Size-Dependent Free Vibration of Non-Rectangular Gradient Elastic Thick Microplates
Abstract
1. Introduction
2. Governing Equations of Gradient Elastic Thick Microplates
3. Solution Procedure
3.1. Navier Method
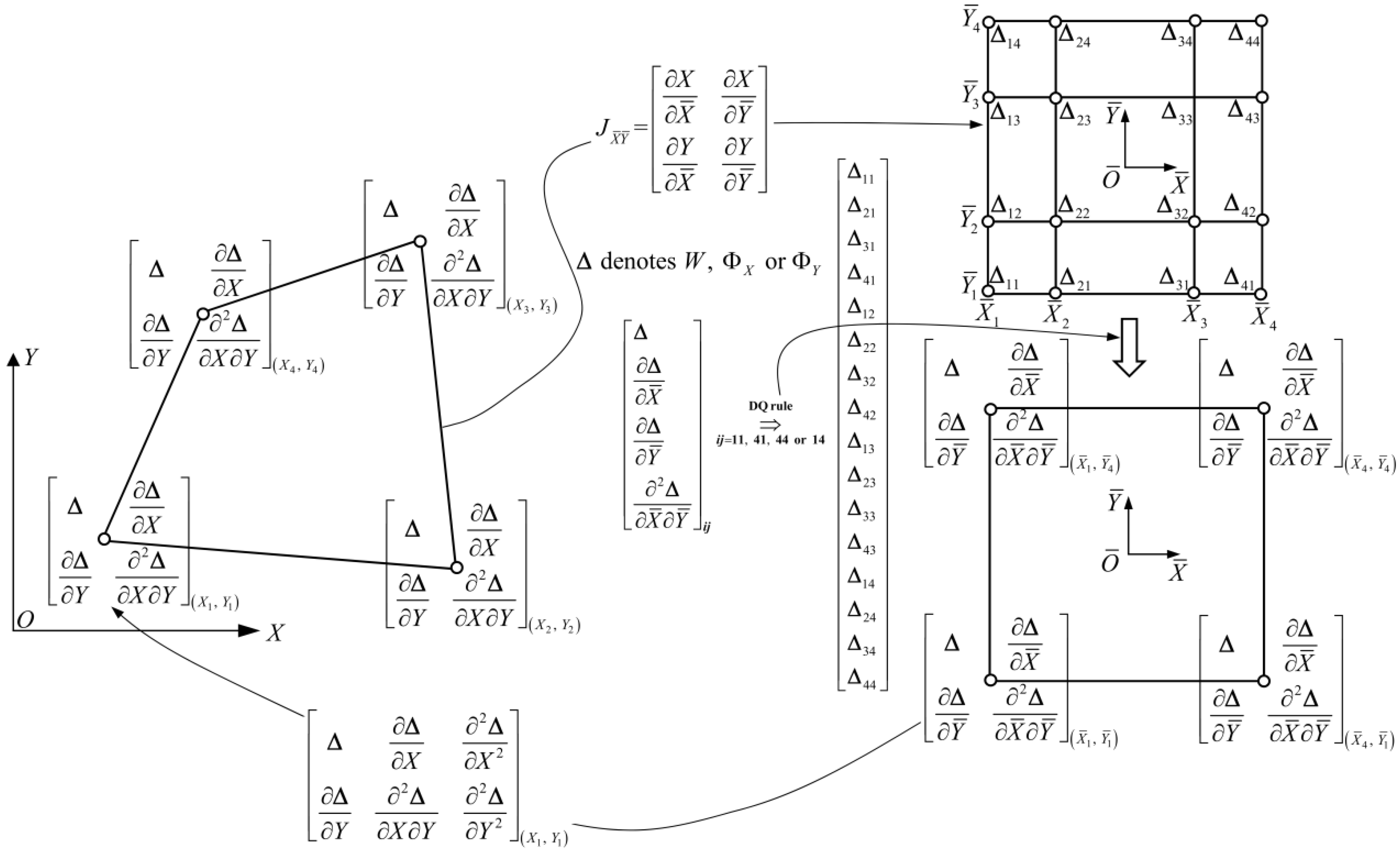
3.2. Differential Quadrature Finite Element Method (DQFEM)
4. Numerical Results and Discussion
4.1. Model Validation
4.2. Parameter Settings
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Bui, T.Q.; Doan, D.H.; Van Do, T.; Hirose, S.; Duc, N.D. High frequency modes meshfree analysis of Reissner–Mindlin plates. J. Sci. Adv. Mater. Devices 2016, 1, 400–412. [Google Scholar] [CrossRef]
- Nam, V.H.; Nam, N.H.; Vinh, P.V.; Khoa, D.N.; Thom, D.V.; Minh, P.V. A New Efficient Modified First-Order Shear Model for Static Bending and Vibration Behaviors of Two-Layer Composite Plate. Adv. Civ. Eng. 2019, 2019, 6814367. [Google Scholar] [CrossRef]
- Tran, T.T.; Nguyen, N.H.; Do, T.V.; Minh, P.V.; Duc, N.D. Bending and thermal buckling of unsymmetric functionally graded sandwich beams in high-temperature environment based on a new third-order shear deformation theory. J. Sandw. Struct. Mater. 2019, 23, 906–930. [Google Scholar] [CrossRef]
- Thai, L.M.; Luat, D.T.; Phung, V.B.; Minh, P.V.; Thom, D.V. Finite element modeling of mechanical behaviors of piezoelectric nanoplates with flexoelectric effects. Arch. Appl. Mech. 2022, 92, 163–182. [Google Scholar] [CrossRef]
- Doan, D.H.; Zenkour, A.M.; Van Thom, D. Finite element modeling of free vibration of cracked nanoplates with flexoelectric effects. Eur. Phys. J. Plus 2022, 137, 447. [Google Scholar] [CrossRef]
- Duc, N.D.; Trinh, T.D.; Do, T.V.; Doan, D.H. On the buckling behavior of multi-cracked FGM plates. In Proceedings of the International Conference on Advances in Computational Mechanics, Phu Quoc Island, Vietnam, 2–4 August 2017; pp. 29–45. [Google Scholar]
- Choudhary, V.; Iniewski, K. Mems: Fundamental Technology and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lam, D.C.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Lei, J.; He, Y.; Guo, S.; Li, Z.; Liu, D. Size-dependent vibration of nickel cantilever microbeams: Experiment and gradient elasticity. AIP Adv. 2016, 6, 105202. [Google Scholar] [CrossRef]
- Li, Z.; He, Y.; Zhang, B.; Lei, J.; Guo, S.; Liu, D. Experimental investigation and theoretical modelling on nonlinear dynamics of cantilevered microbeams. Eur. J. Mech. A/Solids 2019, 78, 103834. [Google Scholar] [CrossRef]
- Liu, D.; He, Y.; Tang, X.; Ding, H.; Hu, P.; Cao, P. Size effects in the torsion of microscale copper wires: Experiment and analysis. Scr. Mater. 2012, 66, 406–409. [Google Scholar] [CrossRef]
- Polyzos, D.; Huber, G.; Mylonakis, G.; Triantafyllidis, T.; Papargyri-Beskou, S.; Beskos, D. Torsional vibrations of a column of fine-grained material: A gradient elastic approach. J. Mech. Phys. Solids 2015, 76, 338–358. [Google Scholar] [CrossRef]
- Polizzotto, C. A gradient elasticity theory for second-grade materials and higher order inertia. Int. J. Solids Struct. 2012, 49, 2121–2137. [Google Scholar] [CrossRef]
- Dontsov, E.V.; Tokmashev, R.D.; Guzina, B.B. A physical perspective of the length scales in gradient elasticity through the prism of wave dispersion. Int. J. Solids Struct. 2013, 50, 3674–3684. [Google Scholar] [CrossRef]
- Koiter, W. Couple stresses in the theory of elasticity, I and II. Roy. Neth. Acad. Sci. B 1964, 67, 0964. [Google Scholar]
- Mindlin, R.; Tiersten, H. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Mindlin, R.; Eshel, N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Toupin, R.A. Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal. 1964, 17, 85–112. [Google Scholar] [CrossRef]
- Aifantis, E.C. On the role of gradients in the localization of deformation and fracture. Int. J. Eng. Sci. 1992, 30, 1279–1299. [Google Scholar] [CrossRef]
- Ru, C.Q.; Aifantis, E.C. A simple approach to solve boundary-value problems in gradient elasticity. Acta Mech. 1993, 101, 59–68. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 2011, 48, 1962–1990. [Google Scholar] [CrossRef]
- Cordero, N.M.; Forest, S.; Busso, E.P. Second strain gradient elasticity of nano-objects. J. Mech. Phys. Solids 2016, 97, 92–124. [Google Scholar] [CrossRef]
- Kong, S.; Zhou, S.; Nie, Z.; Wang, K. Static and dynamic analysis of micro beams based on strain gradient elasticity theory. Int. J. Eng. Sci. 2009, 47, 487–498. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. On the Dynamics of a Visco–Piezo–Flexoelectric Nanobeam. Symmetry 2020, 12, 643. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, J.; Zhou, S. A micro scale Timoshenko beam model based on strain gradient elasticity theory. Eur. J. Mech. A/Solids 2010, 29, 591–599. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Gan, Z.; Shen, L. Size-dependent functionally graded beam model based on an improved third-order shear deformation theory. Eur. J. Mech. A/Solids 2014, 47, 211–230. [Google Scholar] [CrossRef]
- Papargyri-Beskou, S.; Giannakopoulos, A.; Beskos, D. Variational analysis of gradient elastic flexural plates under static loading. Int. J. Solids Struct. 2010, 47, 2755–2766. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, S.; Zhao, J.; Chen, X. A size-dependent Kirchhoff micro-plate model based on strain gradient elasticity theory. Eur. J. Mech. A/Solids 2011, 30, 517–524. [Google Scholar] [CrossRef]
- Ma, H.; Gao, X.-L.; Reddy, J. A non-classical Mindlin plate model based on a modified couple stress theory. Acta Mech. 2011, 220, 217–235. [Google Scholar] [CrossRef]
- Ke, L.-L.; Wang, Y.-S.; Yang, J.; Kitipornchai, S. Free vibration of size-dependent Mindlin microplates based on the modified couple stress theory. J. Sound Vib. 2012, 331, 94–106. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Shen, L.; Lei, J. An efficient size-dependent plate theory for bending, buckling and free vibration analyses of functionally graded microplates resting on elastic foundation. Appl. Math. Model. 2015, 39, 3814–3845. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Shen, L.; Lei, J. Free vibration analysis of four-unknown shear deformable functionally graded cylindrical microshells based on the strain gradient elasticity theory. Compos. Struct. 2015, 119, 578–597. [Google Scholar] [CrossRef]
- Papargyri-Beskou, S.; Beskos, D. Stability analysis of gradient elastic circular cylindrical thin shells. Int. J. Eng. Sci. 2009, 47, 1379–1385. [Google Scholar] [CrossRef]
- Roudbari, M.A.; Jorshari, T.D.; Lü, C.; Ansari, R.; Kouzani, A.Z.; Amabili, M. A review of size-dependent continuum mechanics models for micro-and nano-structures. Thin-Walled Struct. 2022, 170, 108562. [Google Scholar] [CrossRef]
- Kong, S. A Review on the Size-Dependent Models of Micro-beam and Micro-plate Based on the Modified Couple Stress Theory. Arch. Comput. Methods Eng. 2021, 29, 1–31. [Google Scholar] [CrossRef]
- Lim, C.; Zhang, G.; Reddy, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. A unified nonlocal strain gradient model for nanobeams and the importance of higher order terms. Int. J. Eng. Sci. 2017, 119, 265–277. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. Size-dependent vibration analysis of nanobeams based on the nonlocal strain gradient theory. Int. J. Eng. Sci. 2017, 116, 12–24. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. On the mechanics of Kirchhoff and Mindlin plates incorporating surface energy. Int. J. Eng. Sci. 2018, 124, 24–40. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Bahaadini, R.; Sheibani, H.R. Nonlocal, strain gradient and surface effects on vibration and instability of nanotubes conveying nanoflow. Mech. Adv. Mater. Struct. 2018, 27, 586–598. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M. Nonlocal strain gradient shell model for axial buckling and postbuckling analysis of magneto-electro-elastic composite nanoshells. Compos. Part B Eng. 2018, 132, 258–274. [Google Scholar] [CrossRef]
- Ma, L.H.; Ke, L.L.; Reddy, J.N.; Yang, J.; Kitipornchai, S.; Wang, Y.S. Wave propagation characteristics in magneto-electro-elastic nanoshells using nonlocal strain gradient theory. Compos. Struct. 2018, 199, 10–23. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.; Zhao, J. A unified size-dependent plate model based on nonlocal strain gradient theory including surface effects. Appl. Math. Model. 2019, 68, 583–602. [Google Scholar] [CrossRef]
- Chen, W.; Wang, L.; Dai, H. Stability and Nonlinear Vibration Analysis of an Axially Loaded Nanobeam Based on Nonlocal Strain Gradient Theory. Int. J. Appl. Mech. 2019, 11, 1950069. [Google Scholar] [CrossRef]
- Zhang, B.; Shen, H.; Liu, J.; Wang, Y.; Zhang, Y. Deep postbuckling and nonlinear bending behaviors of nanobeams with nonlocal and strain gradient effects. Appl. Math. Mech. 2019, 40, 515–548. [Google Scholar] [CrossRef]
- Lu, L.; Zhu, L.; Guo, X.; Zhao, J.; Liu, G. A nonlocal strain gradient shell model incorporating surface effects for vibration analysis of functionally graded cylindrical nanoshells. Appl. Math. Mech. 2019, 40, 1695–1722. [Google Scholar] [CrossRef]
- Xu, X.-J.; Deng, Z.-C.; Meng, J.-M.; Zhang, K. Bending and vibration analysis of generalized gradient elastic plates. Acta Mech. 2014, 225, 3463–3482. [Google Scholar] [CrossRef]
- Qi, L.; Zhou, S. A size-dependent spherical microshell model based on strain gradient elasticity theory. Eur. J. Mech. A/Solids 2020, 84, 104087. [Google Scholar] [CrossRef]
- Movassagh, A.A.; Mahmoodi, M.J. A micro-scale modeling of Kirchhoff plate based on modified strain-gradient elasticity theory. Eur. J. Mech. A/Solids 2013, 40, 50–59. [Google Scholar] [CrossRef]
- Wang, B.; Huang, S.; Zhao, J.; Zhou, S. Reconsiderations on boundary conditions of Kirchhoff micro-plate model based on a strain gradient elasticity theory. Appl. Math. Model. 2016, 40, 7303–7317. [Google Scholar] [CrossRef]
- Thai, S.; Thai, H.T.; Vo, T.P.; Patel, V.I. Size-dependant behaviour of functionally graded microplates based on the modified strain gradient elasticity theory and isogeometric analysis. Comput. Struct. 2017, 190, 219–241. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Atroshchenko, E.; Ngo, T.; Nguyen-Xuan, H.; Vo, T.P.J.E.S. Vibration of cracked functionally graded microplates by the strain gradient theory and extended isogeometric analysis. Eng. Struct. 2019, 187, 251–266. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Atroshchenko, E.; Nguyen-Xuan, H.; Vo, T.P. Geometrically nonlinear isogeometric analysis of functionally graded microplates with the modified couple stress theory. Comput. Struct. 2017, 193, 110–127. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Nguyen, T.N.; Abdel-Wahab, M.; Bordas, S.; Nguyen-Xuan, H.; Vo, T.P. A refined quasi-3D isogeometric analysis for functionally graded microplates based on the modified couple stress theory. Comput. Methods Appl. Mech. Eng. 2017, 313, 904–940. [Google Scholar] [CrossRef]
- Niiranen, J.; Kiendl, J.; Niemi, A.H.; Reali, A. Isogeometric analysis for sixth-order boundary value problems of gradient-elastic Kirchhoff plates. Comput. Methods Appl. Mech. Eng. 2017, 316, 328–348. [Google Scholar] [CrossRef]
- Balobanov, V.; Kiendl, J.; Khakalo, S.; Niiranen, J. Kirchhoff–Love shells within strain gradient elasticity: Weak and strong formulations and an H3-conforming isogeometric implementation. Comput. Methods Appl. Mech. Eng. 2019, 344, 837–857. [Google Scholar] [CrossRef]
- Babu, B.; Patel, B. A new computationally efficient finite element formulation for nanoplates using second-order strain gradient Kirchhoff’s plate theory. Compos. Part B Eng. 2019, 168, 302–311. [Google Scholar] [CrossRef]
- Wang, X. Novel differential quadrature element method for vibration analysis of hybrid nonlocal Euler–Bernoulli beams. Appl. Math. Lett. 2018, 77, 94–100. [Google Scholar] [CrossRef]
- Ishaquddin, M.; Gopalakrishnan, S. A novel weak form quadrature element for gradient elastic beam theories. Appl. Math. Model. 2020, 77, 1–16. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Wang, J.; Shen, H. Strain gradient differential quadrature beam finite elements. Comput. Struct. 2019, 218, 170–189. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Zhang, X.; Feng, Z. Weak-form differential quadrature finite elements for functionally graded micro-beams with strain gradient effects. Acta Mech. 2021, 232, 4009–4036. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Shen, H.; Zhang, X. Size-dependent static and dynamic analysis of Reddy-type micro-beams by strain gradient differential quadrature finite element method. Thin-Walled Struct. 2020, 148, 106496. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Shen, H.; Zhang, X. Size-dependent vibration and stability of moderately thick functionally graded micro-plates using a differential quadrature-based geometric mapping scheme. Eng. Anal. Bound. Elem. 2019, 108, 339–365. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Zhang, X.; Feng, Z. Strain gradient differential quadrature finite element for moderately thick micro-plates. Int. J. Numer. Methods Eng. 2020, 121, 5600–5646. [Google Scholar] [CrossRef]
- Bo, Z.; Li, H.; Kong, L.; Zhang, X.; Shen, H. Strain gradient differential quadrature Kirchhoff plate finite element with the C2 partial compatibility. Eur. J. Mech. A/Solids 2020, 80, 103879. [Google Scholar]
- Zhang, B.; Li, H.; Liu, J.; Shen, H.; Zhang, X. Surface energy-enriched gradient elastic Kirchhoff plate model and a novel weak-form solution scheme. Eur. J. Mech. A/Solids 2021, 85, 104118. [Google Scholar] [CrossRef]
- Zhang, B.; Li, H.; Kong, L.; Zhang, X.; Feng, Z. Variational formulation and differential quadrature finite element for freely vibrating strain gradient Kirchhoff plates. ZAMM-J. Appl. Math. Mech. 2021, 101, e202000046. [Google Scholar] [CrossRef]
- Duan, Y.; Zhang, B.; Li, X.; Zhang, X.; Shen, H. Size-Dependent Elastic Buckling of Two-Variable Refined Microplates Embedded in Elastic Medium. Int. J. Appl. Mech. 2022, 14, 2250039. [Google Scholar] [CrossRef]
- Liew, K.-M.; Xiang, Y.; Kitipornchai, S.; Wang, C. Vibration of Mindlin Plates: Programming the p-Version Ritz Method; Elsevier: Oxford, UK, 1998. [Google Scholar]

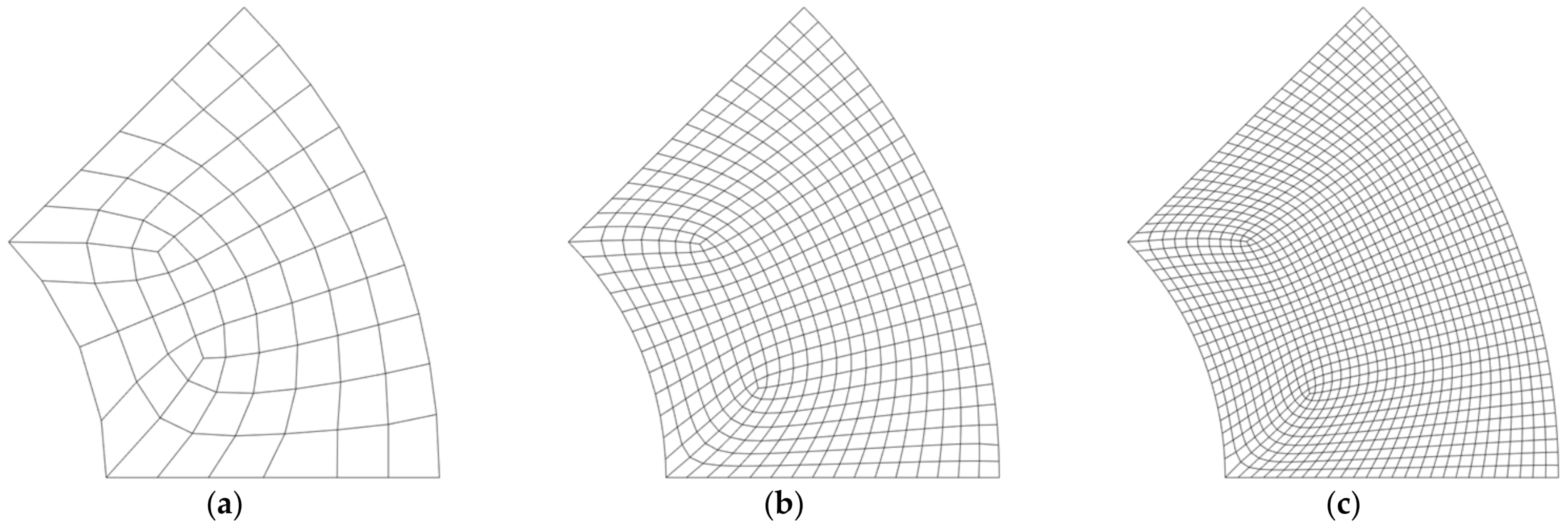
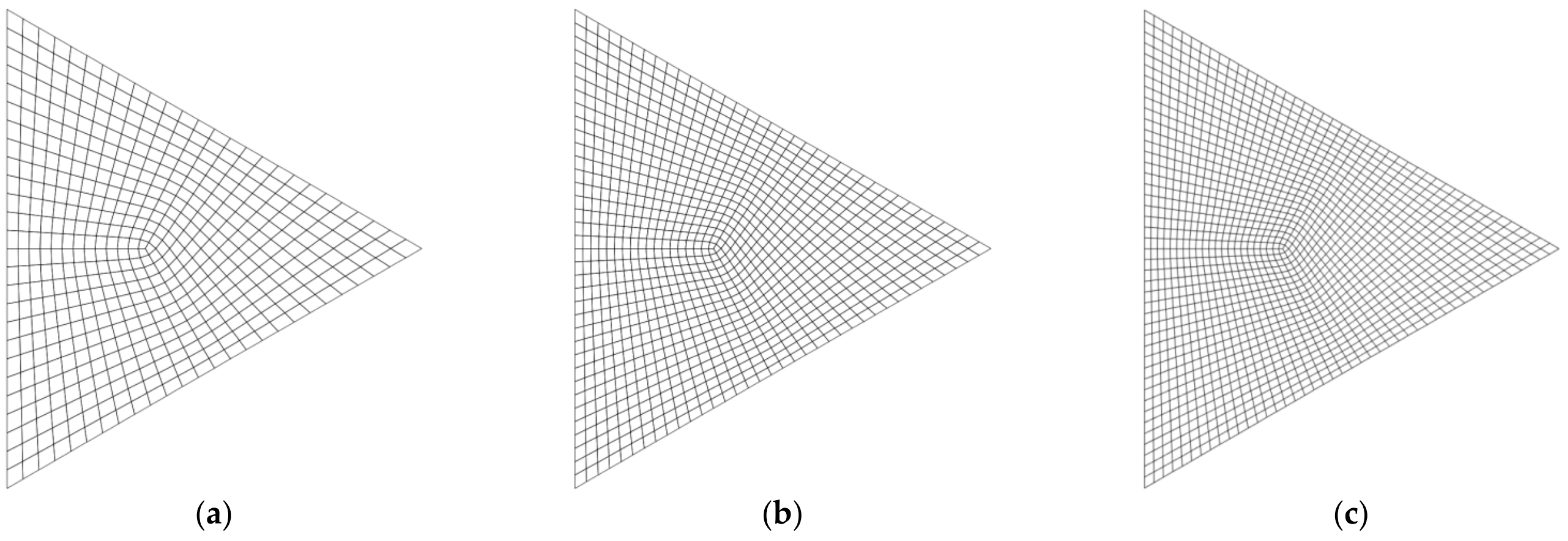

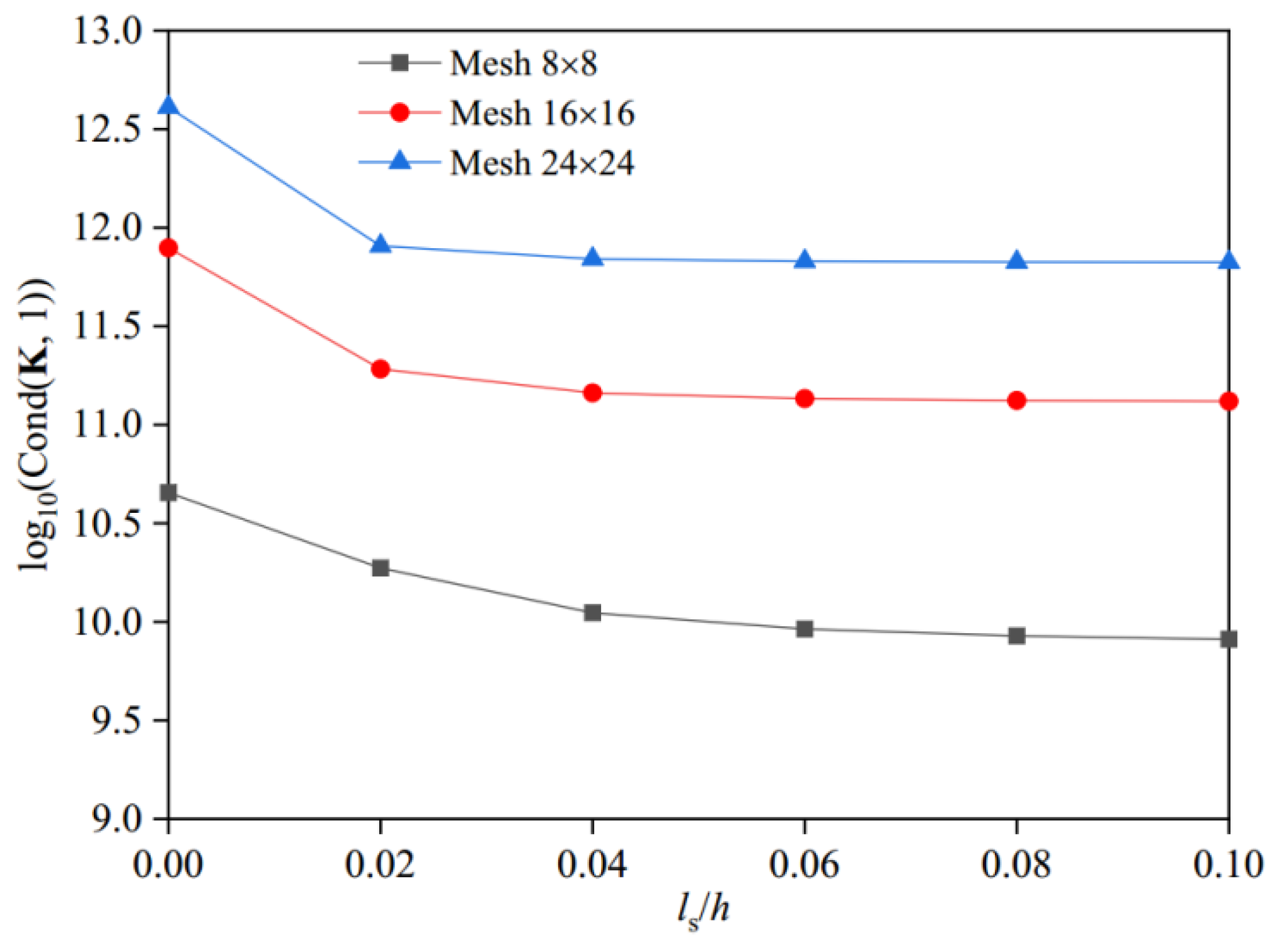
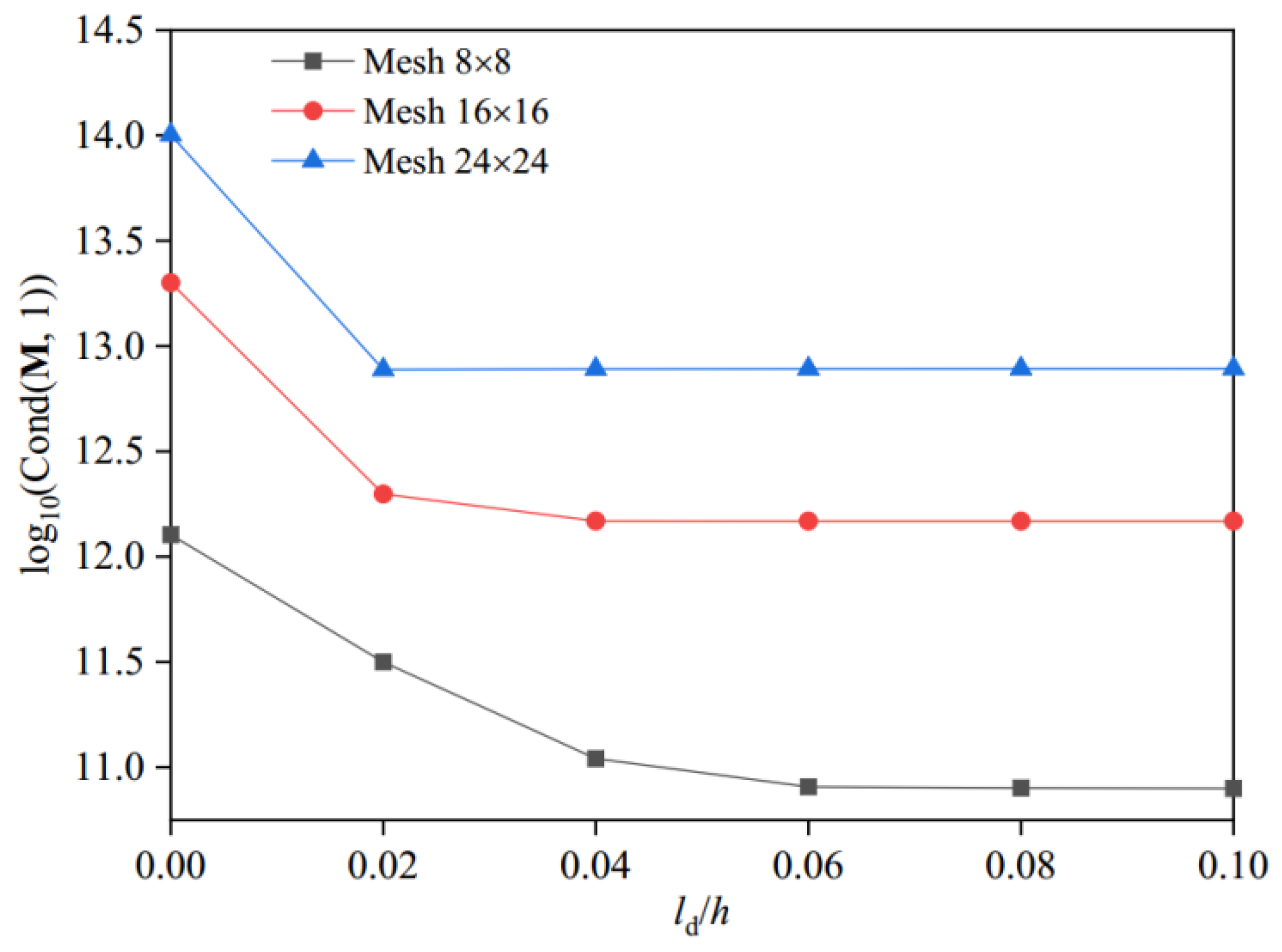


| Plate Type | Source | Dimensionless Frequency | |||||
|---|---|---|---|---|---|---|---|
 | Mesh I | 81.6282 | 131.5274 | 170.5684 | 204.4813 | 213.2321 | 273.2040 (19.7‰) |
| Mesh II | 83.3317 | 133.4009 | 173.9067 | 207.6397 | 217.9088 | 278.5504 (0.54‰) | |
| Mesh III | 83.3762 | 133.5073 | 173.9903 | 207.7985 | 218.1862 | 278.6688 (0.11‰) | |
| Ref. [71] | 83.39 | 133.5 | 174.0 | 207.8 | 218.2 | 278.7 (0.00‰) | |
| ABAQUS | 83.4149 | 133.6469 | 174.2138 | 208.1828 | 218.3593 | 278.9532 | |
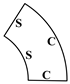 | Mesh I | 79.7667 | 139.6404 | 163.5869 | 212.3000 | 215.0767 | 267.0375 (13.5‰) |
| Mesh II | 80.7754 | 142.1242 | 165.5137 | 217.2101 | 218.9190 | 270.4049 (1.10‰) | |
| Mesh III | 80.9566 | 142.2275 | 165.6100 | 217.3999 | 219.1845 | 270.5344 (0.61‰) | |
| Ref. [71] | 81.01 | 142.2 | 165.8 | 217.4 | 219.3 | 270.7 (0.00‰) | |
| ABAQUS | 81.1477 | 142.8058 | 166.1301 | 217.8956 | 220.0316 | 270.9513 | |
| Plate Type | Source | Dimensionless Frequency | |||||
|---|---|---|---|---|---|---|---|
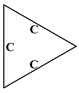 | Mesh I | 77.6961 | 132.1974 | 132.1974 | 188.2262 | 196.6173 | 196.6173 (1.94‰) |
| Mesh II | 77.7317 | 132.2817 | 132.2817 | 188.3909 | 196.8075 | 196.8075 (0.98‰) | |
| Mesh III | 77.7419 | 132.3057 | 132.3057 | 188.4393 | 196.8628 | 196.8628 (0.69‰) | |
| Ref. [71] | 77.79 | 132.3 | 132.3 | 188.6 | 197.0 | 197.0 (0‰) | |
| ABAQUS | 77.9299 | 132.7202 | 132.7202 | 189.1298 | 197.6068 | 197.6068 | |
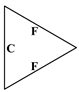 | Mesh I | 8.6418 | 31.3613 | 34.7885 | 75.3018 | 76.0219 | 86.9152 (1.20‰) |
| Mesh II | 8.6433 | 31.3884 | 34.7981 | 75.3645 | 76.0880 | 86.9775 (0.49‰) | |
| Mesh III | 8.6438 | 31.3968 | 34.8010 | 75.3841 | 76.1084 | 86.9971 (0.26‰) | |
| Ref. [71] | 8.646 | 31.41 | 34.81 | 75.40 | 76.15 | 87.02 (0.00‰) | |
| ABAQUS | 8.6460 | 31.4342 | 34.8360 | 75.5201 | 76.2471 | 87.1583 | |
| Mode | Mesh Density | Navier Method | |||||
|---|---|---|---|---|---|---|---|
| 1.7737 | 1.7747 | 1.7747 | 1.7747 | 1.7747 | 1.7747 | 1.7747 | |
| 3.9638 | 3.9502 | 3.9488 | 3.9485 | 3.9485 | 3.9484 | 3.9484 | |
| 6.0028 | 5.9862 | 5.9839 | 5.9833 | 5.9831 | 5.9830 | 5.9830 | |
| 7.1447 | 7.0213 | 7.0113 | 7.0094 | 7.0088 | 7.0086 | 7.0085 | |
| 9.0701 | 8.9722 | 8.9628 | 8.9607 | 8.9601 | 8.9598 | 8.9595 | |
| 11.7753 | 10.8629 | 10.8185 | 10.8101 | 10.8077 | 10.8068 | 10.8063 | |
| 12.0071 | 11.8812 | 11.8680 | 11.8649 | 11.8638 | 11.8634 | 11.8630 | |
| 13.5871 | 12.7407 | 12.7007 | 12.6928 | 12.6904 | 12.6895 | 12.6883 | |
| Plate Type | |||||
|---|---|---|---|---|---|
| 0.2 nm | 1.0 nm | ||||
| Ref. [68] | Present | Ref. [68] | Present | ||
| SFSF | 0.0 nm | 0.9774 | 0.9802 | 0.9878 | 0.9920 |
| 0.2 nm | 0.9735 | 0.9761 | 0.9839 | 0.9864 | |
| 0.5 nm | 0.9539 | 0.9553 | 0.9640 | 0.9688 | |
| 1.0 nm | 0.8922 | 0.8945 | 0.9017 | 0.9079 | |
| SCSF | 0.0 nm | 3.6907 | 3.6967 | 4.6619 | 4.6668 |
| 0.2 nm | 3.6556 | 3.6620 | 4.6160 | 4.6198 | |
| 0.5 nm | 3.4858 | 3.4887 | 4.3949 | 4.3968 | |
| 1.0 nm | 3.0268 | 3.0302 | 3.8032 | 3.8046 | |
| Plate Type | Dimensionless Frequency | ||||||
|---|---|---|---|---|---|---|---|
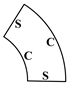 | (0, 0) | 81.5207 | 130.4961 | 168.5017 | 202.1629 | 211.4280 | 268.4294 |
| (0.5, 0) | 95.3423 | 153.3994 | 207.0074 | 256.5577 | 272.0939 | 364.4674 | |
| (0, 0.5) | 72.2138 | 104.7030 | 131.3718 | 146.1192 | 152.6934 | 182.6297 | |
| (1, 0) | 124.5375 | 203.0303 | 281.0181 | 366.8073 | 393.5932 | 534.6659 | |
| 1.5277 | 1.5558 | 1.6677 | 1.8144 | 1.8616 | 1.9918 | ||
| (0, 1) | 55.9479 | 72.3129 | 88.2711 | 93.1260 | 97.2287 | 110.6023 | |
| 0.6863 | 0.5541 | 0.5239 | 0.4606 | 0.4599 | 0.4120 | ||
| (1, 1) | 87.4697 | 112.4565 | 143.7237 | 165.9530 | 178.1079 | 203.0451 | |
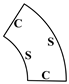 | (0, 0) | 74.2015 | 138.7872 | 149.6016 | 208.7868 | 211.5255 | 251.4064 |
| (0.5, 0) | 86.4273 | 165.6917 | 178.8613 | 266.6957 | 273.2989 | 334.9031 | |
| (0, 0.5) | 65.5494 | 111.5257 | 116.0503 | 150.6620 | 153.5407 | 169.7088 | |
| (1, 0) | 111.5916 | 220.7434 | 239.4153 | 380.8189 | 393.0436 | 493.3882 | |
| 1.5039 | 1.5905 | 1.6004 | 1.8240 | 1.8581 | 1.9625 | ||
| (0, 1) | 50.6369 | 76.9966 | 77.9073 | 95.9221 | 98.1906 | 104.1261 | |
| 0.6824 | 0.5548 | 0.5208 | 0.4642 | 0.4594 | 0.4142 | ||
| (1, 1) | 76.1093 | 121.2415 | 125.4321 | 170.5555 | 175.3253 | 194.4725 | |
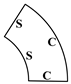 | (0, 0) | 79.2224 | 138.5925 | 161.0288 | 210.7184 | 212.4034 | 261.4489 |
| (0.5, 0) | 93.0171 | 165.6100 | 195.9620 | 270.9050 | 275.0648 | 353.2054 | |
| (0, 0.5) | 69.8781 | 111.4121 | 125.3498 | 152.8662 | 153.3883 | 177.4652 | |
| (1, 0) | 122.1085 | 221.8823 | 266.1490 | 387.9548 | 399.3468 | 519.6088 | |
| 1.5413 | 1.6010 | 1.6528 | 1.8411 | 1.8801 | 1.9874 | ||
| (0, 1) | 53.7549 | 76.9914 | 84.3009 | 97.4848 | 97.8276 | 109.4238 | |
| 0.6785 | 0.5555 | 0.5235 | 0.4626 | 0.4606 | 0.4185 | ||
| (1, 1) | 84.5940 | 124.0212 | 138.3856 | 174.6448 | 181.5263 | 198.7258 | |
| Plate Type | Dimensionless Frequency | ||||||
|---|---|---|---|---|---|---|---|
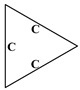 | (0, 0) | 76.2249 | 128.9764 | 128.9764 | 183.0821 | 191.1030 | 191.1030 |
| (0.5, 0) | 84.1899 | 152.6676 | 152.6676 | 228.2820 | 238.8048 | 238.8048 | |
| (0, 0.5) | 68.9814 | 106.9641 | 106.9641 | 140.7625 | 143.9840 | 143.9840 | |
| (1, 0) | 101.3952 | 200.9779 | 200.9779 | 317.4252 | 331.8159 | 331.8159 | |
| 1.3302 | 1.5583 | 1.5583 | 1.7338 | 1.7363 | 1.7363 | ||
| (0, 1) | 55.0620 | 76.0369 | 76.0369 | 94.0234 | 94.1282 | 94.1282 | |
| 0.7224 | 0.5895 | 0.5895 | 0.5136 | 0.4926 | 0.4926 | ||
| (1, 1) | 75.4742 | 120.1357 | 120.6292 | 158.4080 | 158.7861 | 165.5730 | |
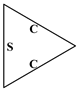 | (0, 0) | 66.3187 | 119.6351 | 119.8490 | 174.2392 | 183.0867 | 183.8417 |
| (0.5, 0) | 72.0779 | 138.4393 | 140.1666 | 213.9839 | 225.1839 | 227.1890 | |
| (0, 0.5) | 59.7884 | 98.9798 | 99.1781 | 133.2975 | 137.7091 | 138.4922 | |
| (1, 0) | 84.7178 | 176.6627 | 182.8545 | 292.5272 | 308.8696 | 313.9850 | |
| 1.2774 | 1.4767 | 1.5257 | 1.6789 | 1.6870 | 1.7079 | ||
| (0, 1) | 47.5424 | 70.3561 | 70.5703 | 88.5408 | 90.0805 | 90.7414 | |
| 0.7169 | 0.5881 | 0.5888 | 0.5082 | 0.4920 | 0.4936 | ||
| (1, 1) | 61.6449 | 104.5859 | 108.3691 | 147.1023 | 148.1694 | 153.0898 | |
 | (0, 0) | 8.4766 | 30.0886 | 33.8771 | 72.8753 | 73.1805 | 85.1658 |
| (0.5, 0) | 11.6780 | 32.8524 | 38.9259 | 84.5572 | 84.8922 | 94.7538 | |
| (0, 0.5) | 8.2626 | 25.6136 | 30.7860 | 56.8479 | 60.8161 | 67.2185 | |
| (1, 0) | 16.5950 | 37.9233 | 48.0417 | 104.3431 | 105.8601 | 114.3535 | |
| 1.9577 | 1.2604 | 1.4181 | 1.4318 | 1.4466 | 1.3427 | ||
| (0, 1) | 7.7009 | 18.7560 | 24.9306 | 38.7446 | 42.6922 | 46.7500 | |
| 0.9085 | 0.6234 | 0.7359 | 0.5317 | 0.5834 | 0.5489 | ||
| (1, 1) | 15.2310 | 23.1984 | 34.8584 | 54.2883 | 55.8119 | 67.2840 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Li, C.; Zhang, L.; Xie, F. Size-Dependent Free Vibration of Non-Rectangular Gradient Elastic Thick Microplates. Symmetry 2022, 14, 2592. https://doi.org/10.3390/sym14122592
Zhang B, Li C, Zhang L, Xie F. Size-Dependent Free Vibration of Non-Rectangular Gradient Elastic Thick Microplates. Symmetry. 2022; 14(12):2592. https://doi.org/10.3390/sym14122592
Chicago/Turabian StyleZhang, Bo, Cheng Li, Limin Zhang, and Feng Xie. 2022. "Size-Dependent Free Vibration of Non-Rectangular Gradient Elastic Thick Microplates" Symmetry 14, no. 12: 2592. https://doi.org/10.3390/sym14122592
APA StyleZhang, B., Li, C., Zhang, L., & Xie, F. (2022). Size-Dependent Free Vibration of Non-Rectangular Gradient Elastic Thick Microplates. Symmetry, 14(12), 2592. https://doi.org/10.3390/sym14122592







