Numerical Simulations of the Fractional Systems of Volterra Integral Equations within the Chebyshev Pseudo-Spectral Method
Abstract
1. Introduction
2. Definitions and Preliminaries Concept
3. Chebyshev Pseudo-Spectral Method (CPM)
4. Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bisquert, J.; Garcia-Belmonte, G.; Fabregat-Santiago, F.; Compte, A. Anomalous transport effects in the impedance of porous film electrodes. Electrochem. Commun. 1999, 1, 429–435. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 1–21. [Google Scholar] [CrossRef]
- Reyes-Melo, E.; Martinez-Vega, J.; Guerrero-Salazar, C.; Ortiz-Mendez, U. Application of fractional calculus to the modeling of dielectirc relaxtion phenomena in polymetric materials. J. Appl. Polym. Sci. 2005, 98, 923. [Google Scholar] [CrossRef]
- Picozzi, S.; West, B.J. Fractional Langevin model of memory in financial market. Phys. Rev. E 2002, 66, 046118. [Google Scholar] [CrossRef]
- Henry, B.I.; Wearne, S.L. Existance of Turing instabilities in a two-species fractional reaction-diffusion system. SIAM J. Appl. Math. 2002, 62, 870. [Google Scholar] [CrossRef]
- Xie, Z.; Feng, X.; Chen, X. Partial least trimmed squares regression. Chemom. Intell. Lab. Syst. 2022, 221, 104486. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Fedorov, R.V.; Karpukhina, T.V.; Simos, T.E.; Tsitouras, C. Sixth Order Numerov-Type Methods with Coefficients Trained to Perform Best on Problems with Oscillating Solutions. Mathematics 2021, 9, 2756. [Google Scholar] [CrossRef]
- Shao, Z.; Zhai, Q.; Han, Z.; Guan, X. A linear AC unit commitment formulation: An application of data-driven linear power flow model. Int. J. Electr. Power Energy Syst. 2023, 145, 108673. [Google Scholar] [CrossRef]
- Mandelbrot, B. Some noises with i/f spectrum, a bridge between direct current and white noise. IEEE Trans. Inf. Theory 1967, 13, 289–298. [Google Scholar] [CrossRef]
- Baillie, R.T. Long memory processes and fractional integration in econometrics. J. Econom. 1996, 73, 5–59. [Google Scholar] [CrossRef]
- He, J.H. Nonlinear oscillation with fractional derivative and its applications. In Proceedings of the International Conference on Vibrating Engineering, Dalian, China, 6–9 August 1998; Volume 98, pp. 288–291. [Google Scholar]
- Magin, R.L. Fractional calculus in bioengineering, part 1. Crit. Rev. Biomed. Eng. 2004, 32, 1–104. [Google Scholar] [CrossRef] [PubMed]
- Vinagre, B.M.; Podlubny, I.; Hernandez, A.; Feliu, V. Some approximations of fractional order operators used in control theory and applications. Fract. Calc. Appl. Anal. 2000, 3, 231–248. [Google Scholar]
- Smit, W.; De Vries, H. Rheological models containing fractional derivatives. Rheol. Acta 1970, 9, 525–534. [Google Scholar] [CrossRef]
- Cuesta, E.; Fernandez-Manso, A.; Quintano, C. Generalized fractional integrals in advanced remote sensing. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–4. [Google Scholar]
- Salo, M.; Tuusa, H. A vector controlled current-source pwm rectifier with a novel current damping method. IEEE Trans. Power Electron. 2000, 15, 464–470. [Google Scholar] [CrossRef]
- Metzler, R.; Schick, W.; Kilian, H.-G.; Nonnenmacher, T.F. Relaxation in filled polymers: A fractional calculus approach. J. Chem. Phys. 1995, 103, 7180–7186. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fishers equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Alyobi, S.; Shah, R.; Khan, A.; Shah, N.A.; Nonlaopon, K. Fractional Analysis of Nonlinear Boussinesq Equation under Atangana-Baleanu-Caputo Operator. Symmetry 2022, 14, 2417. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgul, A.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Liu, K.; Yang, Z.; Wei, W.; Gao, B.; Xin, D.; Sun, C.; Wu, G. Novel detection approach for thermal defects: Study on its feasibility and application to vehicle cables. High Volt. 2022, 1–10. [Google Scholar] [CrossRef]
- Liu, P.; Shi, J.; Wang, Z.-H. Pattern formation of the attraction-repulsion Keller-Segel system. Discret. Contin. Dyn. Syst.-B 2013, 18, 2597–2625. [Google Scholar] [CrossRef]
- Wang, H.; Fu, H.M.; Zhang, H.F.; Hu, Z.Q. A practical thermodynamic method to calculate the best glass-forming composition for bulk metallic glasses. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 171–178. [Google Scholar] [CrossRef][Green Version]
- Xu, L.; He, J.H.; Liu, Y. Electrospun nanoporous spheres with Chinese drug. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 199–202. [Google Scholar] [CrossRef]
- Sun, F.Z.; Gao, M.; Lei, S.H.; Zhao, Y.; Wang, K.; Shi, Y.T.; Wang, N.H. The fractal dimension of the fractal model of dropwise condensation and its experimental study. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 211–222. [Google Scholar] [CrossRef]
- Bo, T.L.; Xie, L.; Zheng, X.J. Numerical approach to wind ripple in desert. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 223–228. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Hashim, I.; Abdulaziz, O.; Momani, S. Homotopy analysis method for fractional ivps. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 674–684. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S.; Erturk, V.S. Generalized differential transform method: Application to differential equations of fractional order. Appl. Math. Comput. 2008, 197, 467–477. [Google Scholar] [CrossRef]
- Brunner, H.; Makroglou, A.; Miller, R.K. Mixed interpolation collocation methods for first and second order volterra integro-differential equations with periodic solution. Appl. Numer. Math. 1997, 23, 381–402. [Google Scholar] [CrossRef]
- Rawashdeh, E.A. Numerical solution of fractional integro-differential equations by collocation method. Appl. Math. Comput. 2006, 176, 1–6. [Google Scholar] [CrossRef]
- Volk, W. The iterated galerkin method for linear integro-differential equations. J. Comput. Appl. Math. 1988, 21, 63–74. [Google Scholar] [CrossRef]
- Pedas, A.; Tamme, E. Spline collocation method for integro-differential equations with weakly singular kernels. J. Comput. Appl. Math. 2006, 197, 253–269. [Google Scholar] [CrossRef][Green Version]
- Yousefi, S.; Razzaghi, M. Legendre wavelets method for the nonlinear volterra-fredholm integral equations. Math. Comput. Simul. 2005, 70, 1–8. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. New numerical approximation for Chua attractor with fractional and fractal-fractional operators. Alex. Eng. J. 2020, 59, 3275–3296. [Google Scholar] [CrossRef]
- Mekkaoui, T.; Atangana, A.; Araz, S.I. Predictor-corrector for non-linear differential and integral equation with fractal-fractional operators. Eng. Comput. 2021, 37, 2359–2368. [Google Scholar] [CrossRef]
- Subasi, M.; Araz, S.I.; Gungor, H. On the numerical solution of two dimensional Schrodinger equation. Int. J. Math. Res. 2017, 6, 1–12. [Google Scholar] [CrossRef][Green Version]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- He, J.H.; Li, Z.B.; Wang, Q.L. A new fractional derivative and its application to explanation of polar bear hairs. J. King Saud-Univ.-Sci. 2016, 28, 190–192. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Khader, M. A Chebyshev pseudo-spectral method for solving fractional-order integro-differential equations. ANZIAM J. 2010, 51, 464–475. [Google Scholar] [CrossRef]





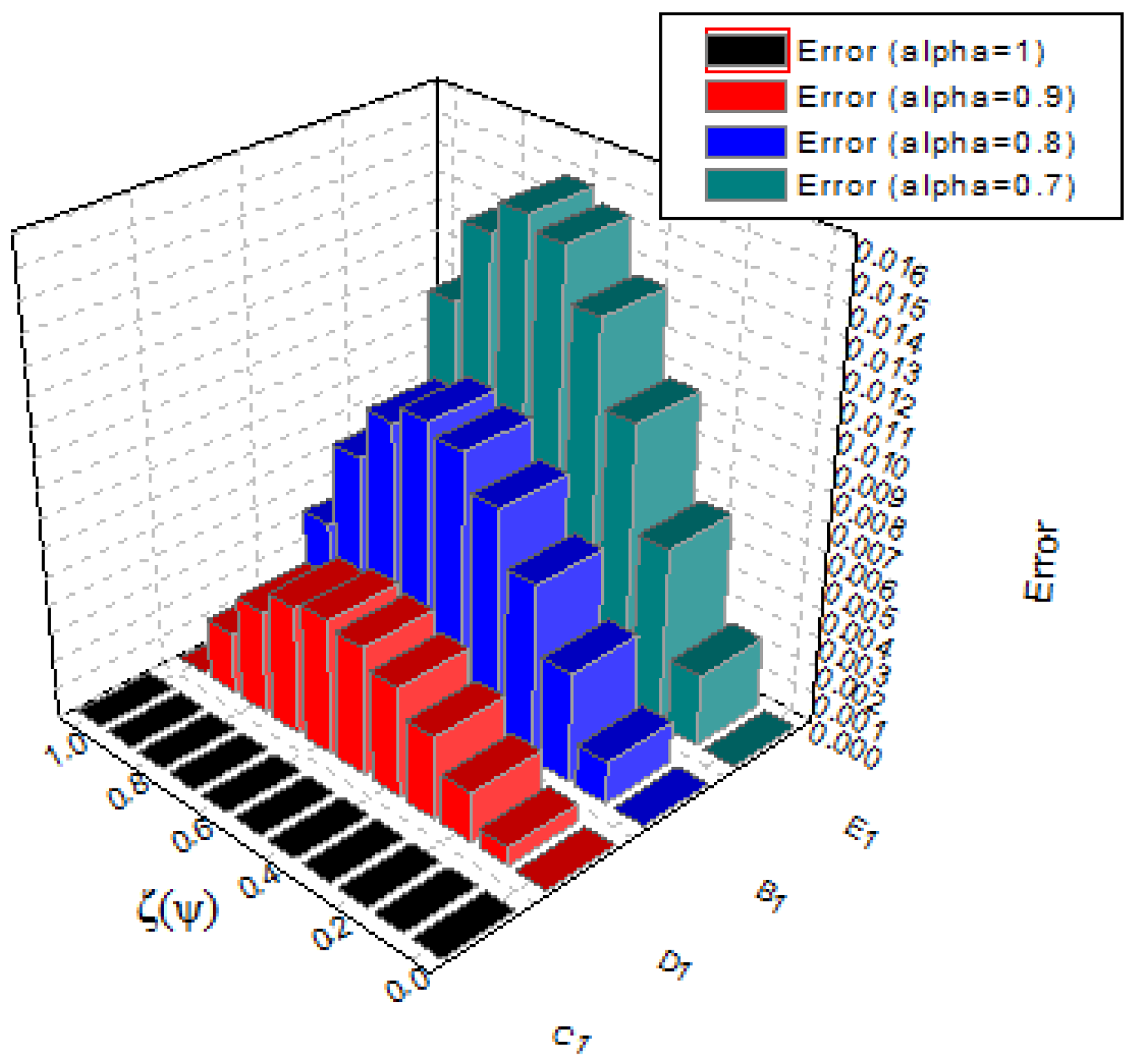
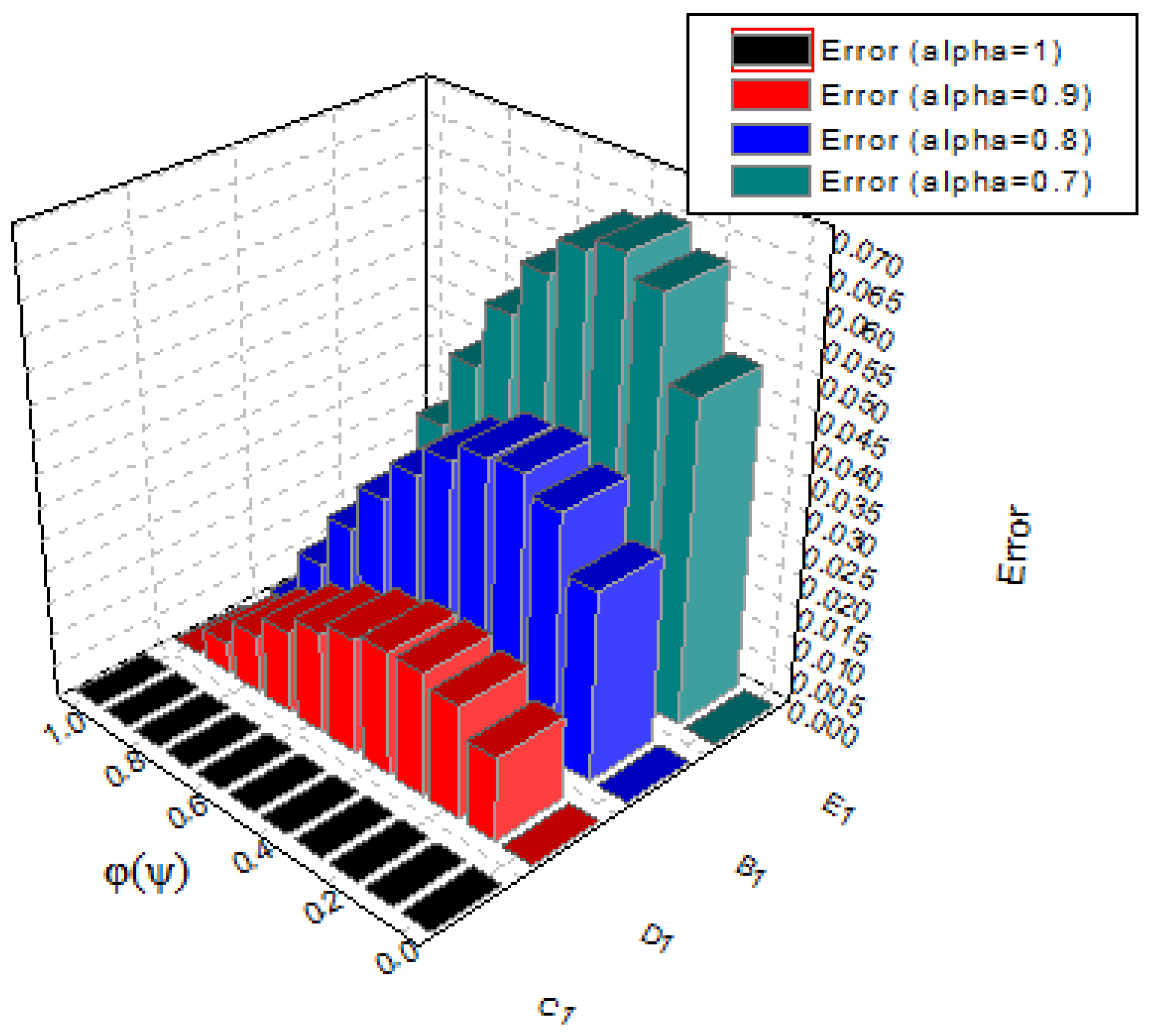
| E.S | E.S | CPM | CPM | CWM | CWM | |
|---|---|---|---|---|---|---|
| 0 | 0.0000000 | 0.0000000 | 0.0000000000 | 0.0000000000 | −0.000026070 | 0.000222296 |
| 0.2 | 0.0400000 | 0.2000000 | 0.0399999999 | 0.2000000000 | 0.039987035 | 0.199964603 |
| 0.4 | 0.1600000 | 0.4000000 | 0.1599999999 | 0.4000000000 | 0.159982615 | 0.400041558 |
| 0.6 | 0.3600000 | 0.6000000 | 0.3599999999 | 0.6000000000 | 0.360047897 | 0.599977336 |
| 0.8 | 0.6400000 | 0.8000000 | 0.6400000000 | 0.7999999999 | 0.639966461 | 0.799997734 |
| 1.0 | 1.0000000 | 1.0000000 | 1.0000000000 | 0.9999999999 | 1.000185856 | 0.999922349 |
| 0 | 0.00000 | 0.00000 | 0.00002607 | 0.0002222 | 7.54 | 2.09 |
| 0.2 | 1.60000 | 1.00000 | 0.00001296 | 0.0000353 | 2.28 | 5.70 |
| 0.4 | 3.00000 | 1.00000 | 0.00001738 | 0.0000415 | 1.98 | 4.79 |
| 0.6 | 3.00000 | 0.00000 | 0.00004789 | 0.0000226 | 1.16 | 6.33 |
| 0.8 | 4.00000 | 2.00000 | 0.00003353 | 0.0000022 | 3.80 | 1.29 |
| 1.0 | 3.00000 | 1.30000 | 0.00018585 | 0.0000776 | 5.82 | 3.89 |
| E.S | E.S | CPM | CPM | CWM | CWM | |
|---|---|---|---|---|---|---|
| 0 | 0.00000000000 | 1.0000000000 | 0.00000000000 | 0.99999999999 | −0.000001403 | 1.000000319 |
| 0.2 | 0.19866933079 | 0.9800665778 | 0.19866933072 | 0.98006657786 | 0.1986696393 | 0.9800669460 |
| 0.4 | 0.38941834230 | 0.9210609940 | 0.38941834202 | 0.92106099406 | 0.3894165787 | 0.9210604974 |
| 0.6 | 0.56464247339 | 0.8253356149 | 0.56464247340 | 0.82533561482 | 0.5646433964 | 0.8253349025 |
| 0.8 | 0.71735609089 | 0.6967067093 | 0.71735609079 | 0.69670670928 | 0.7173557641 | 0.6967067839 |
| 1.0 | 0.84147098480 | 0.5403023058 | 0.84147098076 | 0.54030230757 | 0.8414719842 | 0.5403020838 |
| s | ||||
|---|---|---|---|---|
| 0 | 0.0000000000 | 0.0000000000 | 0.0000014037 | 0.000000319 |
| 0.2 | 6.7443073256 | 1.9129717529 | 0.0000003085 | 0.0000003682 |
| 0.4 | 2.8634095988 | 6.3350567575 | 0.0000001763 | 0.0000004966 |
| 0.6 | 1.4540273872 | 8.3812136477 | 0.000000923 | 0.0000007124 |
| 0.8 | 1.0840388114 | 6.5764647225 | 0.0000003268 | 0.0000000746 |
| 1.0 | 4.0385798791 | 1.7087357128 | 0.0000009994 | 0.0000002221 |
| E.S | E.S | E.S | CPM | CPM | CPM | |
|---|---|---|---|---|---|---|
| 0 | 1.000000000000 | 1.50000000 | 0.6666666666 | 1.000000000 | 1.50000000 | 0.6666666666 |
| 0.1 | 1.002500000000 | 1.50333333 | 0.7166666666 | 1.002500000 | 1.50333333 | 0.7166666666 |
| 0.2 | 1.010000000000 | 1.51333333 | 0.7666666666 | 1.009999999 | 1.51333333 | 0.7666666666 |
| 0.3 | 1.022500000000 | 1.53000000 | 0.8166666666 | 1.022500000 | 1.53000000 | 0.8166666666 |
| 0.4 | 1.040000000000 | 1.55333333 | 0.8666666666 | 1.040000000 | 1.55333333 | 0.8666666666 |
| 0.5 | 1.062500000000 | 1.58333333 | 0.9166666666 | 1.062499999 | 1.58333333 | 0.9166666666 |
| 0.6 | 1.090000000000 | 1.62000000 | 0.9666666666 | 1.090000000 | 1.62000000 | 0.9666666666 |
| 0.7 | 1.122500000000 | 1.66333333 | 1.0166666666 | 1.122500000 | 1.66333333 | 1.0166666666 |
| 0.8 | 1.160000000000 | 1.71333333 | 0.0666666666 | 1.160000000 | 1.71333333 | 1.0666666666 |
| 0.9 | 1.202500000000 | 1.77000000 | 1.1166666666 | 1.202499999 | 1.77000000 | 1.1166666666 |
| 1.0 | 1.250000000000 | 1.83333333 | 1.1666666666 | 1.249999999 | 1.83333333 | 1.1666666666 |
| 0 | 0.00000 | 1.00000 | 3.100000 | 0.000001158 | 0.000000642 | 0.0000097282 |
| 0.2 | 1.00000 | 0.00000 | 4.100000 | 0.000000959 | 0.000000460 | 0.0000008219 |
| 0.4 | 1.00000 | 1.00000 | 2.100000 | 0.000000024 | 0.000000079 | 0.0000030059 |
| 0.6 | 0.00000 | 2.00000 | 3.100000 | 0.000002301 | 0.000001072 | 0.0000071362 |
| 0.8 | 4.00000 | 0.00000 | 2.100000 | 0.000004458 | 0.000002475 | 0.0000081324 |
| 1.0 | 6.40000 | 5.20000 | 8.100000 | 0.000022945 | 0.00001326 | 0.0000439496 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunthrayuth, P.; Naeem, M.; Shah, N.A.; Shah, R.; Chung, J.D. Numerical Simulations of the Fractional Systems of Volterra Integral Equations within the Chebyshev Pseudo-Spectral Method. Symmetry 2022, 14, 2575. https://doi.org/10.3390/sym14122575
Sunthrayuth P, Naeem M, Shah NA, Shah R, Chung JD. Numerical Simulations of the Fractional Systems of Volterra Integral Equations within the Chebyshev Pseudo-Spectral Method. Symmetry. 2022; 14(12):2575. https://doi.org/10.3390/sym14122575
Chicago/Turabian StyleSunthrayuth, Pongsakorn, Muhammad Naeem, Nehad Ali Shah, Rasool Shah, and Jae Dong Chung. 2022. "Numerical Simulations of the Fractional Systems of Volterra Integral Equations within the Chebyshev Pseudo-Spectral Method" Symmetry 14, no. 12: 2575. https://doi.org/10.3390/sym14122575
APA StyleSunthrayuth, P., Naeem, M., Shah, N. A., Shah, R., & Chung, J. D. (2022). Numerical Simulations of the Fractional Systems of Volterra Integral Equations within the Chebyshev Pseudo-Spectral Method. Symmetry, 14(12), 2575. https://doi.org/10.3390/sym14122575






