A Shift-Deflation Technique for Computing a Large Quantity of Eigenpairs of the Generalized Eigenvalue Problems

Abstract

In this paper, we propose a shift-deflation technique for the generalized eigenvalue problems. This technique consists of the following two stages: the shift of converged eigenvalues to zeros, and the deflation of these shifted eigenvalues. By performing the above technique, we construct a new generalized eigenvalue problem with a lower dimension which shares the same eigenvalues with the original generalized eigenvalue problem except for the converged ones. In addition, we consider the relations of the eigenvectors before and after performing the technique. Finally, numerical experiments show the effectiveness and robustness of the proposed method.

1. Introduction

In this paper, we consider the computation of a large quantity of eigenpairs of a large-scale generalized eigenvalue problem (GEP)

$$Ax=\lambda Bx\mathrm{and}{y}^{*}A=\lambda y^{*}B,$$

(1)

where $A,B\in {\mathbb{C}}^{n\times n}$ are the coefficient matrices, and the notation ∗ denotes the conjugate transposition. The scalar $\lambda$ is an eigenvalue of the GEP (1) if and only if $\lambda$ is a root of $det(A-\lambda B)$, where $det(·)$ denotes the determinant of a matrix. The nonzero vectors x and y are called the right and left eigenvectors corresponding to $\lambda$, respectively. Together, $(\lambda ,x)$ or $(\lambda ,x,y)$ is called an eigenpair of the GEP (1). $({\lambda }_i,x_i,y_i)(1\le i\le r\le n)$ are r eigenpairs of the GEP (1), and let

$${\Lambda }_1=\mathrm{diag}({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_r),X_1=[x_1,x_2,\dots ,x_r]\mathrm{and}{Y}_1=[y_1,y_2,\dots ,y_r],$$

(2)

where $\mathrm{diag}({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_r)$ denotes a diagonal matrix with diagonal entries ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_r$, then the pair $({\Lambda }_1,X_1,Y_1)\in {\mathbb{C}}^{r\times r}\times {\mathbb{C}}^{n\times r}\times {\mathbb{C}}^{n\times r}$ is also called an eigenpair of the GEP (1), which satisfies

$$A{X}_1=B{X}_1{\Lambda }_1\mathrm{and}{Y}_1^{*}A={\Lambda }_1{Y}_1^{*}B.$$

(3)

The GEP (1) arises in a number of applications, such as structural analysis [1], magneto-hydrodynamics [2], fluid–structure interaction [3] and the boundary integral equation [4]. For the small and medium-sized GEP, we can compute the eigenpairs using the QZ algorithm [5], the Riemannian nonlinear conjugate gradient method [6] and so on. For the large-scale GEP, the methods in [7,8,9,10,11,12,13] only find a few extreme eigenpairs or interior eigenpairs with eigenvalues close to a given shift. In order to compute a cluster of eigenvalues and associated eigenvectors successively, it is necessary to develop a shift-deflation technique for the GEP (1).

Assume that we have already computed some eigenvalues ${\lambda }_i$$(1\le i\le r)$ of the GEP (1), our goal is to construct a new GEP with coefficient matrices $(\widehat{A},\widehat{B})$ whose eigenvalues are just those of the GEP (1) except for the computed eigenvalues ${\left\{{\lambda }_i\right\}}_{i=1}^r$. To do this, there are two stages, namely, shift and deflation. In the shift stage, we shift the converged eigenvalues ${\left\{{\lambda }_i\right\}}_{i=1}^r$ to zeros while keeping the remaining eigenvalues unchanged. To this purpose, we define a new GEP with coefficient matrices $(\tilde{A},\tilde{B})$ whose eigenvalues are r zeros and ${\left\{{\lambda }_i\right\}}_{i=r+1}^n$. In the deflation stage, we deflate the shifted r zeros of the shifted GEP with coefficient matrices $(\tilde{A},\tilde{B})$. For this purpose, we construct a new GEP with coefficient matrices $(\widehat{A},\widehat{B})$ whose eigenvalues are just ${\left\{{\lambda }_i\right\}}_{i=r+1}^n$. The relationship between the eigenvectors of the two GEPs with coefficient matrices $(A,B)$ and $(\widehat{A},\widehat{B})$ are also shown in this paper.

Throughout this paper, we use the following notations. $I_n$ denotes the $n\times n$ identity matrix. $e_j$ and $E_j$ denote the j-th column and the first j columns of the identity matrix, respectively. The superscript ∗ denotes the conjugate transpose for a vector or a matrix. ${\parallel ·\parallel }_2$ denotes the Euclidean vector norm, and ${\parallel ·\parallel }_F$ denotes the Frobenius matrix norm. We also adopt the following MATLAB notations: $A(i:j,k:l)$ denotes the submatrix of the matrix A that consists of the inrersection of the rows i to j and the columns k to l, $A(i:j,:)$ and $A(:,k:l)$ select the rows i to j and the columns k to l of A, respectively.

2. Shift Technique

In this section, we describe how to move the eigenvalues of the GEP (1) to zeros and keep the corresponding eigenvectors and the remaining eigenvalues unchanged.

Theorem 1.

Assume that $({\lambda }_i,x_i,y_i)(1\le i\le n)$ are the eigenpairs of the GEP (1) with ${\lambda }_i\ne 0$, the pair $({\Lambda }_1,X_1,Y_1)$ is defined as (2) with $Y_1^{*}{X}_1=I_r$ and ${\lambda }_i\ne {\lambda }_j$ where $1\le i\le r$ and $r<j\le n$. Construct a new GEP

$$\tilde{A}\tilde{x}=\tilde{\lambda }\tilde{B}\tilde{x}and{\tilde{y}}^{*}\tilde{A}=\tilde{\lambda }{\tilde{y}}^{*}\tilde{B},$$

(4)

where the coefficient matrices $\tilde{A}$ and $\tilde{B}$ are defined as

$$\left\{\begin{array}{c}\tilde{A}=A-B{X}_1{\Lambda }_1{Y}_1^{*},\hfill \\ \tilde{B}=B,\hfill \end{array}\right.$$

(5)

and $({\tilde{\lambda }}_i,{\tilde{x}}_i,{\tilde{y}}_i)(1\le i\le n)$ are the eigenpairs of the shifted GEP (4) with

$${\tilde{\lambda }}_i=\left\{\begin{array}{c}0,1\le i\le r,\hfill \\ {\lambda }_i,r<i\le n,\hfill \end{array}\right.{\tilde{x}}_i=\left\{\begin{array}{c}{x}_i,1\le i\le r,\hfill \\ (I_n-{\lambda }_i^{-1}{X}_1{\Lambda }_1{Y}_1^{*})x_i,r<i\le n,\hfill \end{array}\right.and{\tilde{y}}_i=\left\{\begin{array}{c}{\tilde{y}}_i,1\le i\le r,\hfill \\ y_i,r<i\le n.\hfill \end{array}\right.$$

(6)

Proof. 

We first verify the case of $1\le i\le r$. From the assumption $Y_1^{*}{X}_1=I_r$, we have $Y_1^{*}{x}_i=e_i$ and

$$\tilde{A}{x}_i=(A-B{X}_1{\Lambda }_1{Y}_1^{*})x_i=A{x}_i-B{X}_1{\Lambda }_1{e}_i=A{x}_i-{\lambda }_{i}B{x}_i=0.$$

Therefore, $(0,x_i,{\tilde{y}}_i)(1\le i\le r)$ are the eigenpairs of the shifted GEP (4) which implies that the shift technique (5) indeed moves the nonzero eigenvalues ${\left\{{\lambda }_i\right\}}_{i=1}^r$ to zeros while keeping the corresponding right eigenvectors ${\left\{x_i\right\}}_{i=1}^r$ unchanged.

Next, we consider the case of $r<i\le n$. In fact, by using (3) we obtain

$$\begin{array}{cc}\hfill (\tilde{A}-{\lambda }_i\tilde{B}){\tilde{x}}_i& =(A-B{X}_1{\Lambda }_1{Y}_1^{*}-{\lambda }_{i}B)(I_n-{\lambda }_i^{-1}{X}_1{\Lambda }_1{Y}_1^{*})x_i\hfill \\ \hfill & =(A-{\lambda }_i^{-1}A{X}_1{\Lambda }_1{Y}_1^{*}+{\lambda }_i^{-1}B{X}_1{\Lambda }_1^2{Y}_1^{*}-{\lambda }_{i}B)x_i\hfill \\ \hfill & =(A-{\lambda }_{i}B)x_i-{\lambda }_i^{-1}(A{X}_1-B{X}_1{\Lambda }_1){\Lambda }_1{Y}_1^{*}{x}_i\hfill \\ \hfill & =0\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill {\tilde{y}}_i^{*}(\tilde{A}-{\lambda }_i\tilde{B})& =y_i^{*}(A-B{X}_1{\Lambda }_1{Y}_1^{*}-{\lambda }_{i}B)\hfill \\ \hfill & =y_i^{*}(A-{\lambda }_i)B-y_i^{*}B{X}_1({\lambda }_i{I}_r-{\Lambda }_1){\Lambda }_1{({\lambda }_i{I}_r-{\Lambda }_1)}^{-1}{Y}_1^{*}\hfill \\ \hfill & =y_i^{*}(A-{\lambda }_i)B+y_i^{*}(A-{\lambda }_{i}B)X_1{\Lambda }_1{({\lambda }_i{I}_r-{\Lambda }_1)}^{-1}{Y}_1^{*}\hfill \\ \hfill & =y_i^{*}(A-{\lambda }_i)B\left(I_n+X_1{\Lambda }_1{({\lambda }_i{I}_r-{\Lambda }_1)}^{-1}{Y}_1^{*}\right)\hfill \\ \hfill & =0\hfill \end{array}$$

(8)

A combination of (7) and (8) indicates that $({\lambda }_i,{\tilde{x}}_i,{\tilde{y}}_i)(r<i\le n)$ are the eigenpairs of the shifted GEP (4), which implies that the shift technique (5) indeed keeps the remaining eigenvalues ${\left\{{\lambda }_i\right\}}_{i=r+1}^n$ along with the corresponding left eigenvectors ${\left\{y_i\right\}}_{i=r+1}^n$ unchanged.    □

Remark 1.

Some remarks of Theorem 1 are illustrated as follows.

(1) 

From (6), we can see that the eigenvalues ${\left\{{\lambda }_i\right\}}_{i=1}^r$, the right eigenvectors ${\left\{x_i\right\}}_{i=r+1}^n$ and the left eigenvectors ${\left\{y_i\right\}}_{i=1}^r$ have changed after implementing the shift technique (5). Moreover, the new right eigenvectors ${\left\{{\tilde{x}}_i\right\}}_{i=r+1}^n$ are explicitly available in (6), and the new left eigenvectors ${\left\{{\tilde{y}}_i\right\}}_{i=1}^r$ can be obtained by solving ${\tilde{y}}_i^{*}A=0$.

(2) 

A similar shift technique can be observed where the coefficient matrix $\tilde{A}$ in (5) is defined by $\tilde{A}=A-X_1{\Lambda }_1{Y}_1^{*}B$. At this moment, the changes of the left eigenvectors ${\left\{y_i\right\}}_{i=1}^r$ are available while those of the right eigenvectors ${\left\{x_i\right\}}_{i=1}^r$ are unavailable. Moreover, we need to solve a homogeneous system using a certain numerical method if we want both the left and right eigenvectors.

(3) 

A similar shift technique can be observed where the coefficient matrix $\tilde{A}$ in (5) is defined by $\tilde{A}=A-B{X}_1{\Lambda }_1{X}_1^{*}$. At this moment, the left eigenvectors ${\left\{y_i\right\}}_{i=1}^r$ are not needed, and $Y_1$ in both the condition $Y_1^{*}{X}_1=I_r$ and the relation ${\tilde{x}}_i=(I_n-{\lambda }_i^{-1}{X}_1{\Lambda }_1{Y}_1^{*})x_i$ should be replaced by $X_1$.

The above theorem and remarks lead to the following corollary directly.

Corollary 1.

Assume that $({\lambda }_i,x_i)(1\le i\le n)$ are the eigenpairs of the GEP (1) with ${\lambda }_i\ne 0$, and $({\lambda }_1,x_1)$ is a converged eigenpair with $x_1^{*}{x}_1=1$ and ${\lambda }_1\ne {\lambda }_j$, where $2\le j\le n$. Construct the new GEP (4) where the coefficient matrices $\tilde{A}$ and $\tilde{B}$ are defined as

$$\left\{\begin{array}{c}\tilde{A}=A-{\lambda }_{1}B{x}_1{x}_1^{*},\hfill \\ \tilde{B}=B,\hfill \end{array}\right.$$

(9)

then $({\tilde{\lambda }}_i,{\tilde{x}}_i)(1\le i\le n)$ are the eigenpairs of the new GEP (4) with

$${\tilde{\lambda }}_i=\left\{\begin{array}{c}0,i=1,\hfill \\ {\lambda }_i,2\le i\le n,\hfill \end{array}\right.and{\tilde{x}}_i=\left\{\begin{array}{c}{x}_i,i=1,\hfill \\ (I_n-\frac{{\lambda }_1}{{\lambda }_i}{x}_1{x}_1^{*})x_i,2\le i\le n.\hfill \end{array}\right.$$

(10)

Remark 2.

Some remarks of Corollary 1 are shown as follows.

(1) 

If ${\lambda }_1=0$, then the shift technique (9) is not needed. If ${\lambda }_1=\infty$, then the shift technique (9) will fail due to the fact $B{x}_1=0$. In practice, eigenvalues can be sorted into modules ascending order, i.e., $|{\lambda }_1|\le |{\lambda }_2|\le \cdots \le |{\lambda }_n|$, and we are interested in finding the smallest eigenvalues of the GEP (1).

(2) 

The relation of the left eigenvectors $y_i$ and ${\tilde{y}}_i$ can also be given as $y_i=(I_n-\frac{{\lambda }_1}{{\lambda }_1-{\lambda }_i}{y}_1{y}_1^{*}){\tilde{y}}_i$ when $2\le i\le n$. However, it will fail if ${\lambda }_i={\lambda }_1$ for a certain i. In order to remedy this issue, we should shift this eigenpair $({\lambda }_i,x_i)$ together with the converged eigenpair $({\lambda }_1,x_1)$ by applying the shift technique referred to in Remark 1 (3).

(3) 

We can also shift ${\lambda }_1$ to infinity by using the following shift technique

$$\left\{\begin{array}{c}\tilde{A}=A,\hfill \\ \tilde{B}=B-B{x}_1{x}_1^{*},\hfill \end{array}\right.$$

(11)

while keeping the corresponding right eigenvector $x_1$ and the remained eigenvalues ${\left\{{\lambda }_i\right\}}_{i=2}^n$ unchanged. Moreover, we have the relation that ${\tilde{x}}_i=(I_n-\frac{{\lambda }_i}{{\lambda }_1}{x}_1{x}_1^{*})x_i$ and $x_i=(I_n-\frac{{\lambda }_i}{{\lambda }_1-{\lambda }_i}{x}_1{x}_1^{*}){\tilde{x}}_i$ when $2\le i\le n$.

3. Deflation Technique

In this section, we deflate the shifted r zeros. To this end, we construct a new GEP with dimension $(n-r)\times (n-r)$ whose eigenvalues are the remaining eigenvalues of the shifted GEP (4) except for zeros. The following theorem shows the feasibility of the deflation technique under certain assumptions.

Theorem 2.

Assume that $({\lambda }_i,x_i,y_i)(1\le i\le n)$ are the eigenpairs of the GEP (1) with ${\lambda }_i=0$ and ${\lambda }_j\ne 0$ where $1\le i\le r$ and $r<j\le n$, $X,Y\in {\mathcal{C}}^{n\times r}$ are both full column rank matrices with $AX=0$ and $Y^{*}A=0$, H and K are both nonsingular matrices with $H{E}_r=Y$ and $K{E}_r=X$, and $R=Y^{*}BX$ is nonsingular. Construct a new GEP

$$\widehat{A}\widehat{x}=\widehat{\lambda }\widehat{B}\widehat{x}and{\widehat{y}}^{*}\widehat{A}=\widehat{\lambda }{\widehat{y}}^{*}\widehat{B},$$

(12)

where the coefficient matrices $\widehat{A}$ and $\widehat{B}$ are defined as

$$\widehat{A}=A_1(r+1:n,r+1:n),\widehat{B}=B_1(r+1:n,r+1:n),$$

with

$$\left\{\begin{array}{c}{A}_1=H^{*}AK,\hfill \\ B_1=H^{*}(I_n-BX{R}^{-1}{Y}^{*})BK,\hfill \end{array}\right.$$

then, $({\lambda }_i,{\widehat{x}}_i,{\widehat{y}}_i)(r<i\le n)$ are the eigenpairs of the new GEP (12) with

$$x_i=K\left(\begin{array}{c}-R^{-1}S{\widehat{x}}_i\\ {\widehat{x}}_i\end{array}\right),y_i=H\left(\begin{array}{c}-{\left(R^{-1}\right)}^{*}{T}^{*}{\widehat{y}}_i\\ {\widehat{y}}_i\end{array}\right),$$

(13)

where $S=S_1(:,r+1:n)\in {\mathcal{C}}^{r\times (n-r)},S_1=Y^{*}BK,T=T_1(r+1:n,:)\in {\mathcal{C}}^{(n-r)\times r}$ and $T_1=H^{*}BX$.

Proof. 

We first prove that ${\lambda }_i(r<i\le n)$ are the eigenvalues of the deflated GEP (12). Let $L\left(\lambda \right)=A-\lambda B$, $L_1\left(\lambda \right)=H^{*}L\left(\lambda \right)K$ and $V\left(\lambda \right)=L_1\left(\lambda \right)(r+1:n,r+1:n)$. We can easily verify that $L_1\left(\lambda \right)$ shares the same spectrum with $L\left(\lambda \right)$. Moreover, we can have the following relations,

$$\begin{array}{cc}\hfill E_r^T{L}_1\left(\lambda \right)E_r& =Y^{*}(A-\lambda B)X=-\lambda R,\hfill \\ \hfill E_r^T{L}_1\left(\lambda \right)e_j& =Y^{*}(A-\lambda B)K{e}_j=-\lambda Y^{*}BK{e}_j,\hfill \\ \hfill e_j^T{L}_1\left(\lambda \right)E_r& =e_j^T{H}^{*}(A-\lambda B)X=-\lambda e_j^T{H}^{*}BX,\hfill \end{array}$$

(14)

where $r<j\le n$. Based on (14), we obtain

$$L_1\left(\lambda \right)=\left(\begin{array}{cc}\lambda I_r& \\ & I_{n-r}\end{array}\right)\left(\begin{array}{cc}-R& -S\\ -\lambda T& V\left(\lambda \right)\end{array}\right).$$

Let $D\left(\lambda \right)=V\left(\lambda \right)+\lambda T{R}^{-1}S$, then $det\left(L_1\left(\lambda \right)\right)={(-1)}^r{\lambda }^{r}det\left(R\right)det\left(D\left(\lambda \right)\right)$. Therefore, ${\lambda }_i(r<i\le n)$ are the roots of $det\left(D\right(\lambda \left)\right)$. Denote $L_2\left(\lambda \right)=A_1-\lambda B_1$, then we have

$$\begin{array}{cc}\hfill L_2\left(\lambda \right)& =H^{*}AK-\lambda H^{*}BK+\lambda \left(H^{*}BX\right)R^{-1}\left(Y^{*}BK\right)\hfill \\ \hfill & =L_1\left(\lambda \right)+\lambda \left(\begin{array}{c}R\\ T\end{array}\right)R^{-1}\left(\begin{array}{cc}R& S\end{array}\right)\hfill \\ \hfill & =L_1\left(\lambda \right)+\lambda \left(\begin{array}{cc}R& S\\ T& T{R}^{-1}S\end{array}\right)=\left(\begin{array}{cc}0& 0\\ 0& D\left(\lambda \right)\end{array}\right),\hfill \end{array}$$

which implies $D\left(\lambda \right)=\widehat{A}-\lambda \widehat{B}$.

Now, we prove the relations (13). Denote

$${\omega }_i=K^{-1}{x}_i=\left(\begin{array}{c}{\omega }_{i1}\\ {\omega }_{i2}\end{array}\right),$$

where ${\omega }_{i1}\in \mathcal{C}$, ${\omega }_{i2}\in {\mathcal{C}}^{n-1}$ and $r<i\le n$. Since $L_1\left({\lambda }_i\right){\omega }_i=H^{*}L\left({\lambda }_i\right)x_i=0$, we have

$$\left\{\begin{array}{c}-{\lambda }_{i}R{\omega }_{i1}-{\lambda }_{i}S{\omega }_{i2}=0,\hfill \\ -{\lambda }_{i}T{\omega }_{i1}+V\left({\lambda }_i\right){\omega }_{i2}=0.\hfill \end{array}\right.$$

(15)

According to the assumption that ${\lambda }_i\ne 0$ and R is nonsingular, we have ${\omega }_{i1}=-R^{-1}S{\omega }_{i2}$ from the first equation of (15). Therefore, we have $(V\left({\lambda }_i\right)+{\lambda }_{i}T{R}^{-1}S){\omega }_{i2}=D\left({\lambda }_i\right){\omega }_{i2}=0$, which implies ${\omega }_{i2}$ is a right eigenvector with respect to ${\lambda }_i$. Without loss of generality, we let ${\omega }_{i2}={\widehat{x}}_i$; then, the first relation in (13) is obtained. The rest of the proof of the second relation in (13) can be given analogously.    □

Remark 3.

Some remarks of Theorem 2 are shown below.

(1) 

If we apply the shift technique (5) and solve a homogeneous system $y^{*}A=0$ for columns of Y as suggested by Remark 1 (1), the full column rank matrices $X,Y\in {\mathcal{C}}^{n\times r}$ are obtained with $AX=0$ and $Y^{*}A=0$.

(2) 

The nonsingularity of $R=Y^{*}BX$ is essential in Theorem 2. If R is singular, then the deflation technique fails.

From the above theorem, we can obtain the following corollary directly.

Corollary 2.

Assume that $({\lambda }_i,x_i,y_i)(1\le i\le n)$ are the eigenpairs of the GEP (1) with ${\lambda }_1=0$ and ${\lambda }_i\ne 0(2\le i\le n)$, $x,y\in {\mathcal{C}}^n$ are both nonzero vectors with $Ax=0,y^{*}A=0$, H and K are both nonsingular and matrices with $H{e}_1=y,K{e}_1=x$, and $\gamma =y^{*}Bx\ne 0$. Construct a new GEP (12) where the coefficient matrices $\widehat{A}$ and $\widehat{B}$ are defined as

$$\widehat{A}=A_1(2:n,2:n),\widehat{B}=B_1(2:n,2:n),$$

(16)

with

$$\left\{\begin{array}{c}{A}_1=H^{*}AK,\hfill \\ B_1=H^{*}(I_n-\frac{1}{\gamma }Bx{y}^{*})BK,\hfill \end{array}\right.$$

(17)

then $({\lambda }_i,{\widehat{x}}_i,{\widehat{y}}_i)(2\le i\le n)$ are the eigenpairs of the new GEP (12) with

$$x_i=K\left(\begin{array}{c}-\frac{1}{\gamma }s{\widehat{x}}_i\\ {\widehat{x}}_i\end{array}\right),y_i=H\left(\begin{array}{c}-\frac{1}{\overline{\gamma }}{t}^{*}{\widehat{y}}_i\\ {\widehat{y}}_i\end{array}\right),$$

(18)

where $s=s_1(:,2:n)\in {\mathcal{C}}^{1\times (n-1)},s_1=y^{*}BK,t=t_1(2:n,:)\in {\mathcal{C}}^{n-1}$ $t_1=H^{*}Bx$ and $\overline{\gamma }$ denotes the conjugation of γ.

Remark 4.

Some remarks of Corollary 2 are given below.

(1) 

There are a lot of choices of the matrices H and K. In actual computation, we choose the nonsingular matrices H and K to be the Householder matrices such that $Hy={\parallel y\parallel }_2{e}_1$ and $Kx={\parallel x\parallel }_2{e}_1$, which guarantees the low computational cost and the numerical stability.

(2) 

The condition $\gamma =y^{*}Bx\ne 0$ is needed in Corollary 2. If $\gamma =0$, the deflation technique fails. To circumvent this problem, we can shift ${\lambda }_1$ to infinity by using the shift technique (11) without deflation, and continue to compute the next eigenvalue of interest.

4. Shift-Deflation Technique

In this section, we synthesize the shift technique in Section 2 and the deflation technique in Section 3 to deflate some known eigenpairs $({\Lambda }_1,X_1,Y_1)\in {\mathcal{C}}^{r\times r}\times {\mathcal{C}}^{n\times r}\times {\mathcal{C}}^{n\times r}$, and to find a large number of eigenpairs corresponding to the smallest eigenvalues in the module of the GEP (1).

We first consider the situation that $r=1$. Assume that $({\lambda }_1,x_1)$ is a simple eigenpair of the GEP (1) with ${\lambda }_1\ne 0$ and $\parallel x_1{\parallel }_2=1$. Define the matrices $\tilde{A}$ and $\tilde{B}$ as (9); then, $\tilde{A}{x}_1=0$. Solve $y^{*}\tilde{A}=0$ for seeking the vector ${\tilde{y}}_1$ with $\parallel {\tilde{y}}_1{\parallel }_2=1$, choose Householder matrices H and K such that $K{e}_1=x_1,H{e}_1={\tilde{y}}_1$, and define the matrices $\widehat{A}$ and $\widehat{B}$ as (16) and (17) where the matrices A and B in (17) are replaced by $\tilde{A}$ and $\tilde{B}$, respectively. If $\gamma ={\tilde{y}}_1^{*}\tilde{B}{x}_1\ne 0$, the shift-deflation technique can be completed, otherwise we shift ${\lambda }_1$ to infinity by using the shift technique (11).

If ${\lambda }_1$ is not a simple eigenvalue, that is $r>1$, we should shift all eigenvalues which are equal to ${\lambda }_1$ by using the shift technique referred to in Remark 1 (3). Moreover, we may obtain more than one converged set of eigenpairs by a certain numerical method at one iteration. Due to the advantage that a low computational cost and numerical stability can be guaranteed if we choose H and K as Householder matrices when $r=1$, we try to deflate these eigenpairs one by one with the relations (10) and (18). A numerical algorithm is summarized as follows.

The first step in Algorithm 1 can be seen as an inner iteration; therefore, it should have its own stopping criterion; for example,

$${\alpha }_i=\frac{\parallel A{x}_i-{\lambda }_{i}B{x}_i{\parallel }_2}{{\parallel A\parallel }_F+|{\lambda }_i{|\parallel B\parallel }_F}<{\tau }_1,$$

(19)

where A and B are the coefficient matrices after implementing the shift-deflation technique, and ${\tau }_1$ is a given tolerance. Then, we can denote ${\alpha }_i$ as the shift-deflated relative residual norm of the shift-deflated GEP. If we are interested in the accuracy of the approximation ${\lambda }_i$ of the original GEP, that is, the coefficient matrices are the input matrices A and B, we can simply test the following stopping criterion:

$${\sigma }_i={\sigma }_{min}(A-{\lambda }_{i}B)<{\tau }_2,$$

(20)

where ${\tau }_2$ is also a given tolerance. If we are also interested in the accuracy of the approximation $x_i$ corresponding to ${\lambda }_i$, we can repeat using the recursions (18) and (10) to backtrack with the computed eigenpair of the shift-deflated GEP during the iterations in Algorithm 1. To this end, we should save all the converged eigenpairs, the scalars $\gamma$, the vectors s, and the nonsingular matrices H and K. If we choose H and K as Householder matrices, we also need to save two vectors. With the backtracked eigenvector $x_i$, we can test the accuracy of approximation $x_i$ with the following stopping criterion

$${\beta }_i=\frac{\parallel A{x}_i-{\lambda }_{i}B{x}_i{\parallel }_2}{{\parallel A\parallel }_F+|{\lambda }_i{|\parallel B\parallel }_F}<{\tau }_3,$$

(21)

where A and B are the input matrices, and ${\tau }_3$ is a given tolerance. Then, we can denote ${\beta }_i$ as the original relative residual norm of the GEP (1) with the input matrices A and B.

Algorithm 1 Shift-deflationtechnique for the GEP.

Input: matrices A, B and the number k of the desired eigenpairs. Output: k approximate eigenpairs and their relative residuals.   1: Seek some (denoted by $r\ge 1$) eigenpairs ${\left\{({\lambda }_i,x_i)\right\}}_{i=1}^r$ with smallest eigenvalues in modules of the GEP with coefficient matrices A and B by a certain numerical method;   2: Backtrack the original eigenvectors by using the recursions (18) and (10) and compute their original relative residuals if necessary;   3: If k, approximate eigenpairs are obtained, then stop; otherwise, set $l=1$;   4: Compute $x_1=\frac{x_l}{\parallel x_l{\parallel }_2}$. If ${\lambda }_l$ is a multiple (denoted by $m\ge 2$) eigenvalue, shift all eigenvalues which are equal to ${\lambda }_l$ by using the shift technique referred in Remark 1 (3), and go to (6); otherwise, set $m=1$;   5: If ${\lambda }_l\ne 0$, compute the shifted matrices $\tilde{A}$ and $\tilde{B}$ as (9); otherwise, set $\tilde{A}=A$ and $\tilde{B}=B$;   6: Compute the eigenvectors ${\tilde{x}}_i(l+m\le i\le r)$ as (10);   7: Solve a homogeneous system $y^{*}\tilde{A}=0$ for seeking the m independent unit vectors ${\left\{{\tilde{y}}_i\right\}}_{i=1}^m$, and set $j=1$;   8: Choose Householder matrices H and K such that $K{e}_1=x_1,H{e}_1={\tilde{y}}_j$;   9: Compute $\gamma ={{\tilde{y}}_j}^{*}\tilde{B}{x}_1$. If $\gamma =0$, shift this eigenvalue ${\lambda }_{l+j-1}$ to infinity by using the shift technique (11), and set $A=\tilde{A},B=\tilde{B}$; otherwise, compute matrices $\widehat{A}$ and $\widehat{B}$ as (16) and (17) and eigenvectors ${\widehat{x}}_i(l+j\le i\le r)$ as (18), and set $A=\widehat{A},B=\widehat{B}$;  10: If $j<m$, set $j=j+1$ and go to (8);  11: If $l<r$, set $l=l+1$ and go to (4); otherwise, go to (1).

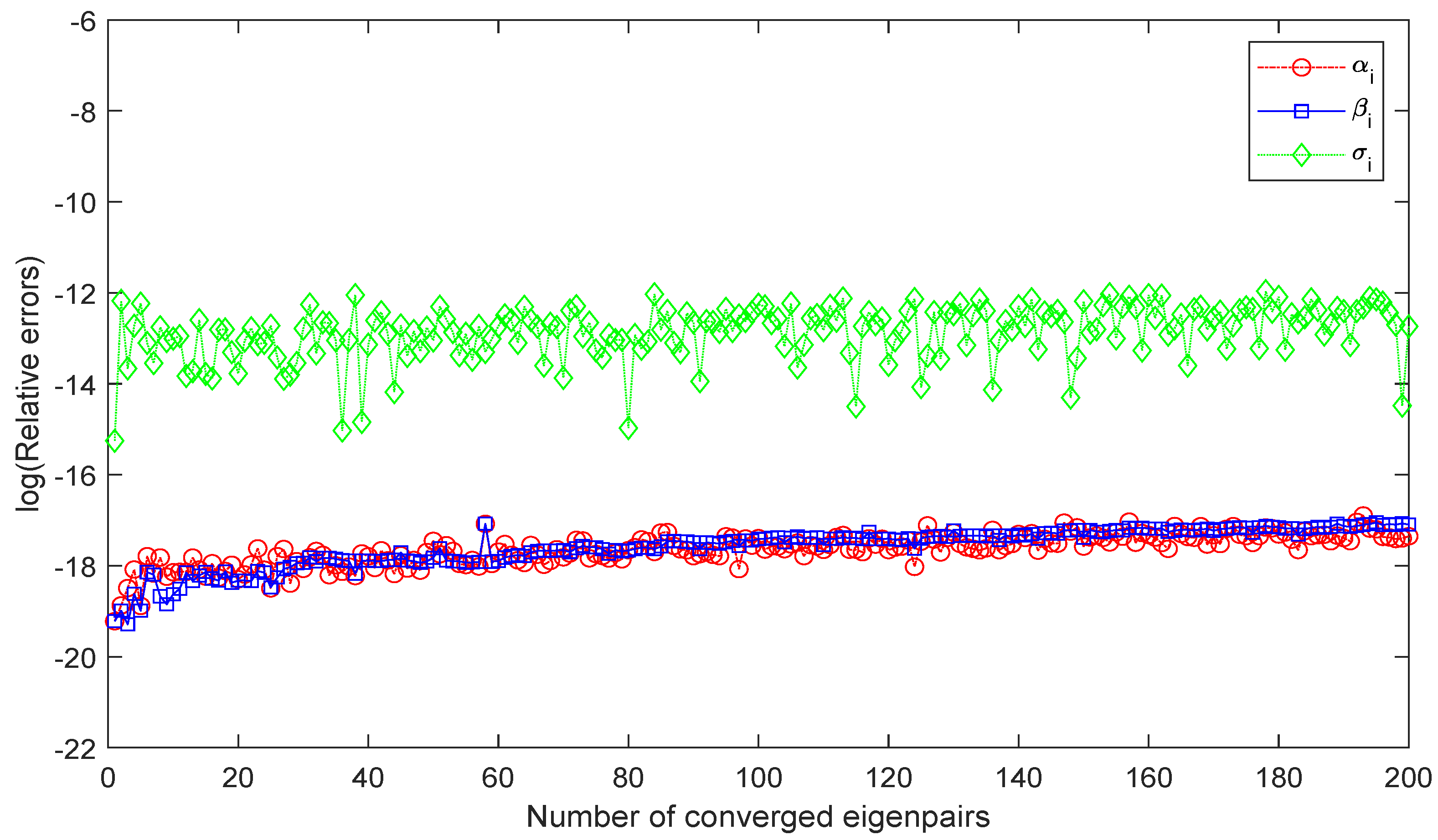
5. Numerical Results

In this section, we report some numerical examples to illustrate the effectiveness of the shift-deflation technique for the GEP. All examples are performed in Matlab R2015b on an Intel Core 2.9 GHz PC with 4 GB memory under a Windows 7 system. For simplicity, we use the Matlab built-in function ‘eigs’ to seek some eigenpairs, with the smallest modulus eigenvalues in the first iteration of Algorithm 1, and ‘svds’ to compute ${\sigma }_{min}$. The integer r in Algorithm 1 is randomly chosen but does not exceed a given threshold $r_{max}$ due to using the Matlab built-in function ‘eigs’. We denote n by the dimension of the GEP (1), and denote k by the number of the desired eigenpairs.

Example 1.

We consider the GEP (1) where the coefficient matrices are given as

$$A=\left(\begin{array}{cccccc}3& -1& 0& -2& 0& -9\\ 0& 1& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 3\\ 1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\end{array}\right),B=\left(\begin{array}{cccccc}1& -1& -1& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right).$$

We can easily obtain all eigenpairs by using the MATLAB built-in function ‘eig’, which are shown in

Table 1. The eigenpairs of Example 1.

i	1	2	3	4	5	6
${\lambda }_i$	0	1	1	2	3	∞
$x_i$	$\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ 1\\ 0\end{array}\right)$	$\left(\begin{array}{c}0\\ 1\\ 0\\ 0\\ 1\\ 0\end{array}\right)$	$\left(\begin{array}{c}1\\ 0\\ 0\\ 1\\ 0\\ 0\end{array}\right)$	$\left(\begin{array}{c}1\\ 0\\ 0\\ \frac{1}{2}\\ 0\\ 0\end{array}\right)$	$\left(\begin{array}{c}0\\ 0\\ -1\\ 0\\ 1\\ -\frac{1}{3}\end{array}\right)$	$\left(\begin{array}{c}-1\\ 0\\ -1\\ 0\\ 0\\ 0\end{array}\right)$
$y_i$	$\left(\begin{array}{c}0\\ -1\\ 0\\ 0\\ 1\\ 0\end{array}\right)$	$\left(\begin{array}{c}0\\ 1\\ 0\\ 0\\ 0\\ 0\end{array}\right)$	$\left(\begin{array}{c}\frac{1}{4}\\ 0\\ 1\\ -\frac{1}{2}\\ 0\\ \frac{3}{4}\end{array}\right)$	$\left(\begin{array}{c}\frac{1}{5}\\ \frac{1}{5}\\ 1\\ -\frac{1}{5}\\ 0\\ \frac{3}{5}\end{array}\right)$	$\left(\begin{array}{c}0\\ 0\\ -1\\ 0\\ 0\\ -1\end{array}\right)$	$\left(\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\right)$

.

From Table 1, we can see that it is not necessary to apply the shift technique to ${\lambda }_1$. Thus, the deflation condition scalar is $\gamma =y_1^{*}B{x}_1=1$ if we deflate this to zero. By performing Algorithm 1 for seeking all the six eigenpairs, we can obtain the following numerical results in

Table 2. Numerical results of Example 1.

Computed Eigenvalues	${\mathit{\alpha }}_{\mathit{i}}$	${\mathit{\sigma }}_{\mathit{i}}$
0	0	0
1.0000	$0.7476\times {10}^{-16}$	$0.4342\times {10}^{-16}$
1.0000	$0.6000\times {10}^{-16}$	$0.1462\times {10}^{-15}$
2.0000	$0.7793\times {10}^{-16}$	$0.7610\times {10}^{-16}$
3.0000	$0.9278\times {10}^{-16}$	$0.6686\times {10}^{-15}$
$0.6525\times {10}^{+16}$	0	$0.1083\times {10}^{-15}$

. We find that our proposed deflation technique is highly accurate from the first and last columns of Table 2.

Example 2.

We consider the GEP (1) where the coefficient matrices come from the Harwell-Boeing test matrices [14] bcsstk07 and bcsstm07. These matrices are $420\times 420$.

We implement Algorithm 1 with $k=10$ and $r_{max}=4$, and show the numerical results in

Table 3. Numerical results of Example 2.

r	${\mathit{\alpha }}_{\mathit{i}}$	${\mathit{\beta }}_{\mathit{i}}$	${\mathit{\sigma }}_{\mathit{i}}$
1	$0.3041\times {10}^{-18}$	$0.3041\times {10}^{-18}$	$0.6831\times {10}^{-7}$
4	$0.5173\times {10}^{-17}$	$0.3549\times {10}^{-17}$	$0.4019\times {10}^{-7}$
	$0.9864\times {10}^{-17}$	$0.2849\times {10}^{-16}$	$0.9069\times {10}^{-7}$
	$0.4854\times {10}^{-17}$	$0.1315\times {10}^{-16}$	$0.2009\times {10}^{-7}$
	$0.6373\times {10}^{-17}$	$0.1133\times {10}^{-16}$	$0.6716\times {10}^{-7}$
3	$0.1214\times {10}^{-16}$	$0.1419\times {10}^{-16}$	$0.5347\times {10}^{-9}$
	$0.4649\times {10}^{-17}$	$0.9685\times {10}^{-17}$	$0.1777\times {10}^{-6}$
	$0.1473\times {10}^{-16}$	$0.2073\times {10}^{-16}$	$0.1500\times {10}^{-6}$
2	$0.1525\times {10}^{-16}$	$0.2238\times {10}^{-16}$	$0.9081\times {10}^{-7}$
	$0.1005\times {10}^{-16}$	$0.1829\times {10}^{-16}$	$0.3821\times {10}^{-7}$

. We can see that the computed eigenpairs are quite accurate from the last two columns of Table 3.

Example 3.

In this example, the coefficient matrices A and B are symmetric and sparse, and given by

$$A=\left(\begin{array}{cccc}1& 1& & \\ -1& 2& \ddots & \\ & \ddots & \ddots & 1\\ & & -1& n\end{array}\right),B=\left(\begin{array}{cccc}1& -1& & 1\\ -1& 1& \ddots & \\ & \ddots & \ddots & -1\\ 1& & -1& 1\end{array}\right).$$

It is obvious that some structural properties of coefficient matrices will no longer hold after performing the shift-deflation technique, such as symmetry and sparsity. However, we can still use some properties of the input coefficient matrices implicitly. In the above case, we can keep implementing sparse operations even after preforming several shift-deflation techniques as long as all converged eigenpairs, the scalars $\gamma$ (or the matrices R), the vectors s (or the matrices S) and the nonsingular matrices H and K are saved during the iterations. The numerical results for Algorithm 1 with the parameters n = 10,000, $r_{max}=10$ and $k=200$ are shown in Figure 1.

From Figure 1, we can see that both the original smallest singular values ${\sigma }_i$ and the original relative residual norms ${\beta }_i$ have a high accuracy even though the shift-deflation technique is performed 200 times. Moreover, the original relative residual norm ${\beta }_i$ has a similar (slightly larger in most cases) accuracy to the shift-deflated relative residual norm ${\alpha }_i$ which is obtained with the Matlab built-in function ‘eigs’. Therefore, the numerical results show that the shift-deflation technique for the large-scale GEP is effective and robust.