Abstract
A d-dimensional, nth-order topological insulator or superconductor has localized eigenmodes at its -dimensional boundaries (). In this work, we apply periodic driving fields to two-dimensional superconductors, and obtain a wide variety of Floquet second-order topological superconducting (SOTSC) phases with many Majorana corner modes at both zero and quasienergies. Two distinct Floquet SOTSC phases are found to be separated by three possible kinds of transformations, i.e., a topological phase transition due to the closing/reopening of a bulk spectral gap, a topological phase transition due to the closing/reopening of an edge spectral gap, or an entirely different phase in which the bulk spectrum is gapless. Thanks to the strong interplay between driving and intrinsic energy scales of the system, all the found phases and transitions are highly controllable via tuning a single hopping parameter of the system. Our discovery not only enriches the possible forms of Floquet SOTSC phases, but also offers an efficient scheme to generate many coexisting Majorana zero and corner modes, which may find applications in Floquet quantum computation.
1. Introduction
Floquet topological phases appear in time-periodic driven systems with nontrivial topological properties (see Refs. [1,2,3,4] for reviews). Their characteristic features include symmetry classifications unique to nonequilibrium states [5,6,7,8], anomalous bulk-boundary correspondence with no static analogy [9,10,11,12], and substantial numbers of edge states induced by driving fields [13,14,15,16,17]. The observation of Floquet topological matter in various physical settings, including solids [18,19,20,21], cold atoms [22,23,24,25] and optical systems [26,27,28,29], further promotes their applications in ultrafast electronics [30] and topological quantum computing [31].
In recent years, the approach of Floquet engineering has been applied to generate and control higher order topological phases [32,33,34,35,36,37,38,39,40]. A gapped topological phase of order n in d-spatial dimensions () usually holds topological edge states along its -dimensional boundaries (see Refs. [41,42,43,44] for reviews). For example, a two-dimensional (2D), second-order topological insulator has localized eigenstates at the corners of the lattice on which it is defined. The conventional topological insulator can, thus, be viewed as a first-order topological phase. Besides insulating [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66] and semi-metallic [67,68,69,70,71] setups, periodic driving fields have also been applied to engineer Floquet SOTSC phases [72,73,74,75,76,77,78,79,80]. The latter could possess two types of symmetry-protected Majorana corner states with zero and quasienergies, which might be adopted in topological quantum computation as substitutions of the more conventional Majorana edge modes. Till now, the studies of Floquet second-order topological superconductors focus on either models with unconventional d-wave pairings and up to eight Floquet bands [78,79,80], or applications in Floquet quantum computation utilizing at most four Majorana corner modes at both zero and quasienergies [73,74]. It remains unclear whether we could obtain as many as possible of the Majorana zero and corner modes together in Floquet SOTSC phases following simple driving protocols, similar to what has been achieved for Floquet second-order topological insulators [45]. Moreover, phase transitions in higher order topological matter could happen by closing either a gap between the bulk bands (type-I) or a gap between the edge bands (type-II) [81,82,83,84,85,86,87]. Following which type of topological phase transition Floquet Majorana corner modes could emerge deserves to be further clarified.
In this work, we couple a superconductor in two dimensions to time-periodic driving fields, and obtain rich Floquet SOTSC phases with many normal and anomalous Majorana corner modes at zero and quasienergies, respectively. In Section 2, we introduce our model and its driving protocol, discuss the symmetries of the model, and explain how to find its spectrum and eigenmodes under different boundary conditions. In Section 3, we explore the topological phases and phase transitions in our system with gradually increased generality. Floquet SOTSC phases with different numbers of Majorana zero and corner modes are obtained, and they are found to be separated by the closing/reopening of bulk spectral gaps, edge band gaps or even emerging new phases with gapless Floquet spectra. In Section 4, we summarize our results and discuss potential future directions. Throughout this work, we set the Floquet driving period and the Planck constant . Other system parameters have been properly scaled and set in dimensionless units.
2. Model
We start with a lattice model that describes a 2D superconductor. It may be viewed as a simplified version of the model introduced in Equation (1) of Ref. [73]. A schematic diagram of our model is shown in Figure 1, whose static Hamiltonian takes the form
where
and
Here, () and () are the creation (annihilation) operators of fermions on the sublattices A and B of a unit cell at the location of the 2D lattice. The sublattice structure is originated from the dimerized superconducting pairing amplitudes () along the y-direction of the lattice. J and denote the hopping amplitudes along the x- and y-directions. is the chemical potential and is the pairing amplitude along the x-direction. By solving the eigenvalue equation , one can obtain the spectrum and Majorana corner states of the static system, with typical examples shown in Figure 2. We observe that there are two possible phases, with one of them being topologically trivial and the other one possessing four zero-energy Majorana eigenmodes at the four corners of the lattice. For the parameter domains considered in Figure 2, these Majorana corner modes emerge once, . Similar results are observed in the previous study of a slightly more complicated model [73], where the hopping amplitude and chemical potential are also dimerized in space. In Ref. [73], it was shown that with a harmonic (sinusoidal) driving field added to the chemical potential , the system could become a Floquet second-order topological superconductor with four Majorana corner modes at both the zero and quasienergies. Note that the model used in Ref. [73] further assumes the lattice dimerization in the hopping amplitude and chemical potential . In our model above, the hopping and chemical potential terms are instead uniform along the two spatial dimensions. In addition, the Floquet driving field in Ref. [73] was added to the dimerized chemical potential there. In our case, the driving field will be coupled to the superconducting pairing amplitude, as discussed below. The possibility of generating more Floquet Majorana zero/ corner modes and inducing multiple topological transitions by periodic driving fields were also not considered in Ref. [73], as the sinusoidal modulation applied there could not achieve such goals.
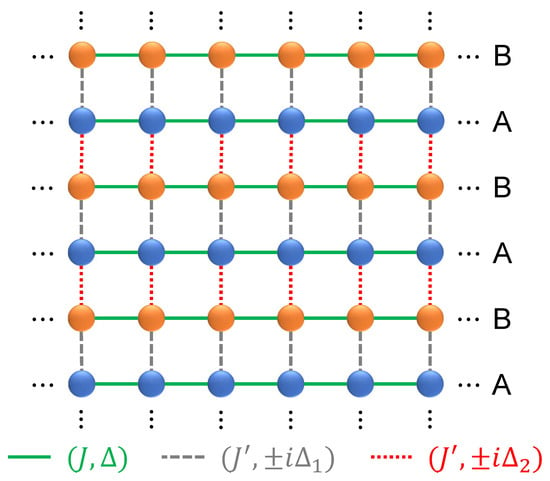
Figure 1.
An illustration of the 2D lattice model. The chains A (blue balls) and B (orange balls) are related to the operators and in . A uniform chemical potential is applied to each site. In the Floquet model, the superconducting pairing amplitude is replaced by .
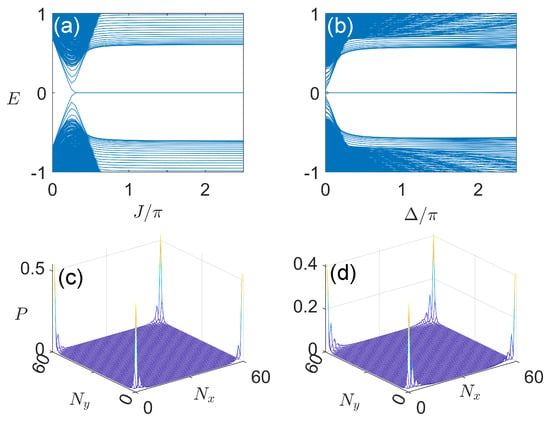
Figure 2.
Typical spectra and Majorana corner modes of the static SOTSC under open boundary conditions along x and y directions. (a,b) show the energy spectra E of versus J and , with other system parameters chosen to be . (c,d) show the probability distributions of the four Majorana corner modes with in (a,b) at and , respectively. The lattice sizes are set as for all panels.
In this work, we consider a different driving protocol by applying time-periodic kicks to the superconducting pairing amplitude along the x-direction, i.e., by setting in Equation (2) to . In one-dimensional Floquet topological superconductors, this type of driving and its physical relevance has been considered in [88]. The Floquet operator of the system, which describes its evolution over a complete driving period (e.g., from ) then takes the form
where
and
The Floquet spectrum and eigenstates of can be obtained from the eigenvalue equation , whose solution describes a Floquet state with the quasienergy (defined modulus ). Under open boundary conditions (OBCs) along both the x- and y-directions, we refer to a corner-localized eigenmode of with the quasienergy () as a Floquet Majorana zero () corner mode. In Section 3, we will show that many such Floquet Majorana corner modes could emerge in our system. Moreover, their numbers can be tuned by changing the system parameter across different types of topological phase transitions.
Under periodic boundary conditions (PBCs) along both the x- and y-directions, we can apply Fourier transformations to the creation and annihilation operators, i.e.,
Here, denotes the total number of unit cells, with () being the number of cells along the x (y) direction of the lattice. The unit cell index is , where and . We thus identify and for the second-quantized operators. The 2D quasimomentum is , with () being the quasimomentum along the x (y) direction. Therefore, we also identify and . After the Fourier transformation, we find the components and of the driven Hamiltonian as
Here, is the creation operator in the Nambu basis. The Hamiltonian matrices and in the Nambu spinor representation are given by
where are Pauli matrices and is the two-by-two identity matrix. In the momentum space, the Floquet operator now takes the form
where
The Floquet spectrum and eigenstates of the system in -space are then obtained by solving the eigenvalue equation , yielding four quasienergy bands for . When there exists j and l such that or , the bulk Floquet spectral gap may close at the center or boundary of the first quasienergy Brillouin zone . In Section 3, we will explore the Floquet spectra and gap-closing conditions of our system for cases with gradually increased complexity. We will further relate the gap closing/reopening transitions of the bulk Floquet spectra with topological phase transitions accompanied by the adjustment of Floquet corner modes under OBCs.
The topological properties of the system are closely related to the symmetries of . Upon unitary transformations, we can express the Floquet operator in a pair of symmetric time frames [89,90,91,92] as
When the hopping amplitude , it is not hard to verify that both and possess the chiral symmetry , in the sense that for . Since unitary transformations do not change the quasienergy spectrum, the chiral symmetry enforces the degeneracy of the eigenmodes of when their quasienergies are equal to zero or under the condition . This will be the situation in the first three cases explored in Section 3. When , the chiral symmetry is broken. However, and still possess the particle-hole symmetry , making the Floquet spectrum of symmetric with respect to the quasienergy . With the particle-hole symmetry only, we may obtain at most four Floquet Majorana corner modes at the quasienergies zero and when a rectangle geometry and the OBCs along both x and y directions are taken for the system. This will be the case encountered in Section 3.4.
In higher order topological phases, the change in topological corner modes can be induced not only by closing/reopening a bulk spectrum gap, but also by closing/reopening a gap between different edge bands. The former (latter) is usually called a type-I (type-II) topological phase transition [81,82,83,84,85,86,87]. To unveil the possibility of generating these two types of phase transitions in Floquet systems, we will also consider the solution of the system under the PBC (OBC) along the x (y) direction of the lattice, or vice versa. In the former case, we can apply the Fourier transformation only along the x direction, i.e.,
The Floquet operator under the PBC (OBC) along x (y) direction then takes the form
where
and
The Floquet spectrum and eigenstates are then obtained by diagonalizing at all different quasimomenta . Similarly, under the PBC (OBC) along the y (x) direction of the lattice, we can apply the Fourier transformation along the y direction, i.e.,
The resulting Floquet operator takes the form
where
and
The Floquet spectrum and eigenstates can now be found by diagonalizing at all different quasimomenta . The spectrum of and could provide useful information for us to understand different types of phase transitions in Floquet second-order topological superconductors, as will be shown in the following section.
3. Results
In this section, we study the emerging Floquet SOTSC phases in our system with gradually increasing complexity. We start with a minimal model which, yet, possesses rich Floquet SOTSC phases, many Majorana zero/ corner modes and different classes of topological phase transitions in Section 3.1. How will these intriguing states and transitions be modified by the presence of finite chemical potential and intracell superconducting pairing are further explored in Section 3.2 and Section 3.3. The most general case with nonvanishing hopping amplitude is, finally, discussed in Section 3.4.
3.1. Case 1:
We start with the simplest construction that allows us to have Floquet SOTSC phases with Majorana corner modes in our system. Assuming the chemical potential , hopping amplitude and intracell pairing amplitude along the y direction to be zero, we arrive at the following Floquet operator in momentum space from Equations (12)–(14), i.e.,
It is clear that the tensor product matrices , , and are anti-commute with one another. We can, thus, apply the Taylor expansion to each exponential term in Equation (28). After recombining relevant terms in the expansion, we find the quasienergy band dispersions
This gives us two quasienergy bands, with each of them being twofold degenerate. Moreover, the dispersions are independent of , which means that all the Floquet bands of our system in Case 1 are flat along . Since the two pairs of bands are symmetric with respect to the zero quasienergy, they could touch each other either at (the center of the quasienergy Brillouin zone) or at (the edge of the quasienergy Brillouin zone). The Floquet spectrum could then become gapless if
whose solution yields the phase boundary equation in parameter space
That is, when the system parameters satisfy this equation, the bulk quasienergy spectrum becomes gapless at either or . To investigate gap-closing transitions induced by the change in system parameters, we introduce the following quasienergy gap functions
Here, the in front is a scaling factor which restricts the ranges of both and to . It is clear that () once the spectrum gap closes at the quasienergy zero (). In Figure 3a, we show the gap functions and versus the hopping amplitude J for a typical set of system parameters in Case 1. For our choice of system parameters, we have , and according to Equation (31), the phase transition points appear at for assuming . They coincide with the locations where or vanish in Figure 3a. Moreover, we observe a series of gap-closing transitions with the increase in J, and more such transitions are expected to happen at larger values of J, which are yet absent in the static limit of the system. Therefore, the periodic driving allows us to create multiple gap-closing/reopening transitions in the quasienergy spectrum of the Floquet system.
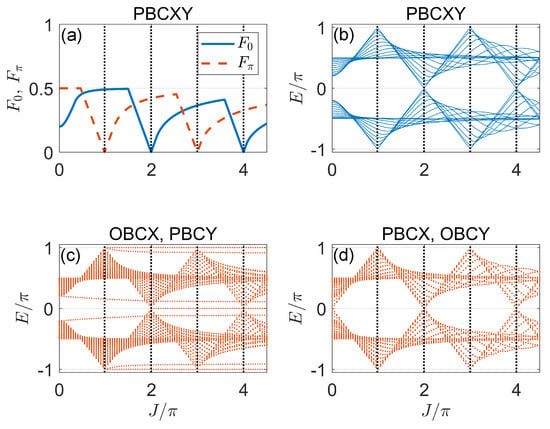
Figure 3.
Gap functions and Floquet spectrum versus J under different boundary conditions in Case 1. (a) Gap functions under PBCXY. (b) Floquet spectrum under PBCXY. (c) Floquet spectrum under OBCX, PBCY. (d) Floquet spectrum under PBCX, OBCY. The crossing points between the vertical dotted lines and the horizontal axis show the bulk gap-closing points predicted by Equation (31). Other system parameters are set as . The number of cells along x and y directions are .
In Figure 3b,c, we report the Floquet spectrum of the system at different hopping amplitudes J under the PBCs along both directions (denoted by PBCXY) and under the open (periodic) boundary condition along the x (y) direction (denoted by OBCX, PBCY). The gap-closing points at and in the bulk spectrum are found to be the same as those observed in Figure 3a. Meanwhile, some curves representing the dispersion of edge bands are observed in Figure 3c due to the open boundary condition taken along the x-direction. Note that the quasienergies of edge states in Figure 3c are not equal to zero and , even though they look very close to them in some parameter regions. In Figure 3d, we present the quasienergies under the periodic (open) boundary condition along the x (y) direction of the lattice (denoted by PBCX, OBCY). Interestingly, despite the bulk gap-closing points already seen in Figure 3a, we observe another gap-closing point at around . This point goes beyond the prediction of the bulk phase boundary according to Equation (31). As we will soon notice, this point corresponds to a closing of the quasienergy gap between different edge bands under the given boundary condition. It will, thus, be related to a type-II topological phase transition [87] in our Floquet SOTSC system.
To deepen our understanding of the gap-closing transitions observed in Case 1, we show the Floquet spectrum of the system under the OBCs along both x and y directions (denoted by OBCXY) in Figure 4. We find that more and more eigenmodes with or emerge following each gap-closing transition of the bulk, as predicted by Equation (31). In addition, the numbers of these eigenmodes are integer multiples of four, which strongly suggests that they are Floquet Majorana zero/ modes localized around the four corners of the lattice. In Figure 5a–e, we report the probability distributions of these zero/ modes in the lattice for a typical case [], with their quasienergies displayed in Figure 4b,c. The results confirm that they are indeed Majorana corner modes in the Floquet system. Compared with the Floquet SOTSC phases found in Ref. [73], we could now obtain many quartets of Majorana zero and corner modes, which may give more room for the realization of topological qubits and the operation of Floquet quantum computing protocols, as suggested previously [73]. In addition, with the increase in J, we could, in principle, obtain unbounded numbers of Floquet zero/ Majorana corner modes in the thermodynamic limit. This again demonstrates one key advantage of Floquet engineering, i.e., to generate many topological nontrivial states and topological phase transitions in a controlled manner.
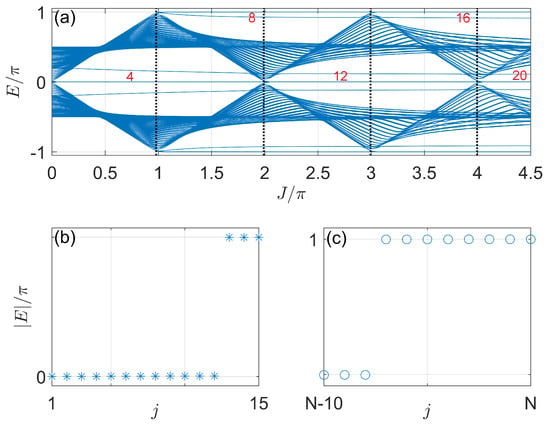
Figure 4.
Floquet spectrum versus J under OBCs in Case 1. (a) Quasienergies at different J under OBCs along both x and y directions (OBCXY). The crossing points between the vertical dotted lines and the horizontal axis show the bulk gap-closing points predicted by Equation (31). The numbers in red denote the numbers of Floquet corner modes at zero and quasienergies. (b,c) show the absolute values of quasienergies of the first fifteen (in stars) and last eleven (in circles) Floquet eigenstates indexed by j at . Other system parameters are . The number of cells along x and y directions are . The total number of Floquet eigenstates is 14,400.
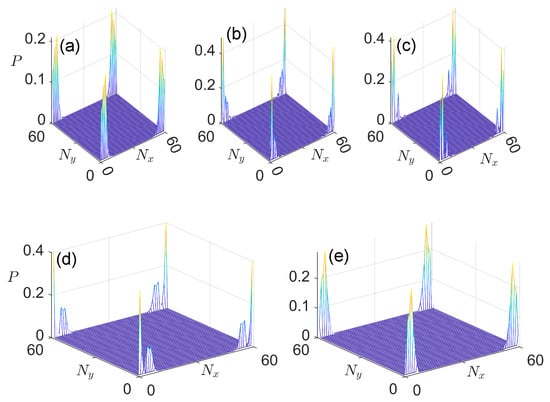
Figure 5.
Probability distributions of Floquet corner modes in Case 1 with zero and quasienergies in panels (a–c) and panels (d,e), respectively. Other system parameters are chosen to be . The number of cells along x and y directions are .
Finally, we are left to understand the transition at in Figure 4a, following which four Floquet Majorana corner modes appear at . However, the bulk Floquet spectral gap remains open throughout this transition, as observed clearly in Figure 3b. By diagonalizing the in Equation (18), we obtain the Floquet spectrum of the system versus under the PBCX, OBCY, as reported in Figure 6a–c for , and , respectively. We observe that while the bulk gaps close at and in the latter two cases, only edge states develop crossings at when . For comparison, we obtain the Floquet spectrum versus the quasimomentum under the OBCX, PBCY by diagonalizing the in Equation (24), as reported in Figure 6d–f. We again find the closings of bulk spectrum gaps at and for and , respectively. These are the bulk transition points predicted by Equation (31). Yet, the spectrum is found to be well-gapped at for in Figure 6d. Altogether, we conclude that under the condition in Equation (31), Floquet zero/ corner modes emerge following type-I topological phase transitions (with bulk-band touchings) in Case 1. Meanwhile, the Floquet zero corner modes could also appear following a type-II higher order topological phase transition (with edge-band touchings) at . There are, thus, two types of topological phase transitions in our Floquet SOTSC system, with each of them being able to generate more Floquet Majorana corner modes. This is another key difference between our system and that explored before [73].
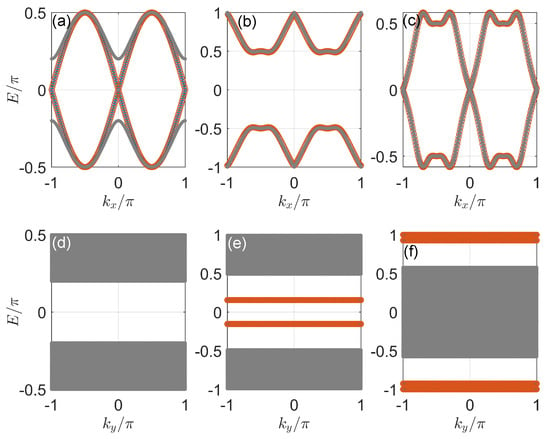
Figure 6.
Floquet spectrum versus () in Case 1 under PBCX, OBCY (OBCX, PBCY) in panels (a–c) [(d–f)]. The gray dots, red circles and blue stars highlight the bulk states, and states localized around the left edge and the right edge of the lattice. The value of hopping amplitude is set to for panels (a,d), to the first bulk gap-closing point at for panels (b,e), and to the first bulk gap-closing point at for panels (c,f). Other system parameters are set as .
The model presented in Case 1 thus forms a “minimal” model of Floquet second-order topological superconductors with rich and different types of topological phase transitions, along with unbounded numbers of Floquet Majorana zero/ corner modes. All of them are induced by a simple time-periodic driving protocol applied to the superconducting pairing amplitude. In the following subsections, we explore more general situations and check how the introducing of extra onsite, pairing and hopping terms could affect the corner modes and the phase transitions found in our system.
3.2. Case 2:
In a slightly more general situation, we allow the system to possess a finite chemical potential . From Equations (12)–(14), the resulting Floquet operator in momentum space now takes the form
Similar to Case 1, the tensor product matrices , , and are anti-commute with one another. Therefore, we can obtain the bulk quasienergy dispersion relation as
There are again two pairs of quasienergy bands with each of them been twofold degenerate and flat along . Setting or , we find the gapless condition of Floquet spectrum to be
yielding the phase boundary equation in the parameter space as
In contrast to Equation (31), we see that the general effect of a nonvanishing is to split each transition point of Case 1 into two distinct points separated by a distance ∼ on the phase diagram. We would, thus, expect richer gap-closing/reopening transitions in the parameter space of Case 2 compared with Case 1. Meanwhile, the gap functions in Case 2 share the same forms as Equation (32) of Case 1, as the systems possess two pairs of twofold-degenerate Floquet bands in both cases.
In Figure 7a, we present the gap functions and versus J for a typical set of system parameters in Case 2. The first interesting observation is that each gap-closing transition point located originally at (for , ) in Figure 3a now splits into two points residing at in Figure 7a, as also predicted by the phase boundary Equation (36). Therefore, the presence of a finite chemical potential endues the system with richer transition patterns in its spectrum. This is further confirmed by the quasienergies with respect to J under three different boundary conditions, as reported in Figure 7b–d. The bulk gap-closing points in each figure are found to be consistent with the prediction of Equation (36). Notably, we observe in Figure 7d a gapless point in the Floquet spectrum at , which is not captured by Equation (36). We will see that this point is again related to a touching of the edge bands instead of the bulk spectrum, similar to what we encountered at in Case 1.
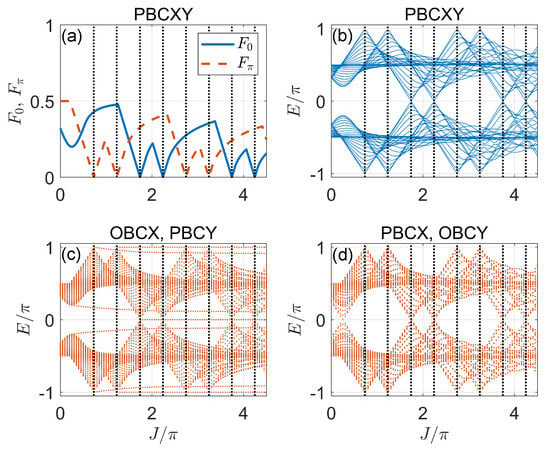
Figure 7.
Gap functions and Floquet spectrum versus J under different boundary conditions in Case 2. (a) Gap functions under PBCXY. (b) Floquet spectrum under PBCXY. (c) Floquet spectrum under OBCX, PBCY. (d) Floquet spectrum under PBCX, OBCY. The crossing points between the vertical dotted lines and the horizontal axis show the bulk gap-closing points predicted by Equation (36). Other system parameters are set as . The number of cells along x and y directions are .
The spectrum of our system in Case 2 under OBCs is shown in Figure 8. We observe that following each gap-closing transition, there are indeed more eigenmodes that emerge at the quasienergy zero or . Their numbers in each phase are denoted by the numbers in red in Figure 8a. Similar to Case 1, here the numbers of zero and Floquet eigenmodes are both integer multiples of four, implying that they are fourfold degenerate Majorana corner states in Floquet SOTSC phases. However, across each bulk gap-closing transition, the number of Floquet zero or eigenmodes now only changes by 4 instead of 8. This is originated from the splitting of each gapless point into two in the phase diagram with a nonvanishing . Following each of the new generated transitions, the change in Floquet zero/ eigenmode number is just half of the original transition in Case 1. We will further digest this point by investigating the momentum space spectrum of the system later in this subsection. In addition, we observe monotonic increases in the numbers of zero and Floquet eigenmodes with the increase in J following the consecutive spectrum transitions. This implies that we could also obtain a great deal of Floquet zero and corner modes at large J in the thermodynamic limit when . Meanwhile, four Floquet zero corner modes emerge from a transition at , which is not captured by the bulk phase boundary Equation (36). As mentioned before, we will trace it back to the touching of edge state bands, i.e., a type-II topological phase transition.
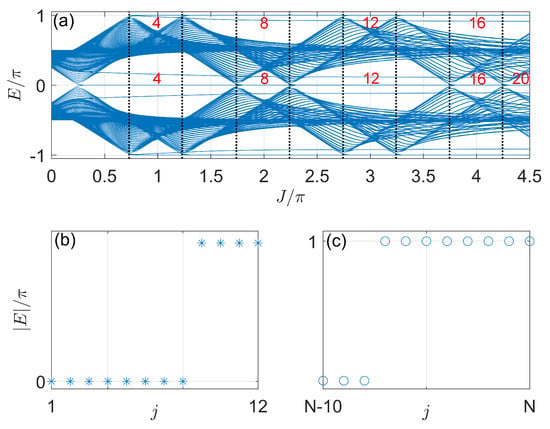
Figure 8.
Floquet spectrum versus J under OBCs in Case 2. (a) Quasienergies at different J under OBCXY. The crossing points between the vertical dotted lines and the horizontal axis show the bulk gap-closing points predicted by Equation (36). The numbers in red denote the numbers of Floquet corner modes at zero and quasienergies. (b,c) show the absolute values of quasienergies of the first twelve (in stars) and last eleven (in circles) Floquet eigenstates indexed by j at . Other system parameters are . The number of cells along x and y directions are . The total number of Floquet eigenstates is 14,400.
To confirm that the zero and Floquet eigenmodes observed in the spectrum are indeed Majorana corner modes, we plot their probability distributions in the lattice for a typical choice of system parameters in Figure 9. The plotted profiles correspond to the first eight and the last eight eigenstates shown in Figure 8b,c. The numbers of zero and eigenmodes are in this case, according to Figure 8a, and we see that they are indeed localized around the four corners of the lattice. Therefore, we could obtain many quartets of zero and Majorana corner modes in our Floquet SOTSC system, even with . This goes beyond the situation encountered before, where only four Majorana zero and corner modes were found to coexist in a continuously driven system [73]. The many corner Majorana states discovered here may again give us more freedom to implement Floquet quantum computing schemes [73].
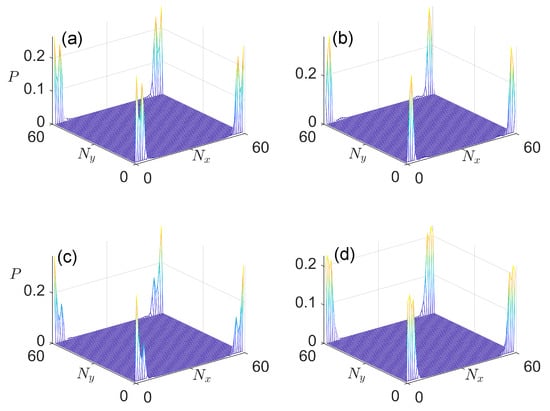
Figure 9.
Probability distributions of Floquet corner modes in Case 2 with quasienergies zero and in panels (a,b) and panels (c,d), respectively. Other system parameters are set as . The number of cells along x and y directions of the lattice are .
To understand the difference between the anomalous transition observed at and the other bulk gap-closing transitions, we present the spectra of the system under the PBCX, OBCY versus and under the OBCX, PBCY versus at three critical points , and , in Figure 10. These spectra were obtained by diagonalizing and in Equations (18) and (24), respectively. We find that for the transitions at and , the bulk Floquet bands of the system indeed touch at and in Figure 10b,e and Figure 10c,f. This is consistent with the prediction of the bulk phase boundary in Equation (36). In addition, a comparison between Figure 10b,c and Figure 6b,c also helps us to understand why the change in zero/ corner mode numbers is four instead of eight across each topological transition when . That is, in Case 1, the Floquet bands touch at two distinct points along [ in Figure 6b,c] at the bulk phase-transition point. Meanwhile, in Case 2, the Floquet bands only touch at a single point along [ in Figure 10b,c] at each bulk phase-transition point, yielding a smaller change in the number of Majorana corner modes across the transition.
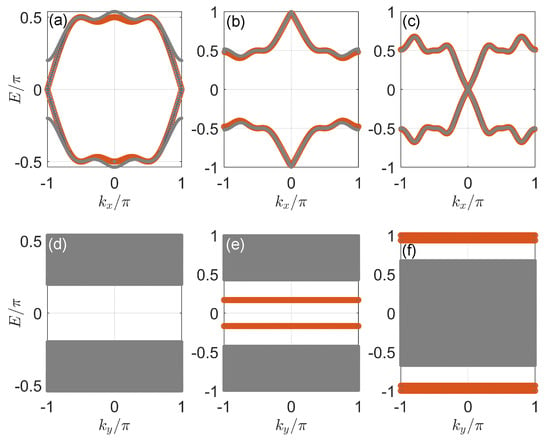
Figure 10.
Floquet spectrum versus () in Case 2 under PBCX, OBCY (OBCX, PBCY) in panels (a–c) [(d–f)]. The gray dots, red circles and blue stars highlight the bulk states, and states localized around the left edge and the right edge of the lattice. The value of hopping amplitude is set to for panels (a,d), to the first bulk gap-closing point at for panels (b,e), and to the first bulk gap-closing point at for panels (c,f). Other system parameters are chosen to be .
Finally, we realize that at , the edge state bands touch at under the PBCX, OBCY in Figure 10a, while no edge states and band touching are observed under the OBCX, PBCY in Figure 10d. This observation confirms that the four Floquet Majorana zero corner modes indeed emerge out of a type-II topological phase transition mediated by an edge-band touching at in Figure 9a. Therefore, we also encounter two types of topological phase transitions in Case 2, after which more Floquet Majorana zero/ corner modes appear with the increase in the hopping amplitude J in our system. This tendency will continue in more general situations, as will be discussed in the following subsection.
3.3. Case 3:
We now consider the case with only . In this case, all the pairing terms are switched on. Following Equations (12)–(14), the Floquet operator in momentum space takes the form
Using again the anti-commuting nature of tensor product matrices , , , and the Taylor expansion, we find the quasienergy dispersions of to be
As before, we obtain two pairs of twofold-degenerate Floquet bands. However, the quasienergies now depend on both the quasimomenta and due to the nonvanishing . Setting to zero or , we obtain the gapless condition of the spectrum as
Without loss of generality, we now assume all system parameters in Case 3 to be positive. One can then deduce from Equation (39) that the gap between the two sets of Floquet bands vanishes at or when the inequality
is satisfied for . This relation suggests a rather different situation compared with Cases 1 and 2, i.e., the Floquet spectrum could now become gapless at the quasienergy zero or in finite domains of the parameter space. Therefore, our model in Case 3 could possess gapless phases with semimetal-like Floquet band structures. Two different Floquet SOTSC phases may then be separated by a finite gapless region instead of a gap-closing point in the spectrum. In the meantime, we can still define the gap functions as in Equation (32) in Case 1.
In Figure 11a, we plot the gap functions and versus J for a typical set of system parameters in Case 3. Interestingly, we observe that with a finite intracell pairing , the gap-closing points in Case 2 now broaden into regions of finite widths along the J axis. The boundaries of these gapless bulk regions are highlighted by the vertical dotted lines in Figure 11, which are further determined theoretically by Equation (40). Therefore, in the presence of a finite , the transitions between different Floquet SOTSC phases can be mediated by other phases with gapless Floquet spectra instead of isolated critical points in the parameter space. The existence of these gapless phases is further confirmed by the Floquet spectrum presented in Figure 11b–d under different boundary conditions. We could thus obtain richer patterns of Floquet phases and spectral transitions with a nonvanishing . This is distinct from the situation considered previously, where the gapless phases are not observed in a harmonically driven setting [73]. Despite the many transitions occurring with the increase in J, we observe another isolated transition at that is not described by Equation (40). As discussed in previous subsections, this transition is also expected to originate from the touching of edge state bands instead of bulk bands.
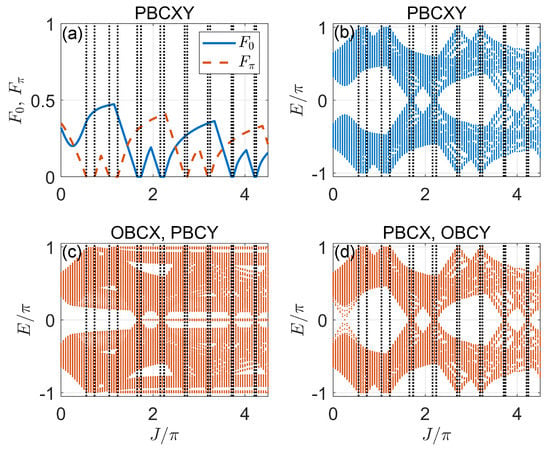
Figure 11.
Gap functions and Floquet spectrum versus J under different boundary conditions in Case 3. (a) Gap functions under PBCXY. (b) Floquet spectrum under PBCXY. (c) Floquet spectrum under OBCX, PBCY. (d) Floquet spectrum under PBCX, OBCY. The crossing points between the vertical dotted lines and the horizontal axis show the bulk gap-closing points predicted by Equation (40). Other system parameters are set as . The number of cells along x and y directions are .
In Figure 12, we report the Floquet spectrum of the system under OBCs along both directions. Following either the transition at or the transition mediated by a gapless phase at or , we obtain more eigenmodes at the quasienergy zero or with the increase in J, whose numbers are highlighted in red in Figure 12a. The quantization of these eigenmode numbers again suggests that they are localized states around the four corners of the lattice. Similar to the previous two cases, we could foresee an unbounded number of quartets of eigenmodes at and with in the thermodynamic limit. This demonstrates a controllable generation of these topological modes in our Floquet SOTSC model under a simple driving protocol. The main impact of a finite pairing amplitude is, thus, to generate gapless regions between different Floquet SOTSC phases, while preserving the zero and Floquet eigenmodes in the gapped phases of the bulk. In addition, four Floquet zero modes emerge through the transition at , where the bulk spectrum is expected to be gapped due to Equation (40). This transition will also be understood as a type-II transition following the closing of a gap between the edge bands at .
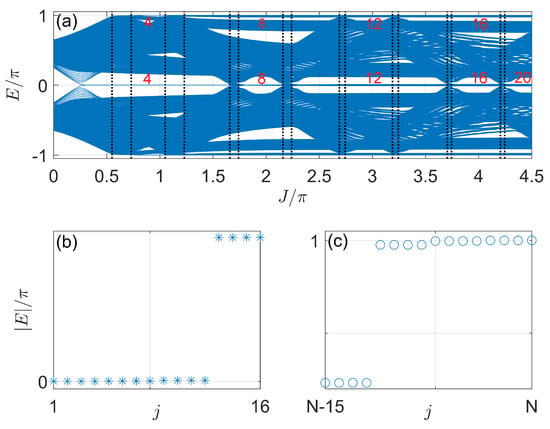
Figure 12.
Floquet spectrum versus J under OBCs in Case 3. (a) Quasienergies at different J under OBCXY. The crossing points between the vertical dotted lines and the horizontal axis show the bulk gap-closing points predicted by Equation (40). The numbers in red denote the numbers of Floquet corner modes at zero and quasienergies. (b,c) show the absolute values of quasienergies of the first sixteen (in stars) and last sixteen (in circles) Floquet eigenstates indexed by j at . Other system parameters are . The number of cells along x and y directions are . The total number of Floquet eigenstates is 14,400.
In Figure 13, we plot the probability distributions of the first twelve and the last twelve Floquet eigenmodes in Figure 12b,c, respectively. It is clear that they are indeed Floquet Majorana corner modes at the quasienergies zero and . We could, thus, obtain many such quartets of Majorana modes in our Floquet SOTSC system with . Furthermore, their appearances follow transitions over gapless phases instead of critical transition points of the system (except at ), which are different from those occurring in Cases 1 and 2. The large numbers of Majorana corner modes found here may also allow us to implement Floquet quantum computing protocols in more general situations [73].
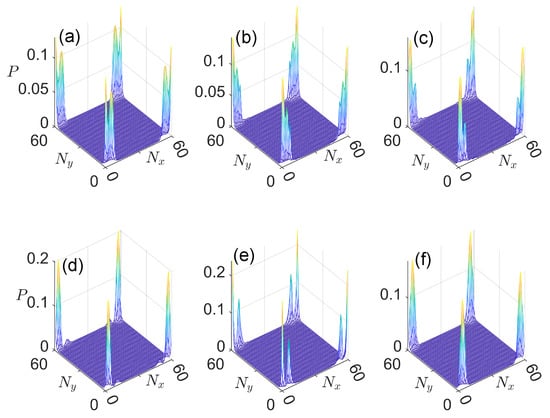
Figure 13.
Probability distributions of Floquet corner modes in Case 3 with quasienergies zero and in panels (a–c) and panels (d–f), respectively. Other system parameters are set as . The number of cells along x and y directions are .
We are left to understand the transition at . Similar to what we have carried out in the last two subsections, we obtain the Floquet spectrum of and in Equations (18) and (24) under the PBCX, OBCY and OBCX, PBCX, respectively, and present them in Figure 14a–c and Figure 14d–f for , , and . In the latter two cases, the transitions happen through the touching of bulk bands at and with the quasimomentum . This coincides with the prediction of the bulk phase boundary in Equation (40). They are, thus, conventional type-I topological phase transition in the Floquet SOTSC system. Instead, we find that the Floquet spectrum versus is gapped for , while it is gapless at through a touching of edge state bands at . Combining this observation with the emerging zero corner modes after the first transition in Figure 12a, we conclude that the transition at is indeed a type-II topological phase transition induced by an edge band touching, and it is not modified by the presence of a finite intracell pairing strength along the y direction of the lattice. It deserves to be mentioned that the edge bands in Figure 14a have vanishing net chiralities even though they traverse the band gap, yielding Floquet bands with zero Chern numbers.
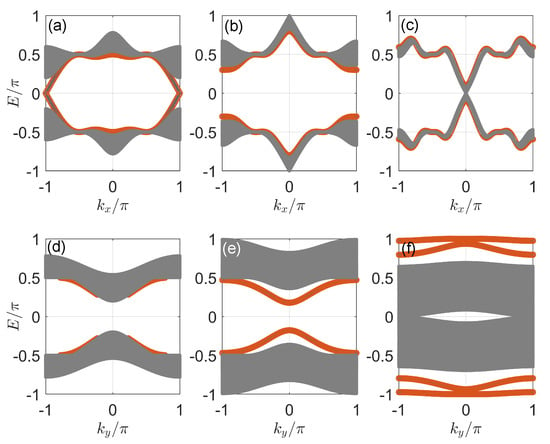
Figure 14.
Floquet spectrum versus () in Case 3 under PBCX, OBCY (OBCX, PBCX) in panels (a–c) [(d–f)]. The gray dots, red circles and blue stars highlight the bulk states, and states localized around the left edge and the right edge of the lattice. The value of hopping amplitude is set to for panels (a,d), to the first bulk gap-closing point at for panels (b,e), and to the first bulk gap-closing point at for panels (c,f). Other system parameters are set as .
Altogether, we find two types of topological phase transitions in Cases 1–3. With the increase in the hopping amplitude J, more and more Floquet Majorana zero/ corner modes emerge within our system, and richer patterns of topological phases and transitions appear in the cases with nonvanishing and . We now arrive at the stage of discussing what will happen if a finite hopping amplitude along the y direction is turned on. This will be our task in the following subsection, in which we treat the effect of essentially as a perturbation.
3.4. Case 4: General Situation
We finally discuss the general case with . The Floquet operator of our model in momentum space now takes the form of Equation (12), i.e.,
In this case, a simple expression of the quasienergy bands cannot be obtained from the Taylor expansion of , as the tensor products of Pauli matrices and are not anti-commute with all other matrices. We thus devolve to numerical calculations of the spectrum and states. Note that the gap functions and for Case 4 should be defined more generally as
where labels all possible quasienergies of at each .
In Figure 15a, we show the gap functions versus J in Case 4 for a typical set of system parameters. We see that with a nonvanishing but small , the general pattern of spectral transitions in Case 3 is preserved. That is, with the increase in J, the system could enter a series of gapped Floquet phases in the bulk (with and ), which are separated by multiple gapless phases (with or ). The main difference, caused by a finite , is that the regions of gapless phases are broadened in the parameter space. This is also confirmed by the Floquet spectrum versus J plotted under different boundary conditions in Figure 15b–d. Therefore, we expect the gapped Floquet SOTSC phases to be robust to certain numbers of hoppings along the y directions. Notably, the anomalous transition at , which is not related to the closing of a bulk spectral gap, is also observed in Figure 15d, which implies that this type-II topological transition remains intact when .
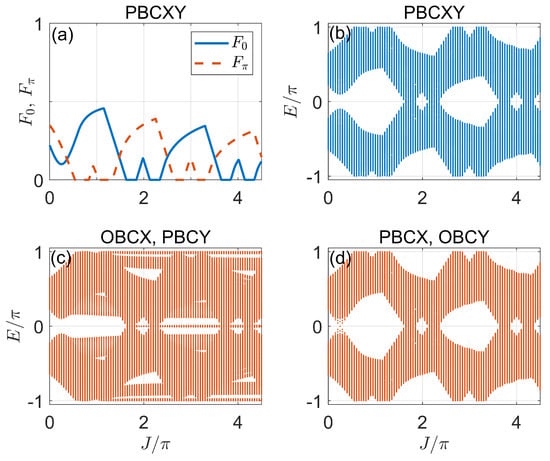
Figure 15.
Gap functions and Floquet spectrum versus J under different boundary conditions in Case 4. (a) Gap functions under PBCXY. (b) Floquet spectrum under PBCXY. (c) Floquet spectrum under OBCX, PBCY. (d) Floquet spectrum under PBCX, OBCY. Other system parameters are set as . The number of cells along x and y directions are .
To further understand the fate of Floquet Majorana zero/ corner modes in the presence of a finite , we plot the spectrum under OBCs along both the two spatial dimensions in Figure 16a. The results suggest that with the increase in J, there are still eigenmodes with zero and quasienergies coming out of the gap-closing transition at and the transitions through other gapless regions. Meanwhile, in the gapped phases, we notice that the spectra become broadened around and compared with Cases 1–3. In Figure 16b,c, we show the absolute values of quasienergy for the first sixteen and the last sixteen eigenstates in the spectrum at . In this case, we only find four eigenmodes with the quasienergies and , which means that not all the zero and Floquet Majorana corner modes are robust to the perturbation introduced by . A possible explanation of this observation is that with , the chiral symmetry of the Floquet system is broken. Yet, the particle-hole symmetry is preserved, as mentioned in Section 2, which enables the system to possess at most four Floquet Majorana corner modes at the quasienergies zero and . However, since we do not expect a spectral gap closing between bulk or edge bands when goes from zero up to a small value ( here), the emerging eigenmodes away from but close to and in Figure 16b,c should still have profiles localized around the four corners of the lattice, since they have no chance of mixing with other bulk or edge states under the perturbation.
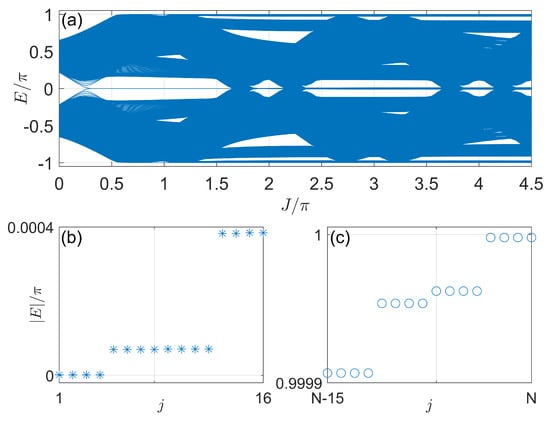
Figure 16.
Floquet spectrum versus J under OBCs in Case 4. (a) Quasienergies at different J under OBCXY. (b,c) show the absolute values of quasienergies of the first sixteen (in stars) and last sixteen (in circles) Floquet eigenstates indexed by j at . Other system parameters are . The number of cells along the x and y directions are . The total number of Floquet eigenstates is 14,400.
In Figure 17a–c and Figure 17d–f, we present the probability distributions of the first twelve and the last twelve eigenstates in Figure 16b,c, respectively. Indeed, we find that all these modes are localized around the four corners of the lattice, even though only eight of them are Majorana zero and corner modes of the Floquet SOTSC phase [in Figure 17a,d]. The fourfold-degenerate corner modes with are not topologically protected, as their quasienergies can vary with the change in . It remains an interesting issue to explore whether these non-topological corner modes could also find applications in Floquet quantum computing schemes. In our calculations, we also checked the effects of dimerized hopping amplitude and chemical potential on our results. These dimerization terms are introduced in the same way as the and used in the Equation (1) of Ref. [73]. Our numerical results suggest that the main observations about Floquet spectrum and corner modes presented in this subsection hold when these dimerization terms are introduced to our model as small perturbations.
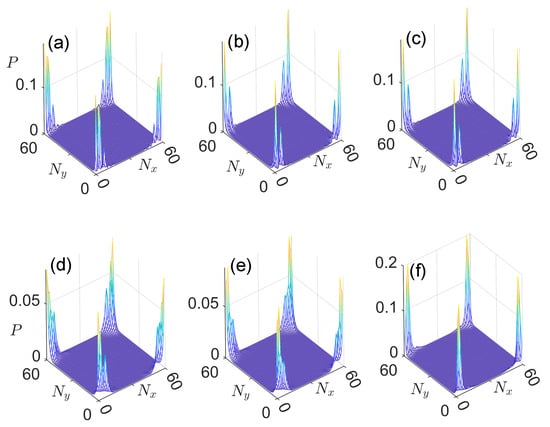
Figure 17.
Probability distributions of Floquet corner modes in Case 4 with quasienergies at or close to zero and in panels (a–c) and panels (d–f), respectively. Other system parameters are set as . The number of cells along x and y directions are .
4. Discussion and Conclusions
In this work, we explored the generation of many Majorana zero/ corner modes and multiple phase transitions in Floquet second-order topological superconductors. By applying time-periodic kicking to the pairing amplitude of a generic 2D superconductor with dimerized superconducting pairing, we obtained rich Floquet SOTSC phases with arbitrarily many Majorana corner modes at zero and quasieneriges, in principle, in the thermodynamic limit. Moreover, two different Floquet SOTSC phases are found to be separated by either a type-I topological phase transition with the closing/reopening of a bulk spectral gap, a type-II topological phase transition with the closing/reopening of an edge band gap, or a third phase with gapless quasienergy spectrum. The multiple quartets of Floquet Majorana zero/ corner modes are found to be protected by the chiral and particle-hole symmetries of the system. When the chiral symmetry is lifted by a perturbation which couples different sites along the y direction, four out of the many Majorana zero and corner modes could still survive, which represents the most stable higher order topological modes in the system. Our work, thus, extends the present understanding of topological phases and transitions in Floquet SOTSC setups. It further provides an efficient means to generate many Majorana corner modes, which may give us more choices and freedoms to design topological quantum computing schemes.
From the perspective of bulk-corner correspondence, there should exist a pair of integer-quantized topological invariants that can characterize the two types of Floquet Majorana corner modes at zero and quasienergies in our system, similar to what has been identified before for Floquet second-order topological insulators [45]. In practice, due to the complicated patterns of phase transitions and Floquet corner modes in our model, the topological winding numbers introduced in Ref. [45] could not fully characterize all the Majorana corner modes and bulk-corner correspondence in our system. In future work, it remains an interesting issue to explore suitable topological invariants that could predict the numbers of Majorana corner modes in the different Floquet SOTSC phases found here.
In our Floquet model, the periodic driving is introduced via a delta-kicked superconducting pairing amplitude. We expect similar results as those reported in Section 3 if the delta kick is replaced by a piecewise quench applied successively to and the other terms of within each driving period. With a sinusoidal driving field, much fewer Floquet zero and Majorana corner modes and more restricted patterns of topological phase transitions are expected in our system, similar to what has been identified before, in Ref. [73]. Meanwhile, in the presence of two sinusoidal drivings with different frequencies, there are still opportunities to find rich Floquet phases with many topological boundary states and multiple topological transitions [93]. It is, thus, interesting to consider the Floquet engineering of SOTSC phases by multi-frequency harmonic driving fields in future studies.
In our system, we numerically checked that when the time-periodic delta kicking is applied to the hopping amplitude J instead of the pairing amplitude , similar results could be obtained as those reported in Section 3. That is, we can now find many Floquet Majorana zero and corner modes together with multiple topological phase transitions with the increase in when J is kicked. Interestingly, substantial differences were observed with the periodic delta kicking applied to the pairing versus hopping amplitudes in the chaotic dynamics of interacting Floquet models [94]. Therefore, the signature of quantum chaos in many-body Floquet SOTSC systems under different kicking protocols deserves to be revealed in future studies.
The effects of disorder and boundary confinements form major challenges in the experimental study of Majorana bound states in topological superconductors [95,96]. In the present work, we focus on the theoretical possibility of generating many Majorana zero/ corner modes and multiple topological phase transitions with the help of Floquet driving fields. For completeness, we also numerically checked the effects of disorder on Majorana corner modes for the different cases considered in Section 3. We found that for Cases 1–3, the Floquet Majorana corner modes are robust to disorder in the forms of , , and . Here, , , , and vary randomly in space over different sites and bonds. The values for each of them are taken separately from a uniform distribution with the range (we take in our numerical calculations). Note that these forms of disorder do not break the chiral symmetry of the model. The many Floquet Majorana corner modes in our system are found to be well-localized around the corners as long as they are well-separated in quasienergies from the other bulk or edge states in the presence of disorder. In Case 4, the four Majorana zero/ corner modes are further found to be robust to weak disorder in the form of , where varies over bonds along the y-direction and taking values randomly in a uniform distribution with the range . Other forms of disorder and boundary confinements may also change the fate of Majorana corner modes in our system, which deserves to be investigated more thoroughly in a potential future work.
Finally, it would be interesting to explore the engineering of Floquet SOTSC phases in other symmetry classes, in higher spatial dimensions and with many-body interactions. The application of the multiple Floquet zero/ Majorana corner modes found here to different quantum computing protocols also deserves to be investigated in detail.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 11905211, 12275260), the Young Talents Project at Ocean University of China (Grant No. 861801013196), and the Applied Research Project of Postdoctoral Fellows in Qingdao (Grant No. 861905040009).
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Cayssol, J.; Dóra, B.; Simon, F.; Moessner, R. Floquet topological insulators. Phys. Status Solidi RRL 2013, 7, 101. [Google Scholar] [CrossRef]
- Eckardt, A. Colloquium: Atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 2017, 89, 011004. [Google Scholar] [CrossRef]
- Harper, F.; Roy, R.; Rudner, M.S.; Sondhi, S. Topology and Broken Symmetry in Floquet Systems. Annu. Rev. Condens. Matter Phys. 2020, 11, 345. [Google Scholar] [CrossRef]
- Rudner, M.; Lindner, N. Band structure engineering and non-equilibrium dynamics in Floquet topological insulators. Nat. Rev. Phys. 2020, 2, 229. [Google Scholar] [CrossRef]
- Nathan, F.; Rudner, M.S. Topological singularities and the general classification of Floquet-Bloch systems. New J. Phys. 2015, 17, 125014. [Google Scholar] [CrossRef]
- Potter, A.C.; Morimoto, T.; Vishwanath, A. Classification of Interacting Topological Floquet Phases in One Dimension. Phys. Rev. X 2016, 6, 041001. [Google Scholar] [CrossRef]
- Roy, R.; Harper, F. Periodic table for Floquet topological insulators. Phys. Rev. B 2017, 96, 155118. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, R.-X.; Song, Z.-D. Dynamical symmetry indicators for Floquet crystals. Nat. Commun. 2021, 12, 5985. [Google Scholar] [CrossRef] [PubMed]
- Rudner, M.S.; Lindner, N.H.; Berg, E.; Levin, M. Anomalous Edge States and the Bulk-Edge Correspondence for Periodically Driven Two-Dimensional Systems. Phys. Rev. X 2013, 3, 031005. [Google Scholar] [CrossRef]
- Titum, P.; Berg, E.; Rudner, M.S.; Refael, G.; Lindner, N. Anomalous Floquet-Anderson Insulator as a Nonadiabatic Quantized Charge Pump. Phys. Rev. X 2016, 6, 021013. [Google Scholar] [CrossRef]
- Zhou, L.; Gong, J. Recipe for creating an arbitrary number of Floquet chiral edge states. Phys. Rev. B 2018, 97, 245430. [Google Scholar] [CrossRef]
- Zhang, Z.; Delplace, P.; Fleury, R. Superior robustness of anomalous non-reciprocal topological edge states. Nature 2021, 598, 293–297. [Google Scholar] [CrossRef] [PubMed]
- Ho, D.Y.H.; Gong, J. Quantized Adiabatic Transport In Momentum Space. Phys. Rev. Lett. 2012, 109, 010601. [Google Scholar] [CrossRef]
- Tong, Q.-J.; An, J.-H.; Gong, J.; Luo, H.-G.; Oh, C.H. Generating many Majorana modes via periodic driving: A superconductor model. Phys. Rev. B 2013, 87, 201109. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, H.; Ho, D.Y.H.; Gong, J. Aspects of Floquet bands and topological phase transitions in a continuously driven superlattice. Eur. Phys. J. B 2014, 87, 204. [Google Scholar] [CrossRef]
- Li, Z.-Z.; Lam, C.-H.; You, J.Q. Floquet engineering of long-range p-wave superconductivity: Beyond the high-frequency limit. Phys. Rev. B 2017, 96, 155438. [Google Scholar] [CrossRef]
- Zhou, L.; Gong, J. Floquet topological phases in a spin-1/2 double kicked rotor. Phys. Rev. A 2018, 97, 063603. [Google Scholar] [CrossRef]
- Wang, Y.H.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Observation of Floquet-Bloch States on the Surface of a Topological Insulator. Science 2013, 342, 453–457. [Google Scholar] [CrossRef]
- Yang, K.; Zhou, L.; Ma, W.; Kong, X.; Wang, P.; Qin, X.; Rong, X.; Wang, Y.; Shi, F.; Gong, J.; et al. Floquet dynamical quantum phase transitions. Phys. Rev. B 2019, 100, 085308. [Google Scholar] [CrossRef]
- McIver, J.W.; Schulte, B.; Stein, F.-U.; Matsuyama, T.; Jotzu, G.; Meier, G.; Cavalleri, A. Light-induced anomalous Hall effect in graphene. Nat. Phys. 2020, 16, 38–41. [Google Scholar] [CrossRef]
- Chen, B.; Li, S.; Hou, X.; Ge, F.; Zhou, F.; Qian, P.; Mei, F.; Jia, S.; Xu, N.; Shen, H. Digital quantum simulation of Floquet topological phases with a solid-state quantum simulator. Photon. Res. 2021, 9, 81–87. [Google Scholar] [CrossRef]
- Jotzu, G.; Messer, M.; Desbuquois, R.; Lebrat, M.; Uehlinger, T.; Greif, D.; Esslinger, T. Experimental realization of the topological Haldane model with ultracold fermions. Nature 2014, 515, 237–240. [Google Scholar] [CrossRef] [PubMed]
- Fläschner, N.; Rem, B.S.; Tarnowski, M.; Vogel, D.; Lühmann, K.; Sengstock, K.; Weitenberg, C. Experimental reconstruction of the Berry curvature in a Floquet Bloch band. Science 2016, 352, 1091–1094. [Google Scholar] [CrossRef]
- Asteria, L.; Tran, D.T.; Ozawa, T.; Tarnowski, M.; Rem, B.S.; Fläschner, N.; Sengstock, K.; Goldman, N.; Weitenberg, C. Measuring quantized circular dichroism in ultracold topological matter. Nat. Phys. 2019, 15, 449–454. [Google Scholar] [CrossRef]
- Wintersperger, K.; Braun, C.; Ünal, F.N.; Eckardt, A.; Liberto, M.D.; Goldman, N.; Bloch, I.; Aidelsburger, M. Realization of an anomalous Floquet topological system with ultracold atoms. Nat. Phys. 2020, 16, 1058–1063. [Google Scholar] [CrossRef]
- Kitagawa, T.; Broome, M.A.; Fedrizzi, A.; Rudner, M.S.; Berg, E.; Kassal, I.; Aspuru-Guzik, A.; Demler, E.; White, A.G. Observation of topologically protected bound states in photonic quantum walks. Nat. Commun. 2012, 3, 882. [Google Scholar] [CrossRef] [PubMed]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Pillay, J.C.; Wu, K.; Pasek, M.; Shum, P.P.; Chong, Y.D. Measurement of a Topological Edge Invariant in a Microwave Network. Phys. Rev. X 2015, 5, 011012. [Google Scholar] [CrossRef]
- Mukherjee, S.; Spracklen, A.; Valiente, M.; Andersson, E.; Öhberg, P.; Goldman, N.; Thomson, R.R. Experimental observation of anomalous topological edge modes in a slowly driven photonic lattice. Nat. Commun. 2017, 8, 13918. [Google Scholar] [CrossRef]
- Oka, T.; Kitamura, S. Floquet Engineering of Quantum Materials. Annu. Rev. Condens. Matter Phys. 2019, 10, 387–408. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Gong, J. Simulation of Non-Abelian Braiding in Majorana Time Crystals. Phys. Rev. Lett. 2018, 120, 230405. [Google Scholar] [CrossRef]
- Sitte, M.; Rosch, A.; Altman, E.; Fritz, L. Topological Insulators in Magnetic Fields: Quantum Hall Effect and Edge Channels with a Nonquantized θ Term. Phys. Rev. Lett. 2012, 108, 126807. [Google Scholar] [CrossRef]
- Zhang, F.; Kane, C.L.; Mele, E.J. Surface State Magnetization and Chiral Edge States on Topological Insulators. Phys. Rev. Lett. 2013, 110, 046404. [Google Scholar] [CrossRef] [PubMed]
- Slager, R.-J.; Rademaker, L.; Zaanen, J.; Balents, L. Impurity-bound states and Green’s function zeros as local signatures of topology. Phys. Rev. B 2015, 92, 085126. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Quantized electric multipole insulators. Science 2017, 357, 61–66. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 2017, 96, 245115. [Google Scholar] [CrossRef]
- Langbehn, J.; Peng, Y.; Trifunovic, L.; von Oppen, F.; Brouwer, P.W. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 2017, 119, 246401. [Google Scholar] [CrossRef]
- Song, Z.; Fang, Z.; Fang, C. (d − 2)-Dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 2017, 119, 246402. [Google Scholar] [CrossRef]
- Schindler, F.; Cook, A.M.; Vergniory, M.G.; Wang, Z.; Parkin, S.S.P.; Bernevig, B.A.; Neupert, T. Higher-order topological insulators. Sci. Adv. 2018, 4, eaat0346. [Google Scholar] [CrossRef]
- Geier, M.; Trifunovic, L.; Hoskam, M.; Brouwer, P.W. Second-order topological insulators and superconductors with an order-two crystalline symmetry. Phys. Rev. B 2018, 97, 205135. [Google Scholar] [CrossRef]
- Kim, M.; Jacob, Z.; Rho, J. Recent advances in 2D, 3D and higher-order topological photonics. Light Sci. Appl. 2020, 9, 130. [Google Scholar] [CrossRef]
- Schindler, F. Dirac equation perspective on higher-order topological insulators. J. Appl. Phys. 2020, 128, 221102. [Google Scholar] [CrossRef]
- Trifunovic, L.; Brouwer, P.W. Higher-Order Topological Band Structures. Phys. Status Solidi B 2021, 258, 2000090. [Google Scholar] [CrossRef]
- Xie, B.; Wang, H.-X.; Zhang, X.; Zhan, P.; Jiang, J.-H.; Lu, M.; Chen, Y. Higher-order band topology. Nat. Rev. Phys. 2021, 3, 520–532. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Zhou, L.; Pan, J.; Gong, J. Coupled-wire construction of static and Floquet second-order topological insulators. Phys. Rev. B 2019, 99, 045441. [Google Scholar] [CrossRef]
- Seshadri, R.; Dutta, A.; Sen, D. Generating a second-order topological insulator with multiple corner states by periodic driving. Phys. Rev. B 2019, 100, 115403. [Google Scholar] [CrossRef]
- Peng, Y.; Refael, G. Floquet Second-Order Topological Insulators from Nonsymmorphic Space-Time Symmetries. Phys. Rev. Lett. 2019, 123, 016806. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Vega, M.; Kumar, A.; Seradjeh, B. Higher-order Floquet topological phases with corner and bulk bound states. Phys. Rev. B 2019, 100, 085138. [Google Scholar] [CrossRef]
- Nag, T.; Juričić, V.; Roy, B. Out of equilibrium higher-order topological insulator: Floquet engineering and quench dynamics. Phys. Rev. Res. 2019, 1, 032045. [Google Scholar] [CrossRef]
- Huang, B.; Liu, W.V. Floquet Higher-Order Topological Insulators with Anomalous Dynamical Polarization. Phys. Rev. Lett. 2020, 124, 216601. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Huang, B.; Zhao, E.; Liu, W.V. Dynamical Singularities of Floquet Higher-Order Topological Insulators. Phys. Rev. Lett. 2020, 124, 057001. [Google Scholar] [CrossRef]
- Pan, J.; Zhou, L. Non-Hermitian Floquet second order topological insulators in periodically quenched lattices. Phys. Rev. B 2020, 102, 094305. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Paul, G.C.; Saha, A. Higher order topological insulator via periodic driving. Phys. Rev. B 2020, 101, 235403. [Google Scholar] [CrossRef]
- Meng, Y.; Chen, G.; Jia, S. Second-order topological insulator in a coinless discrete-time quantum walk. Phys. Rev. A 2020, 102, 012203. [Google Scholar] [CrossRef]
- Zhu, W.; Chong, Y.D.; Gong, J. Floquet higher-order topological insulator in a periodically driven bipartite lattice. Phys. Rev. B 2021, 103, L041402. [Google Scholar] [CrossRef]
- Bhat, R.V.; Bera, S. Out of equilibrium chiral higher order topological insulator on a π-flux square lattice. J. Phys. Condens. Matter 2021, 33, 164005. [Google Scholar] [CrossRef]
- Franca, S.; Hassler, F.; Fulga, I.C. Simulating Floquet topological phases in static systems. SciPost Phys. Core 2021, 4, 007. [Google Scholar] [CrossRef]
- Zhang, R.-X.; Yang, Z.-C. Tunable fragile topology in Floquet systems. Phys. Rev. B 2021, 103, L121115. [Google Scholar] [CrossRef]
- Zhu, W.; Chong, Y.D.; Gong, J. Symmetry analysis of anomalous Floquet topological phases. Phys. Rev. B 2021, 104, L020302. [Google Scholar] [CrossRef]
- Zhou, L. Floquet Second-Order Topological Phases in Momentum Space. Nanomaterials 2021, 11, 1170. [Google Scholar] [CrossRef]
- Zhu, W.; Xue, H.; Gong, J.; Chong, Y.; Zhang, B. Time-periodic corner states from Floquet higher-order topology. Nat. Commun. 2022, 13, 11. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; He, L.; Lu, J.; Mele, E.J.; Zhen, B. Floquet Quadrupole Photonic Crystals Protected by Space-Time Symmetry. Phys. Rev. Lett. 2022, 129, 063902. [Google Scholar] [CrossRef]
- Franca, S.; Hassler, F.; Fulga, I.C. Topological reflection matrix. Phys. Rev. B 2022, 105, 155121. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Nag, T.; Saha, A. Systematic generation of the cascade of anomalous dynamical first- and higher-order modes in Floquet topological insulators. Phys. Rev. B 2022, 105, 115418. [Google Scholar] [CrossRef]
- Ning, Z.; Fu, B.; Xu, D.-H.; Wang, R. Tailoring quadrupole topological insulators with periodic driving and disorder. Phys. Rev. B 2022, 105, L201114. [Google Scholar] [CrossRef]
- Lei, Y.; Luo, X.-W.; Zhang, S. Second-order topological insulator in periodically driven optical lattices. Opt. Express 2022, 30, 24048–24061. [Google Scholar] [CrossRef]
- Huang, B.; Novičenko, V.; Eckardt, A.; Juzeliūnas, G. Floquet chiral hinge modes and their interplay with Weyl physics in a three-dimensional lattice. Phys. Rev. B 2021, 104, 104312. [Google Scholar] [CrossRef]
- Wang, B.-Q.; Wu, H.; An, J.-H. Engineering exotic second-order topological semimetals by periodic driving. Phys. Rev. B 2021, 104, 205117. [Google Scholar] [CrossRef]
- Zhu, W.; Umer, M.; Gong, J. Floquet higher-order Weyl and nexus semimetals. Phys. Rev. Res. 2021, 3, L032026. [Google Scholar] [CrossRef]
- Ghosh, S.; Saha, K.; Sengupta, K. Hinge-mode dynamics of periodically driven higher-order Weyl semimetals. Phys. Rev. B 2022, 105, 224312. [Google Scholar] [CrossRef]
- Du, X.-L.; Chen, R.; Wang, R.; Xu, D.-H. Weyl nodes with higher-order topology in an optically driven nodal-line semimetal. Phys. Rev. B 2022, 105, L081102. [Google Scholar] [CrossRef]
- Plekhanov, K.; Thakurathi, M.; Loss, D.; Klinovaja, J. Floquet second-order topological superconductor driven via ferromagnetic resonance. Phys. Rev. Res. 2019, 1, 032013. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Gong, J. Measurement-only quantum computation with Floquet Majorana corner modes. Phys. Rev. B 2020, 101, 085401. [Google Scholar] [CrossRef]
- Bomantara, R.W. Time-induced second-order topological superconductors. Phys. Rev. Res. 2020, 2, 033495. [Google Scholar] [CrossRef]
- Peng, Y. Floquet higher-order topological insulators and superconductors with space-time symmetries. Phys. Rev. Res. 2020, 2, 013124. [Google Scholar] [CrossRef]
- Chaudhary, S.; Haim, A.; Peng, Y.; Refael, G. Phonon-induced Floquet topological phases protected by space-time symmetries. Phys. Rev. Res. 2020, 2, 043431. [Google Scholar] [CrossRef]
- Vu, D.; Zhang, R.-X.; Yang, Z.-C.; Sarma, S.D. Superconductors with anomalous Floquet higher-order topology. Phys. Rev. B 2021, 104, L140502. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Nag, T.; Saha, A. Floquet generation of a second-order topological superconductor. Phys. Rev. B 2021, 103, 045424. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Nag, T.; Saha, A. Floquet second order topological superconductor based on unconventional pairing. Phys. Rev. B 2021, 103, 085413. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Nag, T.; Saha, A. Dynamical construction of quadrupolar and octupolar topological superconductors. Phys. Rev. B 2022, 105, 155406. [Google Scholar] [CrossRef]
- Liu, F.; Wakabayashi, K. Novel Topological Phase with a Zero Berry Curvature. Phys. Rev. Lett. 2017, 118, 076803. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.-B.; Li, K.; Duan, L.-M.; Xu, Y. Type-II quadrupole topological insulators. Phys. Rev. Res. 2020, 2, 033029. [Google Scholar] [CrossRef]
- Ezawa, M. Edge-corner correspondence: Boundary-obstructed topological phases with chiral symmetry. Phys. Rev. B 2020, 102, 121405. [Google Scholar] [CrossRef]
- Asaga, K.; Fukui, T. Boundary-obstructed topological phases of a massive Dirac fermion in a magnetic field. Phys. Rev. B 2020, 102, 155102. [Google Scholar] [CrossRef]
- Li, C.-A.; Fu, B.; Hu, Z.-A.; Li, J.; Shen, S.-Q. Topological Phase Transitions in Disordered Electric Quadrupole Insulators. Phys. Rev. Lett. 2020, 125, 166801. [Google Scholar] [CrossRef]
- Khalaf, E.; Benalcazar, W.A.; Hughes, T.L.; Queiroz, R. Boundary-obstructed topological phases. Phys. Rev. Res. 2021, 3, 013239. [Google Scholar] [CrossRef]
- Jia, W.; Zhou, X.-C.; Zhang, L.; Zhang, L.; Liu, X.-J. Unified characterization for higher-order topological phase transitions. arXiv 2022, arXiv:2209.10394. [Google Scholar]
- Zhou, L. Non-Hermitian Floquet topological superconductors with multiple Majorana edge modes. Phys. Rev. B 2020, 101, 014306. [Google Scholar] [CrossRef]
- Asbóth, J.K.; Obuse, H. Bulk-boundary correspondence for chiral symmetric quantum walks. Phys. Rev. B 2013, 88, 121406. [Google Scholar] [CrossRef]
- Asbóth, J.K.; Tarasinski, B.; Delplace, P. Chiral symmetry and bulk-boundary correspondence in periodically driven one-dimensional systems. Phys. Rev. B 2014, 90, 125143. [Google Scholar] [CrossRef]
- Ho, D.Y.H.; Gong, J. Topological effects in chiral symmetric driven systems. Phys. Rev. B 2014, 90, 195419. [Google Scholar] [CrossRef]
- Zhou, L.; Du, Q. Floquet topological phases with fourfold-degenerate edge modes in a driven spin-1/2 Creutz ladder. Phys. Rev. A 2020, 101, 033607. [Google Scholar] [CrossRef]
- Liu, X.; Tan, S.; Wang, Q.-h.; Zhou, L.; Gong, J. Floquet band engineering with Bloch oscillations. arXiv 2022, arXiv:2208.05260. [Google Scholar]
- Roy, D.; Prosen, T. Random matrix spectral form factor in kicked interacting fermionic chains. Phys. Rev. E 2020, 102, 060202. [Google Scholar] [CrossRef]
- Kells, G.; Meidan, D.; Brouwer, P.W. Near-zero-energy end states in topologically trivial spin-orbit coupled superconducting nanowires with a smooth confinement. Phys. Rev. B 2012, 86, 100503. [Google Scholar] [CrossRef]
- Roy, D.; Bondyopadhaya, N.; Tewari, S. Topologically trivial zero-bias conductance peak in semiconductor Majorana wires from boundary effects. Phys. Rev. B 2013, 88, 020502. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).