Abstract
In this article, we present an overview of the application of X-ray self-emission methods for the imaging of hydrodynamic astrophysical phenomena in laboratory-scale experiments. Typical diagnostic approaches, their advantages, drawbacks, and application perspectives are considered. We show that X-ray imaging and spectroscopy methods with 2D and even 1D spatial resolution are valuable for numerous laboratory astrophysical problems. Furthermore, the methods revealed the hydrodynamic evolution, the spatial shape and structure, and spatial features of important parameters such as electron density and plasma temperature of astrophysical objects and related phenomena, which are also required for the verification of astrophysical models.
1. Introduction
The idea of using lasers to create high-temperature plasma was first publicly pro-posed by N.G. Basov in 1961 at a meeting of the Presidium of the Academy of Sciences of the USSR; it was theoretically substantiated in 1964 [1]. The work [1] caused a worldwide sensation and laid the foundation for a new field, inertial thermonuclear fusion. As part of this field, huge facilities with pulsed high-power lasers were built in the Russian Federation, the USA, Japan, England, France, and Germany.
Although Basov’s research was concerned with the generation of plasma primarily for a controlled thermonuclear reaction, its fundamental and applied significance proved immeasurably more far-reaching. From a fundamental point of view, it generated the possibility of creating a laboratory object with well-controlled parameters and ultra-high energy density to study the physical processes taking place within. From an applied point of view, it led to the creation of powerful sources of coherent (X-ray laser) and thermal radiation that became extremely useful in several scientific fields that are not directly related. One example is X-ray spectroscopy of multiply charged ions, which is both experimentally and theoretically important. For experimentalists, laser plasma has become an object where ions with a very high ionization multiplicity can be obtained relatively easily. The good controllability of the parameters of the plasma also made it possible to perform fairly accurate spectral measurements. The results of these measurements made it possible to benchmark the results of theoretical calculations of the spectra of multiply charged ions, even in situations where relativistic effects, where the significance increases with ion charge, become very important.
Another good example is laboratory astrophysics, which allows the dynamics of short-lived plasmas to be studied experimentally in the laboratory and is scalable to the long-lived astrophysical objects. It turned out that the plasma generated by high-power lasers is extremely suitable for the experimental modelling of various astrophysical phenomena under laboratory conditions (see e.g., [2,3,4,5,6]). Thus, N.G. Basov’s proposal has indeed played a crucial role in the emergence of this field of research, although not intended.
Laboratory astrophysics started at the beginning of the 20th century with the work of Kristian Birkeland in the so-called “Terrella experiments” [7] and became more widespread only recently after the work of Ryutov, Falize, and Podgorny/Sagdeev [8,9,10]. Observations of astrophysical plasma objects only provide information about the current state of the object, which has slowly evolved over millions of years. This means that researchers have no experimental material describing the dynamics of such objects. Even data obtained over 10 years refers to almost the same moment in time in the evolution of most astrophysical objects. Therefore, until recently, our understanding of many astrophysical processes depended exclusively on computer simulations. Verification of the adequacy of such simulations could only be based on a comparison of theoretical and experimental results obtained for a single temporal point.
The aim of the emerging research field was to generate complex dynamical phenomena to study hydrodynamic mixing, supersonic plasma flows, shock wave physics, radiative hydrodynamics, plasma photoionization, etc. All these processes contribute to the understanding of the physics associated with a variety of astrophysical objects and phenomena, including protostars and active galactic nuclei, supernova explosions, the successive formation of molecular cloud remnants, instabilities, the formation of accretion columns in astrophysical systems, etc. The questions of scaling between laboratory and astrophysical plasmas and the applicability of this method are considered in detail in the following papers [8,9,10,11,12]. It should be noted that other configurations can be used for laboratory modelling [11], e.g., powerful Z-pulsed facilities [13,14,15] and spheromak-like jets [16,17]. However, the role and contribution of laser-induced plasma in this research field is most significant.
For the quantitative and qualitative analysis of astrophysical processes, it is therefore crucial to determine the dynamics and parameters of the laboratory plasma, which requires the use of different imaging techniques with high spatial resolution, a suitable field of view, and within a certain energy range. Research in the X-ray range is extremely important as it helps to reveal the emission parameters in the high-energy part of the spectrum, which is used to determine the dynamics and parameters of the object when optical methods are not applicable, and also to determine the plasma structure and ionization composition [18]. In this case, it is not always possible to use radiographic methods, i.e., methods with a backlighting illumination source, due to the limitations of the setup or the geometry of the plasma formation in the experiment.
Therefore, in this review, we focus on the methods for visualizing and determining the parameters of astrophysically-relevant objects modelled with laser-generated plasma in the laboratory. First, we will look at the methods of X-ray self-emission imaging used in laser plasma experiments (Section 2), then show the results of some of these methods in laboratory astrophysics (Section 3), and finally discuss their advantages/drawbacks and perspective applications (Section 3 and Section 4).
2. Basic Aspects of Laser-Induced Plasma X-ray Imaging
In general, self-emission imaging of laboratory plasma can be carried out in the following two ways: with the use of dispersive optical elements (for example, crystals, gratings, mirrors) and without them, when emission without reflection and refraction hits the detector, as, for example, in a pinhole camera.
2.1. Imaging of Laboratory Plasma without the Use of Dispersive Elements
In a pinhole camera, an optical image occurs when light from an object passes through a small hole and creates an inverted image on the detector (Figure 1a). Temporal resolution can be achieved if applied to detectors with a fast shutter. For X-ray imaging in a specific spectral range, the self-emission from the object is typically filtered using a simple filter system with the desired bandwidth. It is not always sufficient due to the low flexibility of the filter used or the presence of a high-energy tail in the distribution of hot particles on the detector. A detector that responds only to X-ray photons can also be used. The numerical magnification and geometric spatial resolution of the pinhole camera are shown below [19,20]:
where is the distance from the object to the hole, is the distance from the image to the pinhole, and is the size of the hole. Thus, the spatial resolution is very close to the hole size itself at sufficiently high magnifications. When using optical schemes with a magnification less than 1, the hole size must be significantly smaller than the source size so that the resolution of the entire system is less than the image size.
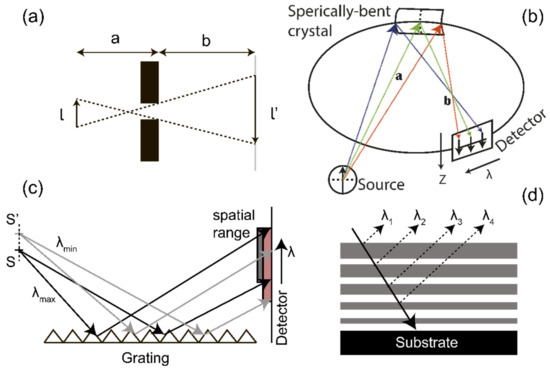
Figure 1.
Optical schemes showing basic methods of X-ray emission imaging. (a) Pinhole camera. (b) Construction of spectrally selected images based on spherically curved crystals. (c) Schematic of imaging with reflective diffraction gratings. (d) Multilayer mirror with a variable coating thickness [25]. The figure (c) shows that the vertical size of the source, without being limited by a special horizontal slit or a pinhole, leads to strong smearing of the spectral data.
It is worth noting that the pinhole camera cannot provide extremely high image sharpness, which is usually determined by a combination of spatial resolution and image contrast. When the pinhole diameter is reduced, sharpness increases up to a certain limit, and when it is reduced too much, the effects of light diffraction at the pinhole occur, making the image less sharp [19]:
where is the wavelength and is the resolution limit due to diffraction.
In laboratory astrophysical experiments, however, quite large plasma structures with a spatial scale of approximately 1 mm are often studied [21,22,23], and so a resolution of the order of tens of microns is typically required. In this case, for a wavelength of approximately 10 Å and a distance to the object of approximately 50 cm, Equation (2) gives a spatial resolution of ~20 µm, which satisfies the above requirements. Moreover, the actual spatial resolution is often limited by the size of the detector pixel. For example, conventional fluorescence image plate type detectors provide a spatial resolution of 25 µm at best, which is defined by resolution of the scanning system [24].
According to Formula (2), it makes no sense to use a pinhole with a size smaller than the diffraction limit. However, in this mode, the pinhole camera can register X-ray images without applying additional filters in the optical and ultraviolet ranges. It is also worth mentioning that pinhole cameras are difficult to use when the target is irradiated with high-power laser pulses due to the strong background in the hard X-ray range [26]. In this case, combined methods can be implemented by using auxiliary X-ray optics, such as mirrors or crystals.
Thus, using a pinhole camera and the necessary detecting devices (image plate, streak-camera, X-ray film, etc.), it is possible to register X-ray images in a wide range of energies. However, due to the absence of the photon energy dispersion, it is impossible to determine spectrally dependent parameters of the object under investigation. Currently, one of the most effective methods for diagnosing high-temperature plasma is the spatially resolved X-ray spectroscopy of the emission of multiply charged ions that provided not only spatial characteristics, but also spectral characteristics, of objects using various dispersive elements in the path of X-ray emission from the object. This makes it possible to measure important spatial profiles of plasma parameters, such as electron temperature, density, emissivity, etc.
Therefore, at present, the solution for the most urgent problem in X-ray spectral studies of high-temperature dense plasma is based on increasing the luminosity and spectral resolution of diagnostics, as well as on creating the new types of imaging spectroscopy devices, which, at a reasonable luminosity, simultaneously have a high spectral and spatial resolution.
2.2. Imaging Using Dispersing Elements
Of the multitude of spectral devices for the wavelength range of 1–20 Å, in principle, only spectrographs with a crystal dispersive element can provide the required spectral resolution in the experiment. Application of flat crystals is the conventional and simplest technique for studying the spectral and spatial properties of plasma objects. Together with the Bragg selectivity of the crystals, spatial resolution is easily achieved here by the insertion of a narrow slit lying in a plane perpendicular to the direction of dispersion. The main disadvantage of this scheme is that the spatial resolution depends on the size of the slit and the spectral resolution depends strongly on the size of the source [27]. To improve the spectral resolution, the distance between the crystal and the detector must be increased, and it is desirable to work with small Bragg angles that are close to zero. This leads firstly to an increase in the width of the rocking curve of the crystal, which worsens the spectral resolution, and secondly, the luminosity decreases since it is inversely proportional to the square of the total distance between source–crystal–registration plane. Alternatively, if the cylindrical profile of crystals is used as defocusing spectrographs [28], the spectral range of the measured emission lies in the entire wavelength range from to . However, due to the increased divergence of the emission when reflected from a convex surface and the rather small aperture used, in practice, defocusing spectrographs can only be used to study high intensity X-ray sources. For astrophysical laboratory objects, the intensity of the self-emission is usually not strong enough, so dispersive elements and measurement schemes with higher luminosity are desired [29,30].
The use of cylindrical crystals as dispersive elements in a mode where the emission is reflected from the inner concave surface of the crystal, such as in the schemes of Von Hamos, Johann, and Cauchois, has significantly increased the luminosity of the technique [31,32]. In this case, the crystal surface, similar to a conventional cylindrical mirror, focuses the reflected emission in the plane of curvature, which increases its intensity in the image plane. However, this system also has serious disadvantages. It is very sensitive to misalignment; if one moves the source away from the axis of the cylinder, this leads to a shift out of focus and a loss of resolving power. A slight disorientation of the registration plane relative to the axis of the cylinder leads to blurring and distortion of the spectral lines, resulting in large errors in the measurement of their wavelengths and intensities. Moreover, the spectral resolution is still inversely proportional to the size of the source, and such spectrometers based on cylindrical or flat crystals require the additional use of slits to achieve the required spatial resolution in the sagittal direction. In terms of geometrical optics, the dispersion plane or the plane containing the Rowland circle is the meridional plane and the plane perpendicular to the plane of the Rowland circle is the sagittal plane.
In the mid-1990s, in connection with the development of a high-quality bending technique for spherical surfaces of crystals of sufficient size and with radii of curvature down to 80 mm, it became possible to develop a new type of X-ray spectrograph that has not only dispersive but also focusing properties [33]. The design was called “Focusing Spectrometer with Spatial Resolution” (FSSR) and it typically uses spherically bent crystals with radii of curvature R = 100–500 mm in laser-plasma experiments (e.g., [34,35,36,37]). In addition to measuring the spectral composition of the emission, it is possible to obtain images of plasma objects in different spectral lines or narrow ranges. The main advantage over traditionally used devices is the high luminosity combined with a high spatial resolution (up to 10 µm), while maintaining the maximum possible spectral resolution for this dispersive element (up to ). The general features of this spectrograph are discussed below.
The formation of a spectrometric image on a detector using a spherically bent crystal (Figure 1b, FSSR) is based on both the properties of conventional geometrical optics and the use of Bragg diffraction for short wavelengths [38]. The properties of the recorded images are determined by the initial parameters of the scheme: type of crystal (material and lattice parameters) and its radius of curvature; distances between the source and the crystal, as well as between the crystal and the detector; relative angular position between the crystal and the detector; etc. When reflecting with a crystal for a given Bragg angle, the initial condition for the point-like source must satisfy the following equation:
where is the interplane distance for the crystal lattice, is the Bragg angle, is the wavelength, and is the order of reflection. In practice, this equation is valid near a certain angle, considering the rocking curve of the crystal. An important parameter is usually the central wavelength, i.e., the wavelength that, in Equation (3), corresponds to the angle at which the beam from the source hits the center of the spherical surface of the crystal. At the same time, the central wavelength does not correspond to the center of the image due to the non-linearity of the dispersion curve. The Young–Abbe equations, which describe the propagation of elementary beams when reflected from a spherical mirror, have the following form for the sagittal plane:
and for the meridional plane:
where is the distance from the source to the center of the crystal, is the angle of incidence, is the radius of curvature of the crystal, and and are the distances from the crystal to the sagittal and meridional planes of the image [39].
The dispersion scheme when the detector is on the Rowland circle is shown in Figure 1b. In this special case, the position of the detector must correspond to the position of the sagittal focus for central beams. According to the properties of the Rowland circle, the spectral resolution in the measured image does not depend on the size of the source. With such a scheme, it is therefore possible to obtain spectrally resolved images with one-dimensional resolution. If the detector is moved away from the Rowland circle and at the same time the condition (4) for the distances and is maintained, the image becomes two-dimensional. The magnification (for 1D and 2D schemes) in the sagittal plane is defined by the following equation, as for the usual optical scheme:
For a scheme with one-dimensional resolution, the relation is satisfied, where is the angle of incidence for the central wavelength. This leads to the definition of the distance between the source and the crystal as follows:
For a 2D scheme with a given central wavelength λ0 and the required linear magnification in the sagittal plane :
The linear magnification in the meridional plane is equal to the ratio of the distance between the Rowland circle and the plane of registration to the distance from the source to the Rowland circle. With the help of Equation (8) and the knowledge that the distance from the crystal to the Rowland circle is R cosφ0, one can easily find out:
It follows from Equations (6) and (9) that and an anamorphic image is formed in the image plane of the 2D scheme. In most practical cases, the coefficient of anamorphosis is . If the distance between the object and the center of the crystal is equal to twice the sagittal focal length ( then both magnifications are equal to one: . Note, schemes based on spherically-bent crystals can also be used to visualize X-ray images in a rather narrow spectral range if the detector is placed in the meridional plane of the image or even between the sagittal and meridional planes [39].
Thus, with a certain relative position of the crystal and the detector, systems based on spherically-bent crystals can be used both as a conventional imager with two spatial axes and as an excellent instrument for measuring plasma profiles of parameters due to the high spectral resolution and luminosity. Limitations of the applicability of these spectrographs include the inability to operate with wavelengths 30 Å.
In addition to spherically-bent crystals, systems with toroidal crystals are also worth mentioning [40,41], which are also characterized by high luminosity and spatial resolution. With unequal radii of curvature, toroidal crystals can be made astigmatism-free, so that any Bragg angle can be chosen, even in the 1D scheme, for which there is a limitation in spectrometers with a spherically curved crystal (FSSR in 1D geometry is used for a Bragg angle of more than 45°).
Visualization schemes based on diffraction gratings are similar to the ones based on crystals. The concept is shown schematically in Figure 1c for the concave reflecting grating. The reflecting grating consists of grooves superimposed on a reflecting surface, while the transmitting one is superimposed on a transparent surface. Basically, diffraction grating is a set of elements (reflective or transmissive, depending on the type) systematically divided by a distance comparable to the wavelength of light and where a spatial modulation of the refractive index is observed. Therefore, the use of a diffraction grating is limited from below, as it is currently not possible to produce gratings with elements divided by units of Angstrom. In diffraction, an electromagnetic wave incident on the grating changes the amplitude of its electric field and/or its phase in a predictable manner due to periodic changes in the refractive index near the grating surface. Spectral resolution is achieved by focusing the signal on a portion of the Rowland circle or plane when the grating is concave, taking aberrations into account.
The dispersion of the diffraction grating is given by a diffraction equation similar to the Bragg equation in the case of crystals as follows:
where is the diffraction order, and are the angles of incidence and diffraction, and is the nominal distance between the grating grooves. The distance to the image is determined by the geometric scheme. To improve spectral and spatial resolution, slits are often used here to limit the size of the source reflected from the grating surface. The spatial resolution is thus determined by the slit, as in a pinhole camera. The maximum achievable theoretical resolution is determined by the wavelength and the width of the grating [42]: . However, the spectral resolution depends not only on the parameters of the grating, but also on the size and position of the slit used, as well as on the detector and the source sizes. Thus, if there is no slit, the size of the plasma source strongly blurs the received signal (Figure 1c). After convolution, the typical spectral resolution is usually of the order of [43,44]. However, it is worth noting that the reflection efficiency and spectral range are quite high compared to crystals. An example of a spectrometer based on a reflective diffraction grating is the VSG spectrometer with a concave grating [45].
Application of X-ray mirrors is also a good method to obtain X-ray emission images. For the classical case of a near grazing incidence of the X-rays on the mirror, the refraction angle is close to 90 degrees, so that the refracted wave does not penetrate deeply but travels along the surface. In view of this, there is a critical angle , at which complete external reflection occurs [46]:
where β describes the absorption, n is the refractive index, and δ is a function of the electron density, the wavelength, and the scattering factor [46]. For the soft X-ray range, this usually means that only single-layer mirrors with an interface between the vacuum and the reflecting surface are used [47]. For hard X-rays, however, multilayer structures can also be used (Figure 1d), where the signal absorption is not as high [25].
Mirrors with a grazing angle of incidence can be used with typical reflection in the soft X-ray range up to 2–10 keV [48,49]. In particular, a 16-channel Kirkpatrick–Baez microscope [49,50] can be used, where each channel uses two orthogonal parabolic mirrors with a grazing angle of incidence. The first reflection focuses the signal into a line, which is then focused into a point by the second mirror. Therefore, X-rays can be focused with better spatial resolution and efficiency than with traditionally used pinhole cameras [49], which can be used in combination with gated cameras that take multiple frames at once. However, the spatial field of view of such a device is limited to a few hundred µm as the spatial resolution decreases rapidly with an increasing field of view due to the serious off-axis aberration. Therefore, construction of such a microscope is a rather complicated process as each mirror must be set to exactly the same field of view and certain ratios between the mirrors have to be maintained. In the mentioned project, the mirrors were cut to fit together in the shape of a perfect 16-sided polygon, i.e., a hexagon. In particular, modification of the ideal hexagonal arrangement of the mirrors is used [49], which allows the images to be shifted so that they fall on rectangular camera strips with fast framing. The focus is adjusted as follows:
where is the distance from the object to the mirror, is the distance from the image to the mirror, is the bending radius, and is the angle of incidence of the X-ray beam. The basic concept is to simultaneously move and tilt the mirror to maintain the focus state when the image position changes. Thus, a template of 16 images can be moved such that it is projected onto the cathode strips of a high-speed framing camera, which are normally spaced apart. It is worth noting that this geometry with X-ray optics at a grazing angle is not the only system; there are many systems based, for example, on Wolter or Montel mirrors, or optics such as the “lobster eye” [51,52,53], etc.
As mentioned before, the absorption in the deposition layers limits the final properties of a multilayer mirror. However, in the case of a multilayer structure [47], this allows reflection at angles greater than the critical angle of reflection of X-rays for that material. This concept is based on the structural interference of waves reflected from different media interfaces. Reflection from mirrors also obeys Bragg’s law, as in crystals (Formula (3)), using the period of the layer structure instead of the distance between the planes. Therefore, the thickness of the required deposition depends on the angle of incidence of the X-rays [47]. The typical thickness of such depositions is more than ~10 Å [54], which is due to the complexity of coating smooth atomic structures, limiting their use only to soft X-rays (except at grazing incidence angle). The reflection at the boundary between the deposited interfaces obeys the Fresnel equations, where the amplitudes of the reflected and refracted waves correspond to the incident wave. The spectral resolution depends on the quality of the deposited surface, or its flatness , and is significantly reduced at small wavelengths.
The spatial resolution of flat multilayer mirrors is determined by the size of the slit to be inserted. With a curved substrate, such as crystals, it is possible to work with spatial resolution without slits because of the shape of the surface; however, in this case, it becomes more difficult to achieve good surface quality.
Fresnel lenses, which can combine the properties of diffraction gratings and multilayer mirrors or crystals, should also be mentioned as optics used in experiments. For example, there are schemes for using multilayer transmissive gratings as well as for depositing grooves on crystals [33,55]. Mostly, such systems are used for active visualization with a backlight source; however, the use of spherically bent crystals makes it especially possible to use this approach for imaging self-emission spectra. The spatial resolution of the Bragg–Fresnel structure is determined by the width of the last zone and depends on the diffraction order . The distance between two resolved points in the radial direction is , and the resolution in the axial direction is proportional to [56]. Thus, the spatial resolution can be fractions of µm [57,58], which extends the application range of classical crystals and multilayer mirrors.
3. The Use of X-ray Images and Spectrograms with Spatial Resolution in Laboratory Astrophysical Plasma Research
In the last 10–15 years, the methods described above have been actively used in the study of astrophysical laboratory plasmas. In the following section, we give a number of examples of such recent studies, showing the possibilities and prospects of X-ray imaging methods for laboratory astrophysics.
3.1. Application of X-ray Pinhole Camera in Laboratory Astrophysics Experiments
Although the pinhole camera usually has relatively low spatial resolution for high energy density physics, the flexibility of laboratory scaling allows the use of this diagnostic device without obvious limitations due to scaling laws and the use of ~mm scale plasmas in many experiments. Here, we will mention only a few of them. The additional use of fast gated cameras makes it possible to obtain a time evolution of about 10–100 ns for a plasma object, which is particularly useful when optical methods are no longer available due to high density. In one study [59], for example, a four-frame X-ray pinhole camera was used to study the generation of a magnetic field and the magnetization of an astrophysical plasma. For this purpose, a laboratory experiment was conducted at the Prague Asterix Laser System (PALS, Prague, Czech Republic). The laser pulse (~1016 W/cm2) irradiated targets with a special shape in the form of a “snail” to generate a controlled spontaneous magnetic field. This approach is extremely interesting as it allows a high magnetic field strength to be maintained over a long period of time, while the resulting plasma structure is sufficiently stable and equilibrated.
A four-frame pinhole camera with an exposure time of about 1 ns and a delay of 3 ns between frames measured the extreme ultraviolet and soft X-ray region of the laser-induced plasma. The self-emission of the plasma was transferred to a microchannel plate (MCP) connected to a Nikon D600 digital camera at a magnification of ~4. This experimental geometry, including a pinhole diameter of 35 µm, resulted in a spatial resolution of approximately 45 µm. The MCP detector is sensitive to photons in the energy range 10-10,000 eV. The use of a 0.9 µm thick Mylar filter made it possible to cut off photons with an energy of less than 100 eV. The spatial and temporal resolution achieved made it possible to capture the self-emission of hot plasma (Figure 2a,b) in the X-ray region inside the ‘snail’ target and to register the moment when the plasma explodes in the center of the target. It was confirmed that the grazing incidence of the laser on a curved surface leads to a continuous reflection of the light along the inner wall of the target.
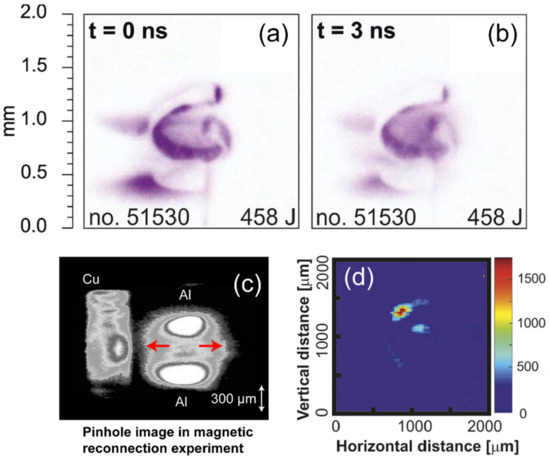
Figure 2.
(a,b) Images in the soft X-ray region taken with a four-frame pinhole camera [59] showing evolution of the self-emission of the snail-shaped target at 0 and 3 ns. (c) X-ray images on a pinhole camera with signal integration on the time for the magnetic reconnection experiment [60]. The red lines indicate the direction of the jet. (d) 2D image [59] taken with a spherically curved quartz crystal on an image plate and in a narrow spectral region near Cu Ka and for the same target as in figure (a,b).
For the experimental study of plasma jets with astrophysical similarity, the same approach was used in [61]. Although the pinhole camera does not provide photon intensity spectra, one of the channels of a fast gated camera can be used to filter a single frame and compare the signal with an unfiltered image. In one study [61], this approach was used to measure the electron temperature, which was Te = 50–150 eV in a jet and Te ≈ 150 eV in a copper plasma with shock heating. It should be noted, however, that such a measurement is not very reliable and is more of an estimate of the temperature from below since it is based on a rough estimate of the bremsstrahlung in a rather broad spectral range.
The experiment at the PALS facility used four elliptical pinholes for the X-ray pinhole camera, one of which was covered with 0.2 µm thick Fe foil. The pinhole images were projected onto a four-quadrant detector with a gold-plated microchannel plate (MCP) connected to a phosphor screen and was visualized with a Nikon D1X CCD digital camera. The exposure time was 2 ns and the adjustable intervals between quadrants were configured so that imaging occurred at three different times, two of which measured open and filtered emission simultaneously. The MCP was sensitive to photon energy in the range 10–1000 eV.
The experimental approach was based on a relatively simple method of generating supersonic jets using a defocused laser (3ω = 0.438 µm with a pulse duration of 250 ps and an energy of 100 J) on targets with a high atomic number [62]. The jets are produced by the collision of an ablated plasma converging on one axis, which is due to a combination of the annular laser intensity profile on the surface of the target and the radiative cooling [63]. X-ray diagnostics with spatial resolution made it possible to determine the parameters of the plasma jet and shock wave and to study their structure and evolution in detail, starting from the initial ionization of the background plasma and the formation of the jet to their subsequent interaction over a period of approximately 15 ns. The result showed a strong shock compression in the copper plasma with a ten-fold increase in density compared to the argon background plasma. The characteristic velocities of the jet and the shock wave were also measured. The X-ray pinhole camera showed that the structure and evolution of the shock wave depend strongly on the density of the neutral gas, both through the properties of the interaction during the formation of the shock wave and through its influence on the initial formation of the jet and its structure. It was concluded that the copper flow was re-oriented, resulting in a narrower and better collimated jet at low gas pressures.
In a similar experiment [64], using an X-ray pinhole camera, the interaction of such collimated laser-induced plasma jets with He and Ar gas flows was studied in two irradiation geometries as follows: with a perpendicular laser incidence on the target surface and with an inclination (30 ° relative to the normal of the target) to minimize the heating of the surrounding gas by the laser beam. With the geometry of the inclined interaction, the effect of double shock formation in the surrounding gas was demonstrated. Experiments conducted to test the generation of a plasma jet in this new geometry have clearly shown that even with an inclined case, well-formed plasma jets have parameters that are no worse than those of a normal incidence. The generated plasma structure, registered by an X-ray pinhole camera, is characterized by a sharp, elongated peak of luminosity along the symmetry axis of the laser beam propagation.
In the following studies [65,66], strong stochastic magnetic fields generated in a turbulent plasma during the collision of two inhomogeneous, asymmetric, weakly magnetized plasma jets were studied at the Omega Laser Facility. The X-ray diagnostics of the experiment visualized the bremsstrahlung in the soft X-ray region in a fully ionized CH plasma using a fast frame X-ray pinhole camera (XRFC) configured with a two-band microchannel plate (MCP) and a CCD camera. The 50-µm array of pinholes was located at 9.14 cm from the center of the target and the main detector at a distance of 27.4 cm, resulting in a 2× magnification of the image. A thin filter consisting of 0.5 µm polypropylene and a 150 nm thick aluminum coating was placed in front of the MCP and removed emission with a photon energy of ≤100 eV. Two temporally integrated images were taken with an interval of 1 ns. The image resolution and the choice of filtering were sufficient to observe the finger-shaped fluctuations of the plasma jets. These fluctuations were explained by density inhomogeneities in the plasma, whose origin can be explained by the effect of turbulent motion. The X-ray images obtained in the work show that the external magnetic field has only a limited influence on the dynamics of the plasma in the experiment, in the case of two individual plasma jets located in an external magnetic field. It was found that for a turbulent laser plasma with supercritical magnetic Reynolds numbers, the magnetic fields enhanced by the dynamo effect are determined by the turbulent dynamics and not by the initial fields or moderate changes in the initial dynamics of the plasma stream, which is consistent with theoretical expectations and modelling. The results suggest the possibility that plasma turbulence caused by strong displacement can generate fields more efficiently than would be expected with the idealized modelling of the magnetohydrodynamics (MHD) of a non-spiral dynamo. This discovery could help explain the large-scale fields obtained from observations of astrophysical systems.
It is worth mentioning that it is not always necessary to use pinhole cameras with multiple channels. Moreover, it can be more interesting to look at the evolution of the process from several lines of observation [67]. In the article [60], X-ray imaging was used to confirm the effect of magnetic reconnection of lines of force. For this purpose, two synchronized laser beams from the Shenguang (SG) II laser system were focused on one side of the aluminum foil at a distance of 400–600 µm, while the other two laser beams symmetrically irradiated the other side. The target was a loop of aluminum foil and a copper target attached to it. Each beam was focused to a focal spot diameter of 50–100 µm (FWHM), resulting in an incident laser intensity of 5 × 1015 W/cm2. In this experimental approach, X-ray emission was measured from the front, back and side using three X-ray pinhole cameras. The image was taken with a 10-µm pinhole and a 50-µm beryllium filter, resulting in X-rays (Figure 2b) over ~1 keV being registered on the X-ray film with a higher sensitivity in the range of 1–10 keV.
3.2. Application of Dispersive X-ray Optics in Alboratory Astrophysics Experiments
3.2.1. 2D X-ray Imagers Based on Spherically-Bent Crystals at Small Angles of Incidence
To obtain more detailed information about the laser-plasma interaction, methods with a combination of different optics are used. In particular, 2D imagers based on spherically curved crystals at near-normal X-ray incidence are worth mentioning. Image plates or time-resolved X-ray streak cameras are most commonly used as detectors in this case. In contrast to a pinhole camera, this approach allows us to obtain visual information about the emission of ions or hot electrons in a rather narrow, one could say monochromatic, spectral range.
In one study [59], for which images of a four-frame camera are shown in Figure 2a, a quartz crystal (422) with a bending radius R = 380 mm was used to obtain 2D-resolved images of Cu Kα emission (Figure 2c). The use of such a crystal with 2d = 1.5414 Å leads to the registration of the image in the line Ka (λ = 1.54056 Å) at an almost normal angle to the target and to minor distortions due to deviations from the sagittal and meridional planes of the crystal. The disadvantage of this configuration is the small spectral range of the emission, which can be shorter than the width of the Kα line due to the strong heating of the target by the laser. In this case, the absolute measurements of the X-ray yield in Kα line may be inaccurate, especially since the line profile may shift towards higher energies when the temperature changes. However, the spatial and temporal parameters of such a technique are very important for the interpretation of the obtained experimental data. It is also worth noting that visualization in such a narrow range results in a lower signal intensity on the detector than using a pinhole camera.
The image was registered on FUJI BAS MS image plates, which were then scanned using a Fujifilm BAS-1800 scanner with a pixel size of 50 × 50 microns. The system provided a magnification of . The measured X-ray data were interpreted in terms of the hot electron generation and the efficiency of conversion of laser energy into hot electrons. This approach made it possible to show a map of the intensity of hot electron generation for a snail target and to demonstrate the formation of a dense hot plasma, similar to a theta-pinch, and the distribution of a large magnetic field penetrating the target.
3.2.2. 1D and 2D of Spectrometers Based on Spherical Crystals with Spectral Resolution
Optical schemes based on spherical crystals and detectors placed in the sagittal plane of the image make it possible to visualize laser-plasma processes not only with spatial but also with spectral resolution. This is particularly important when a plasma object has a large aspect ratio. In this case, one of the tasks is the ability to investigate the parameters over the entire length of the plasma. For example, in research [29,68,69] conducted at the ELFIE facility (LULI, Polytechnique), a plasma jet with a high aspect ratio was studied for laboratory modelling of Herbig–Haro type astrophysical ejections from young stellar objects (YSOs). A large aspect ratio was achieved using an external magnetic field of 20 T, in which a Teflon target (CF2) was irradiated with a laser pulse with an energy of about ~40 J and a duration of about ~1 ns. An example of an image obtained by 2D spatially resolved X-ray spectroscopy based on a spherical mica crystal (2d = 19.9376 Å) is shown in Figure 3. The image was composed of three different frames with high repeatability of results (due to the long focal length (approximately 2 m) of a nanosecond laser beam and a homogeneous magnetic field) using the image plate detector. To investigate the full length of the jet propagation, the target was placed at different positions along the laser axis inside the magnetic coil. With each image, the parameters of the jet were measured in a range of 5–7 mm per shot.

Figure 3.
An X-ray image of a plasma jet composed of three successive frames taken for different shots of a heating laser at different target distances within the Helmholtz coil.
As a result of this approach, important spatial profiles of plasma parameters are given in [68,69], which are the electronic density and the temperature, as they are of great importance for modelling most physical quantities and for comparisons with astrophysical models. Figure 4 shows an example of such profiles in the experiment mentioned above. It is obvious that the high spatial resolution (approximately 100 µm of the source) allows the measurement of plasma parameters with high accuracy using modern techniques over a wide range of distances, including the laser-induced target surface itself.
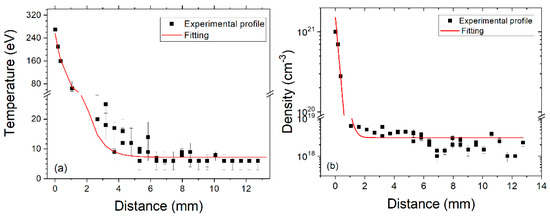
Figure 4.
The measurement is dependent on the electron temperature (a), the electron density of the plasma (b), and on the distance to the target surface in the presence of a magnetic field (black squares). The approximation of the profile by an exponential function is shown in red.
As mentioned earlier, this scheme is characterized by a stronger astigmatism and a larger magnification along the jet axis than in the case of the radial direction (i.e., the direction of spectral dispersion). In the sagittal plane, the spatial resolution is determined by the aberrations of the spherical surface in the sagittal plane. In the meridional plane, the spatial resolution is determined by aberrations as well as by the size of the source, the width of the spectral line, and the width of the rocking curve of the crystal. Therefore, it is necessary to correct for spatial distortions for extended sources, otherwise the estimates for the plasma parameters can deviate significantly from the truth due to an incorrect comparison of the relative intensities of the spectral lines.
To illustrate this, Figure 5a shows an X-ray image registered by us in a laboratory experiment when the collision of two plasma flows was studied in the presence of an external magnetic field and a gas medium (Nitrogen) between two simultaneously laser-irradiated solid CF2 targets. The irradiation parameters and the image registration scheme were identical to those given for a single jet, as shown in Figure 3. A focusing spectrometer with spatial resolution based on a spherically-bent mica crystal was used. It is obvious that long wavelengths occupy a shorter spatial extent in the image than shorter wavelengths. This was corrected in Figure 5b using the authors’ anti-distortion code written in Python, which allows the user to graphically select the points of change in magnification while preserving the initial emissivity integral. By correcting the distortions and considering the scaling coefficients on both axes, it is possible to obtain both an X-ray image of a plasma source and spatial profiles of the plasma.

Figure 5.
The original (a) and the processed spectrometric image (b) in the experimental campaign. In this case, there are two laser-irradiated targets in the field of view, between which plasma jets interact in an external gas. From left to right, the wavelengths increase. The mark corresponds to the position of the central wavelength (part of the spectrum is cut off on the right-hand side because there is no useful information).
Figure 6a shows an example of a 2D X-ray image of a plasma jet for the fluorine line with equal magnification coefficients in the radial and axial directions in an experiment simulating the collimation of astrophysical flows [70]. For this purpose, the scaling coefficients were used (the magnification according to Formulae (6) and (9) was = 0.048 in the meridional direction and = 0.26 mm in the sagittal direction) and the distortion effect of the optical system was taken into account. Since the magnification factor on one axis was much larger, the averaged values of the neighboring pixels were placed between the stretched points. For the construction, only the (−3:+3) radial neighborhood of the maximum value of the spectral line of each line was used, while the background was completely cut off. In Figure 6a, only the line F He 4p-1s () is shown, while the behavior of the other lines is very similar. The resolution in sagittal and meridional directions was approximately 100 and 500 µm, respectively. The images are composed of several frames (represented by dotted rectangles), each taken for a separate shot with a target at different distances from the diagnostic window of the Helmholtz coil.
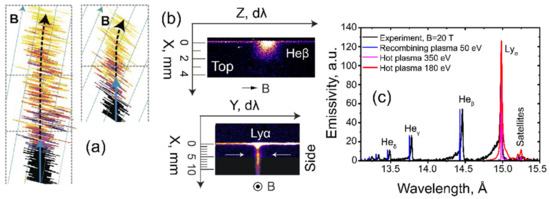
Figure 6.
(a) X-ray image [70] of a plasma jet obtained by a FSSR spectrometer [33] along a spectral line with minimal distortion (transition in fluorine atom F He 4p-1s, closest to the central wavelength) at 20 T when the inclination of the target was 10 and 20 degrees to the normal. (b) X-ray images of the self-emission of the fluorine spectral line obtained by diagnosis of the 3D plasma from the side and from above at a transverse magnetic field of 20 T [34]. (c) The analytical approach of the two-component plasma.
In these images, the bending of the expanding plasma can be clearly seen, with two phases being distinguished. First, near the target, both diagnostics show that the propagation of the plasma jet does not depend on the variation of the angle of the magnetic field near the laser-irradiated target surface. Moreover, this propagation is perpendicular to the target surface and is identical to the case where there is no magnetic field. The reason for this behavior is the kinetic gas pressure of the plasma , which far exceeds the pressure of the magnetic field in this region, where the electron temperature and density are expected to be above 100 eV and 1 × 1019 cm−3, respectively. The results of the X-ray diagnostics thus helped to establish that the modulation of the jet can be interpreted as a sign of a change in the flow angle or the surrounding field over time, and that a change in the direction of the jet can be a sign of changes in the direction of the surrounding field.
The simultaneous use of multiple spectrometers makes it possible to reconstruct or prove the dynamics of plasma propagation on a 3-dimensional scale. For example, in one study [34], two spectrometers were used with an observation line orthogonal to each other and with spatial resolution along the axis of the plasma expansion. Since the spectrometers were installed in a 2D scheme, the experiment (Figure 6b) was able to compare two projections of an X-ray source with a magnetic field perpendicular to the plasma expansion, as occurs in a variety of astrophysical environments, e.g., at the edge of discs surrounding young stars or when coronal mass ejections (CME) [71] propagate from the star [72]. Note, that images in Figure 6b are integrated over time and measured simultaneously in one shot by two focusing spectrometers with spatial resolution (FSSR) used in the experiment. The white arrows in the side view indicate an increase in the emissivity in the spatial region of ≈ 4 mm.
As a result of this approach, the morphology of the plasma flow was confirmed, which is characterized by expansion in one plane and compression in another. Furthermore, an approach based on the comparison of spatial profiles of the emissivity and the measured electron density and temperature was used to estimate the propagation velocity of the plasma flows. In this way, it was possible to determine the separation of the plasma into two components as follows: dense, slow plasma that is increasingly compressed towards the target as the magnetic field increases, and fast, low-density plasma that is redirected by the magnetic field along the axis. It is noteworthy that the ability of the plasma observed here to propagate against a transverse magnetic field could be of interest for the physics of the edges of the disc, namely to enable the ejections from the disc to cross the gap separating the disc from the star and thus participate in the deceleration of the disc, as postulated in Shakura and Sunyaev [73].
3.2.3. Investigations of Laboratory Astrophysical Plasma by X-ray Spectral Composition
The relative intensities of the spectral lines obtained or the spectral composition itself cannot often be described by only one plasma component. It is concluded that there are additional zones that are not resolved along a particular axis [2,74,75]. This is particularly useful, for example, when the sensitivity of the detector is not sufficient to make reliable measurements with time resolution. In the following studies [2,74], focusing spectrometers based on spherically curved crystals were used to obtain fluorine ion emission spectra when simulating CTTS accretion columns directed along the magnetic field lines connecting the surrounding material to the star. To study the dynamics of accretion in the laboratory, a collimated narrow (diameter ~1.5 mm) plasma flow was used by superimposing an external (B = 6–30 T) and a homogeneous poloidal magnetic field on an expanding laser-induced plasma (laser duration 0.6 ns, intensity ~1013 W/cm2). The plasma flow propagated with a velocity of parallel to the lines of a large-scale external magnetic field, as in the present picture of mass accretion in CTTS encountering a solid obstacle simulating a high-density region in the stellar chromosphere. In most of the shots, the obstacle was located at 11.7 mm from the main target. The emission spectra were taken with spatial resolution in the direction of laser propagation near the obstacle surface. Since the X-ray images in the experiments were recorded integrally in time, the spectrometer recorded, at each spatial point, the sum of the spectra emitted first by a laser plume expanded freely from the target and then by the plasma generated by the collision of the initial plasma flow and the plasma generated on a solid obstacle. Of course, the plasma parameters at early and late times can be very different, and the resulting spectrograms only give some average values of the plasma parameters. To solve this problem, targets and obstacles with different chemical compositions were used, namely polyvinyl chloride, or PVC (C2H3Cl)n, aluminum, and Teflon (CF2). These materials were used for both the main and obstacle targets so that the plasma of incident and induced flows could be observed separately, registering the spectral lines of fluorine, chlorine, and aluminum, respectively.
The spectra obtained near the obstacle surface have demonstrated that the data obtained cannot be described by a single set of parameters. This is due to the presence of dielectric satellites to the line (hot plasma with a temperature much higher than 100 eV, exceeding the ionization potential for the L-shell) and to the recombinant nature of the emission of the helium series, where high intensities for high transitions are observed (Figure 6c). The conclusion on the possible presence of an additional plasma component made it possible to use a two-plasma approach, where the parameters of a dense and cold core and a hot and less dense shell were determined. The colder plasma was estimated with a recombination model [76], while the parameters of the hot part were measured with the PrismSPECT code [77] from the ratio of the intensities of the dielectric satellites to the Lya resonance line. The results on the spatial distribution of the components were then confirmed by optical methods and modelling. Despite the low sensitivity of the system to conduct time-resolved measurements, such an approach was able to detect the formation of a plasma shell, which in the astrophysical case of accretion columns can lead to significant absorption of X-rays.
3.2.4. Diffraction Gratings
In experiments to study the propagation of plasma flows in a perpendicular magnetic field [34], as well as to study the slanted accretion [30], a spectrometer based on a diffraction grating with variable line spacing (VSG: variable spatial grating) was used. This VSG spectrometer allows the investigation of a wider spectral range (400–2000 eV) than the FSSR, but with a lower spectral resolution [45].
The spectrometer consists of a diffraction grating (average 1200 points per inch), a spectrometer body, and a removable front cone that can accommodate slits for spatial resolution measurements. The image was also captured using an image plate TR. In the experiments, the front part of the spectrometer body was equipped with a vertical slit that allowed spatial resolution of the X-ray emission of the plasma along the horizontal axis, which was one of the expansion points of the plasma. In this case, the grating had its lines in the horizontal direction, resulting in horizontal spatial and vertical spectral resolution on the VSG detector.
Figure 7a shows the X-ray image where only a vertical slit was used instead of a pinhole at the entrance of the VSG spectrometer. In this case, the spectrum on the vertical axis is not purely spectral but mixed with space (different emitting points of the plasma at different heights (along the r-axis) appear at different heights on the IP—see Figure 1c). Another effect of using a vertical slit is that tilted targets also appear tilted on the IP detector (as seen in Figure 7a). It is therefore necessary to consider the convolution of the spectrum in relation to the size of the source. Setting an additional horizontal slit with a size of 500 μm [78] leads to a much better resolution (Figure 7b) with ~20, which is sufficient for visual observation of the Lyβ line of carbon. Due to the wide observation range and the high reflection efficiency, this diagnostic was useful for the qualitative observation of plasma dynamics. In particular, thanks to this diagnostic, it was possible to show that the confinement of the plasma along the axis of incidence strongly decreases as the incoming flow becomes more and more slanted.
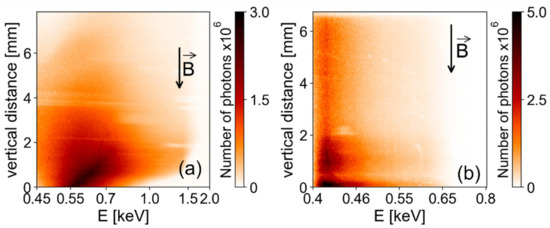
Figure 7.
Energy spectra of the plasma self-emission in the soft X-ray region, measured with VSG. (a) Use of a grating without a space-limiting slit in the direction of the dispersion axis. (b) A horizontal slit with a size of 500 µm was used. Spectrum (b) shows the characteristic carbon line detected in the CF2 plasma. An increase in emissivity at a distance of 1–2 mm from the target corresponds to the injection of a gas jet from a supersonic nozzle.
The use of transmission diffraction gratings is also worth mentioning. In papers [79,80] dealing with the laboratory investigation of photoionized plasma generated in a high-power laser facility GEKKO-XII, a spectrometer with a transmission grating was used to measure the absolute intensities of the plasma emission in the range of 1–6 keV. This diagnostic helped to control and measure the Planck spectrum of the central plasma. An example of a photoionized plasma can be the stellar wind around compact objects.
4. Discussion and Perspectives
As discussed in Section 3 and Section 4, not all existing imaging methods are currently provided in the study of astrophysical-relevant laser-induced plasmas. In particular, systems based on multilayer mirrors, flat and cylindrical curved crystals, and Fresnel lenses are not used conventionally. The reason for this is perhaps the high demands for self-emission imaging systems. They must be easily adjustable, quickly tunable, and reliable in construction; have high luminosity; and allow easy variation of the spectral range and magnification. Unfortunately, these properties are not characteristic of systems using multilayer mirrors or Fresnel lenses.
The Kirkpatrick-Baez multichannel microscope, for example, has a small spatial range of ~0.5 mm [81] and requires a long time to adjust. Therefore, it has been used mainly in unique experiments on inertial thermonuclear fusion [49]. In laboratory astrophysics experiments, one might expect such devices to be used at a rather small (less than 0.5 mm) spatial scale of the plasma under investigation, as is the case, for example, in magnetic reconnection studies [60,82]; however, so far, to our knowledge, they have not served these purposes.
X-ray imaging diagnostics based on Fresnel lenses are very promising as the field of view is of the order of 1 mm and even higher, and the spatial resolution can reach hundreds of nm [83]. The obvious disadvantage of such diagnostics is the presence of the chromatic effect, which reduces the contrast of the image and leads to the need to use a rather narrow spectral range. The spectrographs with flat or curved crystals used so far have a satisfactory spectral resolution but cannot always provide sufficient luminosity and spatial resolution when it comes to obtaining images of plasma sources. Spectrometers with toroidal schemes do not have these disadvantages, but their surface is much more difficult to fabricate and the resulting schemes are difficult to set up because of the limitation in all six degrees of freedom [39].
In contrast, simple multiframe pinhole cameras as well as spectrometers based on diffraction gratings and spherically curved crystals are quite easy to handle and allow spectroscopic studies of an X-ray source with high luminosity and high resolution. Thanks to recent technological advances, it is possible to use such multichannel systems in conjunction with X-ray streak or gated cameras with high temporal resolution instead of the traditionally used image plates or photographic films [84,85]. Furthermore, such systems can easily be used simultaneously with multiple dispersive elements projecting an image onto a detector, as in the case of toroidal crystals [40], allowing an extension of the spectral range.
The availability and wide choice of X-ray optics and methods for acquiring X-ray images of plasmas have led to significant advances in astrophysical laboratory investigations. In particular, emission visualization methods have helped to reveal many details of various astrophysical phenomena, such as the evolution of young stars [4,29,61,86], the evolution and luminosity of accretion columns [2,30], the collimation of astrophysical flows in Herbig–Haro objects [64,70], coronal mass ejections [34], and the generation and reconnection of magnetic field lines [59,60]. It should not go unmentioned that further increases in the sensitivity and temporal resolution of elemental detection will undoubtedly enable significant advances not only in laboratory astrophysics but also in many other fields, including thermonuclear inertial fusion.
Author Contributions
Writing—review, E.D.F. and I.Y.S.; editing and data curation, E.D.F., I.Y.S., T.A.P. and K.F.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by The Ministry of Science and Higher Education of the Russian Federation (Agreement with Joint Institute for High Temperatures RAS No 075 15 2020 785).
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank team of LULI facility and J. Fuchs for the opportunity to participate in experiments in laboratory astrophysics in laboratory LULI, Ecole Polytechnique.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Basov, N.G.; Krokhin, O.N. Conditions for Heating up of a Plasma by the Radiation from an Optical Generator. Sov. Phys. JETP 1964, 19, 171–175. [Google Scholar]
- Revet, G.; Chen, S.N.; Bonito, R.; Khiar, B.; Filippov, E.; Argiroffi, C.; Higginson, D.P.; Orlando, S.; Béard, J.; Blecher, M.; et al. Laboratory Unravelling of Matter Accretion in Young Stars. Sci. Adv. 2017, 3, e1700982. [Google Scholar] [CrossRef] [PubMed]
- Rigon, G.; Casner, A.; Albertazzi, B.; Michel, T.; Mabey, P.; Falize, E.; Ballet, J.; Van Box Som, L.; Pikuz, S.; Sakawa, Y.; et al. Rayleigh-Taylor Instability Experiments on the LULI2000 Laser in Scaled Conditions for Young Supernova Remnants. Phys. Rev. E 2019, 100, 021201. [Google Scholar] [CrossRef] [PubMed]
- Albertazzi, B.; Ciardi, A.; Nakatsutsumi, M.; Vinci, T.; Béard, J.; Bonito, R.; Billette, J.; Borghesi, M.; Burkley, Z.; Chen, S.N.; et al. Laboratory Formation of a Scaled Protostellar Jet by Coaligned Poloidal Magnetic Field. Science 2014, 346, 325–328. [Google Scholar] [CrossRef]
- Drake, R.P.; Doss, F.W.; McClarren, R.G.; Adams, M.L.; Amato, N.; Bingham, D.; Chou, C.C.; DiStefano, C.; Fidkowski, K.; Fryxell, B.; et al. Radiative Effects in Radiative Shocks in Shock Tubes. High Energy Density Phys. 2011, 7, 130–140. [Google Scholar] [CrossRef]
- Falize, É.; Loupias, B.; Ravasio, A.; Gregory, C.D.; Dizière, A.; Koenig, M.; Michaut, C.; Cavet, C.; Barroso, P.; Leidinger, J.-P.P.; et al. The Scalability of the Accretion Column in Magnetic Cataclysmic Variables: The POLAR Project. Astrophys. Space Sci. 2011, 336, 81–85. [Google Scholar] [CrossRef]
- Egeland, A. Kristian Birkeland: The First Space Scientist. J. Atmos. Solar-Terr. Phys. 2009, 71, 1749–1755. [Google Scholar] [CrossRef]
- Ryutov, D.; Drake, R.P.; Kane, J.; Liang, E.; Remington, B.A.; Wood-Vasey, W.M. Similarity Criteria for the Laboratory Simulation of Supernova Hydrodynamics. Astrophys. J. 1999, 518, 821–832. [Google Scholar] [CrossRef]
- Falize, É.; Michaut, C.; Bouquet, S. Similarity Properties and Scaling Laws of Radiation Hydrodynamic Flows in Laboratory Astrophysics. Astrophys. J. 2011, 730, 96. [Google Scholar] [CrossRef]
- Podgornyi, I.M.; Sagdeev, R.Z. Physics of Interplanetary Plasma and Laboratory Experiments. Sov. Phys. Uspekhi 1970, 12, 445–462. [Google Scholar] [CrossRef]
- Remington, B.A.; Drake, R.P.; Ryutov, D.D. Experimental Astrophysics with High Power Lasers and Z Pinches. Rev. Mod. Phys. 2006, 78, 755–807. [Google Scholar] [CrossRef]
- Ryutov, D.D.; Drake, R.P.; Remington, B.A. Criteria for Scaled Laboratory Simulations of Astrophysical MHD Phenomena. Astrophys. J. Suppl. Ser. 2000, 127, 465–468. [Google Scholar] [CrossRef]
- Lebedev, S.V.; Ciardi, A.; Ampleford, D.J.; Bland, S.N.; Bott, S.C.; Chittenden, J.P.; Hall, G.N.; Rapley, J.; Jennings, C.A.; Frank, A.; et al. Magnetic Tower Outflows from a Radial Wire Array Z-Pinch. Mon. Not. R. Astron. Soc. 2005, 361, 97–108. [Google Scholar] [CrossRef][Green Version]
- Ampleford, D.J.; Lebedev, S.V.; Ciardi, A.; Bland, S.N.; Bott, S.C.; Hall, G.N.; Naz, N.; Jennings, C.A.; Sherlock, M.; Chittenden, J.P.; et al. Supersonic Radiatively Cooled Rotating Flows and Jets in the Laboratory. Phys. Rev. Lett. 2008, 100, 035001. [Google Scholar] [CrossRef] [PubMed]
- Ciardi, A.; Lebedev, S.V.; Frank, A.; Suzuki-Vidal, F.; Hall, G.N.; Bland, S.N.; Harvey-Thompson, A.; Blackman, E.G.; Camenzind, M. Episodic Magnetic Bubbles and Jets: Astrophysical Implications from Laboratory Experiments. Astrophys. J. 2009, 691, L147–L150. [Google Scholar] [CrossRef]
- Hsu, S.C.; Bellan, P.M. Experimental Identification of the Kink Instability as a Poloidal Flux Amplification Mechanism for Coaxial Gun Spheromak Formation. Phys. Rev. Lett. 2003, 90, 4. [Google Scholar] [CrossRef] [PubMed]
- Bellan, P.M.; You, S.; Hsu, S.C. Simulating Astrophysical Jets in Laboratory Experiments. In High Energy Density Laboratory Astrophysics; Springer: Dordrecht, The Netherlands, 2005; Volume 298, pp. 203–209. [Google Scholar]
- Faenov, A.Y.Y.; Skobelev, I.Y.Y.; Rosmej, F.B.B. High Resolution X-ray Spectroscopy of Laser Generated Plasmas. Phys. Scr. 1999, 80, 43–45. [Google Scholar] [CrossRef]
- Pikuz, S.A.; Shelkovenko, T.A.; Hammer, D.A. X-Pinch. Part I. Plasma Phys. Rep. 2015, 41, 291–342. [Google Scholar] [CrossRef]
- Thomas, C.; Rehm, G.; Martin, I.; Bartolini, R. X-ray Pinhole Camera Resolution and Emittance Measurement. Phys. Rev. Spec. Top.-Accel. Beams 2010, 13, 022805. [Google Scholar] [CrossRef]
- Albertazzi, B.; Falize, E.; Pelka, A.; Brack, F.; Kroll, F.; Yurchak, R.; Brambrink, E.; Mabey, P.; Ozaki, N.; Pikuz, S.; et al. Experimental Platform for the Investigation of Magnetized-Reverse-Shock Dynamics in the Context of POLAR. High Power Laser Sci. Eng. 2018, 6, e43. [Google Scholar] [CrossRef]
- Higginson, D.P.; Korneev, P.; Béard, J.; Chen, S.N.; d’Humières, E.; Pépin, H.; Pikuz, S.; Pollock, B.; Riquier, R.; Tikhonchuk, V.; et al. A Novel Platform to Study Magnetized High-Velocity Collisionless Shocks. High Energy Density Phys. 2015, 17, 190–197. [Google Scholar] [CrossRef]
- Casner, A.; Mailliet, C.; Rigon, G.; Khan, S.F.; Martinez, D.; Albertazzi, B.; Michel, T.; Sano, T.; Sakawa, Y.; Tzeferacos, P.; et al. From ICF to Laboratory Astrophysics: Ablative and Classical Rayleigh-Taylor Instability Experiments in Turbulent-like Regimes. Nucl. Fusion 2019, 59, 032002. [Google Scholar] [CrossRef]
- Meadowcroft, A.L.; Bentley, C.D.; Stott, E.N. Evaluation of the Sensitivity and Fading Characteristics of an Image Plate System for X-ray Diagnostics. Rev. Sci. Instrum. 2008, 79, 113102. [Google Scholar] [CrossRef]
- Joensen, K.D.; Voutov, P.; Szentgyorgyi, A.; Roll, J.; Gorenstein, P.; Høghøj, P.; Christensen, F.E. Design of Grazing-Incidence Multilayer Supermirrors for Hard-X-ray Reflectors. Appl. Opt. 1995, 34, 7935. [Google Scholar] [CrossRef]
- Wang, C.; An, H.H.; Xiong, J.; Fang, Z.H.; Wang, Y.W.; Zhang, Z.; Hua, N.; Sun, J.R.; Wang, W. A Pinhole Camera for Ultrahigh-Intensity Laser Plasma Experiments. Rev. Sci. Instrum. 2017, 88, 113501. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Gao, Y.; Zhang, X.; Lu, D.; Hu, W.; Gao, M.; Chen, W.; Zou, Y. High Resolution Flat Crystal Spectrometer for the Shanghai EBIT. Rev. Sci. Instrum. 2008, 79, 093101. [Google Scholar] [CrossRef]
- Baronova, E.O.; Stepanenko, M.M.; Pereira, N.R. Cauchois-Johansson X-ray Spectrograph for 1.5–400 KeV Energy Range. Rev. Sci. Instrum. 2001, 72, 1416–1420. [Google Scholar] [CrossRef]
- Higginson, D.P.; Khiar, B.; Revet, G.; Béard, J.; Blecher, M.; Borghesi, M.; Burdonov, K.; Chen, S.N.; Filippov, E.; Khaghani, D.; et al. Enhancement of Quasistationary Shocks and Heating via Temporal Staging in a Magnetized Laser-Plasma Jet. Phys. Rev. Lett. 2017, 119, 255002. [Google Scholar] [CrossRef]
- Burdonov, K.; Revet, G.; Bonito, R.; Argiroffi, C.; Béard, J.; Bolanõs, S.; Cerchez, M.; Chen, S.N.; Ciardi, A.; Espinosa, G.; et al. Laboratory Evidence for an Asymmetric Accretion Structure upon Slanted Matter Impact in Young Stars. Astron. Astrophys. 2020, 642, A38. [Google Scholar] [CrossRef]
- Hoszowska, J.; Dousse, J.C.; Kern, J.; Rhême, C. High-Resolution von Hamos Crystal X-ray Spectrometer. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1996, 376, 129–138. [Google Scholar] [CrossRef]
- Skobelev, I.Y.; Faenov, A.Y.; Bryunetkin, B.A.; Dyakin, V.M. Investigating the Emission Properties of Plasma Structures with X-ray Imaging Spectroscopy. J. Exp. Theor. Phys. 1995, 81, 692–718. [Google Scholar]
- Faenov, A.Y.; Pikuz, S.A.; Erko, A.I.; Bryunetkin, B.A.; Dyakin, V.M.; Ivanenkov, G.V.; Mingaleev, A.R.; Pikuz, T.A.; Romanova, V.M.; Shelkovenko, T.A. High-Performance X-ray Spectroscopic Devices for Plasma Microsources Investigations. Phys. Scr. 1994, 50, 333–338. [Google Scholar] [CrossRef]
- Filippov, E.D.; Makarov, S.S.; Burdonov, K.F.; Yao, W.; Revet, G.; Béard, J.; Bolaños, S.; Chen, S.N.; Guediche, A.; Hare, J.; et al. Enhanced X-ray Emission Arising from Laser-Plasma Confinement by a Strong Transverse Magnetic Field. Sci. Rep. 2021, 11, 8180. [Google Scholar] [CrossRef] [PubMed]
- Condamine, F.P.; Filippov, E.; Angelo, P.; Pikuz, S.A.; Renner, O.; Rosmej, F.B. High-Resolution Spectroscopic Study of Hot Electron Induced Copper M-Shell Charge States Emission from Laser Produced Plasmas. High Energy Density Phys. 2019, 32, 89–95. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, H.; Shi, J.; Tang, C.; Liu, S. Shenye Liu High Resolution X-ray Spherically Bent Crystal Spectrometer for Laser-Produced Plasma Diagnostics. Chin. Opt. Lett. 2009, 7, 92–94. [Google Scholar] [CrossRef]
- Bitter, M.; Hill, K.W.; Efthimion, P.C.; Delgado-Aparicio, L.; Pablant, N.; Lu, J.; Beiersdorfer, P.; Chen, H. A New Spectrometer Design for the X-ray Spectroscopy of Laser-Produced Plasmas with High (Sub-Ns) Time Resolutiona). Rev. Sci. Instrum. 2014, 85, 11D627. [Google Scholar] [CrossRef]
- Pikuz, S.A.; Douglass, J.D.; Shelkovenko, T.A.; Sinars, D.B.; Hammer, D.A.C. Wide band focusing X-ray spectrograph with spatial resolution. Rev. Sci. Instrum. 2008, 79, 013106. [Google Scholar] [CrossRef]
- Koch, J.A.; Aglitskiy, Y.; Brown, C.; Cowan, T.; Freeman, R.; Hatchett, S.; Holland, G.; Key, M.; MacKinnon, A.; Seely, J.; et al. 4.5- and 8-KeV Emission and Absorption X-ray Imaging Using Spherically Bent Quartz 203 and 211 Crystals (Invited). Rev. Sci. Instrum. 2003, 74, 2130. [Google Scholar] [CrossRef]
- Jiang, C.; Xu, J.; Mu, B.; Wang, X.; Li, M.; Li, W.; Pu, Y.; Ding, Y. Four-Channel Toroidal Crystal X-ray Imager for Laser-Produced Plasmas. Opt. Express 2021, 29, 6133–6146. [Google Scholar] [CrossRef]
- Pisani, F.; Koenig, M.; Batani, D.; Hall, T.; Desenne, D.; Bruneau, J.; Reverdin, C. Toroidal Crystal Spectrometer for Time-Resolved X-ray Absorption Diagnostic in Dense Plasmas. Rev. Sci. Instrum. 1999, 70, 3314. [Google Scholar] [CrossRef]
- Palmer, C. Diffraction Grating Handbook, 8th ed.; Loewen, E., Ed.; THERMO RGL: Rochester, NY, USA, 2020. [Google Scholar]
- Cone, K.V.; Dunn, J.; Schneider, M.B.; Baldis, H.A.; Brown, G.V.; Emig, J.; James, D.L.; May, M.J.; Park, J.; Shepherd, R.; et al. Development of a Time-Resolved Soft X-ray Spectrometer for Laser Produced Plasma Experimentsa). Rev. Sci. Instrum. 2010, 81, 10E318. [Google Scholar] [CrossRef]
- Fäustlin, R.R.; Zastrau, U.; Toleikis, S.; Uschmann, I.; Förster, E.; Tschentscher, T.H. A Compact Soft X-ray Spectrograph Combining High Efficiency and Resolution. J. Instrum. 2010, 5, P02004. [Google Scholar] [CrossRef][Green Version]
- Kita, T.; Harada, T.; Nakano, N.; Kuroda, H. Mechanically Ruled Aberration-Corrected Concave Gratings for a Flat-Field Grazing-Incidence Spectrograph. Appl. Opt. 1983, 22, 512. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.P. Grazing Incidence Optics for X-ray Astronomy: X-ray Optics. J. Opt. 2011, 40, 88–95. [Google Scholar] [CrossRef]
- Kozhevnikov, I.V.; Vinogradov, A.V. Multilayer X-ray Mirrors. J. Russ. Laser Res. 1995, 16, 343–385. [Google Scholar] [CrossRef]
- Hudec, R. Kirkpatrick-Baez (KB) and Lobster Eye (LE) Optics for Astronomical and Laboratory Applications. X-ray Opt. Instrum. 2010, 2010, 139148. [Google Scholar] [CrossRef]
- Marshall, F.J.; Bahr, R.E.; Goncharov, V.N.; Glebov, V.Y.; Peng, B.; Regan, S.P.; Sangster, T.C.; Stoeckl, C. A Framed, 16-Image Kirkpatrick–Baez X-ray Microscope. Rev. Sci. Instrum. 2017, 88, 093702. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Zhang, Z.; Huang, Q.; Zhang, Z.; Wang, Z.; Wei, L.; Liu, D.; Cao, L.; Gu, Y. Note: Tandem Kirkpatrick–Baez Microscope with Sixteen Channels for High-Resolution Laser-Plasma Diagnostics. Rev. Sci. Instrum. 2018, 89, 036105. [Google Scholar] [CrossRef]
- Angel, J.R.P. Lobster Eyes as X-ray Telescopes. Astrophys. J. 1979, 233, 364. [Google Scholar] [CrossRef]
- Montel, M. X-ray Microscopy and Microradiography; Academic Press: New York, NY, USA, 1957; Volume 177. [Google Scholar]
- Lider, V.V. Kirkpatrick–Baez and Wolter X-ray Focusing Optics (Review). J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2019, 13, 670–682. [Google Scholar] [CrossRef]
- Mondal, B.; Vadawale, S.V.; Mithun, N.P.S.; Vaishnava, C.S.; Tiwari, N.K.; Goyal, S.K.; Panini, S.S.; Navalkar, V.; Karmakar, C.; Patel, M.R.; et al. DarpanX: A Python Package for Modeling X-ray Reflectivity of Multilayer Mirrors. Astron. Comput. 2021, 34, 100446. [Google Scholar] [CrossRef]
- Agafonov, Y.A.; Bryunetkin, B.A.; Erko, A.I.; Mingaleev, A.R.; Pikuz, S.A.; Romanova, V.T.; Skobelev, I.Y.; Faenov, A.Y.; Shelkovenko, T.A. Imaging Spectroscopy of Microscopic Plasmas by Means of a Mica Crystal with a Zone-Plate Surface Structure. Quantum Electron. 1993, 23, 172–174. [Google Scholar] [CrossRef]
- Aristov, V.V.; Erko, A.I. X-ray Optics; Nauka: Moscow, Russia, 1991. [Google Scholar]
- Aglitskiy, Y.; Obenschain, S.; Yunkin, V. Bent Bragg–Fresnel Lenses for X-ray Imaging Diagnostics. Rev. Sci. Instrum. 2003, 74, 2228. [Google Scholar] [CrossRef]
- Cauchon, G.; Pichet-Thomasset, M.; Sauneuf, R.; Dhez, P.; Idir, M.; Ollivier, M.; Troussel, P.; Boutin, J.Y.; Le Breton, J.P. Imaging of Laser Produced Plasma at 1.43 KeV Using Fresnel Zone Plate and Bragg–Fresnel Lens. Rev. Sci. Instrum. 1998, 69, 3186. [Google Scholar] [CrossRef]
- Pisarczyk, T.; Gus’kov, S.Y.; Zaras-Szydłowska, A.; Dudzak, R.; Renner, O.; Chodukowski, T.; Dostal, J.; Rusiniak, Z.; Burian, T.; Borisenko, N.; et al. Magnetized Plasma Implosion in a Snail Target Driven by a Moderate-Intensity Laser Pulse. Sci. Rep. 2018, 8, 17895. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Li, Y.; Wang, X.; Wang, J.; Dong, Q.; Xiao, C.; Wang, S.; Liu, X.; Zhang, L.; An, L.; et al. Modelling Loop-Top X-ray Source and Reconnection Outflows in Solar Flares with Intense Lasers. Nat. Phys. 2010, 6, 984–987. [Google Scholar] [CrossRef]
- Bohlin, H.; Brack, F.E.; Cervenak, M.; Chodukowski, T.; Cikhardt, J.; Dostál, J.; Dudžák, R.; Hubner, J.; Huo, W.; Jelinek, S.; et al. Radiative Characterization of Supersonic Jets and Shocks in a Laser-Plasma Experiment. Plasma Phys. Control. Fusion 2021, 63, 045026. [Google Scholar] [CrossRef]
- Kasperczuk, A.; Pisarczyk, T.; Borodziuk, S.; Ullschmied, J.; Krousky, E.; Masek, K.; Rohlena, K.; Skala, J.; Hora, H. Stable Dense Plasma Jets Produced at Laser Power Densities around 1014W/cm2. Phys. Plasmas 2006, 13, 062704. [Google Scholar] [CrossRef]
- Kasperczuk, A.; Pisarczyk, T.; Demchenko, N.N.; Gus’Kov, S.Y.; Kalal, M.; Ullschmied, J.; Krousky, E.; Masek, K.; Pfeifer, M.; Rohlena, K.; et al. Experimental and Theoretical Investigations of Mechanisms Responsible for Plasma Jets Formation at PALS. Laser Part. Beams 2009, 27, 415–427. [Google Scholar] [CrossRef]
- Kasperczuk, A.; Pisarczyk, T.; Nicolai, P.; Stenz, C.; Tikhonchuk, V.; Kalal, M.; Ullschmied, J.; Krousky, E.; Masek, K.; Pfeifer, M.; et al. Investigations of Plasma Jet Interaction with Ambient Gases by Multi-Frame Interferometric and X-ray Pinhole Camera Systems. Laser Part. Beams 2009, 27, 115–122. [Google Scholar] [CrossRef]
- Bott, A.F.A.; Chen, L.; Tzeferacos, P.; Palmer, C.A.J.; Bell, A.R.; Bingham, R.; Birkel, A.; Froula, D.H.; Katz, J.; Kunz, M.W.; et al. Insensitivity of a Turbulent Laser-Plasma Dynamo to Initial Conditions. Matter Radiat. Extrem. 2022, 7, 046901. [Google Scholar] [CrossRef]
- Bott, A.F.A.; Tzeferacos, P.; Chen, L.; Palmer, C.A.J.; Rigby, A.; Bell, A.R.; Bingham, R.; Birkel, A.; Graziani, C.; Froula, D.H.; et al. Time-Resolved Turbulent Dynamo in a Laser Plasma. Proc. Natl. Acad. Sci. USA 2021, 118, e2015729118. [Google Scholar] [CrossRef] [PubMed]
- Dozières, M.; Hansen, S.; Forestier-Colleoni, P.; McGuffey, C.; Kawahito, D.; Bailly-Grandvaux, M.; Bhutwala, K.; Krauland, C.M.; Wei, M.S.; Gourdain, P.; et al. Characterization of an Imploding Cylindrical Plasma for Electron Transport Studies Using X-ray Emission Spectroscopy. Phys. Plasmas 2020, 27, 023302. [Google Scholar] [CrossRef]
- Filippov, E.D.; Pikuz, S.A.; Skobelev, I.Y.; Ryazantsev, S.N.; Higginson, D.P.; Khaghani, D.; Revet, G.; Chen, S.N.; Fuchs, J. Parameters of Supersonic Astrophysically-Relevant Plasma Jets Collimating via Poloidal Magnetic Field Measured by X-ray Spectroscopy Method. J. Phys. Conf. Ser. 2016, 774, 012114. [Google Scholar] [CrossRef]
- Higginson, D.P.; Revet, G.; Khiar, B.; Béard, J.; Blecher, M.; Borghesi, M.; Burdonov, K.; Chen, S.N.; Filippov, E.; Khaghani, D.; et al. Detailed Characterization of Laser-Produced Astrophysically-Relevant Jets Formed via a Poloidal Magnetic Nozzle. High Energy Density Phys. 2017, 23, 48–59. [Google Scholar] [CrossRef]
- Revet, G.; Khiar, B.; Filippov, E.; Argiroffi, C.; Béard, J.; Bonito, R.; Cerchez, M.; Chen, S.N.; Gangolf, T.; Higginson, D.P.; et al. Laboratory Disruption of Scaled Astrophysical Outflows by a Misaligned Magnetic Field. Nat. Commun. 2021, 12, 762. [Google Scholar] [CrossRef]
- Tun, S.D.; Vourlidas, A. Derivation of the Magnetic Field in a Coronal Mass Ejection Core via Multi-Frequency Radio Imaging. Astrophys. J. 2013, 766, 130. [Google Scholar] [CrossRef]
- Argiroffi, C.; Reale, F.; Drake, J.J.; Ciaravella, A.; Testa, P.; Bonito, R.; Miceli, M.; Orlando, S.; Peres, G. A Stellar Flare−Coronal Mass Ejection Event Revealed by X-ray Plasma Motions. Nat. Astron. 2019, 3, 742–748. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Shakura, N.I.; Zilitinkevich, S.S. On the Turbulent Energy Transport in Accretion Discs. Astron. Astrophys. 1978, 62, 179–187. [Google Scholar]
- Filippov, E.D.; Skobelev, I.Y.; Revet, G.; Chen, S.N.; Khiar, B.; Ciardi, A.; Khaghani, D.; Higginson, D.P.; Pikuz, S.A.; Fuchs, J. X-ray Spectroscopy Evidence for Plasma Shell Formation in Experiments Modeling Accretion Columns in Young Stars. Matter Radiat. Extrem. 2019, 4, 064402. [Google Scholar] [CrossRef]
- Alkhimova, M.A.; Faenov, A.Y.; Skobelev, I.Y.; Pikuz, T.A.; Nishiuchi, M.; Sakaki, H.; Pirozhkov, A.S.; Sagisaka, A.; Dover, N.P.; Kondo, K.; et al. High Resolution X-ray Spectra of Stainless Steel Foils Irradiated by Femtosecond Laser Pulses with Ultra-Relativistic Intensities. Opt. Express 2017, 25, 29501. [Google Scholar] [CrossRef]
- Ryazantsev, S.N.; Skobelev, I.Y.; Faenov, A.Y.; Pikuz, T.A.; Grum-Grzhimailo, A.N.; Pikuz, S.A. X-ray Spectroscopy Diagnostics of a Recombining Plasma in Laboratory Astrophysics Studies. JETP Lett. 2015, 102, 707–712. [Google Scholar] [CrossRef]
- MacFarlane, J.J.; Golovkin, I.E.; Woodruff, P.R.; Welch, D.R.; Oliver, B.V.; Melhorn, T.A.; Campbell, R.B.; Mehlhorn, T.A.; Campbell, R.B. Simulation of the Ionization Dynamics of Aluminum Irradiated by Intense Short-Pulse Lasers. Proc. Inert. Fusion Sci. Appl. (Am. Nucl. Soc. La Grange Park. IL) 2003, 457, 1–4. [Google Scholar]
- Burdonov, K.F. Ambient Plasma Impact onto Accretion Dynamics of YSOs Modelled in the Laboratory. 2023, manuscript in preparation.
- Fujioka, S.; Takabe, H.; Yamamoto, N.; Salzmann, D.; Wang, F.; Nishimura, H.; Li, Y.; Dong, Q.; Wang, S.; Zhang, Y.; et al. X-ray Astronomy in the Laboratory with a Miniature Compact Object Produced by Laser-Driven Implosion. Nat. Phys. 2009, 5, 821–825. [Google Scholar] [CrossRef]
- Fujioka, S.; Nishimura, H.; Takabe, H.; Yamamoto, N.; Nishihara, K.; Salzmann, D.; Norimatsu, T.; Miyanaga, N.; Mima, K.; Azechi, H.; et al. Laser-Produced Plasmas as Unique X-ray Souces for Industry and Astrophysics. J. Phys. Conf. Ser. 2010, 244, 012001. [Google Scholar] [CrossRef]
- Yi, S.Z.; Dong, J.Q.; Jiang, L.; Huang, Q.S.; Guo, E.F.; Wang, Z.S. Simultaneous High-Resolution X-ray Backlighting and Self-Emission Imaging for Laser-Produced Plasma Diagnostics Using a Two-Energy Multilayer Kirkpatrick–Baez Microscope. Matter Radiat. Extrem. 2021, 7, 015902. [Google Scholar] [CrossRef]
- Bolanos, S.; Sladkov, A.; Smets, R.; Chen, S.N.; Grisollet, A.; Filippov, E.; Henares, J.L.; Nastasa, V.; Pikuz, S.; Riquier, R.; et al. Laboratory Evidence of Magnetic Reconnection Hampered in Obliquely Interacting Flux Tubes. Nat. Commun. 2022, 13, 6426. [Google Scholar] [CrossRef]
- Wang, X.-F.F.; Wang, J.-Y.Y.; Chen, X.-H.H.X.-G.G.; Chen, X.-H.H.X.-G.G.; Wei, L. Large Field-of-View X-ray Imaging by Using a Fresnel Zone Plate. Laser Part. Beams 2012, 30, 87–93. [Google Scholar] [CrossRef]
- Bitter, M.; Hill, K.W.; Gao, L.; Kraus, B.F.; Efthimion, P.C.; Delgado-Aparicio, L.; Pablant, N.; Stratton, B.; Schneider, M.; Coppari, F.; et al. A New Toroidal X-ray Crystal Spectrometer for the Diagnosis of High Energy Density Plasmas at the National Ignition Facility. Rev. Sci. Instrum. 2018, 89, 10F118. [Google Scholar] [CrossRef] [PubMed]
- Shiraga, H.; Miyanaga, N.; Heya, M.; Nakasuji, M.; Aoki, Y.; Azechi, H.; Yamanaka, T.; Mima, K. Ultrafast Two-Dimensional X-ray Imaging with X-ray Streak Cameras for Laser Fusion Research (Invited). Rev. Sci. Instrum. 1998, 68, 745. [Google Scholar] [CrossRef]
- Gregory, C.D.; Dizière, A.; Aoki, H.; Tanji, H.; Ide, T.; Falize, É.; Loupias, B.; Michaut, C.; Morita, T.; Pikuz, S.A.; et al. Experiments to Investigate the Effects of Radiative Cooling on Plasma Jet Collimation. High Energy Density Phys. 2014, 11, 12–16. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).