Quantum Fluctuations in the Small Fabry–Perot Interferometer

Abstract

Spectra of the small Fabry–Perot interferometer (FPI) of the size of the order of the wavelength, with the main mode excited by a quantum field from a nano–LED or a laser, are investigated. The input field is detuned from the FPI mode with only a few photons. We formulate the convenient model for the FPI interacting with a quantum field, and provide novel explicit expressions for the field and the photon number fluctuation spectra inside and outside the FPI, with clearly identified contributions of the quantum and the classical noise. As a result, we found the spectra structures are quite different for the field, the photon number fluctuations inside the FPI, for the transmitted and the reflected fields and note asymmetries in spectra. The quantum noise is colored (or white) inside (or outside) the FPI, which explains differences in spectra. As another novel result, we calculate the second-order time auto–correlation functions for the FPI field; they oscillate and are negative under certain conditions. Results will help the study, design, manufacture, and use of the small elements of quantum optical integrated circuits, such as delay lines or optical transistors.

1. Introduction

The Fabry–Perot interferometer (FPI), invented in 1899 [1], is widely used in optics, optoelectronics, and laser physics [2,3]. FPIs can be met, in particular, in telecommunications for wavelength–division multiplexing [4], as laser cavities [5], in spectroscopy to control and measure the wavelengths of light [6], and in precision displacement measurements (chapter 5.10.1.1 of [7]), in optical integrated circuits [8,9,10]. Recent technological progress leads to a considerable reduction of the optical element size [11,12] and the appearance of photonic quantum technologies (PQT) [13]. PQT requires experimental research and theoretical studies of quantum phenomena in small optical elements, with the size of the order of the optical wavelength, such as the small FPI, operating with a few photons at a significant quantum noise. The paper contributes to the quantum theory of such a small FPI.

The particular motivation for the quantum consideration of the small FPI is making the background for the theoretical model of the small quantum, a single-photon optical transistor for PQT. It is well-known that the FPI with the nonlinear medium has, in certain conditions, dispersive optical bistability [14,15,16] and operates as an optical transistor [17]. Some attractive phenomena have been predicted in the quantum optical transistor based at FPI, for example, the noiseless amplification [18,19]. Thus, the bistable miniature FPI is an essential element for the quantum photonic circuits, necessary for ultra-low power signal processing [20,21].

In this paper, we calculate, in particular, the photon number fluctuation spectrum of the FPI with the quantum input field detuned from the center of the FPI mode. It is a necessary step for analyzing the bistability in the quantum nonlinear FPI with only a few photons. We will do such analysis in the future with the method developed in [22] and related papers [23,24,25,26]. The method of [22] permits solving nonlinear operator equations and generalizes a cumulant–neglect closure approach of the classical stochastic theory [27,28] to spectral analysis of open quantum nonlinear systems such as lasers and nonlinear optical devices. The cumulant–neglect closure approach has been used previously for quantum systems in the cluster expansion method [29,30] for calculations of high–order correlations.

Another motivation of the present study is the investigation of the field, the field power fluctuation spectra, and the auto-correlation functions of the small FPI with a mode detuned from the quantum input field. We find spectral profiles different from Lorentzian (or, Airy) spectral distributions well-known from the classical theory of FPI [3]. We see that spectra are asymmetric, with a noticeable contribution of quantum fluctuations. Spectra have different shapes inside and outside the FPI.

Quantum analysis has been made previously in the relation with various applications of the FPI. For example, the quantum limits of measurements with FPI have been considered in [31]. A quantum description of FPI, modeled as a beam splitter with frequency–dependent transmissivity and reflectivity coefficients, predicts the antibunching [32] necessary for non–classical light generation. A reduction of the effective finesse of the FPI cavity with regard to quantum noise has been found in [33] for the gravitational wave measurements. However, previous theories should pay more attention to the quantum FPI spectra.

Some applications of the FIP with the incoherent input have been studied. For example, the incoherent input field has been applied to FPI in experiments for the characterization of optical Fabry–Perot cavities [34].

We model the FPI as the quantum harmonic oscillator excited by the quantum stochastic force. The oscillator with a stochastic excitation is one of the basic models in the stochastic theory [35,36] including the quantum case [37]. There is a high interest in quantum phenomena in dynamical systems in general. For example, quantum corrections increase the number of equilibrium points in the Hill system considered in relation to the stability of satellites [38,39,40]. We hope that this paper contributes to the spectral theory of open quantum harmonic oscillators and helps to extend the method of [22] from the laser theory to general quantum devices and objects [41] modeled as sets of oscillators.

We present general formulas for the photon number fluctuation spectra inside the FPI and the field power fluctuation spectra outside the FPI; formulate the model for the FPI interacting with a quantum field; and find explicit expressions for the FPI spectra in Section 2.

We show and describe spectra and auto–correlation functions of the FPI, interacting with the quantum field, in Section 3.

The discussion of the results of Section 3 is given in Section 4. The conclusion is in Section 5.

2. Methods: Formulas for Spectra and Quantum Model of the FPI

In this section, we derive formulas for the photon number fluctuation (the field power) spectra for fields inside (outside) the FPI, whose scheme is shown in Figure 1.

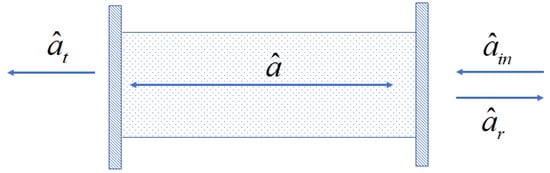
Figure 1. Fabry–Perot interferometer with two semitransparent mirrors, the input (reflected) field amplitude operators ${\widehat{a}}_{in}$ (${\widehat{a}}_r$) on the right, transmitted field ${\widehat{a}}_t$ on the left, and the field $\widehat{a}$ inside.

A quazi–monochromatic external field with Bose–operator ${\widehat{a}}_{in}\left(t\right)e^{-i{\omega }_{l}t}$, with the amplitude operator ${\widehat{a}}_{in}\left(t\right)$ and the carrier frequency ${\omega }_l$, enters the FPI, shown in Figure 1, through the semitransparent mirror on the right. ${\omega }_l$ is close to the frequency ${\omega }_0$ of the center of the FPI mode spectrum. The FPI mode has Bose–operator $\widehat{a}\left(t\right)e^{-i{\omega }_{0}t}$ and is excited by the external field. Detuning $\delta ={\omega }_0-{\omega }_l\ll {\omega }_0,{\omega }_l$. The small FPI in Figure 1 has the size $\sim \lambda /2$, where $\lambda$ is the wavelength of the FPI mode. For certainty, we suppose that the main mode of the small FPI is excited, so the FPI free spectral range is of the order of ${\omega }_0$ or ${\omega }_l$. We assume the FPI cavity quality factor $Q\sim {10}^3$; it can be achieved, for example, in photonic crystal cavities [42]. In the future, we want to satisfy conditions for the dispersive bistability in the FPI with a nonlinear medium [16], so we take $\kappa \le \delta \le$ few $\kappa$, where $\kappa$ is the half–width (HWHM) of the excited FPI mode. For such parameters, we, with a negligibly small error $\sim \delta /\kappa Q\ll 1$, neglect the excitation of all FPI modes but the main FPI mode.

2.1. General Formula for the Photon Number Fluctuation Spectrum in the Cavity

We make Fourier–expansions of the amplitude operators of the field $\widehat{a}\left(t\right)$ inside the FPI cavity and ${\widehat{a}}_{in}\left(t\right)$ of the input field entering the cavity through the semitransparent mirror

$$\widehat{a}\left(t\right)=\frac{1}{\sqrt{2\pi }}\underset{-\infty }{\overset{\infty }{\int }}\widehat{a}\left(\omega \right)e^{-i\omega t}d\omega ,\mathrm{and}{\widehat{a}}_{in}\left(t\right)=\frac{1}{\sqrt{2\pi }}\underset{-\infty }{\overset{\infty }{\int }}{\widehat{a}}_{in}\left(\omega \right)e^{-i\omega t}d\omega ,$$

(1)

where $\widehat{a}\left(\omega \right)$ and ${\widehat{a}}_{in}\left(\omega \right)$ are the Fourier–component operators; $\omega ={\omega }_{opt}-{\omega }_l$ is the deviation of the field optical frequency ${\omega }_{opt}$ from ${\omega }_l$. We consider $T⟨:\widehat{n}\left(t\right)\widehat{n}\left(t^{\prime }\right):⟩$, where $\widehat{n}$ is a photon number operator, $:\widehat{n}\left(t\right)\widehat{n}\left(t^{\prime }\right):$ means the normal ordering, T is the time ordering and $⟨...⟩$ is the quantum averaging; see [43], Section 12.2.2. Using $\widehat{n}\left(t\right)={\widehat{a}}^{+}\left(t\right)\widehat{a}\left(t\right)$ and the first of Fourier–expansions (1), we write

$$T⟨:\widehat{n}\left(t\right)\widehat{n}\left(t^{\prime }\right):⟩=\frac{1}{{\left(2\pi \right)}^2}\underset{-\infty }{\overset{\infty }{\int }}d{\omega }_{1}d{\omega }_{2}d{\omega }_{3}d{\omega }_4⟨:{\widehat{a}}^{+}(-{\omega }_1)\widehat{a}\left({\omega }_2\right){\widehat{a}}^{+}(-{\omega }_3)\widehat{a}\left({\omega }_4\right):⟩T\left[e^{-i({\omega }_1+{\omega }_2)t-i({\omega }_3+{\omega }_4)t^{\prime }}\right],$$

(2)

so we separate the time and the normal–ordering operations.

Fourier–component operators of different frequencies commute; they are uncorrelated with each other, so the mean $⟨{\widehat{a}}^{+}(-{\omega }_1)\widehat{a}\left({\omega }_2\right){\widehat{a}}^{+}(-{\omega }_3)\widehat{a}\left({\omega }_4\right)⟩$ is not zero if ${\omega }_1=-{\omega }_2$ and ${\omega }_3=-{\omega }_4$, or ${\omega }_1=-{\omega }_4$ and ${\omega }_3=-{\omega }_2$. The commutator of the field Bose operators inside the cavity is

$$\left[\widehat{a}\left({\omega }_2\right),{\widehat{a}}^{+}(-{\omega }_3)\right]=c\left({\omega }_2\right)\delta ({\omega }_2+{\omega }_3),$$

(3)

with ${\left(2\pi \right)}^{-1}\underset{-\infty }{\overset{\infty }{\int }}c\left(\omega \right)d\omega =1$[44]. Note that the cavity modifies the density of states of the quantum field, respectively, to the free space [45], so commutation relations (3) for Fourier–component operators in the cavity differ from commutation relations (12) in the free space. $c\left(\omega \right)$ for the FPI cavity is given by Equation (23).

Using (3), we make the normal ordering in (2) exchanging $\widehat{a}\left({\omega }_2\right)$ and ${\widehat{a}}^{+}(-{\omega }_3)$

$$⟨:{\widehat{a}}^{+}(-{\omega }_1)\widehat{a}\left({\omega }_2\right){\widehat{a}}^{+}(-{\omega }_3)\widehat{a}\left({\omega }_4\right):⟩=$$

(4)

$$n\left({\omega }_2\right)n\left({\omega }_4\right)\delta ({\omega }_1+{\omega }_2)\delta ({\omega }_3+{\omega }_4)+n\left({\omega }_2\right)\left[n\left({\omega }_4\right)+c\left({\omega }_4\right)\right]\delta ({\omega }_1+{\omega }_4)\delta ({\omega }_3+{\omega }_2).$$

We insert Equation (4) into Equation (2), calculate the integral in Equation (2) with $\delta$–functions, and see that the integral from the first term in Equation (4) is $n^2$ so that

$$T⟨:\widehat{n}\left(t\right)\widehat{n}\left(t^{\prime }\right):⟩=n^2+\frac{1}{{\left(2\pi \right)}^2}\underset{-\infty }{\overset{\infty }{\int }}d{\omega }_{2}d{\omega }_{4}n\left({\omega }_2\right)\left[n\left({\omega }_4\right)+c\left({\omega }_4\right)\right]T\left[e^{i({\omega }_4-{\omega }_2)(t-t^{\prime })}\right].$$

(5)

The time–ordering operation in Equation (5) is

$$T\left[e^{i({\omega }_4-{\omega }_2)(t-t^{\prime })}\right]=\left\{\begin{array}{c}{e}^{i({\omega }_4-{\omega }_2)(t-t^{\prime })},t\ge t^{\prime }\\ e^{i({\omega }_4-{\omega }_2)(t^{\prime }-t)},t<t^{\prime }\end{array}\right.=e^{i({\omega }_4-{\omega }_2)\left|t-t^{\prime }\right|}.$$

(6)

Replacing in Equation (5) ${\omega }_2$ by a new variable $\omega ={\omega }_2-{\omega }_4$ and ${\omega }_4$ by ${\omega }^{\prime }$, we find the second–order auto–correlation function ${\delta }^{2}n\left(\tau \right)$ for the photon number fluctuations

$${\delta }^{2}n\left(\tau \right)\equiv T⟨:\widehat{n}\left(t\right)\widehat{n}\left(t^{\prime }\right):⟩-n^2=\frac{1}{{\left(2\pi \right)}^2}\underset{-\infty }{\overset{\infty }{\int }}d\omega d{\omega }^{\prime }n(\omega +{\omega }^{\prime })\left[n\left({\omega }^{\prime }\right)+c\left({\omega }^{\prime }\right)\right]e^{-i\omega \left|\tau \right|},$$

(7)

where $\tau =t-t^{\prime }$. The Wiener–Khinchin theorem ([46], page 102) tells us that the spectrum ${\delta }^{2}n\left(\omega \right)$ of the photon number fluctuations is related to ${\delta }^{2}n\left(\tau \right)$ by the Fourier–transform

$${\delta }^{2}n\left(\tau \right)={\left(2\pi \right)}^{-1}\underset{-\infty }{\overset{\infty }{\int }}{\delta }^{2}n\left(\omega \right)e^{-i\omega \tau }d\omega ,$$

(8)

so we find ${\delta }^{2}n\left(\omega \right)$ by the Fourier–transform of Equation (7). In such a transform, the integral over $d\tau$ is split into two parts: from $-\infty$ to 0 and from 0 to ∞, taking into account the multiplier $exp(-i\omega |\tau \left|\right)$. We carry out the Fourier–transform and come to

$${\delta }^{2}n\left(\omega \right)=\frac{1}{4\pi }\underset{-\infty }{\overset{\infty }{\int }}{\left[n({\omega }^{\prime }+\omega )+n({\omega }^{\prime }-\omega )\right]\left[n\left({\omega }^{\prime }\right)+c\left({\omega }^{\prime }\right)\right]d\omega }^{\prime }$$

(9)

Making the replacement ${\omega }^{\prime }\to {\omega }^{″}={\omega }^{\prime }+\omega$, we see that $\underset{-\infty }{\overset{\infty }{\int }}{n({\omega }^{\prime }+\omega )n\left({\omega }^{\prime }\right)d\omega }^{\prime }=\underset{-\infty }{\overset{\infty }{\int }}{n\left({\omega }^{″}\right)n({\omega }^{″}-\omega )d\omega }^{″}$, so we re–write Equation (9) as

$${\delta }^{2}n\left(\omega \right)=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}{n(\omega +{\omega }^{\prime })n\left({\omega }^{\prime }\right)d\omega }^{\prime }+\frac{1}{4\pi }\underset{-\infty }{\overset{\infty }{\int }}{\left[n({\omega }^{\prime }+\omega )+n({\omega }^{\prime }-\omega )\right]c\left({\omega }^{\prime }\right)d\omega }^{\prime }.$$

(10)

The first term in Equation (10) is the same as for the classical field fluctuations ([43], Section 9.8.3). One can obtain this term without the time and the normal orderings, considering $\widehat{a}$ in Equation (2) as a classical fluctuating variable. The second term in Equation (10) appears due to quantum fluctuations applying the time and the normal orderings. Below, we call the first term of (10) a classical contribution, and the second one a quantum contribution to the photon number fluctuation spectrum.

We see in Equation (10) that ${\delta }^{2}n\left(\omega \right)={\delta }^{2}n\left(-\omega \right)$ as it must be for real ${\delta }^{2}n\left(\tau \right)$. The photon number variance ${\delta }^{2}n\equiv {\left(2\pi \right)}^{-1}\underset{-\infty }{\overset{\infty }{\int }}{\delta }^{2}n\left(\omega \right)d\omega =n\left(n+1\right)$ corresponds to Bose–Einstein distribution.

The meaning of $\omega$ in ${\delta }^{2}n\left(\omega \right)$ is different from the meaning of $\omega$ in $n\left(\omega \right)$ or $\widehat{a}\left(\omega \right)$. $\omega$ in ${\delta }^{2}n\left(\omega \right)$ is the radio frequency. Otherwise, $\omega$ in $n\left(\omega \right)$ or $\widehat{a}\left(\omega \right)$ is the deviation of the optical frequency ${\omega }_{opt}$ of the field inside the FPI from the central frequency ${\omega }_l$ of the input field spectra.

2.2. Photon Number Fluctuation Spectra Outside FPI: General Formula

We write the field power operator (in photons per second) in the free space ${\widehat{p}}_{\alpha }\left(t\right)={\widehat{a}}_{\alpha }^{+}\left(t\right){\widehat{a}}_{\alpha }\left(t\right)$ for the input $\alpha =in$, output $\alpha =out$ fields, and the field reflected from the input mirror of the interferometer $\alpha =out$. We will find

$$T⟨:{\widehat{p}}_{\alpha }\left(t\right){\widehat{p}}_{\alpha }\left(t^{\prime }\right):⟩=\frac{1}{{\left(2\pi \right)}^2}\underset{-\infty }{\overset{\infty }{\int }}d{\omega }_{1}d{\omega }_{2}d{\omega }_{3}d{\omega }_4⟨:{\widehat{a}}_{\alpha }^{+}(-{\omega }_1){\widehat{a}}_{\alpha }\left({\omega }_2\right){\widehat{a}}_{\alpha }^{+}(-{\omega }_3){\widehat{a}}_{\alpha }\left({\omega }_4\right):⟩T\left[e^{-i({\omega }_1+{\omega }_2)t-i({\omega }_3+{\omega }_4)t^{\prime }}\right]$$

(11)

We carry out the normal ordering in Equation (11) using commutation relations for Bose operators in free space [44]

$$\left[{\widehat{a}}_{\alpha }\left(\omega \right),{\widehat{a}}_{\alpha }^{+}(-{\omega }^{\prime })\right]=\delta (\omega +{\omega }^{\prime })$$

(12)

so that

$$⟨{\widehat{a}}_{\alpha }^{+}(-{\omega }_1){\widehat{a}}_{\alpha }\left({\omega }_2\right){\widehat{a}}_{\alpha }^{+}(-{\omega }_3){\widehat{a}}_{\alpha }\left({\omega }_4\right)⟩=⟨{\widehat{a}}_{\alpha }^{+}(-{\omega }_1){\widehat{a}}_{\alpha }^{+}(-{\omega }_3){\widehat{a}}_{\alpha }\left({\omega }_2\right){\widehat{a}}_{\alpha }\left({\omega }_4\right)⟩+⟨{\widehat{a}}_{\alpha }^{+}(-{\omega }_1){\widehat{a}}_{\alpha }\left({\omega }_4\right)⟩\delta ({\omega }_2+{\omega }_3).$$

Similar to the case of Equation (2), we note that operators of different frequencies commute and do not correlate with each other; therefore,

$$⟨{\widehat{a}}_{\alpha }^{+}(-{\omega }_1){\widehat{a}}_{\alpha }\left({\omega }_2\right){\widehat{a}}_{\alpha }^{+}(-{\omega }_3){\widehat{a}}_{\alpha }\left({\omega }_4\right)⟩=⟨{\widehat{a}}_{\alpha }^{+}\left({\omega }_2\right){\widehat{a}}_{\alpha }\left({\omega }_2\right)⟩⟨{\widehat{a}}_{\alpha }^{+}\left({\omega }_4\right){\widehat{a}}_{\alpha }\left({\omega }_4\right)⟩\delta ({\omega }_1+{\omega }_2)\delta ({\omega }_3+{\omega }_4)+$$

$$⟨{\widehat{a}}_{\alpha }^{+}\left({\omega }_4\right){\widehat{a}}_{\alpha }\left({\omega }_4\right)⟩\left[⟨{\widehat{a}}_{\alpha }^{+}\left({\omega }_2\right){\widehat{a}}_{\alpha }\left({\omega }_2\right)⟩+1\right]\delta ({\omega }_1+{\omega }_2)\delta ({\omega }_3+{\omega }_4)$$

(13)

Inserting Equation (13) into the integral in Equation (11), we see that the first term in Equation (13) is the mean power square ${⟨{\widehat{p}}_{\alpha }\left(t\right)⟩}^2\equiv p_{\alpha }^2$. Taking the integral in Equation (11) over $d{\omega }_1$ and $d{\omega }_3$, inserting there the power spectra $p_{\alpha }\left({\omega }_{2,4}\right)=⟨{\widehat{a}}_{\alpha }^{+}\left({\omega }_{2,4}\right){\widehat{a}}_{\alpha }\left({\omega }_{2,4}\right)⟩$, we come to the auto–correlation function for the field power fluctuations in free space

$${\delta }^2{p}_{\alpha }\left(\tau \right)\equiv ⟨{\widehat{p}}_{\alpha }\left(t\right){\widehat{p}}_{\alpha }\left(t^{\prime }\right)⟩-p_{\alpha }^2=\frac{1}{{\left(2\pi \right)}^2}\underset{-\infty }{\overset{\infty }{\int }}d{\omega }^{\prime }d\omega p_{\alpha }({\omega }^{\prime }-\omega )\left[p_{\alpha }\left({\omega }^{\prime }\right)+1\right]e^{-i\omega \left|\tau \right|},$$

(14)

where $\tau =t-t^{\prime }$, and we replace ${\omega }_4$ by $\omega ={\omega }_2-{\omega }_4$; ${\omega }_2$ by ${\omega }^{\prime }$. The integral over $d{\omega }_2$ in the second term in Equation (14) leads to ${\left(2\pi \right)}^{-1}\underset{-\infty }{\overset{\infty }{\int }}d{\omega }_2{p}_{\alpha }({\omega }_2-\omega )=p_{\alpha }$, the integral over $d\omega$ in this term gives ${\left(2\pi \right)}^{-1}\underset{-\infty }{\overset{\infty }{\int }}{e}^{-i\omega \left|\tau \right|}d\omega =\delta \left(\tau \right)$, so the auto–correlation function is

$${\delta }^2{p}_{\alpha }\left(\tau \right)=\frac{1}{{\left(2\pi \right)}^2}\underset{-\infty }{\overset{\infty }{\int }}d{\omega }^{\prime }{p}_{\alpha }({\omega }^{\prime }-\omega )p_{\alpha }\left({\omega }^{\prime }\right)e^{-i\omega \left|\tau \right|}d\omega +p_{\alpha }\delta \left(\tau \right).$$

(15)

The Fourier transform of Equation (15) leads to the spectrum ${\delta }^2{p}_{\alpha }\left(\omega \right)$ of the field power fluctuations in the free space

$${\delta }^2{p}_{\alpha }\left(\omega \right)=\frac{1}{4\pi }\underset{-\infty }{\overset{\infty }{\int }}\left[p_{\alpha }({\omega }^{\prime }-\omega )p_{\alpha }\left({\omega }^{\prime }\right)+p_{\alpha }({\omega }^{\prime }+\omega )p_{\alpha }\left({\omega }^{\prime }\right)\right]d{\omega }^{\prime }+p_{\alpha }.$$

(16)

Since $\underset{-\infty }{\overset{\infty }{\int }}d{\omega }^{\prime }{p}_{\alpha }({\omega }^{\prime }-\omega )p_{\alpha }\left({\omega }^{\prime }\right)=\underset{-\infty }{\overset{\infty }{\int }}d{\omega }^{\prime }{p}_{\alpha }({\omega }^{\prime }+\omega )p_{\alpha }\left({\omega }^{\prime }\right)$, we write Equation (16) as

$${\delta }^2{p}_{\alpha }\left(\omega \right)=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}{p}_{\alpha }({\omega }^{\prime }-\omega )p_{\alpha }\left({\omega }^{\prime }\right)d{\omega }^{\prime }+p_{\alpha }.$$

(17)

The first term in Equation (17) is a “colored” part of the spectrum. The second term is a white noise with constant spectrum power density $p_{\alpha }$. The first term in Equation (17) is the classical contribution, similar to the first term in Equation (10). The second one is the quantum contribution.

Equation (17) is different from the result for the classical field ([43], Section 9.8.3) in the second term $p_{\alpha }$, which is the spectral density of the “white” quantum noise. Note the difference between the quantum (the second) terms in Equations (10) and (17). The quantum term in Equation (10) is a convolution of “colored” quantum noise with the field spectrum in the cavity, while there is a “white” quantum noise term in Equation (17) for the free space.

Dimensionalities of $n\left(\omega \right)$ and ${\delta }^{2}n\left(\omega \right)$ are the photon number per Hz and the photon number square per Hz, respectively. Dimensionalities of $p_{\alpha }\left(\omega \right)$ (${\delta }^2{p}_{\alpha }\left(\omega \right)$) are the photon number (the photon number square) per second per Hz.

2.3. The Model of the FPI with Quantum Input Field

We consider the field and the photon number fluctuation spectra inside and outside the small FPI; the main FPI cavity mode is excited by the quasi–monochromatic quantum field taken, for example, from a LED or a laser. Figure 2 shows the scheme of the FPI (on the left) and the input field source (on the right).

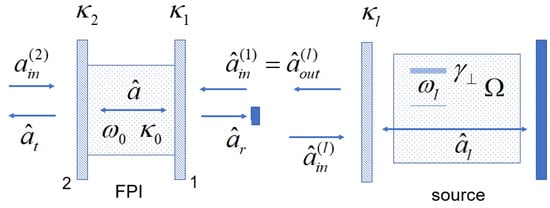
Figure 2. FPI (on the left) with the source of the quantum field (on the right). The field ${\widehat{a}}_r$, reflected from the FPI input mirror 1, is isolated from the source. FPI parameters are explained in the main text, and parameters of the field source are described in Appendix A.

Bose–operator $\widehat{a}$ of the FPI mode amplitude satisfies the equation

$$\dot{\widehat{a}}=-\left(i\delta +{\kappa }_t\right)\widehat{a}+\sqrt{2{\kappa }_0}{\widehat{a}}_{in}^{\left(0\right)}+\sqrt{2{\kappa }_1}{\widehat{a}}_{in}^{\left(1\right)}+\sqrt{2{\kappa }_2}{\widehat{a}}_{in}^{\left(2\right)},$$

(18)

written with the help of the input–output theory [44]. In Equation (18), ${\kappa }_t={\kappa }_1+{\kappa }_2+{\kappa }_0$ is the decay rate of the mode due to the field escape through the FPI semitransparent mirrors 1 and 2 with rates ${\kappa }_{1,2}$ and the absorption inside the FPI with the rate ${\kappa }_0$. Bose–operators ${\widehat{a}}_{in}^{\left(0\right)}$ and ${\widehat{a}}_{in}^{\left(2\right)}$ correspond to zero temperature baths, uncorrelated with each other and related with the absorption and the field escape through the FPI mirror 2. The input field with the Bose–operator ${\widehat{a}}_{in}^{\left(1\right)}$ is the output ${\widehat{a}}_{out}^{\left(l\right)}$ of the source in Figure 2.

Making the Fourier transform in Equation (18) and solving the equation for Fourier–component operators, we find the Fourier–component operator of the FPI mode

$$\widehat{a}\left(\omega \right)=\frac{\sqrt{2{\kappa }_0}{\widehat{a}}_{in}^{\left(0\right)}\left(\omega \right)+\sqrt{2{\kappa }_1}{\widehat{a}}_{in}^{\left(1\right)}\left(\omega \right)+\sqrt{2{\kappa }_2}{\widehat{a}}_{in}^{\left(2\right)}\left(\omega \right)}{{\kappa }_t+i\left(\delta -\omega \right)},$$

(19)

where $\omega ={\omega }_{opt}-{\omega }_0$, ${\omega }_{opt}$ is the optical frequency of the mode, ${\widehat{a}}_{in}^{(0,2)}\left(\omega \right)$ and ${\widehat{a}}_{in}^{\left(1\right)}\left(\omega \right)$ are Fourier–component operators of baths and the input field. The baths and the input field operators obey the free space Bose–commutation relations [44]

$$[{\widehat{a}}_{in}^{\left(\alpha \right)}\left(\omega \right),{\widehat{a}}_{in}^{+\left(\alpha \right)}\left({\omega }^{\prime }\right)]=\delta (\omega +{\omega }^{\prime }),$$

(20)

$\alpha =0,1,2$. Substituting the expression (19) into the relation $⟨{\widehat{a}}^{+}(-\omega )\widehat{a}\left({\omega }^{\prime }\right)⟩=n\left(\omega \right)\delta (\omega +{\omega }^{\prime })$, we obtain the spectrum $n\left(\omega \right)$ of the FPI mode

$$n\left(\omega \right)=\frac{{\kappa }_1}{{\kappa }_t}{p}_{in}\left(\omega \right)L(\delta -\omega ,{\kappa }_t),$$

(21)

where $p_{in}\left(\omega \right)$ is the input field spectrum satisfying $⟨{\widehat{a}}_{in}^{\left(1\right)+}(-\omega ){\widehat{a}}_{in}^{\left(1\right)}\left({\omega }^{\prime }\right)⟩=p_{in}\left(\omega \right)\delta (\omega +{\omega }^{\prime })$. In Equation (21) and below, we denote the Lorenz spectrum

$$L(\omega ,\kappa )=\frac{2\kappa }{{\omega }^2+{\kappa }^2},{\left(2\pi \right)}^{-1}\underset{-\infty }{\overset{\infty }{\int }}L(\omega ,\kappa )d\omega =1.$$

(22)

Using Equation (19) and Bose–commutation relations (20), we find

$$[\widehat{a}\left({\omega }^{\prime }\right),{\widehat{a}}^{+}(-\omega )]=L(\delta -\omega ,{\kappa }_t)\delta (\omega +{\omega }^{\prime })\equiv c\left(\omega \right)\delta (\omega +{\omega }^{\prime }),$$

(23)

where $c\left(\omega \right)$ is a “commutator spectrum”; see Equation (3).

The input field spectrum is

$$p_{in}\left(\omega \right)=p_{in}L(\omega ,{\gamma }_l),{\gamma }_l=\frac{{\gamma }_{max}}{1+p_{in}/{\kappa }_l},$$

(24)

where $p_{in}$ is the input power in photons per second, ${\gamma }_l$ is the spectrum HWHM with the maximum value ${\gamma }_{max}$; ${\kappa }_l$ is the input field emission rate from the mirror of the source in Figure 2. When $p_{in}$ increases, ${\gamma }_l$ decreases. We identify the LED, the intermediate, and the lasing regime when ${\gamma }_l\gg {\kappa }_l$, ${\gamma }_l\sim {\kappa }_l$, and ${\gamma }_l\ll {\kappa }_l$, correspondingly. The derivation of expressions (24) is in the Appendix A.

2.4. Explicit Expressions for Spectra Inside FPI

Equations (21) and (24) give the field spectrum $n\left(\omega \right)$ inside the FPI. Using

${\left(2\pi \right)}^{-1}\underset{-\infty }{\overset{\infty }{\int }}L(\omega ,{\gamma }_1)L(\delta -\omega ,{\gamma }_2)d\omega =L(\delta ,{\gamma }_1+{\gamma }_2)$ we calculate the integral

$n={\left(2\pi \right)}^{-1}\underset{-\infty }{\overset{\infty }{\int }}n\left(\omega \right)d\omega$ and find the mean photon number in the FPI mode

$$n=\frac{{\kappa }_1}{{\kappa }_t}{p}_{in}L(\delta ,{\kappa }_t+{\gamma }_l).$$

(25)

With $n\left(\omega \right)$ from Equation (21) and $c\left(\omega \right)$ from Equation (23), we obtain, from Equation (10), the FPI mode photon number (or the field power) fluctuation spectrum

$${\delta }^{2}n\left(\omega \right)={\left(\frac{p_{in}{\kappa }_1}{{\kappa }_t}\right)}^2{J}_0\left(\omega \right)+\frac{p_{in}{\kappa }_1}{{\kappa }_t}{J}_1\left(\omega \right),$$

(26)

where

$$J_0\left(\omega \right)=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}L({\omega }^{\prime }-\omega ,{\gamma }_l)L({\omega }^{\prime }-\omega -\delta ,{\kappa }_t)L({\omega }^{\prime },{\gamma }_l)L({\omega }^{\prime }-\delta ,{\kappa }_t)d{\omega }^{\prime },$$

(27)

$$J_1\left(\omega \right)=\frac{1}{4\pi }\underset{-\infty }{\overset{\infty }{\int }}\left[L({\omega }^{\prime }-\omega ,{\gamma }_l)L({\omega }^{\prime }-\omega -\delta ,{\kappa }_t)+L({\omega }^{\prime }+\omega ,{\gamma }_l)L({\omega }^{\prime }+\omega -\delta ,{\kappa }_t)\right]L({\omega }^{\prime }-\delta ,{\kappa }_t)d{\omega }^{\prime }$$

(28)

One can find some cumbersome explicit expressions for $J_{0,1}\left(\omega \right)$. We do not write them here.

2.5. Explicit Spectra Outside FPI

2.5.1. The Field Spectra

Spectra of the transmitted $p_t\left(\omega \right)$, the absorbed $p_0\left(\omega \right)$ fields, and the transmitted $p_t$ and the absorbed $p_0$ field powers are

$$p_{t,0}\left(\omega \right)=2{\kappa }_{2,0}n\left(\omega \right),p_{t,0}=2{\kappa }_{2,0}n.$$

(29)

The reflected field is ${\widehat{a}}_r=\sqrt{2{\kappa }_1}\widehat{a}-{\widehat{a}}_{in}^{\left(1\right)}$, according to the boundary conditions on the FPI input mirror 1 in Figure 2. Taking $\widehat{a}\left(\omega \right)$ from Equation (19), we see that the reflected field Fourier component is

$${\widehat{a}}_r\left(\omega \right)=2\sqrt{{\kappa }_1}\frac{\sqrt{{\kappa }_0}{\widehat{a}}_{in}^{\left(0\right)}\left(\omega \right)+\sqrt{{\kappa }_1}{\widehat{a}}_{in}^{\left(1\right)}\left(\omega \right)+\sqrt{{\kappa }_2}{\widehat{a}}_{in}^{\left(2\right)}\left(\omega \right)}{{\kappa }_t+i\left(\delta -\omega \right)}-{\widehat{a}}_{in}^{\left(1\right)}\left(\omega \right)$$

(30)

Inserting Equation (30) into $⟨{\widehat{a}}_r^{+}(-\omega ){\widehat{a}}_r\left({\omega }^{\prime }\right)⟩=p_r\left(\omega \right)\delta (\omega +{\omega }^{\prime })$, taking into account that only the input field ${\widehat{a}}_{in}^{\left(1\right)}\left(\omega \right)$ gives a non–zero contribution to $p_r\left(\omega \right)$, calculating the mean values and expressing the result in terms of Lorenz spectra (22), we obtain the reflected field spectrum

$$p_r\left(\omega \right)=p_{in}\left[1-\frac{2{\kappa }_1({\kappa }_2+{\kappa }_0)}{{\kappa }_t}L(\omega -\delta ,{\kappa }_t)\right]L(\omega ,{\gamma }_l).$$

(31)

One can see that $p_r\left(\omega \right)+p_t\left(\omega \right)+p_0\left(\omega \right)=p_{in}\left(\omega \right)$, as it must be.

2.5.2. The Field Power Fluctuation Spectra

We substitute $p_t\left(\omega \right)$ and $p_t$ from Equation (29) into Equation (17), carry out the integration, and find the power fluctuation spectrum of the transmitted field

$${\delta }^2{p}_t\left(\omega \right)=2{\kappa }_2\left[{\left(\frac{{\kappa }_1}{{\kappa }_t}{p}_{in}\right)}^2{J}_0\left(\omega \right)+n\right],$$

(32)

where $J_0\left(\omega \right)$ is given by Equation (27).

We insert $p_r\left(\omega \right)$ from Equation (31) and $p_r$ from Equation (29) into Equation (17), calculate integrals, and find the spectrum of the reflected field power fluctuations

$${\delta }^2{p}_r\left(\omega \right)=p_{in}^2\left\{L(\omega ,2{\gamma }_l)-\frac{2{\kappa }_1({\kappa }_2+{\kappa }_0)}{{\kappa }_t}{J}_2\left(\omega \right)+{\left(\frac{2{\kappa }_1({\kappa }_2+{\kappa }_0)}{{\kappa }_t}\right)}^2{J}_0\left(\omega \right)\right\}+p_r,$$

(33)

where

$$J_2\left(\omega \right)=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}L({\omega }^{\prime }-\omega ,{\gamma }_l)L({\omega }^{\prime },{\gamma }_l)\left[L({\omega }^{\prime }-\omega -\delta ,{\kappa }_t)+L({\omega }^{\prime }-\delta ,{\kappa }_t)\right]d{\omega }^{\prime }$$

(34)

and $J_0\left(\omega \right)$ is given by Equation (27).

2.5.3. Reflection and Transmission Coefficients

We calculate the reflected field power $p_r$ integrating Equation (31) and find the coefficient R of the reflection from the FPI input mirror 1 in Figure 2

$$R\equiv \frac{p_r}{p_{in}}=1-\frac{2{\kappa }_1({\kappa }_2+{\kappa }_0)}{{\kappa }_t}L(\delta ,{\kappa }_t+{\gamma }_l).$$

(35)

Taking $p_t=2{\kappa }_{2}n$ and the expression (25) for n, we find the FPI transmission coefficient

$$T\equiv \frac{p_t}{p_{in}}=\frac{2{\kappa }_1{\kappa }_2}{{\kappa }_t}L(\delta ,{\kappa }_t+{\gamma }_l).$$

(36)

When ${\kappa }_0=0$, the absorption inside the FPI is absent, then $T+R=1$. When ${\gamma }_l\to 0$, Equations (35) and (36) come to expressions for the T and R for the FPI with the monochromatic input [47].

3. Results

We demonstrate examples of spectra of the FPI with quantum input at the different input field powers. Suppose that the FPI input is taken from the small field source as the quantum dot LED or laser with the photonic crystal cavity [42]. The source cavity quality factor is $Q={10}^3$; the frequency of the center of the input field spectrum corresponds to the wavelength ${\lambda }_l=1.55$ μm. Such a field source with the mean cavity photon number $n_l=1$ produces about $8·{10}^{11}$ photons per second (≈0.07 μWt). We take the rate ${\kappa }_l=4·{10}^{11}$ rad/s of the field escape from the source cavity as a normalizing factor.

We will see fascinating features of FPI spectra by changing the normalized FPI input power $p_{in}/{\kappa }_l=2n_l$ in the range from 0 to 50. $n_l$ in the range $0<n_l\le 25$ corresponds to the LED ($n_l<1$), the intermediate ($n_l\sim 1$), and the lasing ($n_l\gg 1$) radiation. $n_l\le 25$ obtained in the photonic crystal laser with 100–1000 resonant emitters (quantum dots) with the small lasing mode volume V, for example, $V\sim 10{\left({\lambda }_l/2n_r\right)}^3$, where ${\left({\lambda }_l/2n_r\right)}^3$ is the minimum cavity mode volume, and $n_r$ is the refractive index inside the source cavity.

We take ${\gamma }_{max}=3{\kappa }_l$ in Equation (24); see the expression for ${\gamma }_{max}$ in Appendix A. We suppose that the FPI is from the photonic crystal, similar to the cavity of the input field source, so we take the decay rates in the FPI cavity of the order of ${\kappa }_l$, namely ${\kappa }_1/{\kappa }_l={\kappa }_2/{\kappa }_l=0.5$, ${\kappa }_0/{\kappa }_l=0.1$. We set the detuning $\delta /{\kappa }_l=5$, which is relatively large, respectively, to the FPI mode total decay rate ${\kappa }_t/{\kappa }_l=1.1$. Relatively large detuning is necessary for the optical bistability in the small FPI with a quantum field and nonlinear medium [14,15], which we will consider in the future. The chosen $\delta$ is not too large, so the main FPI mode is effectively excited by the input field, while the excitation of the other FPI modes is negligibly small.

For $\delta /{\kappa }_l=5$, the mean FPI cavity photon number $n\sim 1$, even for high power of the input field $p_{in}/{\kappa }_l=50$, when the input is practically coherent radiation of a narrow spectrum, with a small HWHM ${\gamma }_l/{\kappa }_l\ll 1$; see Figure 3a. Such a small number of photons in the FPI cavity confirms the importance of quantum analysis.

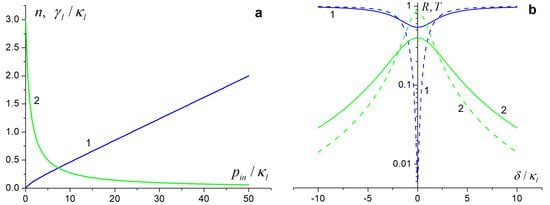
Figure 3. (a) The mean photon number n in the FPI mode (curve 1) and the HWHM ${\gamma }_l$ of the input field spectrum (curve 2) versus the power $p_{in}$ of the input field for the detuning $\delta /{\kappa }_l=5$. Note that $n\sim 1$, at a high input power $p_{in}/{\kappa }_l\gg 1$; (b) reflection R (curves 1) and transmission T (curves 2) coefficients of the FPI versus the detuning $\delta$. Solid curves are for the input field spectrum of a finite HWHM ${\gamma }_l/{\kappa }_l=1.5$ (at $p_{in}/{\kappa }_l=1$), dashed curves are for the monochromatic input with ${\gamma }_l/{\kappa }_l\to 0$, values of other parameters given in the text. Near $\delta /{\kappa }_l=0$, the transmittance for the finite spectral width field is low, and the reflection is higher than for the monochromatic field—compare the solid and the dashed curves with the same numbers.

3.1. Reflection and Transmission Coefficients

The reflection $R\left(\delta \right)$ and the transmission $T\left(\delta \right)$ coefficients characterize the FPI. Equation (35) defines $R\left(\delta \right)$ and $T\left(\delta \right)$, shown in Figure 3b, for the FPI with quantum input. $R\left(\delta \right)$ and $T\left(\delta \right)$ are symmetric relative to $\delta =0$. We see from Figure 3b that the FPI has a lower transmission and higher reflection for the finite spectral width input than for the monochromatic input field. Indeed, the non–monochromatic input field includes the frequency components detuned from the exact resonance with the FPI mode even at $\delta =0$.

3.2. Field Spectra

The field spectra outside the FPI have the spectrum power densities $p_{\alpha }({\omega }_{opt}-{\omega }_l)$ (in photons per second per Hz): transmitted $\alpha =t$, see Equation (29); input $\alpha =in$, Equation (24); and reflected from the mirror of the FPI, $\alpha =r$, Equation (31). The physical meaning of, for example, $p_r\left(\omega \right)d\omega /p_{in}$ is the part of the input field power in a narrow frequency interval ${\omega }_l+\omega ÷{\omega }_l+\omega +d\omega$ reflected from the FPI input mirror.

Figure 4a–d show $p_{\alpha }({\omega }_{opt}-{\omega }_l)$. The input field power $p_{in}$ increased, and the input field spectra HWHM ${\gamma }_l$ decreased from Figure 4a–d. The reflected field spectrum $p_r({\omega }_{opt}-{\omega }_l)$ (green curves 1) has the same structure at any $p_{in}$ and ${\gamma }_l$. There is the peak at the center of the input field spectrum at ${\omega }_{opt}={\omega }_l$ and the gap at the center of the FPI mode spectrum at ${\omega }_{opt}={\omega }_0$. The peak is narrower and higher, and the gap has a smaller depth at the higher $p_{in}$ and smaller ${\gamma }_l$; see the green curves 1.

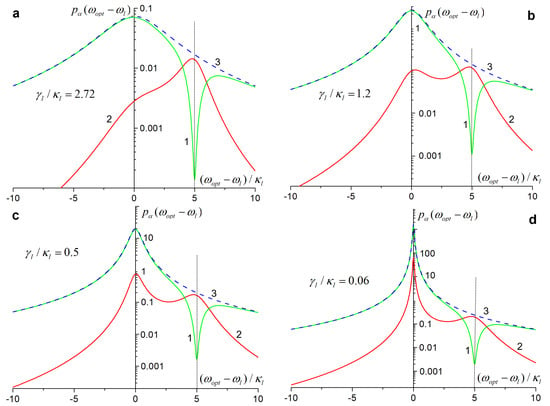
Figure 4. Spectral power densities $p_{\alpha }({\omega }_{opt}-{\omega }_l)$ are shown for reflected (curves 1), transmitted (2), and input (3) fields. The power $p_{in}$ increases from (a) to (d): $p_{in}/{\kappa }_l=0.1$ (a), 1.5 (b), 5 (c), and 50 (d). The input field spectrum HWHM ${\gamma }_l$ decreases with the $p_{in}$; ${\gamma }_l/{\kappa }_l$ values are in the figures. The minima of the transmitted and local maxima of the reflected field spectra correspond to the center of the FPI mode marked by the vertical dashed line. Maxima at ${\omega }_{opt}={\omega }_l$ (the horizontal axis zero) correspond to the center of the input field spectrum.

The structure of the transmitted field spectrum (the red curves 2) changed with $p_{in}$ and ${\gamma }_l$. For Figure 4a, the FPI mode is excited by a weak broadband input field with $p_{in}/{\kappa }_l=0.1$ and ${\gamma }_l/{\kappa }_l=2.72>{\kappa }_t/{\kappa }_l=1.1$, so the input field spectrum is broader than the empty FPI mode spectrum. The transmitted field spectrum in Figure 4a is broad and asymmetric, with a single maximum at the center ${\omega }_{opt}={\omega }_0$ of the FPI mode.

When we go from Figure 4a–d, the input power $p_{in}$ grows with the narrowing of the input field spectrum. For Figure 4b, $p_{in}/{\kappa }_l=1.5$, and ${\gamma }_l/{\kappa }_l=1.2$—close to the HWHM ${\kappa }_t/{\kappa }_l=1.1$ of the empty FPI mode. The peak at ${\omega }_{opt}-{\omega }_l=\delta$ appears in the transmitted field spectrum in Figure 4b. Parameters of Figure 4b are such that both maxima in the transmitted field spectra have approximately the same height. The maxima slightly shifted toward each other relative to the maxima of the input field spectra (at zero in Figure 4) and the FPI mode spectra (marked by the vertical dashed line).

With further increase of $p_{in}$ and narrowing of the input field spectra, the maximum of the transmitted FPI spectrum at the input field frequency (at zero in Figure 4) increases and narrows as in Figure 4c,d.

If we separate the transmitted field spectra at their local minimum at ${\omega }_{opt}-{\omega }_l=\delta /2$, we see that 48, 70, and 95% of the transmitted field energy are in the left part, near the maximum of the input field spectrum—for Figure 4b,c, and d correspondingly. Thus, a large amount of the transmitted field energy is in the spectral range of the input of a narrow spectrum, as for Figure 4c,d. The situation is the opposite for a broadband input, as in Figure 4a, where the principal part of the transmitted field energy is near the maximum of the FPI mode spectrum marked by the vertical dashed line.

Figure 5a shows the field spectrum $n({\omega }_{opt}-{\omega }_l)$ inside the FPI cavity, normalized to ${\kappa }_l^{-1}$ and given by Equation (21).

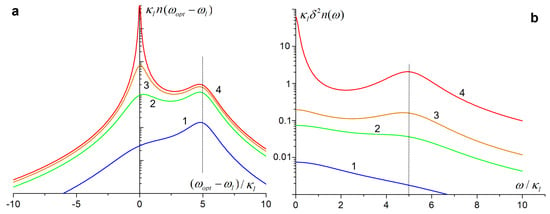
Figure 5. (a) The field $n({\omega }_{opt}-{\omega }_l)$ and (b) the photon number fluctuation ${\delta }^{2}n\left(\omega \right)$ spectra of the FPI cavity mode for $p_{in}/{\kappa }_l=0.1$ [${\gamma }_l/{\kappa }_l=2.5$] (curves 1); 1.5 [1.1] (2); 5 [0.45] (3); and 50 [0.05] (4). The field spectra have two maxima, similar to the transmitted field spectra in Figure 4. ${\delta }^{2}n\left(\omega \right)$ has the sideband maxima at $\omega =\delta$ (shown by the vertical dashed line) in curve 3,4 for a high input field power.

In Figure 5, the input field power (the linewidth) increases (decreases) from curve 1 to curve 4. $n({\omega }_{opt}-{\omega }_l)$ spectra have two peaks at a large input field, similar to the transmitted field spectrum curves shown in Figure 4. Note that the shape of $n({\omega }_{opt}-{\omega }_l)$ curves in Figure 5a is different from the well–known Lorenzian (or Airy function) curves of the field mode spectra of the empty FPI [3].

3.3. Photon Number Fluctuation Spectra

Figure 5b shows ${\delta }^{2}n\left(\omega \right)$, given by Equation (26), for the same parameters as for the FPI field spectra in Figure 5a. In Figure 5b, the width of the input field spectrum exceeds the width of the empty FPI mode for curves 1 and 2, so $\delta n\left(\omega \right)$ is broad with a single maximum at $\omega =0$. When the input power $p_{in}$ increases and the input field spectrum narrows, the second local peak appears in ${\delta }^{2}n\left(\omega \right)$ at $\omega =\delta$ in curve 3. The peak at $\omega =0$ is higher and narrower while the $p_{in}$ increases. The sideband maximum at $\omega =\delta$ grows with the $p_{in}$ but not so rapidly as the maximum at $\omega =0$ in curve 4.

It is interesting to compare the classical and the quantum contributions in ${\delta }^{2}n\left(\omega \right)$ given by the first and the second terms in Equation (26), correspondingly. Figure 6a–d present ${\delta }^{2}n\left(\omega \right)$ curves, the same as in Figure 5b, together with the quantum and the classical contributions to them.

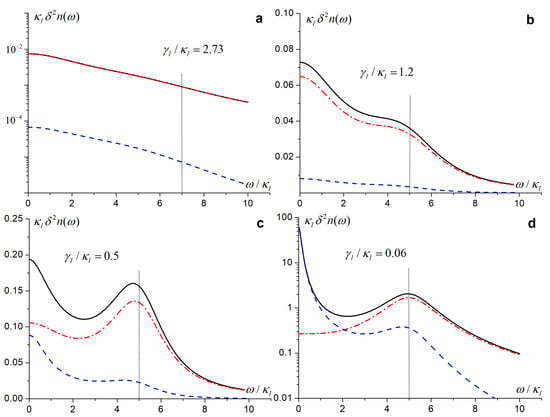
Figure 6. Photon number fluctuation spectra in the FPI mode (solid curves) and their classical (dashed curves) and quantum (dash–dotted curves) components. Solid curves in Figures (a–d) are the same as curves 1–4, correspondingly, in Figure 5b. The vertical dashed lines mark $\omega =\delta$.

Figure 6a corresponds to a broadband spectrum of the input field with the HWHM ${\gamma }_l>{\kappa }_t$. Large quantum fluctuations contribute to ${\delta }^{2}n\left(\omega \right)$. The broad ${\delta }^{2}n\left(\omega \right)$ spectrum has only one maximum at $\omega =0$.

With the increase of $p_{in}$ and the reduction of ${\gamma }_l$ up to ${\gamma }_l\sim {\kappa }_t$, a structure of ${\delta }^{2}n\left(\omega \right)$ appears near $\omega =\delta$ in Figure 6b; quantum fluctuations still give a significant contribution to ${\delta }^{2}n\left(\omega \right)$. With further $p_{in}$ growth and the input field spectrum narrowing, the quantum and the classical contributions to ${\delta }^{2}n\left(\omega \right)$ become similar; see the peaks at $\omega =0$ and $\omega =\delta$ in Figure 6c. With a large $p_{in}$, when ${\gamma }_l\ll {\kappa }_l,{\kappa }_t$, and when the input field source approaches a lasing regime, the spike in ${\delta }^{2}n\left(0\right)$ is high and narrow, while the side–band peak in $\omega =\delta$ still presents in Figure 6d. Photon number fluctuations in the FPI cavity give a considerable contribution to ${\delta }^{2}n\left(\omega \right)$ near the FPI mode maximum at $\omega =\delta$, marked by the vertical dashed lines in Figure 6.

Photon number fluctuations have the maximum at the center of the FPI cavity mode, shifted on $\delta$, respectively, to the center of the input field spectrum. This explains the noticeable contribution of quantum fluctuations near $\omega =\delta$.

Figure 7 show the power fluctuation spectra of the transmitted ${\delta }^2{p}_t\left(\omega \right)$ and the reflected ${\delta }^2{p}_r\left(\omega \right)$ fields given by Equations (32) and (33). Profiles of the spectra in Figure 7 differ from the power fluctuation spectra inside the FPI in Figure 5b and Figure 6.

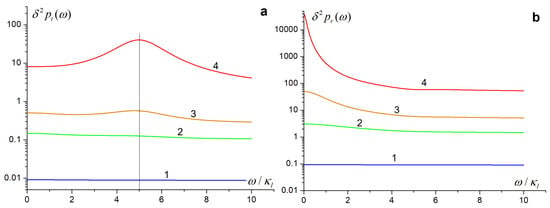
Figure 7. Power fluctuation spectra of the transmitted (a) and reflected (b) fields for the same parameters as for curves 1–4 in Figure 5. The input field power (the HWHM) increases (decreases) from curves 1 to 4. There is only one peak at $\omega =\delta$ in the transmitted field and $\omega =0$ in the reflected field spectra: compare with two peaks in curves inside the FPI shown in Figure 5.

${\delta }^2{p}_t\left(\omega \right)$ has the maximum at $\omega =\delta$, while ${\delta }^2{p}_r\left(\omega \right)$—at $\omega =0$. Maxima observed if the input field power is large. The quantum part of the transmitted and the reflected power fluctuation spectra does not depend on the frequency, as in Equations (17), (32) and (33). Quantum contributions only shift the spectra up from the horizontal axis. They do not influence the structure of spectra, which is different from the power fluctuation spectra inside the FPI cavity in Figure 6.

3.4. Auto–Correlation Functions

Inverse Fourier–transforms of the photon number fluctuation spectrum (26), transmitted (32), and reflected (33) field power fluctuation spectra lead to auto–correlation functions. Equations (8) and (26) determine the auto–correlation function ${\delta }^{2}n\left(\tau \right)$ of the FPI cavity photon number fluctuations. The first term in Equation (26) is responsible for the classical component of ${\delta }^{2}n\left(\tau \right)$, and the second is responsible for the quantum component.

Figure 8 shows examples of ${\delta }^{2}n\left(\tau \right)$ and their quantum and classical components. ${\delta }^{2}n\left(\tau \right)$ in Figure 8a decreases monotonically with $\tau$ and is determined mostly by quantum fluctuations with a small contribution from classical fluctuations. It is for a small power $p_{in}/{\kappa }_l=0.1$ and a wide input field spectrum with HWHM ${\gamma }_l/{\kappa }_l=2.73$. ${\delta }^{2}n\left(\tau \right)$ starts to oscillate at larger $p_{in}/{\kappa }_l=1.5$ and the smaller the spectrum HWHM ${\gamma }_l/{\kappa }_l=1.2$, as shown in Figure 8b; ${\delta }^{2}n\left(\tau \right)$ still includes a large part of quantum fluctuations. ${\delta }^{2}n\left(\tau \right)$ oscillates, with its quantum part, and accepts negative values at greater $p_{in}/{\kappa }_l=5$ and smaller ${\gamma }_l/{\kappa }_l=0.5$ in Figure 8c. At large $p_{in}/{\kappa }_l=50$ and small ${\gamma }_l/{\kappa }_l=0.06$, ${\delta }^{2}n\left(\tau \right)$ is positive and displays oscillations in the quantum part of ${\delta }^{2}n\left(\tau \right)$, as shown in Figure 8d.

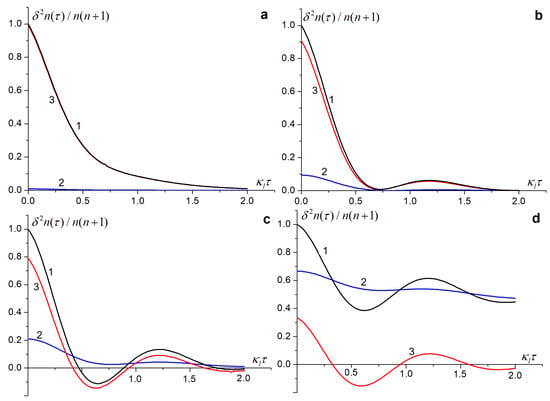
Figure 8. Auto−correlation functions for the photon number fluctuations in the FPI cavity (curves 1) consisted of the classical (curves 2) and the quantum (curves 3) contributions. The input field power increases from (a–d) with the same values of parameters as for Figure 6a–d, correspondingly.

The slow decay of ${\delta }^{2}n\left(\tau \right)$ in Figure 8d is related to a narrow line and, correspondingly, the long coherency time of the input field.

Figure 9 shows the auto–correlation function ${\delta }^2{\tilde{p}}_t\left(\tau \right)$ for the transmitted field power fluctuations. ${\delta }^2{\tilde{p}}_t\left(\tau \right)$ does not contain the term $p_t\delta \left(\tau \right)$ presented in ${\delta }^2{p}_t\left(\tau \right)$ in Equation (15). We find ${\delta }^2{\tilde{p}}_t\left(\tau \right)$ by the inverse Fourier–transform of Equation (32) without $2{\kappa }_{2}n$, which corresponds to the quantum part of the transmitted field auto–correlation function. Quantum contributions, proportional to the delta–function $\delta \left(\tau \right)$, are not shown in Figure 9. Normalizing factor ${\delta }^2{\tilde{p}}_t$, used in Figure 9, is the integral over frequencies of the expression (32), taken without $2{\kappa }_{2}n$.

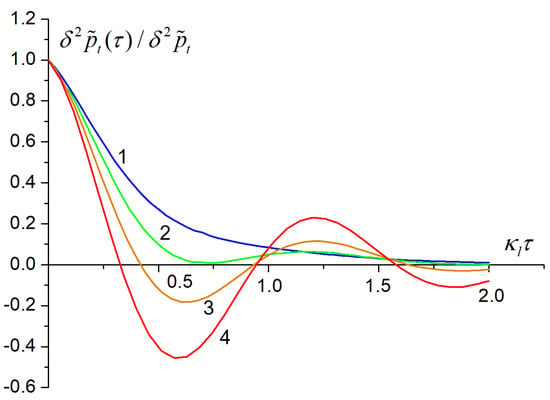
Figure 9. Auto−correlation functions for the transmitted field with parameters for curves 1–4 as for Figure 8a–d. Delta functions at $\tau =0$, corresponding to quantum noise contributions, are not shown.

We see in Figure 9 that ${\delta }^2{\tilde{p}}_t\left(\tau \right)$ starts to oscillate and takes negative values with the increase of the input field power $p_{in}$ and the narrowing of the input field spectrum—from curve 1 to curve 4. Such behavior is related to beatings between the FPI mode and the input field at the non–zero detuning $\delta$ of centers of the FPI mode and the input field spectra.

The first term in Equation (33) dominates in the auto–correlation function ${\delta }^2{\tilde{p}}_r\left(\tau \right)$ of the reflected field at chosen parameter values. Thus, ${\delta }^2{\tilde{p}}_r\left(\tau \right)$ (taken without delta–function at $\tau =0$) is very well approximated by $e^{-2{\gamma }_l\left|\tau \right|}$, and we do not show ${\delta }^2{\tilde{p}}_r$ on figures.

4. Discussion

We derived Formulas (10) and (17) for the photon number and the transmitted/reflected field power fluctuation spectra. We found transmission/reflection coefficients; transmission, reflection, and the cavity mode field spectra; the photon number (the field power) fluctuation spectra inside (outside) the FPI. We calculate the auto–correlation functions of the FPI—for the FPI excited by a finite spectrum width field when maxima of the FPI cavity mode and the input field spectra detuned on $\delta$. We take the detuning $\delta$ several times larger than HWHMs of spectra of the FPI mode and the input field. Detuning $\delta$ considered for using the results in the future investigation of the optical bistability [14,15] in the miniature FPI with the nonlinear medium and quantum field with only a few, one, or less than one photon in the cavity. Different from well–known “macroscopic” FPI [3], quantum fluctuations are significant in the small FPI with a detuning.

We found the transmission T and the reflection R coefficients of the FPI. T (or R) reduced (or increased) with the broadening of the input field spectrum; see Figure 3b. This is because the finite spectrum width field includes the frequency components shifted from the resonance with the FPI mode even at the detuning $\delta =0$. The effective FPI mode HWHM is ${\kappa }_t+{\gamma }_l$ in expressions for T and R, where ${\kappa }_t$ and ${\gamma }_l$ is HWHM of the empty FPI mode and the input field spectra—see Equations (35) and (36) for R and T.

We investigate the FPI field spectra. The structure of the reflected field spectra (shown by curves 1 in Figure 4) remains the same for any width of the input field spectrum. The reflected field spectrum contains the peak at the input field frequency and the gap at the FPI mode frequency. The peak becomes higher and narrower with the narrowing of the input field spectrum.

The FPI transmitted field spectrum, shown in curves 2 in Figure 4, changes its structure with the narrowing of the input field spectrum. The transmitted field has one broad maximum at the FPI mode frequency for broad–band input, see Figure 4a. There are two maxima of similar height—when the input field spectral width is of the order of the FPI mode spectral width; see Figure 4b,c. The first high and narrow peak is at the input field frequency. The second broad local maximum is at the FPI mode frequency if the input field has high power and a narrow spectrum; see Figure 4d.

Figure 5a shows the FIP field spectra evolution with the narrowing of the input field spectrum. It is similar to the transmitted field spectra in Figure 4. It is impossible to separate quantum and classical contributions in the field spectra.

The two–peak structure in the photon number fluctuation spectra ${\delta }^{2}n\left(\omega \right)$ inside the FPI appeared with the narrowing of the input field spectrum. We see it in Figure 5b. This structure is related to the beating between the input field and the FPI mode field when the input field spectrum is narrower or of the order of the FPI mode spectrum. ${\delta }^{2}n\left(\omega \right)$ in Figure 5b has only the maximum at $\omega =0$ for the weak broad–band input field.

It is possible to separate the quantum and the classical contributions in the photon number fluctuation spectra inside FPI, such contributions shown in Figure 6. The broad–band quantum fluctuations dominate in ${\delta }^{2}n\left(\omega \right)$ with the maximum at $\omega =0$. It is for a weak input field in Figure 6a. With the increase of the input field power, the beatings between quantum fluctuations in the FPI mode and the input field appear, leading to the side–band maximum in ${\delta }^{2}n\left(\omega \right)$ at $\omega =\delta$, see Figure 6b,c. Quantum fluctuations contribute near the FPI mode spectrum maximum. They are high near the local maximum at $\omega =\delta$ in Figure 6c,d.

It is not possible to measure ${\delta }^{2}n\left(\omega \right)$ inside FPI directly. However, the photon number fluctuations influence, for example, the interaction of the quantum field with the nonlinear medium inside the FPI. Photon number fluctuation spectra shown in Figure 5 and Figure 6 help identify the frequency domains where quantum fluctuation dominates. It is meaningful, in particular, if we insert the nonlinear resonant medium inside the small FPI cavity for absorptive bistability or other purposes, for investigating the quantum field spectra by FPI.

Field power fluctuation spectra ${\delta }^2{p}_t\left(\omega \right)$ for the transmitted (Figure 7a) and ${\delta }^2{p}_r\left(\omega \right)$ for the reflected (Figure 7b) fields are different from the photon number fluctuation spectra inside FPI in Figure 5 and Figure 6. ${\delta }^2{p}_t\left(\omega \right)$ has the maximum at $\omega =\delta$, while ${\delta }^2{p}_r\left(\omega \right)$ has the maximum at $\omega =0$ if the input field has a high power and a narrow spectrum. ${\delta }^2{p}_{r,t}\left(\omega \right)$ are flat (or almost flat) for a weak and broad–band input field. The white quantum noise does not beat the transmitted (reflected) fields. Thus, there is only one peak in the transmitted (reflected) field power spectra at $\omega =\delta$ ($\omega =0$).

Auto–correlation functions inside the FPI, shown in Figure 8, have the quantum and the classical components. The quantum component dominates at a weak and a broad–band input, and the classical—at a strong and a narrow spectrum input. We see in Figure 8b–d oscillations of ${\delta }^{2}n\left(\tau \right)$ related with a beating between the detuned FPI mode and the input field mode. Beatings disappear at a weak input field and significant quantum noise. Then, ${\delta }^{2}n\left(\tau \right)$ decays monotonically, as in Figure 8a. The auto–correlation function takes negative values when the contribution of the quantum noise is comparable with the classical part of ${\delta }^{2}n\left(\tau \right)$; see Figure 8c.

The output field power auto–correlation function ${\delta }^2{p}_t\left(\tau \right)$ in Figure 9 oscillates, similar to the auto–correlation function inside FPI. ${\delta }^2{p}_t\left(\tau \right)$ accepts negative values when the input field has a high power and a narrow spectrum. Negative values of ${\delta }^2{p}_t\left(\tau \right)$ are a “trace” of the quantum interference of the FPI mode noise and the input field inside the FPI. The quantum part of ${\delta }^2{p}_t\left(\tau \right)$ is a delta function at $\tau =0$. We do not show this part in Figure 9. The difference in quantum contributions to the field power fluctuation spectra inside and outside the FPI is related to a broad–band white quantum noise outside and a narrow–band “colored” quantum noise inside the FPI cavity.

5. Conclusions

We performed the quantum analysis of the small, of the size of wavelength Fabry–Perot interferometer (FPI) with only a few photons in the cavity. The quantum input field is taken from a LED or a laser with the finite spectral width detuned from the FPI mode. The method of study is based on general formulas for the photon number fluctuation spectra inside and outside the FPI derived in Section 2. We obtain explicit analytical expressions for the field and the photon number fluctuation spectra inside and outside the FPI in Section 2 and investigate the spectra in Section 3. The FPI spectra have asymmetry, and the structure depends on the input field spectral width and power. We identify the classical and the quantum contributions in the photon number fluctuation spectra and investigate the evolution of such contributions with the increase of the input field power and the narrowing of the input field spectra. We found that spectra structures are quite different inside and outside the FPI. The different noise explains differences in spectra: the colored (the white) quantum noise inside (outside) the FPI. We also calculate the second–order time auto–correlation functions for the FPI field; they oscillate and become negative under certain conditions. Section 3 and Section 4 describe details and reasons for the evolution of the spectra and the auto–correlation functions.

We will apply the present results for the future investigation of the optical bistability in the quantum FPI with a nonlinear medium. In general, results will help the study, design, manufacture, and use of the small elements of quantum optical integrated circuits, such as delay lines and optical transistors. We hope that the present results will stimulate experimental investigations of the quantum fluctuations and the fluctuation spectra in the small FPI.