Visual Analysis of Mixed Algorithms with Newton and Abbasbandy Methods Using Periodic Parameters

Abstract

In this paper, we proposed two mixed algorithms of Newton’s and Abbasbandy’s methods using a known iteration scheme from fixed point theory in polynomiography. We numerically investigated some properties of the proposed algorithms using periodic sequence parameters instead of the constant parameters that are mostly used by many authors. Two pseudo-Newton algorithms were introduced based on the mixed iterations for the purpose of generating polynomiographs. The properties of the obtained polynomiographs were studied with respect to their graphics, turning effects and computation time. Moreover, some of these polynomiographs exhibited symmetrical properties when the degree of the polynomial was even.

1. Introduction

Polynomiography has many applications in our everyday life, from painting to animation. It has been used to create images that have inspired several hand-painted artworks, lead to the creation of elegant carpet designs, provided a great source for the production of many tapestries and served as a useful technique in the content of both education and art in the generation of several animations [1]. Polynomiography may also be used in textile design. According to Kalantari [1], polynomiography is described as the art or science of creating graphics based on the approximation of zeros of complex polynomials. These graphical images can be fractals or nonfractals and are created using mathematical convergence properties of iteration functions. A single image created via polynomiography is referred to as a polynomiograph. Although polynomiographs belong to the same class of images as fractals (an earlier word for an image produced from iteration functions), they, however, differ in the sense that their shapes and designs can be controlled more predictably by using different iteration methods. More so, polynomiographs are sensitive to small changes in the control parameters of the iteration functions, polynomials or scales of the graphics, whereas fractals are self-similar, have a typical structure and are independent of scale. In general, polynomiography has found several applications in design, education, art and science [2,3,4].

According to the fundamentals of algebra, a complex polynomial p of degree n with coefficients $\{a_n,a_{n-1},\dots ,a_1\}$, which can be written as

$$p\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0,$$

has n roots (zeros), which may or may not be distinct. In a polynomiograph, the degree of the polynomial describes the number of basins of attraction the polynomial has. In addition, the localization of the basins is controlled by placing roots on the complex plane manually. Polynomiographs are colored based on the number of iterations needed to obtain the approximation of the root within a chosen accuracy. One of the most popular methods for finding the roots of a polynomial p is Newton’s method. This method has served as a motivation for the introduction of several generalized methods for finding roots of polynomials in real and complex domains. Recently, polynomiographs have been created using the modified Newton’s method together with several iterations from the theory of fixed points. A major contribution towards the development of pseudo-Newton algorithms for locating the maximum modulus of a polynomial on the unit disk is attributed to Kalantari [5]. Gdawiec et al. [6,7,8,9] modified and studied Kalanrari’s pesudo-Newton method with other known methods for approximating fixed points, resulting in new algorithms to solve the local maxima of polynomial modulus problems. Instead of using the standard Picard iteration, they used several different iterations, such as the Mann, Ishikawa, Noor, S and SP iterations. Many other authors have proposed several polynomiographs obtained using generalized versions of Newton’s method with different iteration processes, for instance, [10,11] and references therein. Moreover, a survey of stability analysis for solving systems of nonlinear equations can be found in [12,13].

In this paper, we introduced two mixed algorithms consisting of Newton’s method and Abbasbandy’s method for generating polynomiographs. We modified the mixed processes by using a known iterative scheme that was used for finding the common fixed points of two nonlinear mappings. We also investigated some properties of these algorithms by using periodic sequence parameters instead of constant parameters, which have been mostly used by many authors. Using these processes, we obtained several polynomiographs with interesting properties from an artistic and aesthetic point of view.

2. Iterative Methods

In this section, some iterative methods for finding the fixed points of a mapping are recalled. Let $(X,d)$ be a complete metric space and $T:X\to X$ be a mapping. A point $x\in X$ is called a fixed point T if $Tx=x.$ For approximating the fixed point of $T,$ the following iterative methods are well known. Take $x_0\in X$ as a starting point, then we have the following:

(i)

The standard Picard iteration [14] is defined by

$$z_{n+1}=T{z}_n,n\ge 0;$$

(1)

(ii)

The Mann iteration [15] is given by

$$z_{n+1}=(1-{\xi }_n)z_n+{\xi }_{n}T{z}_n,n\ge 0,$$

where ${\xi }_n\in (0,1];$

(iii)

The Ishikawa iteration [16], which is a two-step process, is given by

$$\left\{\begin{array}{c}{z}_{n+1}=(1-{\xi }_n)z_n+{\xi }_{n}T{y}_n,\hfill \\ y_n=(1-{\eta }_n)z_n+{\eta }_{n}T{z}_n,n\ge 0,\hfill \end{array}\right.$$

where ${\xi }_n\in (0,1]$ and ${\eta }_n\in [0,1];$

(iv)

The Picard–Mann iteration of Khan [17] is given as

$$\left\{\begin{array}{c}{z}_{n+1}=T{y}_n\hfill \\ y_n=(1-{\xi }_n)z_n+{\xi }_{n}T{z}_n,n\ge 0,\hfill \end{array}\right.$$

where ${\xi }_n\in (0,1].$

In the celebrated Banach fixed-point theorem [14], the standard Picard iteration is used to ensure the existence of a fixed point of a contraction mapping $T.$ The Mann and Ishikawa iterations allow the weakening of the assumption on the mapping T to be nonexpansive. It is easy to see that the Ishikawa iteration with ${\eta }_n=0$ is a Mann iteration, and for ${\eta }_n=0,{\xi }_n=1$ it is a Picard iteration. The Mann iteration with ${\xi }_n=1$ is a Picard iteration. In addition, the Picard–Mann iteration with ${\xi }_n=0$ is the Picard iteration.

Recently, Khan et al. [18] introduced a new iteration for finding common fixed points of two mappings $S,T:X\to X,$ as follows: given $x_0\in X,$

$$\left\{\begin{array}{c}{x}_{n+1}=T{y}_n\hfill \\ y_n=S((1-{\xi }_n)w_n+{\xi }_{n}T{w}_n)\hfill \\ w_n=(1-{\eta }_n)x_n+{\eta }_{n}S{x}_n,n=0,1,2,\cdots ,\hfill \end{array}\right.$$

(2)

where $\left\{{\xi }_n\right\}$ and $\left\{{\eta }_n\right\}$ are sequences in $(0,1).$ It is easy to see that (2) is more general than the Picard, Mann, Ishikawa and Picard–Mann iterations. In the sequel, we take the space $X=\mathbb{C}$, which is clearly a Banach one, $z_0=(x_0,y_0)\in {\mathbb{R}}^2$ and ${\xi }_n=\xi ,$ ${\eta }_n=\eta$ such that $0<\xi \le 1$ and $0\le \eta \le 1.$

Mixed Algorithms

Let $p\left(z\right)$ be a complex polynomial. Newton’s method for finding the roots of p is given by the formula

$$z_{n+1}=z_n-\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)},n=0,1,2,\cdots ,$$

(3)

where $z_0\in \mathbb{C}$ is a starting point and $p^{\prime }$ is the first derivative of $p.$ Newton’s method was introduced in the 17th century and has continued to be a very important tool in mathematics. It is well known that Newton’s method converges quadratically.

Using the technique of domain decomposition, Abbasbandy [19] introduced the following generalization of Newton’s method:

$$z_{n+1}=z_n-\frac{p\left(z_n\right)}{p^{\prime }\left(z_n\right)}-\frac{p^2\left(z_n\right)p^{″}\left(z_n\right)}{2{\left(p^{\prime }\left(z_n\right)\right)}^3}-\frac{p^3\left(z_n\right)p^{‴}\left(z_n\right)}{6{\left(p^{\prime }\left(z_n\right)\right)}^4}.$$

(4)

It was shown that the Abbasbandy method (4) converges cubically, and, hence, has a better rate of convergence than Newton’s method.

Next, we define the following mixed iteration process using (2) with Newton’s and Abbasbandy’s methods:

$$\left\{\begin{array}{c}{z}_{n+1}=N\left(v_n\right),\hfill \\ v_n=B((1-\eta )w_n+\eta N\left(w_n\right)),\hfill \\ w_n=(1-\xi )z_n+\eta B\left(z_n\right),\hfill \end{array}\right.$$

(5)

and

$$\left\{\begin{array}{c}{z}_{n+1}=B\left(v_n\right),\hfill \\ v_n=N((1-\eta )w_n+\eta B\left(w_n\right)),\hfill \\ w_n=(1-\xi )z_n+\xi N\left(z_n\right),\hfill \end{array}\right.$$

(6)

where $n\in \mathbb{N},$$z_0\in \mathbb{C},$

$$N\left(z\right)=z-\frac{p\left(z\right)}{p^{\prime }\left(z\right)},$$

and

$$B\left(z\right)=z-\frac{p\left(z\right)}{p^{\prime }\left(z\right)}-\frac{p^2\left(z\right)p^{″}\left(z\right)}{2{\left(p^{\prime }\left(z\right)\right)}^3}-\frac{p^3\left(z\right)p^{‴}\left(z\right)}{6{\left(p^{\prime }\left(z\right)\right)}^4}.$$

If the sequence $\left\{z_n\right\}$ (the orbit of point $z_0$) converges to a root $z^{*}$ of $p,$ then we say that $z_0$ is attracted to $z^{*}.$ The set of all starting points $z_0$, for which $\left\{z_n\right\}$ converges to $z^{*}$, is called the basin of attraction of $z^{*}.$ The boundaries among basins are usually fractals in nature. The above mixed iteration processes are convergent to the roots of the polynomial $p.$ More so, the speed of convergence is different and the polynomiographs created by each process look different. The application of each iteration perturbs the shape of the polynomiographs, which is interesting from an aesthetic point of view.

3. Escape Criterion Results

In this section, we present some escape criterion for the mixed algorithm presented in (5) and (6). We used the general polynomial $z^n+c$ and $z^n+az+r$ to repsent Newton’s and Abbassbany’s methods, respectively. In the sequel, we took $z_0\in \mathbb{C}$ and $\xi ,\eta \in (0,1].$ The escape criterion is important in the analysis of Julia sets, Mandelbrot sets and their generalizations.

The following theorem describes the escape criterion for (5).

Theorem 1.

Let $N_c\left(z\right)=z_n+c$ and $B_{a,r}\left(z\right)=z_n+az+r$. Suppose

$$\left|z\right|\ge \left|r\right|>\frac{2(1+|a\left|\right)}{\xi |r^{n-2}|}and\left|z\right|\ge \left|c\right|>\frac{2}{\eta |c^{n-2}|},$$

where $\xi ,\mu \in (0,1]$ and $r,c,a\in \mathbb{C}.$ Define $\left\{z^n\right\}$ by the iteration in (5). Then, $|z^n|\to \infty$ as $n\to \infty .$

Proof. 

From (5), we consider

$$\begin{array}{ccc}\hfill \left|w\right|& =& |(1-\xi )z+\xi B_{a,r}\left(z\right)|\hfill \\ & =& |(1-\xi )z+\xi (z^n+az+r)|\hfill \\ & \ge & |(1-\xi )z+\xi (z^n+az)|-\xi |r|\hfill \\ & \ge & |(1-\xi )z+\xi (z^n+az)|-\xi |z|\hfill \\ & \ge & \xi |z^n|-(1-\xi +\xi \left|a\right|\left)\right|z|-\xi |z|\hfill \\ & =& \xi |z^n|-(1+\xi \left|a\right|\left)\right|z|\hfill \\ & =& \left|z\right|\left(\xi \right|z^{n-1}|-(1+\xi \left|a\right|\left)\right).\hfill \end{array}$$

Since $\xi \in (0,1]$ and $\left|z\right|>\left|r\right|,$ then

$$\begin{array}{ccc}\hfill \left|w\right|& \ge & \left|z\right|\left(\xi \right|z\left|\right|z^{n-2}|-(1+\xi \left|a\right|\left)\right)\hfill \\ & \ge & \left|z\right|\left(\xi \right|z\left|\right|r^{n-2}|-(1+\left|a\right|\left)\right)\hfill \\ & =& \left|z\right|(1+\left|a\right|)\left(\frac{\xi \left|z\right||r^{n-2}|}{1+\left|a\right|}-1\right).\hfill \end{array}$$

From the hypothesis of our theorem, we get

$$\begin{array}{c}\hfill \left|z\right|>\frac{2(1+|a\left|\right)}{\xi |r^{n-2}|},\end{array}$$

which implies that

$$\begin{array}{c}\hfill \frac{\xi \left|z\right||r^{n-2}|}{1+\left|a\right|}-1>1.\end{array}$$

(7)

Therefore,

$$\left|w\right|>\left|z\right|.$$

Furthermore, set $u=(1-\eta )w+\eta N_C\left(w\right),$ then

$$\begin{array}{ccc}\hfill \left|u\right|& =& |(1-\eta )w+\eta N_c\left(w\right)|\hfill \\ & =& |(1-\eta )w+\eta (w^n+c)|\hfill \\ & \ge & |(1-\eta )w+\eta w^n|-\eta |w|\hfill \\ & \ge & \eta |w^n|-(1-\eta )|w|-\eta |w|\hfill \\ & \ge & \left|w\right|\left(\eta \right|w\left|\right|c^{n-2}|-1).\hfill \end{array}$$

In addition, since $\left|w\right|\ge \left|z\right|,$ thus

$$\begin{array}{cc}\hfill \left|u\right|& \ge \left|z\right|\left(\eta \right|z\left|\right|c^{n-2}|-1).\end{array}$$

Again, $\left|z\right|>\frac{2}{\eta |c^{n-2}|},$ so $\eta \left|z\right|c^{n-2}-1>1,$ hence,

$$\left|u\right|\ge \left|z\right|.$$

Then,

$$\begin{array}{ccc}\hfill \left|v\right|& =& |B_{a,r}\left(u\right)|\hfill \\ & =& |u^n+au+r|\hfill \\ & \ge & |u^n+au|-|r|\hfill \\ & \ge & |u^n+au|-|u|.\hfill \end{array}$$

Since $\xi \in (0,1],$ then

$$\begin{array}{ccc}\hfill \left|v\right|& \ge & \xi |u^n|-|a\left|\right|u|-|u|\hfill \\ & =& \left|u\right|\left(\xi \right|u\left|\right|u^{n-2}|-(1+\left|a\right|\left)\right).\hfill \end{array}$$

(8)

Since $\left|u\right|>\left|z\right|,$ then

$$\begin{array}{ccc}\hfill \left|v\right|& \ge & \left|u\right|\left(\xi \right|u\left|\right|u^{n-2}|-(1+\left|a\right|\left)\right)\hfill \\ & >& \left|z\right|\left(\xi \right|z\left|\right|r^{n-2}|-(1+\left|a\right|\left)\right)\hfill \\ & \ge & \left|z\right|\left(\frac{\xi \left|z\right||r^{n-2}|}{1+\left|a\right|}-1\right).\hfill \end{array}$$

Hence (7), we get

$$\begin{array}{c}\hfill \left|v\right|\ge \left|z\right|.\end{array}$$

More so, from (5), we obtain

$$\begin{array}{ccc}\hfill |z_1|& =& |N_c\left(v\right)|\hfill \\ & =& |v^n+c|\hfill \\ & \ge & |v^n|-|c|\hfill \\ & \ge & \eta |v^n|-|v|\hfill \\ & =& \left|v\right|\left(\eta \right|v\left|\right|c^{n-2}|-1)\hfill \\ & \ge & \left|z\right|\left(\eta \right|z\left|\right|c^{n-2}|-1).\hfill \end{array}$$

Since $\left|z\right|>\frac{2}{\eta |c^{n-2}|}$, which implies that $\eta \left|z\right||c^{n-2}|-1>1,$ then there exists a real number $\lambda >0$ such that

$$\begin{array}{c}\hfill \frac{2}{\eta |c^{n-2}|}-1>1+\lambda .\end{array}$$

Therefore, $|z_1|>(1+\lambda )|z|.$ Hence by induction, we have

$$|z_n{|>(1+\lambda )}^n\left|z\right|.$$

This means that $|z_n|\to \infty$ as $n\to \infty .$    □

Next, we prove the escape criterion for (6).

Theorem 2.

Let $N_c\left(z\right)=z_n+c$ and $B_{a,r}\left(z\right)=z_n+az+r$. Suppose

$$\left|z\right|\ge \left|r\right|>\frac{2(1+|a\left|\right)}{\eta |r^{n-2}|}and\left|z\right|\ge \left|c\right|>\frac{2}{\xi |c^{n-2}|},$$

(9)

where $\xi ,\mu \in (0,1]$ and $r,c,a\in \mathbb{C}.$ Define $\left\{z^n\right\}$ by the iteration in (5). Then, $|z^n|\to \infty$ as $n\to \infty .$

Proof. 

From (6), we get

$$\begin{array}{ccc}\hfill \left|w\right|& =& |(1-\xi )z+\xi N_c\left(z\right)|\hfill \\ & =& |(1-\xi )z+\xi (z^n+c)|\hfill \\ & \ge & |(1-\xi )z+\xi z^n|-\xi |c|\hfill \\ & \ge & |(1-\xi )z+\xi z^n|-\xi |z|\hfill \\ & \ge & \xi |z^n|-|z|\hfill \\ & =& \left|z\right|\left(\xi \right|z\left|\right|c^{n-2}|-1).\hfill \end{array}$$

From (9), we obtain $\left|z\right|>\frac{2}{\xi \left|z\right||c^{n-2}|}.$ Thus $\xi \left|z\right||c^{n-2}|-1>1.$ Hence,

$$\left|w\right|\ge \left|z\right|.$$

Similarly, put $p=(1-\eta )w+\eta B_{a,r}\left(w\right).$ Then,

$$\begin{array}{ccc}\hfill \left|p\right|& =& |(1-\eta )w+\eta B_{a,r}\left(w\right)|\hfill \\ & =& |(1-\eta )w+\eta (w^n+aw+r)|\hfill \\ & \ge & |(1-\eta )w+\eta (w^n+aw)|-\eta |r|\hfill \\ & \ge & |(1-\eta )w+\eta (w^n+aw)|-\eta |w|\hfill \\ & \ge & \eta |w^n|-(1-\eta +\eta \left|a\right|\left)\right|w|-\eta |w|\hfill \\ & \ge & \eta |w^n|-(1+\eta \left|a\right|\left)\right|w|.\hfill \end{array}$$

Since $\eta \in (0,1]$, then

$$\begin{array}{ccc}\hfill \left|p\right|& \ge & \eta |w^n|-(1+\eta \left|a\right|\left)\right|w|\hfill \\ & \ge & \eta |w^n|-(1+\left|a\right|\left)\right|w|\hfill \\ & =& \left|w\right|\left(\eta \right|w\left|\right|w^{n-2}|-(1+\left|a\right|\left)\right).\hfill \end{array}$$

In addition, since $\left|z\right|\ge \left|r\right|,$ then

$$\begin{array}{ccc}\hfill \left|p\right|& \ge & \left|w\right|\left(\eta \right|w\left|\right|w^{n-2}|-(1+\left|a\right|\left)\right)\hfill \\ & \ge & \left|w\right|\left(\eta \right|w\left|\right|r^{n-2}|-(1+\left|a\right|\left)\right)\hfill \\ & =& \left|w\right|\left(\frac{\left|w\right|\eta |r^{n-2}|}{1+\left|a\right|}-1\right).\hfill \end{array}$$

Hence by (9), we have

$$\begin{array}{c}\hfill \left|w\right|>\frac{2(1+|a\left|\right)}{\eta |r^{n-2}|},\end{array}$$

which implies that

$$\begin{array}{c}\hfill \frac{\left|w\right|\eta |r^{n-2}|}{1+\left|a\right|}-1>1.\end{array}$$

(10)

Therefore $\left|p\right|>\left|w\right|.$ Consequently,

$$\begin{array}{ccc}\hfill \left|v\right|& =& |N_c\left(p\right)|\hfill \\ & =& |p^n+c|\hfill \\ & \ge & |p^n|-|c|\hfill \\ & \ge & \xi |p^n|-|p|\hfill \\ & =& \left|p\right|\left(\xi \right|p\left|\right|p^{n-2}|-1)\hfill \\ & \ge & \left|z\right|\left(\xi \right|z\left|\right|c^{n-2}|-1).\hfill \end{array}$$

From the hypothesis of our theorem, we have $\left|v\right|\ge \left|z\right|.$ Hence,

$$\begin{array}{ccc}\hfill |z_1|& =& |B_{a,r}\left(v\right)|\hfill \\ & =& |v^n+av+r|\hfill \\ & \ge & |v^n+av|-|r|\hfill \\ & \ge & |v^n+av|-|v|.\hfill \end{array}$$

Similarly since $\eta \in (0,1]$, then

$$\begin{array}{ccc}\hfill |z_1|& \ge & \eta |v^n|-|a\left|\right|v|-|v|\hfill \\ & =& \left|v\right|\left(\eta \right|v\left|\right|v^{n-2}|-(1+\left|a\right|\left)\right)\hfill \\ & \ge & \left|z\right|\left(\eta \right|z\left|\right|r^{n-2}|-(1+\left|a\right|\left)\right)\hfill \\ & =& \left|z\right|\left(\frac{\eta \left|z\right||r^{n-2}|}{1+\left|a\right|}-1\right).\hfill \end{array}$$

From (10), we get

$$\begin{array}{c}\hfill \frac{\eta \left|z\right||r^{n-2}|}{1+\left|a\right|}-1>1.\end{array}$$

This implies that there exists a real number $\rho >0$ such that

$$\frac{2(1+|a\left|\right)}{\eta |r^{n-2}|}-1>1+\rho .$$

Therefore,

$$\begin{array}{c}\hfill |z_1|>(1+\rho )|z|.\end{array}$$

Then, by induction, we have

$$\begin{array}{c}\hfill |z_n{|>(1+\rho )}^n\left|z\right|.\end{array}$$

This means that $|z_n|\to \infty$ as $n\to \infty .$    □

4. Polynomiographs Generation

4.1. Algorithms

To generate a polynomiograph, we selected a polynomial $p,$ parameters ${\xi }_n$ and ${\eta }_n$ for the mixed algorithms, and the maximum number of iterations $M.$ Then, for each starting point $z_0$ in the area $A\subset \mathbb{C}$ (the area was discretized depending on the resolution of the graphics), we used the mixed iteration processes to iterate the root of the polynomial. The iteration proceeded until the following convergence test was satisfied:

$$|z_{n+1}-z_n|<ϵ,$$

where $ϵ>0$ is the accuracy of computation, or the maximum number of iterations was reached. Finally, when the iteration process stopped, we determined a color for the starting point by mapping the number n of performed iterations to a color in the color map. The algorithms for generating the polynomiographs were presented as follows.

4.2. Visualization of Polynomiographs

In this subsection, we present some polynomiographs, which were obtained by using Algorithms 1 and 2. Furthermore, we compare the performance of the algorithms using the time taken by each algorithm to generate a polynomiograph.

Algorithm 1: Mixed Algorithm 1 for generating polynomiography

Input: Choose $$\begin{array}{c}\hfill \begin{array}{ccc}p\in \mathbb{C}\left[\mathbb{Z}\right]& --& \mathrm{polynomial}\mathrm{of}\mathrm{degree}\ge 2,\\ z_0\in \mathbb{C}& --& \mathrm{starting}\mathrm{point},\\ {\xi }_n\in (0,1],{\eta }_n\in [0,1]& --& \mathrm{parameters}\mathrm{of}\mathrm{mixed}\mathrm{iteration},\\ M& --& \mathrm{maximum}\mathrm{number}\mathrm{of}\mathrm{iteration},\\ A\in \mathbb{C}& --& \mathrm{area}\mathrm{for}\mathrm{the}\mathrm{polynomiographs}.\end{array}\end{array}$$ (11) While:$n\le M$, compute $$\left\{\begin{array}{c}{w}_n=(1-{\xi }_n)z_n+{\eta }_{n}B\left(z_n\right)\hfill \\ v_n=B((1-{\eta }_n)w_n+{\eta }_{n}N\left(w_n\right))\hfill \\ z_{n+1}=N\left(v_n\right)\hfill \end{array}\right.$$ (12) Stopping criterion:$|z_{n+1}-z_n|<ϵ$. Output: color c of $z_0.$

Algorithm 2: Mixed Algorithm 2 for generating polynomiography

Input: Choose $$\begin{array}{c}\hfill \begin{array}{ccc}p\in \mathbb{C}\left[\mathbb{Z}\right]& --& \mathrm{polynomial}\mathrm{of}\mathrm{degree}\ge 2,\\ z_0\in \mathbb{C}& --& \mathrm{starting}\mathrm{point},\\ {\xi }_n\in (0,1],{\eta }_n\in [0,1]& --& \mathrm{parameters}\mathrm{of}\mathrm{mixed}\mathrm{iteration},\\ M& --& \mathrm{maximum}\mathrm{number}\mathrm{of}\mathrm{iteration},\\ A\in \mathbb{C}& --& \mathrm{area}\mathrm{for}\mathrm{the}\mathrm{polynomiographs}.\end{array}\end{array}$$ (13) While:$n\le M$, compute $$\left\{\begin{array}{c}{w}_n=(1-{\xi }_n)z_n+{\eta }_{n}N\left(z_n\right)\hfill \\ v_n=N((1-{\eta }_n)w_n+{\eta }_{n}B\left(w_n\right))\hfill \\ z_{n+1}=B\left(v_n\right)\hfill \end{array}\right.$$ (14) Stopping criterion:$|z_{n+1}-z_n|<ϵ$. Output: color c of $z_0.$

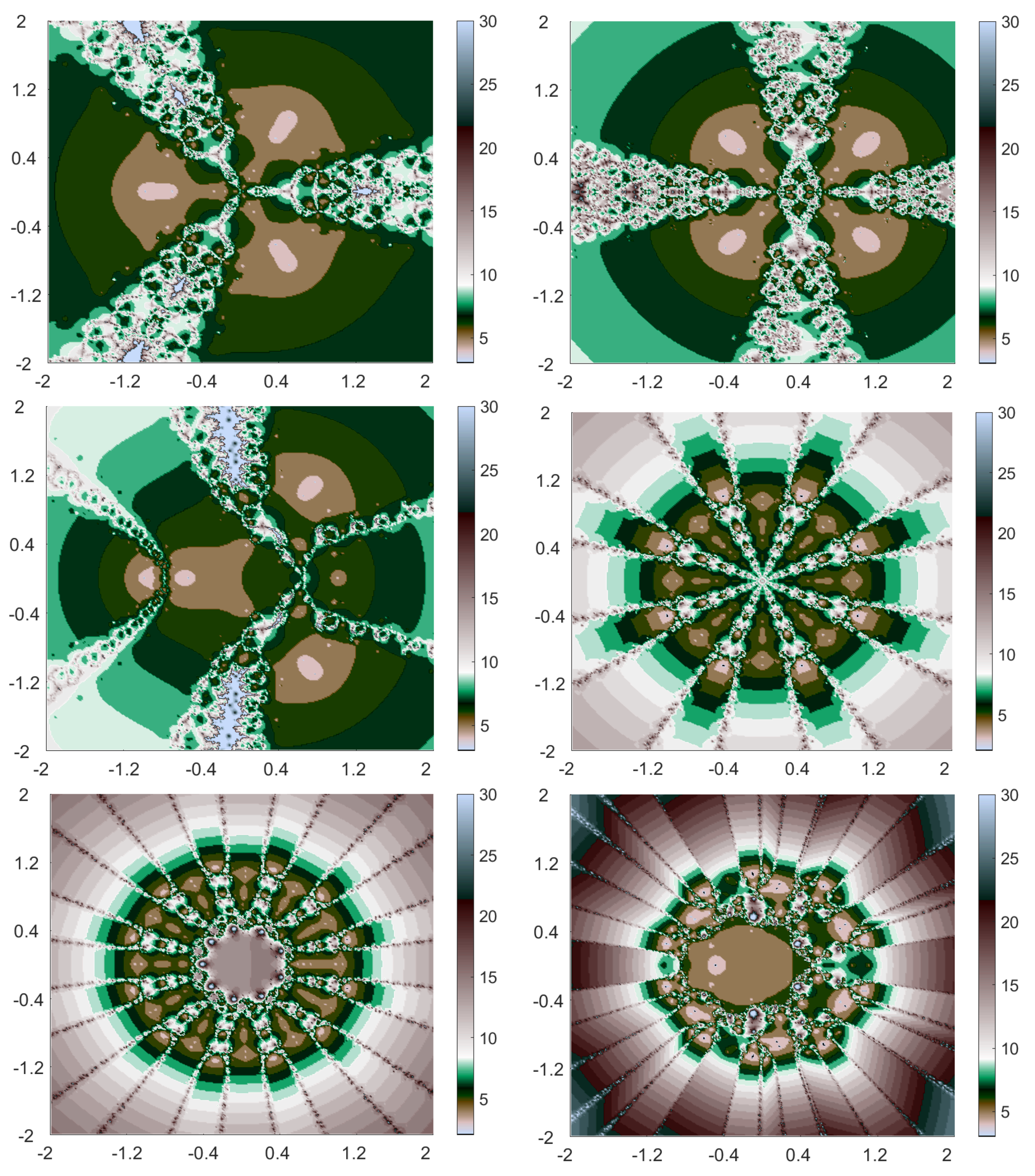
Example 1.

In the first example, we used six various polynomials to generate different polynomiographs with Algorithms 1 and 2. We chose ${\xi }_n=\frac{1}{n+1},{\eta }_n=\frac{2n}{5n^2+8},M=30,ϵ=0.0001$ and $A={[-2,2]}^2.$ The control parameter was chosen arbitrarily such that ${\xi }_n,{\eta }_n\in [0,1].$ In particular, we considered the following polynomials:

Case I

$p\left(z\right)=z^3+1$;

Case II

$p\left(z\right)=2z^4-3z^3+z^2+2$;

Case III

$p\left(z\right)=z^4+2z-1$;

Case IV

$p\left(z\right)=z^8-1$;

Case V

$p\left(z\right)=z^{12}+2z-3$;

Case VI

$p\left(z\right)=z^{17}+8z^8+2z^7-z-1.$

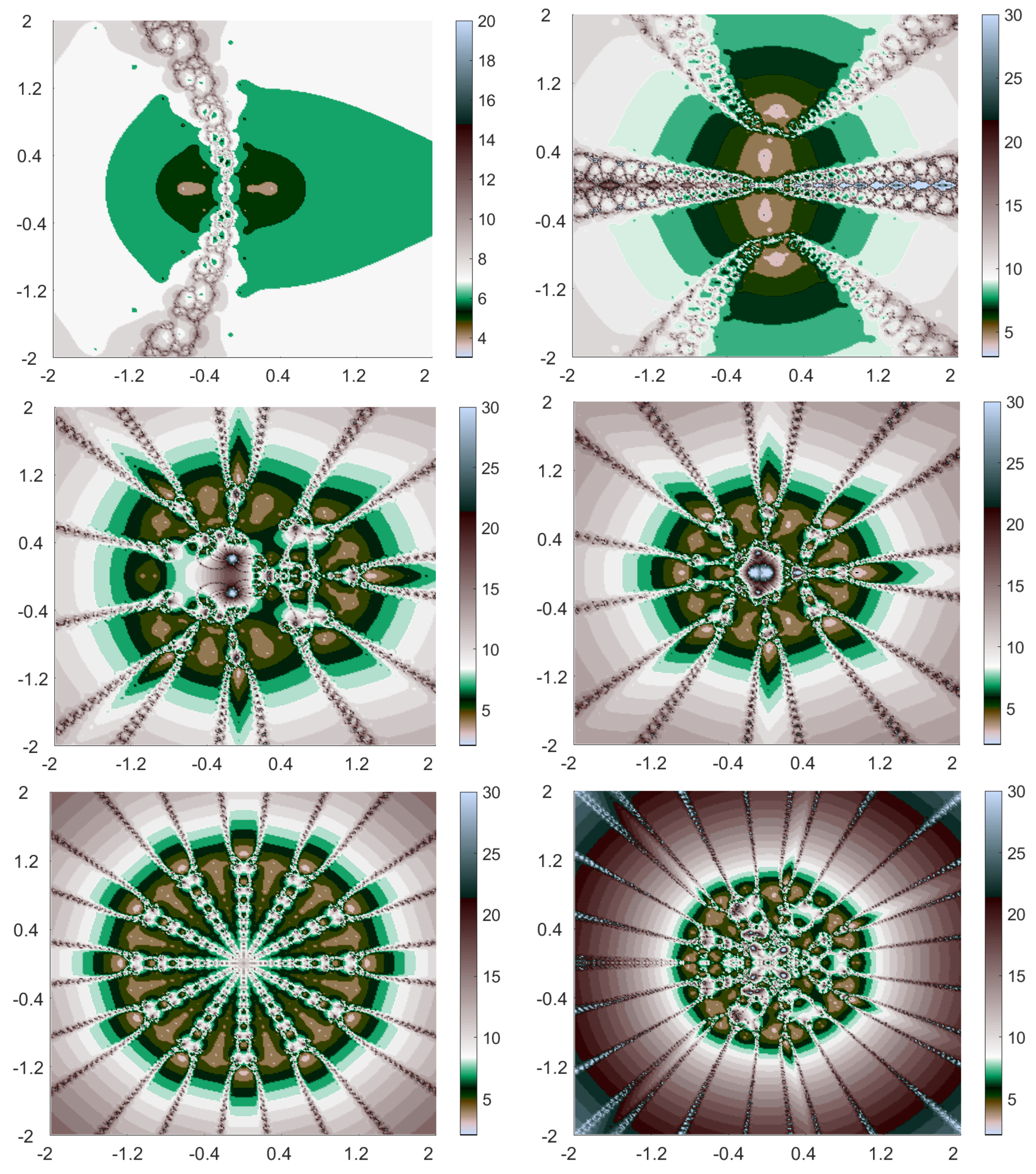
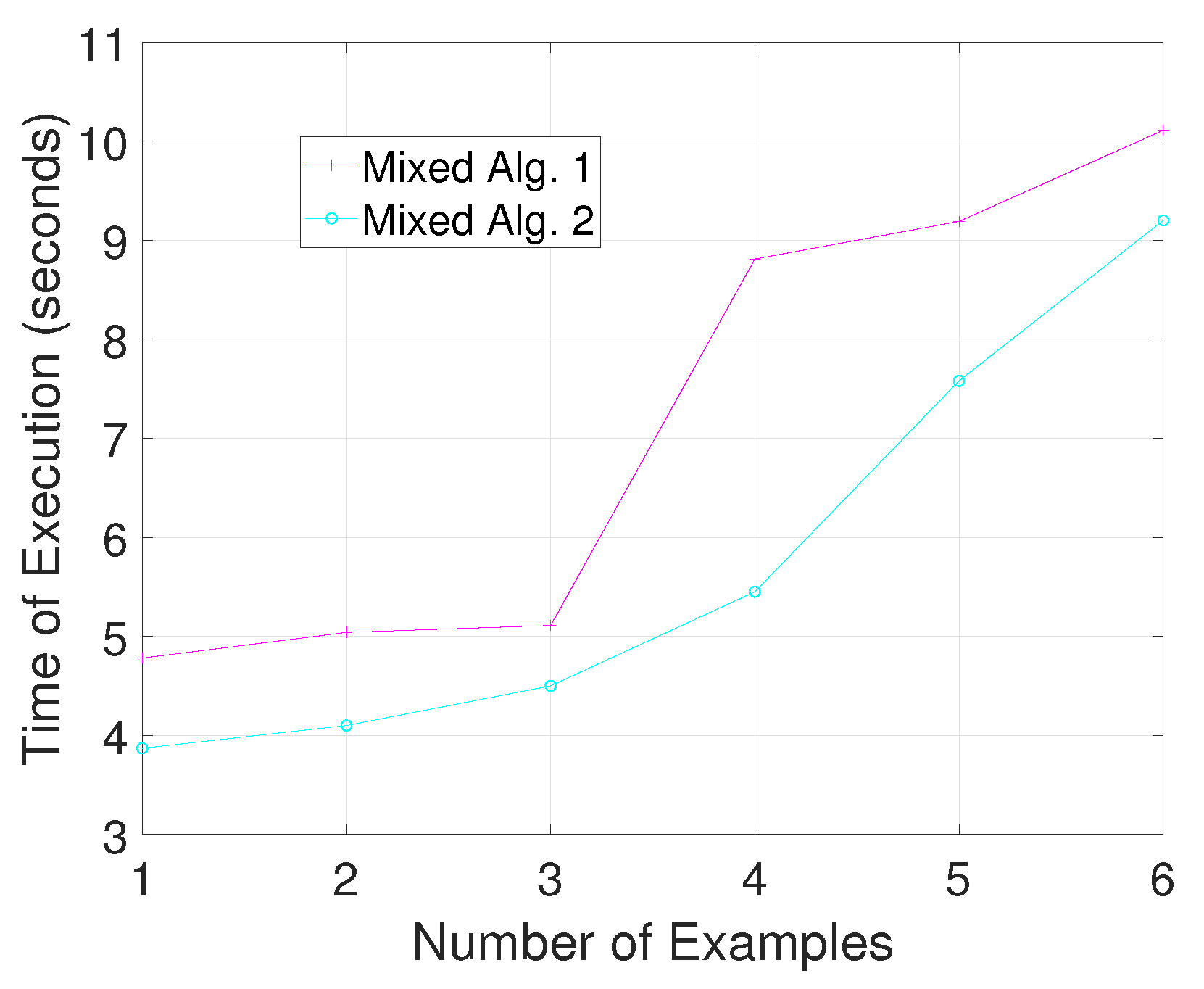
The polynomiographs generated by Algorithm 1 are shown in Figure 1 and those generated by Algorithm 2 are shown in Figure 2. More so, the graph of time of execution against the number of examples is shown in Figure 3.

From Figure 1 and Figure 2, we see that both algorithms were able to generate distinct polynomiographs, which were artistically appealing. Figure 3 shows that the average time of execution for Algorithm 1 was less than the average time of execution for Algorithm 2.

Example 2.

For the second example, we used periodic control parameter ${\xi }_n=sin\left(2n\right),{\eta }_n=cos(n+1)$ together with the following polynomials to generate our polynomiographs:

Case I:

$p\left(z\right)=z^3-5z^2-2z+1$;

Case II:

$p\left(z\right)=10z^5-2z^4+3\pi z+1$;

Case III:

$p\left(z\right)=$ −$5z^6+7z^3+2z^2+z-10$;

Case IV:

$p\left(z\right)=$ −$50z^8+5z^7+6z^6+7z^5+3z^3$ − $7z^2+4z-10$;

Case V:

$p\left(z\right)=z^{12}-1$;

Case VI:

$p\left(z\right)=20z^{12}+9z^3+2z+3.$

Similar to Example 1, the mixed algorithms were used for generating distinct polyomiographs. The polynomiographs generated by Algorithm 1 are shown in Figure 4 and the polynomiographs generated by Algorithm 2 are shown in Figure 5.The time of execution against the number of cases is shown in Figure 6. In this case, the average time of execution for Algorithm 2 was less than the average time of execution for Algorithm 1.

5. Conclusions and Future Work

In this paper, we introduced two new mixed algorithms, which consisted of Newton’s and Abbasbandy’s methods with a known iteration process in fixed point theory. We investigated some properties of the algorithms while generating polynomiographs using periodic parameters. The use of periodic parameters gave the obtained polynomiographs more interesting patterns. More so, numerical results showed that the change in the parameters did not have any significant effect on the convergence of the algorithms. These results were new and interesting from an artistic point of view.

The results of this paper could be further modified by using other known methods for approximating the roots of complex polynomials. In addition, the mixed algorithms could be modified by using other iteration methods from fixed point theory. We could also define different periodic functions for the parameters, as well as measure the comparison of the mixed algorithms using the mean number of iterations and the convergence area index.