Liquid Crystal-Based Geometric Phase-Enhanced Platform for Polarization and Wavefront Analysis Techniques with the Short-TeraHertz FEL Oscillator TerRa@BriXSinO

Abstract

In this work, we propose to design a liquid crystal–based modular and extendable platform of cutting-edge optical technologies for studying materials based on the analysis of polarization and wavefront of light in the wavelength range of 10–50 μm, which is considered to work even in the longer wavelengths range. This platform will be driven by the future THz-FEL source TerRa@BriXSinO that produces high power radiation in THz-range from 6 THz up to 30 THz (Mid-/Far-IR). The lack of optical infrastructures in this range has been tackled by fabricating liquid crystal–based geometric phase components that have been specifically designed for this purpose. This is in order to optimally exploit all the source’s potential for maximum accuracy and efficiency in determining polarization- and wavefront-sensitive properties of materials. We present an overview of a few experiments for characterizing bulk inhomogeneities, dielectric anisotropy, surface roughness, cracks, impact damages, and stress and strain effects with special emphasis on non-destructive tests on composite structures. The tools for wavefront shaping developed within our platform will be exploited to add a further degree of freedom, i.e., orbital angular momentum, to nonlinear optics techniques, such as Terahertz Hyper-Raman spectroscopy, for investigating chiral agents’ properties.

1. Introduction

The capability of reconstructing polarization states and wavefronts of light waves is the key to disclosing a wealth of information about the objects the waves have interacted with along their path. In addition to dielectric properties, high significance is taken on by morphological properties of objects, on both macroscopic and mesoscopic scales, since they have the peculiarity of directly affecting the wavefront shape and/or the local polarization state of the incident light wave. Morphological properties, for instance, include: dielectric inhomogeneities, which cause bulk granularity and surface roughness; the overall shape of an object, which underpins its operation as an idolic as well as an anidolic optical component (lens, mirror, prism, free-from optics, etc.) [1]; the local deformation pattern superposed to the object shape, which gives rise to optical aberrations or is the signal of anomalies, defects, cracks, stress, or strains in the bulk or over the surface of the object, just to mention a few. Such properties can be detected by exploiting both polarization and wavefront analyses, which can be profitably used simultaneously to unveil complementary aspects of each single property. Subjected to mechanical stresses, an object made of transparent isotropic material, for instance, may suffer a deformation in shape—suitable for wavefront analysis—and become optically anisotropic [2]—a phenomenon known as stress birefringence or photo-elastic effect—suitable for polarization analysis. The quantitative estimation of mechanical stress–induced deformations turns to be of vital importance in studying mechanical strength and resilience of innovative materials, such as composite structures [3] or in monitoring possible damages in structures and infrastructures in multiple areas, such as the construction sectors, the automotive industry, or the aerospace industry. Similar comments apply to the investigation of form birefringence [2], a property originating from an ordered arrangement of similar particles of optically isotropic material over a scale large compared to the molecular dimensions. Form birefringence often occurs in manufacturing processes as an unwanted effect, as in lens manufacturing [4]. Not seldom, however, is it deliberately induced for fabricating high-birefringence materials [5]. Modern polarimetry and wavefront sensing, based on both interferometric and non-interferometric methods, as well as polarization and wavefront shaping, have nowadays achieved unprecedented capabilities in the visible domain—including Near IR and Long-Wave UV. A host of powerful and effective methods are nowadays available. A survey of basic methods and perspective in polarization and wavefront shaping and sensing can be found in Refs. [6,7]. It is no doubt that optical technologies based on Diffractive Optical Elements (DOEs) and Geometric Phase Elements (GPEs) have contributed to boost the development of this area [8,9,10].

In Mid- and Far-Infrared, however, things are quite different: available testing methods are few and they are not continuously widespread over all the wavelength range. Because this wavelength range is rather large, four times wider than the visible range, we will subdivide them into sub-domains. The long-wavelength side of the far-IR, customarily referred to as the THz wavelength range (∼1–3 THz or ∼100–300 μm) and henceforth mentioned as Long wavelength T-waves or LT-waves), has drawn a great deal of interest for a wide variety of optoelectronic, sensing, and imaging applications both in fundamental research and in industrial sectors [11,12]: many novel technologies have been developed in this field since the first pulsed THz Time-Domain Spectroscopic (TDS) system was invented more than 30 years ago, and electromagnetic waves in this domain appear now less elusive than in the past, including Terahertz DOEs [13]. In addition, the shorter wavelength region of Far-IR (∼20–100 μm) and that straddling the border between Far- and Mid-IR (∼10–20 μm), have received little attention thus far, despite being a wavelength range of potential interest for remote morphological characterization of objects, as well as for explosives detection [14], chemical and biological spectroscopy [15,16], and astrophysics applications. Within the conventional Terahertz domain, remote morphological Non Destructive Tests (NDTs) have been developing for years, and highly promising results have been achieved. For example, remote scanning methods of surface textures, during metal production and processing, have been worked out in order to enable fast real-time identification and discrimination of protrusions and dents [17], having a millimeter-scale width and a height or depth down to 5 μm. In this analysis, T-waves take advantage over visible light since they are insensitive to micron- and submicron-scale surface roughness and circumvent the constraint of a large working distance between the sample and the measurement system—usually of the order of several tens of centimeters. To increase the resolution to sub-millimeter-scale width, without reducing scattering insensitivity or the working distance, it would be highly desirable exploiting shorter wavelength T-waves. Any other method developed in the terahertz range for morphological analysis of materials and devices could be profitably extended from LT-waves to shorter wavelength T-waves, such as terahertz polarization imaging for high-resolution topography or stress-induced anisotropy, just as for instance [12,18].

Exploring and exploiting any wavelength range requires a full optical toolkit, including sources, detectors, and any sort of optical components such as lenses, beamsplitters, polarizers, and filters. Metrology applications based on polarimetry and wavefront sensing, however, are particularly demanding and high performing sources, detectors and optical systems accomplishing very specific tasks are needed. In the ∼10–100 μm wavelength range, such components and optical systems are few and do not cover continuously all the range. This is mainly due to the strong phonon absorption of semiconductor materials, which are the most prominent optical materials in the infrared domain and represent the basis of almost all the optoelectronic devices. The wavelength range ∼10–100 μm is therefore sometimes referred to as the semiconductors Reststrahlen band. In this view, it would be more appropriate to distinguish two wavelength intervals:

• The wavelength range ∼20–100 μm, corresponding to the Reststrahlen band of III–V materials, henceforth mentioned as Medium T-waves or MT-waves;
• The wavelength range ∼10–20 μm, corresponding to the Reststrahlen band of wide bandgap materials (SiC, diamond, III-nitrides), henceforth mentioned as Short T-waves or ST-waves.

To our best knowledge, whereas some preliminary studies have been done in the MT range [19], the ST range is still under-explored. Nevertheless, Short T-waves could ideally combine advantages of both Long T-waves and visible light, at least in morphological tests, by enabling remote high-resolution surface or bulk topography of objects while averaging over scattering due to micron-sized irregularities. Achieving metrology-grade standards in this wavelength domain, however, requires the following basic conditions to be satisfied:

• The sources employed for tests should match state-of-art spectral brightness, pulse energies, and stability specifications so as to compensate for high losses due to atmospheric absorption or to multiple reflections from the host of optical components required for building the measurement systems; to provide detection signals affected by comparatively small fluctuations; and for high spatial and time coherence for stable and reliable interferometric analyses.
• It is mandatory to design and fabricate highly performing optical components and devices for manipulating polarization as well as for structuring light and sensing wavefronts.

Meeting this challenge would not only enable the sort of analyses hereafter proposed in great detail—by their own already highly comprehensive method—but it would also allow for developing the whole sector of Short T-waves optics for the most diverse applications.

In this work, we present the layout of a complex extendable optical platform designed for multiple integrated analyses of materials and devices in the Short Wavelengths Terahertz domain. The main purpose is to test dielectric and, above all, morphologic properties of material objects over a variable lateral scale ranging from hundreds down to few tens of micrometers and a variable depth scale from few nanometers up to few tenths of micrometers. The source, for which the platform is designed, is the future THz-FEL TerRa@BriXSinO, which provides a narrow bandwidth and high power—up to 10³ W, on average—with tunability over a wide frequency range in Short Wavelengths THz region from 6 THz up to 30 THz (≈10–50 μm), with a peak of efficiency between 10 and 25 μm. The setup includes high performance optical components exploiting the concept of liquid crystal–based (LC-based) Spatially Varying Axis Plate (SVAP) [9,10]. Such components are based on Pancharatnam-Berry or Geometric Phase. To our best knowledge, there are a very few works reporting a successful employment of LC-based SVAPs for vortex beam generation in the terahertz domain [20]. As illustrated in the following, multiple optical components can be fabricated as an LC SVAP, such as lenses, prisms, beam splitters, spiral phase plates, and, of course, any kind of retardation waveplates. These components have been designed and tailored specifically for TerRa@BriXSinO source, in order to allow for efficient management of light polarization as well as wavefront structuring and sensing. High birefringence, THz-specific liquid crystals are required to achieve this goal. At present only a few liquid crystals having the correct features exist [21] and material research in this sense should be stimulated. Importantly, a high-power source is imperative in building complex layouts including a host of optical components with many interposed free-space layers, especially in view of the non-negligible absorption at $\lambda \ge 15\mathsf{\mu }\mathrm{m}$ ($\nu \le 20$ THz), mainly due to CO₂ and water vapor. Considering the prominent role played by Geometric Phase in the development of the platform, we have baptized the system Geometric Phase Enhanced Short wavelength Terahertz, or GEST (the acrostic GEST means ‘Tale of adventures’) platform.

The paper is organized as follows. In Section 2, we introduce the source TerRa and provide its envisioned parameters. In Section 3, we introduce the problem of measuring polarization states and wavefronts of electromagnetic waves, as dual manifestations of the field transverse phase. We underline the relationship between such measurements and the possibility of providing a full morphological remote characterization of objects over a sub-millimeter up to micrometric transverse scale, as further illustrated in Section 3.1, thanks to combined measurement of both wavefront and polarization. In Section 3.2, we explain which methods we have selected for building the platform, accounting for both their advantages and disadvantages as tools for tackling the challenges of this research activity. The prominent role of the geometric phase optical elements in meeting these challenges is clearly stated. In Section 4, we introduce the basic principles of Geometric Phase and illustrate its use working principle underpinning optical elements operation. Specifically, we describe in details how the Geometric Phase can be exploited to reshape an input wavefront through the above-mentioned liquid crystal–based retardation waveplates with spatially varying axis. In Section 5, we illustrate in detail the general layout of the platform. Beyond the laser source, two beam manipulation stages are inserted: a wavefront shaper, for generating scalar as well as vector beams; and the sample to be analyzed, which involves several detection stages for gathering different information about the sample. The different detection stages can be operated in combination. In Section 6, Section 7, Section 8 and Section 9, the anticipated experiments using TerRa and GEST are explained: shearography for stress tests on composite structures and surface characterization; twisted light for detecting chiral agents via THz Hyper-Raman spectroscopy; measuring mean and variance of orbital angular momentum exchanged between THz radiation and matter for detecting bulk inhomogeneities; and simulations of planet–star systems for developing coronagraphic high-contrast imaging in the THz domain.

2. The BriXSinO Project

The BriXSinO project is developed by INFN (Istituto Nazionale di Fisica Nucleare), Section of Milan and Naples, in collaboration with other Italian National Institutions and Universities, and will be located at LASA (INFN- Mi/University of Milan, Italy).

Its accelerator is constituted by Super-Conducting (SC) cavities accelerating the electron beam up to 22–40 MeV. In the zero dispersion zones of the arc, the electron beam interacts by Inverse Compton Scattering with the photons of a laser in a Fabry–Perot cavity, producing hard X-rays. On the opposite side of the arc, a THz FEL radiation source, named TerRa, is placed. The two radiation sources can be alimented either independently or in sequence, thus generating synchronized radiation pulses in two different frequency ranges, namely, X-rays and THz. The primary objective of the BriXSinO project is to analyse and demonstrate the physics of the two-pass two-way acceleration scheme [22,23]; however, thanks to the wide versatility of its beam lines, BriXSinO exhibits strong potentiality as a user facility for both X-rays and THz radiation. As are many other THz FELs, TerRa@BriXSinO is configured as a multi-pass FEL oscillator, thus fully exploiting the large repetition rate of the SC accelerator, which delivers 50–200 pC electron beams at about 100 MHz, as shown in

Table 1. Electron beam parameters of TerRa@BriXSinO. ${ϵ}_{n_{x,y}}$ is the slice transverse normalized emittance and $\Delta E/E$ is the slice relative energy spread.

Quantity	Value	Quantity	Value
Energy E (MeV)	22–45	Charge (pC)	50–100
Rep rate (MHz)	50–100	Peak current (A)	8–12
${ϵ}_{n_{x,y}}$ (mm mrad)	1.2–1.7	$\Delta E/E$ (%)	0.05

.

The scientific case of TerRa indicates strong interest in radiation of wavelengths between 10 and 50 μm (3–17 THz). Emission in this range can be generated with undulators with period in the range $k_w$ = 3.5–4.5 cm, with magnetic fields up to 1 T (see

Table 2. Undulator modules for TeRra@BriXSinO. Permanent magnet undulators with linear polarization. TU (Terahertz Undulator), IO (Infrared Oscillator). ${\lambda }_w$ undulator period, B peak on-axis magnetic field, $\lambda$ emission wavelength, $L_w$ undulator length.

Und.	TU	IO
${\lambda }_w$ (cm)	3.5	3
B (T)	0.5–1	0.5–1
$\lambda$ (μm)	5–50	3.5–35
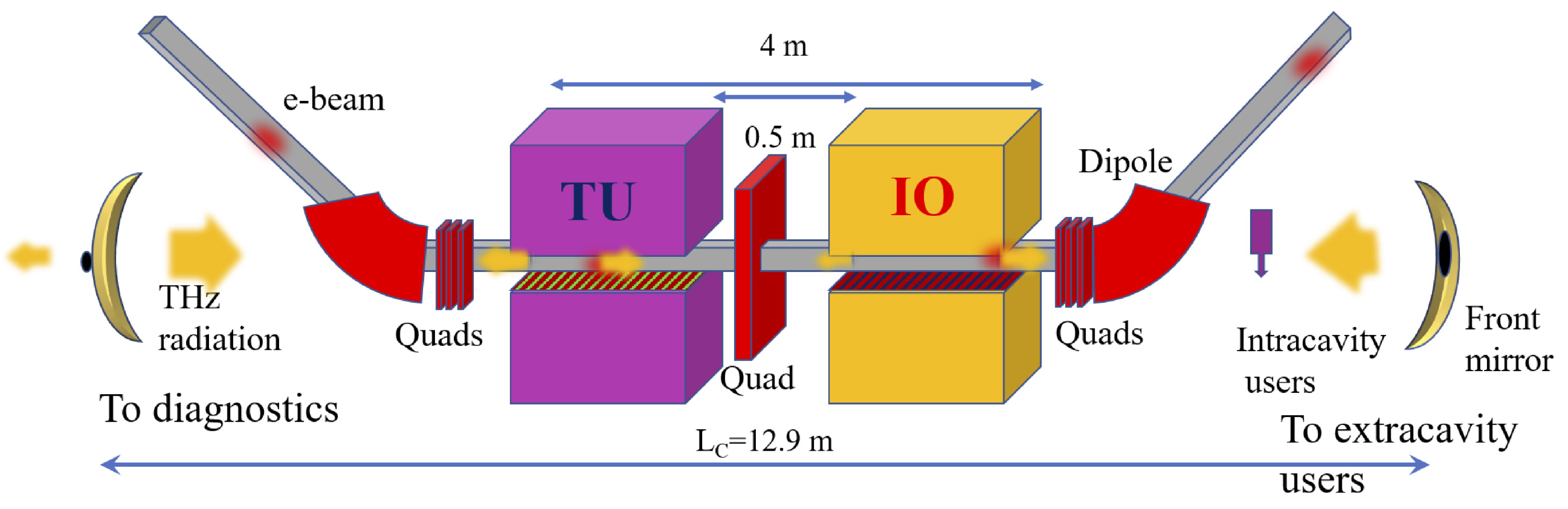
$L_w$ (m)	1.75	1.75

). The source has been designed to have the peak efficiency around 20 μm. TerRa@BriXSinO, whose scheme is shown in Figure 1, is conceived as composed by two undulator segments, separated by a drift where a quadrupole, phase shifters, diagnostics, and correctors are allocated, and embedded into an optical cavity equipped with mirrors suitable to the considered frequency range. The two undulator modules can work either tuned at the same wavelength or can deliver different wavelengths.

The numerical simulation of TerRa has been performed with the three-dimensional, time-dependent FEL code Genesis 1.3 [24], starting from the electron beam parameters listed in Table 1. The jitters of the bunch train have been modeled by injecting into the undulator a sequence of randomly prepared electron beams, each different from one other both microscopically and macroscopically.

For each electron bunch passing through, the produced radiation is cycled to the entrance of the undulator, taking into account the details of the optical line.

The study has been performed for radiation wavelengths from 10 to 50 μm, whose main properties are reported in

Table 3. THz radiation properties of TerRa@BriXSinO. IC=Intra-cavity, EC=extra-cavity. For cases (a) and (b): I = 12 A; case (c): I = 20 A; case (d): I = 25 A. The divergence of the THz radiation is on the order of mrad, for $\lambda$ = 20 μm it is 4.5 mrad.

Quantity	(a)	(b)	(c)	(d)
Wavelength (μm)	20	30	35	50
Beam energy (MeV)	40	33.2	30	26
Beam peak current (A)	12	12	20	25
IC energy (μJ)	355	300	952	560
EC energy (μJ)	17.7	15	46.6	16.8
EC average power (kW)	1.77	1.5	4.66	1.68
Peak power (MW)	250	100	250	100
Bandwidth (%)	0.6	1.6	2.7	1.3
RMS waist (mm)	2.6	3.5	4.5	5

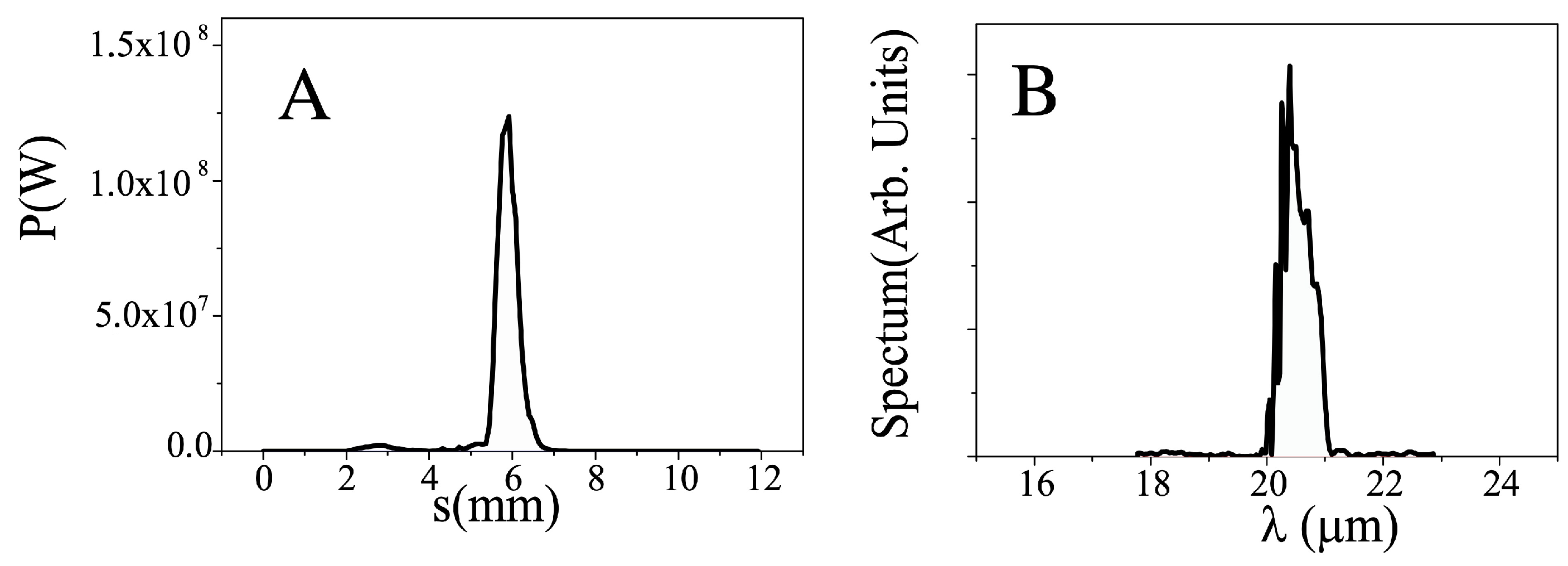
. Figure 2A shows the longitudinal power profile and Figure 2B shows the spectrum of the radiation at $\lambda$ = 20 μm. They appear to be single spiked, with an intra-cavity (IC) single shot energy of 355 μJ (meaning 17.7 μJ of extra-cavity (EC) energy and 1.77 kW of average output power). TerRa could open up also new research opportunities for the run of high field two-color THz spectroscopy measurements or X-ray pump/THz probe experiments.

3. Transverse Phase Measurements for Polarization and Wavefront Sensing

Despite polarization and wavefronts are both originated from the transverse phase of electromagnetic waves and are tied to each other by the transversality constraint, they are deeply different in nature: the former is a manifestation of the vector nature of the field; the latter provides a measure of the beam spreading due to diffraction during propagation. The polarization state of an electromagnetic wave is specified by a finite and small number of parameters, i.e., the three reduced Stokes parameters, and multiple accurate reliable methods are currently available for their measurement [25]. Many different methods for accurately reconstructing wavefronts exist, but the picture here is far more complicated, in that the parameters eligible for determining the wavefront passing through an observation point of space are neither unique nor a little. A wavefront could be determined directly by measuring the phase difference between any two points across a plane transverse to the propagation direction, in combination with the wave intensity profile over the same plane [26]. However, the derivative of the phase difference over the transverse plane is usually more easily affordable [27]. When the wavefront is not too ruffled—and the slow transverse envelope approximation applies—the wavefront can be reconstructed by measuring the tilt of the emerging rays or, alternatively, collecting the intensity distributions over distinct neighboring transverse planes [28]. The higher complexity of wavefront measurements against polarization reflects the infinite-dimensional nature of spatial wavefunctions and the Orbital angular momentum (OAM) of photons over the two-dimensional space of polarization and Spin Angular Momentum (SAM). Nevertheless, as it will appear clearer in what follows, wavefront and polarization, due to their intimate connection, have to be measured always in combination [29,30].

Selecting which method is the most appropriate for measuring wavefronts strongly depends on whether the subject of study is a source of radiation or an object that the source interacts with. In the former case, in fact, the source is unknown, while in the latter, the source is well-known and under the control of the observer, so it can be used to probe the object.

Studying the source—as typical in Astronomy—requires preliminary spectroscopic investigations aimed at discriminating, first, the emission wavelength band and brightness. This test enables to properly select detectors and materials for building the optical setup according to the most adequate measurement method. Then spatial and time coherence analyses follow. Moreover, in optical test of materials, preliminary spectroscopic analyses, providing the absorbance as a function of wavelength, enable the selection of the source of radiation required to test all the other optical properties.

In the case of studying an object, a distinction must be drawn between dielectric and morphologic properties, as already emphasized in Section 1. The former include dielectric tensor spectral dependence (dispersion), anisotropy (birefringence), and inhomogeneity (bulk scattering); the latter, on the other hand, include shape and roughness of thin film layers or boundary surfaces of bulky objects. In measuring dielectric inhomogeneities of bulk materials or topographic signatures of irregular surfaces, not only the material absorbance, but also the characteristic length of the spatial changes of the local refractive index as well as the sizes of surface protrusions and dents, place strong constraints on the wavelengths of the waves that can be used for probing. Metal surfaces, for instance, can be tested by reflection techniques from THz-FIR to visible domain and, of course, the spatial resolution achievable is increasingly higher as wavelengths reduce. Nevertheless, the larger the wavelength, the smoother the average information and the less the sensitivity to scattering; at the end, the wavelength is chosen to match the typical characteristic lengths of the textures of the tested surfaces. Long wavelength THz sensing techniques turn to be ideal for reconstructing the texture of optically rough surfaces of materials, such as rolled steel [12], as well as for testing the surface figure of telescope mirrors, as in the case of dish antennae for millimeter- and submillimeter-wave astronomical missions, where high accuracy is mandatory. As an example, consider the recently concluded Planck mission [31], in which the temperature fluctuations of the cosmic background radiation have been measured all over the sky at nine different frequencies with a target accuracy of one part in a million. Of course, particulate contamination, surface irregularities, and micro-cracking of the mirror surface were all potential issues that might have limited the target accuracy [32] and a remote testing of surface issues might have been useful.

3.1. Interdependent Measurements of Wavefront and Polarization Distribution

Reconstructing wavefronts generally entails measuring the phase change across any two points over planes transverse to the propagation direction. Reconstructing the polarization distribution over a wavefront, on the other hand, requires measuring, point by point, the phase change between two orthogonal components of field associated to the same ray. Indeed, the phase of an electromagnetic wave is a polymorphous and ubiquitous object, occurring in multiple experiments involving distinct properties of the wave. In scalar optics—in which the vectorial nature of light is kept silent, viz. image construction in geometric optics or wavefront reshaping in Kirchhoff diffraction theory— the phase appears as a relativistic invariant describing the time-space dependence of the field. In this guise, it is also known as dynamic phase—by contrast with the geometric phase, which will be introduced hereinafter—and is related to the lengths of the optical paths followed by rays in wave propagation. It determines the wavefronts as equal-phase surfaces. The wavefront geometry of a scalar field reflects the symmetry properties of the source and includes the deformations induced by the media interposed between the source and the observer. Deformations do occur when rays transmitted or reflected by the interposed media follow optical paths of unequal lengths due to inhomogeneities of the refractive index, local curvature, and roughness of the boundary surfaces, just to mention a few. The scalar theory ignores polarization and does not account for transversality, which couples polarization to the wavevector direction. However, in the paraxial approximation, the scalar theory can be adapted to obey transversality and to include polarization, in a consistent manner within terms of the first order in $2\pi w^2/\lambda$, w being the characteristic length scale of variation of the wavefront. Similarly, the polarization state of an electromagnetic wave reflects the dynamical properties of the source and suffers changes due to several anisotropies of the bodies that light propagates through. Polarization-affecting anisotropies include anisotropic phase-change upon reflection/refraction on boundaries between different dielectrics; bulk propagation through dichroic media (polarization-selective absorption); and bulk propagation through birefringent media, in which ordinary and extraordinary rays follow optical paths of different lengths. Due to the transversality constraint imposed by Maxwell’s equations, wavefront and polarization transformations are interlocked and accurate consistent wavefront analyses cannot be carried out independently of polarization. The coupling between wavefront and polarization ultimately reflects the intrinsic inseparability of SAM and OAM of electromagnetic radiation [29,33]. In general, a paraxial wavefield can be represented as

$$\begin{array}{ccc}\mathit{E}(x,y)\hfill & =\hfill & {\mathit{E}}_1(x,y)+{\mathit{E}}_2(x,y)=A_1(x,y)e^{\mathrm{i}{\psi }_1(x,y)}{\mathit{e}}_1+A_2(x,y)e^{\mathrm{i}{\psi }_2(x,y)}{\mathit{e}}_2,\hfill \end{array}$$

(1)

where ${\mathit{E}}_1(x,y)$ and ${\mathit{E}}_2(x,y)$ are two monochromatic orthogonally polarized wavefields, i.e., ${\mathit{e}}_1·{\mathit{e}}_2^{*}=0$ (where * denotes complex conjugation), having distinct complex amplitudes, $A_1(x,y)e^{\mathrm{i}{\psi }_1(x,y)}$ and $A_2(x,y)e^{\mathrm{i}{\psi }_2(x,y)}$, and therefore two distinct wavefronts. The total field $\mathit{E}(x,y)$ will appear as an inhomogenously polarized wavefield over an intensity landscape $|A_1{(x,y)|}^2+{\left|A_2(x,y)\right|}^2$ [10] and a joined polarization-wavefront analysis turns to be inescapable. This behavior is not uncommon: it occurs in artificially engineered materials and/or peculiar devices, such as metamaterials [34], form-birefringent space-variant inhomogeneous materials [35], liquid crystal–based spatially varying axis plates (SVAPs) [9,10], and it also occurs in polycrystalline or isotropic materials, such as crown glass, subject to mechanical stresses or exhibiting form birefringence [2]. The latter, in turn, helps in gathering information about submicroscopic particles that give rise to form birefringence or in recognizing unwanted polarization issues in fabrication processes of plastic or glass products, such as lenses, mirrors, filters, and others [4].

In summary, we here emphasize that polarimetry and wavefront sensing must be carried out in combination. They enable not only the characterization of a light source, but also the quality test of optical materials and the geometry of optical components. They provide information about texture and imperfections of optical surfaces and quality of coatings of single components and can be exploited to test performance of a whole optical system. Indeed, in free-space or guided optical communications, the ability of measuring polarization and wavefront of light is essential for the development of a receiving station decoding optical information encoded into the emitted signal. Of course, this entails the capability of manipulating at will the polarization state and wavefront of the electromagnetic field.

3.2. General Remarks on Methods for Carrying Out Polarimetry and Wavefront Sensing

The overwhelming majority of the devices adopted for measuring wavefronts or polarization are based on the analysis of peculiar intensity patterns known as interferograms or polarigrams, when the wavefront shape depends on the selected polarization state. Specifically, a polarimeter enables to reconstruct polarization ellipse by measuring the Stokes parameters in a selected frame reference [2], viz.

$$\begin{array}{ccc}{S}_0(x,y)& =& |E_x{(x,y)|}^2+{\left|E_y(x,y)\right|}^2\hfill \\ \\ S_1(x,y)& =& |E_x{(x,y)|}^2-{\left|E_y(x,y)\right|}^2\hfill \\ \\ S_2(x,y)& =& {\left|{\displaystyle \frac{E_x(x,y)+E_y(x,y)}{\sqrt{2}}}\right|}^2-{\left|{\displaystyle \frac{E_x(x,y)-E_y(x,y)}{\sqrt{2}}}\right|}^2\hfill \\ \\ S_3(x,y)& =& {\left|{\displaystyle \frac{E_x(x,y)+\mathrm{i}{E}_y(x,y)}{\sqrt{2}}}\right|}^2-{\left|{\displaystyle \frac{E_x(x,y)-\mathrm{i}{E}_y(x,y)}{\sqrt{2}}}\right|}^2.\hfill \end{array}$$

(2)

The phase change between the two copropagating orthogonal components $E_x$ and $E_y$ of the wavefield is determined by measuring their relative in-phase and quadrature parts, respectively represented by $S_2$ and $S_3$. The former is measured by projecting $E_x$ and $E_y$ along two orthogonal common directions forming $\pm {45}^{\circ }$ with the horizontal axis and by making them interfere. Analogously, $S_3$ is measured by projecting $E_x$ and $E_y$ along a clockwise and counterclockwise rotating directions having the same frequency as the electromagnetic wave and by making them interfere. For scalar fields, all the polarigrams displaying the Stokes parameters are proportional to $S_0(x,y)$. Consequently, though each of them can have a different peak intensity, they all exhibit the same intensity distribution, so that the normalized Stokes parameters $s_i=S_i(x,y)/S_0(x,y)$ are all uniform over the transverse plane. This is not the case for vector fields, in which $|E_x{(x,y)|}^2$ is not proportional $|E_y{(x,y)|}^2$. Though multiple schemes of polarimeters have been designed, they differ from one another only with respect to the method adopted for measuring the Stokes parameters [25].

A wavefront sensor, on the other hand, enables to reconstruct equal-phase surfaces based on both interferometric and non-interferometric methods. Here, we are not going to examine all the methods for reconstructing wavefronts; in Section 1, we have already suggested classical textbooks of technical optics for a comprehensive review. We emphasize, however, that we have not included into our platform double-path interferometers, as a reference plane wave is required for providing the transverse phase profile. In contrast, in common-path interferometers, there is no need for a reference plane wave to be superposed to the wavefront to be analyzed. In particular, we have selected several types of shearing interferometers to be inserted into GEST platform. Generally speaking, a shearing interferometer splits the test wavefront into two shifted replicas and subsequently makes them interfere. In its basic form, a shearing interferometer enables to superposes different parts of the same wavefront. Properly operated, it provides the derivative of the input wavefront, as will be explained in Section 5.4. Common-path interferometers, moreover, have remarkable stability and in some cases are very compact and do not require high-coherence lengths. To pass through the difficulty in finding out appropriate optical components and devices, a shearing interferometer based on geometric phase will be realized specifically for our platform [36]. No Hartmann–Shack wavefront sensor has been planned for the GEST platform, as efficient lenslet arrays for ST-waves are not available on the market. We envisage the possibility to design and fabricate such a wavefront sensor in future, as a potential extension of GEST.

It is worth noticing that wavefront analysis underpins a variety of diverse and seemingly unrelated applications such as microscopy [37], holography [38], optical testing [39], adaptive optics [40], ophthalmology [41], and other applications of interferometric metrology [42].

4. Geometric Phase Optical Elements

Since Geometric Phase Elements (GPEs) or Pancharatnam–Berry Phase elements are of vital importance for GEST, we judge it to be appropriate illustrating some basic related concepts in the present section [43].

In quantum mechanics, when the Hamiltonian of a dynamical system gradually glides through a succession of forms which are slightly different from each other, the $n^{th}$ eigenstate of the initial Hamiltonian $H^i$ gradually slides into the $n^{th}$ eigenstate of the final Hamiltonian $H^f$, provided that no energy-level crossing occurs [44]. In doing so, the $n^{th}$ eigenstate acquires a global phase as a result of two distinct contributions [45]:

• The ‘dynamical phase’, due to time evolution independently of the Hamiltonian variation and given by the time integral of the (slowly varying) energy $E_n$ divided by the reduced Planck constant $\hslash =h/\left(2\pi \right)$;
• The ‘geometric phase’, due to the quasi-static evolution of the Hamiltonian as a consequence of the parameters dragging, independently of the time duration.

The ‘geometric phase’ is also designated as the Berry phase, after its discoverer. The Berry phase concept applies beyond the boundaries of quantum mechanics [46]. In the field of optics, the geometric phase basically appears in two forms:

• ‘Spin redirection’ (also known as the Rytov–Vladimirskii–Berry phase), arising when varying the wavevector direction of a light beam;
• The Pancharatnam–Berry phase, which is induced by a sequence of polarization manipulations occurring in anisotropic media [47].

Throughout this paper, only the latter will be object of our attention.

The dynamical phase accumulated by an optical wave across a birefringent (uniform) medium is defined as ${\gamma }_d=2\pi \overline{n}d/\lambda$, where $\overline{n}={cos}^2\theta n_o+{sin}^2\theta n_e$ is the average refractive index; $n_o$ and $n_e$ are the ordinary and extraordinary indices, respectively; and $\theta$ is the angle formed by the input linear polarization direction with the ordinary (fast) axis in the transverse plane. If the input polarization is elliptical, $\theta$ is similarly defined by the projection angle of the input electric field onto the ordinary axis (see Figure 3A). When using standard birefringent waveplates, such as half-wave or quarter-wave plates, $\theta$ is determined by the orientation of the waveplate axis with respect to the input polarization. In particular, in all cases in which the waveplate axis is oriented at 45${}^{\circ }$ with respect to a linear input polarization or if the input light is circularly polarized (in the latter case, independently of the waveplate orientation), the average index reduces to $\overline{n}=(n_o+n_e)/2$. Representing the polarization states as points on the Poincaré sphere, all these cases correspond to rotating around an axis orthogonal to the direction defined by the initial point on the sphere, and hence, they correspond to moving along a geodesic arc on the sphere, i.e., an arc of a great circle. For the sake of clarity, we remind that a geodesic arc between two points on the sphere (or a general curved surface) is the minimum-length path connecting the points: it is a concept that generalizes the notion of a ‘straight line’ over a sphere (or a general curved space).

Apart from a dynamical phase, birefringent media also introduce an extra phase shift, determined only by the geometry of the polarization-evolution path on the Poincaré sphere and independent of the propagation length. Specifically, for any cyclic evolution, the extra phase over the cycle is given by ${\gamma }_g=-\mathsf{\Omega }/2$, $\mathsf{\Omega }$ being the solid angle subtended by the closed path. The extra phase here described corresponds to the above mentioned geometric phase. Consider, for instance, the ‘geodesic triangle’ $ABC$ in Figure 3B. The geometric phase ${\gamma }_g$ is then proportional to the solid angle $\mathsf{\Omega }(A,B,C)$ subtended by the closed path $ABC$ on the Poincaré sphere. Given any expansion or contraction of the geodesic triangle performed by a suitable rotation of waveplates, but the connecting lines remain arcs of great circles, the phase change will only be given by the variations of ${\gamma }_g$, because the dynamical phase will remain constant.

In addition, the phase difference between two distinct optical transformations sharing the same initial and final states has a geometric nature: it can be immediately traced back to the phase variation of a single cyclic transformation by reversing one of the two transformations. Consider the case in which the transformation relates a given input circular polarization state (left or right) to the opposite one. This can be easily achieved by the action of a single half-wave plate whose birefringent optic axis orientation is specified by the angle $\alpha$ (measured with respect to a fixed reference axis in the transverse plane). We are interested in the phase change determined by this transformation for any arbitrary angle $\alpha$, relative to that obtained for a reference angle such as, for instance, ${\alpha }_0=0$. This can be interpreted as the phase difference between two distinct transformations from left to right circular polarization or vice versa. For a circularly polarized input, the half-wave plate provides a geodesic arc on the Poincaré sphere, corresponding to the “meridian” located at 45${}^{\circ }+2\alpha$ (relative to the reference direction), so that the two transformations subtend an overall solid angle $\pm 4\alpha$ and, hence, have a geometric phase difference given by ${\gamma }_g=\pm 2\alpha$, the sign being determined by the input polarization (in ${\gamma }_g$, it is + for left circular input and − for right circular input). Hence, the optical phase of the outgoing wave can be controlled by simply rotating the half-wave plate. In contrast, the dynamical phase is independent of $\alpha$ and, therefore, plays no role.

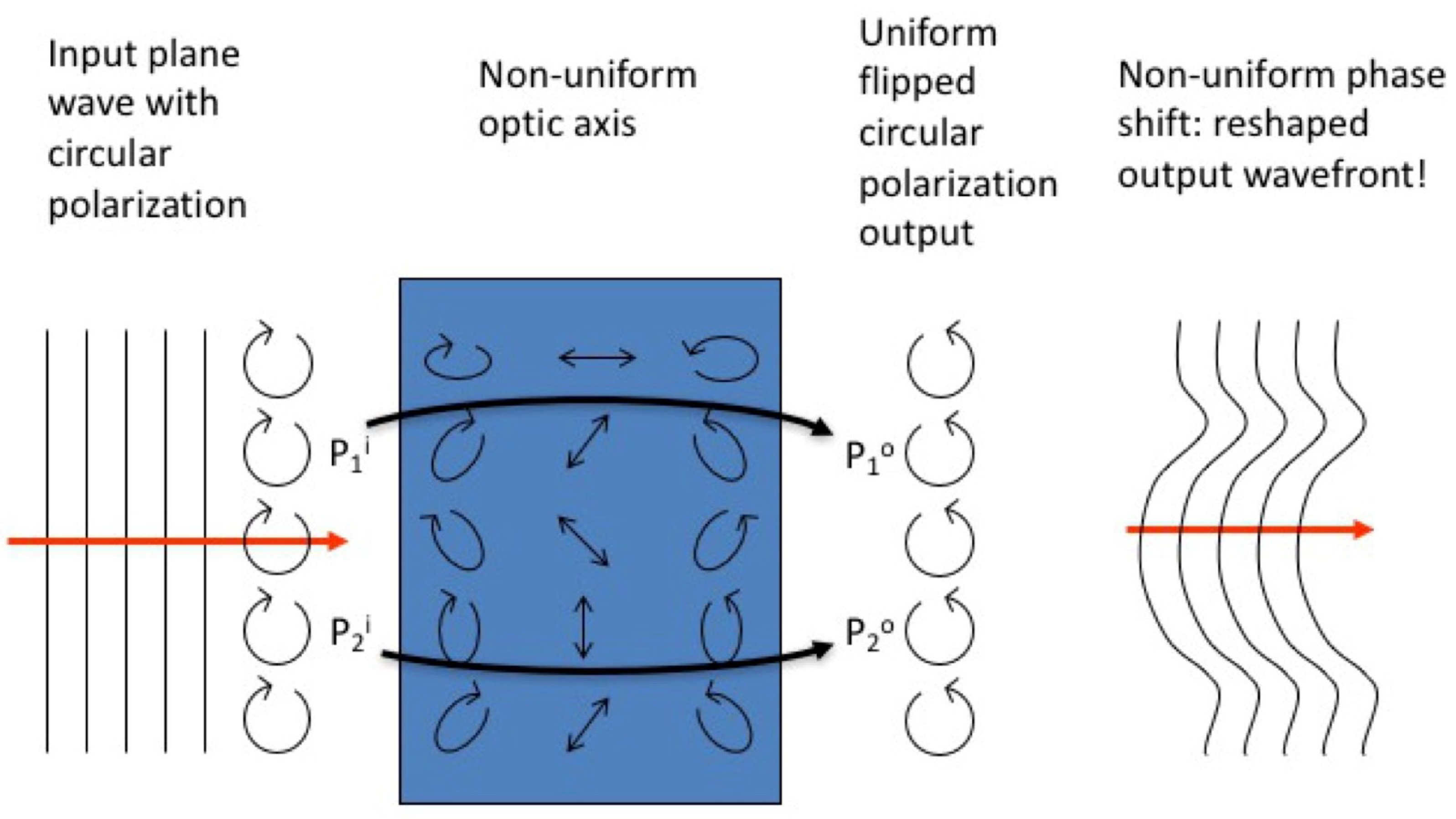
The simplest possible design of a GPE is a Spatially Varying optic Axis birefringent half-wave Plate (SVAP), so that the above-mentioned geometric phase in the transverse directions and results into a reshaped optical wavefront. When the input light is circularly polarized, only phase effects will arise. The output will be also circularly polarized with opposite handedness. The resulting optical phase component has a uniform thickness, but arbitrarily large phase differences can anyway be induced across the plate. Opposite handedness of the input circularly polarized light induces opposite phase retardations across the plate, and the wavefront outputs come to be reciprocally “conjugate”. The working principle of the device is illustrated pictorially in Figure 4.

The standard materials used for making birefringent optics are crystals, whose optic axis cannot be patterned. Liquid crystals are particularly well-suited for making SVAPs, as they are as birefringent as many ordinary crystals (actually, they typically have a fairly large birefringence), but their optic axis can be easily made non-uniform and controlled with patterned surface treatments or external fields. More importantly, the overall retardation $\delta$ of a SVAP can be continuously changed between 0 and $2\pi$—we say that SVAP retardation can be ‘tuned’ to match any wavelength—by applying a weak (∼ 1-2 V rms voltage) external AC electric field. This capability originates from sensitivity of liquid-crystals molecular director to external electric fields. In practice, to apply an external voltage to liquid crystals, the substrates of the SVAP cell are coated with a conductive transparent material.

The main challenges to be met in transferring liquid crystals–based SVAP technology from visible to T-waves involve the correct selection of the cell substrates and of the conductive transparent material for voltage application, and, importantly, of the transparency and birefringence magnitude of liquid-crystalline materials suitable for Short-wavelength Terahertz domain. The ideal substrate material is diamond Type IIA. A cheaper but less efficient choice is represented by germanium semiconductor. A typical conductive material for application in the visible range is Indium tin oxide (ITO), i.e., a ternary composition of indium, tin, and oxygen in varying proportions, deposited on glass or fused silica substrates by sputtering or evaporation. Unfortunately, it is unsuitable for applications to Mid-/Far-IR. A recently proposed material more suitable for this task is the poly(3,4-ethylenedioxythiophene) polystyrene sulfonate (PEDOT:PSS) [48], whose conductivity is not smaller than ITO’s.

5. Design of the Optical Layout of GEST Platform

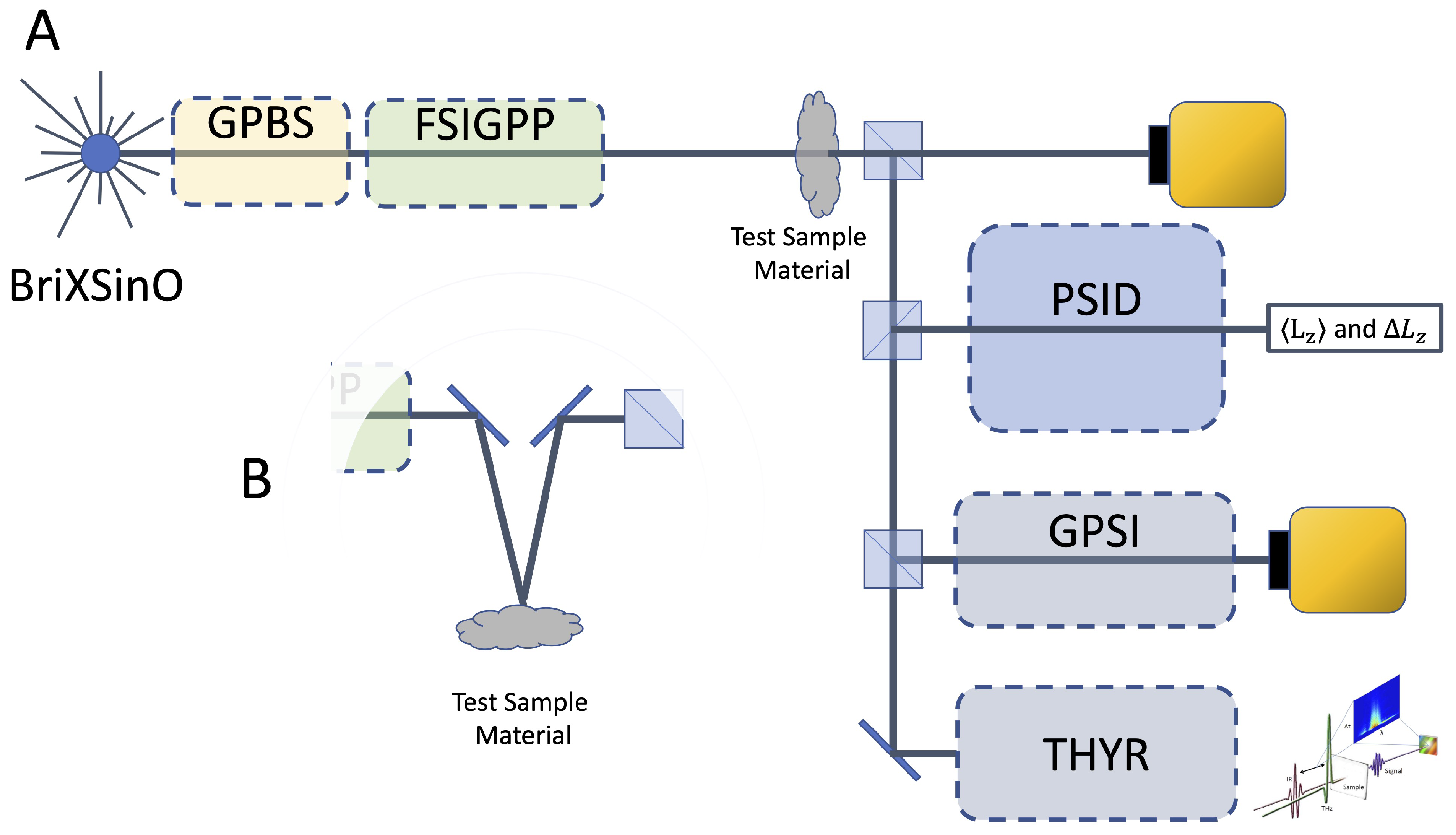
The designed layout for GEST platform is sketched in Figure 5A,B. TerRa@BriXino provides a linearly polarized pulsed wave in the frequency range between 6 THz ($\lambda =50\mathsf{\mu }\mathrm{m}$) and 30 THz ($\lambda =10\mathsf{\mu }\mathrm{m}$) with an output power on the order of 1 kW. The output beam has a divergence of 4.5 mrad. The output power could present high order transverse modes, that require to be adjusted to a clean TEM₀₀ mode before any further utilization for metrology applications. 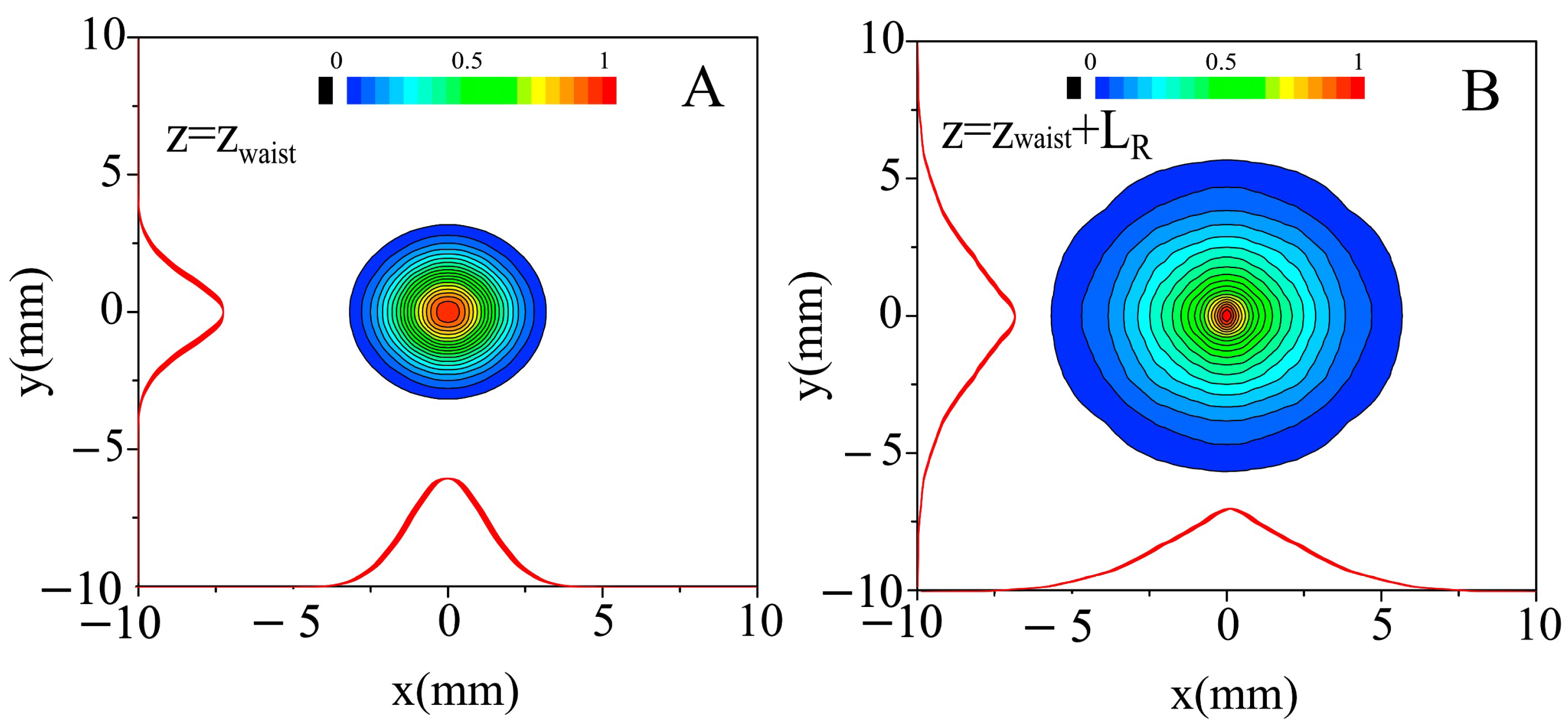Figure 6A shows the transverse power profile in correspondence to the waist ($z=z_{waist}$) and Figure 6B shows the profile after one Rayleigh length. For this purpose, the beam has been focused and re-collimated by means of two confocal biconvex diamond (Type IIA) lenses, $L_1$ and L₂, with focal lengths, respectively, $f_1=25$ mm and $f_2=50$ mm. For spatial filtering, a small circular aperture is placed at the common intermediate focus of this simple-telescope. The aperture diameter should be at least on the order of $2f_1\lambda /\pi w_0$. Depending on the test type, polarization state and wavefront shape can be easily modified through the versatile electro-optical system represented by Module for Geometric Phase Beam Shaping (GPBS). It includes several liquid crystals–based electro-optically driven homogeneous retardation waveplates and SVAPs. The latter have suitably shaped optic axis distributions that can be tailored to sculpt the wavefront or the polarization transverse distribution as required [9,10]. The modules for polarization and wavefront analyses will be described in greater detail in Section 5.2, Section 5.3 and Section 5.4. The sample is then inserted. Depending on the sample material and/or the test type, transmitted or reflected light is analyzed. An optical system has been provided to switch from transmitted to reflected light analysis and vice versa (Figure 5B).

Consistently with what has been explained in Section 3.1, in order to perform combined polarization and wavefront analyses, the GEST platform includes an electro-optically driven Full-Stokes Imaging Geometric Phase Polarimeter (FSIGPP) that we have specifically designed for the platform. Such device consists of a wiregrid polarizer and six liquid-crystal retardation wave plates, that can be electrically tuned independently from each other (SUAP or Spatially Uniform Axis Plates). In this way, any desired retardation can be achieved and any required polarization component can be selected for subsequent wavefront analysis. Two 50:50 beam splitters, $B{S}_1$ and $B{S}_2$, and the mirror M are cascaded in order to generate three replicas of the output beam from the polarimeter to be injected in the following systems for subsequent intensity measurements and wavefront analyses:

• Direct output from the polarimeter (FSIGPP) for pure polarization analysis and measurement of the Spin Angular Momentum (SAM) transferred from light to matter and vice versa;
• Sagnac Polarizing Interferometer containing a Dove prism (PSID), delivering the mean and variance of the Orbital Angular Momentum (OAM) transferred from light to matter and vice versa;
• Geometric Phase-based Shearing Interferometer (GPSI), delivering the phase derivative of the input wavefront with respect to multiple coordinates depending on the shearing core device and the wavefront shape impinging on the sample, for optical devices aberrometry and for surface profilometry;
• Twisted Light Terahertz Hyper-Raman (THYR) Spectroscopy in both frequency and time domains can be implemented by exploiting FSIGPP to prepare wavefront and polarization of the pump/probe beams used to generate and detect a THz-optical four wave mixing in the investigated material.

THYR spectroscopy technique is illustrated in detail in Section 7. The frequencies of the generated signal correspond to a large variety of material excitations, such as $\mathsf{\Gamma }$-point phonons, polaritons, and phonons out of the $\mathsf{\Gamma }$-point, which can be usually observed only by neutron scattering techniques. Twisted light adds a further degree of freedom to the technique and enables to investigate chiral molecular agents, which have high relevance in Biology and Medicine.

Some detection stages in this layout include a high-performance camera, such as a NEC IRV-T0831 uncooled microbolometer array ($320\times 240$ pixels, 23.5 μm pixel size). Microbolometers are originally designed for thermal imaging at the long wavelength infrared (LWIR) region at 7–14 μm, but they are known to retain sensitivity at THz frequencies and have been effectively used for THz beam profiling and imaging at longer wavelengths (14–300 μm) [49]. All the beamsplitters included into in the platform are Germanium-protected multilayer KBr beamsplitters designed for flat spectral response from Spectral Systems.

In the GEST platform, the Pancharatnam–Berry or Geometric Phase underpins the operation principle not only of optical components and devices deployed all over the optical layout, but also of entire building blocks, such as the preparation stage of both polarization and wavefront of the beam irradiating the sample, as well as the detection stage of polarization and, of course, the GPSI. At present, Geometric-Phase-based optical devices and systems are not available on the market and we will fabricate them in the Photonics Lab of the Department of Physics "E. Pancini" at University of Naples “Federico II”. The design and fabrication of liquid crystal–based SVAPs for ST-waves are extremely challenging and require a fairly cunning strategy to be realized in practice, as explained in Section 4, namely, selection of the most appropriate liquid crystals for this wavelength range; selection of substrates transparent over a very large spectral range for enabling optical writing at short wavelengths and operation at long wavelengths; and conductive transparent film for voltage control of retardation enabling retardation tuning.

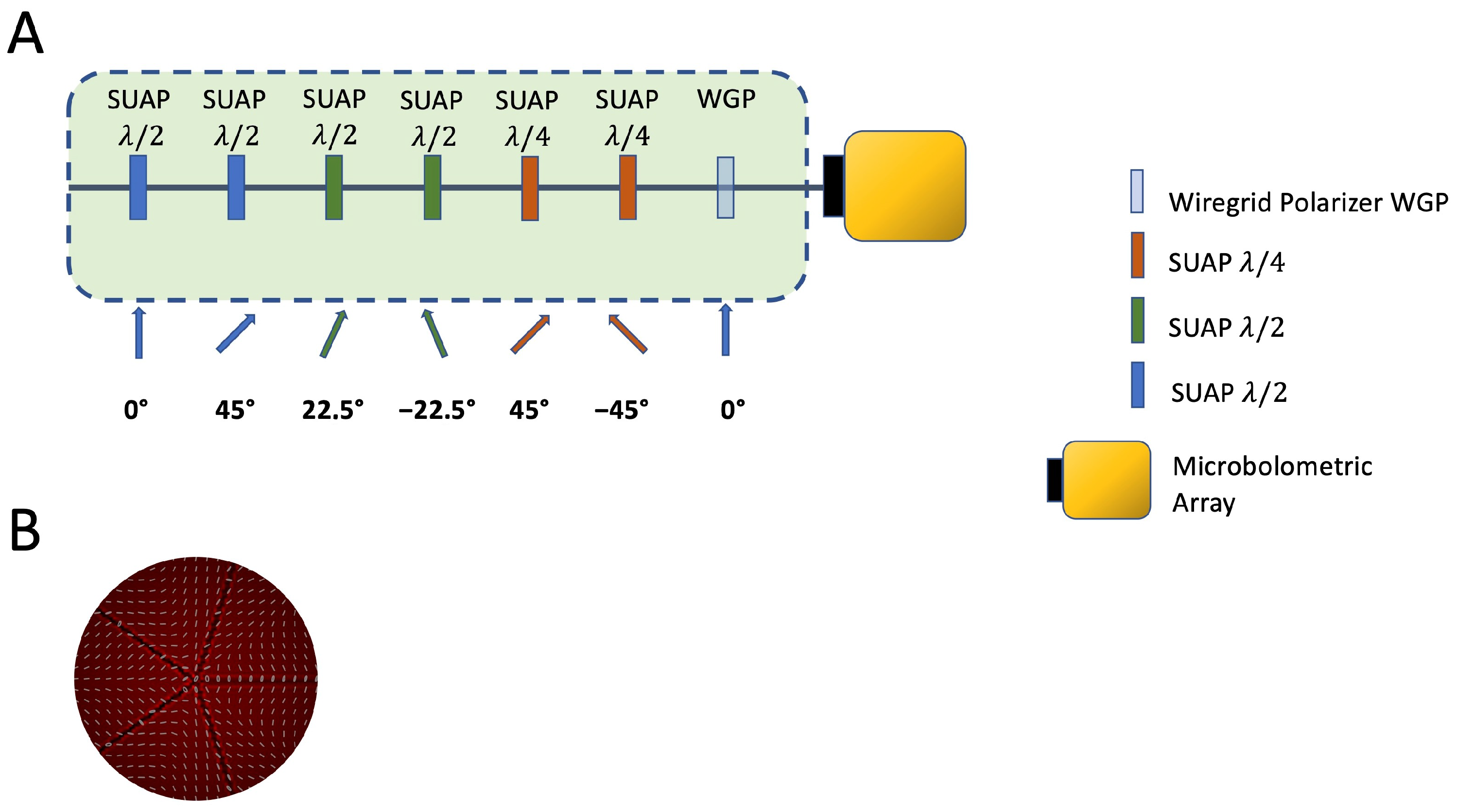
5.1. Test Beam Preparation: Setting the Polarization and the Wavefront of the Beam Output from Future TerRa@BriXSinO Source

TerRa@BriXSinO generates an output beam linearly polarized in the vertical direction with contrast ratio that can reach values of the order of 10.000:1, in the transverse fundamental gaussian mode TEM₀₀ with waist w = 5 mm. The polarization state can be homogeneously changed at will by using a couple of electrically tunable liquid crystal–based retardation waveplates with uniform optic axis distribution or Spatially Uniform Axis Plates (SUAPs), fabricated in our Photonics Lab in Naples (Figure 7A). The axis of the first SUAP is oriented at 45${}^{\circ }$ with respect to the linear polarization direction of TerRa@BriXSinO output. Its retardation ${\delta }_1$ can be tuned to any value between 0 and $2\pi$ with resolution of ≈${10}^{-2}\pi$. The second waveplate retardation is set to an appropriate value ${\delta }_2=\pi /2$ for Half-Wave Plate (HWP) operation and the axis can be rotated in order to set at will the orientation of the polarization ellipse. SUAPs fabricated in our lab take advantage against ordinary retardation waveplates tunability: the retardation ${\delta }_1$ or ${\delta }_2$, as explained in Section 4, can be changed to perfectly match the peak wavelength of the laser pulse by changing the amplitude of the AC voltage signal applied to the SUAP.

In order to impart the beam a transversely inhomogeneous polarization, a suitably designed SVAP is required [10], as shown in Figure 7B. In generating vector beams, SVAPs are by far more efficient than interferometric devices: they are easy to use, compact, and, above all, when operated as Quarter-Wave Plates (QWPs), the polarization distribution is coincident with the optic axis distribution. To reshape the wavefront while maintaining the polarization uniform and preserving input power, a suitably designed SVAP is again required, but the input polarization has to be preliminarily converted from linear into circular by means of a 45${}^{\circ }$ oriented SUAP with retardation $\delta =\pi /2$ [9]. Most probably, q-plates are the most well-known examples of such [29].

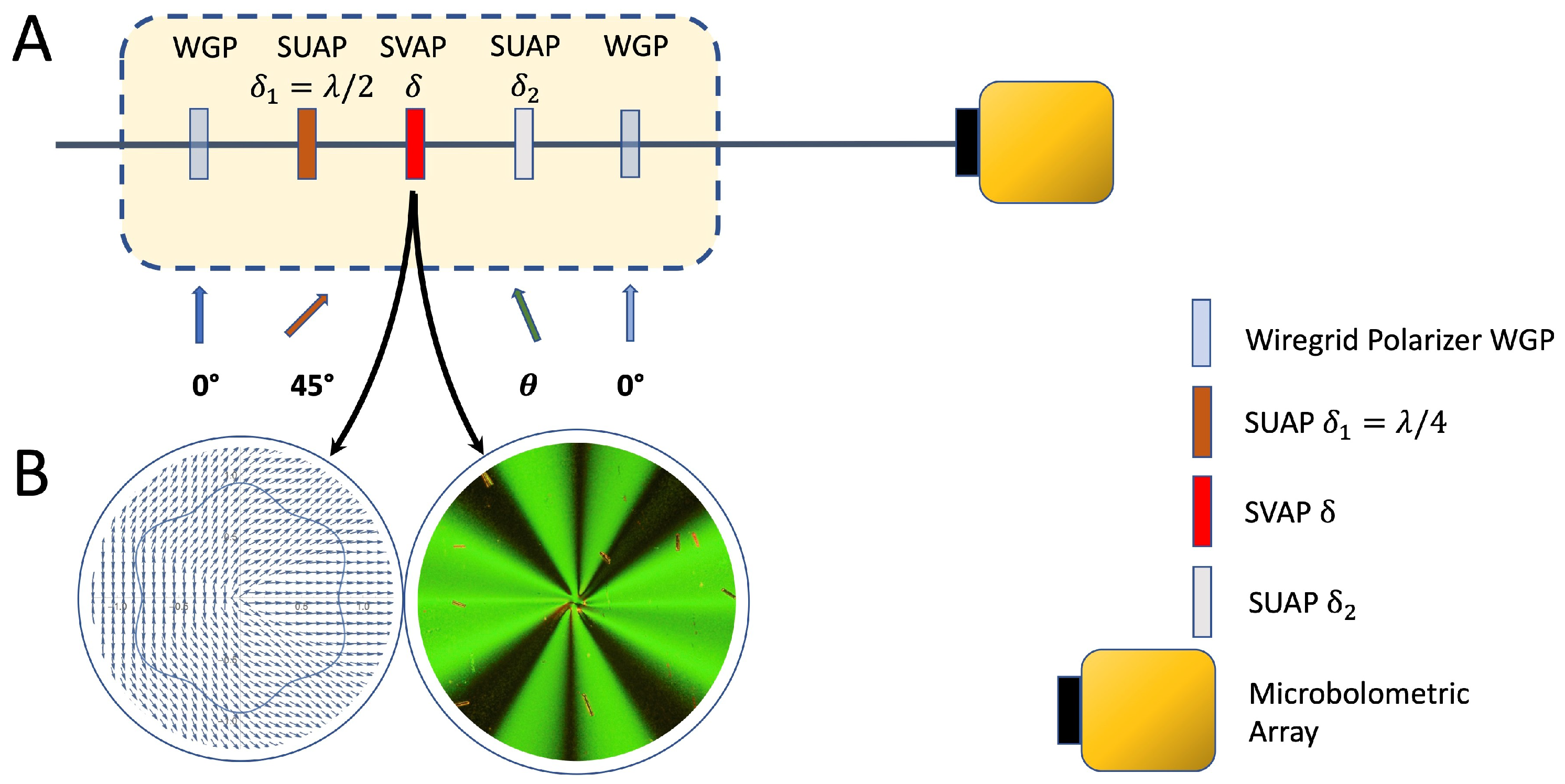
5.2. Polarization Detection Stage

Beyond the test sample, a geometric phase-based polarimeter is posed. It consists of six SUAPs and a wire-grid polarizer (WGP) model P03 from InfraSpecs (Figure 8A). WGP is a high contrast Far-Infrared and Mid-Infrared substrate-free wire-grid polarizer P03, with extinction ratio 10.000:1. All the SUAPs, as well as the WGP, are mounted on stepper-motor-driven rotary tables having angular resolution 0.02${}^{\circ }$. Combined with the NEC IRV-T0831 microbolometric camera, our system enables full-Stokes imaging; hence, the name of the subsystem, Full-Stokes Imaging Geometric Phase Polarimeter (FSIGPP). The polarization inhomogeneity map of the light transmitted or reflected by an object can be reconstructed with a resolution depending on the specifications of the camera and the magnification of the optical system adopted to locally scan the sample. The magnification system consists of an infinity-corrected microscope objective (reflective objective LMM-UVV by Thorlabs) with a predetermined magnification ratio mounted on a stepper-motor-drive XYZ translation stage for both transverse and longitudinal scanning. Full-Stokes parameters measurements through a single SUAP is allowed thanks to the possibility to set the retardation $\delta$ for both HWP and QWP operation all over the wavelength range of interest. Measuring the Stokes parameter $S_3$ enables measuring the local Spin Angular Momentum (SAM) transfer between light and sample.

Such a stage serves as polarization detector as well as polarization selector for subsequent wavefront analysis. Moreover, it enables to select any output polarization state and to encode the corresponding amplitude into a linear polarization state. The orientation of the latter can be rotated to match the beam splitters eigenmodes (vertical or horizontal direction) for maximum visibility beyond the interferometric stages.

5.3. Polarizing Sagnac Interferometer with Dove Prism (PSID)

In a polarizing Sagnac interferometer (Figure 9), two replicas of the input beam propagate in two opposite directions along the same planar path (common-path interferometer) and are linearly polarized along mutually orthogonal directions. A Dove prism whose basis is tilted out of the interferometer plane by an angle $\alpha$ is inserted into the path and provides a rotational shift of the two replicas around their own axes by an angle $2\alpha$. The phase delay between the beams leaving the interferometer is adjusted to $\pi /2$ or $2\pi$ through a SUAP with the optic axis aligned along one of the PSID axis. A second SUAP with $\delta =\pi$ and the optic axis at 45${}^{\circ }$ to the PSID axes is used to make the output beams interfere and, finally, a balanced polarizing homodyne detector is used to provide the contrast ratio between the two output ports. By this method, the mean and variance of the Orbital Angular Momentum (OAM) transferred between light and sample can be directly measured without passing through the determination of its full spectral distribution [30].

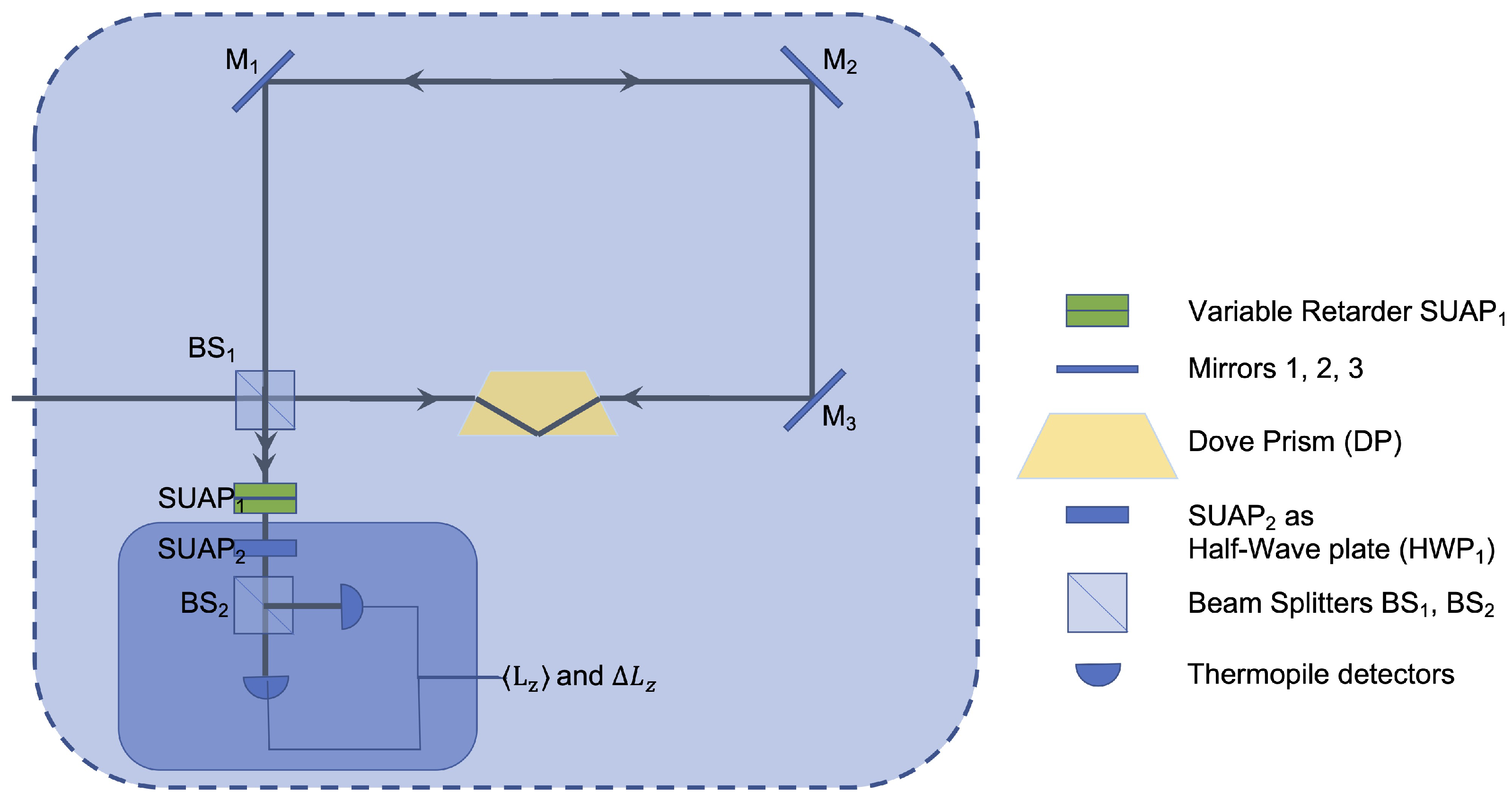
5.4. Geometric Phase–Based Shearing Interferometer (GPSI)

A shearing interferometer is a common-path interferometer delivering the derivative of the optical phase with respect to a given coordinate. The derivative is performed by generating two replicas of the input beam, so that they are slightly shifted with respect to each other along the given coordinate, and making them interfere with opposite phases. This method enables to reconstruct wavefronts without resorting to any reference wave. Indeed, the PSID layout described in Section 5.3 does match such description and represents an ideally perfect azimuthal shearing interferometer. However, in a narrower acceptation, the term ‘shearing interferometer’ is often used to label a compact short-path interferometer perfectly suitable for light beams having limited coherence lengths. We have included into our platform a Geometric Phase-based Shearing Interferometer (GPSI) (Figure 10A), which has been fully developed in our Photonics Lab in Naples and represents the most advanced delivery of shearing interferometry technology [36]. Thanks to its Geometric Phase heart, it enables to perform several types of shearing interferometry, though preserving a robust, compact, and common-path setup. The key elements are two identical parallel SVAPS, which perform the shearing by imparting different geometric phases on the two circular polarization components of a linearly polarized incident wavefront. This setup allows the independent control of the shearing magnitude and the relative phase of the two wavefront replicas. The shearing coordinate depends on the specific axis profile characterizing the SVAPs (Figure 10B). To date, lateral and radial shearing have been successfully implemented. Other coordinates, such as, for instance, the azimuthal polar angle or the quadratic lateral coordinates, are currently under development.

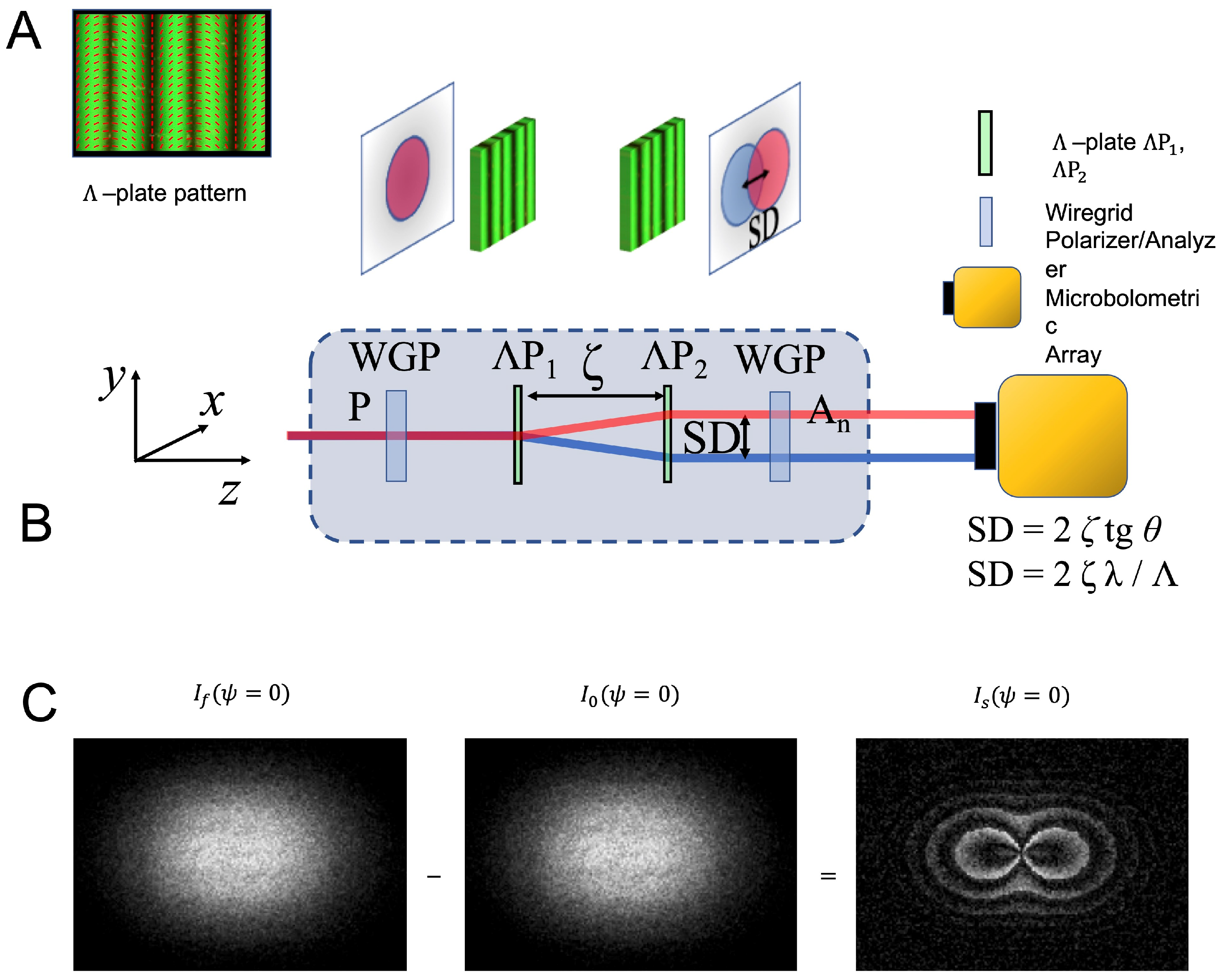
6. Geometric Phase–Based Shearography for Stress Tests on Composite Structures and Surface Profilometry

A composite material consists of two or more materials with different physical and chemical properties, in order to create a novel material suitable for very specific jobs, such as, for instance, materials having mind-boggling properties suitable for spacecrafts. In general, composite materials, such as glass-fiber-reinforced materials, carbon-fiber-reinforced materials, and honeycomb structures, consist of multilayered structures. Separation between layers could occur through an internal defect in one of them (delamination). Moreover, their mechanical properties could be reduced by false adhesion, wrinkle, crack, impact damage, etc., thus causing serious consequences. Therefore, nondestructive testing methods, such as shearometry, play an important role in this technology sector [3]. The GPSI included in the GEST platform could be of great help to unveil, with high reliability, the possible issues. To clarify this point, we focus the attention on the lateral shearing interferometer described in Ref. [36]. This has been realized by using two identical $\mathsf{\Lambda }$-plates with separation $\zeta$, in order to introduce a controlled lateral Shear Distance (SD) between the replicas. A $\mathsf{\Lambda }$-plate is a SVAP in which the fast axis rotates in the transverse plane along the horizontal direction, say x, so that the rotation angle $\mathsf{\Theta }$ of the optic axis increases or decreases linearly with x from 0 to $\pi$ over a distance $\mathsf{\Lambda }$. The latter quantity—dubbing the SVAP—is the spatial period of the plate axis distribution. As a result, a $\mathsf{\Lambda }$-plate deflects light of wavelength $\lambda$ and circular polarization ${\mathit{C}}_{\pm }$ by an angle $\pm arctan(\lambda /\mathsf{\Lambda })$ (Figure 10B). At a distance z from the plate, such deflection induces a lateral shear $\pm z\lambda /\mathsf{\Lambda }$ from the incident propagation direction.

Extending the operation of this technology to TerRa’s wavelength range requires again meeting the challenge of fabricating electrically tunable $\mathsf{\Lambda }$-plates for $\lambda$ in the range 10–50 μm. The GPSI module included in the GEST platform will enable to perform, in the Mid- and Far-IR domain, testing of optical systems and components, surface profilometry of object boundaries. The scheme of the optical layout for the lateral GPSI is shown in Figure 10A. The shearing distance SD depends on both $\mathsf{\Lambda }$ and the distance $\zeta$ between the plates. It can be continuously changed so to enable tailoring the sensitivity and, then, the operation range of the wavefront sensor. The input beam replicas are made to interfere through an output linear analyzer providing a speckle pattern, or speckle interferogram, recorded by the NEC IRV-T0831 camera and then computer stored. The specific shape of the speckle interferogram depends on the angular mismatch $\psi$ between the direction of the input linear polarization and the direction of the axis of the analyzer, according to [36]

$$\begin{array}{ccc}\hfill I\left(\psi \right)& \propto & |E_{+}{\mathrm{e}}^{\mathrm{i}\psi }+E_{-}{\mathrm{e}}^{-\mathrm{i}\psi }{|}^2\hfill \\ & =& {\left|\mathcal{S}\right|}^2{cos}^2\psi +{\left|\mathcal{D}\right|}^2{sin}^2\psi +\mathrm{Im}\left(\mathcal{S}{\mathcal{D}}^{*}\right)sin2\psi ,\hfill \end{array}$$

(3)

where $E_{\pm }$ are the two equally intense circularly-polarized displaced replicas of the input beam, $\mathcal{S}=E_{+}+E_{-}$, $\mathcal{D}=E_{+}-E_{-}$. Notice that, for small SD, $\left|\mathcal{S}\right|\gg \left|\mathcal{D}\right|$. Equation (3) shows that the relative phase difference between the replicas is $\mathrm{SP}$ = 2$\psi$ and that it can be controlled by rotating either the input polarization direction or the output analyzer axis. The most relevant information rests on the last term in Equation (3), i.e., $\mathrm{Im}\left(\mathcal{S}{\mathcal{D}}^{*}\right)$, which is proportional to the wavefront derivative when $\mathrm{SD}\ll w$, w denoting the characteristic length of the surface profile. This term can be experimentally obtained by subtracting the speckle interferogram for $\psi =\pi /4$ and that for $\psi =-\pi /4$

$$\mathrm{Im}\left(\mathcal{S}{\mathcal{D}}^{*}\right)=I(\pi /4)-I(-\pi /4).$$

(4)

Equations (3) and (4) rule the operation of the shearing interferometer for testing of optical systems and for surface profilometry. In the latter case, both transverse and longitudinal resolutions can be enhanced by collecting the light from the sample through the magnification system previously introduced for polarization analysis, i.e., an infinity-corrected microscope objective (reflective objective LMM-UVV by Thorlabs) with a predetermined magnification ratio mounted on a stepper-motor-drive XYZ translation stage for both transverse and longitudinal scanning. General references on this topic, for applications in the visible domain, are found in Ref. [50]. We incidentally notice that, in most shearing interferometry applications reported in literature, the modified Michelson interferometer, no doubt, plays a prominent role. Such shearing device, as a matter of facts, exhibits a simple structure and ease in changing the shearing magnitude and direction. However, tuning the relative phase difference between the input beam replicas requires piezoelectric crystal driven mirrors that change the lengths of the arms of the interferometer. We have included the GPSI into GEST because of its geometric phase heart makes its structure even simpler and handier than the modified Michelson interferometer and, above all, delivers explicitly the phase derivative of the input field. The shearing magnitude amount SD, controlled by $\mathsf{\Lambda }$ and $\zeta$, is totally independent of the shear phase SP, controlled by $\psi$. More importantly, changing the shearing coordinate—which is fully determined by the SVAPs axis profiles—simply requires replacing the SVAPs while preserving the setup. Electrical tunability, finally, enables a single device to be adjusted to all the wavelength within the region of transparency of the nematic liquid crystals exploited in fabricating SVAPs.

Furthermore, digital shearography is based on the same principles described by Equations (3) and (4), but further details of the method have to be described henceforth. For a comprehensive review about digital shearography applied to NDT of composite structures, the recent review in Ref. [3] is suggested for reference. In order to test the mechanical strength of an object or possible defects that might reduce its mechanical properties, both the speckle interferogram of the relaxed object, $I_0\left(\psi \right)$, and that of the loaded object, $I_f\left(\psi \right)$, need to be acquired and subsequently subtracted to each other, i.e., $I_s\left(\psi \right)=|I_f\left(\psi \right)-I_0\left(\psi \right)|$ (Figure 10C). The intensity fringe pattern or shearogram $I_s\left(\psi \right)$ encodes the derivative of the deformation of the object. The latter can be determined based on the relationship between the relative phase change and the relative deformation between any two points separated by the distance SD, determined by $\mathsf{\Lambda }$ and $\zeta$. The method selected for phase decoding the shearogram deeply affects the overall measurement sensitivity. If the phase at each fringe is determined simply by counting the shearogram fringes, the measurement sensitivity will be only one fringe, or $2\pi$, and smaller phase changes will not be accessible. A higher sensitivity in phase measurements can be achieved by recurring to the phase-shift technique, in which four speckle interferograms corresponding to as many distinct supplementary phase delays are subsequently measured and combined to provide the detailed phase distribution [3]. Interpreting speckle interferograms—and then shearograms—provided by GPSI, based on this phase-retrieving technique, is quite simple. In fact, the phase change $\mathsf{\Phi }$ between two points separated by the distance SD over the test surface, is

$$tan\mathsf{\Phi }=\frac{2Im\mathcal{S}{\mathcal{D}}^{*}}{{\left|\mathcal{S}\right|}^2-{\left|\mathcal{D}\right|}^2}=2\frac{I(\pi /4)-I(-\pi /4)}{I\left(0\right)-I\left(\pi \right)},$$

(5)

which involves simply rotating the orientation of either the input or the output polarization. Both transverse and longitudinal spatial resolutions can be enhanced by scanning the wavefront through a high numerical aperture reflective microscope objective, selected depending on the target resolution.

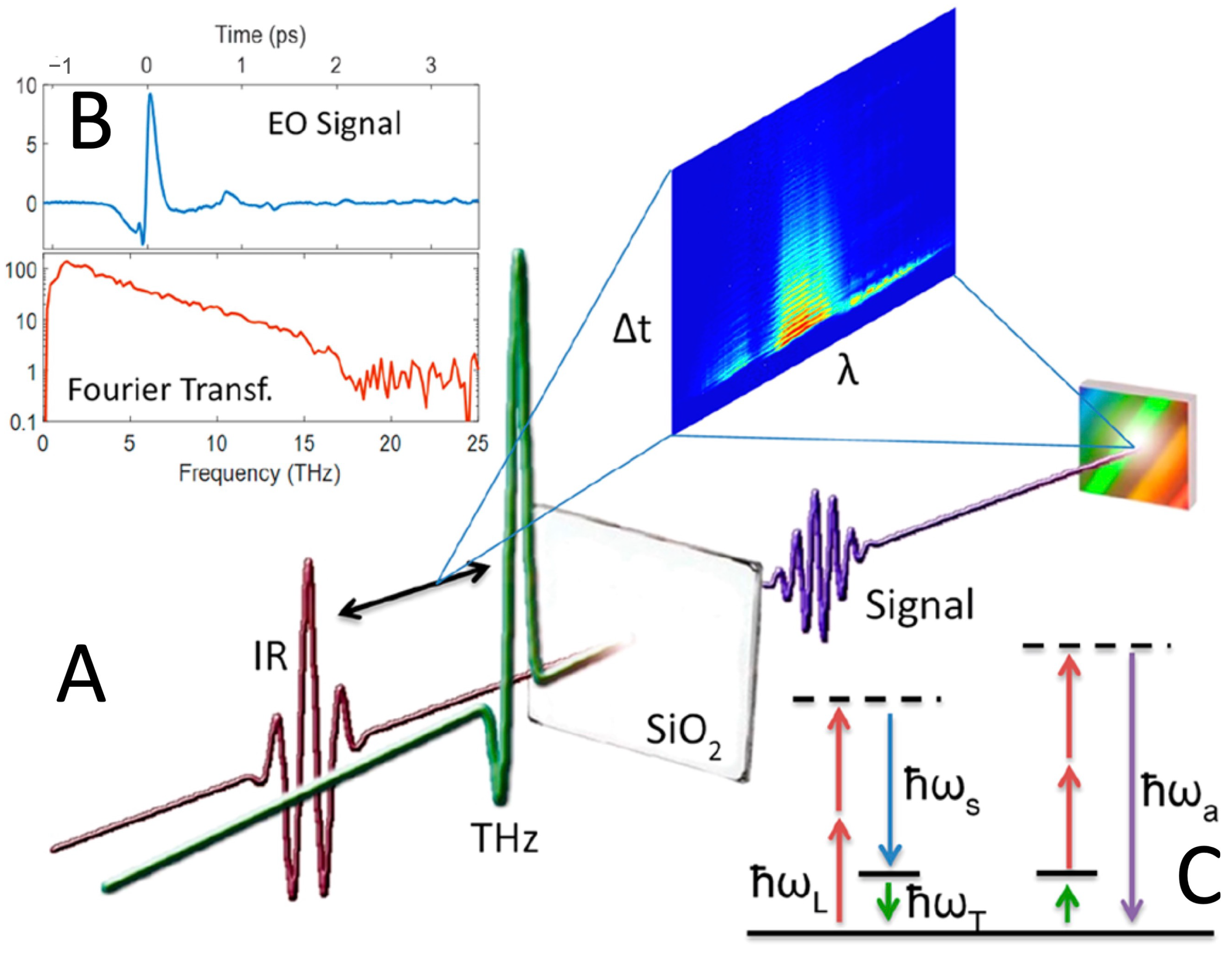
7. THz Hyper-Raman Spectroscopy with Twisted Light for Chiral Agents Detection

Since the initial works [51] in the early 1990s, time-domain THz spectroscopy has become a mature technique with a consequent flourishing of applications in very diverse fields [52]. With the advent of high-power THz sources, the last decade has witnessed a rapid growth of reports on the nonlinear interaction between intense THz pulses and matter, which has paved the way to the topical field of ‘THz nonlinear optics’ [53,54,55,56,57]. This field is still in its infancy, and for its further development, there is a strong need for new intense pulsed THz sources.

Very recently, some of us have demonstrated a new nonlinear technique in the THz domain which combines near-infrared optical pulses and intense sub-ps broadband THz pulses to generate a THz-optical four wave mixing in the investigated material [58,59,60]. We name this effect coherent ‘THz Hyper-Raman’ (THYR) and a schematic representation of the technique is provided in Figure 11A–C. The reason for this name will be clarified henceforth.

Standard hyper-Raman spectroscopy is a modified version of the Raman technique where the scattered light displays a frequency spectrum with components that are close to the double frequency or second harmonic generated (SHG) signal of the fundamental laser frequency ${\omega }_L$. These components are the Stokes (anti-Stokes) frequencies ${\omega }_{s;a}$. The energy conservation law for the hyper-Raman effect can be written as $\hslash {\omega }_{s;a}=2\hslash {\omega }_L\mp \hslash \mathsf{\Omega }$, where $\mathsf{\Omega }$ is a low-energy excitation of the material under investigation. The main advantage of hyper-Raman spectroscopy is that it may provide information on low-energy modes that are suppressed in Raman spectra because of its symmetry selection rules. A second advantage is that detecting the signal close to the $2{\omega }_L$ frequency allows a more effective rejection of the extremely intense radiation at ${\omega }_L$. We will come back to this point below.

Usually, the hyper-Raman signal is very weak, but it may be strongly enhanced in the presence of additional optical fields oscillating at frequency $\mathsf{\Omega }$; hence, it is resonant with the material low-energy modes. To this aim, it would be highly desirable to have an intense THz pulse, which may impulsively excite the material low-energy modes and then mix with the visible light so to generate a stimulated hyper-Raman signal. This is exactly what happens in the THYR effect, where the THz wave at ${\omega }_T$ may directly couple to the $\mathsf{\Omega }$ of the material, thus enhancing the THYR signal when ${\omega }_T=\mathsf{\Omega }$. The energy level diagrams of the THYR process are depicted in in Figure 11C. In the THYR technique, the THz photon at ${\omega }_T$ mixes with the two photons of the visible pulse at ${\omega }_L$ and generates new spectral components at lower (Stokes) and higher (anti-Stokes) frequencies as compared to the SHG central frequency $2{\omega }_L$. In crystalline quartz, in Ref. [58], the THYR signal has been shown to carry information on a large variety of low-energy excitations, including polaritons and phonons far from the $\mathsf{\Gamma }$-point that usually cannot be observed with standard optical techniques.

This phenomenon has been observed by means of a table-top THz source with limited intensity per pulse, which makes the observation of this nonlinear optical effect challenging. Therefore, we propose to extend the frequency range of this novel technique to that covered by the future source TerRa@BriXSinO. The high intensity of the light emitted by this source will unlock the full potentiality of this new technique and allow the exploration of other wave-mixing effects. As mentioned above, detecting the THYR signal about the $2{\omega }_L$ frequency allows a more efficient rejection of the fundamental frequency at ${\omega }_L$, especially when the intensity of the THz beam is much lower than the fundamental one. Since this limitation does not apply to TerRa@BriXSinO source, we propose to explore also the possibility of detecting a sum-frequency generation (SFG) process, i.e., the appearance of a signal at frequency ${\omega }_{SFG}={\omega }_L+\mathsf{\Omega }$, which is close to ${\omega }_L$. The latter is a second-order process with peculiar symmetry rules. Specifically, second-order processes cannot occur in the bulk of centrosymmetric materials but at their surface or at the interface between two centrosymmetric materials in which the inversion symmetry is naturally broken. This makes SFG a spectroscopic tool suitable for investigating surfaces and interfaces with a sub-nanometer vertical resolution. Moreover, the use of a THz frequency in the SFG process add to this technique also chemical specificity as in the case of Raman techniques. We may ‘naively’ say that SFG is the surface version of Raman spectroscopy.

We notice that, in general, Raman spectroscopy is a powerful technique, being extensively used in different fields including chemical and biological analysis [61]. Additionally, when interacting with chiral molecules, the Raman signal exhibit a slight dependence on the handedness of a circularly polarized pumping beam. This effect is known as Raman Optical Activity (ROA) [62]. Since most biomolecules are chiral, ROA has been extensively applied for sensing structure, conformations, and functionalities of chiral biomolecules [63,64]. An additional advantage of ROA is its persistence in aqueous solutions, which makes this technique extremely appealing for investigating biological macromolecules in their own environment, including proteins, carbohydrates, nucleic acids, and viruses [65]. Analogously to chiral molecules, vector beams carrying an optical orbital angular momentum per photon due to their helical phase front structure, are chiral. Note that the orbital angular momentum is quite different from the circular handedness playing a role in ROA. Now, a question naturally rises: May the interaction of vector beams with chiral molecules be somehow enhanced? In particular, may we expect an intensity enhancement or different selection rules for the THYR and THz-SFG signals when a chiral degree of freedom is added to the beams?

From a theoretical point of view, the answer is yes in the case of Raman [66] as well as hyper-Raman and hyper-Rayleigh scattering [67]. These theoretical predictions open the possibility of using THYR and THz-SFG with chiral photons as advanced tools for spectroscopic and microscopic investigations of chiral biological samples in their aqueous environment. However, an experimental demonstration of these predictions in the case of Raman spectroscopies is still lacking, while the case of THz-SFG is fully unexplored from both a theoretical and an experimental point of view. We strongly believe that TerRa@BriXSinO can fully enable these new spectroscopic techniques with unpredictable implications in the field of bio-sensing.

8. Inhomogeneities Detection Using PSID and FSIGPP

Detecting the symmetry properties of inhomogeneities inside materials or over their surface is of vital importance to understand their origin in the fabrication process as well as to predict the possible issues they could provide during operation. Our platform enables to detect such symmetry properties by measuring the SAM and OAM locally exchanged between light and matter. SAM is specifically useful when inhomogeneous birefringent materials are envisaged or when inhomogeneities in isotropic materials have a spatial degree of correlation, such that a form birefringence effect arises within the material [2]. To this purpose, our FSIGPP for Full-Stokes Imaging turns to be useful as demonstrated in the case of artificially realized inhomogeneously polarized structures (Figure 8B) [10]. For unveiling inhomogeneities in isotropic materials, OAM represents un invaluable probe, since OAM is only exchanged when rotational symmetry is broken. Our PSID enables, in one shot, without passing through the measurement of the entire OAM spectrum coefficients, to obtain the amount of such symmetry breaking. This is, in fact, quantified by the overall mean $L_z$ and variance $\Delta L_z$ of the OAM exchanged between light and matter. Of course in this case, we have to set the GPBS beam shaper so that the beam impinging on the sample carries a non zero average OAM.

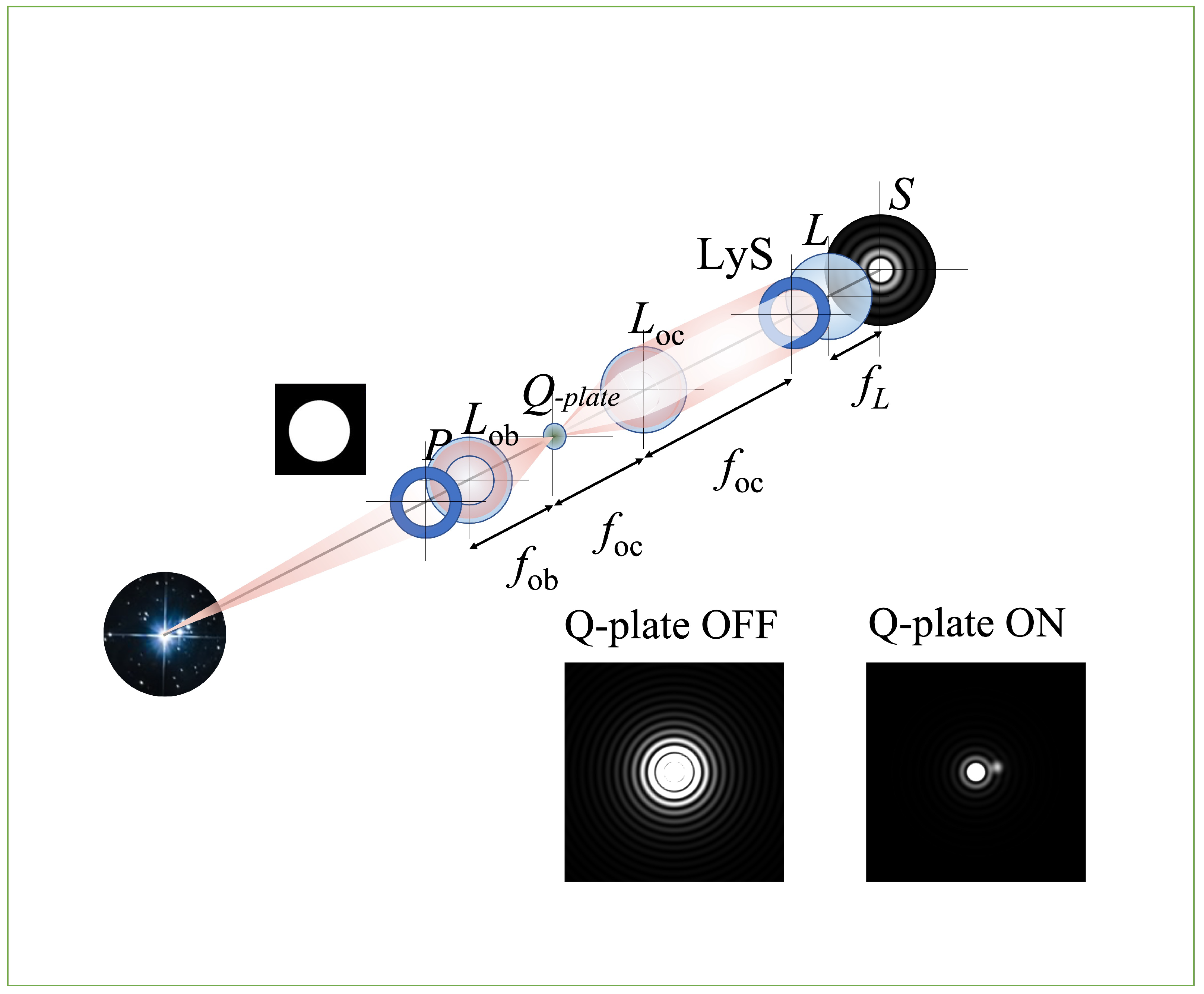
9. Developing Methods for Optical Vortex Coronagraphy for Detecting Exoplanets in the Short T-Waves Range

Coronagraphy is a powerful wavefront analysis method for high-contrast imaging, which is needed in several experimental situations, ranging from measurements of small-angle scattering in radiation–matter interaction, as, for instance, Raman and Brillouin scattering, to imaging faint companions around bright targets, such as the Sun corona (or, in general, stellar coronas), zodiacal light (or extrazodiacal dust), and, above all, circumstellar environments and exoplanets. Indeed, coronagraphy enables to investigate structures in circumstellar disks, identifying locations of forming planets. It provides also a technique for studying the circumnuclear environments in active galaxies and for probing the connection between star-formation and outflows powered by the central supermassive black holes [68].

Coronagraphy was firstly introduced in 1939 by B. Lyot to observe the Sun corona without eclipses [69]. Lyot coronagraph was based on a sharp-edge absorbing obstacle positioned in the focal plane of the objective of an ordinary telescope to push away as much light as possible from the optical axis. The rejection ratio of the on-axis intensity was roughly ${10}^{-3}$ at $3\lambda /D$ (in the 3rd Airy ring of the Sun). The contrast for this kind of coronagraphs is always finite, even ideally, due to diffraction effects beyond the obstacle [70]. In 2005, Foo et al. proposed to replace the sharp-edge obstacle by a vortex phase mask, which was ideally able to fully cancel out the light propagating along the axis [71,72]. A sketch of principle of the vortex coronagraph is reported in Figure 12. Indeed, the contrast quickly degrades as the aberrations of the phase mask increase and only finite values of the contrast are actually available. However, in the second Airy ring, contrast ratios of the order of ${10}^{-5}$–${10}^{-6}$ can be achieved without resorting to further image reduction algorithms [73]. A vortex phase mask can be scalar, when it imparts light a phase change based on Optical Path Difference, or vector, when it imparts light a phase change based on Geometric Phase or Pancharatnam–Berry Phase. Recently, we proposed to use a q-plate as vector vortex mask. The q-plate is the prototype of the electrically tunable Geometric Phase optical components, and it is a half-wave plate showing a topologically charged transverse optic axis distribution, that thanks to photoalignment techniques can be accurately shaped and operated at a required wavelength. We demonstrated the possibility to improve the performance of the phase mask, due to these features. Actually, it turned out that it is possible to realize an electrical tuning of the operation wavelength of the phase mask, and to push imaging contrast as high as possible, thanks to highly accuracy patterning capabilities. Moreover, this technology allowed us to design azimuthally selective masks, to enhance contrast only where this is actually needed [74]. We propose to extend this technology, implemented for the visible and near-infrared regime, in the Short T-waves range, which is nowadays largely unexplored. A laboratory demonstration of this kind of instruments can be of course obtained exploiting GEST platform.

10. Conclusions

In summary, we have presented a detailed plan of the design of the optical platform GEST, aimed at developing metrology techniques for bulk and surface morphological properties of objects over lateral length-scales ranging from hundreds down to few tens of micrometers and axial depth scales from few nanometers up to few tenths of micrometers. This can be achieved exploiting the future high-brilliance THz-FEL source TerRa@BriXSinO, which provides a particular high average power, on the order of 1 kW, in the range of Short T-waves, 6–30 THz. The design of GEST includes high performance geometric phase optical components or systems allowing for efficient management of light polarization as well as wavefront structuring and sensing.The present design consists of four modules: (i) polarization and wavefront beam shaping module, for generating twisted light for detecting chiral agents via THz Hyper-Raman spectroscopy; (ii) Full-Stokes Imaging module for polarization and SAM, for detecting stress-induced birefringence; (iii) PSID module, for measuring mean and variance of orbital angular momentum exchanged between THz radiation and matter for detecting bulk inhomogeneities; and (iv) GPSI, for shearography for stress tests on composite structures and surface characterization.

In short, GEST and TerRa will give access to the still under-explored wavelength range of Short T-waves, leading to new designs of geometric phase optical components, developing techniques for monitoring defects and/or inhomogeneities for industrial application, testing the theoretical predictions of THz Hyper-Raman spectroscopy with twisted light and THz-SFG, and expending astrophysical measurement principles.