Prediction of Marshall Stability and Marshall Flow of Asphalt Pavements Using Supervised Machine Learning Algorithms
Abstract
1. Introduction
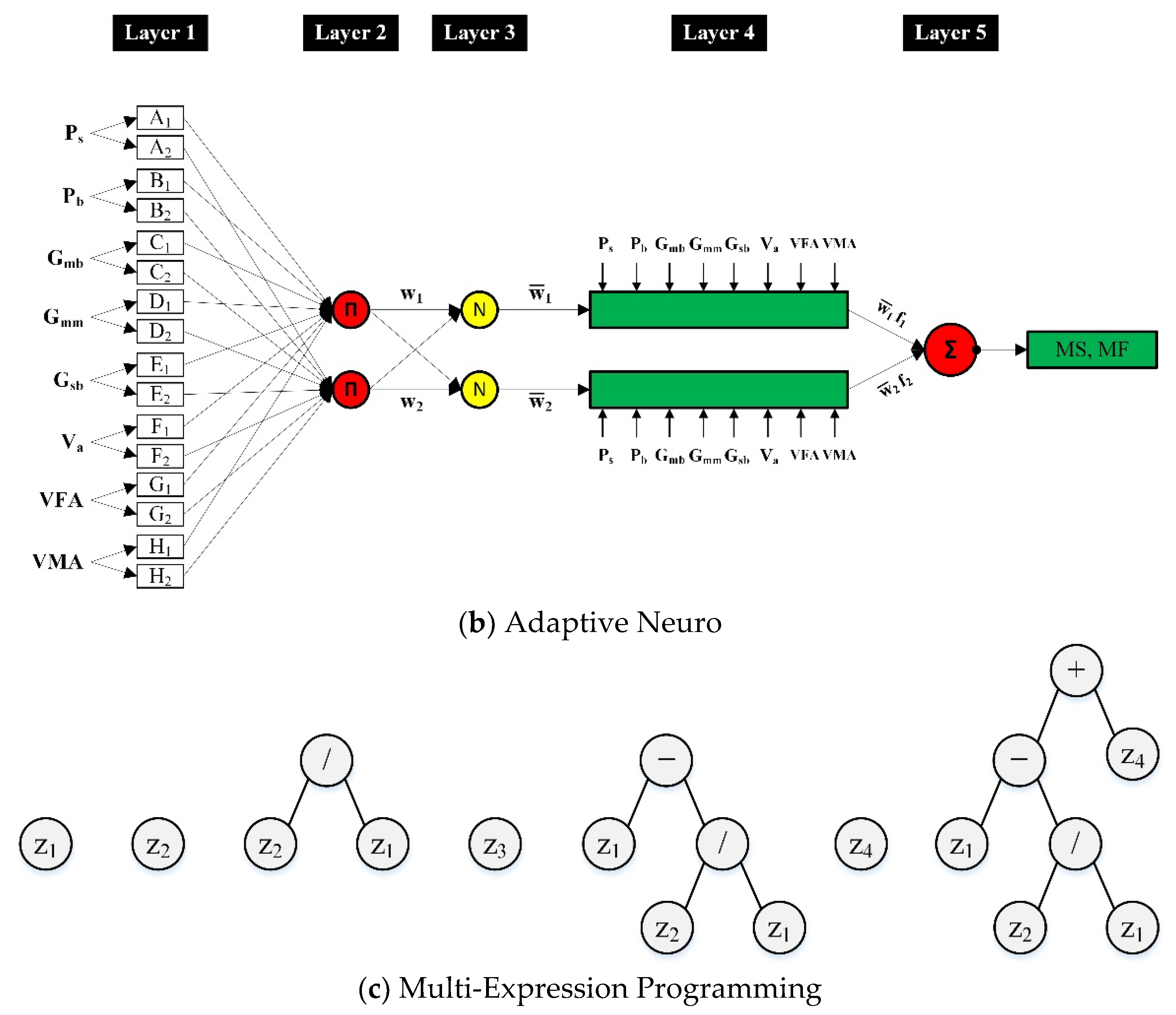
2. Overview of Soft-Computing Approaches
- Using the binary tournament approach, two parents are chosen and recombined with a probability of fixed crossover.
- By recombining the two parents, two offspring are obtained.
- The mutation of the offspring takes place by the replacement of the best individual with the worst in the current population.
- G0: z1
- G1: z2
- G2: G1/G0
- G3: z3
- G4: G0 − G2
- G5: z4
- G6: G4 + G5
3. Research Methodology
3.1. Data Division and Pre-Processing
3.2. Model Structure and Performance
3.3. Evolution Criteria and Performance Measures
4. Results and Discussions
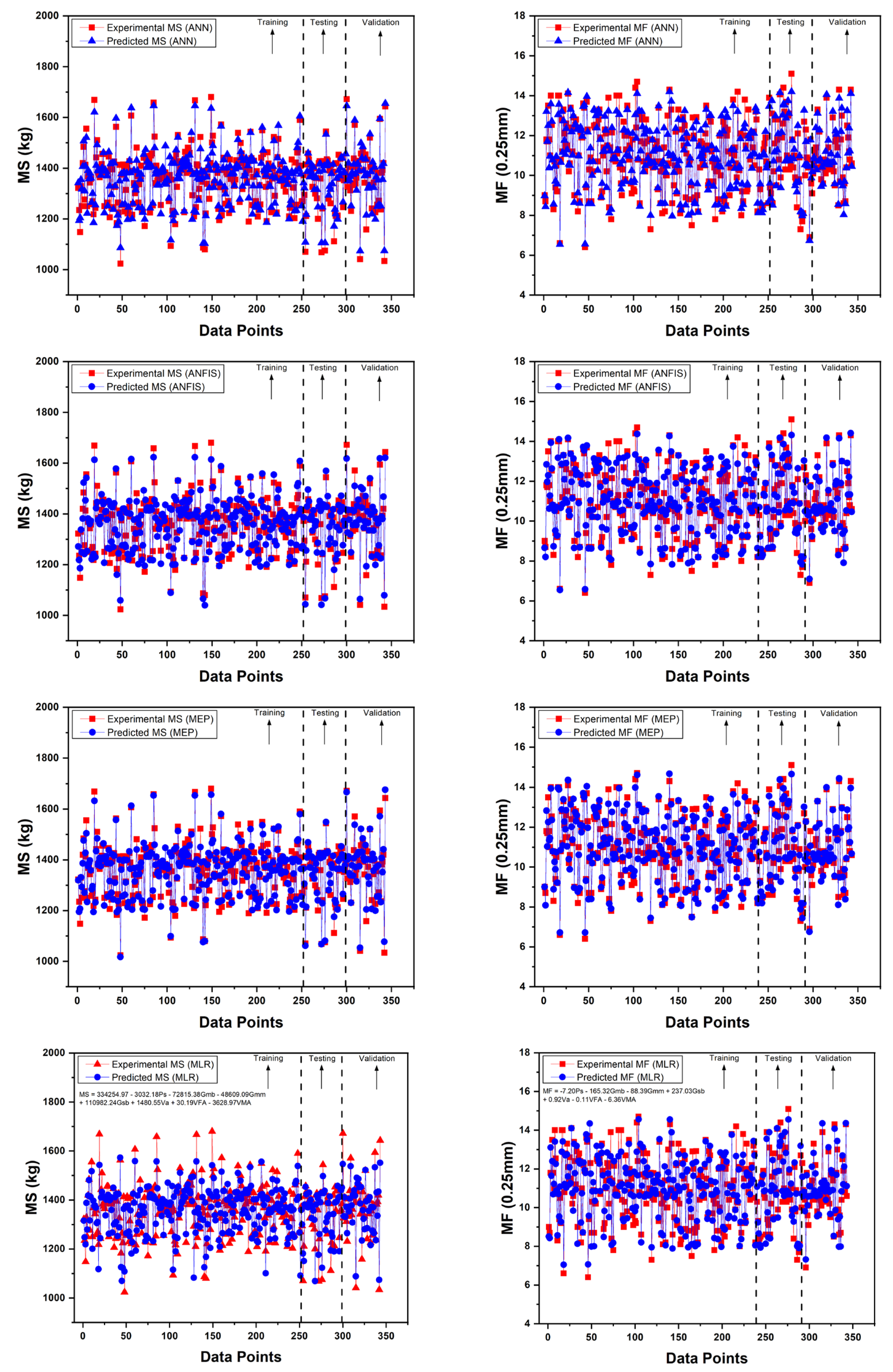
4.1. Comparison Plot for ANN, ANFIS and MEP
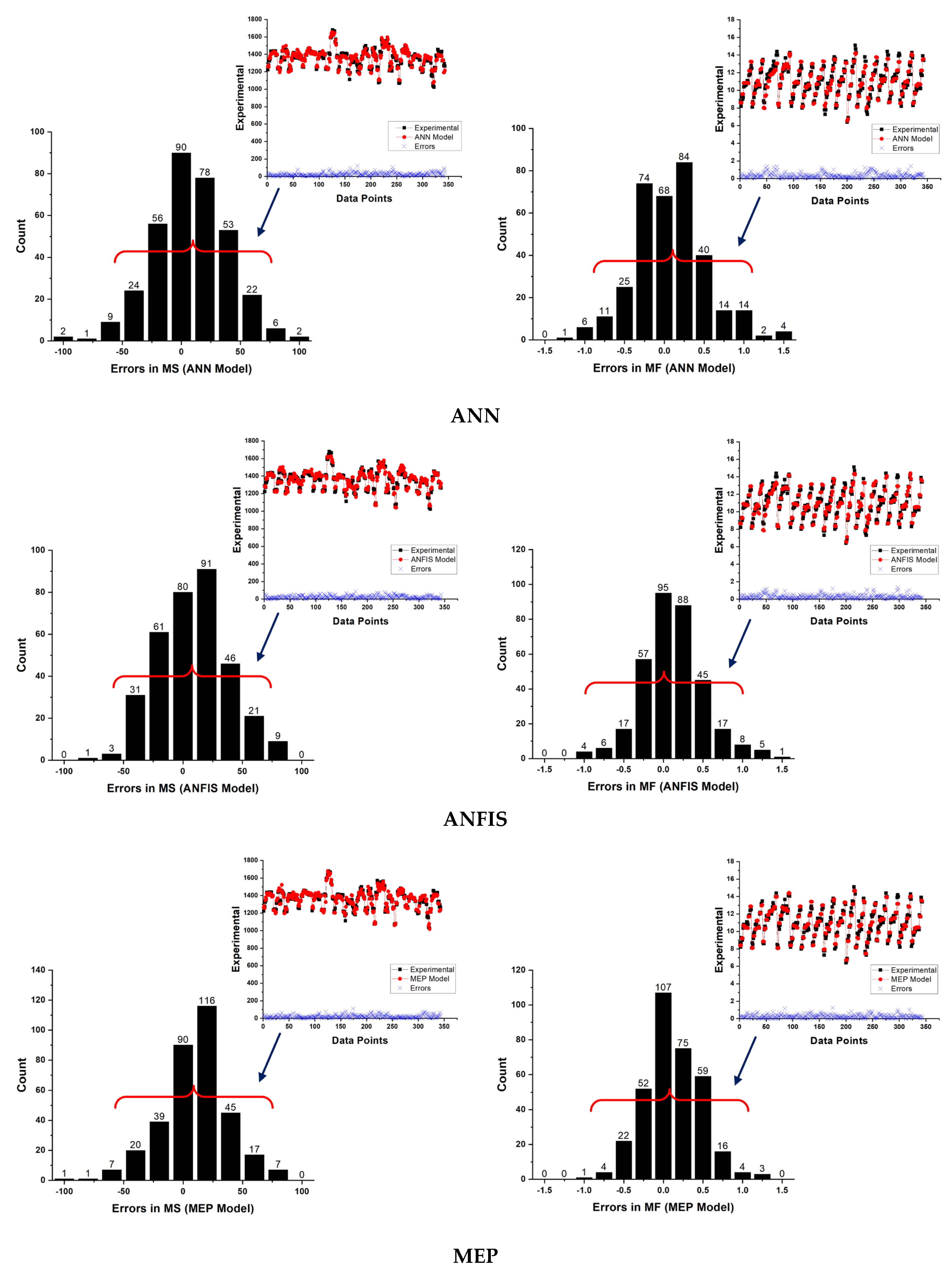
4.2. ANN, ANFIS, and MEP Models Results and Assessment
4.2.1. ANN Model
4.2.2. ANFIS Model
4.2.3. MEP Model
4.2.4. Performance Assessment and Comparison of Developed Models
4.3. Formulation of MS and MF Using MEP
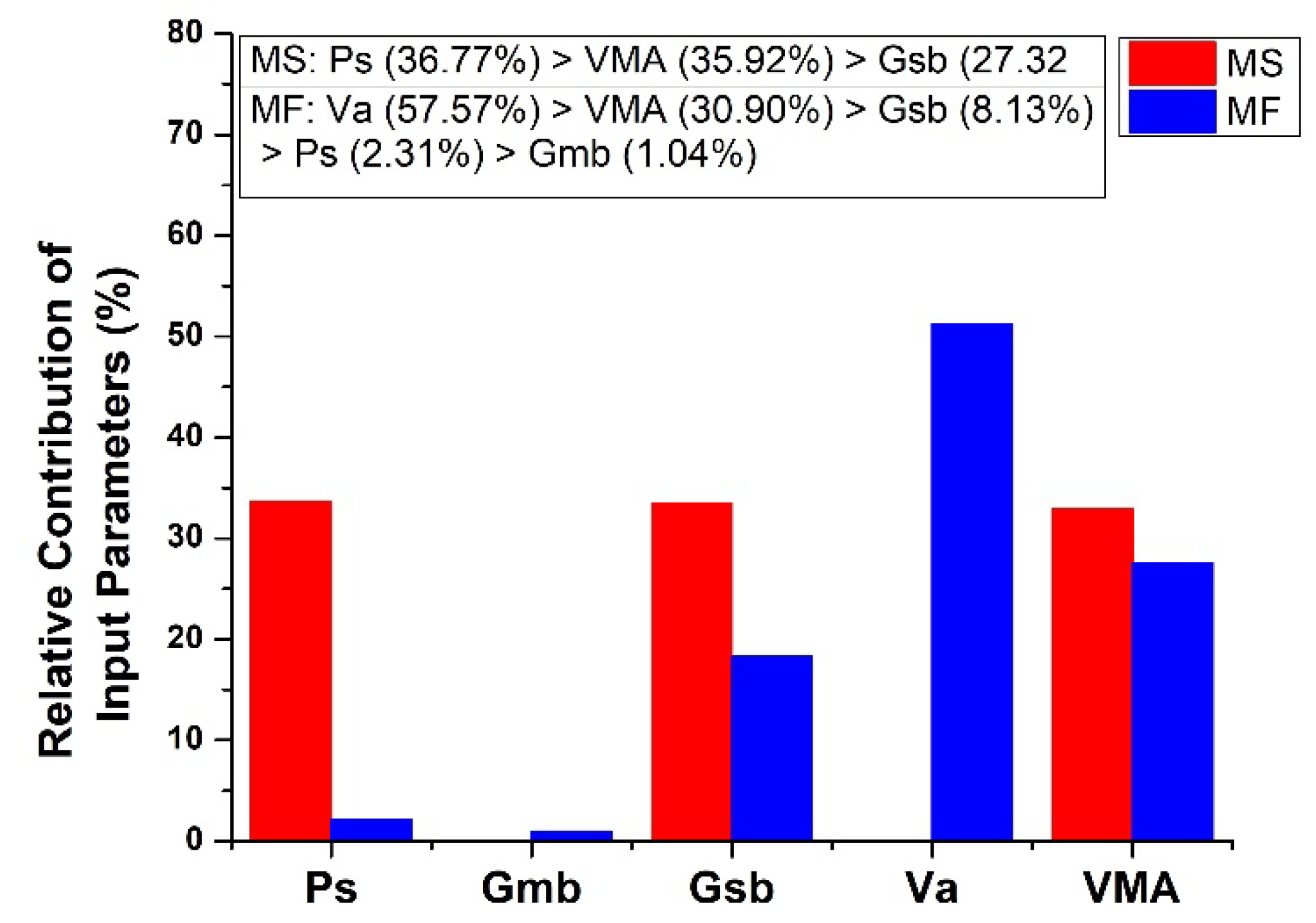
4.4. Sensitivity and Parametric Analysis
5. Conclusions
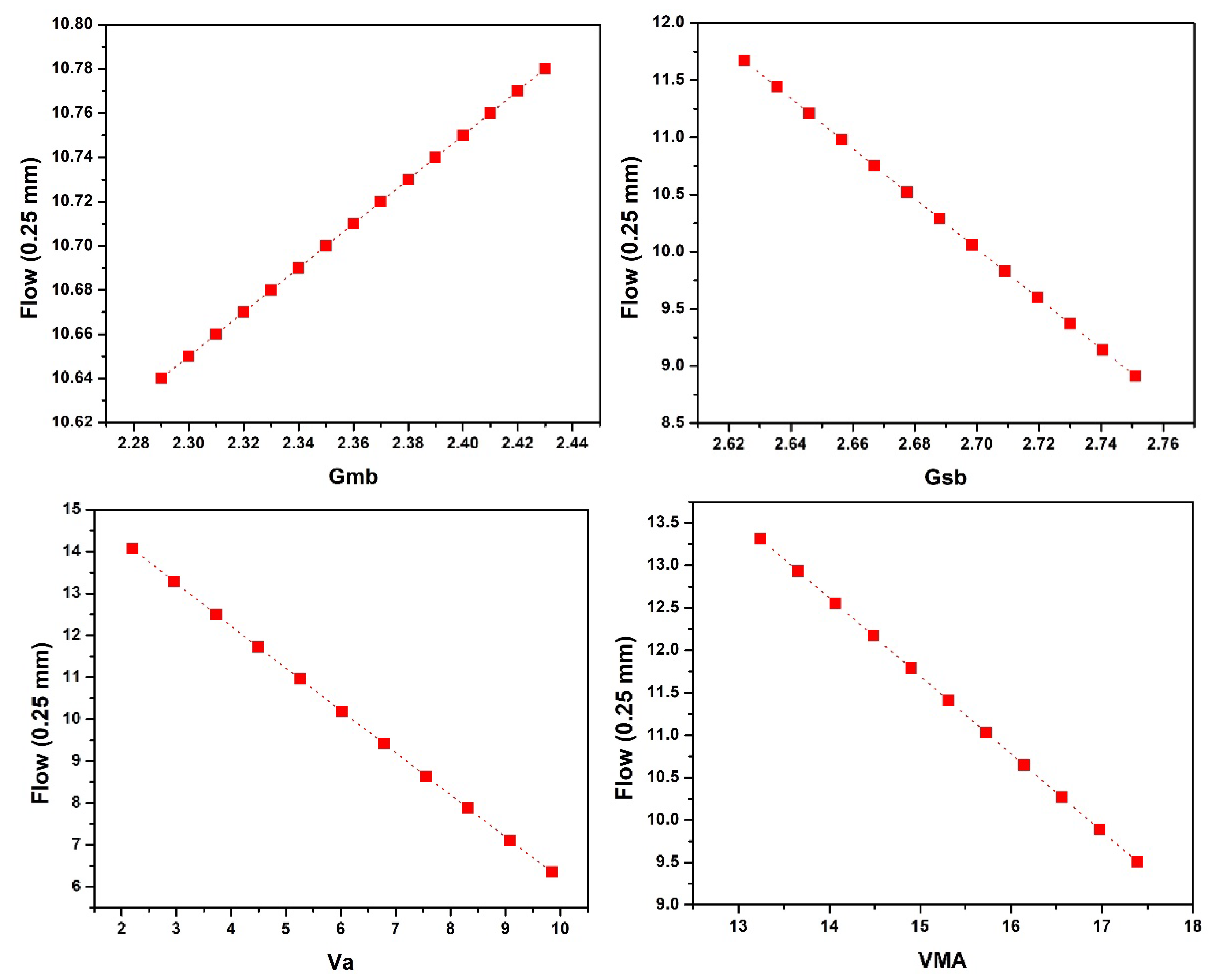
- According to the investigation on the influence of input parameters on MS and MF, it was concluded that with the increase in Ps, the MS first increases then drops, while MF first decreases and then rises. Downward linear trends were found for Gsb and VMA in the case of MS and Gsb, and Va and VMA in the case of MF. While in the case of MF, Gmb followed the upward linear trend.
- Models based on ANN, ANFIS, and MEP have the ability to predict MS and MF with higher accuracy. Additionally, the MS and MF predicted while employing the MEP technique is better than ANN and ANFIS. The MEP approach simplifies the derivation of MS and MF while maintaining a reasonable level of accuracy between simulated and experimental data.
- To avoid the over-fitting of the employed approaches, i.e., ANN, ANFIS, and MEP, a variety of methods, including data division and preprocessing were utilized to minimize the complexity of the developed models. Sensitivity and parametric analysis were carried out, and are covered in length in the paper. The results of the parametric study were found to be inconsistent with the trends of previous research studies.
- All the models were evaluated using RSE, MAE, NSE, RMSE, RRMSE, R2, and R. Overall, the comparison results show that all three approaches are effective and trustworthy for predicting the MS and MF of asphalt pavements; however, MEP technique outperformed ANN and ANFIS based on various statistical checks. MEP’s mathematical expressions (Equations (22) and (23)) are substantially simpler than the proposed models of ANN and ANFIS. The latter strategies, on the other hand, suffer from overfitting of data, NN’s limitations, and complexity in the network’s structure. It is suggested that the developed MEP models be used in everyday practice.
- The existing models can be used to estimate the MS and MF of asphalt pavements using basic geotechnical indices, which is an efficient, cost-effective, reliable, and time-saving solution to deal with the hectic and time-consuming process involved in the determination of MS and MF, leading to sustainable construction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miani, M.; Dunnhofer, M.; Rondinella, F.; Manthos, E.; Valentin, J.; Micheloni, C.; Baldo, N. Bituminous Mixtures Experimental Data Modeling Using a Hyperparameters-Optimized Machine Learning Approach. Appl. Sci. 2021, 11, 11710. [Google Scholar] [CrossRef]
- Zhou, F.; Scullion, T.; Sun, L. Verification and modeling of three-stage permanent deformation behavior of asphalt mixes. J. Transp. Eng. 2004, 130, 486–494. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H.; Mirzahosseini, M.R.; Nejad, F.M. Nonlinear genetic-based models for prediction of flow number of asphalt mixtures. J. Mater. Civ. Eng. 2011, 23, 248–263. [Google Scholar] [CrossRef]
- Alavi, A.H.; Ameri, M.; Gandomi, A.H.; Mirzahosseini, M.R. Formulation of flow number of asphalt mixes using a hybrid computational method. Constr. Build. Mater. 2011, 25, 1338–1355. [Google Scholar] [CrossRef]
- Dias, J.F.; Picado-Santos, L.; Capitão, S. Mechanical performance of dry process fine crumb rubber asphalt mixtures placed on the Portuguese road network. Constr. Build. Mater. 2014, 73, 247–254. [Google Scholar] [CrossRef]
- Liu, Q.T.; Wu, S.P. Effects of steel wool distribution on properties of porous asphalt concrete. In Key Engineering Materials; Trans Tech Publications Ltd.: Zurich, Switzerland, 2014; pp. 150–154. [Google Scholar]
- García, A.; Norambuena-Contreras, J.; Bueno, M.; Partl, M.N. Influence of Steel Wool Fibers on the Mechanical, Termal, and Healing Properties of Dense Asphalt Concrete; ASTM International: West Conshohocken, PN, USA, 2014. [Google Scholar]
- Pasandín, A.; Pérez, I. Overview of bituminous mixtures made with recycled concrete aggregates. Constr. Build. Mater. 2015, 74, 151–161. [Google Scholar] [CrossRef]
- Zaumanis, M.; Mallick, R.B.; Frank, R. 100% hot mix asphalt recycling: Challenges and benefits. Transp. Res. Procedia 2016, 14, 3493–3502. [Google Scholar] [CrossRef]
- Wang, L.; Gong, H.; Hou, Y.; Shu, X.; Huang, B. Advances in pavement materials, design, characterisation, and simulation. Road Mater. Pavement Des. 2017, 18, 1–11. [Google Scholar] [CrossRef]
- Erkens, S.; Liu, X.; Scarpas, A. 3D finite element model for asphalt concrete response simulation. Int. J. Geomech. 2002, 2, 305–330. [Google Scholar] [CrossRef]
- Giunta, M.; Pisano, A.A. One-Dimensional Visco-Elastoplastic Constitutive Model for Asphalt Concrete. Multidiscip. Model. Mater. Struct. 2006, 2, 247–264. [Google Scholar] [CrossRef]
- Underwood, S.B.; Kim, R.Y. Viscoelastoplastic continuum damage model for asphalt concrete in tension. J. Eng. Mech. 2011, 137, 732–739. [Google Scholar] [CrossRef]
- Yun, T.; Richard Kim, Y. Viscoelastoplastic modeling of the behavior of hot mix asphalt in compression. KSCE J. Civ. Eng. 2013, 17, 1323–1332. [Google Scholar] [CrossRef]
- Pasetto, M.; Baldo, N. Computational analysis of the creep behaviour of bituminous mixtures. Constr. Build. Mater. 2015, 94, 784–790. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Sauzéat, C.; Clec’h, P. Anisotropy of bituminous mixture in the linear viscoelastic domain. Mech. Time Depend. Mater. 2016, 20, 281–297. [Google Scholar] [CrossRef]
- Pasetto, M.; Baldo, N. Numerical visco-elastoplastic constitutive modelization of creep recovery tests on hot mix asphalt. J. Traffic Transp. Eng. 2016, 3, 390–397. [Google Scholar] [CrossRef]
- Darabi, M.K.; Huang, C.-W.; Bazzaz, M.; Masad, E.A.; Little, D.N. Characterization and validation of the nonlinear viscoelastic-viscoplastic with hardening-relaxation constitutive relationship for asphalt mixtures. Constr. Build. Mater. 2019, 216, 648–660. [Google Scholar] [CrossRef]
- Anwar, M.K.; Shah, S.A.R.; Sadiq, A.N.; Siddiq, M.U.; Ahmad, H.; Nawaz, S.; Javead, A.; Saeed, M.H.; Khan, A.R. Symmetric performance analysis for mechanical properties of sustainable asphalt materials under varying temperature conditions: An application of DT and NDT digital techniques. Symmetry 2020, 12, 433. [Google Scholar] [CrossRef]
- Arifuzzaman, M.; Aniq Gul, M.; Khan, K.; Hossain, S.Z. Application of artificial intelligence (ai) for sustainable highway and road system. Symmetry 2020, 13, 60. [Google Scholar] [CrossRef]
- Kim, S.-H.; Kim, N. Development of performance prediction models in flexible pavement using regression analysis method. KSCE J. Civ. Eng. 2006, 10, 91–96. [Google Scholar] [CrossRef]
- Laurinavičius, A.; Oginskas, R. Experimental research on the development of rutting in asphalt concrete pavements reinforced with geosynthetic materials. J. Civ. Eng. Manag. 2006, 12, 311–317. [Google Scholar] [CrossRef]
- Shukla, P.K.; Das, A. A re-visit to the development of fatigue and rutting equations used for asphalt pavement design. Int. J. Pavement Eng. 2008, 9, 355–364. [Google Scholar] [CrossRef]
- Rahman, A.A.; Mendez Larrain, M.M.; Tarefder, R.A. Development of a nonlinear rutting model for asphalt concrete based on Weibull parameters. Int. J. Pavement Eng. 2019, 20, 1055–1064. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, R.; Wu, C.; Goh, A.T.C.; Lacasse, S.; Liu, Z.; Liu, H. State-of-the-art review of soft computing applications in underground excavations. Geosci. Front. 2020, 11, 1095–1106. [Google Scholar] [CrossRef]
- Dobrescu, C. Dynamic Response of the Newton Voigt–Kelvin Modelled Linear Viscoelastic Systems at Harmonic Actions. Symmetry 2020, 12, 1571. [Google Scholar] [CrossRef]
- Li, H.; Wu, A.; Wang, H. Evaluation of short-term strength development of cemented backfill with varying sulphide contents and the use of additives. J. Environ. Manag. 2019, 239, 279–286. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Dholakia, M.; Prakash, I.; Pham, H.V. A comparative study of least square support vector machines and multiclass alternating decision trees for spatial prediction of rainfall-induced landslides in a tropical cyclones area. Geotech. Geol. Eng. 2016, 34, 1807–1824. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Roke, D.A. Assessment of artificial neural network and genetic programming as predictive tools. Adv. Eng. Softw. 2015, 88, 63–72. [Google Scholar] [CrossRef]
- Sathyapriya, S.; Arumairaj, P.; Ranjini, D. Prediction of unconfined compressive strength of a stabilised expansive clay soil using ANN and regression analysis (SPSS). Asian J. Res. Soc. Sci. Humanit. 2017, 7, 109–123. [Google Scholar] [CrossRef]
- Alade, I.O.; Bagudu, A.; Oyehan, T.A.; Abd Rahman, M.A.; Saleh, T.A.; Olatunji, S.O. Estimating the refractive index of oxygenated and deoxygenated hemoglobin using genetic algorithm-support vector regression model. Comput. Methods Programs Biomed. 2018, 163, 135–142. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Liu, Q.-f.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef]
- Wu, Q.; Wu, B.; Hu, C.; Yan, X. Evolutionary Multilabel Classification Algorithm Based on Cultural Algorithm. Symmetry 2021, 13, 322. [Google Scholar] [CrossRef]
- Shahin, M.A. Genetic programming for modelling of geotechnical engineering systems. In Handbook of Genetic Programming Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 37–57. [Google Scholar]
- Li, L.-L.; Liu, J.-Q.; Zhao, W.-B.; Dong, L. Fault Diagnosis of High-Speed Brushless Permanent-Magnet DC Motor Based on Support Vector Machine Optimized by Modified Grey Wolf Optimization Algorithm. Symmetry 2021, 13, 163. [Google Scholar] [CrossRef]
- Çanakcı, H.; Baykasoğlu, A.; Güllü, H. Prediction of compressive and tensile strength of Gaziantep basalts via neural networks and gene expression programming. Neural Comput. Appl. 2009, 18, 1031–1041. [Google Scholar] [CrossRef]
- Ozbek, A.; Unsal, M.; Dikec, A. Estimating uniaxial compressive strength of rocks using genetic expression programming. J. Rock Mech. Geotech. Eng. 2013, 5, 325–329. [Google Scholar] [CrossRef]
- Khan, M.A.; Shah, M.I.; Javed, M.F.; Khan, M.I.; Rasheed, S.; El-Shorbagy, M.; El-Zahar, E.R.; Malik, M. Application of random forest for modelling of surface water salinity. Ain Shams Eng. J. 2022, 13, 101635. [Google Scholar] [CrossRef]
- Das, S.K. 10 Artificial neural networks in geotechnical engineering: Modeling and application issues. Metaheuristics Water Geotech Transp. Eng. 2013, 45, 231–267. [Google Scholar]
- Giustolisi, O.; Doglioni, A.; Savic, D.A.; Webb, B. A multi-model approach to analysis of environmental phenomena. Environ. Model. Softw. 2007, 22, 674–682. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Recent advances and future challenges for artificial neural systems in geotechnical engineering applications. Adv. Artif. Neural Syst. 2009, 2009, 308239. [Google Scholar] [CrossRef]
- Mohammadzadeh, S.D.; Kazemi, S.-F.; Mosavi, A.; Nasseralshariati, E.; Tah, J.H. Prediction of compression index of fine-grained soils using a gene expression programming model. Infrastructures 2019, 4, 26. [Google Scholar] [CrossRef]
- Zhang, Q.; Barri, K.; Jiao, P.; Salehi, H.; Alavi, A.H. Genetic programming in civil engineering: Advent, applications and future trends. Artif. Intell. Rev. 2021, 54, 1863–1885. [Google Scholar] [CrossRef]
- Awan, H.H.; Hussain, A.; Javed, M.F.; Qiu, Y.; Alrowais, R.; Mohamed, A.M.; Fathi, D.; Alzahrani, A.M. Predicting Marshall Flow and Marshall Stability of Asphalt Pavements Using Multi Expression Programming. Buildings 2022, 12, 314. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Zacarias-Morales, N.; Pancardo, P.; Hernández-Nolasco, J.A.; Garcia-Constantino, M. Attention-inspired artificial neural networks for speech processing: A systematic review. Symmetry 2021, 13, 214. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Artificial neural network applications in geotechnical engineering. Aust. Geomech. 2001, 36, 49–62. [Google Scholar]
- Yaman, M.A.; Abd Elaty, M.; Taman, M. Predicting the ingredients of self compacting concrete using artificial neural network. Alex. Eng. J. 2017, 56, 523–532. [Google Scholar] [CrossRef]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Sugeno, M. Industrial Applications of Fuzzy Control; Elsevier Science Inc.: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Mazari, M.; Rodriguez, D.D. Prediction of pavement roughness using a hybrid gene expression programming-neural network technique. J. Traffic Transp. Eng. 2016, 3, 448–455. [Google Scholar] [CrossRef]
- Oltean, M.; Dumitrescu, D. Multi expression programming. J. Genet. Program. Evolvable Mach. 2002. Available online: https://www.researchgate.net/publication/2918165_Multi_Expression_Programming (accessed on 19 September 2022).
- Baykasoğlu, A.; Güllü, H.; Çanakçı, H.; Özbakır, L. Prediction of compressive and tensile strength of limestone via genetic programming. Expert Syst. Appl. 2008, 35, 111–123. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H.; Sahab, M.G.; Gandomi, M. Multi expression programming: A new approach to formulation of soil classification. Eng. Comput. 2010, 26, 111–118. [Google Scholar] [CrossRef]
- Alavi, A.H.; Mollahasani, A.; Gandomi, A.H.; Bazaz, J.B. Formulation of secant and reloading soil deformation moduli using multi expression programming. Eng. Comput. 2012, 29, 173–197. [Google Scholar] [CrossRef]
- Cabalar, A.F.; Cevik, A. Genetic programming-based attenuation relationship: An application of recent earthquakes in turkey. Comput. Geosci. 2009, 35, 1884–1896. [Google Scholar] [CrossRef]
- Tapkın, S.; Çevik, A.; Uşar, Ü. Prediction of Marshall test results for polypropylene modified dense bituminous mixtures using neural networks. Expert Syst. Appl. 2010, 37, 4660–4670. [Google Scholar] [CrossRef]
- Nguyen, H.-L.; Le, T.-H.; Pham, C.-T.; Le, T.-T.; Ho, L.S.; Le, V.M.; Pham, B.T.; Ly, H.-B. Development of hybrid artificial intelligence approaches and a support vector machine algorithm for predicting the marshall parameters of stone matrix asphalt. Appl. Sci. 2019, 9, 3172. [Google Scholar] [CrossRef]
- Saffarzadeh, M.; Heidaripanah, A. Effect of asphalt content on the marshall stability of asphalt concrete using artificial neural networks. Sci. Iran. 2009, 16, 98–105. [Google Scholar]
- Ozgan, E. Artificial neural network based modelling of the Marshall Stability of asphalt concrete. Expert Syst. Appl. 2011, 38, 6025–6030. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Miani, M. Stiffness modulus and marshall parameters of hot mix asphalts: Laboratory data modeling by artificial neural networks characterized by cross-validation. Appl. Sci. 2019, 9, 3502. [Google Scholar] [CrossRef]
- Shah, S.A.R.; Anwar, M.K.; Arshad, H.; Qurashi, M.A.; Nisar, A.; Khan, A.N.; Waseem, M. Marshall stability and flow analysis of asphalt concrete under progressive temperature conditions: An application of advance decision-making approach. Constr. Build. Mater. 2020, 262, 120756. [Google Scholar] [CrossRef]
- Morova, N.; Sargin, Ş.; Terzi, S.; Saltan, M.; Serin, S. Modeling Marshall Stability of light asphalt concretes fabricated using expanded clay aggregate with Artificial Neural Networks. In Proceedings of the 2012 International Symposium on Innovations in Intelligent Systems and Applications, Trabzon, Turkey, 2–4 July 2012; pp. 1–4. [Google Scholar]
- Morova, N.; Eriskin, E.; Terzi, S.; Karahancer, S.; Serin, S.; Saltan, M.; Usta, P. Modelling Marshall Stability of fiber reinforced asphalt mixtures with ANFIS. In Proceedings of the 2017 IEEE International Conference on INnovations in Intelligent SysTems and Applications (INISTA), Gdynia, Poland, 3–5 July 2017; pp. 174–179. [Google Scholar]
- Serin, S.; Morova, N.; Sargın, Ş.; Terzi, S.; Saltan, M. Modeling Marshall stability of lightweight asphalt concretes fabricated using expanded clay aggregate with anfis. In Proceedings of the BCCCE—International Balkans Conference on Challenges of Civil Engineering, Epoka, Albania, 23–25 May 2013. [Google Scholar]
- Mistry, R.; Roy, T.K. Predicting Marshall stability and flow of bituminous mix containing waste fillers by the adaptive neuro-fuzzy inference system. Rev. Construcción 2020, 19, 209–219. [Google Scholar] [CrossRef]
- Fabani, M.P.; Capossio, J.P.; Román, M.C.; Zhu, W.; Rodriguez, R.; Mazza, G. Producing non-traditional flour from watermelon rind pomace: Artificial neural network (ANN) modeling of the drying process. J. Environ. Manag. 2021, 281, 111915. [Google Scholar] [CrossRef]
- Venkatesh, K.; Bind, Y.K. ANN and neuro-fuzzy modeling for shear strength characterization of soils. Proc. Natl. Acad. Sci. USA 2020, 92, 243–249. [Google Scholar] [CrossRef]
- Khan, M.A.; Aslam, F.; Javed, M.F.; Alabduljabbar, H.; Deifalla, A.F. New prediction models for the compressive strength and dry-thermal conductivity of bio-composites using novel machine learning algorithms. J. Clean. Prod. 2022, 350, 131364. [Google Scholar] [CrossRef]
- Sada, S.; Ikpeseni, S. Evaluation of ANN and ANFIS modeling ability in the prediction of AISI 1050 steel machining performance. Heliyon 2021, 7, e06136. [Google Scholar] [CrossRef]
- Kourgialas, N.N.; Dokou, Z.; Karatzas, G.P. Statistical analysis and ANN modeling for predicting hydrological extremes under climate change scenarios: The example of a small Mediterranean agro-watershed. J. Environ. Manag. 2015, 154, 86–101. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Zafar, A.; Farooq, F.; Javed, M.F.; Alyousef, R.; Alabduljabbar, H.; Khan, M.I. Geopolymer concrete compressive strength via artificial neural network, adaptive neuro fuzzy interface system, and gene expression programming with K-fold cross validation. Front. Mater. 2021, 8, 621163. [Google Scholar] [CrossRef]
- Koçak, Y.; Şiray, G.Ü. New activation functions for single layer feedforward neural network. Expert Syst. Appl. 2021, 164, 113977. [Google Scholar] [CrossRef]
- Cai, C.; Xu, Y.; Ke, D.; Su, K. Deep neural networks with multistate activation functions. Comput. Intell. Neurosci. 2015, 2015, 721367. [Google Scholar] [CrossRef]
- Tang, C.; Luktarhan, N.; Zhao, Y. SAAE-DNN: Deep Learning Method on Intrusion Detection. Symmetry 2020, 12, 1695. [Google Scholar] [CrossRef]
- Ramachandran, P.; Zoph, B.; Le, Q. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Xu, B.; Huang, R.; Li, M. Revise saturated activation functions. arXiv 2016, arXiv:1602.05980. [Google Scholar]
- Naresh Babu, K.; Edla, D.R. New algebraic activation function for multi-layered feed forward neural networks. IETE J. Res. 2017, 63, 71–79. [Google Scholar] [CrossRef]
- Malinov, S.; Sha, W.; McKeown, J. Modelling the correlation between processing parameters and properties in titanium alloys using artificial neural network. Comput. Mater. Sci. 2001, 21, 375–394. [Google Scholar] [CrossRef]
- Tahani, M.; Vakili, M.; Khosrojerdi, S. Experimental evaluation and ANN modeling of thermal conductivity of graphene oxide nanoplatelets/deionized water nanofluid. Int. Commun. Heat Mass Transf. 2016, 76, 358–365. [Google Scholar] [CrossRef]
- Tang, Y.-J.; Zhang, Q.-Y.; Lin, W. Artificial neural network based spectrum sensing method for cognitive radio. In Proceedings of the 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Shenzhen, China, 23–25 September 2010; pp. 1–4. [Google Scholar]
- Dorofki, M.; Elshafie, A.H.; Jaafar, O.; Karim, O.A.; Mastura, S. Comparison of artificial neural network transfer functions abilities to simulate extreme runoff data. Int. Proc. Chem. Biol. Environ. Eng. 2012, 33, 39–44. [Google Scholar]
- Hanandeh, S.; Ardah, A.; Abu-Farsakh, M. Using artificial neural network and genetics algorithm to estimate the resilient modulus for stabilized subgrade and propose new empirical formula. Transp. Geotech. 2020, 24, 100358. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H. A robust data mining approach for formulation of geotechnical engineering systems. Eng. Comput. 2011, 28, 242–274. [Google Scholar] [CrossRef]
- Nosratabadi, S.; Mosavi, A.; Duan, P.; Ghamisi, P.; Filip, F.; Band, S.S.; Reuter, U.; Gama, J.; Gandomi, A.H. Data science in economics: Comprehensive review of advanced machine learning and deep learning methods. Mathematics 2020, 8, 1799. [Google Scholar] [CrossRef]
- Shahin, M.A. Artificial intelligence in geotechnical engineering: Applications, modeling aspects, and future directions. In Metaheuristics in Water, Geotechnical and Transport Engineering; Elsevier: Amsterdam, The Netherlands, 2013; pp. 169–204. [Google Scholar]
- Sperotto, A.; Molina, J.-L.; Torresan, S.; Critto, A.; Marcomini, A. Reviewing Bayesian Networks potentials for climate change impacts assessment and management: A multi-risk perspective. J. Environ. Manag. 2017, 202, 320–331. [Google Scholar] [CrossRef]
- Khan, K.; Ashfaq, M.; Iqbal, M.; Khan, M.A.; Amin, M.N.; Shalabi, F.I.; Faraz, M.I.; Jalal, F.E. Multi Expression Programming Model for Strength Prediction of Fly-Ash-Treated Alkali-Contaminated Soils. Materials 2022, 15, 4025. [Google Scholar] [CrossRef]
- Akan, R.; Keskin, S.N. The effect of data size of ANFIS and MLR models on prediction of unconfined compression strength of clayey soils. SN Appl. Sci. 2019, 1, 843. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
- Sadeghizadeh, A.; Ebrahimi, F.; Heydari, M.; Tahmasebikohyani, M.; Ebrahimi, F.; Sadeghizadeh, A. Adsorptive removal of Pb (II) by means of hydroxyapatite/chitosan nanocomposite hybrid nanoadsorbent: ANFIS modeling and experimental study. J. Environ. Manag. 2019, 232, 342–353. [Google Scholar] [CrossRef] [PubMed]
- Khan, K.; Jalal, F.E.; Khan, M.A.; Salami, B.A.; Amin, M.N.; Alabdullah, A.A.; Samiullah, Q.; Arab, A.M.A.; Faraz, M.I.; Iqbal, M. Prediction Models for Evaluating Resilient Modulus of Stabilized Aggregate Bases in Wet and Dry Alternating Environments: ANN and GEP Approaches. Materials 2022, 15, 4386. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.; Jaafar, W.Z.W.; Hin, L.S.; Osman, N.; Hossain, A.; Mohd, N.S. Development of an intelligent system based on ANFIS model for predicting soil erosion. Environ. Earth Sci. 2018, 77, 186. [Google Scholar] [CrossRef]
- Khan, S.; Ali Khan, M.; Zafar, A.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Predicting the ultimate axial capacity of uniaxially loaded cfst columns using multiphysics artificial intelligence. Materials 2021, 15, 39. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
- Khan, M.A.; Memon, S.A.; Farooq, F.; Javed, M.F.; Aslam, F.; Alyousef, R. Compressive strength of fly-ash-based geopolymer concrete by gene expression programming and random forest. Adv. Civ. Eng. 2021, 2021, 6618407. [Google Scholar] [CrossRef]
- Javed, M.F.; Farooq, F.; Memon, S.A.; Akbar, A.; Khan, M.A.; Aslam, F.; Alyousef, R.; Alabduljabbar, H.; Rehman, S.K.U. New prediction model for the ultimate axial capacity of concrete-filled steel tubes: An evolutionary approach. Crystals 2020, 10, 741. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H.; Nejad, H.C.; Mollahasani, A.; Rashed, A. Design equations for prediction of pressuremeter soil deformation moduli utilizing expression programming systems. Neural Comput. Appl. 2013, 23, 1771–1786. [Google Scholar] [CrossRef]
- Cheng, Z.-L.; Zhou, W.-H.; Garg, A. Genetic programming model for estimating soil suction in shallow soil layers in the vicinity of a tree. Eng. Geol. 2020, 268, 105506. [Google Scholar] [CrossRef]
- Wang, H.-L.; Yin, Z.-Y. High performance prediction of soil compaction parameters using multi expression programming. Eng. Geol. 2020, 276, 105758. [Google Scholar] [CrossRef]
- Chu, H.-H.; Khan, M.A.; Javed, M.; Zafar, A.; Khan, M.I.; Alabduljabbar, H.; Qayyum, S. Sustainable use of fly-ash: Use of gene-expression programming (GEP) and multi-expression programming (MEP) for forecasting the compressive strength geopolymer concrete. Ain Shams Eng. J. 2021, 12, 3603–3617. [Google Scholar] [CrossRef]
- Khan, M.A.; Farooq, F.; Javed, M.F.; Zafar, A.; Ostrowski, K.A.; Aslam, F.; Malazdrewicz, S.; Maślak, M. Simulation of depth of wear of eco-friendly concrete using machine learning based computational approaches. Materials 2021, 15, 58. [Google Scholar] [CrossRef] [PubMed]
- Aldrees, A.; Khan, M.A.; Tariq, M.A.U.R.; Mustafa Mohamed, A.; Ng, A.W.M.; Bakheit Taha, A.T. Multi-Expression Programming (MEP): Water Quality Assessment Using Water Quality Indices. Water 2022, 14, 947. [Google Scholar] [CrossRef]
- Oltean, M.; Grosan, C. A comparison of several linear genetic programming techniques. Complex Syst. 2003, 14, 285–314. [Google Scholar]
- Maeda, T. How to Rationally Compare the Performances of Different Machine Learning Models? PeerJ Prepr. 2018, 6, 2167–9843. [Google Scholar]
- Abunama, T.; Othman, F.; Ansari, M.; El-Shafie, A. Leachate generation rate modeling using artificial intelligence algorithms aided by input optimization method for an MSW landfill. Environ. Sci. Pollut. Res. 2019, 26, 3368–3381. [Google Scholar] [CrossRef]
- Shah, M.I.; Javed, M.F.; Abunama, T. Proposed formulation of surface water quality and modelling using gene expression, machine learning, and regression techniques. Environ. Sci. Pollut. Res. 2021, 28, 13202–13220. [Google Scholar] [CrossRef]
- Papadimitriou, F. What is Spatial Complexity? In Spatial Complexity; Springer: Berlin/Heidelberg, Germany, 2020; pp. 3–18. [Google Scholar]
- Papadimitriou, F. The Probabilistic Basis of Spatial Complexity. In Spatial Complexity; Springer: Berlin/Heidelberg, Germany, 2020; pp. 51–61. [Google Scholar]
- Papadimitriou, F. Modelling spatial landscape complexity using the Levenshtein algorithm. Ecol. Inform. 2009, 4, 48–55. [Google Scholar] [CrossRef]
- Rekha, M. MLmuse: Correlation and Collinearity—How They Can Make or Break a Model. Correlation Analysis and Collinearity|Data Science|Multicollinearity|Clairvoyant Blog (clairvoyantsoft.com). 2019. Available online: https://blog.clairvoyantsoft.com/correlation-and-collinearity-how-they-can-make-or-break-a-model-9135fbe6936a (accessed on 11 June 2022).
- Shrestha, N. Detecting multicollinearity in regression analysis. Am. J. Appl. Math. Stat. 2020, 8, 39–42. [Google Scholar] [CrossRef]
- Kim, J.H. Multicollinearity and misleading statistical results. Korean J. Anesthesiol. 2019, 72, 558–569. [Google Scholar] [CrossRef]
- Al-Jamimi, H.A.; Bagudu, A.; Saleh, T.A. An intelligent approach for the modeling and experimental optimization of molecular hydrodesulfurization over AlMoCoBi catalyst. J. Mol. Liq. 2019, 278, 376–384. [Google Scholar] [CrossRef]
- Alawi, M.; Rajab, M. Determination of optimum bitumen content and Marshall stability using neural networks for asphaltic concrete mixtures. In Proceedings of the 9th WSEAS International Conference on Computers, World Scientific and Engineering Academy and Society (WSEAS), Athens, Greece, 11–13 July 2005. [Google Scholar]
- Kandil, K.A. Modeling marshall stability and flow for hot mix asphalt using artificial intelligence techniques. Nat. Sci. 2013, 11, 106–112. [Google Scholar]
- Ogundipe, O.M. Marshall stability and flow of lime-modified asphalt concrete. Transp. Res. Procedia 2016, 14, 685–693. [Google Scholar] [CrossRef]
- Mozumder, R.A.; Laskar, A.I. Prediction of unconfined compressive strength of geopolymer stabilized clayey soil using artificial neural network. Comput. Geotech. 2015, 69, 291–300. [Google Scholar] [CrossRef]
- Jalal, M.; Grasley, Z.; Nassir, N.; Jalal, H. RETRACTED: Strength and dynamic elasticity modulus of rubberized concrete designed with ANFIS modeling and ultrasonic technique. Constr. Build. Mater. 2020, 240, 117920. [Google Scholar] [CrossRef]
- Alade, I.O.; Abd Rahman, M.A.; Saleh, T.A. Predicting the specific heat capacity of alumina/ethylene glycol nanofluids using support vector regression model optimized with Bayesian algorithm. Sol. Energy 2019, 183, 74–82. [Google Scholar] [CrossRef]
- Alade, I.O.; Abd Rahman, M.A.; Saleh, T.A. Modeling and prediction of the specific heat capacity of Al2O3/water nanofluids using hybrid genetic algorithm/support vector regression model. Nano Struct. Nano Objects 2019, 17, 103–111. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Tombul, M. Modeling rainfall-runoff process using soft computing techniques. Comput. Geosci. 2013, 51, 108–117. [Google Scholar] [CrossRef]
- Shahin, M.A. Use of evolutionary computing for modelling some complex problems in geotechnical engineering. Geomech. Geoengin. 2015, 10, 109–125. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Bahman, K.; Bateni, S.M.; Ghorbani, H.; Marofpoor, I.; Nielson, J.R. Estimation of soil dispersivity using soft computing approaches. Neural Comput. Appl. 2017, 28, 207–216. [Google Scholar] [CrossRef]
- Aslam, F.; Elkotb, M.A.; Iqtidar, A.; Khan, M.A.; Javed, M.F.; Usanova, K.I.; Khan, M.I.; Alamri, S.; Musarat, M.A. Compressive strength prediction of rice husk ash using multiphysics genetic expression programming. Ain Shams Eng. J. 2022, 13, 101593. [Google Scholar] [CrossRef]
- Erzin, Y. Artificial neural networks approach for swell pressure versus soil suction behaviour. Can. Geotech. J. 2007, 44, 1215–1223. [Google Scholar] [CrossRef]
- Frank, I.E.; Todeschini, R. The Data Analysis Handbook; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Dao, D.V.; Ly, H.-B.; Trinh, S.H.; Le, T.-T.; Pham, B.T. Artificial intelligence approaches for prediction of compressive strength of geopolymer concrete. Materials 2019, 12, 983. [Google Scholar] [CrossRef]
- Roy, P.P.; Roy, K. On some aspects of variable selection for partial least squares regression models. QSAR Comb. Sci. 2008, 27, 302–313. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Javed, M.F.; Rauf, M.; Azim, I.; Ashraf, M.; Yang, J.; Liu, Q.-f. Sustainable utilization of foundry waste: Forecasting mechanical properties of foundry sand based concrete using multi-expression programming. Sci. Total Environ. 2021, 780, 146524. [Google Scholar] [CrossRef]
- Trucchia, A.; Frunzo, L. Surrogate based Global Sensitivity Analysis of ADM1-based Anaerobic Digestion Model. J. Environ. Manag. 2021, 282, 111456. [Google Scholar] [CrossRef]
- Derbel, M.; Hachicha, W.; Aljuaid, A.M. Sensitivity Analysis of the Optimal Inventory-Pooling Strategies According to Multivariate Demand Dependence. Symmetry 2021, 13, 328. [Google Scholar] [CrossRef]
- Khan, M.A.; Zafar, A.; Akbar, A.; Javed, M.F.; Mosavi, A. Application of Gene Expression Programming (GEP) for the prediction of compressive strength of geopolymer concrete. Materials 2021, 14, 1106. [Google Scholar] [CrossRef]



| Parameters | Unit | Mean | Median | Standard Deviation | Coefficient of Variation | Minimum | Maximum | Range | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| OUTPUTS | ||||||||||
| MS | kg | 1358 | 1372 | 109.40 | 8.06 | 1024 | 1680 | 656.000 | −0.129 | 0.838 |
| MF | 0.25 mm | 10.97 | 10.90 | 1.70 | 15.46 | 6.40 | 15.10 | 8.700 | −0.057 | −0.476 |
| INPUTS | ||||||||||
| Ps | % | 95.94 | 95.90 | 0.66 | 0.68 | 94.50 | 97.50 | 3.000 | 0.083 | −0.472 |
| Pb | % | 4.06 | 4.10 | 0.66 | 16.16 | 2.50 | 5.50 | 3.000 | −0.083 | −0.472 |
| Gmb | g/cm3 | 2.363 | 2.355 | 0.032 | 1.344 | 2.290 | 2.431 | 0.141 | 0.413 | −0.474 |
| Gmm | g/cm3 | 2.501 | 2.495 | 0.038 | 1.507 | 2.427 | 2.599 | 0.172 | 0.497 | −0.212 |
| Gsb | g/cm3 | 2.660 | 2.655 | 0.033 | 1.238 | 2.625 | 2.751 | 0.126 | 1.486 | 1.744 |
| Va | % | 5.50 | 5.25 | 1.53 | 27.82 | 2.20 | 9.85 | 7.649 | 0.646 | −0.155 |
| VFA | % | 62.81 | 63.89 | 10.06 | 16.02 | 34.82 | 83.65 | 48.836 | −0.498 | −0.355 |
| VMA | % | 14.79 | 14.68 | 0.72 | 4.87 | 13.24 | 17.39 | 4.142 | 0.692 | 1.192 |
| Ps | Pb | Gmb | Gmm | Gsb | Va | VFA | VMA | MS | |
|---|---|---|---|---|---|---|---|---|---|
| Ps | 1 | ||||||||
| Pb | −1 | 1 | |||||||
| Gmb | −0.3697 | 0.3697 | 1 | ||||||
| Gmm | 0.6758 | −0.6758 | 0.3504 | 1 | |||||
| Gsb | 0.0874 | −0.0874 | 0.6770 | 0.6963 | 1 | ||||
| Va | 0.9321 | −0.9321 | −0.5002 | 0.6356 | 0.0838 | 1 | |||
| VFA | −0.9538 | 0.9538 | 0.4636 | −0.6518 | −0.0245 | −0.9857 | 1 | ||
| VMA | −0.0921 | 0.0921 | −0.3039 | −0.0874 | 0.3075 | 0.1646 | −0.0035 | 1 | |
| MS | 0.0901 | −0.0901 | 0.5236 | 0.2662 | 0.1727 | −0.1788 | 0.0854 | −0.6560 | 1 |
| Ps | Pb | Gmb | Gmm | Gsb | Va | VFA | VMA | MF | |
|---|---|---|---|---|---|---|---|---|---|
| Ps | 1 | ||||||||
| Pb | −1 | 1 | |||||||
| Gmb | −0.3697 | 0.3697 | 1 | ||||||
| Gmm | 0.6758 | −0.6758 | 0.3504 | 1 | |||||
| Gsb | 0.0874 | −0.0874 | 0.6770 | 0.6963 | 1 | ||||
| Va | 0.9321 | −0.9321 | −0.5002 | 0.6356 | 0.0838 | 1 | |||
| VFA | −0.9538 | 0.9538 | 0.4636 | −0.6518 | −0.0245 | −0.9857 | 1 | ||
| VMA | −0.0921 | 0.0921 | −0.3039 | −0.0874 | 0.3075 | 0.1646 | −0.0035 | 1 | |
| MF | −0.9029 | 0.9029 | 0.4555 | −0.5247 | 0.1522 | −0.8625 | 0.9084 | 0.2242 | 1 |
| Parameter | MS & MF |
|---|---|
| Network type | FFBP |
| No. of hidden neurons | 10 |
| Number of hidden layers | 1 |
| Transfer function for hidden layer | TANSIG |
| Transfer function for output layer | PURELIN |
| Training algorithm | Levenberg–Marquardt |
| Learning rate | 0.01 |
| Number of nonlinear parameters | 18 |
| Number of epochs | 35 |
| Parameter | MS & MF |
|---|---|
| Number of linear parameters | 66 |
| Number of nonlinear parameters | 120 |
| Number of fuzzy rules | 6 |
| Number of MFs | 6 |
| Total number of parameter | 186 |
| Training epoch number | 50 |
| Training error goal | 0 |
| Number of nodes | 60 |
| Fuzzy structure | Sugeno |
| FIS type | Sub clustering |
| MF type | Trimf |
| Output function | linear |
| Optimization method | Hybrid |
| Parameters | MS and MF |
|---|---|
| Subpopulation Size | 100 |
| Code Length | 500 |
| Crossover Type | Uniform |
| Measure of Error | MAE |
| Crossover Probability | 0.9 |
| Mathematical Operators | +, −, /, ×, Sqrt, Power, Exp, Sin, Cos, Tan |
| Mutation Probability | 0.01 |
| Functions | 2 |
| Variables | 2 |
| Tournament Size | 2 |
| Num Generations | 1000 |
| Model | Statistical Parameter | ANN | ANFIS | MEP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tra | Tes | Val | Tra | Tes | Val | Tra | Tes | Val | ||
| MS | R | 0.954 | 0.950 | 0.970 | 0.961 | 0.966 | 0.977 | 0.965 | 0.968 | 0.971 |
| MAE | 24.36 | 29.94 | 23.88 | 23.56 | 25.33 | 21.53 | 20.89 | 21.02 | 22.12 | |
| RMSE | 31.46 | 36.33 | 29.30 | 29.25 | 32.22 | 25.47 | 27.58 | 29.01 | 28.34 | |
| RSE | 0.090 | 0.100 | 0.060 | 0.078 | 0.078 | 0.046 | 0.069 | 0.064 | 0.057 | |
| RRMSE | 0.023 | 0.027 | 0.021 | 0.022 | 0.024 | 0.019 | 0.020 | 0.022 | 0.021 | |
| PI | 0.012 | 0.014 | 0.011 | 0.011 | 0.012 | 0.009 | 0.010 | 0.011 | 0.010 | |
| NSE | 0.910 | 0.900 | 0.940 | 0.922 | 0.922 | 0.954 | 0.931 | 0.936 | 0.943 | |
| ObF | 0.044 | 0.044 | 0.044 | |||||||
| MF | R | 0.961 | 0.973 | 0.959 | 0.972 | 0.980 | 0.972 | 0.979 | 0.982 | 0.973 |
| MAE | 0.36 | 0.37 | 0.33 | 0.30 | 0.31 | 0.27 | 0.27 | 0.29 | 0.25 | |
| RMSE | 0.47 | 0.44 | 0.44 | 0.40 | 0.38 | 0.35 | 0.35 | 0.36 | 0.34 | |
| RSE | 0.076 | 0.054 | 0.092 | 0.056 | 0.040 | 0.059 | 0.043 | 0.036 | 0.057 | |
| RRMSE | 0.042 | 0.041 | 0.040 | 0.036 | 0.035 | 0.032 | 0.032 | 0.033 | 0.032 | |
| PI | 0.022 | 0.021 | 0.021 | 0.018 | 0.018 | 0.016 | 0.016 | 0.017 | 0.016 | |
| NSE | 0.924 | 0.946 | 0.909 | 0.944 | 0.960 | 0.941 | 0.957 | 0.964 | 0.943 | |
| ObF | 0.044 | 0.044 | 0.044 | |||||||
| S. No. | Equation | Condition | MEP Model | |
|---|---|---|---|---|
| MS | MF | |||
| 1 | R | 0.8 < R | 0.968 | 0.978 |
| 2 | 0.85 < k < 1.15 | 0.9996 | 0.9997 | |
| 3 | 0.85 < k′ < 1.15 | 1.0000 | 0.9993 | |
| 4 | 1.0000 1.0000 | 1.0000 1.0000 | ||
| 5 | Rm > 0.5 | 0.6959 | 0.7596 | |
| 6 | 1 > m | −0.0698 | −0.0446 | |
| 7 | 1 > n | −0.0699 | −0.0445 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gul, M.A.; Islam, M.K.; Awan, H.H.; Sohail, M.; Al Fuhaid, A.F.; Arifuzzaman, M.; Qureshi, H.J. Prediction of Marshall Stability and Marshall Flow of Asphalt Pavements Using Supervised Machine Learning Algorithms. Symmetry 2022, 14, 2324. https://doi.org/10.3390/sym14112324
Gul MA, Islam MK, Awan HH, Sohail M, Al Fuhaid AF, Arifuzzaman M, Qureshi HJ. Prediction of Marshall Stability and Marshall Flow of Asphalt Pavements Using Supervised Machine Learning Algorithms. Symmetry. 2022; 14(11):2324. https://doi.org/10.3390/sym14112324
Chicago/Turabian StyleGul, Muhammad Aniq, Md Kamrul Islam, Hamad Hassan Awan, Muhammad Sohail, Abdulrahman Fahad Al Fuhaid, Md Arifuzzaman, and Hisham Jahangir Qureshi. 2022. "Prediction of Marshall Stability and Marshall Flow of Asphalt Pavements Using Supervised Machine Learning Algorithms" Symmetry 14, no. 11: 2324. https://doi.org/10.3390/sym14112324
APA StyleGul, M. A., Islam, M. K., Awan, H. H., Sohail, M., Al Fuhaid, A. F., Arifuzzaman, M., & Qureshi, H. J. (2022). Prediction of Marshall Stability and Marshall Flow of Asphalt Pavements Using Supervised Machine Learning Algorithms. Symmetry, 14(11), 2324. https://doi.org/10.3390/sym14112324







