SPM: Sparse Persistent Memory Attention-Based Model for Network Traffic Prediction
Abstract
1. Introduction
- We propose a low-complexity SPM self-attention, which learns the sparse key features in the multivariate network traffic sequence, and carries out persistent memory to effectively use the key features to predict network traffic with more accuracy than the SOTA methods;
- We further develop a symmetric structure of the SPM Encoder and SPM Decoder based on SPM self-attention, which removes the feed-forward sub-layer, simplifies the structure of the model, and thus further reduces the complexity of the model;
- We evaluate SPM on two real-world network traffic datasets. The results demonstrate that SPM is optimal in terms of RMSE, MAE, and . Compared with Transformer, SPM also achieves great promotion in time performance.
2. Related Work
3. SPM for Network Traffic Prediction
3.1. Problem Formulation
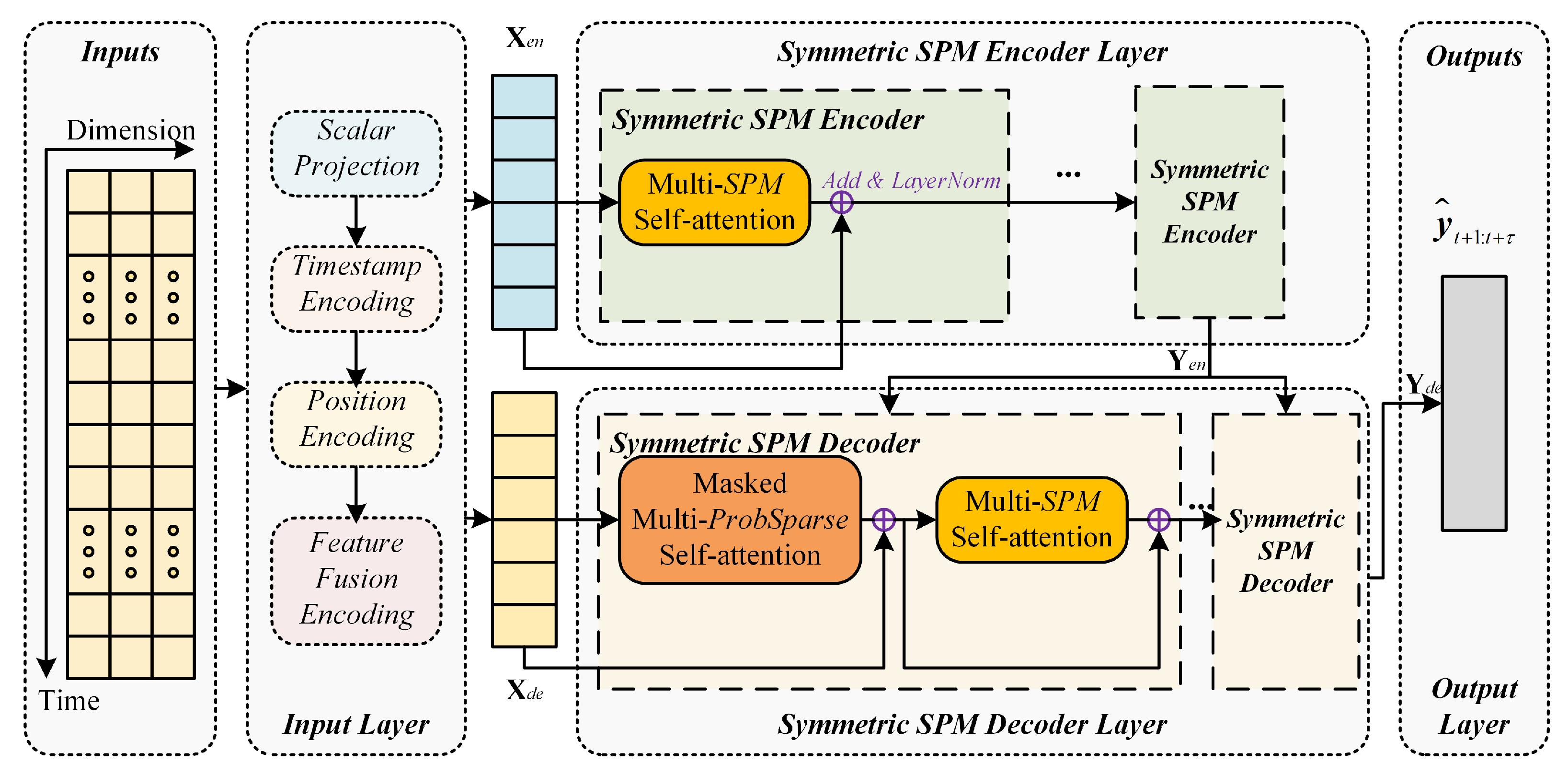
3.2. Overview of SPM
- (1)
- Input Layer
- (2)
- Symmetric SPM Encoder Layer
- (3)
- Symmetric SPM Decoder Layer
- (4)
- Output Layer
3.3. Input Layer
3.3.1. Data Normalization
3.3.2. Scalar Projection
3.3.3. Timestamp Feature Encoding
3.3.4. Position Encoding
3.3.5. Input Feature Fusion Encoding
3.4. Symmetric SPM Encoder Layer
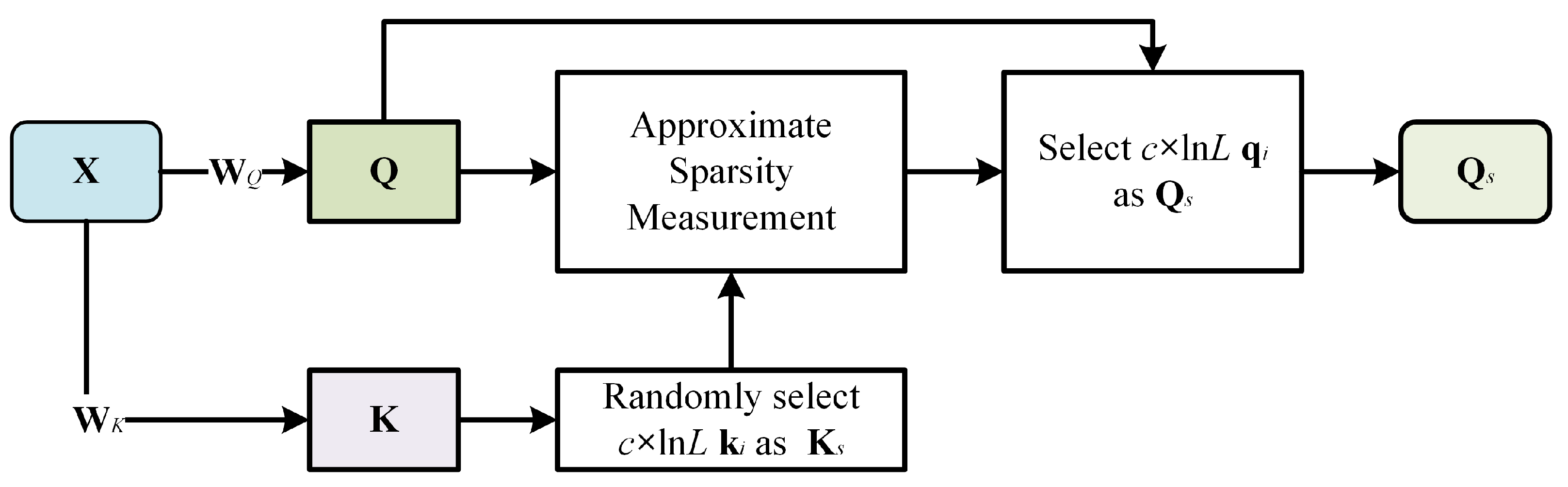
3.4.1. Sparse Query Block
3.4.2. SPM Self-Attention
- (1)
- Concatenation and normalization of sparse key attention weights
- (2)
- Split and fill sparse attention
- (3)
- Fusion sparse key attention
- (4)
- Multi-head SPM self-attention layer
3.4.3. Symmetric SPM Encoder Layer
3.5. Symmetric SPM Decoder Layer
3.5.1. ProbSparse Self-Attention
3.5.2. Symmetric SPM Decoder Layer
3.6. Output Layer
3.7. Cost Function
4. Evaluation
4.1. Dataset Description and Experiment Setup
4.1.1. Dataset Description
4.1.2. Experiment Setup
4.1.3. Evaluated Approaches and Metrics
- ARIMA [11], or autoregressive integrated moving average model, is one of the most classic time series prediction models;
- LSTM [35], or long short-term memory, is an extension of the RNN model;
- GRU [16], or gated recurrent unit, is a variant of LSTM;
- DeepAR [27] is a probabilistic prediction model based on neural networks, and its prediction target is the probability distribution of sequences over time steps;
- Transformer [20] is an improved prediction model based on vanilla Transformer.
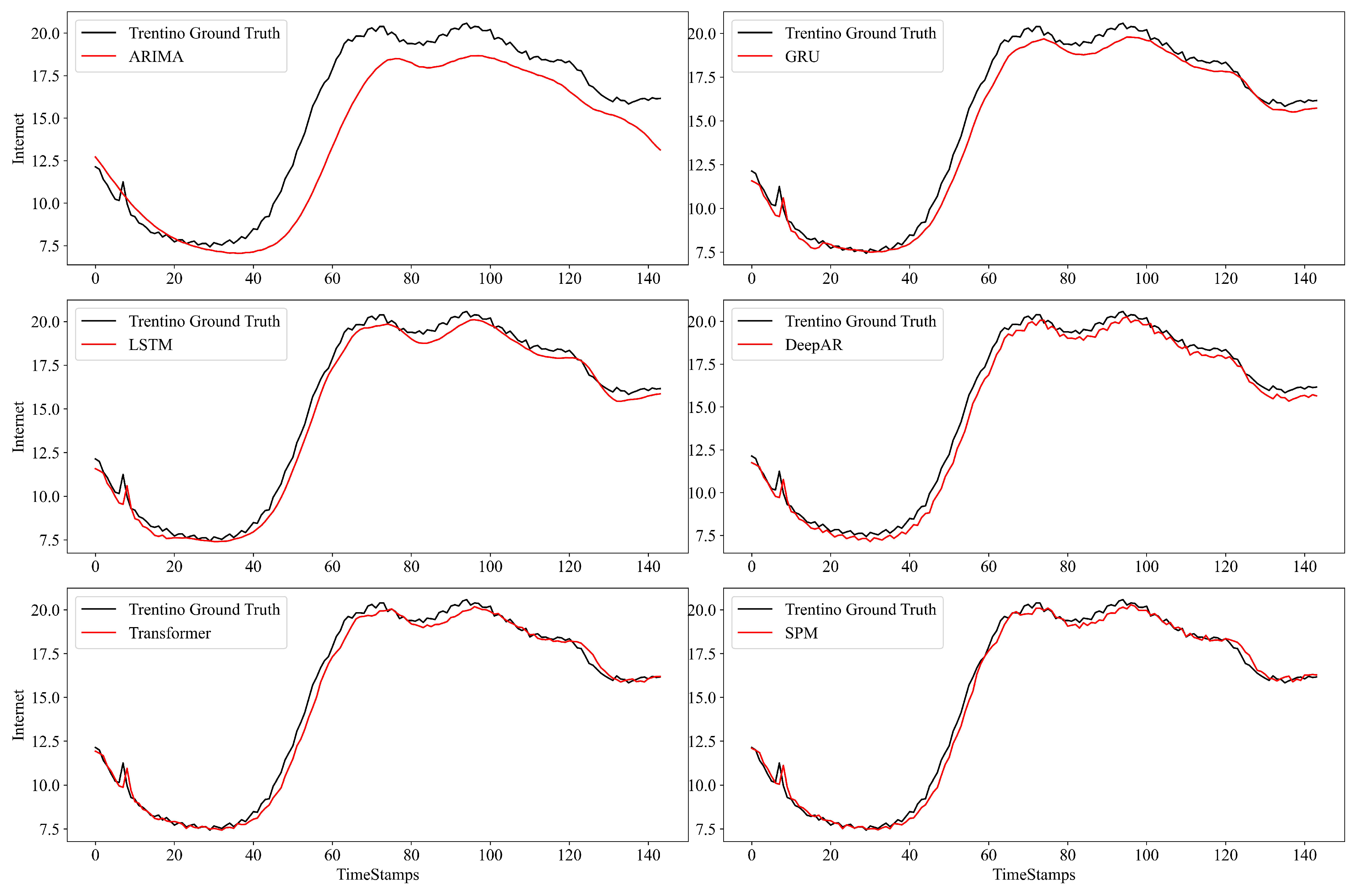
4.2. Evaluation Results
- (1)
- The performance of the classical model (e.g., ARIMA) is generally lower than that of the NN-based approaches, because such classical approaches generally rely on the mean value of history;
- (2)
- Transformer has effective performance when the prediction step is short ( = 144). However, as the prediction step increases ( = 432, 1008), the Transformer pays attention to all the features. It will generate a quadratic complexity, causing its inference speed to be slow. In addition, the key attention feature will also be affected by most other non-critical attention features, resulting in performance degradation, which is lower than the DeepAR;
- (3)
- SPM can decrease the interference of other non-critical attention information and focus on more key attention information, which can effectively improve the prediction performance. For instance, on the Milian dataset ( = 1008), SPM achieves RMSE reductions of 52.7%, 55.9%, and 23.5%, compared with GRU, LSTM, and DeepAR respectively. Moreover, compared with Transformer, SPM reduces the prediction MAE and RMSE by 48.3% and 42.9%, respectively. When measured by , the average of SPM at different prediction steps is about 0.1142 and 0.1553 higher than the sub-optimal baseline in the two datasets, respectively.
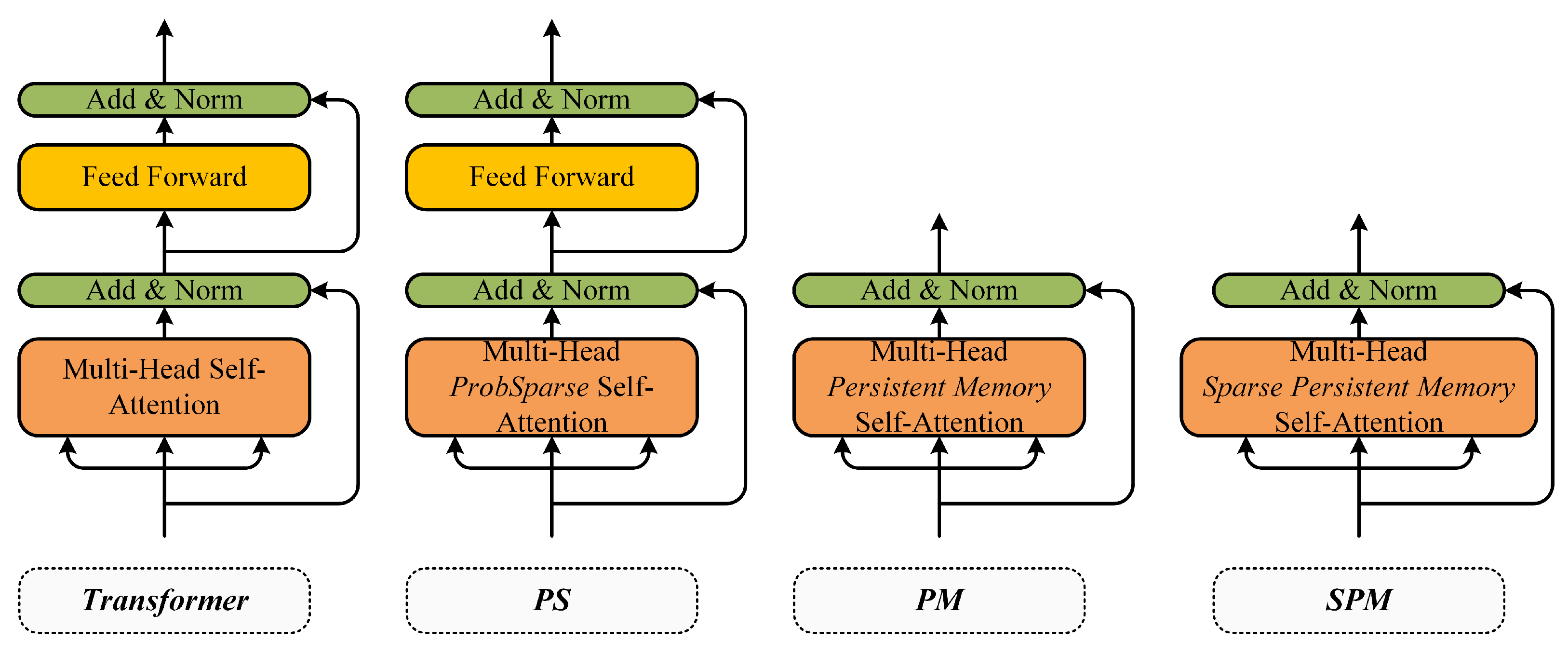
4.3. Ablation Evaluation
- Transformer, an improved prediction model based on vanilla Transformer;
- PS, or ProbSparse Transformer, Ablation model, using the ProbSparse self-attention layer to replace the vanilla self-attention layer;
- PM, or Persistent Memory Transformer, Ablation model, using the persistent memory self-attention layer structure, removing the feed-forward sub-layer;
- SPM, the proposed symmetric model in this paper.
4.3.1. Time Complexity Analysis
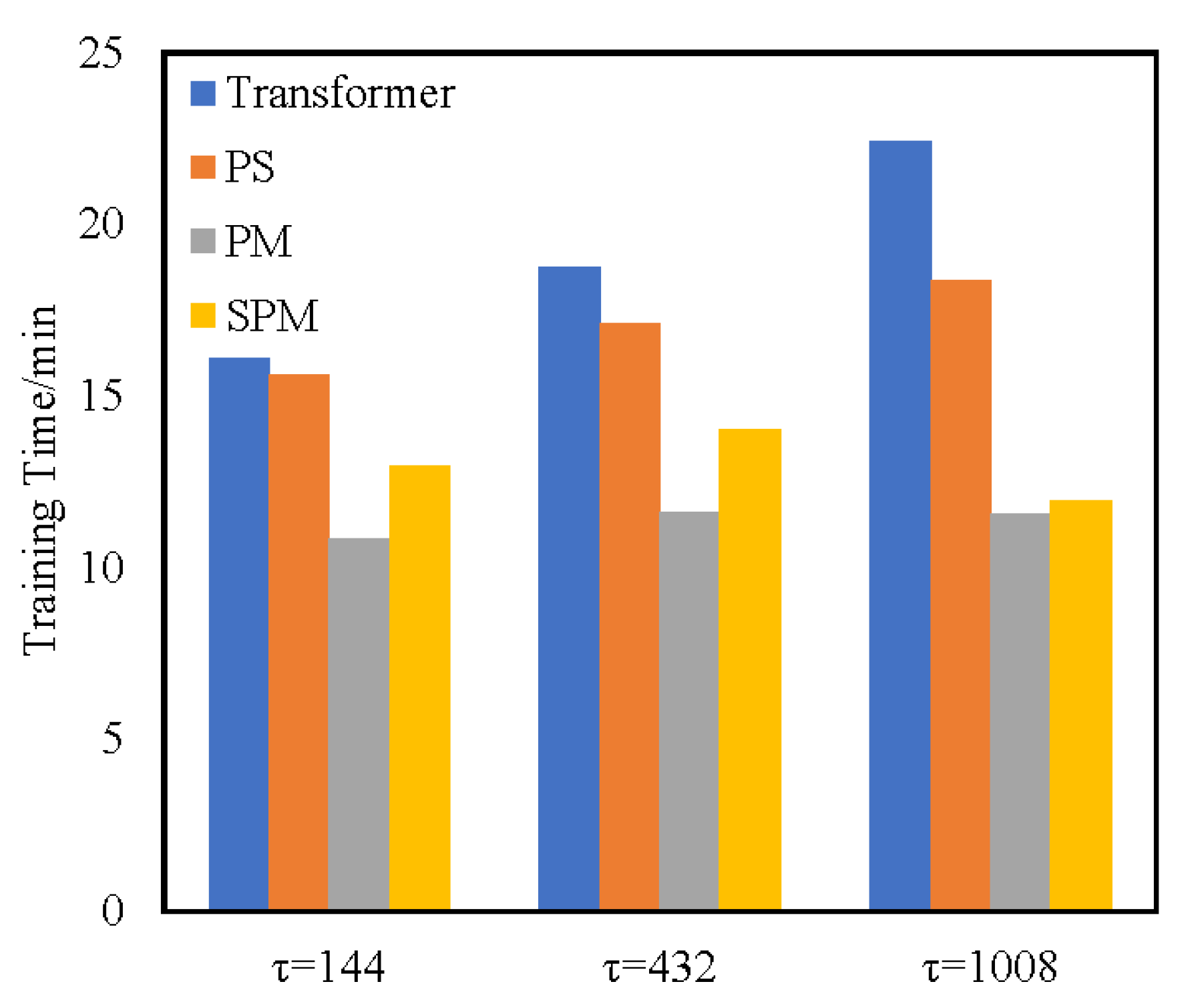
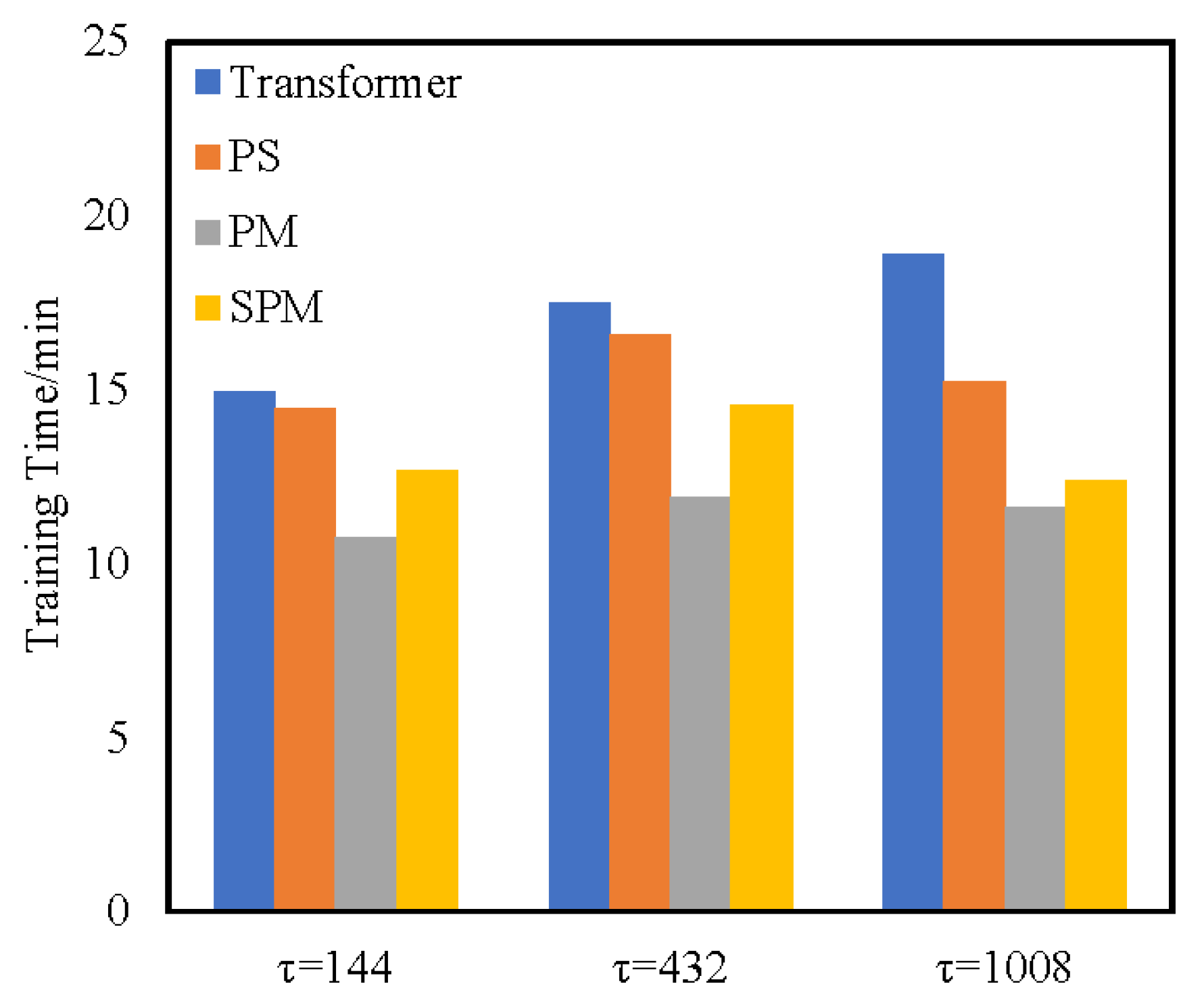
4.3.2. Ablation Evaluation Results of Temporal Performance
- (1)
- The PS Transformer replaces the vanilla attention layer with the ProbSparse self-attention layer. In terms of time performance, the complexity of the ProbSparse self-attention layer has been proved to be lower than that of the original attention layer. Therefore, the training time of the PS Transformer model is shorter than that of the Transformer model.
- (2)
- PM Transformer adopts the structure of the PM self-attention layer, which eliminates the feed-forward sub-layer and has low complexity. In terms of time performance, although the complexity of the self-attention layer is , the calculation method of self-attention is direct and does not calculate other factors. Therefore, the training time of PM is lower than that of SPM models.
- (3)
- SPM utilizes the SPM self-attention layer to obtain key attention information in the form of a sparse query matrix and carries out persistent memory for key attention information to retain the key attention information in a new attention layer. When calculating SPM attention, two attention fragments are calculated by branches and the attention weight is concatenated. Although such a fragmented structure has been shown to be beneficial for accuracy, it could decrease the efficiency because it is unfriendly for devices with strong parallel computing powers such as GPU. It also introduces extra overheads such as kernel launching and synchronization [36]. However, PM uses a simple single-branch calculation method, which can fully make use of the parallel computing powers of GPU and has high training efficiency. Thus, although the theoretical time complexity of SPM has reached a good level, the actual training time may be longer than that of PM. Compared with other methods, SPM removes the high complexity component of the feed-forward layer, and thus the time performance is in sub-optimal performance. Compared with Transformer, the training time of SPM is reduced by 22.2% and 30.4% on two real-world datasets, respectively. Compared with the baseline approaches, the evaluation metric is also optimal on two datasets.
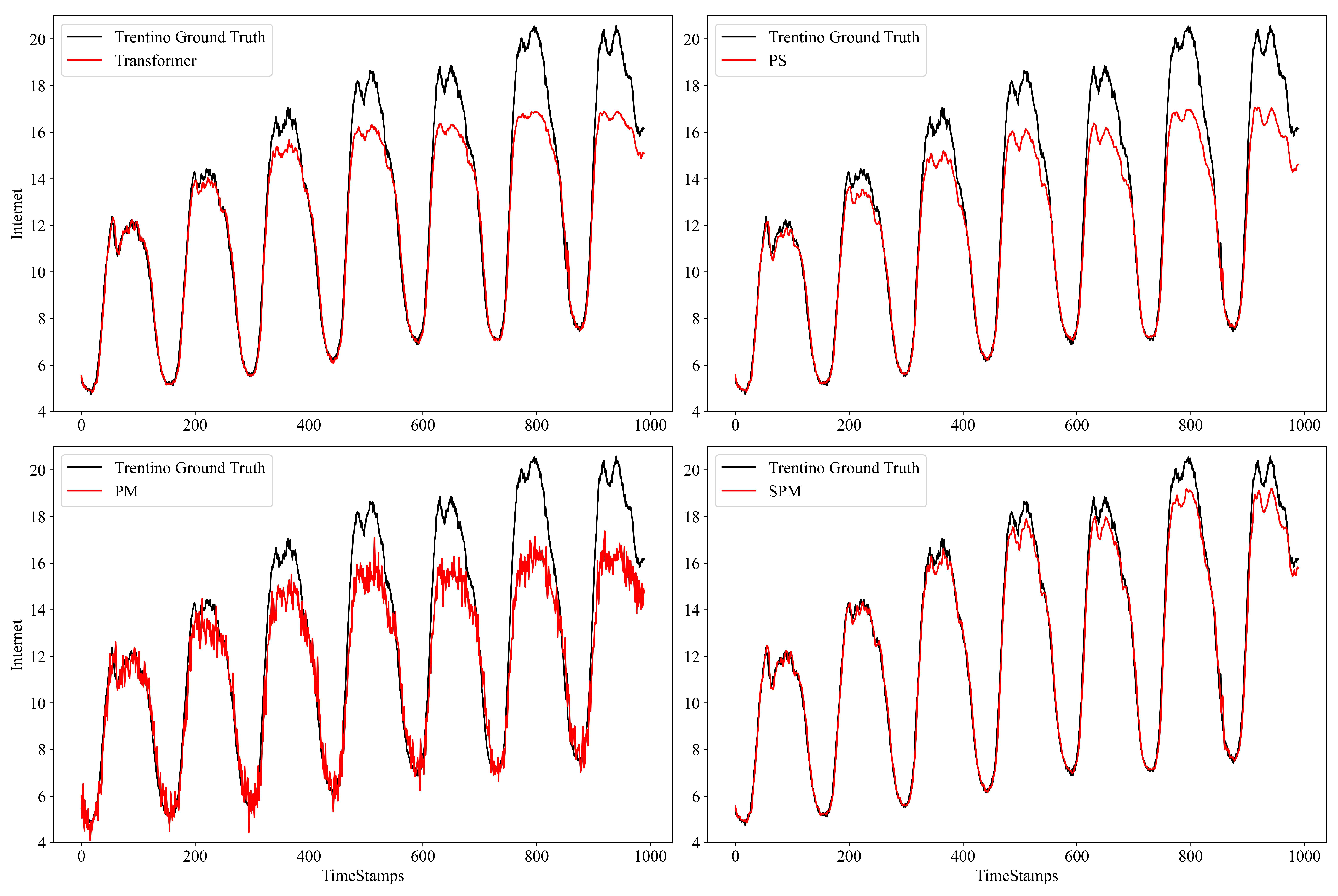
4.3.3. Ablation Evaluation Results of Prediction Performance
- (1)
- The PS Transformer replaces the vanilla self-attention layer with the ProbSparse self-attention layer. Sparse attention will only lead to the loss of partial attention information and can retain some key attention information. Therefore, the performance of RMSE and MAE evaluation indicators is not significantly reduced compared to the Transformer model, and still maintains a certain prediction accuracy;
- (2)
- The PM Transformer removes the feed-forward layer directly. PM calculates all the attention weights and cannot distinguish the key attention values. Moreover, there is no feed-forward sub-layer to further extract the key features, resulting in its poor prediction performance;
- (3)
- SPM utilizes the SPM self-attention layer, obtains key attention information in the form of a sparse query matrix, and carries out persistent memory for key attention information, so as to retain key attention information in the new attention layer, thus obtaining higher prediction accuracy.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, R.; Zhao, Z.; Zhou, X.; Palicot, J.; Zhang, H. The prediction analysis of cellular radio access network traffic: From entropy theory to networking practice. IEEE Commun. Mag. 2014, 52, 234–240. [Google Scholar] [CrossRef]
- Xu, Y.; Yin, F.; Xu, W.; Lin, J.; Cui, S. Wireless traffic prediction with scalable gaussian process: Framework, algorithms, and verification. IEEE J. Sel. Areas Commun. 2019, 37, 1291–1306. [Google Scholar] [CrossRef]
- Zhang, C.; Dang, S.; Shihada, B.; Alouini, M.-S. Dual attention-based federated learning for wireless traffic prediction. In Proceedings of the IEEE INFOCOM 2021—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 10–13 May 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Klaine, P.V.; Imran, M.A.; Onireti, O.; Souza, R.D. A survey of machine learning techniques applied to self-organizing cellular networks. IEEE Commun. Surv. Tutor. 2017, 19, 2392–2431. [Google Scholar] [CrossRef]
- Xu, F.; Lin, Y.; Huang, J.; Wu, D.; Shi, H.; Song, J.; Li, Y. Big data driven mobile traffic understanding and forecasting: A time series approach. IEEE Trans. Serv. Comput. 2016, 9, 796–805. [Google Scholar] [CrossRef]
- Hwang, S.-Y.; Shin, D.-J.; Kim, J.-J. Systematic review on identification and prediction of deep learning-based cyber security technology and convergence fields. Symmetry 2022, 14, 683. [Google Scholar] [CrossRef]
- Abadi, A.; Rajabioun, T.; Ioannou, P.A. Traffic flow prediction for road transportation networks with limited traffic data. IEEE Trans. Intell. Transp. Syst. 2014, 16, 653–662. [Google Scholar] [CrossRef]
- Abbasi, M.; Shahraki, A.; Taherkordi, A. Deep learning for network traffic monitoring and analysis (NTMA): A survey. Comput. Commun. 2021, 170, 19–41. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Qiao, J.; Yuan, D.; Zhang, M. Deep transfer learning for intelligent cellular traffic prediction based on cross-domain big data. IEEE J. Sel. Areas Commun. 2019, 37, 1389–1401. [Google Scholar] [CrossRef]
- Wang, S.; Nie, L.; Li, G.; Wu, Y.; Ning, Z. A multitask learning-based network traffic prediction approach for SDN-enabled industrial internet of things. IEEE Trans. Ind. Inform. 2022, 18, 7475–7483. [Google Scholar] [CrossRef]
- Ariyo, A.A.; Adewumi, A.O.; Ayo, C.K. Stock price prediction using the ARIMA model. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; pp. 106–112. [Google Scholar] [CrossRef]
- Zare Moayedi, H.; Masnadi-Shirazi, M.A. ARIMA model for network traffic prediction and anomaly detection. In Proceedings of the 2008 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–28 August 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Y.-H.; Wu, T.-X.; Zhai, D.-W.; Zhao, C.-H.; Zhou, Y.-F.; Qin, Y.-G.; Su, J.-S.; Qin, H. Hybrid decision based on DNN and DTC for model predictive torque control of PMSM. Symmetry 2022, 14, 693. [Google Scholar] [CrossRef]
- Lohrasbinasab, I.; Shahraki, A.; Taherkordi, A.; Delia Jurcut, A. From statistical- to machine learning-based network traffic prediction. Trans. Emerg. Telecommun. Technol. 2022, 33, e4394. [Google Scholar] [CrossRef]
- Cui, H.; Yao, M.Y.; Zhang, M.K.; Sun, F.; Liu, M.Y. Network traffic prediction based on Hadoop. In Proceedings of the 2014 International Symposium on Wireless Personal Multimedia Communications (WPMC), Sydney, Australia, 7–10 September 2014; pp. 29–33. [Google Scholar]
- Li, C.; Tang, G.; Xue, X.; Saeed, A.; Hu, X. Short-term wind speed interval prediction based on ensemble GRU model. IEEE Trans. Sustain. Energy 2020, 11, 1370–1380. [Google Scholar] [CrossRef]
- Zhang, C.; Patras, P. Long-term mobile traffic forecasting using deep spatio-temporal neural networks. In Proceedings of the Eighteenth ACM International Symposium on Mobile Ad Hoc Networking and Computing, Los Angeles, CA, USA, 26–29 June 2018; pp. 231–240. [Google Scholar]
- Balraj, E.; Harini, R.M.; SB, S.P.; Janani, S. A DNN based LSTM model for predicting future energy consumption. In Proceedings of the 2022 International Conference on Applied Artificial Intelligence and Computing (ICAAIC), Salem, India, 9–11 May 2022; pp. 1667–1671. [Google Scholar]
- Bi, J.; Zhang, X.; Yuan, H.; Zhang, J.; Zhou, M. A hybrid prediction method for realistic network traffic with temporal convolutional network and LSTM. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1869–1879. [Google Scholar] [CrossRef]
- Wu, N.; Green, B.; Ben, X.; O’Banion, S. Deep transformer models for time series forecasting: The influenza prevalence case. arXiv 2020, arXiv:2001.08317. [Google Scholar]
- Yuan, X.; Chen, N.; Wang, D.; Xie, G.; Zhang, D. Traffic prediction models of traffics at application layer in metro area network. J. Comput. Res. Dev. 2009, 46, 434–442. [Google Scholar]
- Jiang, M.; Wu, C.; Zhang, M.; Hu, D. Research on the comparison of time series models for network traffic prediction. Acta Electronica Sin. 2009, 37, 2353–2358. [Google Scholar] [CrossRef]
- Nie, L.; Wang, X.; Wang, S.; Ning, Z.; Obaidat, M.S.; Sadoun, B.; Li, S. Network traffic prediction in industrial internet of things backbone networks: A multitask learning mechanism. IEEE Trans. Ind. Inform. 2021, 17, 7123–7132. [Google Scholar] [CrossRef]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 2342–2350. [Google Scholar]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Stacked bidirectional and unidirectional LSTM recurrent neural network for forecasting network-wide traffic state with missing values. Transp. Res. Part C Emerg. Technol. 2020, 118, 102674. [Google Scholar] [CrossRef]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; pp. 324–328. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 5243–5253. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar] [CrossRef]
- Sukhbaatar, S.; Grave, E.; Lample, G.; Jegou, H.; Joulin, A. Augmenting self-attention with persistent memory. arXiv 2019, arXiv:1907.01470. [Google Scholar]
- Bao, Y.-X.; Shi, Q.; Shen, Q.-Q.; Cao, Y. Spatial-Temporal 3D Residual Correlation Network for Urban Traffic Status Prediction. Symmetry 2022, 14, 33. [Google Scholar] [CrossRef]
- Barlacchi, G.; De Nadai, M.; Larcher, R.; Casella, A.; Chitic, C.; Torrisi, G.; Antonelli, F.; Vespignani, A.; Pentland, A.; Lepri, B. A multi-source dataset of urban life in the city of Milan and the province of Trentino. Sci. Data 2015, 2, 150055. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ali, A.; Hassanein, H.S. Time-series prediction for sensing in smart greenhouses. In Proceedings of the GLOBECOM 2020-2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer: Cham, Switzerland, 2018; pp. 122–138. [Google Scholar]
- Kalaycı, T.A.; Asan, U. Improving classification performance of fully connected layers by fuzzy clustering in transformed feature space. Symmetry 2022, 14, 658. [Google Scholar] [CrossRef]
- Tang, Y.; Pan, Z.; Pedrycz, W.; Ren, F.; Song, X. Viewpoint-based kernel fuzzy clustering with weight information granules. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Tang, Y.; Ren, F.; Pedrycz, W. Fuzzy c-means clustering through SSIM and patch for image segmentation. Appl. Soft Comput. 2020, 87, 105928. [Google Scholar] [CrossRef]
- Yang, J.-Q.; Chen, C.-H.; Li, J.-Y.; Liu, D.; Li, T.; Zhan, Z.-H. Compressed-encoding particle swarm optimization with fuzzy learning for large-scale feature selection. Symmetry 2022, 14, 1142. [Google Scholar] [CrossRef]


| Symbol | Definition and Description |
|---|---|
| Input data | |
| Prediction steps | |
| t | The length of history time series |
| The predicted network traffic target | |
| The input of Symmetric SPM Encoder Layer | |
| The input of Symmetric SPM Decoder Layer | |
| The output of Symmetric SPM Encoder Layer | |
| The output of Symmetric SPM Decoder Layer | |
| Queries matrix | |
| Keys matrix | |
| Values matrix | |
| Dimension parameters | |
| Projection matrix | |
| The parameters of full connection layer | |
| h | Attention heads |
| M | The number of symmetric SPM encoders |
| N | The number of symmetric SPM decoders |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| ARIMA | 190.1470 | 196.6632 | 206.1349 |
| GRU | 99.6861 | 150.1390 | 142.0568 |
| LSTM | 107.0977 | 131.5001 | 152.1568 |
| DeepAR | 89.4358 | 74.2318 | 87.7861 |
| Transformer | 79.8580 | 87.7893 | 126.4511 |
| SPM | 49.1054 | 58.4251 | 67.1300 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| ARIMA | 1.3847 | 1.5369 | 1.6408 |
| GRU | 0.7939 | 1.1959 | 1.1203 |
| LSTM | 0.8931 | 1.0615 | 1.1814 |
| DeepAR | 0.5981 | 0.5570 | 0.6963 |
| Transformer | 0.6378 | 0.6637 | 0.9250 |
| SPM | 0.3839 | 0.3785 | 0.4782 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| ARIMA | 0.8777 | 0.8249 | 0.8128 |
| GRU | 0.9163 | 0.8803 | 0.7832 |
| LSTM | 0.9546 | 0.8183 | 0.8365 |
| DeepAR | 0.9790 | 0.9546 | 0.9177 |
| Transformer | 0.9849 | 0.8072 | 0.6995 |
| SPM | 0.9901 | 0.9630 | 0.9578 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| ARIMA | 89.1283 | 112.846 | 120.8139 |
| GRU | 73.7290 | 93.2989 | 130.0032 |
| LSTM | 54.3140 | 114.9338 | 112.9086 |
| DeepAR | 36.9362 | 57.4856 | 80.1257 |
| Transformer | 31.3617 | 118.3934 | 153.0669 |
| SPM | 25.4240 | 51.8640 | 57.3931 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| ARIMA | 0.6029 | 0.7877 | 0.8477 |
| GRU | 0.5470 | 0.6848 | 0.9567 |
| LSTM | 0.4299 | 0.8825 | 0.7772 |
| DeepAR | 0.2453 | 0.3924 | 0.6811 |
| Transformer | 0.2356 | 0.8722 | 0.9705 |
| SPM | 0.1933 | 0.3794 | 0.3902 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| ARIMA | 0.8612 | 0.7758 | 0.7344 |
| GRU | 0.9050 | 0.8467 | 0.6924 |
| LSTM | 0.9485 | 0.7674 | 0.7680 |
| DeepAR | 0.9762 | 0.9418 | 0.8832 |
| Transformer | 0.9829 | 0.7532 | 0.5736 |
| SPM | 0.9887 | 0.9527 | 0.9401 |
| Model | Self-Attention Layer | Feed-Forward Layer |
|---|---|---|
| Transformer | ||
| PS | ||
| PM | ||
| SPM |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| Transformer | 79.8580 | 87.7893 | 126.4511 |
| PS | 84.8511 | 92.1521 | 117.6370 |
| PM | 112.8224 | 136.8528 | 162.4517 |
| SPM | 49.1054 | 58.4251 | 67.1300 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| Transformer | 0.6378 | 0.6637 | 0.9250 |
| PS | 0.6752 | 0.6837 | 0.9108 |
| PM | 0.8354 | 0.8909 | 1.2974 |
| SPM | 0.3839 | 0.3785 | 0.4782 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| Transformer | 0.9849 | 0.8072 | 0.6995 |
| PS | 0.9766 | 0.8275 | 0.7558 |
| PM | 0.9620 | 0.7752 | 0.5437 |
| SPM | 0.9901 | 0.9630 | 0.9578 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| Transformer | 31.3617 | 118.3934 | 153.0669 |
| PS | 39.0264 | 111.9865 | 137.9754 |
| PM | 49.6851 | 127.8553 | 188.6106 |
| SPM | 25.4240 | 51.8640 | 57.3931 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| Transformer | 0.2356 | 0.8722 | 0.9705 |
| PS | 0.3035 | 0.8279 | 0.8083 |
| PM | 0.3336 | 0.9653 | 1.2941 |
| SPM | 0.1933 | 0.3794 | 0.3902 |
| Methods | = 144 | = 432 | = 1008 |
|---|---|---|---|
| Transformer | 0.9829 | 0.7532 | 0.5736 |
| PS | 0.9734 | 0.7792 | 0.6535 |
| PM | 0.9569 | 0.7121 | 0.3525 |
| SPM | 0.9887 | 0.9527 | 0.9401 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.-S.; Jiang, G.-H.; Zheng, B. SPM: Sparse Persistent Memory Attention-Based Model for Network Traffic Prediction. Symmetry 2022, 14, 2319. https://doi.org/10.3390/sym14112319
Ma X-S, Jiang G-H, Zheng B. SPM: Sparse Persistent Memory Attention-Based Model for Network Traffic Prediction. Symmetry. 2022; 14(11):2319. https://doi.org/10.3390/sym14112319
Chicago/Turabian StyleMa, Xue-Sen, Gong-Hui Jiang, and Biao Zheng. 2022. "SPM: Sparse Persistent Memory Attention-Based Model for Network Traffic Prediction" Symmetry 14, no. 11: 2319. https://doi.org/10.3390/sym14112319
APA StyleMa, X.-S., Jiang, G.-H., & Zheng, B. (2022). SPM: Sparse Persistent Memory Attention-Based Model for Network Traffic Prediction. Symmetry, 14(11), 2319. https://doi.org/10.3390/sym14112319







