The Enhancement of Energy-Carrying Capacity in Liquid with Gas Bubbles, in Terms of Solitons

Abstract

A generalized (3 + 1)-dimensional nonlinear wave is investigated, which defines many nonlinear phenomena in liquid containing gas bubbles. Basic theories of the natural phenomenons are usually described by nonlinear evolution equations, for example, nonlinear sciences, marine engineering, fluid dynamics, scientific applications, and ocean plasma physics. The new extended algebraic method is applied to solve the model under consideration. Furthermore, the nonlinear model is converted into an ordinary differential equation through the next wave transformation. A well-known analytical approach is used to obtain more general solutions of different types with the help of Mathematica. Shock, singular, mixed-complex solitary-shock, mixed-singular, mixed-shock singular, mixed trigonometric, periodic, mixed-periodic, mixed-hyperbolic solutions are obtained. As a result, it is found that the energy-carrying capacity of liquid with gas bubbles and its propagation can be increased. The stability of the considered model is ensured by the modulation instability gain spectrum generated and proposed with acceptable constant values. Two-dimensional, three-dimensional, and contour surfaces are plotted to see the physical properties of the obtained solutions.

1. Introduction

Researchers’ attention has been drawn to liquids through gas bubbles because they are common in physics, engineering, nature, science, and life. Bubble liquid mixture equations have been extended, to express the weakly nonlinear waves through liquids keeping gas bubbles [1,2]. As a result, it is found that the energy-carrying capacity of a liquid and its propagation can be increased with gas bubbles, as seen in some applied and scientific fields, similarly condensed matter physics, fluid mechanics, plasma physics, elastic mechanics, and particle physics [3,4,5,6,7,8,9,10]. There are many nonlinear wave phenomena in nature that can be explained analytically. Therefore, one of the most important achievements in mathematical physics is the study of integrable properties and the finding of exact solutions as nonlinear evolution equations [11]. In recent years, finding the exact solutions of NLEEs has also become important in research. Some nonlinear physical phenomena have been described using nonlinear evolution equations (NLEEs) and the propagation properties of waves [12,13,14,15].

It is well known that generalized and successful methods are available to study nonlinear equations. Namely, the KP hierarchy-reduction method [16], the Hirota’s bilinear method [17,18,19,20,21,22,23], the modified $\left(\frac{G^{\prime }}{G2}\right)$ and $\left(\frac{1}{G^{\prime }}\right)$ expansion method [24], the improved $tan\left(\frac{\varphi }{2}\right)$ expansion method [25], the sine-Gordon expansion [26], the optimal galerkin-homotopy asymptotic method [27], the inverse scattering transformation method [28,29], the homotopy perturbation method [30], the Backlund transformation method [31], Lie symmetry analysis [32], a kind of new $\left(\frac{G^{\prime }}{G}\right)$-expansion method [33], the $(\frac{G^{\prime }}{G},\frac{1}{G})$, and so on. The exact solutions of NLEEs can supply a wealth of physical data and additional understanding into the physical components of the problems [34]. It is important to find the exact solutions to NLEEs, e.g., soliton [35], travelling wave [36] and periodic wave solutions [37]. Accordingly, via Bell-polynomial manipulation [38], the integrability of NLEEs could be defined by a number of significant factors, such as infinite conservation laws, bilinear form, the Painleve test, Lax pairs, and infinite symmetries. As we know that there are many methods, Hirota bilinear methodology [39], Backlund transformation (BT) [40], polynomial expansion methodology [41], and Hirota-Riemann methodology [42] were suggested. According to several studies, the linear acoustic-wave propagation occurs in isothermal bubbly liquids due to the phenomena of one spatial dimension. In the three-dimensional (3D) case, nonlinear waves in liquid containing gas bubbles are considered. The nonlinear evolution equation is given for a description of long nonlinear pressure waves. The Hirota method is used to find multiple solutions to the nonintegrable evolution equation in three dimensions [43]. The model of transcillatory heat transfer is induced by gas bubbles buoyant in liquid. The algorithms for calculating the coefficient of transcillatory transfer have been discovered [44]. Higher-order terms with respect to the small parameter are taken into account in the derivation of the equation for nonlinear waves. For long weakly nonlinear waves, a nonlinear differential equation is derived that takes into consideration liquid viscosity, inter-phase heat transfer, and surface tension [45].

The first analysis of the bubble dynamics issue was carried out by Rayleigh [46]. According to some studies, linear acoustic-wave propagation occurs in isothermal bubbly liquids in the case of one spatial dimension [1]. Nonlinear wave studies have focused on the research of the bubbly liquid, which has drawn the interest of different researchers because liquids with gas bubbles are common in many professions, including engineering and medical science. The generalized (3 + 1) dimensional nonlinear wave equation narrating a liquid through gas bubbles is one of these models [47].

$$\begin{array}{c}\hfill {({\Omega }_t+{\sigma }_1\Omega {\Omega }_x+{\sigma }_2\Omega {\Omega }_{xxx}+{\sigma }_3{\Omega }_x)}_x+{\sigma }_4\Omega {\Omega }_{yy}+{\sigma }_5{\Omega }_{zz}=0,\end{array}$$

(1)

where $\Omega$ is the wave amplitude function of the scaled spatial coordinates $x,y,z$ and the temporal coordinate t is the partial derivative represented by the subscripts $x,y,z$, and t. ${\sigma }_1$, ${\sigma }_2$, ${\sigma }_3$, ${\sigma }_4$, and ${\sigma }_5$ describe the bubble-liquid non-linearity, the bubble-liquid dispersion, the bubble-liquid viscosity, the y transverse perturbation, and the z transverse perturbation. Additionally, ${\sigma }_3=0$ was simplified to the generalized (3 + 1) dimensional Kadomtsev–Petviashvili equation. It is noted that the solutions for its travelling wave, bright-dark soliton, and rogue wave were also derived. The pressure dependency of thermal expansion coefficient conductivity may be the cause of the coefficients’ temporal fluctuation of seawater coupled with the oceanic temperature-salinity relation’s large-scale meridional variation, transforming hydrography from deep to shallow water topography of the continental shelf and other dynamical conditions [48].

Recently, Akbulut et al. [49] explored, using Nnucci’s reduction, increased, and modified, Kudryashov algorithms, and solitary waves for the generalized nonlinear wave equation in (3 + 1) dimensions with gas bubbles successfully determined. Akbulut developed the three different classes of solitary wave solution. This implies that there are many solutions that are not explained yet, and to the best of our knowledge the modulation instability analysis is still a mystery. Our purpose is to develop more propagated structures; we will apply a generalized expansion method and derive thirty-seven different solutions, as well as provide a graphical explanation. The stability of our model will be discussed through the modulational instability gain spectrum.

The main motive of this article is to generalize the (3 + 1) dimensional nonlinear wave equation describing liquid with gas bubbles, in order to find the exact solutions. The new extended direct algebraic method will be used to achieve this goal. In Section 2, the proper details with respect to the method will be presented. In the following section, the different solutions to the provided model will be obtained using the new extended direct algebraic methods. Graphical representations for a derived solution will be described in Section 3 for stability analysis. Finally, the conclusions will be provided.

2. Construction of Analytical Solutions

2.1. New Extended Direct Algebraic Method

The proposed method is successfully applied to the complex nonlinear governing model [50].

We have a nonlinear partial differential equation:

$$\begin{array}{c}\hfill \mathcal{P}(\Omega ,{\Omega }_x,{\Omega }_t,{\Omega }_{xt},{\Omega }_{xx},\dots )=0,\end{array}$$

(2)

where $\mathcal{P}$ is the polynomial function in $\Omega$, and its spatial independent variables and temporal and accommodating $\Omega (x,y,z,t)$ is an unknown function of its partial derivatives.

It can be changed through the ordinary differential equation:

$$\begin{array}{c}\hfill \mathcal{Q}(\mathbb{E},{\mathbb{E}}^{\prime },{\mathbb{E}}^{″},\dots )=0.\end{array}$$

(3)

Apply the following transformation:

$$\Omega (x,y,z,t)=\mathbb{E}\left(\lambda \right),$$

(4)

where $\lambda =k_{1}x+k_{2}y+k_{3}t$. Let Equation (3) have the solution

$$\begin{array}{c}\hfill \mathbb{E}\left(\lambda \right)=\sum _{j=0}^m\left[a_j{\left(\mathbb{R}\left(\lambda \right)\right)}^j\right],\end{array}$$

(5)

where,

$$\begin{array}{c}\hfill {\mathbb{R}}^{\prime }\left(\lambda \right)=log\left[\chi \right]\left(\alpha +\beta \mathbb{R}\left(\lambda \right)+\gamma {\mathbb{R}}^2\left(\lambda \right)\right),\chi \ne 0,1,\end{array}$$

(6)

where, $\alpha$, $\beta$, and $\gamma$ are real constants and $\mathfrak{S}={\beta }^2-4\alpha \gamma$. The general roots regrading the parameters $\alpha$, $\beta$, and $\gamma$ of Equation (6) are

(Family 1): When ${\beta }^2-4\alpha \gamma <0$, and $\gamma \ne 0,$

$$\begin{array}{c}\hfill {\mathbb{R}}_1\left(\lambda \right)=-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }{tan}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{2}\lambda \right),\end{array}$$

(7)

$$\begin{array}{c}\hfill {\mathbb{R}}_2\left(\lambda \right)=-\frac{\beta }{2\gamma }-\frac{\sqrt{-\mathfrak{S}}}{2\gamma }{cot}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{2}\lambda \right),\end{array}$$

(8)

$$\begin{array}{c}\hfill {\mathbb{R}}_3\left(\lambda \right)=-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }\left({tan}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\pm \sqrt{mn}{sec}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\right),\end{array}$$

(9)

$$\begin{array}{c}\hfill {\mathbb{R}}_4\left(\lambda \right)=-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }\left({cot}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\pm \sqrt{mn}{csc}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\right),\end{array}$$

(10)

$$\begin{array}{c}\hfill {\mathbb{R}}_5\left(\lambda \right)=-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{4\gamma }\left({tan}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{4}\lambda \right)-{cot}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{4}\lambda \right)\right).\end{array}$$

(11)

(Family 2): When ${\beta }^2-4\alpha \gamma >0$, and $\gamma \ne 0,$

$$\begin{array}{c}\hfill {\mathbb{R}}_6\left(\lambda \right)=-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{2\gamma }{tanh}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{2}\lambda \right),\end{array}$$

(12)

$$\begin{array}{c}\hfill {\mathbb{R}}_7\left(\lambda \right)=-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{2\gamma }{coth}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{2}\lambda \right),\end{array}$$

(13)

$$\begin{array}{c}\hfill {\mathbb{R}}_8\left(\lambda \right)=-\frac{\beta }{2\gamma }+\frac{\sqrt{\mathfrak{S}}}{2\gamma }\left(-{tanh}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\pm i\sqrt{mn}sec{h}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\right),\end{array}$$

(14)

$$\begin{array}{c}\hfill {\mathbb{R}}_9\left(\lambda \right)=-\frac{\beta }{2\gamma }+\frac{\sqrt{\mathfrak{S}}}{2\gamma }\left(-{coth}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\pm \sqrt{mn}csc{h}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\right),\end{array}$$

(15)

$$\begin{array}{c}\hfill {\mathbb{R}}_{10}\left(\lambda \right)=-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{4\gamma }\left(tan{h}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{4}\lambda \right)+cot{h}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{4}\lambda \right)\right).\end{array}$$

(16)

(Family 3): When $\alpha \gamma >0$ and $\beta =0,$

$$\begin{array}{c}\hfill {\mathbb{R}}_{11}\left(\lambda \right)=\sqrt{\frac{\alpha }{\gamma }}ta{n}_{\chi }\left(\sqrt{\alpha \gamma }\lambda \right),\end{array}$$

(17)

$$\begin{array}{c}\hfill {\mathbb{R}}_{12}\left(\lambda \right)=-\sqrt{\frac{\alpha }{\gamma }}co{t}_{\chi }\left(\sqrt{\alpha \gamma }\lambda \right),\end{array}$$

(18)

$$\begin{array}{c}\hfill {\mathbb{R}}_{13}\left(\lambda \right)=\sqrt{\frac{\alpha }{\gamma }}\left({tan}_{\chi }\left(2\sqrt{\alpha \gamma }\lambda \right)\pm \sqrt{mn}se{c}_{\chi }\left(2\sqrt{\alpha \gamma }\lambda \right)\right),\end{array}$$

(19)

$$\begin{array}{c}\hfill {\mathbb{R}}_{14}\left(\lambda \right)=\sqrt{\frac{\alpha }{\gamma }}\left(-co{t}_{\chi }\left(2\sqrt{\alpha \gamma }\lambda \right)\pm \sqrt{mn}{csc}_{\chi }\left(2\sqrt{\alpha \gamma }\lambda \right)\right),\end{array}$$

(20)

$$\begin{array}{c}\hfill {\mathbb{R}}_{15}\left(\lambda \right)=\frac{1}{2}\sqrt{\frac{\alpha }{\gamma }}\left({tan}_{\chi }\left(\frac{\sqrt{\alpha \gamma }}{2}\lambda \right)-{cot}_{\chi }\left(\frac{\sqrt{\alpha \gamma }}{2}\lambda \right)\right).\end{array}$$

(21)

(Family 4): When $\alpha \gamma <0$ and $\beta =0,$

$$\begin{array}{c}\hfill {\mathbb{R}}_{16}\left(\lambda \right)=-\sqrt{-\frac{\alpha }{\gamma }}{tanh}_{\chi }\left(\sqrt{-\alpha \gamma }\lambda \right),\end{array}$$

(22)

$$\begin{array}{c}\hfill {\mathbb{R}}_{17}\left(\lambda \right)=-\sqrt{-\frac{\alpha }{\gamma }}{coth}_{\chi }\left(\sqrt{-\alpha \gamma }\lambda \right),\end{array}$$

(23)

$$\begin{array}{c}\hfill {\mathbb{R}}_{18}\left(\lambda \right)=\sqrt{-\frac{\alpha }{\gamma }}\left(-{tanh}_{\chi }\left(2\sqrt{-\alpha \gamma }\lambda \right)\pm i\sqrt{mn}sec{h}_{\chi }\left(2\sqrt{-\alpha \gamma }\lambda \right)\right),\end{array}$$

(24)

$$\begin{array}{c}\hfill {\mathbb{R}}_{19}\left(\lambda \right)=\sqrt{-\frac{\alpha }{\gamma }}\left(-{coth}_{\chi }\left(2\sqrt{-\alpha \gamma }\lambda \right)\pm \sqrt{mn}csc{h}_{\chi }\left(2\sqrt{-\alpha \gamma }\lambda \right)\right),\end{array}$$

(25)

$$\begin{array}{c}\hfill {\mathbb{R}}_{20}\left(\lambda \right)=-\frac{1}{2}\sqrt{-\frac{\alpha }{\gamma }}\left({tanh}_{\chi }\left(\frac{\sqrt{-\alpha \gamma }}{2}\lambda \right)+cot{h}_{\chi }\left(\frac{\sqrt{-\alpha \gamma }}{2}\lambda \right)\right).\end{array}$$

(26)

(Family 5): When $\beta =0$ and $\alpha =\gamma ,$

$$\begin{array}{c}\hfill {\mathbb{R}}_{21}\left(\lambda \right)={tan}_{\chi }\left(\alpha \lambda \right),\end{array}$$

(27)

$$\begin{array}{c}\hfill {\mathbb{R}}_{22}\left(\lambda \right)=-{cot}_{\chi }\left(\alpha \lambda \right),\end{array}$$

(28)

$$\begin{array}{c}\hfill {\mathbb{R}}_{23}\left(\lambda \right)={tan}_{\chi }\left(2\alpha \lambda \right)\pm \sqrt{mn}{sec}_{\chi }\left(2\alpha \lambda \right),\end{array}$$

(29)

$${\mathbb{R}}_{24}\left(\lambda \right)=-{cot}_{\chi }\left(2\alpha \lambda \right)\pm \sqrt{mn}{csc}_{\chi }\left(2\alpha \lambda \right),$$

(30)

$$\begin{array}{c}\hfill {\mathbb{R}}_{25}\left(\lambda \right)=\frac{1}{2}\left({tan}_{\chi }\left(\frac{\alpha }{2}\lambda \right)-{cot}_{\chi }\left(\frac{\alpha }{2}\lambda \right)\right).\end{array}$$

(31)

(Family 6): When $\beta =0$ and $\gamma =-\alpha ,$

$$\begin{array}{c}\hfill {\mathbb{R}}_{26}\left(\lambda \right)=-{tanh}_{\chi }\left(\alpha \lambda \right),\end{array}$$

(32)

$$\begin{array}{c}\hfill {\mathbb{R}}_{27}\left(\lambda \right)=-{coth}_{\chi }\left(\alpha \lambda \right),\end{array}$$

(33)

$$\begin{array}{c}\hfill {\mathbb{R}}_{28}\left(\lambda \right)=-{tanh}_{\chi }\left(2\alpha \lambda \right)\pm i\sqrt{mn}sec{h}_{\chi }\left(2\alpha \lambda \right),\end{array}$$

(34)

$$\begin{array}{c}\hfill {\mathbb{R}}_{29}\left(\lambda \right)=-{cot}_{\chi }\left(2\alpha \lambda \right)\pm \sqrt{mn}csc{h}_{\chi }\left(2\alpha \lambda \right),\end{array}$$

(35)

$$\begin{array}{c}\hfill {\mathbb{R}}_{30}\left(\lambda \right)=-\frac{1}{2}\left({tanh}_{\chi }\left(\frac{\alpha }{2}\lambda \right)+{coth}_{\chi }\left(\frac{\alpha }{2}\lambda \right)\right).\end{array}$$

(36)

(Family 7): When ${\beta }^2=4\alpha \gamma$,

$$\begin{array}{c}\hfill {\mathbb{R}}_{31}\left(\lambda \right)=\frac{-2\alpha (\beta \lambda log[\chi ]+2)}{{\beta }^2\lambda log\left[\chi \right]}.\end{array}$$

(37)

(Family 8): When $\alpha =pq,(q\ne 0),\beta =p,$ and $\gamma =0$,

$$\begin{array}{c}\hfill {\mathbb{R}}_{32}\left(\lambda \right)={\chi }^{p\lambda }-q.\end{array}$$

(38)

(Family 9): When $\beta =\gamma =0$,

$$\begin{array}{c}\hfill {\mathbb{R}}_{33}\left(\lambda \right)=\alpha \lambda log\left[\chi \right].\end{array}$$

(39)

(Family 10): When $\beta =\alpha =0$,

$$\begin{array}{c}\hfill {\mathbb{R}}_{34}\left(\lambda \right)=\frac{-1}{\gamma \lambda log\left[\chi \right]}.\end{array}$$

(40)

(Family 11): When $\alpha =0$ and $\beta \ne 0$,

$$\begin{array}{c}\hfill {\mathbb{R}}_{35}\left(\lambda \right)=-\frac{m\beta }{\gamma \left({cosh}_{\chi }\left(\beta \lambda \right)-{sinh}_{\chi }\left(\beta \lambda \right)+m\right)},\end{array}$$

(41)

$$\begin{array}{c}\hfill {\mathbb{R}}_{36}\left(\lambda \right)=-\frac{\beta \left({sinh}_{\chi }\left(\beta \lambda \right)+{cosh}_{\chi }\left(\beta \lambda \right)\right)}{\gamma \left({sinh}_{\chi }\left(\beta \lambda \right)+{cosh}_{\chi }\left(\beta \lambda \right)+n\right)}.\end{array}$$

(42)

(Family 12): When $\gamma =pq,(q\ne 0),\beta =p,$ and $\alpha =0$,

$$\begin{array}{c}\hfill {\mathbb{R}}_{37}\left(\lambda \right)=-\frac{m{\chi }^{p\lambda }}{m-qn{\chi }^{p\lambda }}.\end{array}$$

(43)

$$\begin{array}{c}\hfill {sinh}_{\chi }\left(\lambda \right)=\frac{m{\chi }^{\lambda }-n{\chi }^{-\lambda }}{2},{cosh}_{\chi }\left(\lambda \right)=\frac{m{\chi }^{\lambda }+n{\chi }^{-\lambda }}{2},\end{array}$$

$$\begin{array}{c}\hfill {tanh}_{\chi }\left(\lambda \right)=\frac{m{\chi }^{\lambda }-n{\chi }^{-\lambda }}{m{\chi }^{\lambda }+n{\chi }^{-\lambda }},{coth}_{\chi }\left(\lambda \right)=\frac{m{\chi }^{\lambda }+n{\chi }^{-\lambda }}{m{\chi }^{\lambda }-n{\chi }^{-\lambda }},\end{array}$$

$$\begin{array}{c}\hfill sec{h}_{\chi }\left(\lambda \right)=\frac{2}{m{\chi }^{\lambda }+n{\chi }^{-\lambda }},csc{h}_{\chi }\left(\lambda \right)=\frac{2}{m{\chi }^{\lambda }-n{\chi }^{-\lambda }},\end{array}$$

$$\begin{array}{c}\hfill si{n}_{\chi }\left(\lambda \right)=\frac{m{\chi }^{i\lambda }-n{\chi }^{-i\lambda }}{2i},co{s}_{\chi }\left(\lambda \right)=\frac{m{\chi }^{i\lambda }+n{\chi }^{-i\lambda }}{2},\end{array}$$

$$\begin{array}{c}\hfill {tan}_{\chi }\left(\lambda \right)=-i\frac{m{\chi }^{i\lambda }-n{\chi }^{-i\lambda }}{m{\chi }^{i\lambda }+n{\chi }^{-i\lambda }},{cot}_{\chi }\left(\lambda \right)=i\frac{m{\chi }^{i\lambda }+n{\chi }^{-i\lambda }}{m{\chi }^{i\lambda }-n{\chi }^{-i\lambda }},\end{array}$$

where, $m,n>0$ are arbitrary constant deformation parameters.

2.2. Application of New Extended Direct Algebraic Method

In this portion, we will apply the new extended distinct algebraic methodology to the generalized energy-carrying capacity of liquids in the presence of gas bubbles. To extract the solutions of Equation (1), we set up a traveling wave transformation:

$$\begin{array}{c}\hfill M(x,y,z,t)=\mathbb{E}\left(\lambda \right),\mathrm{where}\lambda =\delta ({\varrho }_{1}x+{\varrho }_{2}y+{\varrho }_{3}z-\varpi t),\end{array}$$

(44)

where $\delta$ is free constant parameter and $\varpi$ is the speed of soliton, and ${\varrho }_1$, ${\varrho }_2$, ${\varrho }_3$ are the direction of the cosine.

$${\varrho }_1^2+{\varrho }_2^2+{\varrho }_3^2=1.$$

Equation (1) takes the form by introducing Equation (44),

$$\begin{array}{c}\hfill 2({\sigma }_3{\varrho }_1^2+{\sigma }_4{\varrho }_2^2+{\sigma }_5{\varrho }_3^2-{\varrho }_3\varpi )\mathbb{E}+{\sigma }_1{\varrho }_1^2{\mathbb{E}}^2+2{\sigma }_2{\delta }^2{\sigma }_2{\varrho }_1^4{\mathbb{E}}^{″}=0.\end{array}$$

(45)

The solution can be revealed by the setting of the homogeneous balancing constant of Equation (45):

$$\begin{array}{c}\hfill \mathbb{E}\left(\lambda \right)=a_0+a_1\mathbb{R}\left(\lambda \right)+a_2\mathbb{R}{\left(\lambda \right)}^2,\end{array}$$

(46)

where,

$$\begin{array}{c}\hfill {\mathbb{R}}^{\prime }\left(\lambda \right)=\alpha ln\left(\chi \right)+\beta \mathbb{R}\left(\xi \right)ln\left(\chi \right)+\gamma {\left(\mathbb{R}\left(\xi \right)\right)}^{2}ln\left(\chi \right),\chi \ne 0,1,\end{array}$$

(47)

now, we plug the solution of Equation (46) into (47) and identify the coefficient of the dissimilar powers:

$$\begin{array}{c}\hfill \begin{array}{cc}& \mathbb{R}{\left(\lambda \right)}^0:2{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_1\beta {\left(ln\left(\chi \right)\right)}^2\alpha +4{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_2{\alpha }^2{\left(ln\left(\chi \right)\right)}^2+{\sigma }_1{{\varrho }_1}^2{a_0}^2-2a_0{\varrho }_1\varpi +2a_0{\sigma }_4{{\varrho }_2}^2\hfill \\ & +2a_0{\sigma }_5{{\varrho }_3}^2+2a_0{\sigma }_3{{\varrho }_1}^2\hfill \\ & {\mathbb{R}\left(\lambda \right)}^1:2{\sigma }_1{{\varrho }_1}^2{a}_0{a}_1+2{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_1{\beta }^2{\left(ln\left(\chi \right)\right)}^2+2a_1{\sigma }_3{{\varrho }_1}^2+2a_1{\sigma }_4{{\varrho }_2}^2+2a_1{\sigma }_5{{\varrho }_3}^2-2a_1{\varrho }_1\varpi \hfill \\ & +4{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_1\gamma {\left(ln\left(\chi \right)\right)}^2\alpha +12{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_2\alpha {\left(ln\left(\chi \right)\right)}^2\beta \hfill \\ & {\mathbb{R}\left(\lambda \right)}^2:16{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_2\alpha {\left(ln\left(\chi \right)\right)}^2\gamma +6{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_1\beta {\left(ln\left(\chi \right)\right)}^2\gamma +8{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_2{\beta }^2{\left(ln\left(\chi \right)\right)}^2\hfill \\ & +2{\sigma }_1{{\varrho }_1}^2{a}_0{a}_2+2a_2{\sigma }_3{{\varrho }_1}^2+2a_2{\sigma }_4{{\varrho }_2}^2+2a_2{\sigma }_5{{\varrho }_3}^2-2a_2{\varrho }_1\varpi +{\sigma }_1{{\varrho }_1}^2{a_1}^2\hfill \\ & {\mathbb{R}\left(\lambda \right)}^3:20{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_2\beta {\left(ln\left(\chi \right)\right)}^2\gamma +4{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_1{\gamma }^2{\left(ln\left(\chi \right)\right)}^2+2{\sigma }_1{{\varrho }_1}^2{a}_1{a}_2\hfill \\ & {\mathbb{R}\left(\lambda \right)}^4:12{\delta }^2{\sigma }_2{{\varrho }_1}^4{a}_2{\gamma }^2{\left(ln\left(\chi \right)\right)}^2+{\sigma }_1{{\varrho }_1}^2{a_2}^2.\hfill \end{array}\end{array}$$

(48)

The algebraic system of Equation (48) is solved with the assistance of maple, and we will obtain the following:

Set 1:

$$\begin{array}{c}\hfill \begin{array}{cc}& [a_0=-\frac{12\alpha {\delta }^2\gamma ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1},a_1=-\frac{12ln{\left(\chi \right)}^2\gamma {\delta }^2{\sigma }_2{\varrho }_1^2\beta }{{\sigma }_1},a_2=-\frac{12ln{\left(\chi \right)}^2{\gamma }^2{\delta }^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\hfill \\ & \varpi =\frac{{\delta }^2{\sigma }_2{\varrho }_1^{4}ln\left(\chi \right)[4\gamma \alpha +{\beta }^2]+{\sigma }_3{\varrho }_1^2+{\sigma }_4{\varrho }_2^2+{\sigma }_5{\varrho }_3^2}{{\varrho }_1}].\hfill \end{array}\end{array}$$

(49)

The general solution of Equation (1) by putting Equation (49) in Equation (46) is

$$\begin{array}{c}\hfill \Omega (x,y,z,t)=-\frac{12\alpha {\delta }^2\gamma ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}-\frac{12ln{\left(\chi \right)}^2\gamma {\delta }^2{\sigma }_2{\varrho }_1^2\beta }{{\sigma }_1}\left[{\mathbb{R}}_i\left(\lambda \right)\right]-\frac{12ln{\left(\chi \right)}^2{\gamma }^2{\delta }^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}{\left[{\mathbb{R}}_i\left(\lambda \right)\right]}^2.\end{array}$$

(50)

Set 2:

$$\begin{array}{c}\hfill \begin{array}{cc}& [a_0=-\frac{2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2(2\alpha \gamma +{\beta }^2)}{{\sigma }_1},a_1=-\frac{12ln{\left(\chi \right)}^2\gamma {\delta }^2{\sigma }_2{\varrho }_1^2\beta }{{\sigma }_1},a_2=-\frac{12ln{\left(\chi \right)}^2{\gamma }^2{\delta }^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1},\hfill \\ & \varpi =\frac{{\delta }^2{\sigma }_2{\varrho }_1^{4}ln\left(\chi \right)[4\gamma \alpha -{\beta }^2]+{\sigma }_3{\varrho }_1^2+{\sigma }_4{\varrho }_2^2+{\sigma }_5{\varrho }_3^2}{{\varrho }_1}].\hfill \end{array}\end{array}$$

(51)

The general solution of Equation (1) by putting Equation (51) in Equation (46) is:

$$\begin{array}{c}\hfill \Omega (x,y,z,t)=-\frac{2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2(2\alpha \gamma +{\beta }^2)}{{\sigma }_1}-\frac{12ln{\left(\chi \right)}^2\gamma {\delta }^2{\sigma }_2{\varrho }_1^2\beta }{{\sigma }_1}\left[{\mathbb{R}}_i\left(\lambda \right)\right]-\frac{12ln{\left(\chi \right)}^2{\gamma }^2{\delta }^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}{\left[{\mathbb{R}}_i\left(\lambda \right)\right]}^2.\end{array}$$

(52)

Set 1: Now, we will derive many different solutions by taking $R_i$ from Equation (7) to Equation (43), respectively.

(Family 1) When ${\beta }^2-4\alpha \gamma <0$, and $\gamma \ne 0,$

The shock solution is obtain as

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_1(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta \left(-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }{tan}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{2}\lambda \right)\right)\hfill \\ & +\gamma {\left(-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }{tan}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{2}\lambda \right)\right)}^2].\hfill \end{array}\end{array}$$

(53)

The singular solution is gain as

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_2(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta \left(-\frac{\beta }{2\gamma }-\frac{\sqrt{-\mathfrak{S}}}{2\gamma }{cot}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{2}\lambda \right)\right)\hfill \\ & +\gamma {\left(-\frac{\beta }{2\gamma }-\frac{\sqrt{-\mathfrak{S}}}{2\gamma }{cot}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{2}\lambda \right)\right)}^2].\hfill \end{array}\end{array}$$

(54)

The mixed complex solitary-shock solution is taken as

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_3(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta (-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }\left({tan}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\right.\hfill \\ & \pm \sqrt{mn}{sec}_{\chi }\left.\left(\sqrt{-\mathfrak{S}}\lambda \right)\right))+\gamma {\left(-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }\left({tan}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\pm \sqrt{mn}{sec}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\right)\right)}^2].\hfill \end{array}\end{array}$$

(55)

The mixed singular solution takes the appearance of

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_4(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta (-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }\left({cot}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\right.\hfill \\ & \pm \sqrt{mn}{csc}_{\chi }\left.\left(\sqrt{-\mathfrak{S}}\lambda \right)\right))+\gamma {\left(-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{2\gamma }\left({cot}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\pm \sqrt{mn}{csc}_{\chi }\left(\sqrt{-\mathfrak{S}}\lambda \right)\right)\right)}^2].\hfill \end{array}\end{array}$$

(56)

The mixed shock singular solution is derived from arrangement of

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_5(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta (-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{4\gamma }\left({tan}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{4}\lambda \right)\right.\hfill \\ & -{cot}_{\chi }\left.\left(\frac{\sqrt{-\mathfrak{S}}}{4}\lambda \right)\right))+\gamma {\left(-\frac{\beta }{2\gamma }+\frac{\sqrt{-\mathfrak{S}}}{4\gamma }\left({tan}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{4}\lambda \right)-{cot}_{\chi }\left(\frac{\sqrt{-\mathfrak{S}}}{4}\lambda \right)\right)\right)}^2].\hfill \end{array}\end{array}$$

(57)

(Family 2): When ${\beta }^2-4\alpha \gamma >0$, and $\gamma \ne 0,$

Then, mixed trigonometric solutions take the following form:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_6(x,y,z,t)=\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta \left(-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{2\gamma }{tanh}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{2}\lambda \right)\right)\hfill \\ & +\gamma {\left(-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{2\gamma }{tanh}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{2}\lambda \right)\right)}^2].\hfill \end{array}\end{array}$$

(58)

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_7(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta \left(-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{2\gamma }{coth}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{2}\lambda \right)\right)\hfill \\ & +\gamma {\left(-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{2\gamma }{coth}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{2}\lambda \right)\right)}^2].\hfill \end{array}\end{array}$$

(59)

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_8(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta (-\frac{\beta }{2\gamma }+\frac{\sqrt{\mathfrak{S}}}{2\gamma }\left(-{tanh}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\right.\hfill \\ & \pm i\sqrt{mn}sech\chi \left.\left(\sqrt{\mathfrak{S}}\lambda \right)\right))+\gamma {\left(-\frac{\beta }{2\gamma }+\frac{\sqrt{\mathfrak{S}}}{2\gamma }\left(-{tanh}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\pm i\sqrt{mn}sech\chi \left(\sqrt{\mathfrak{S}}\lambda \right)\right)\right)}^2].\hfill \end{array}\end{array}$$

(60)

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_9(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta (-\frac{\beta }{2\gamma }+\frac{\sqrt{\mathfrak{S}}}{2\gamma }\left(-{coth}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\right.\hfill \\ & \pm \sqrt{mn}csc{h}_{\chi }\left.\left(\sqrt{\mathfrak{S}}\lambda \right)\right))+\gamma {\left(-\frac{\beta }{2\gamma }+\frac{\sqrt{\mathfrak{S}}}{2\gamma }\left(-{coth}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\pm \sqrt{mn}csc{h}_{\chi }\left(\sqrt{\mathfrak{S}}\lambda \right)\right)\right)}^2].\hfill \end{array}\end{array}$$

(61)

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_{10}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\beta (-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{4\gamma }\left(tan{h}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{4}\lambda \right)\right.\hfill \\ & +{coth}_{\chi }\left.\left(\frac{\sqrt{\mathfrak{S}}}{4}\lambda \right)\right))+\gamma {\left(-\frac{\beta }{2\gamma }-\frac{\sqrt{\mathfrak{S}}}{4\gamma }\left(tan{h}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{4}\lambda \right)+cot{h}_{\chi }\left(\frac{\sqrt{\mathfrak{S}}}{4}\lambda \right)\right)\right)}^2].\hfill \end{array}\end{array}$$

(62)

(Family 3): When $\alpha \gamma >0$ and $\beta =0,$ we obtained results in the expression of the shock solution,

$$\begin{array}{c}\hfill {\Omega }_{11}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[\alpha +\gamma {\left(\sqrt{\frac{\alpha }{\gamma }}ta{n}_{\chi }\left(\sqrt{\alpha \gamma }\lambda \right)\right)}^2\right].\end{array}$$

(63)

We take the singular solution as

$$\begin{array}{c}\hfill {\Omega }_{12}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[\alpha +\gamma {\left(-\sqrt{\frac{\alpha }{\gamma }}co{t}_{\chi }\left(\sqrt{\alpha \gamma }\lambda \right)\right)}^2\right].\end{array}$$

(64)

The dissimilar solutions of the complex combo class is derived as

$$\begin{array}{c}\hfill {\Omega }_{13}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[\alpha +\gamma {\left(\sqrt{\frac{\alpha }{\gamma }}\left({tan}_{\chi }\left(2\sqrt{\alpha \gamma }\lambda \right)\pm \sqrt{mn}se{c}_{\chi }\left(2\sqrt{\alpha \gamma }\lambda \right)\right)\right)}^2\right].\end{array}$$

(65)

$$\begin{array}{c}\hfill {\Omega }_{14}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[\alpha +\gamma {\left(\sqrt{\frac{\alpha }{\gamma }}\left(-co{t}_{\chi }\left(2\sqrt{\alpha \gamma }\lambda \right)\pm \sqrt{mn}{csc}_{\chi }\left(2\sqrt{\alpha \gamma }\lambda \right)\right)\right)}^2\right].\end{array}$$

(66)

$$\begin{array}{c}\hfill {\Omega }_{15}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[\alpha +\gamma {\left(\frac{1}{2}\sqrt{\frac{\alpha }{\gamma }}\left({tan}_{\chi }\left(\frac{\sqrt{\alpha \gamma }}{2}\lambda \right)-{cot}_{\chi }\left(\frac{\sqrt{\alpha \gamma }}{2}\lambda \right)\right)\right)}^2\right].\end{array}$$

(67)

(Family 4): When $\alpha \gamma <0$ and $\beta =0,$ we obtain trigonometric solutions as

$$\begin{array}{c}\hfill {\Omega }_{16}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[\alpha +\gamma {\left(-\sqrt{-\frac{\alpha }{\gamma }}{tanh}_{\chi }\left(\sqrt{-\alpha \gamma }\lambda \right)\right)}^2\right].\end{array}$$

(68)

$$\begin{array}{c}\hfill {\Omega }_{17}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[\alpha +\gamma {\left(-\sqrt{-\frac{\alpha }{\gamma }}{coth}_{\chi }\left(\sqrt{-\alpha \gamma }\lambda \right)\right)}^2\right].\end{array}$$

(69)

The mixed trigonometric solutions are obtained as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_{18}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\gamma (\sqrt{-\frac{\alpha }{\gamma }}\left(-{tanh}_{\chi }\left(2\sqrt{-\alpha \gamma }\lambda \right)\right.\hfill \\ & \pm i\sqrt{mn}sec{h}_{\chi }\left.\left(2\sqrt{-\alpha \gamma }\lambda \right)\right){)}^2].\hfill \end{array}\end{array}$$

(70)

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_{19}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\gamma (\sqrt{-\frac{\alpha }{\gamma }}\left(-{coth}_{\chi }\left(2\sqrt{-\alpha \gamma }\lambda \right)\right.\hfill \\ & \pm \sqrt{mn}csc{h}_{\chi }\left.\left(2\sqrt{-\alpha \gamma }\lambda \right)\right){)}^2].\hfill \end{array}\end{array}$$

(71)

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_{20}(x,y,z,t)=-\frac{12\gamma {\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [\alpha +\gamma (-\frac{1}{2}\sqrt{-\frac{\alpha }{\gamma }}\left({tanh}_{\chi }\left(\frac{\sqrt{-\alpha \gamma }}{2}\lambda \right)\right.\hfill \\ & +cot{h}_{\chi }\left.\left(\frac{\sqrt{-\alpha \gamma }}{2}\lambda \right)\right){)}^2].\hfill \end{array}\end{array}$$

(72)

(Family 5): When $\beta =0$ and $\alpha =\gamma ,$ the periodic and mixed periodic solutions have been derived in the formation of the periodic and mixed-periodic family,

$$\begin{array}{c}\hfill {\Omega }_{21}(x,y,z,t)=-\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left({tan}_{\chi }\left(\alpha \lambda \right)\right)}^2\right].\end{array}$$

(73)

$$\begin{array}{c}\hfill {\Omega }_{22}(x,y,z,t)=-\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left(-{cot}_{\chi }\left(\alpha \lambda \right)\right)}^2\right].\end{array}$$

(74)

$$\begin{array}{c}\hfill {\Omega }_{23}(x,y,z,t)=-\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left({tan}_{\chi }\left(2\alpha \lambda \right)\pm \sqrt{mn}{sec}_{\chi }\left(2\alpha \lambda \right)\right)}^2\right].\end{array}$$

(75)

$$\begin{array}{c}\hfill {\Omega }_{24}(x,y,z,t)=-\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left(-{cot}_{\chi }\left(2\alpha \lambda \right)\pm \sqrt{mn}{csc}_{\chi }\left(2\alpha \lambda \right)\right)}^2\right].\end{array}$$

(76)

$$\begin{array}{c}\hfill {\Omega }_{25}(x,y,z,t)=-\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left(\frac{1}{2}\left({tan}_{\chi }\left(\frac{\alpha }{2}\lambda \right)-{cot}_{\chi }\left(\frac{\alpha }{2}\lambda \right)\right)\right)}^2\right].\end{array}$$

(77)

(Family 6): When $\beta =0$ and $\gamma =-\alpha ,$ single and mixed wave compositions are derived in the following class:

$$\begin{array}{c}\hfill {\Omega }_{26}(x,y,z,t)=\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left(-{tanh}_{\chi }\left(\alpha \lambda \right)\right)}^2\right].\end{array}$$

(78)

$$\begin{array}{c}\hfill {\Omega }_{27}(x,y,z,t)=\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left(-{coth}_{\chi }\left(\alpha \lambda \right)\right)}^2\right].\end{array}$$

(79)

$$\begin{array}{c}\hfill {\Omega }_{28}(x,y,z,t)=\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left(-{tanh}_{\chi }\left(2\alpha \lambda \right)\pm i\sqrt{mn}sec{h}_{\chi }\left(2\alpha \lambda \right)\right)}^2\right].\end{array}$$

(80)

$$\begin{array}{c}\hfill {\Omega }_{29}(x,y,z,t)=\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left(-{cot}_{\chi }\left(2\alpha \lambda \right)\pm \sqrt{mn}csc{h}_{\chi }\left(2\alpha \lambda \right)\right)}^2\right].\end{array}$$

(81)

$$\begin{array}{c}\hfill {\Omega }_{30}(x,y,z,t)=\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[1+{\left(-\frac{1}{2}\left({tanh}_{\chi }\left(\frac{\alpha }{2}\lambda \right)+{coth}_{\chi }\left(\frac{\alpha }{2}\lambda \right)\right)\right)}^2\right].\end{array}$$

(82)

(Family 7): When ${\beta }^2=4\alpha \gamma$,

$$\begin{array}{c}\hfill \begin{array}{cc}& {\Omega }_{31}(x,y,z,t)=-\frac{3{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times [{\beta }^2+4\gamma \beta \left(\frac{-2\alpha (\beta \lambda log[\chi ]+2)}{{\beta }^2\lambda log\left[\chi \right]}\right)\hfill \\ & +4{\gamma }^2{\left(\frac{-2\alpha (\beta \lambda log[\chi ]+2)}{{\beta }^2\lambda log\left[\chi \right]}\right)}^2].\hfill \end{array}\end{array}$$

(83)

(Family 8) and (Family 9) have constant solutions.

(Family 10): When $\beta =\alpha =0$

$$\begin{array}{c}\hfill {\Omega }_{34}(x,y,z,t)=-\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[{\left(\frac{-1}{\gamma \lambda log\left[\chi \right]}\right)}^2\right].\end{array}$$

(84)

(Family 11): When $\alpha =0$ and $\beta \ne 0$, the mixed hyperbolic solution has been in formation of the

$$\begin{array}{c}\hfill {\Omega }_{35}(x,y,z,t)=-\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[{\left(-\frac{m\beta }{\gamma \left({cosh}_{\chi }\left(\beta \lambda \right)-{sinh}_{\chi }\left(\beta \lambda \right)+m\right)}\right)}^2\right].\end{array}$$

(85)

$$\begin{array}{c}\hfill {\Omega }_{36}(x,y,z,t)=-\frac{12{\gamma }^2{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[{\left(-\frac{\beta \left({sinh}_{\chi }\left(\beta \lambda \right)+{cosh}_{\chi }\left(\beta \lambda \right)\right)}{\gamma \left({sinh}_{\chi }\left(\beta \lambda \right)+{cosh}_{\chi }\left(\beta \lambda \right)+n\right)}\right)}^2\right].\end{array}$$

(86)

(Family 12): When $\gamma =pq,(q\ne 0),\beta =p,$ and $\alpha =0$

$$\begin{array}{c}\hfill {\Omega }_{37}(x,y,z,t)=-\frac{12p^{2}q{\delta }^{2}ln{\left(\chi \right)}^2{\sigma }_2{\varrho }_1^2}{{\sigma }_1}\times \left[\left(-\frac{m{\chi }^{p\lambda }}{m-qn{\chi }^{p\lambda }}\right)+q{\left(-\frac{m{\chi }^{p\lambda }}{m-qn{\chi }^{p\lambda }}\right)}^2\right].\end{array}$$

(87)

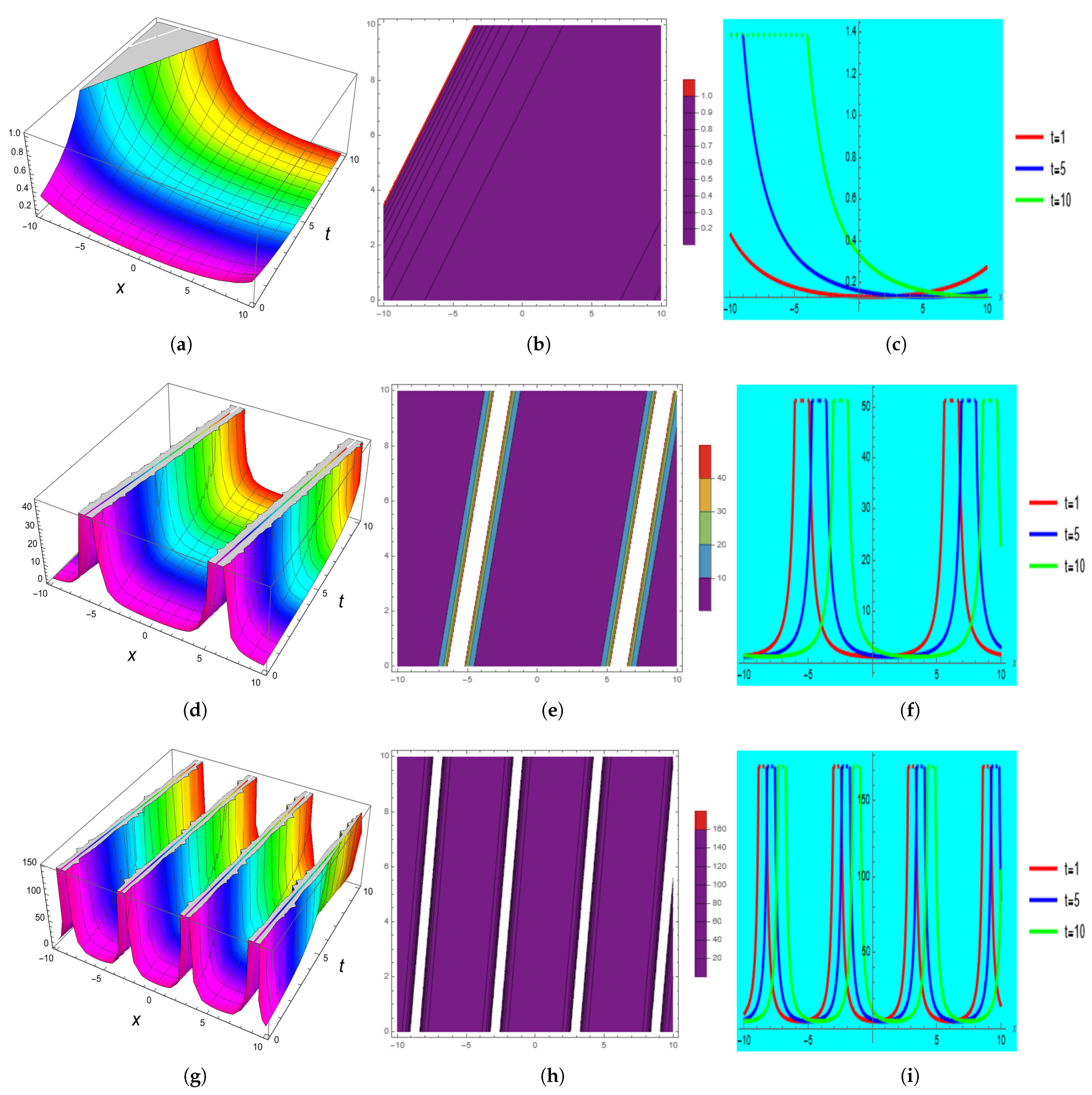
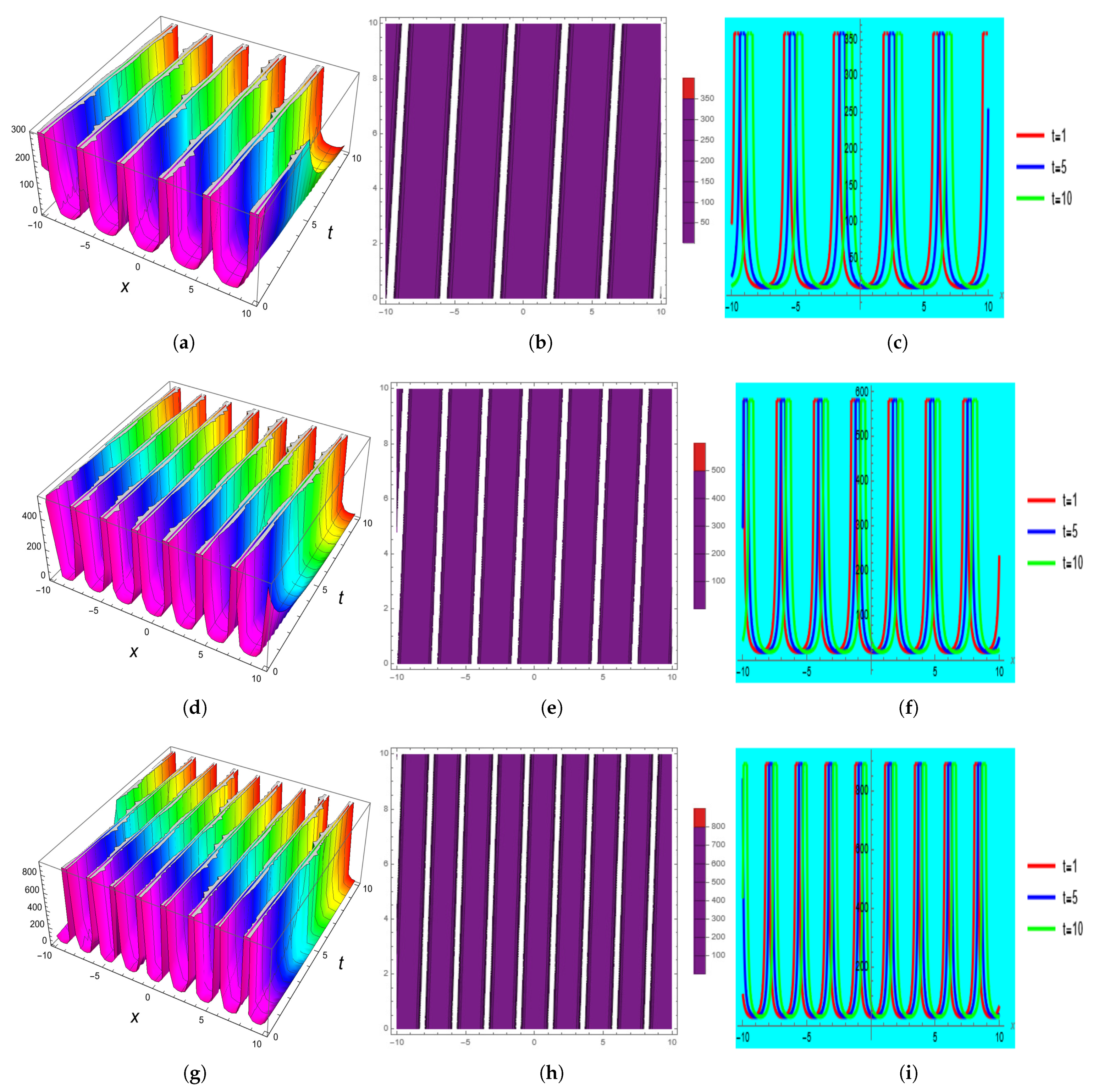
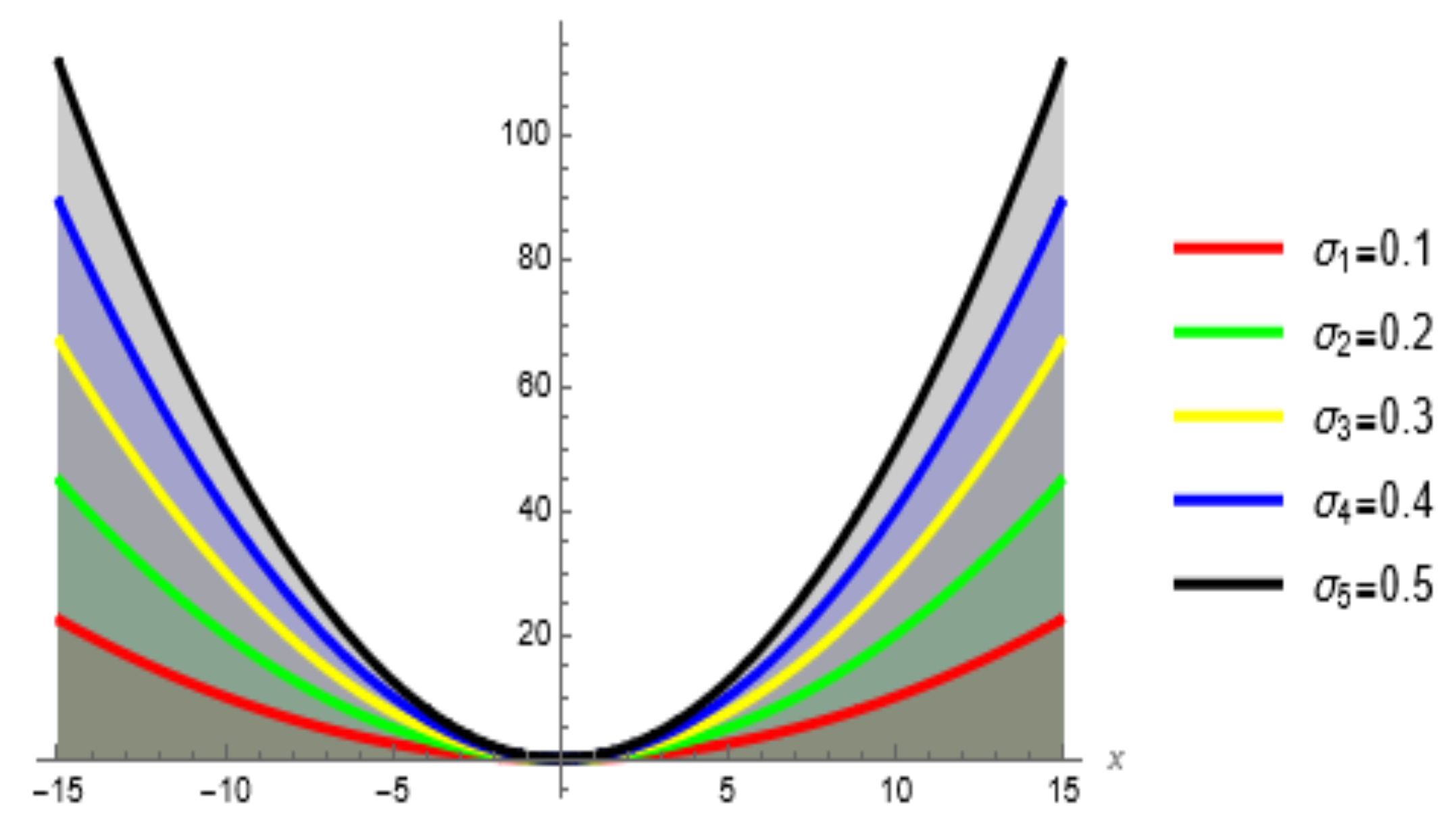
3. Graphical Explanation

In this section, we will discuss the outcomes in graphical form by using distinct values of parameters. It is easy to bring out the complex solitary shock, periodic, singular wave, shock wave, and singular wave. These various kinds of outputs are favorable and have been recently discovered. As we know that waves can transfer energy from one place to another place, the phenomena are explained graphically in this portion. By choosing the different values of the parameter, the diagram of several declared solutions is divided in three dimensions, two dimensions, and their related contours $\gamma =1$, $\delta =0.9$, $\alpha =1$, $\omega =0.1$, ${\sigma }_2=-0.4$, and ${\sigma }_1=0.3$. Therefore, these graphical images of our latest results should help us to examine and accurately predict the results for nonlinear wave problems https://www.academic-agency.com/, accessed on 1 October 2022. Figure 1 and Figure 2 display the shock-wave solution ${\Omega }_{11}(x,y,t)$ at direction cosine ${\varrho }_1=0.1,0.3,0.6,0.9,1.2,1.5$ and speed of soliton $\varpi =0.1$. If we increase the value of the direction cosine, then the amplitude of the shock wave also increases. The amplitude of the wave varies from 1 m to 800 m in the predicted values in this study. Figure 3 and Figure 4 represent the mixed hyperbolic solution wave solution at direction cosine ${\varrho }_1=2,4,6,8,10,12$, and the speed of the soliton is $\varpi =2$. The amplitude of the mixed hyperbolic wave solution ${\Omega }_{35}(x,y,z,t)$ increases as we increase the value of the direction cosine. The amplitude of the wave varies from 0.003 m to 1 m in the predicted values in this study.

Remark 1.

The Figure 1 and Figure 2 is displaying the periodic and periodic singular soliton solution due to variation of direction cosine. Figure 3 and Figure 4 display the anti-kink soliton solution due to variation of direction cosine. Figure 5 and Figure 6 present the 2-dimensional impact of direction of cosine on the obtained solution.

Physical aspects: A wave is an energy-carrying disturbance in a medium that does not include any net particle motion. According to the laws of physics, the amplitude is directly proportional to the energy density. Thus, the obtained solutions predict that the liquid with gas bubbles has more capacity to carry the high amount of energy and also can transfer it more rapidly and smoothly. The results of solution ${\Omega }_{11}(x,y,z,t)$ can be applied to macro-level energy consumption systems and ${\Omega }_{35}(x,y,z,t)$ to micro-level energy consumption systems. The direction cosine controls the capacity and transmission of energy density in liquid with gas bubbles. The use of these results on an industry level is more beneficial to us and improves our work. Physicists and chemists can obtain their required outcomes from these results by using the influence of direction cosine on the wave amplitude. We will discuss this collectively.

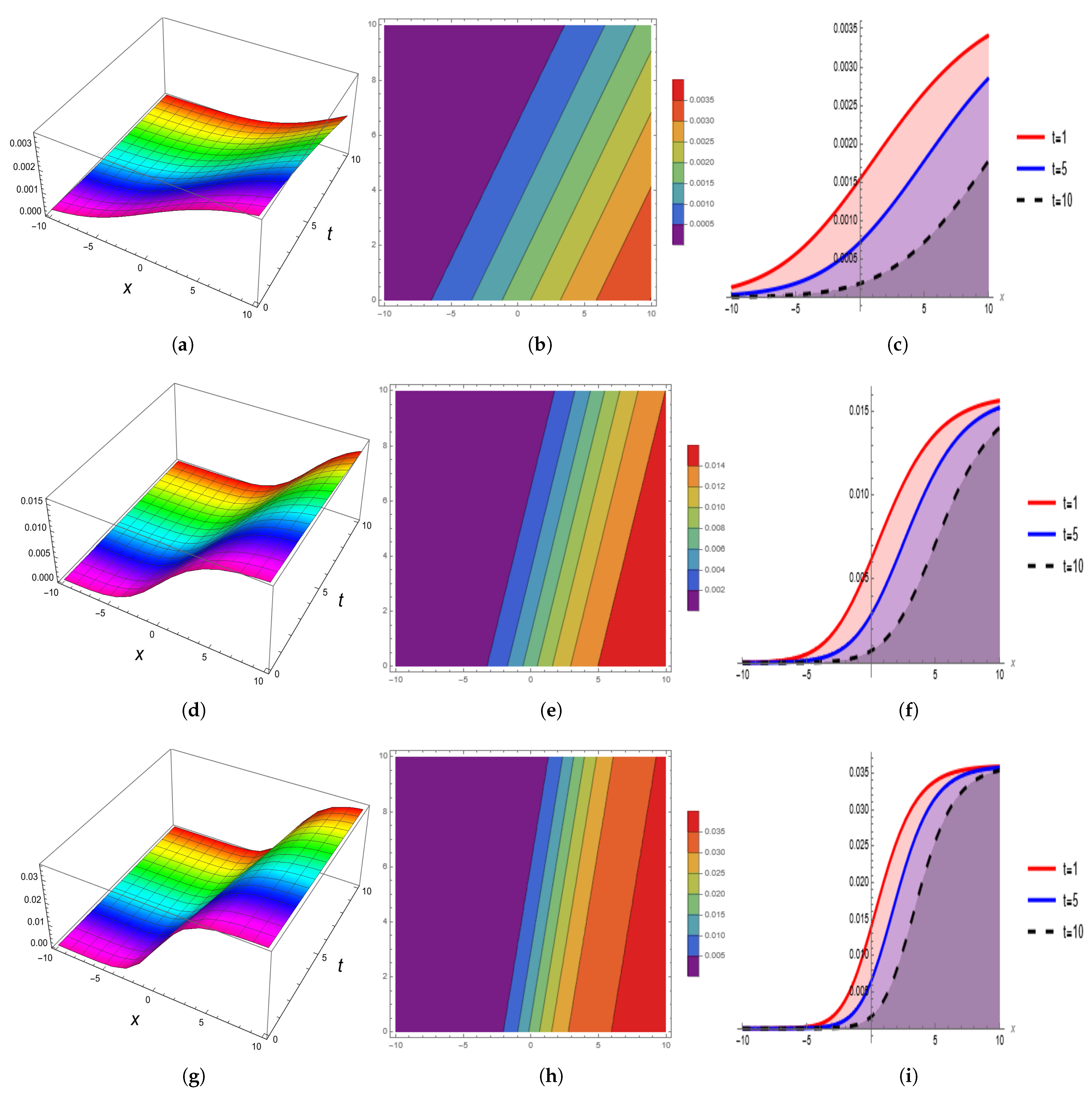
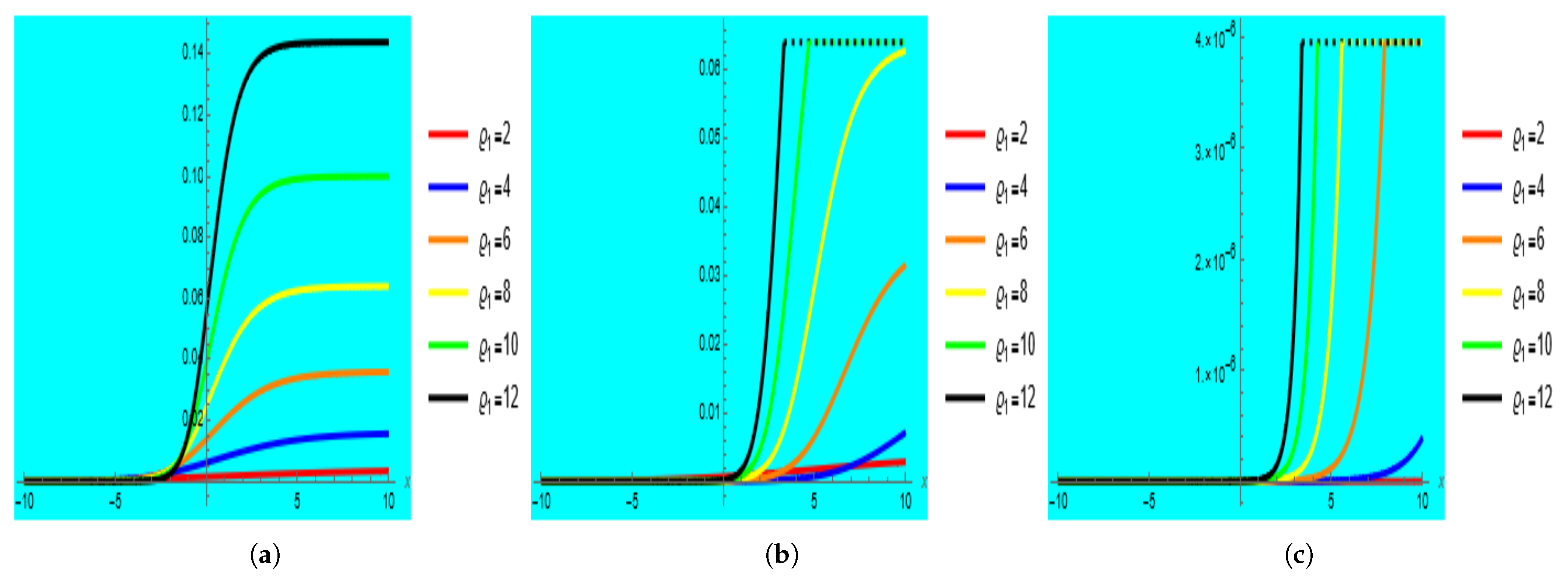
4. Modulation Instability Gain Spectrum

Linear Stability Analysis

In this part of the paper, the goal is to expand the modulation instability (MI) gain of the steady-state solution of the executive system by the decency of the linear stability analysis. The MI can be included in the exponential development of the small perturbation in the stage of optical waves or the amplitude. It is remarkable within nonlinear physics.

Let us suppose a steady-state solution in order to execute a stability analysis

$$\begin{array}{c}\hfill \Omega =\sqrt{p},\end{array}$$

(88)

where p is the initial incidence power(real constant-amplitude). Additionally, the solution (88) converts to the perturbed stationary solutions as

$$\begin{array}{c}\hfill \Omega =\sqrt{P}+\sigma \theta \left(x,y,z,t\right),\end{array}$$

(89)

where $\theta$ is real function of x, y, z, t and the perturbation coefficient parameter is $\sigma <<1$. The perturbed stationary solutions are put into system (1) and obtain the disturbance equation

$$\begin{array}{c}\hfill \begin{array}{cc}& \mu \frac{{\partial }^2}{\partial x\partial t}\theta \left(x,y,z,t\right)+{\sigma }_1\left(\mu \left(\frac{{\partial }^2}{\partial x^2}\theta \left(x,y,z,t\right)\right)\sqrt{P}+{\mu }^2\left(\frac{{\partial }^2}{\partial x^2}\theta \left(x,y,z,t\right)\right)\theta \left(x,y,z,t\right)\right.\hfill \\ & \left.+{\mu }^2{\left(\frac{\partial }{\partial x}\theta \left(x,y,z,t\right)\right)}^2\right)+{\sigma }_2\left(\mu \left(\frac{{\partial }^4}{\partial x^4}\theta \left(x,y,z,t\right)\right)\sqrt{P}+{\mu }^2\left(\frac{{\partial }^4}{\partial x^4}\theta \left(x,y,z,t\right)\right)\theta \left(x,y,z,t\right)\right.\hfill \\ & \left.+{\mu }^2\left(\frac{{\partial }^3}{\partial x^3}\theta \left(x,y,z,t\right)\right)\frac{\partial }{\partial x}\theta \left(x,y,z,t\right)\right)+{\sigma }_3\mu \frac{{\partial }^2}{\partial x^2}\theta \left(x,y,z,t\right)+{\sigma }_4\left(\mu \left(\frac{{\partial }^2}{\partial y^2}\theta \left(x,y,z,t\right)\right)\sqrt{P}\right.\hfill \\ & \left.+{\mu }^2\left(\frac{{\partial }^2}{\partial y^2}\theta \left(x,y,z,t\right)\right)\theta \left(x,y,z,t\right)\right)+{\sigma }_5\mu \frac{{\partial }^2}{\partial z^2}\theta \left(x,y,z,t\right)=0.\hfill \end{array}\end{array}$$

(90)

After linearization, the disturbance Equation (90) can be write down as

$$\begin{array}{c}\hfill \begin{array}{cc}& \mu \frac{{\partial }^2}{\partial x\partial t}\theta \left(x,y,z,t\right)+{\sigma }_1\left(\mu \left(\frac{{\partial }^2}{\partial x^2}\theta \left(x,y,z,t\right)\right)\right)\sqrt{P}+{\sigma }_2\left(\mu \left(\frac{{\partial }^4}{\partial x^4}\theta \left(x,y,z,t\right)\right)\sqrt{P}\right)+\hfill \\ & {\sigma }_3\mu \frac{{\partial }^2}{\partial x^2}\theta \left(x,y,z,t\right)+{\sigma }_4\left(\mu \left(\frac{{\partial }^2}{\partial y^2}\theta \left(x,y,z,t\right)\right)\sqrt{P}\right)+{\sigma }_5\mu \frac{{\partial }^2}{\partial z^2}\theta \left(x,y,z,t\right)=0.\hfill \end{array}\end{array}$$

(91)

Now, we have to organize the $\theta (x,y,t)$ such that

$$\begin{array}{c}\hfill \theta (x,y,z,t)=\Theta e^{\iota (ax+by+cz-dt)}+\Xi e^{-\iota (ax+by+cz-dt)}.\end{array}$$

(92)

The function (92) plugs into (91), and we obtain the system of the homogenous equation

$$\begin{array}{c}\hfill \begin{array}{cc}& \mu \Theta Md{\left(ln\left(e\right)\right)}^{2}a+\mu \Xi Nd{\left(ln\left(e\right)\right)}^{2}a-{\sigma }_1\mu \sqrt{P}\Theta M{a}^2{\left(ln\left(e\right)\right)}^2-\hfill \\ & {\sigma }_1\mu \sqrt{P}\Xi N{a}^2{\left(ln\left(e\right)\right)}^2+{\sigma }_2\mu \sqrt{P}\Theta M{a}^4{\left(ln\left(e\right)\right)}^4+{\sigma }_2\mu \sqrt{P}\Xi N{a}^4{\left(ln\left(e\right)\right)}^4-\hfill \\ & {\sigma }_3\mu \Theta M{a}^2{\left(ln\left(e\right)\right)}^2-{\sigma }_3\mu \Xi N{a}^2{\left(ln\left(e\right)\right)}^2-{\sigma }_3\mu \Theta M{b}^2{\left(ln\left(e\right)\right)}^2-{\sigma }_3\mu \Xi N{b}^2{\left(ln\left(e\right)\right)}^2\hfill \\ & -{\sigma }_4\mu \sqrt{P}\Theta M{b}^2{\left(ln\left(e\right)\right)}^2-{\sigma }_4\mu \sqrt{P}\Xi N{b}^2{\left(ln\left(e\right)\right)}^2=0.\hfill \end{array}\end{array}$$

(93)

$$\begin{array}{c}\hfill \begin{array}{cc}& \mu \Theta d{\left(ln\left(e\right)\right)}^{2}a-{\sigma }_1\mu \Theta a^2{\left(ln\left(e\right)\right)}^2\sqrt{P}+{\sigma }_2\mu \Theta a^4{\left(ln\left(e\right)\right)}^4\sqrt{P}\hfill \\ & -{\sigma }_3\mu \Theta a^2{\left(ln\left(e\right)\right)}^2-{\sigma }_3\mu \Theta b^2{\left(ln\left(e\right)\right)}^2-{\sigma }_4\mu \Theta b^2{\left(ln\left(e\right)\right)}^2\sqrt{P}=0.\hfill \\ & \mu \Xi d{\left(ln\left(e\right)\right)}^{2}a-{\sigma }_1\mu \Xi a^2{\left(ln\left(e\right)\right)}^2\sqrt{P}+{\sigma }_2\mu \Xi a^4{\left(ln\left(e\right)\right)}^4\sqrt{P}-\hfill \\ & {\sigma }_3\mu \Xi a^2{\left(ln\left(e\right)\right)}^2-{\sigma }_3\mu \Xi b^2{\left(ln\left(e\right)\right)}^2-{\sigma }_4\mu \Xi b^2{\left(ln\left(e\right)\right)}^2\sqrt{P}=0.\hfill \end{array}\end{array}$$

(94)

The coefficient matrix of system (94) can be written as follows for $\Theta$ and $\Xi$:

$$\begin{array}{c}\hfill \left[\begin{array}{cc}A& 0\\ 0& B\end{array}\right]\left[\begin{array}{c}\Theta \\ \Xi \end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right],\end{array}$$

(95)

where

$$\begin{array}{c}\hfill \begin{array}{cc}& A=\mu d{\left(ln\left(e\right)\right)}^{2}a-{\sigma }_1\mu a^2{\left(ln\left(e\right)\right)}^2\sqrt{P}+{\sigma }_2\mu a^4{\left(ln\left(e\right)\right)}^4\sqrt{P}-{\sigma }_3\mu a^2{\left(ln\left(e\right)\right)}^4\hfill \\ & -{\sigma }_3\mu b^2{\left(ln\left(e\right)\right)}^2-{\sigma }_4\mu b^2{\left(ln\left(e\right)\right)}^2\sqrt{P},\hfill \\ & B=\mu d{\left(ln\left(e\right)\right)}^{2}a-{\sigma }_1\mu a^2{\left(ln\left(e\right)\right)}^2\sqrt{P}+{\sigma }_2\mu a^4{\left(ln\left(e\right)\right)}^4\sqrt{P}-2{\sigma }_3\mu a^2{\left(ln\left(e\right)\right)}^2\hfill \\ & -{\sigma }_3\mu b^2{\left(ln\left(e\right)\right)}^2-{\sigma }_4\mu b^2{\left(ln\left(e\right)\right)}^2\sqrt{P}.\hfill \end{array}\end{array}$$

(96)

The non-trivial solutions exist for the coefficient matrix (95) when the determinant vanishes. The dispersion relation is derived by modify the determinant of the above coefficient matrix

$$\begin{array}{c}\hfill \begin{array}{cc}& -2{\mu }^{2}d{\left(ln\left(e\right)\right)}^{4}a{\sigma }_4{b}^2\sqrt{P}+2{\sigma }_1{\mu }^2{a}^2{\left(ln\left(e\right)\right)}^4\sqrt{P}{\sigma }_3{b}^2\hfill \\ & +2{\sigma }_1{\mu }^2{a}^2{\left(ln\left(e\right)\right)}^{4}P{\sigma }_4{b}^2-2{\sigma }_2{\mu }^2{a}^4{\left(ln\left(e\right)\right)}^6\sqrt{P}{\sigma }_3{b}^2\hfill \\ & -2{\sigma }_2{\mu }^2{a}^4{\left(ln\left(e\right)\right)}^{6}P{\sigma }_4{b}^2+2{\sigma }_4{\mu }^2{b}^2{\left(ln\left(e\right)\right)}^4\sqrt{P}{\sigma }_3{a}^2\hfill \\ & +2{\sigma }_3{\mu }^2{b}^4{\left(ln\left(e\right)\right)}^4{\sigma }_4\sqrt{P}+{{\sigma }_1}^2{\mu }^2{a}^4{\left(ln\left(e\right)\right)}^{4}P+{{\sigma }_2}^2{\mu }^2{a}^8{\left(ln\left(e\right)\right)}^{8}P\hfill \\ & -{\sigma }_3{\mu }^2{a}^3{\left(ln\left(e\right)\right)}^{6}d+{{\sigma }_3}^2{\mu }^2{a}^2{\left(ln\left(e\right)\right)}^6{b}^2+{{\sigma }_4}^2{\mu }^2{b}^4{\left(ln\left(e\right)\right)}^{4}P\hfill \\ & +{\sigma }_3{\mu }^2{a}^4{\left(ln\left(e\right)\right)}^6{\sigma }_1\sqrt{P}-{\sigma }_3{\mu }^2{a}^6{\left(ln\left(e\right)\right)}^8{\sigma }_2\sqrt{P}-2{\mu }^{2}d{\left(ln\left(e\right)\right)}^4{a}^3{\sigma }_1\sqrt{P}\hfill \\ & +2{\mu }^{2}d{\left(ln\left(e\right)\right)}^6{a}^5{\sigma }_2\sqrt{P}-2{\mu }^{2}d{\left(ln\left(e\right)\right)}^{4}a{\sigma }_3{b}^2-2{\sigma }_1{\mu }^2{a}^6{\left(ln\left(e\right)\right)}^{6}P{\sigma }_2\hfill \\ & +2{\sigma }_1{\mu }^2{a}^4{\left(ln\left(e\right)\right)}^4\sqrt{P}{\sigma }_3-2{\sigma }_2{\mu }^2{a}^6{\left(ln\left(e\right)\right)}^6\sqrt{P}{\sigma }_3\hfill \\ & +{\mu }^2{d}^2{\left(ln\left(e\right)\right)}^4{a}^2+{{\sigma }_3}^2{\mu }^2{b}^4{\left(ln\left(e\right)\right)}^4+2{{\sigma }_3}^2{\mu }^2{a}^4{\left(ln\left(e\right)\right)}^6\hfill \\ & -2{\mu }^{2}d{\left(ln\left(e\right)\right)}^4{a}^3{\sigma }_3+2{{\sigma }_3}^2{\mu }^2{b}^2{\left(ln\left(e\right)\right)}^4{a}^2+{\sigma }_3{\mu }^2{a}^2{\left(ln\left(e\right)\right)}^6{\sigma }_4{b}^2\sqrt{P}=0.\hfill \end{array},\end{array}$$

(97)

It is well known that the generalized nonlinear wave equation in (3 + 1) dimensions with gas bubbles is modulation-stable for any wave number a if and only if four roots d (97) are all positive real numbers. However, it is not a simple task to obtain the roots of (97) since we have to employ the efficient analytical formula and the related phenomena for the roots of a fourth-order polynomial. The results of a dispersion relation (97) are developed as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill d=\frac{1}{a}\left(-{\left(ln\left(e\right)\right)}^2\sqrt{P}{a}^4{\sigma }_2+1/2{\left(ln\left(e\right)\right)}^2{a}^2{\sigma }_3+\sqrt{P}{a}^2{\sigma }_1+\sqrt{P}{b}^2{\sigma }_4+a^2{\sigma }_3+b^2{\sigma }_3-1/2\sqrt{\Psi }\right),\end{array}\end{array}$$

(98)

where

$$\begin{array}{c}\hfill \Psi =ln{\left(e\right)}^4{a}^4{{\sigma }_3}^2-4ln{\left(e\right)}^2{a}^4{{\sigma }_3}^2+4a^4{{\sigma }_3}^2.\end{array}$$

(99)

Thus, one can notice that the modulation instability of the generalized nonlinear wave equation in (3 + 1) dimensions with gas bubbles occurs when either

$$\sqrt{\Psi }<0,$$

or

$$\frac{1}{a}(-{\left(ln\left(e\right)\right)}^2\sqrt{P}{a}^4{\sigma }_2+1/2{\left(ln\left(e\right)\right)}^2{a}^2{\sigma }_3+\sqrt{P}{a}^2{\sigma }_1+\sqrt{P}{b}^2{\sigma }_4+a^2{\sigma }_3+b^2{\sigma }_3-1/2\sqrt{\Psi }<0.$$

Furthermore, the modulation instability gain spectrum MI gain can be deliberated and modified by the maximum absolute value for the imaginary part of the wave number and defined as

$$\begin{array}{c}\hfill \begin{array}{cc}& MIgain=a\Im \left(d\right)=\sqrt{ln{\left(e\right)}^4{a}^4{{\sigma }_3}^2-4ln{\left(e\right)}^2{a}^4{{\sigma }_3}^2+4a^4{{\sigma }_3}^2}.\hfill \end{array}\end{array}$$

(100)

The modulational gain spectrum Figure 7 ensured the stability of the considered model by satisfying the aforementioned conditions.

5. Conclusions

This study examined the generalized (3 + 1) dimensional nonlinear liquid wave equation with gas bubbles in a sort of solitonic theory. The new extended algebraic equation method is used to discuss the explicit solitonic structures and modulational instability gain spectrum developed. As a result,

• The used method generated the plane solution, the mixed-hyperbolic solution, the periodic and mixed-periodic solutions, the mixed-trigonometric solution, the trigonometric solution, the shock solution, the mixed-shock singular solution, the mixed singular solution, the complex solitary shock solution, the singular solution, and shock-wave solutions.
• It is noticed that the energy-carrying capacity of liquid with gas bubbles and its propagation can be increased.
• The modulational instability gain spectrum is developed and ensures the stability of the proposed model.
• The researchers and experts can apply these results in the different fields of modern sciences at macro and micro levels where needed. These results are also beneficial for the industry level.