Generalized Fuzzy Linguistic Bicubic B-Spline Surface Model for Uncertain Fuzzy Linguistic Data
Abstract
1. Introduction
2. Introduction to B-Spline Function
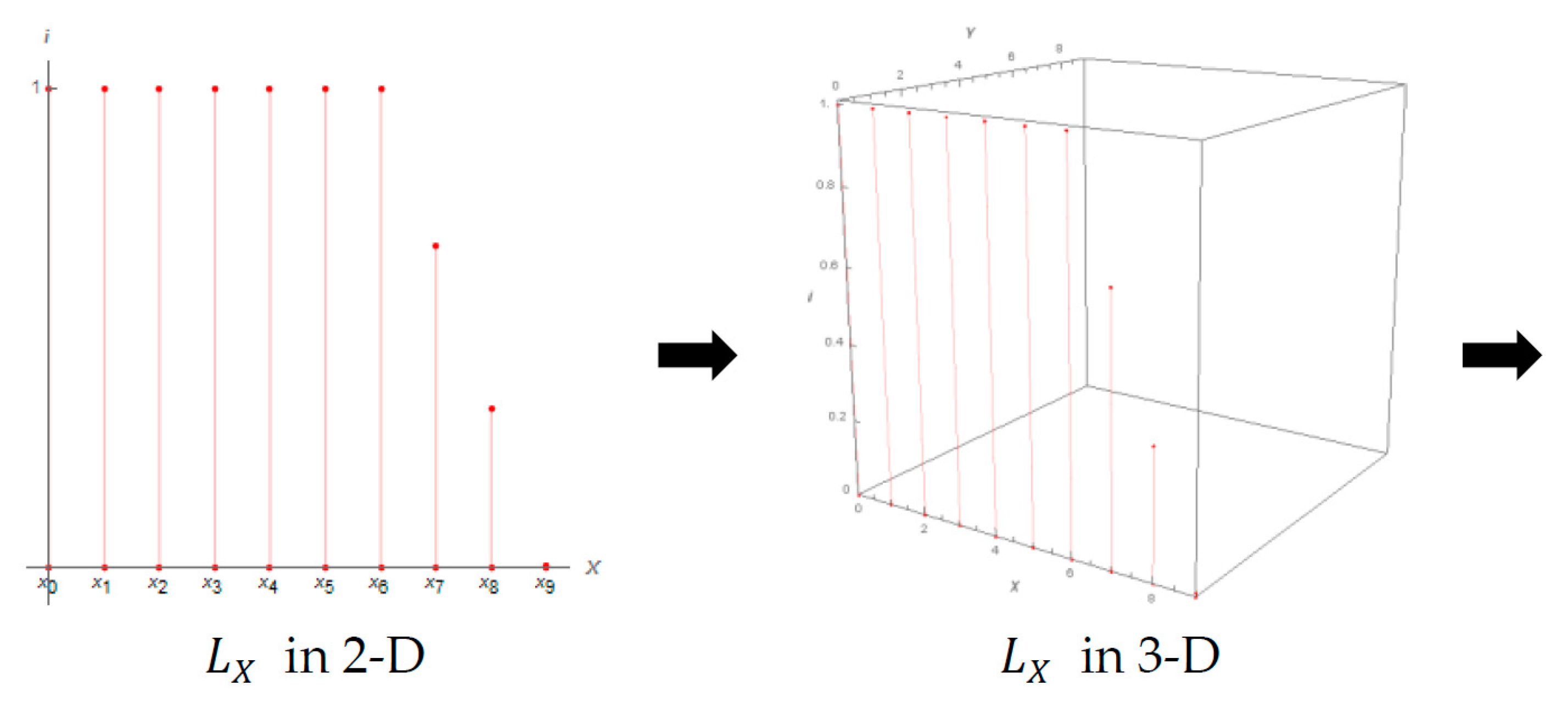
3. Fuzzy Set Approach to B-Spline
4. Literature Review
5. Preliminaries
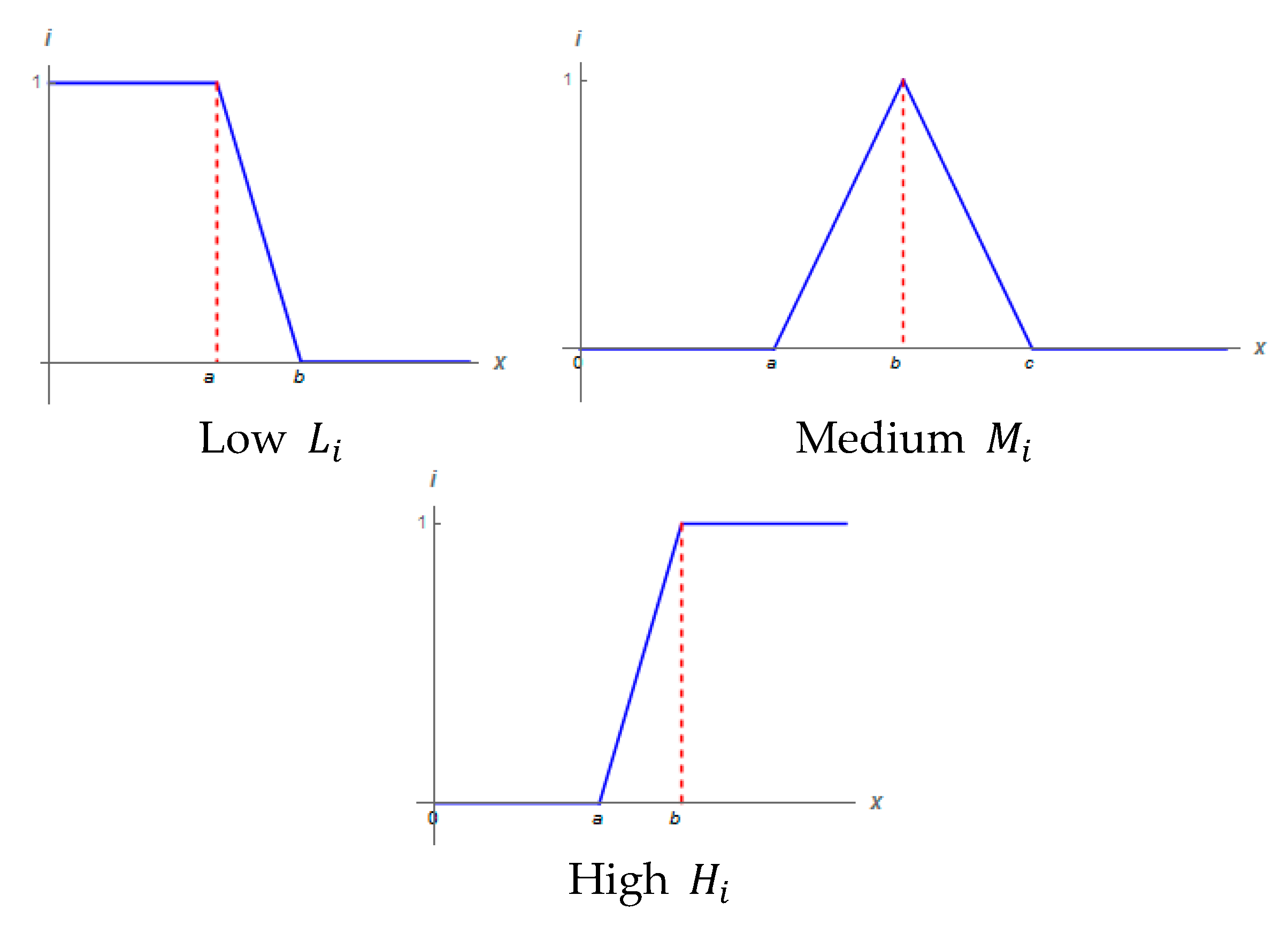
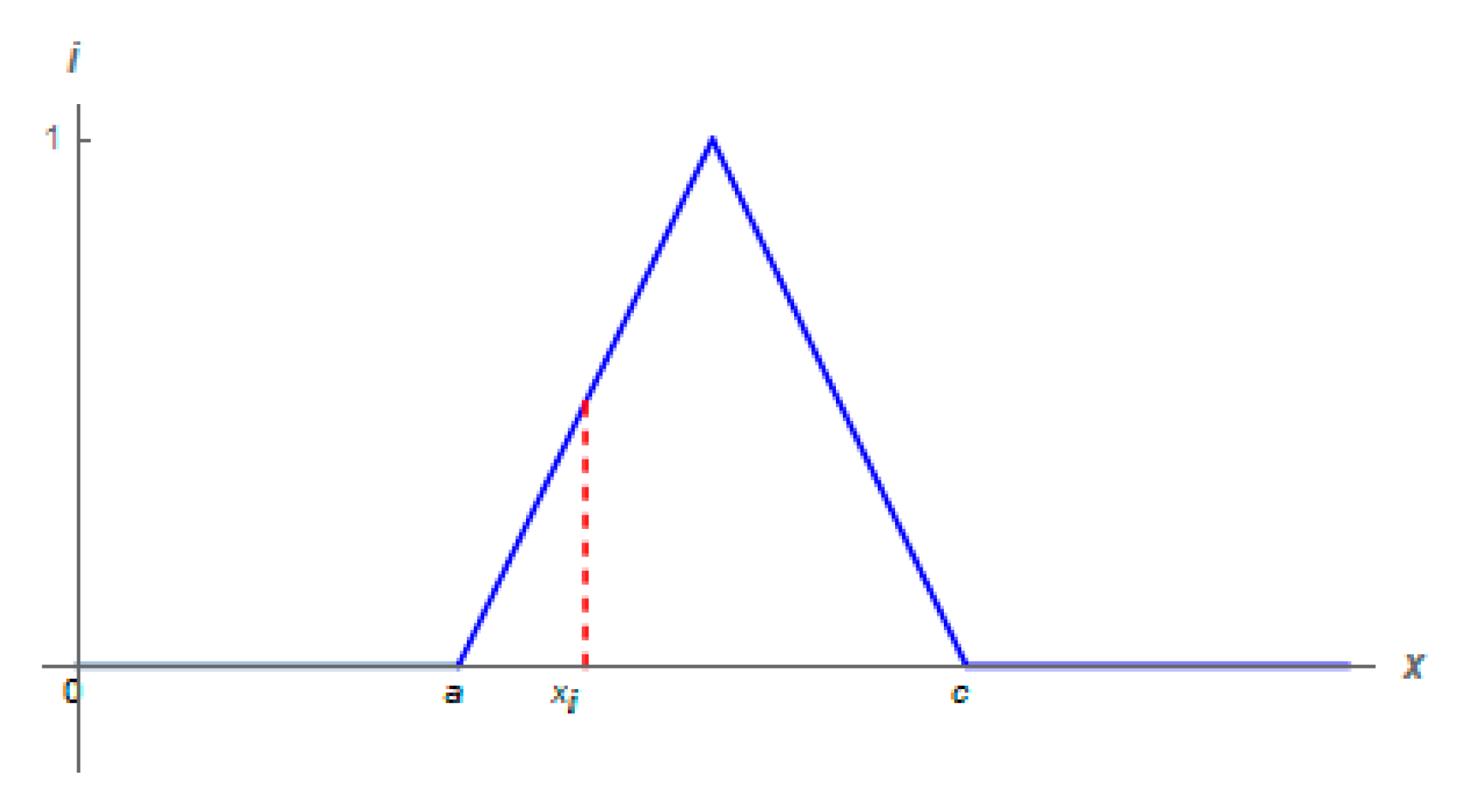
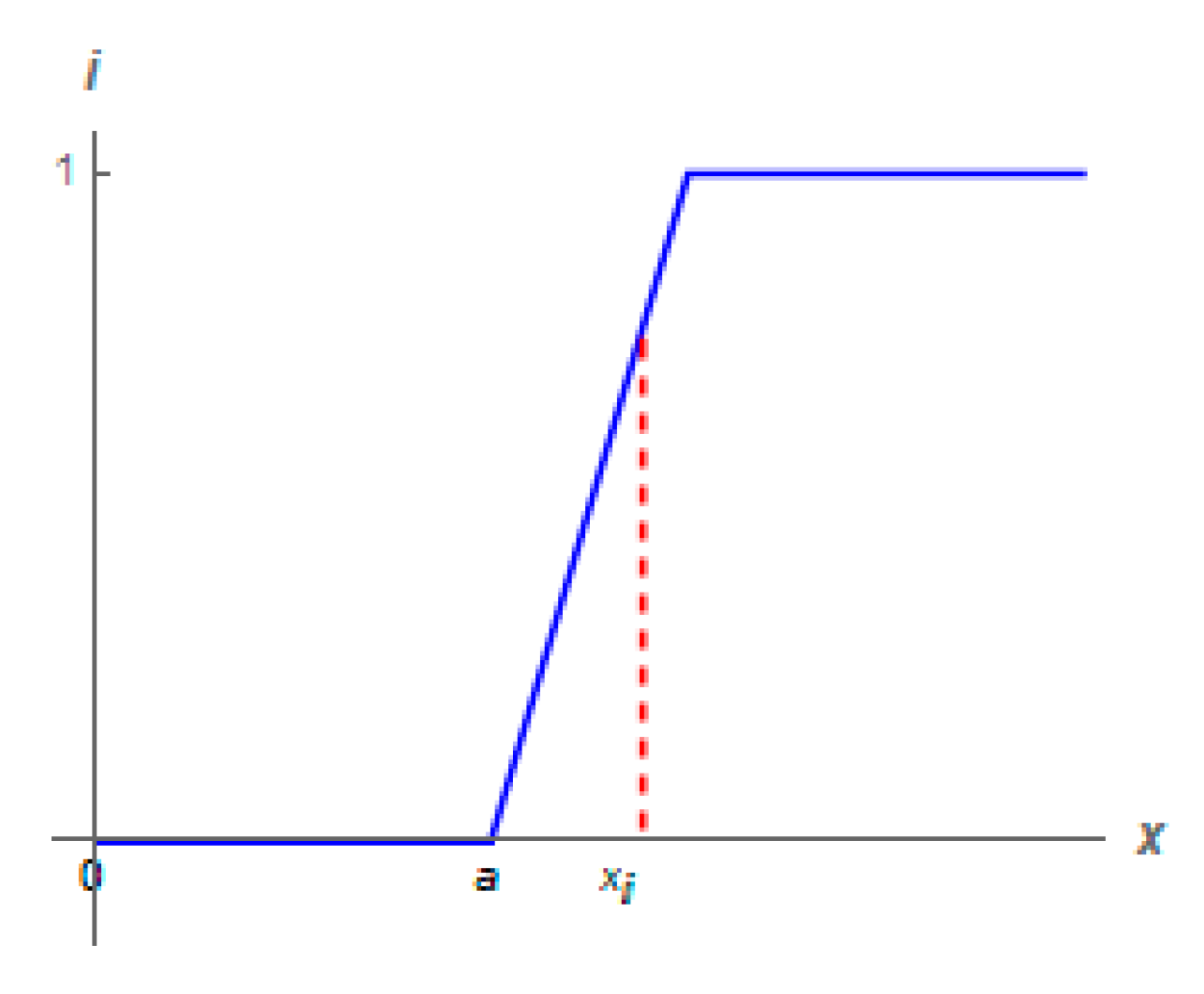
6. Linguistic Variables
7. Fuzzy Linguistic Point Relation
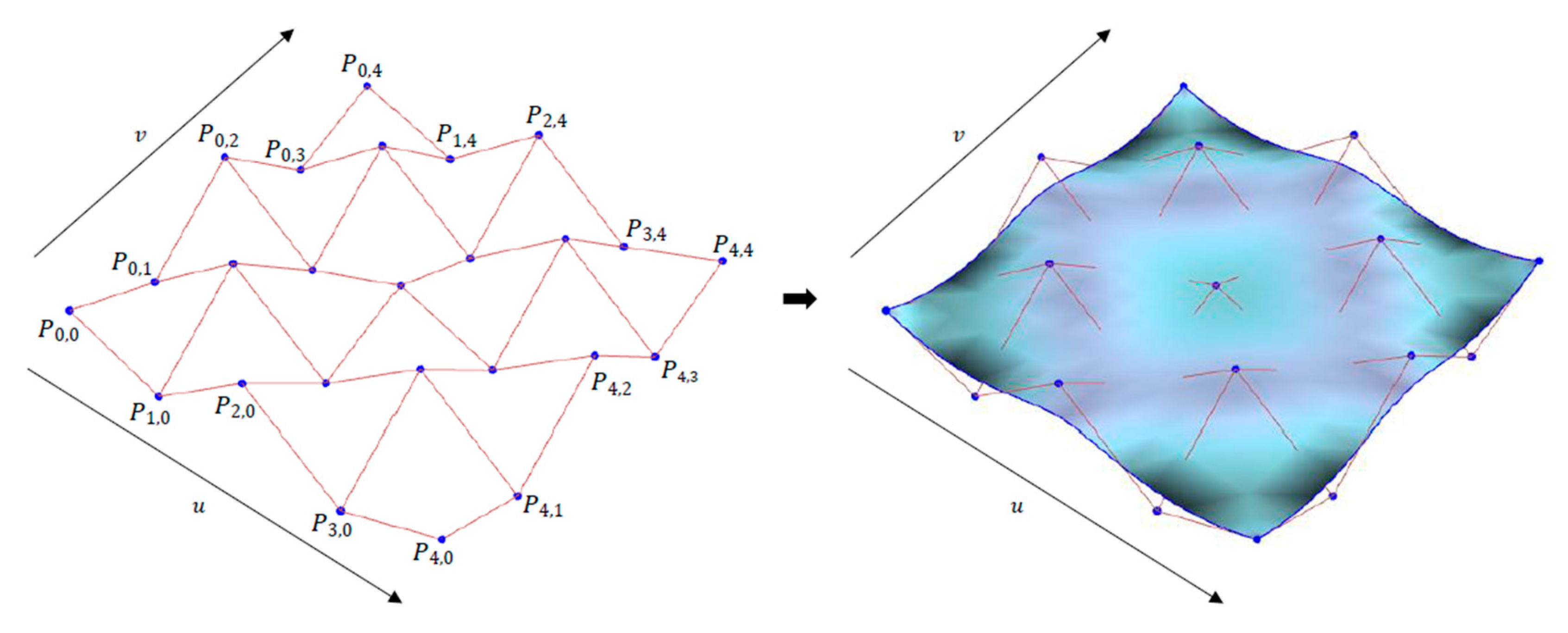
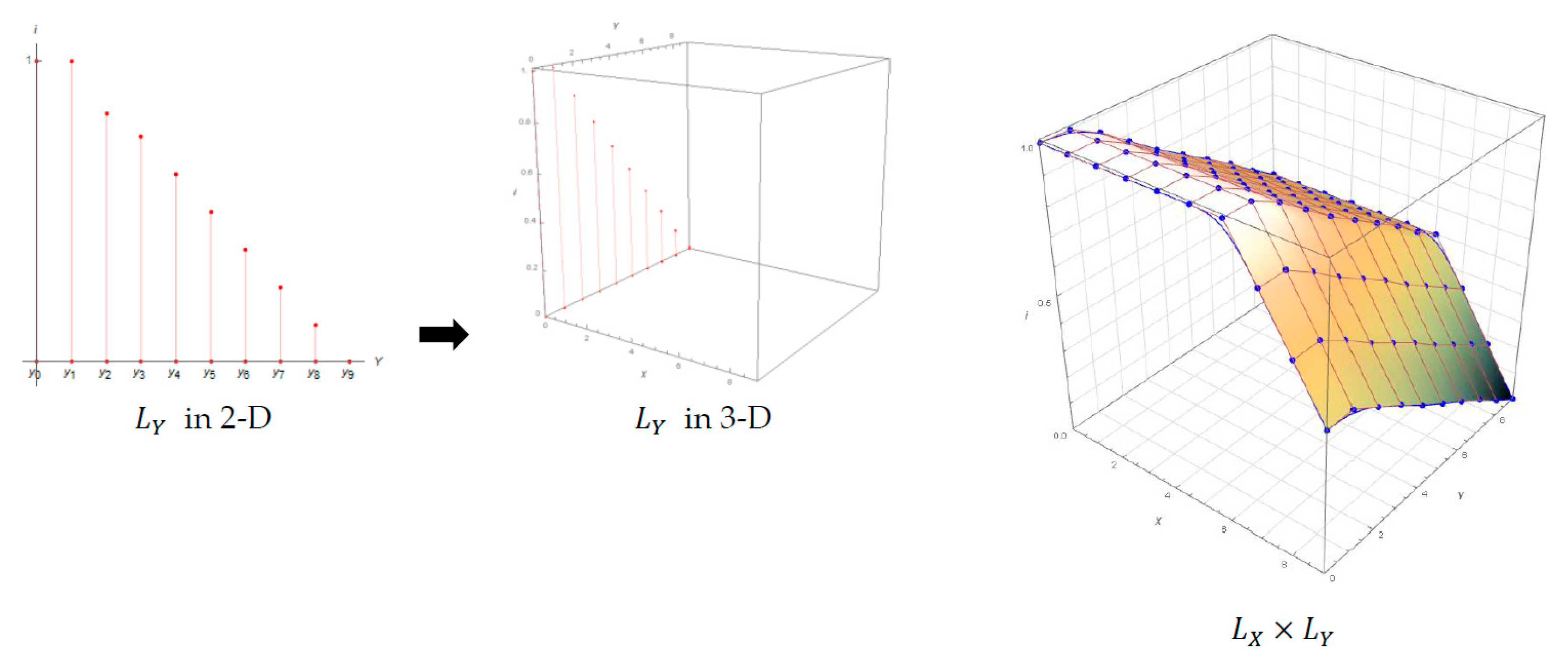
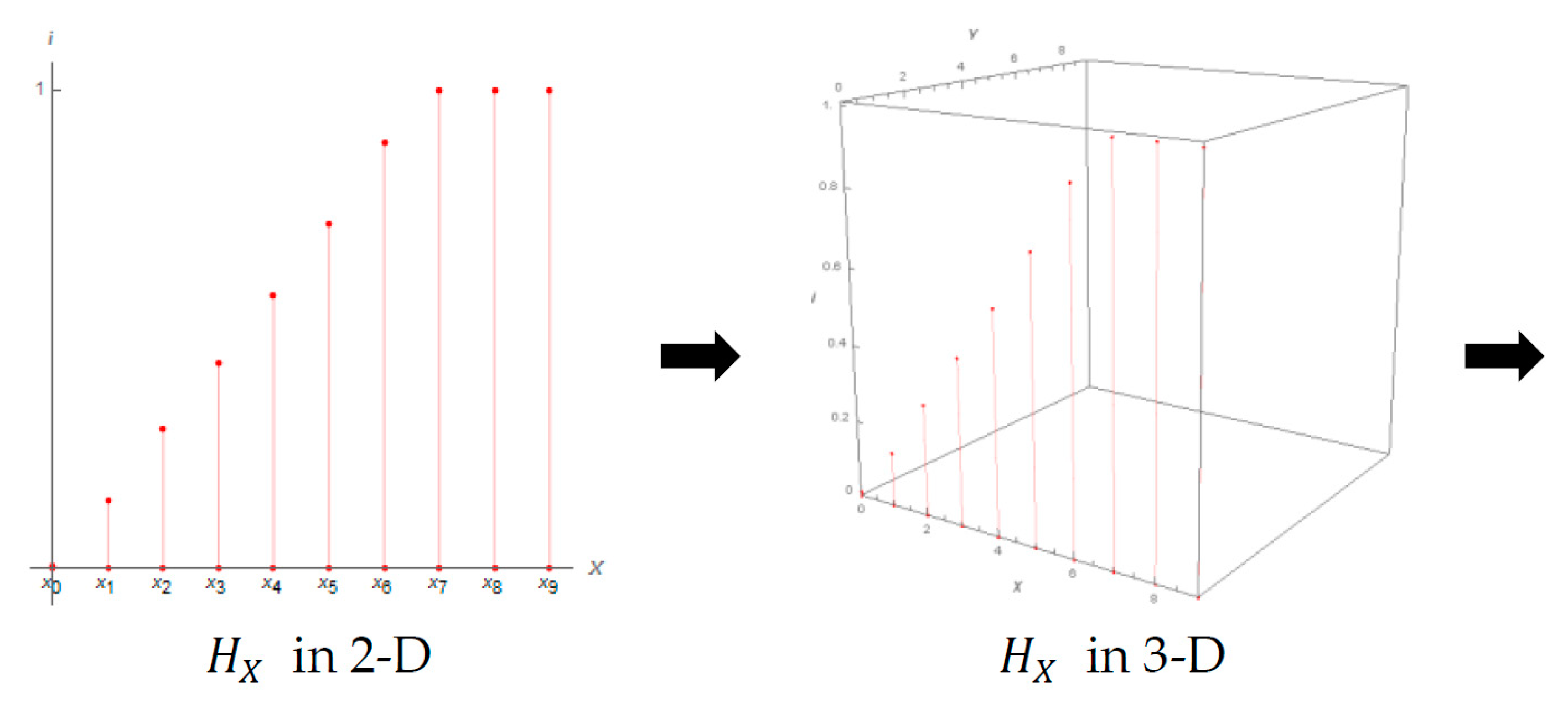
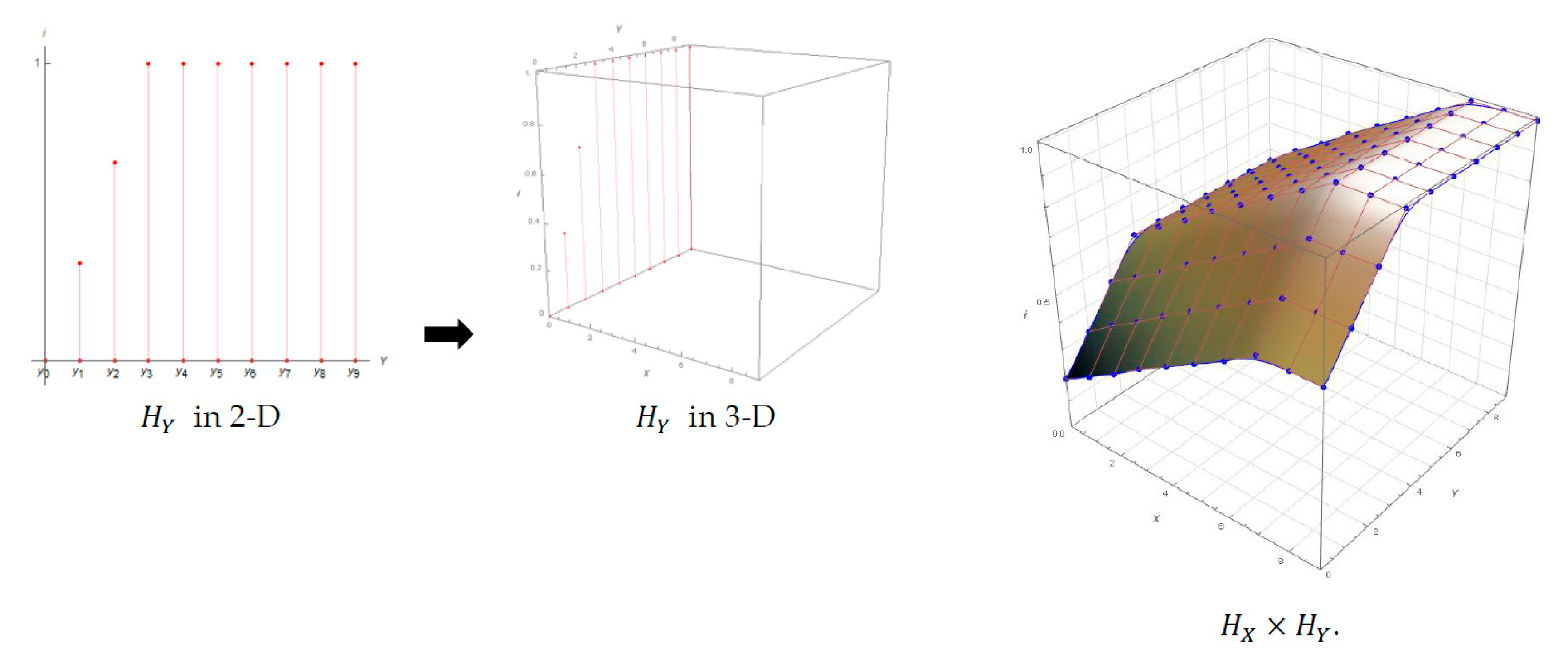
8. Fuzzy Linguistic Bicubic B-Spline Surface Model
| Algorithm 1 Fuzzy linguistic bicubic B-spline surface modeling |
| Step 1: Define all fuzzy data points. Let . |
| Step 2: Define all fuzzy point relations where . |
| Step 3: Define all fuzzy control points where
|
| Step 4: Define all linguistic functions to form fuzzy linguistic control points. |
| Step 5: Develop fuzzy linguistic bicubic B-spline surface model using fuzzy linguistic control points blended with B-spline basis function. |
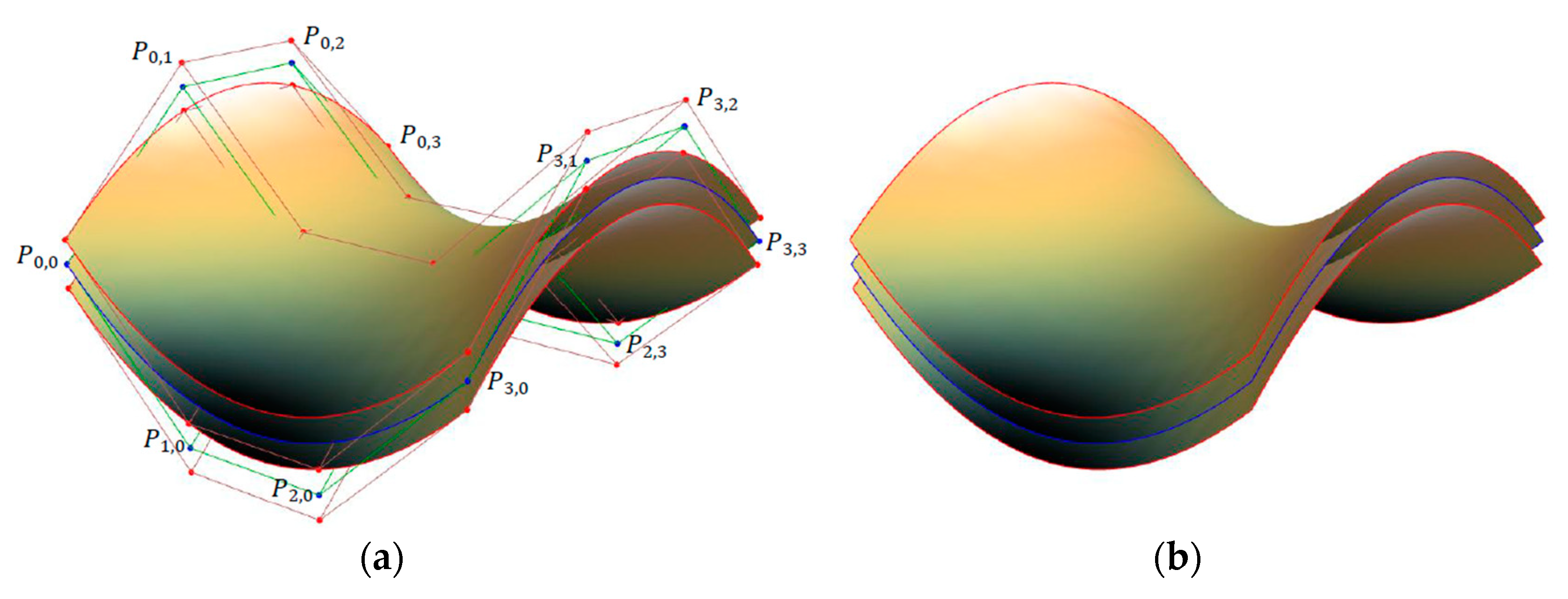
9. Numerical Example and Visualization
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Husain, M.S.; Wahab, A.F.; Gobithaasan, R.U. Generalizations of fuzzy linguistic control points in geometric design. AIP Conf. Proc. 2014, 1605, 244. [Google Scholar]
- Husain, M.S.; Wahab, A.F.; Gobithasaan, R.U. Fuzzy linguistic in geometric modeling. Malays. J. Fundam. Appl. Sci. 2015, 11, 36–41. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- McShane, M.; Nirenburg, S. Linguistics for the Age of AI; MIT Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Li, D.; Du, Y. Artificial Intelligence with Uncertainty; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zakaria, R. Pemodelan Interpolasi Splin-B Kabur Jenis-2 Teritlak Bagi Masalah Ketakpastian Kompleks. Ph.D. Thesis, Universiti Malaysia Terengganu, Terengganu, Malaysia, 2013. [Google Scholar]
- Wahab, A.F.; Husain, M.S. A new types of spline modeling using fuzzy linguistic approach. AIP Conf. Proc. 2016, 1750, 020020. [Google Scholar]
- Schoenberg, I.J. Contributions to the problem of approximation of equidistant data by analytic functions, Part B. On the problem of osculatory interpolation. A second class of analytic approximation formulae. Q. Appl. Math. 1946, 4, 112–141. [Google Scholar] [CrossRef]
- De Boor, C. On calculating with B-splines. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef]
- Dempski, K. Focus on Curves and Surfaces (Focus on Game Development); Course Technology Press: Boston, MA, USA, 2002. [Google Scholar]
- Farin, G.E. Curves and Surfaces for CAGD: A Practical Guide; Morgan Kaufmann: Berkeley, CA, USA, 2002. [Google Scholar]
- Salomon, D. Curves and Surfaces for Computer Graphics; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS Book, 2nd ed.; Springer Science & Business Media: New York, NY, USA, 1997. [Google Scholar]
- Wahab, A.F.; Ali, J.M.; Majid, A.A.; Tap, A.O.M. Fuzzy set in geometric modeling. In Proceedings of the International Conference on Computer Graphics, Imaging and Visualization, 2004 (CGIV 2004), Penang, Malaysia, 2 July 2004; pp. 227–232. [Google Scholar]
- Wahab, A.F.; Ali, J.M.; Majid, A.A. Fuzzy geometric modeling. In Proceedings of the 2009 Sixth International Conference on Computer Graphics, Imaging and Visualization, Tianjin, China, 11–14 August 2009; pp. 276–280. [Google Scholar]
- McWhorter, J.H. Understanding Linguistic: The Science of Language; The Teaching Company: Chantilly, VA, USA, 2008. [Google Scholar]
- Kracht, M. Introduction to Linguistics; Hilgard Avenue: Los Angeles, LA, USA, 2007. [Google Scholar]
- Aikhenvald, A. Evidentiality: Problems and Challenges; John Benjamins: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Maynard, S.K. Linguistic Emotivity: Centrality of Place, the Topic-Comment Dynamic, and an Ideology of Pathos in Japanese Discourse; John Benjamins Publishing: Amsterdam, The Netherlands, 2002; Volume 97. [Google Scholar]
- Kövecses, Z. The “container” metaphor of anger in English, Chinese, Japanese and Hungarian. In From a Metaphorical Point of View: A Multidisciplinary Approach to the Cognitive Content of Metaphor; Walter de Gruyter: Berlin, Germany, 1995; pp. 117–145. [Google Scholar]
- Kövecses, Z. Anger: Its language, conceptualization, and. Lang. Cogn. Construal World 1995, 82, 181. [Google Scholar]
- Soriano, C. Some anger metaphors in Spanish and English. A contrastive review. Int. J. Engl. Stud. 2003, 3, 107–122. [Google Scholar]
- King, B. The Conceptual Structure of Emotional Experience in Chinese; Lulu Press: Morrisville, NC, USA, 2005. [Google Scholar]
- Matsuki, K. Metaphors of anger in Japanese. Lang. Cogn. Construal World 1995, 82, 137–151. [Google Scholar]
- Bonissone, P.P. A fuzzy sets based linguistic approach: Theory and applications. In Proceedings of the 12th conference on Winter simulation, Orlando, FL, USA, 3–5 December 1980. [Google Scholar]
- Delgado, M.; Verdegay, J.L.; Vila, M.A. On aggregation operations of linguistic labels. Int. J. Intell. Syst. 1993, 8, 351–370. [Google Scholar] [CrossRef]
- Bordogna, G.; Pasi, G. A fuzzy linguistic approach generalizing Boolean Information Retrieval: A model and its evaluation. J. Am. Soc. Inf. Sci. 1993, 44, 70–82. [Google Scholar] [CrossRef]
- Khoury, R.; Karray, F.; Sun, Y.; Kamel, M.; Basir, O. Semantic Understanding of General Linguistic Items by Means of Fuzzy Set Theory. IEEE Trans. Fuzzy Syst. 2007, 15, 757–771. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Martinez, L. A Fuzzy Linguistic Methodology to Deal With Unbalanced Linguistic Term Sets. IEEE Trans. Fuzzy Syst. 2008, 16, 354–370. [Google Scholar] [CrossRef]
- Ma, L. Clarification on linguistic applications of fuzzy set theory to natural language analysis. In Proceedings of the 2011 Eighth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Shanghai, China, 26–28 July 2011; pp. 811–815. [Google Scholar]
- Ramos-Soto, A.; Pereira-Fariña, M. Reinterpreting interpretability for fuzzy linguistic descriptions of data. In Proceedings of the International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Cádiz, Spain, 11–15 June 2018; Springer: Cham, Switzerland; pp. 40–51. [Google Scholar]
- Tong, R.M.; Bonissone, P.P. A Linguistic Approach to Decisionmaking with Fuzzy Sets. IEEE Trans. Syst. Man Cybern. 1980, 10, 716–723. [Google Scholar] [CrossRef]
- Herrera, F.; Martinez, L. An Approach for Combining Linguistic and Numerical Information Based on The 2-Tuple Fuzzy Linguistic Representation Model in Decision-Making. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2000, 8, 539–562. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant Fuzzy Linguistic Term Sets for Decision Making. IEEE Trans. Fuzzy Syst. 2011, 20, 109–119. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. A group decision making model dealing with comparative linguistic expressions based on hesitant fuzzy linguistic term sets. Inf. Sci. 2013, 241, 28–42. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Wu, J.-T.; Wang, J.; Zhang, H.-Y.; Chen, X.-H. Interval-valued hesitant fuzzy linguistic sets and their applications in multi-criteria decision-making problems. Inf. Sci. 2014, 288, 55–72. [Google Scholar] [CrossRef]
- Nguyen, H.-T.; Dawal, S.Z.; Nukman, Y.; Aoyama, H.; Case, K. An Integrated Approach of Fuzzy Linguistic Preference Based AHP and Fuzzy COPRAS for Machine Tool Evaluation. PLoS ONE 2015, 10, e0133599. [Google Scholar] [CrossRef] [PubMed]
- Jacas, J.; Monreal, A.; Recasens, J. A model for CAGD using fuzzy logic. Int. J. Approx. Reason. 1997, 16, 289–308. [Google Scholar] [CrossRef]
- Jacas, J.; Monreal, A.; Recasens, J. Similarity Based Fuzzy Interpolation Applied to CAGD. In Proceedings of the IFSA-EUSFLAT 2009 Conference, Lisbon, Portugal, 20–24 July 2009; pp. 1696–1701. [Google Scholar]
- Gallo, G.; Spagnuolo, M. Uncertainty coding and controlled data reduction using fuzzy-B-splines. In Proceedings of the Computer Graphics International 1998 Proceedings, Hannover, Germany, 26 June 1998; pp. 536–542. [Google Scholar]
- Gallo, G.; Spagnuolo, M.; Spinello, S. Fuzzy B-splines: A surface model encapsulating uncertainty. Graph. Models 2000, 62, 40–55. [Google Scholar] [CrossRef]
- Anile, A.; Falcidieno, B.; Gallo, G.; Spagnuolo, M.; Spinello, S. Modeling undertain data with fuzzy B-splines. Fuzzy Sets Syst. 2000, 113, 397–410. [Google Scholar] [CrossRef]
- Wahab, A.F.; Ali, J.M. Penyelesaian Masalah Data Ketakpastian Menggunakan Splin-B Kabur. Sains Malays. 2010, 39, 661–670. [Google Scholar]
- Zakaria, R.; Wahab, A.F.; Gobithaasan, U.R. Fuzzy B-Spline surface modeling. J. Appl. Math. 2014, 2014, 285045. [Google Scholar] [CrossRef]
- Zakaria, R.; Wahab, A.F. Fuzzy B-spline modeling of uncertainty data. Appl. Math. Sci. 2012, 6, 6971–6991. [Google Scholar]
- Zakaria, R.; Wahab, A.F. Pemodelan Titik Data Kabur Teritlak. Sains Malays. 2014, 43, 799–805. [Google Scholar]
- Karim, N.A.A.; Wahab, A.F.; Gobithaasan, R.U.; Zakaria, R. Model of fuzzy B-spline interpolation for fuzzy data. Far East J. Math. Sci. 2013, 72, 269–280. [Google Scholar]
- Bakar, N.A.; Yusoff, B.; Wahab, A.F.; Mamat, M. Modeling Fuzzy B-spline Interpolation Series using α-cut operation for spatial earth surface problem. J. Phys. Conf. Ser. 2021, 1988, 012011. [Google Scholar] [CrossRef]
- Zulkifly, M.I.E.; Wahab, A.F. Intuitionistic fuzzy bicubic Bézier surface approximation. AIP Conf. Proc. 2018, 1974, 020064. [Google Scholar]
- Zulkifly, M.I.E.; Wahab, A.F. 3-Tuple Bézier Surface Interpolation Model for Data Visualization. IAENG Int. J. Appl. Math. 2020, 50, 1–7. [Google Scholar]
- Zulkifly, M.I.E.; Wahab, A.F.; Zakaria, R. B-Spline curve interpolation model by using intuitionistic fuzzy approach. IAENG Int. J. Appl. Math. 2020, 50, 6. [Google Scholar]
- Zulkifly, M.I.E.; Wahab, A.F.; Bidin, M.S.; Embong, A.F.; Hoe, Y.S. Intuitionistic fuzzy piecewise Bézier curve modeling with C1 and G1 continuities for complex data. Adv. Differ. Equ. Control. Process. 2020, 23, 251–260. [Google Scholar] [CrossRef]
- Shah, M.M.; Wahab, A.F. Fuzzy topological digital space and their properties of flat electroencephalography in epilepsy disease. J. Phys. Conf. Ser. 2017, 890, 12114. [Google Scholar] [CrossRef]
- Shah, M.M.; Wahab, A.F.; Zulkifly, M.I.E. Fuzzy Cubic Bézier Curve Approximation in Fuzzy Topological Digital Space. Malays. J. Math. Sci. 2019, 13, 123–137. [Google Scholar]
- Zakaria, R.; Wahab, A.F.; Gobithaasan, R.U. The Representative Curve of Type-2 Fuzzy Data Point Modeling. Mod. Appl. Sci. 2013, 7, 60. [Google Scholar] [CrossRef]
- Zakaria, R.; Wahab, A.F.; Ismail, I.; Zulkifly, M.I.E. Complex uncertainty of surface data modeling via the type-2 fuzzy B-spline model. Mathematics 2021, 9, 1054. [Google Scholar] [CrossRef]
- Wahab, A.F.; Yong, L.K.; Zulkifly, M.I.E. Type-2 Fuzzy Non-uniform Rational B-spline Model with Type-2 Fuzzy Data. Malays. J. Math. Sci. 2017, 11, 35–46. [Google Scholar]
- Adesah, R.S.; Zakaria, R.; Wahab, A.F.; Talibe, A. Type-2 fuzzy curve model. J. Phys. Conf. Ser. 2017, 890, 012088. [Google Scholar] [CrossRef]
- Bidin, M.S.; Wahab, A.F.; Zulkifly, M.I.E.; Zakaria, R. Generalized Fuzzy Linguistic Cubic B-Spline Curve Model for Uncertainty Fuzzy Linguistic Data. Adv. Appl. Discret. Math. 2020, 25, 285–302. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]







| (xn, yn) | y0 | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 |
|---|---|---|---|---|---|---|---|---|---|---|
| x0 | ||||||||||
| x1 | ||||||||||
| x2 | ||||||||||
| x3 | ||||||||||
| x4 | ||||||||||
| x5 | ||||||||||
| x6 | ||||||||||
| x7 | ||||||||||
| x8 | ||||||||||
| x9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bidin, M.S.; Wahab, A.F.; Zulkifly, M.I.E.; Zakaria, R. Generalized Fuzzy Linguistic Bicubic B-Spline Surface Model for Uncertain Fuzzy Linguistic Data. Symmetry 2022, 14, 2267. https://doi.org/10.3390/sym14112267
Bidin MS, Wahab AF, Zulkifly MIE, Zakaria R. Generalized Fuzzy Linguistic Bicubic B-Spline Surface Model for Uncertain Fuzzy Linguistic Data. Symmetry. 2022; 14(11):2267. https://doi.org/10.3390/sym14112267
Chicago/Turabian StyleBidin, Mohd Syafiq, Abd. Fatah Wahab, Mohammad Izat Emir Zulkifly, and Rozaimi Zakaria. 2022. "Generalized Fuzzy Linguistic Bicubic B-Spline Surface Model for Uncertain Fuzzy Linguistic Data" Symmetry 14, no. 11: 2267. https://doi.org/10.3390/sym14112267
APA StyleBidin, M. S., Wahab, A. F., Zulkifly, M. I. E., & Zakaria, R. (2022). Generalized Fuzzy Linguistic Bicubic B-Spline Surface Model for Uncertain Fuzzy Linguistic Data. Symmetry, 14(11), 2267. https://doi.org/10.3390/sym14112267







