Remarks on Fractal-Fractional Malkus Waterwheel Model with Computational Analysis
Abstract
1. Introduction
2. Preliminaries
Effect of Fractal-Fractional on Simple Processes
3. Existence and Uniqueness of a Solution of Fractal-Fractional Differential Equations
4. Numerical Method
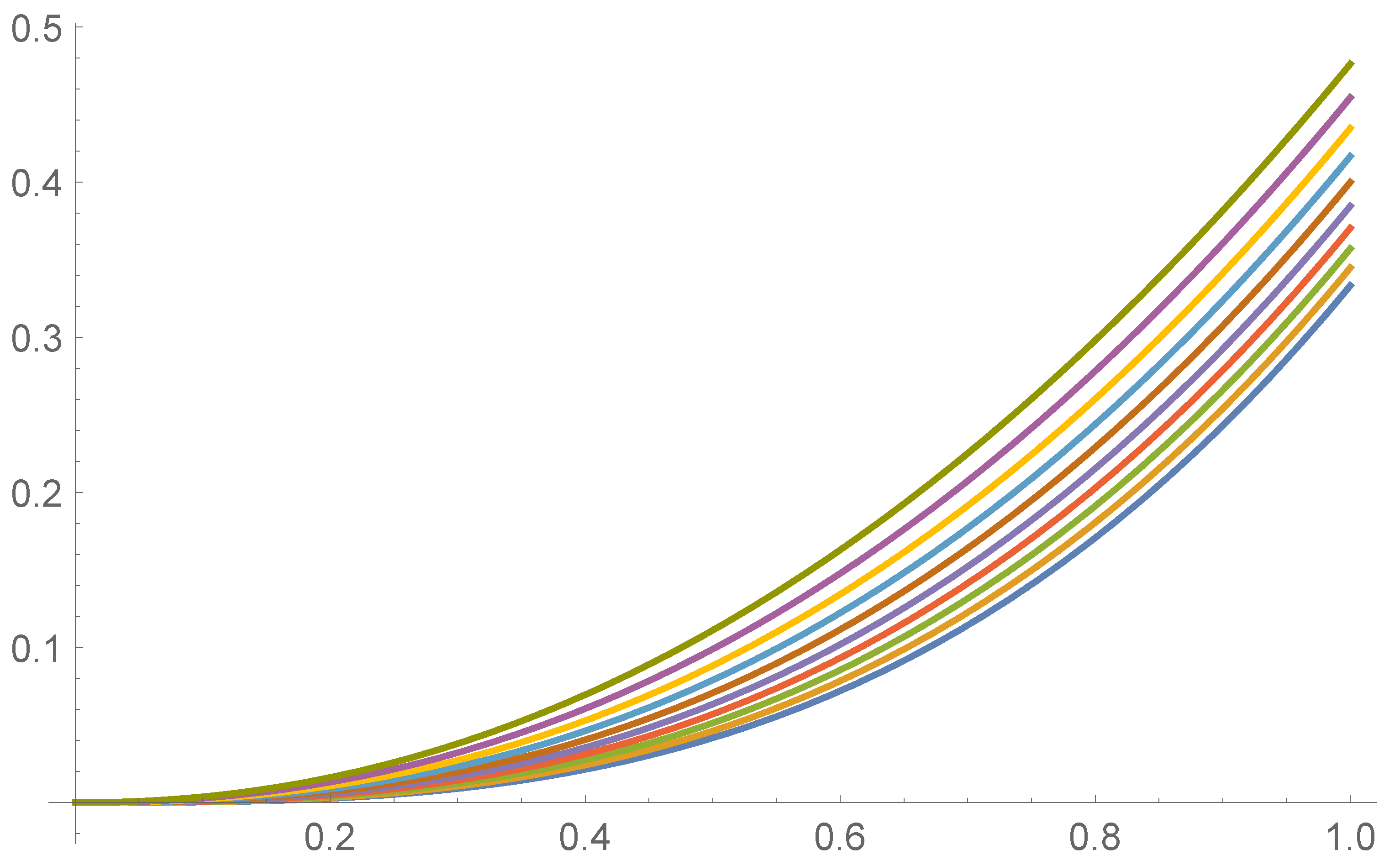
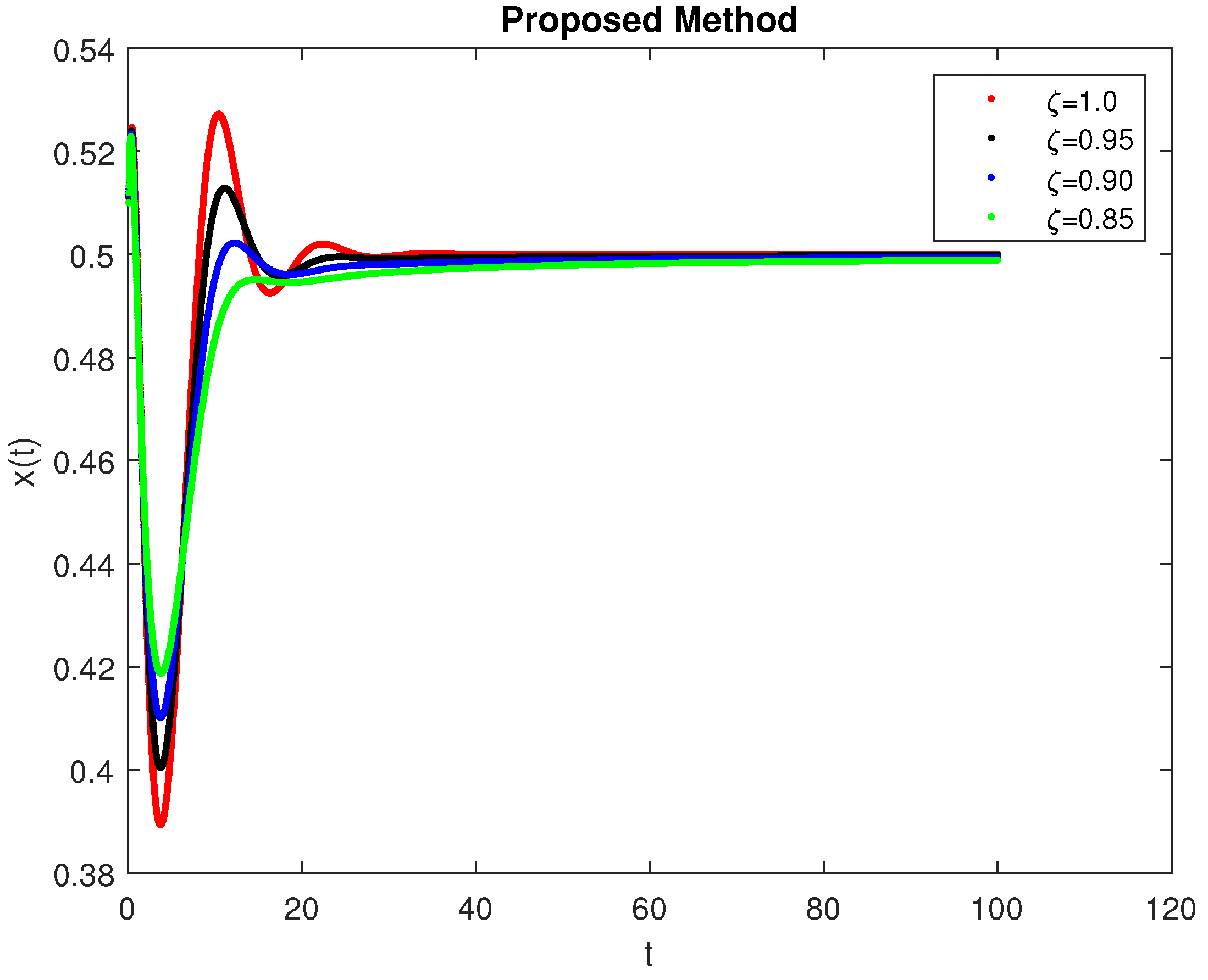
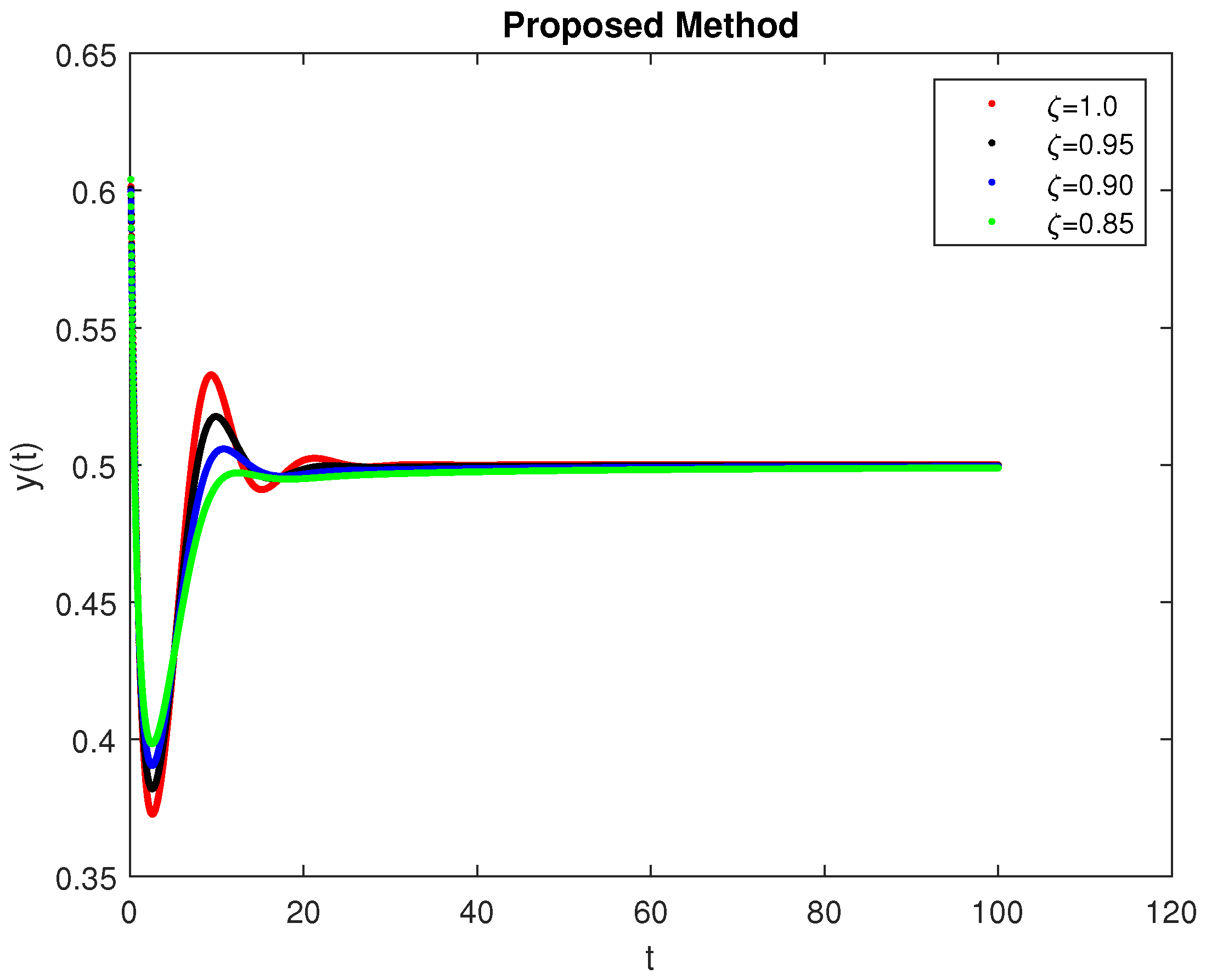
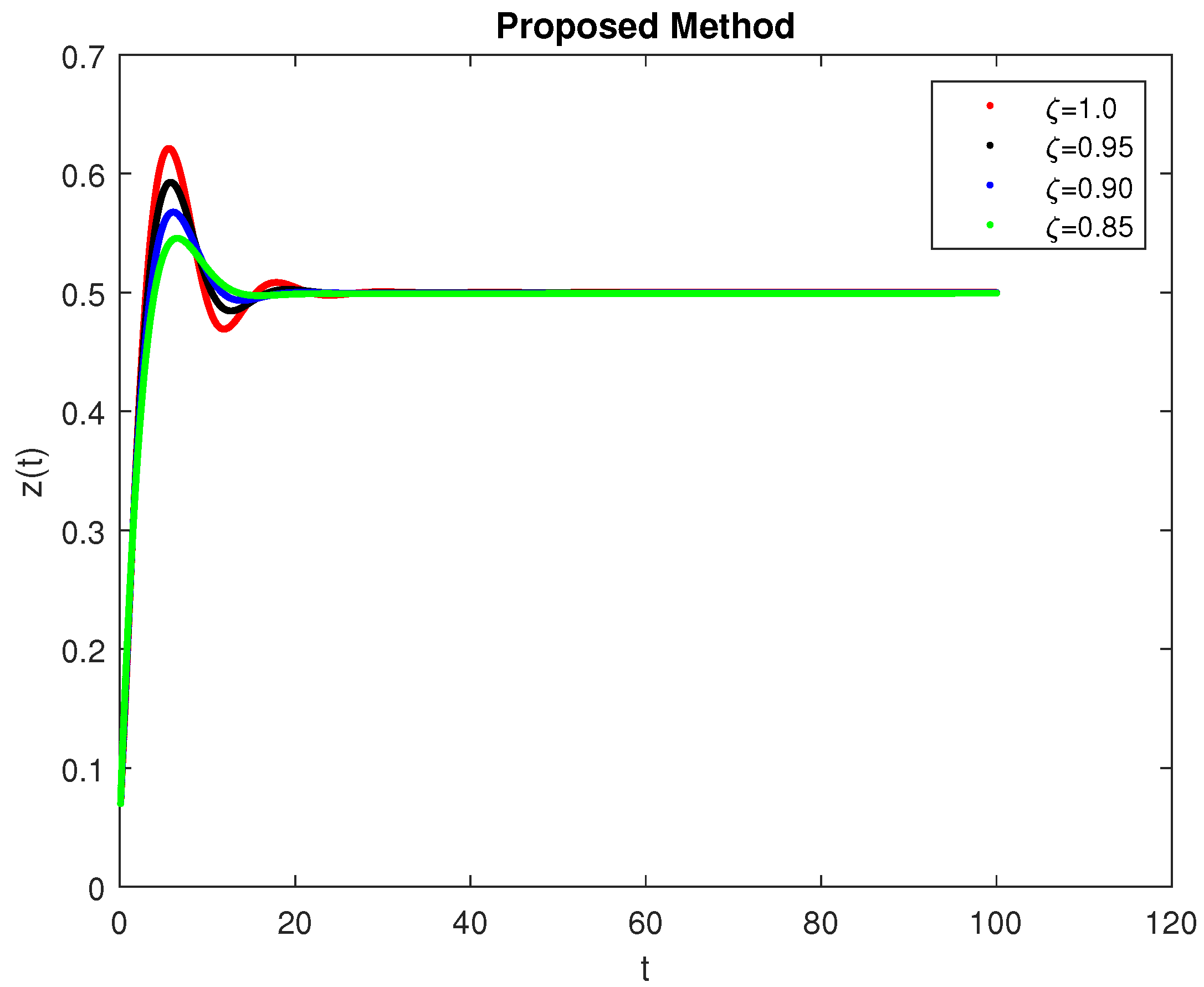
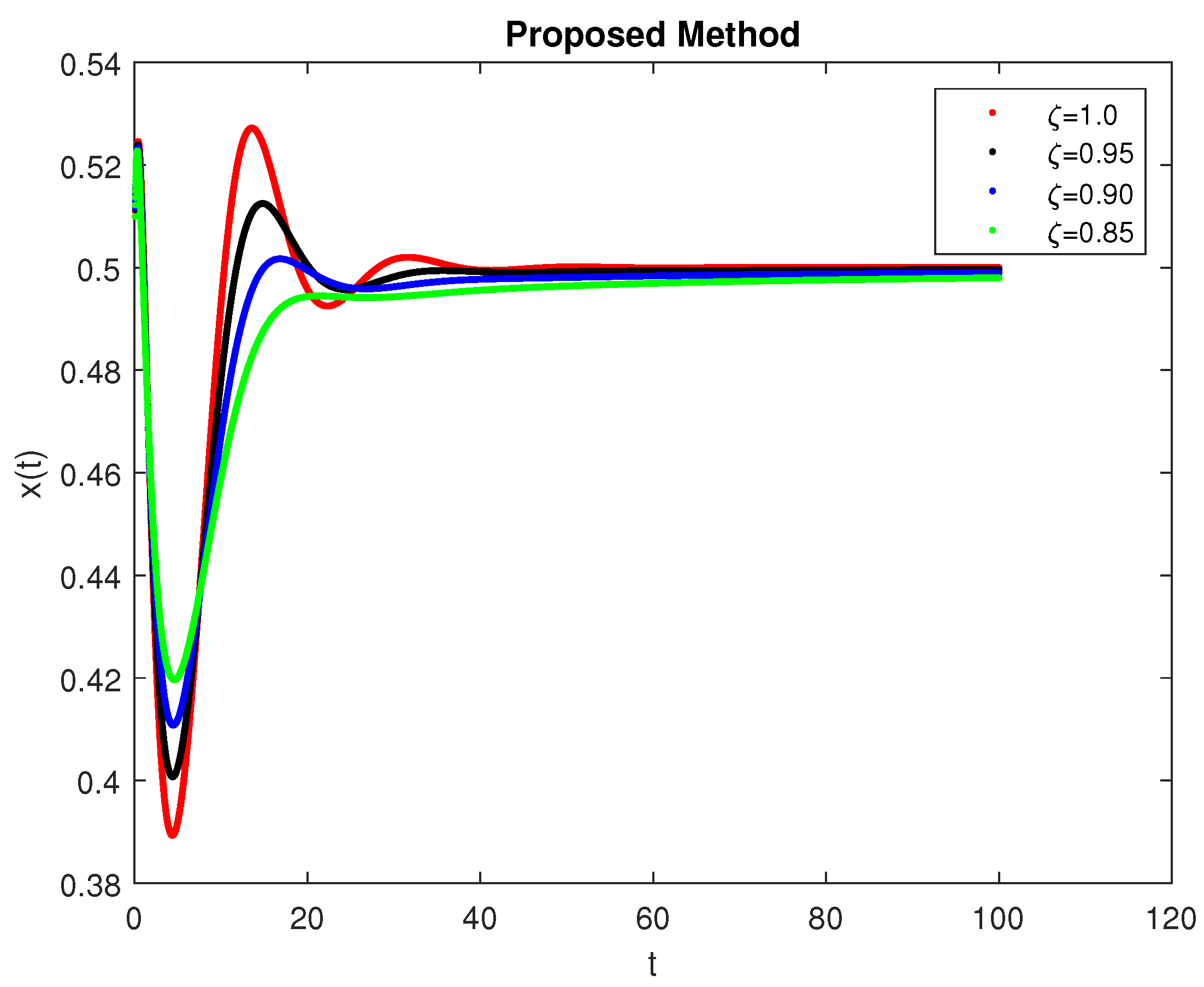
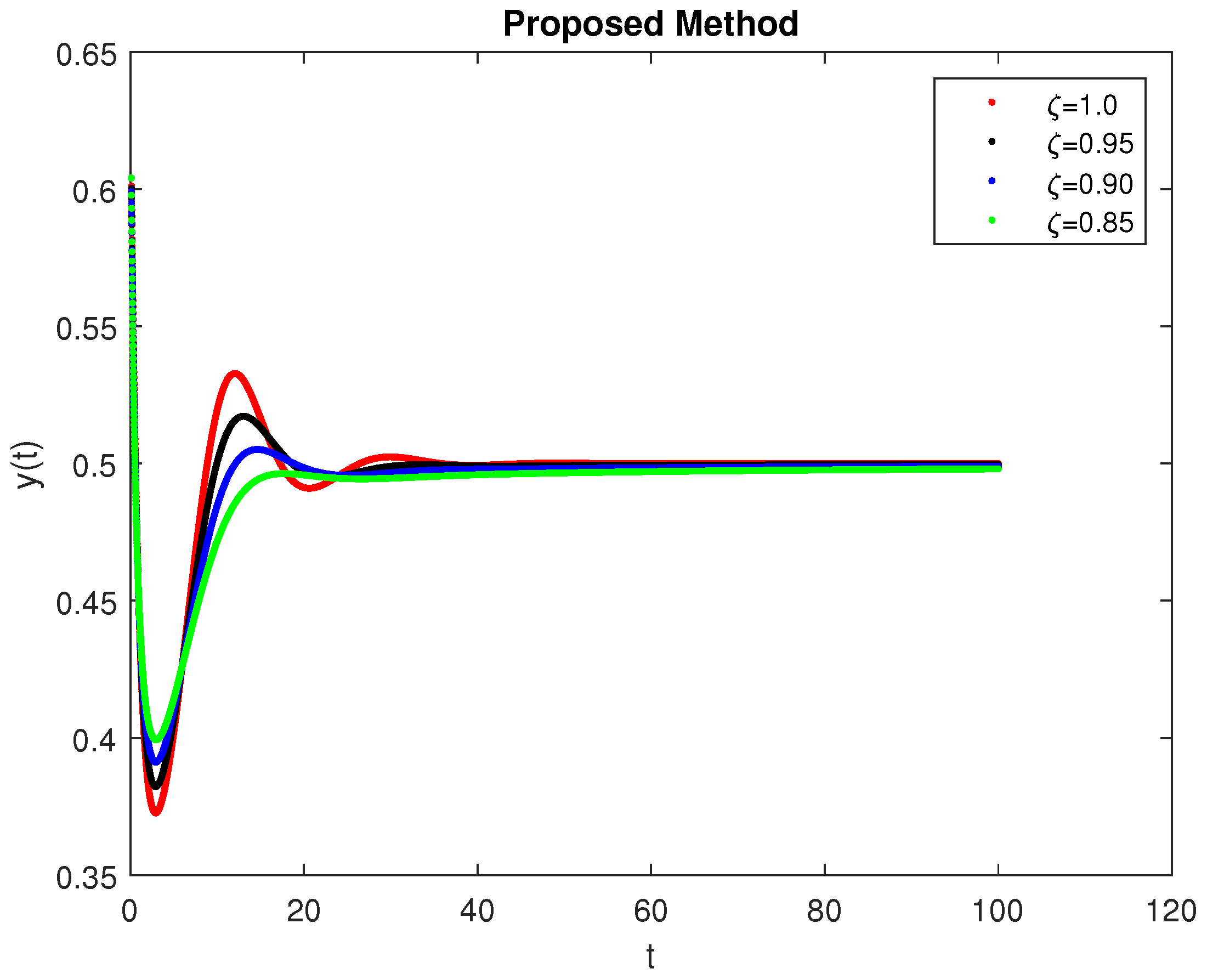
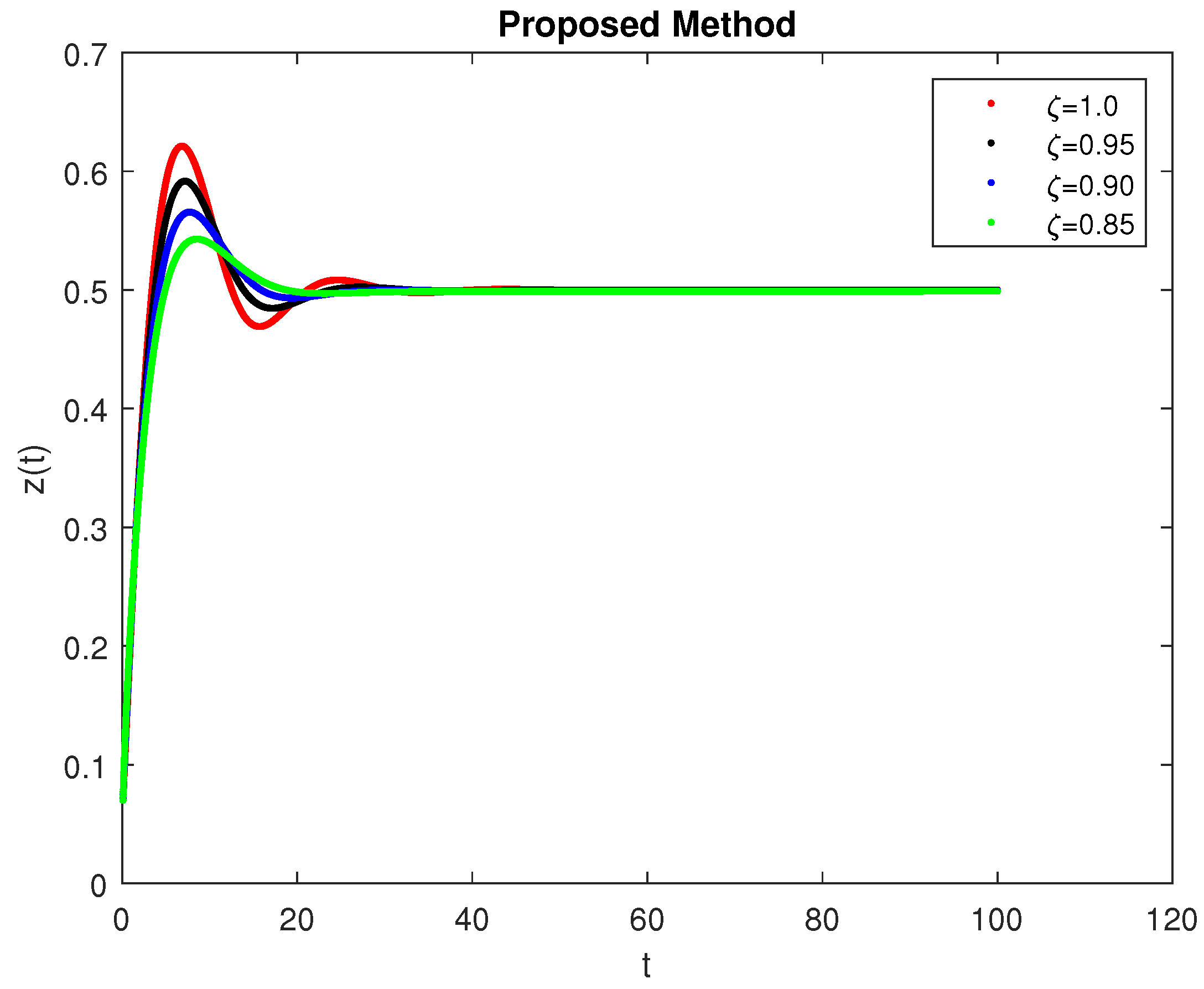
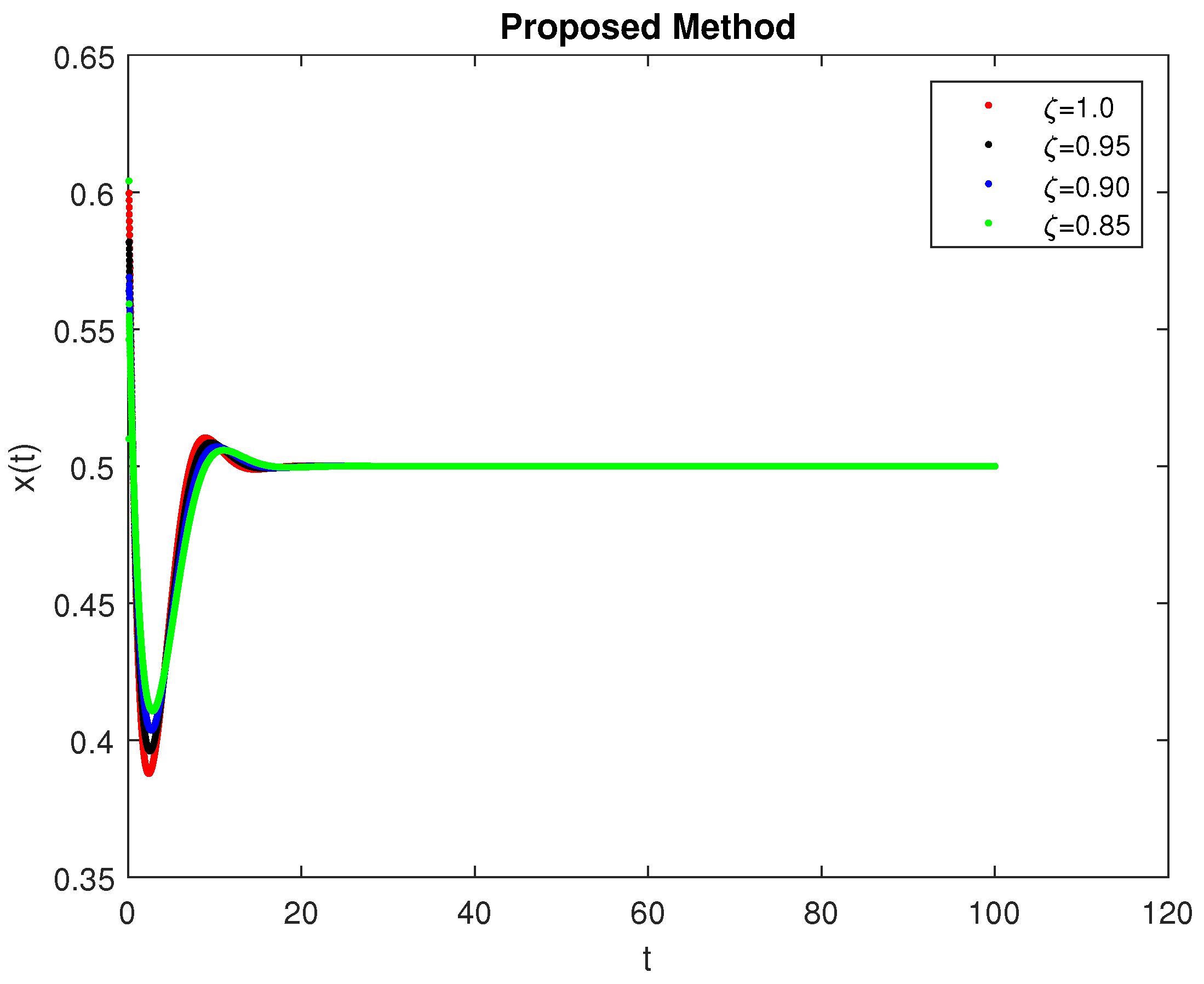
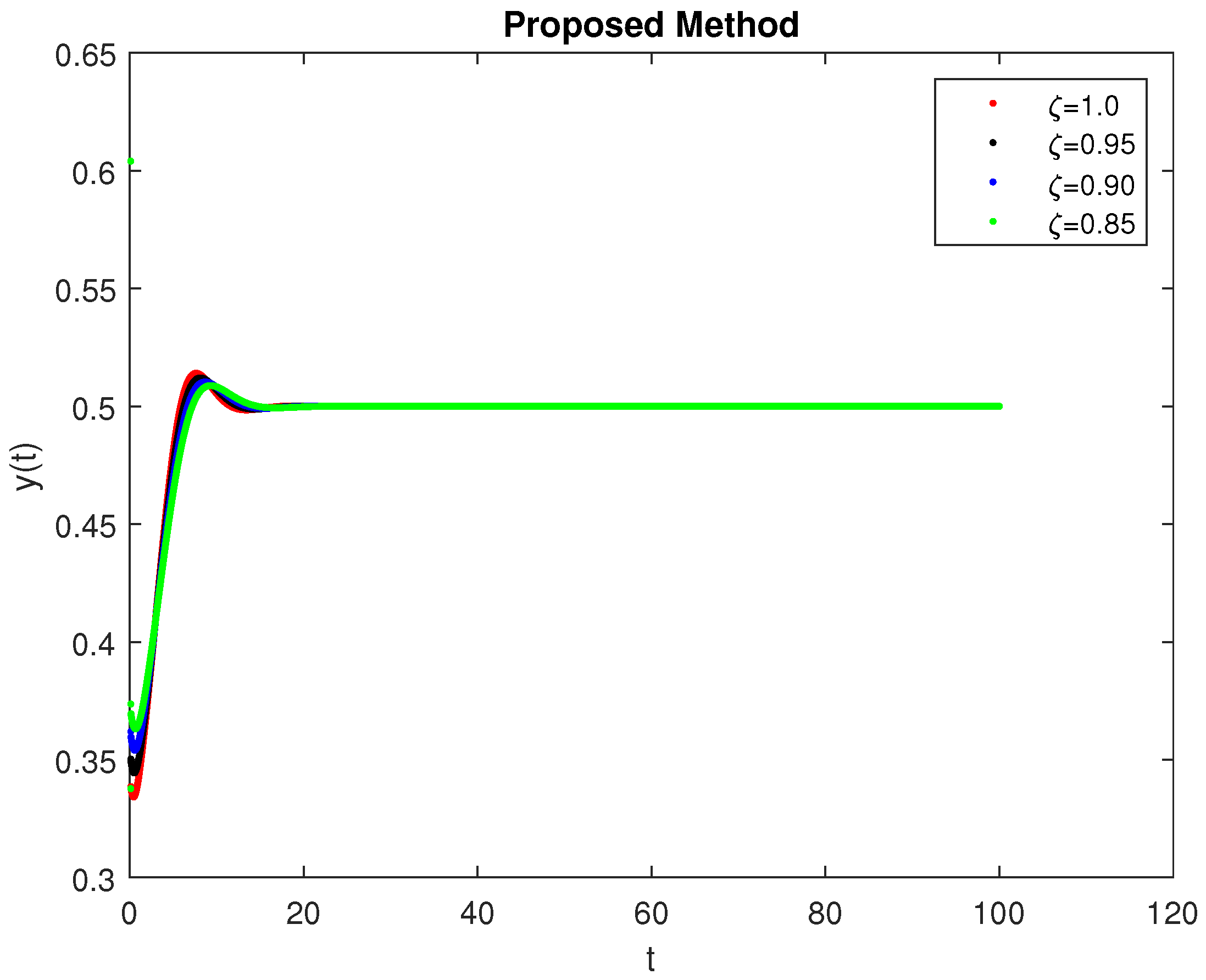
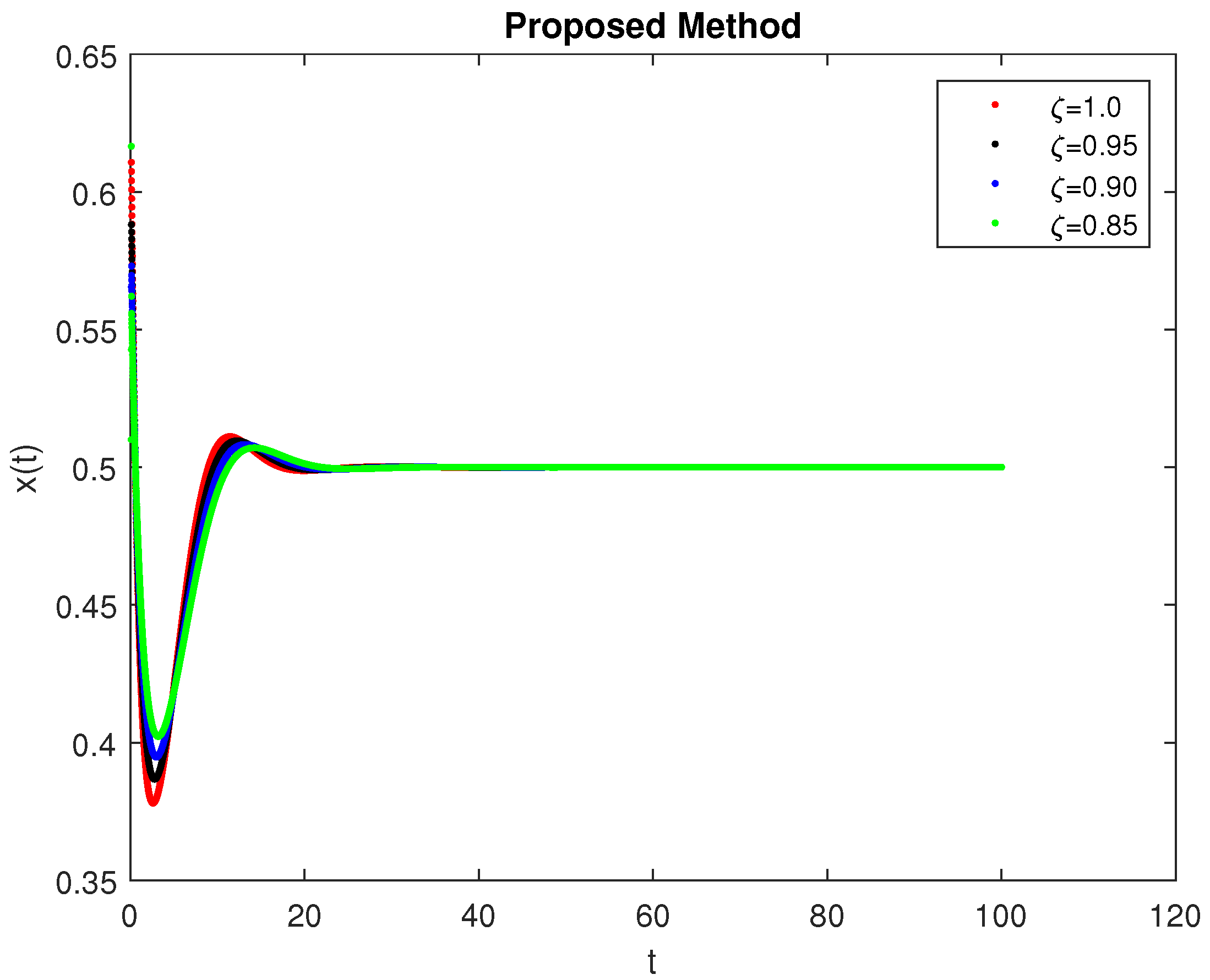
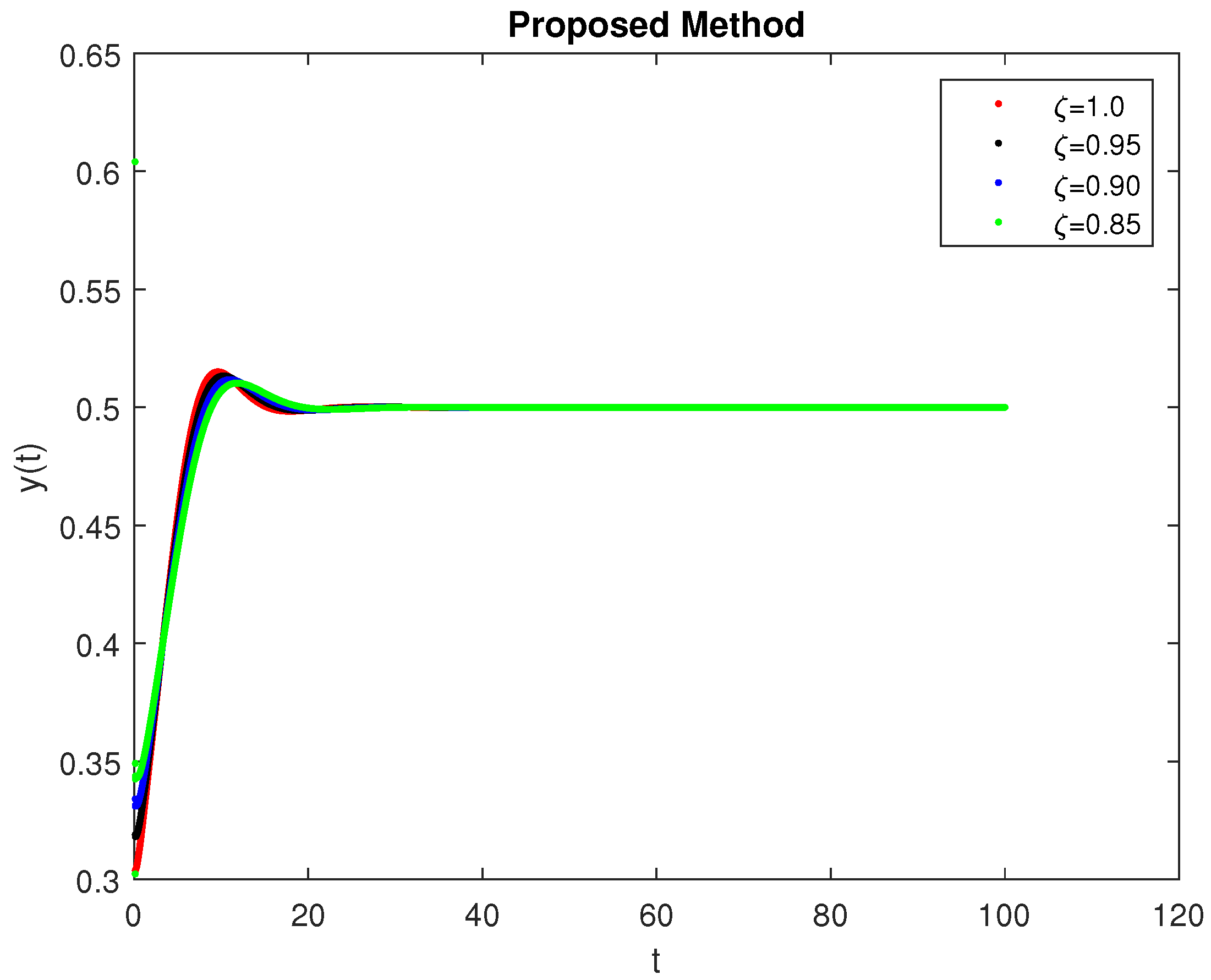
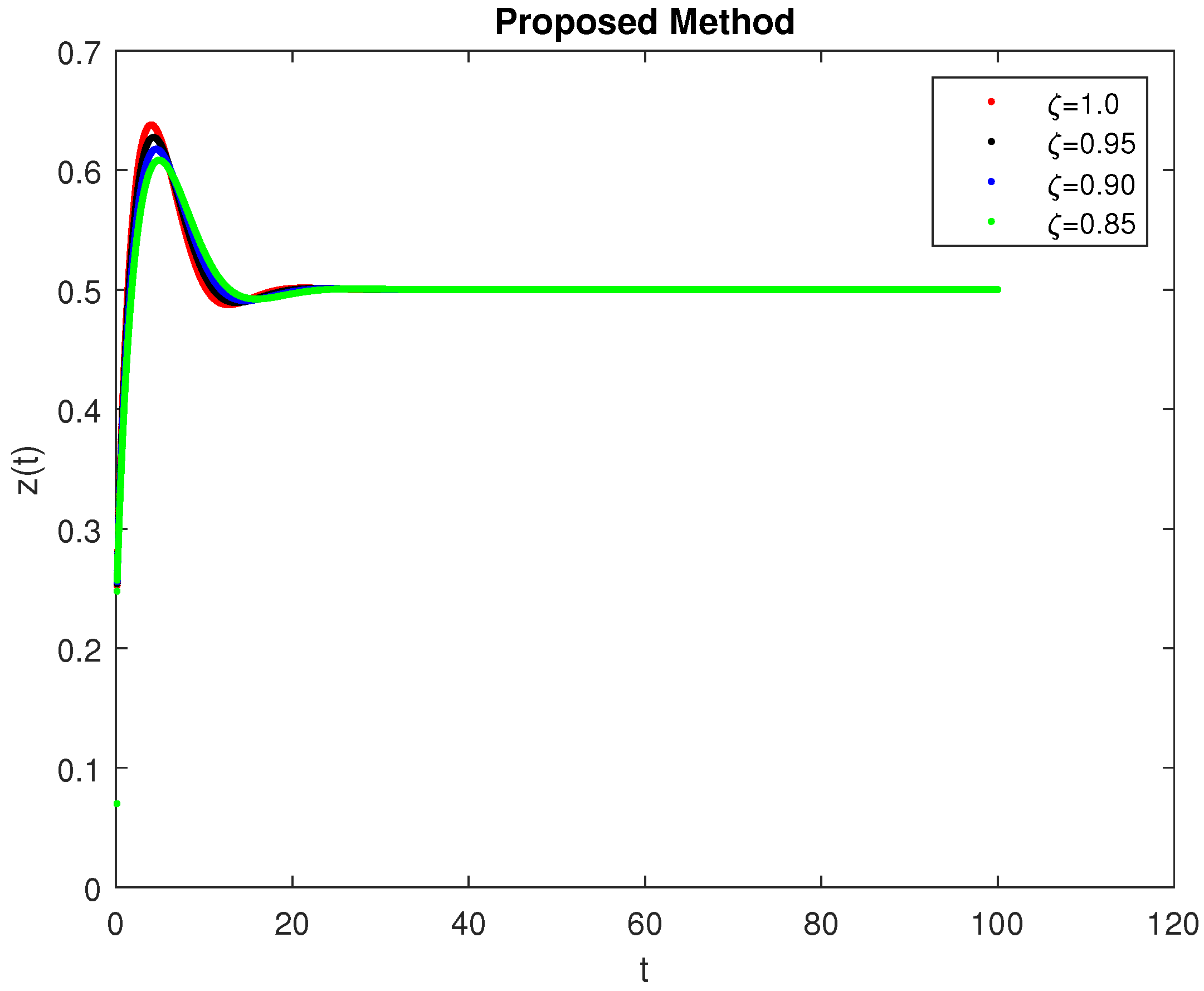
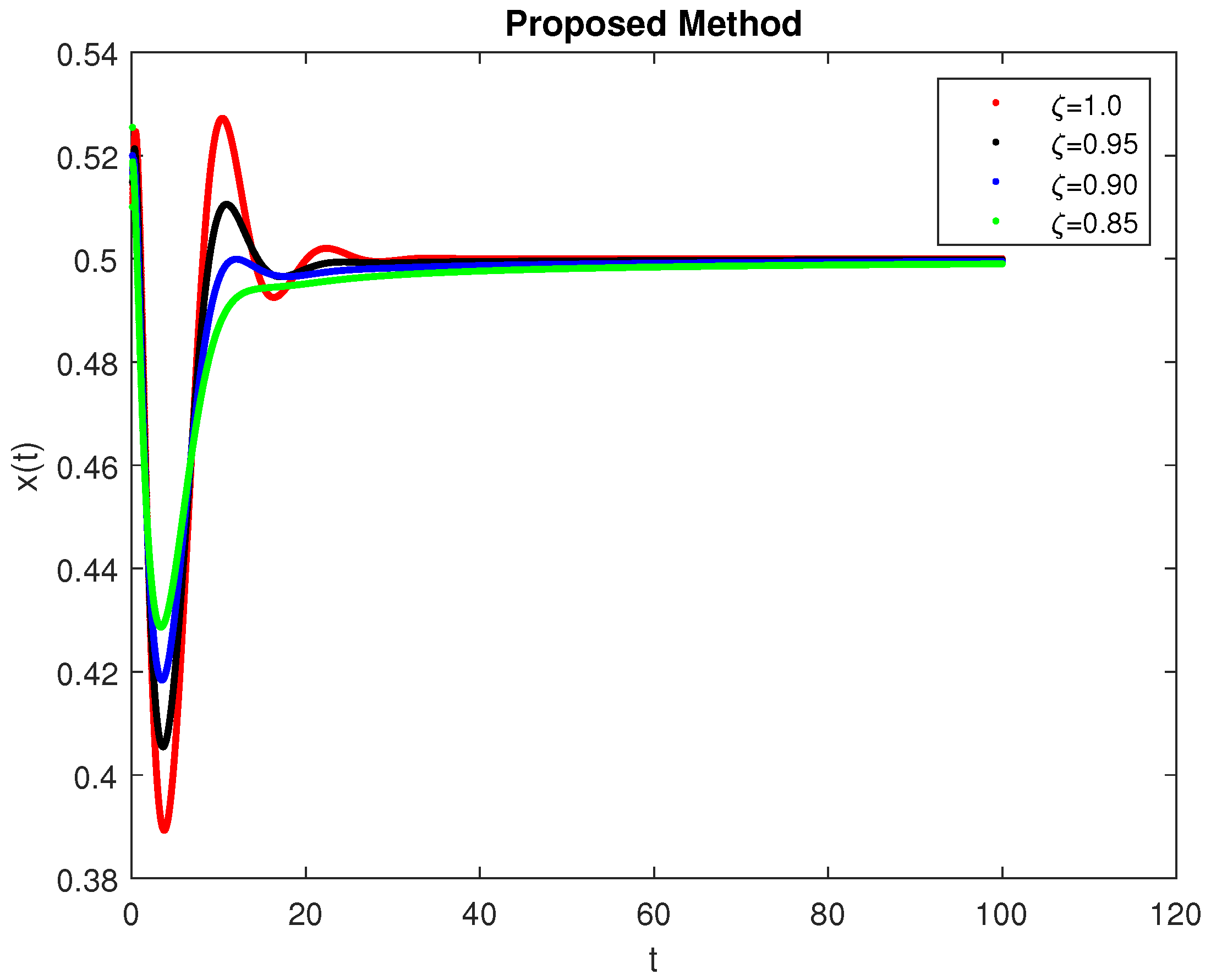
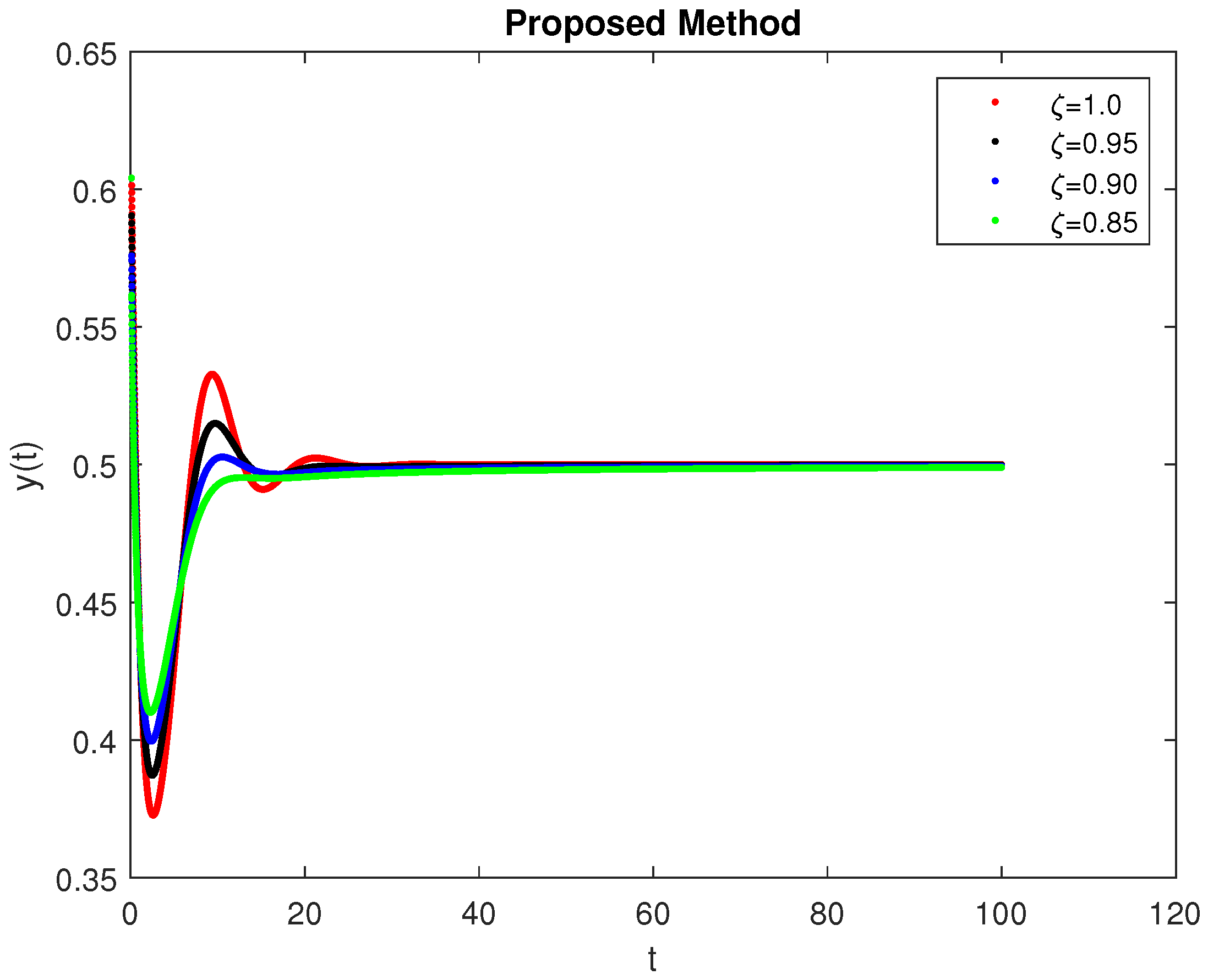
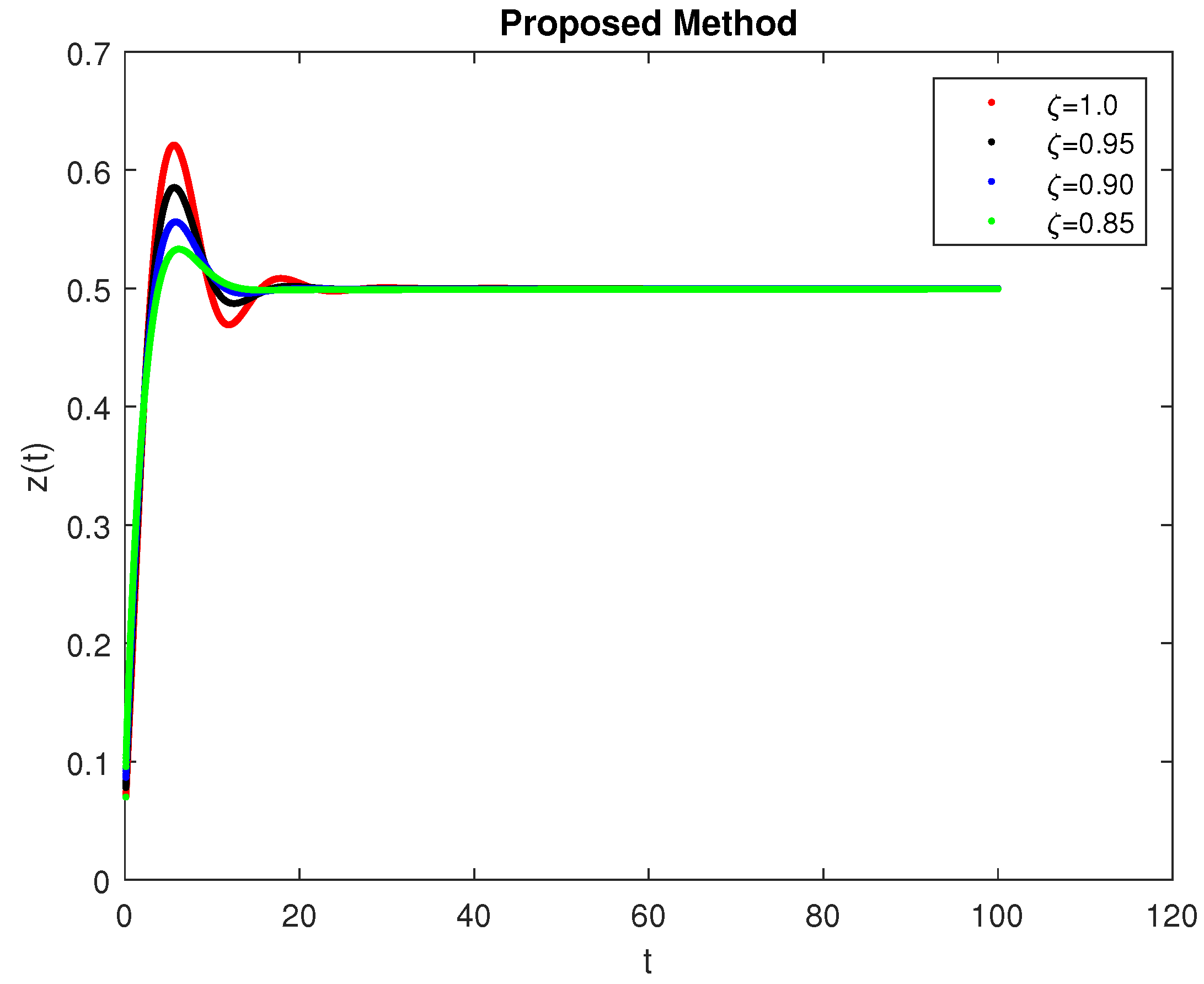
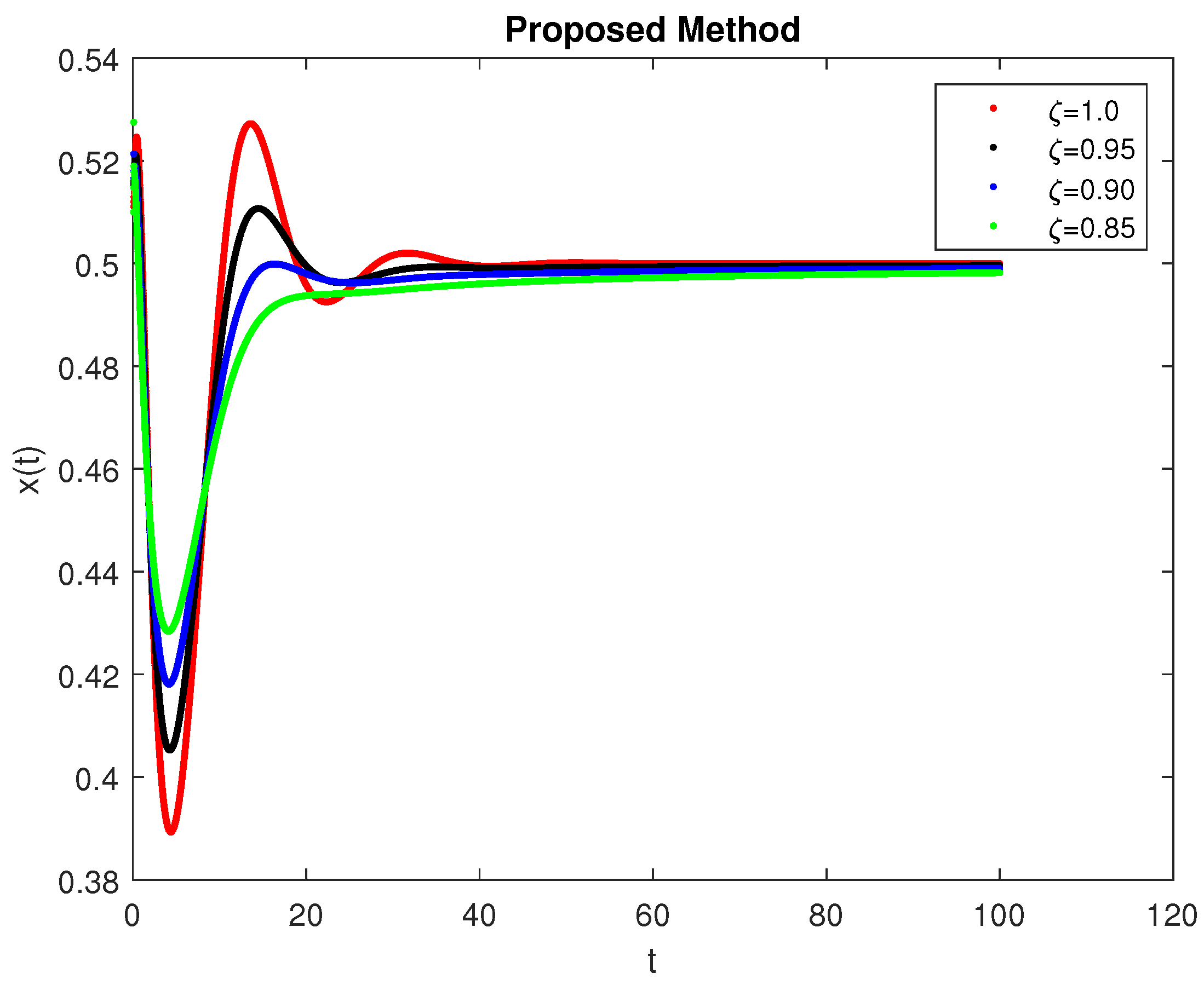
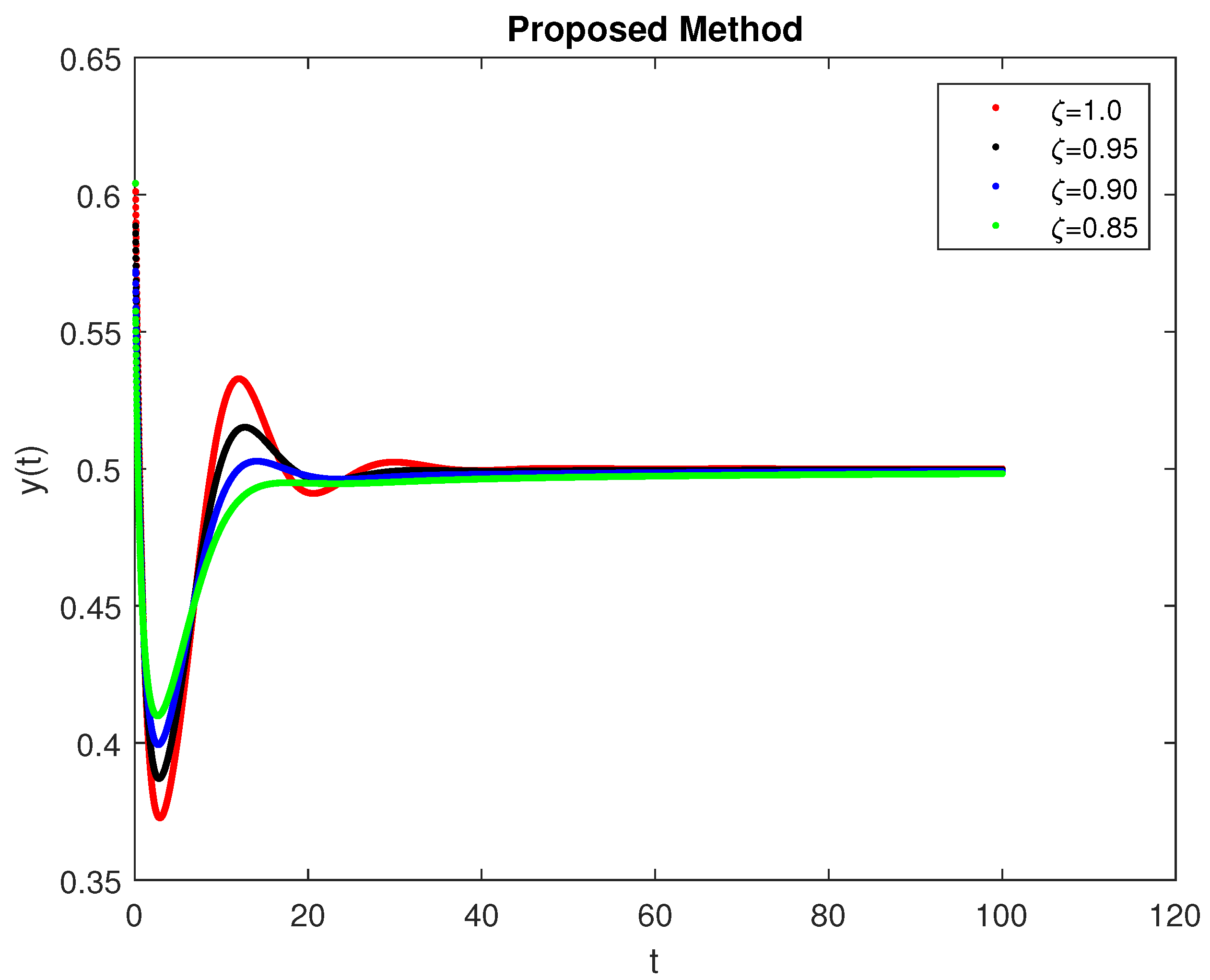
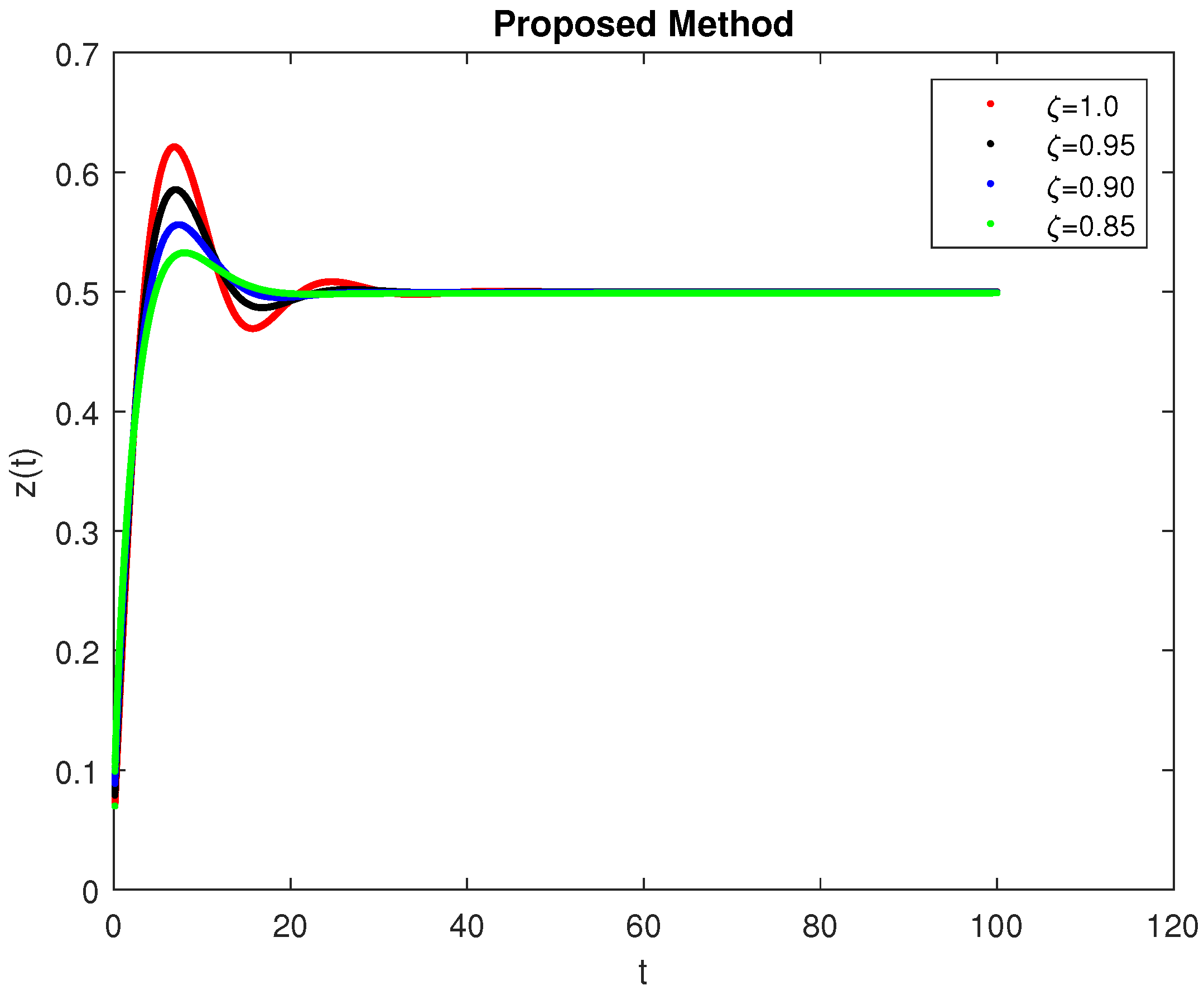
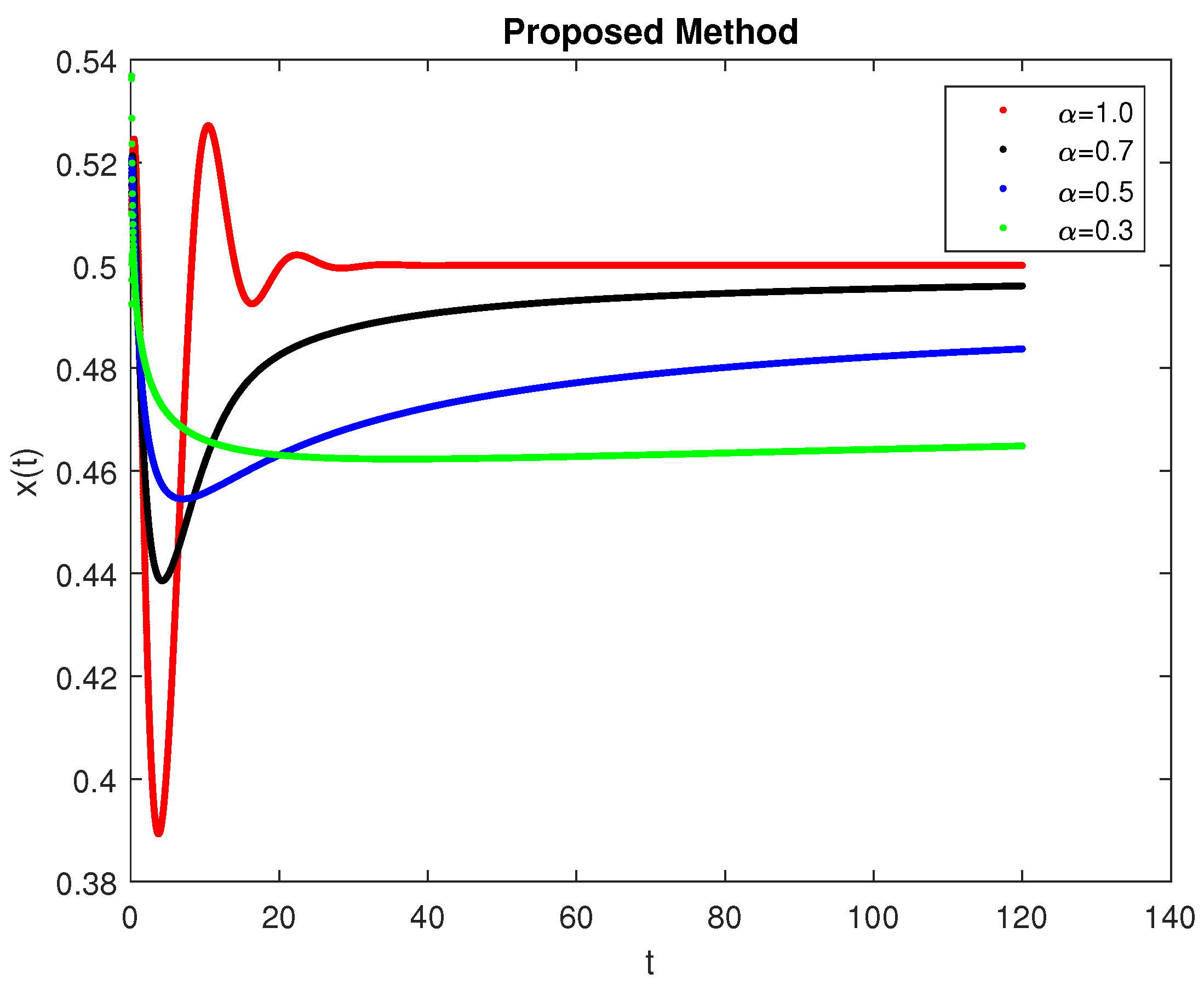
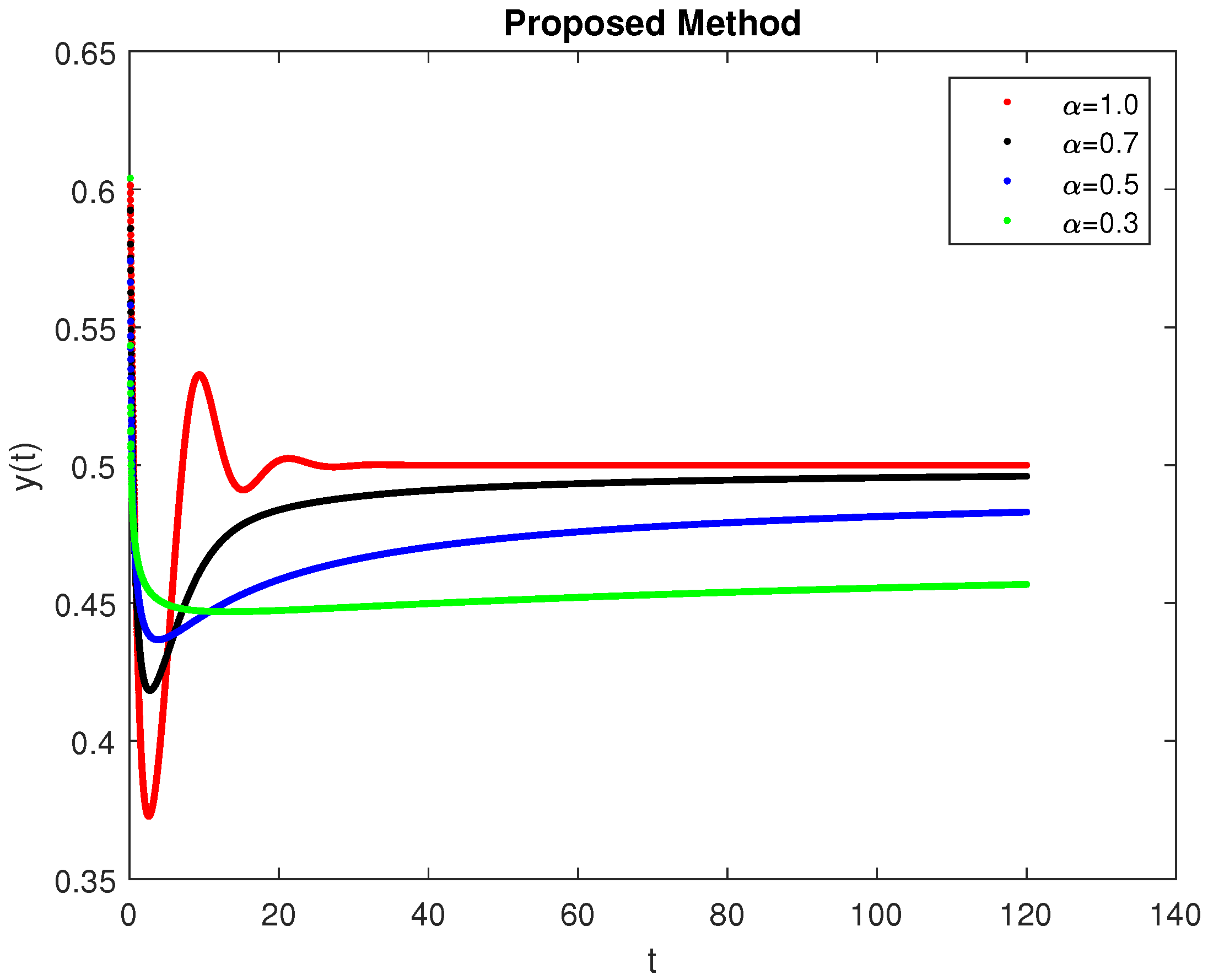
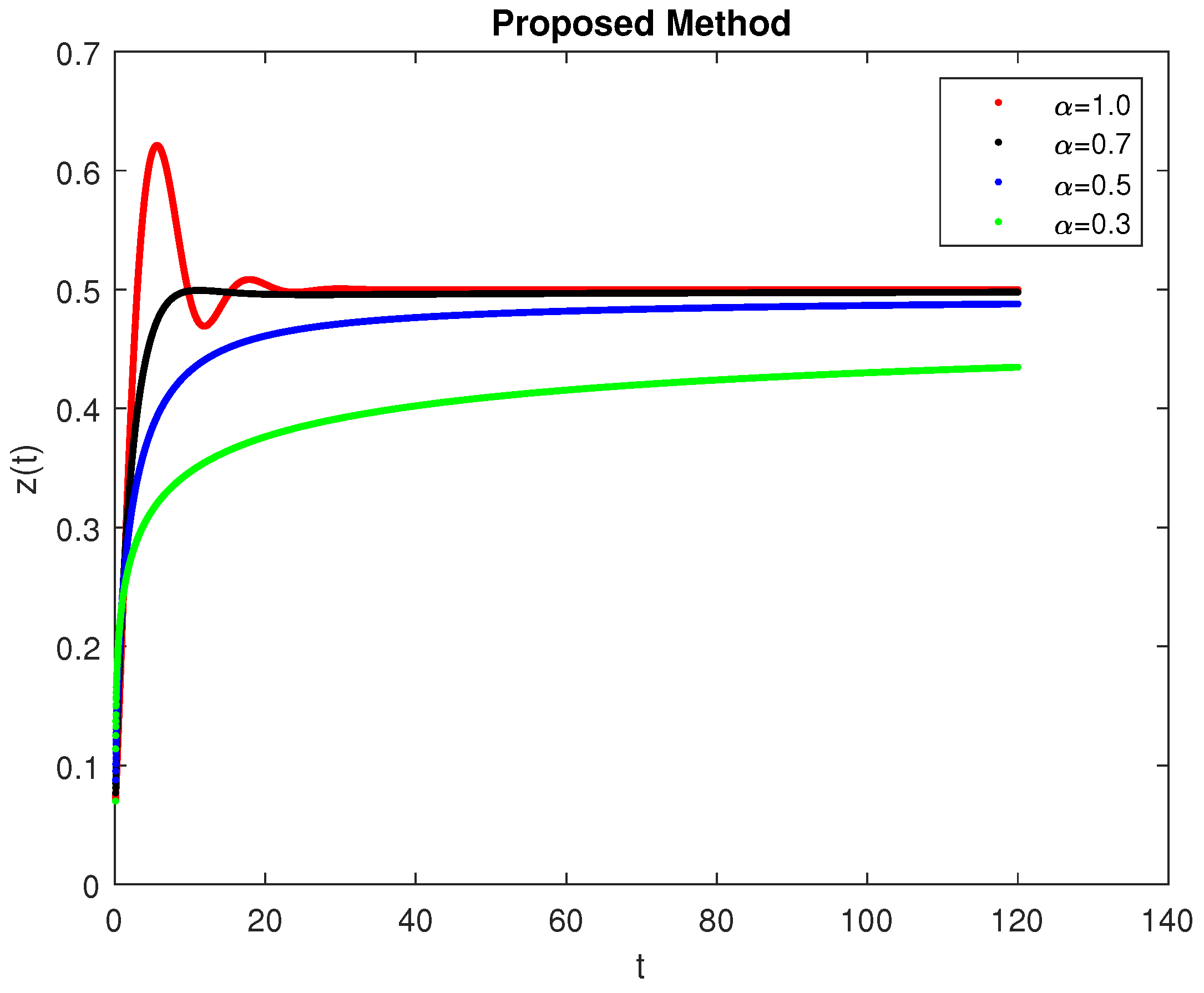
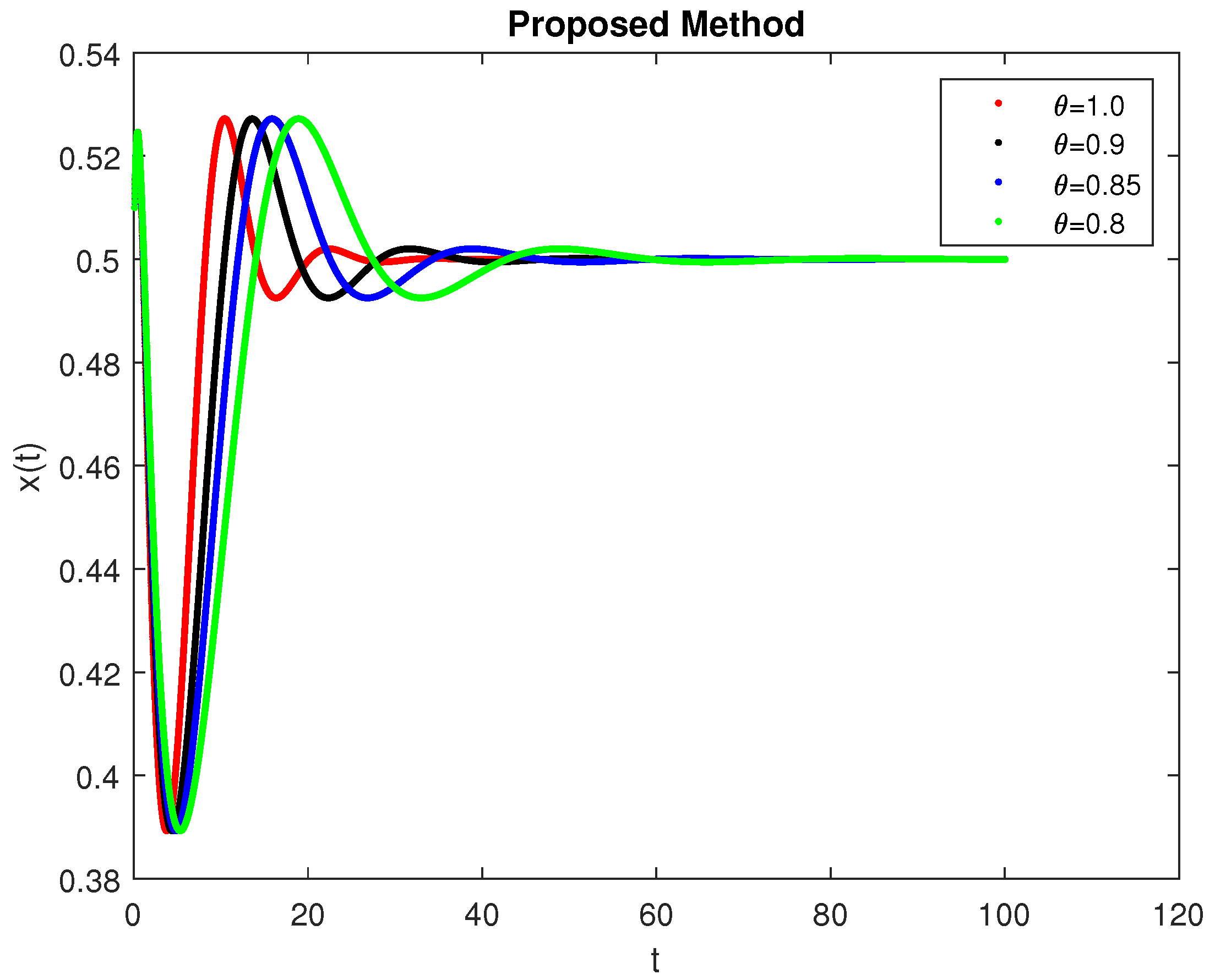
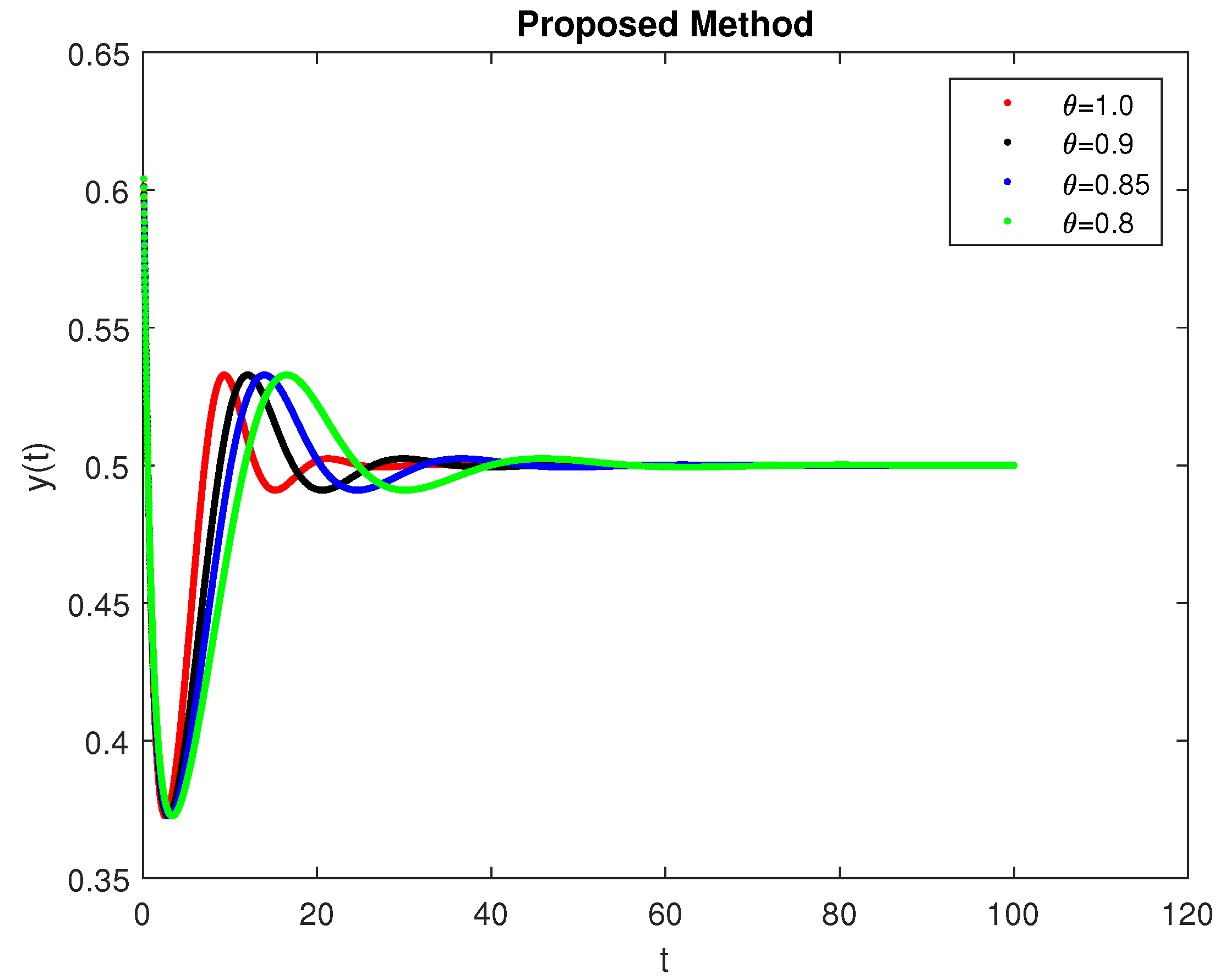
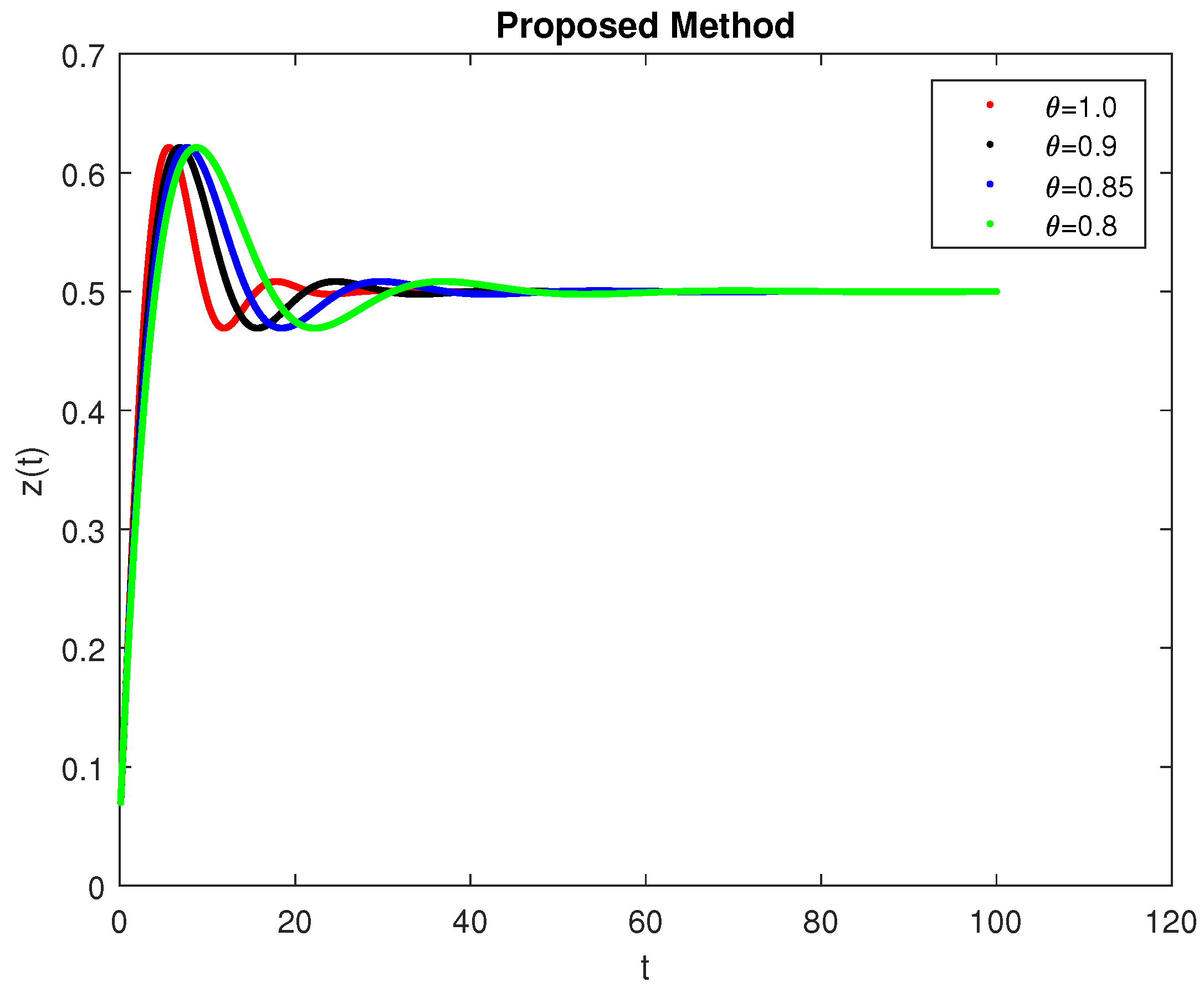
5. Computational Simulations
6. Discussions and Conclusions
Open Questions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morris, S.A.; Pratt, D. Analysis of the Lotka-Volterra competition equations as a technological substitution model. Technol. Forecast. Soc. Chang. 2003, 70, 103–133. [Google Scholar] [CrossRef]
- Lee, S.-J.; Lee, D.-J.; Oh, H.S. Technological forecasting at the Korean stock market: A dynamic competition analysis using Lotka-Volterra model, Technol. Forecast. Soc. Chang. 2005, 72, 1044–1057. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.-J.; Ahn, J. A dynamic competition analysis on the Korean mobile phone market using competitive diffusion model. Comput. Ind. Eng. 2006, 51, 174–182. [Google Scholar] [CrossRef]
- Michalakelis, C.; Christodoulos, C.; Varoutas, D.; Sphicopoulos, T. Dynamic estimation of markets exhibiting a prey-predator behavior. Expert. Syst. Appl. 2012, 39, 7690–7700. [Google Scholar] [CrossRef]
- Lakka, S.; Michalakelis, C.; Varoutas, D.; Martakos, D. Competitive dynamics in the operating systems market: Modeling and policy implications. Technol. Forecast. Soc. Chang. 2013, 80, 88–105. [Google Scholar] [CrossRef]
- Fatmawati; Khan, M.A.; Azizah, M.; Windarto; Ullah, S. A fractional model for the dynamics of competition between commercial and rural banks in Indonesia. Chaos Solitons Fractals 2019, 122, 32–46. [Google Scholar] [CrossRef]
- Wang, W. A comparison study of bank data in fractional calculus. Chaos Solitons Fractals 2019, 126, 369–384. [Google Scholar] [CrossRef]
- Comes, C.A. Banking system: Three level Lotka-Volterra model. Procedia Econ. Financ. 2012, 3, 251–255. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.A.; Farooq, M. A fractional model for the dynamics of TB virus. Chaos Solitons Fractals 2018, 116, 63–71. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, S.; Farooq, M. A new fractional model for tuberculosis with relapse via Atangana-Baleanu derivative. Chaos Solitons Fractals 2018, 116, 227–238. [Google Scholar] [CrossRef]
- Fatmawati, F.; Shaiful, E.; Utoyo, M. A fractional-order model for HIV dynamics in a two-sex population. Int. J. Math. Math. Sci. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Das, S.; Gupta, P. A mathematical model on fractional Lotka-Volterra equations. J. Theor. Biol. 2011, 277, 16. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Hammouch, Z.; Baleanu, D. Modeling the dynamics of hepatitis e via the Caputo-Fabrizio derivative. Math. Model Nat. Phenom. 2019, 14, 311. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Fractional derivatives applied to MSEIR problems: Comparative study with real world data. Eur. Phys. J. Plus 2019, 134, 171. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Modeling chickenpox disease with fractional derivatives: From Caputo to Atangana-Baleanu. Chaos Solitons Fractals 2019, 122, 111–118. [Google Scholar] [CrossRef]
- Atangana, A.; Nieto, J.J. Numerical solution for the model of RLC circuit via the fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1687814015613758. [Google Scholar] [CrossRef]
- Qureshi, S.; Atangana, A. Mathematical analysis of dengue fever outbreak by novel fractional operators with field data. Phys. A 2019, 526, 121–127. [Google Scholar] [CrossRef]
- Atangana, A.; Alqahtani, R.T. A new approach to capture heterogeneity in groundwater problem: An illustration with an earth equation. Math. Model. Nat. Phenom. 2019, 14, 313. [Google Scholar] [CrossRef]
- Toufik, M.; Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 2017, 132, 444. [Google Scholar] [CrossRef]
- Attia, N.; Akgül, A.; Seba, D.; Nour, A.; Riaz, M.B. Reproducing kernel Hilbert space method for solving fractal fractional differential equations. Results Phys. 2022, 35, 105225. [Google Scholar] [CrossRef]
- Zhou, J.C.; Salahshour, S.; Ahmadian, A.; Senu, N. Modeling the dynamics of COVID-19 using fractal-fractional operator with a case study. Results Phys. 2022, 33, 105103. [Google Scholar] [CrossRef] [PubMed]
- Attia, N.; Akgül, A.; Seba, D.; Nour, A.; Asjad, J. A novel method for fractal-fractional differential equations. Alex. Eng. J. 2022, 61, 9733–9748. [Google Scholar] [CrossRef]
- Shloof, A.M.; Senu, N.; Ahmadian, A.; Pakdaman, M.; Salahshour, S. A new iterative technique for solving fractal-fractional differential equations based on artificial neural network in the new generalized Caputo sense. Eng. Comput. 2022; preview. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Shikongo, A.; Atangana, A. Fractal Fractional Derivative Operator Method on MCF-7 Cell Line Dynamics. Stud. Syst. Decis. Control 2022, 373, 319–339. [Google Scholar]
- Saad, K.M. Fractal-fractional Brusselator chemical reaction. Chaos Solitons Fractals 2021, 150, 111087. [Google Scholar] [CrossRef]
- Akgül, A.; Siddique, I. Analysis of MHD Couette flow by fractal-fractional differential operators. Chaos Solitons Fractals 2021, 146, 110893. [Google Scholar] [CrossRef]
- Almalahi, M.A.; Panchal, S.K.; Shatanawi, W.; Abdo, M.S.; Shah, K.; Abodayeh, K. Analytical study of transmission dynamics of 2019-nCoV pandemic via fractal fractional operator. Results Phys. 2021, 24, 104045. [Google Scholar] [CrossRef]
- Shloofa, A.M.; Senua, N.; Ahmadian, A.; Longa, N.M.A.N.; Salahshour, S. Solving fractal-fractional differential equations using operational matrix of derivatives via Hilfer fractal-fractional derivative sense. Appl. Numer. Math. 2022, 178, 386–403. [Google Scholar] [CrossRef]
- Khan, H.; Ahmad, F.; Tunc, O.; Idrees, M. On fractal-fractional Covid-19 mathematical model. Chaos Solitons Fractals 2022, 157, 111937. [Google Scholar] [CrossRef]
- Khan, H.; Alzabut, J.; Shah, A.; Etemad, S.; Rezapour, S.; Park, C. A study on the fractal-fractional tobacco smoking model. Aims Math. 2022, 7, 13887–13909. [Google Scholar] [CrossRef]
- Khan, N.; Ahmad, Z.; Ahmad, H.; Tchier, F.; Zhang, X.Z.; Murtaza, S. Dynamics of chaotic system based on image encryption through fractal-fractional operator of non-local kernel. Aip Adv. 2022, 12, 055129. [Google Scholar] [CrossRef]
- Abro, K.A.; Atangana, A. Role of non-integer and integer order differentiations on the relaxation phenomena of viscoelastic fluid. Phys. Scr. 2020, 95, 035228. [Google Scholar] [CrossRef]
- Martínez, H.Y.; Aguilar, J.F.G.; Atangana, A. First integral method for non-linear differential equations with conformable derivative. Math. Model. Nat. Phenom. 2018, 13, 14. [Google Scholar] [CrossRef]
- Khan, M.A.; Atangana, A. Dynamics of Ebola disease in the framework of different fractional derivatives. Entropy 2019, 21, 303. [Google Scholar] [CrossRef]
- Malkus, W.V.R. Non-periodic convection at high and low Prandtl number. Mem. Soc. R. Sci. Liege Collect. 1972, 6, 125–128. [Google Scholar]
- Mishra, A.A.; Sanghi, S. A study of the asymmetric Malkus waterwheel: The biased Lorenz equations. Chaos 2006, 16, 013114. [Google Scholar] [CrossRef] [PubMed]
- Alonso, D.B.; Tereshko, V. Local and global Lyapunov exponents in a discrete mass waterwheel, In Chaotic Systems; World Scientific: Singapore, 2010; pp. 35–42. [Google Scholar] [CrossRef]
- Illing, L.; Fordyce, R.F.; Saunders, A.M.; Ormond, R. Experiments witha Malkus-Lorenz water wheel: Chaos and synchronization. Am. J. Phys. 2012, 80, 192. [Google Scholar] [CrossRef]
- Illing, L.; Saunders, A.M.; Hahs, D. Multi-parameter identification from scalar time series generated by a Malkus-Lorenz water wheel. Chaos 2012, 22, 013127. [Google Scholar] [CrossRef]
- Kim, H.; Seo, J.; Jeong, B.; Min, C. An experiment of the Malkus–Lorenz whater wheel and its measurement by image processing. Int. J. Bifurcation Chaos 2017, 27, 1750. [Google Scholar] [CrossRef]
- Tusset, A.M.; Balthazar, J.M.; Ribeiro, M.A.; Lenz, W.B.; Marsola, T.C.L.; Pereira, M.F.V. Dynamics analysis and control of the Malkus–Lorenz waterwheel with parametric errors. In Topics in Nonlinear Mechanics and Physics; Belhaq, M., Ed.; Springer: Singapore, 2019; p. 228. [Google Scholar]
- Matson, L.E. The Malkus–Lorenz water wheel revisited. Am. J. Phys. 2007, 75, 1114. [Google Scholar] [CrossRef]
- Tylee, J.L. Chaos in a real system. Simulation 1995, 64, 176–183. [Google Scholar] [CrossRef]
- Alonso, D.B. Deterministic Chaos in Malkus’ Waterwheel: A Simple Dynamical System on the Verge of Low-Dimensional Chaotic Behavior; LAP Lambert Academic Publishing: Saarbrücken, Germany, 2010; ISBN 9783838358642. [Google Scholar]
- Lopez, A.G.; Benito, F.; Sabuco, J.; Delgado-Bonale, A. The thermodynamic efficiency of the Lorenz system. arXiv 2022, arXiv:2202.07653. [Google Scholar] [CrossRef]
- Yavari, M.; Nazemi, A.; Mortezaee, M. On chaos control of nonlinear fractional chaotic systems via a neural collocation optimization scheme and some applications. New Astron. 2022, 94, 101794. [Google Scholar] [CrossRef]
- Platt, J.A.; Penny, S.G.; Smith, T.A.; Chen, T.-C.; Abarbanel, H.D.I. A Systematic Exploration of Reservoir Computing for Forecasting Complex Spatiotemporal Dynamics. arXiv 2022, arXiv:2201.08910. [Google Scholar] [CrossRef] [PubMed]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Chen, W. Time–space fabric underlying anomalous diffusion. Chaos Solitons Fractals 2006, 28, 923–929. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Akinlar, M.A.; Tchier, F.; Inc, M. Chaos control and solutions of fractional-order Malkus waterwheel model. Chaos Solitons Fractals 2020, 135, 109746. [Google Scholar] [CrossRef]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Rezapour, S.; Boulfoul, A.; Tellab, B.; Samei, M.E.; Etemad, S.; George, R. Fixed Point Theory and the Liouville–Caputo Integro-Differential FBVP with Multiple Nonlinear Terms. J. Funct. Spaces 2022, 2022, 6713533. [Google Scholar] [CrossRef]
- Rezapour, S.; Deressa, C.T.; Hussain, A.; Etemad, S.; George, R.; Ahmad, B. A Theoretical Analysis of a Fractional Multi-Dimensional System of Boundary Value Problems on the Methylpropane Graph via Fixed Point Technique. Mathematics 2022, 10, 568. [Google Scholar] [CrossRef]
- Guran, L.; Mitrović, Z.D.; Reddy, G.S.M.; Belhenniche, A.; Radenović, S. Applications of a Fixed Point Result for Solving Nonlinear Fractional and Integral Differential Equations. Fractal Fract. 2021, 5, 211. [Google Scholar] [CrossRef]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione. G. Ist. Ital. Attuari 1933, 4, 83–91. [Google Scholar]
- Marsaglia, G.; Tsang, W.W.; Wang, J. Evaluating Kolmogorov’s Distribution. J. Stat. Softw. 2003, 8, 1–4. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bolboacă, S.D. Performances of Shannon’s Entropy Statistic in Assessment of Distribution of Data. Ovidius Univ. Ann. Chem. 2017, 28, 30–42. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guran, L.; Akgül, E.K.; Akgül, A.; Bota, M.-F. Remarks on Fractal-Fractional Malkus Waterwheel Model with Computational Analysis. Symmetry 2022, 14, 2220. https://doi.org/10.3390/sym14102220
Guran L, Akgül EK, Akgül A, Bota M-F. Remarks on Fractal-Fractional Malkus Waterwheel Model with Computational Analysis. Symmetry. 2022; 14(10):2220. https://doi.org/10.3390/sym14102220
Chicago/Turabian StyleGuran, Liliana, Esra Karataş Akgül, Ali Akgül, and Monica-Felicia Bota. 2022. "Remarks on Fractal-Fractional Malkus Waterwheel Model with Computational Analysis" Symmetry 14, no. 10: 2220. https://doi.org/10.3390/sym14102220
APA StyleGuran, L., Akgül, E. K., Akgül, A., & Bota, M.-F. (2022). Remarks on Fractal-Fractional Malkus Waterwheel Model with Computational Analysis. Symmetry, 14(10), 2220. https://doi.org/10.3390/sym14102220









