Abstract
The transmission of high-speed data over communication channels is the function of digital communication systems. Due to linear and nonlinear distortions, data transmitted through this process is distorted. In a communication system, the channel is the medium through which signals are transmitted. The useful signal received at the receiver becomes corrupted because it is associated with noise, ISI, CCI, etc. The equalizers function at the front end of the receiver to eliminate these factors, and they are designed to make them work efficiently with proper network topology and parameters. In the case of highly dispersive and nonlinear channels, it is well known that neural network-based equalizers are more effective than linear equalizers, which use finite impulse response filters. An alternative approach to training neural network-based equalizers is to use metaheuristic algorithms. Here, in this work, to develop the symmetry-based efficient channel equalization in wireless communication, this paper proposes a modified form of bat algorithm trained with ANN for channel equalization. It adopts a population-based and local search algorithm to exploit the advantages of bats’ echolocation. The foremost initiative is to boost the flexibility of both the variants of the proposed algorithm and the utilization of proper weight, topology, and the transfer function of ANN in channel equalization. To evaluate the equalizer’s performance, MSE and BER can be calculated by considering popular nonlinear channels and adding nonlinearities. Experimental and statistical analyses show that, in comparison with the bat as well as variants of the bat and state-of-the-art algorithms, the proposed algorithm substantially outperforms them significantly, based on MSE and BER.
1. Introduction
Nowadays, high-speed data can be transmitted through communication channels. Transmitted data become corrupted as a result of linear and nonlinear distortions. The effects of linear distortion include intersymbol interference (ISI), co-channel interference (CCI), and adjacent channel interference (ACI) when additive white Gaussian noise is present. A communication pipeline is subject to nonlinear distortion due to impulse noise, modulation, demodulation, amplification, and crosstalk. Adaptive channel equalizers are needed for recuperating information from communication channels [1,2]. In [3], the authors proposed optimal preprocessing strategies for restoring the signals from nonlinear channels. For the perfect reform of discrete data transmission during a channel, Touri et al. [4] have suggested some ideas. Soft computing tools-based adaptive equalizers, such as neural network-based equalizers [5], were developed in the late 80s; for nonlinear and complex channels, it has been observed that these methods are very suitable. Patra et al. [6] used the Chebyshev artificial neural network for the problem of equalization. The JPRNN-based equalizer using RTRL, developed by Zhao H. et al. [7], provides some encouraging results. The amalgamation of the FIR filter and FLNN with an adaptive decision feedback equalizer (DFE) is introduced in [8]. Several types of NN-based equalizers were introduced by Zhao et al. [9,10,11,12,13] to resolve these complex issues. Regarding the problem of equalization [7,8,9,10,11,12,13,14,15], ANN has proven to be a useful tool despite its complexity. Since conventional training algorithms do not work well in many instances [16,17], bio-inspired optimization algorithms are used to train ANNs. PSO remains progressively connected within the zone of figuring insights. Moreover, it loans itself as being appropriate to an assortment of issues of optimization. Das. et al. [18] used PSO to train an NE for nonlinear channels. The ANN [19,20,21,22,23], trained with evolutionary algorithms, are applied in nonlinear channel equalization for channel prediction. Potter et al. [23] used recurrent neural networks (RNN) and the successful application of PSO variants to optimize network parameters. Moreover, intricacy becomes exceptionally large here due to utilizing numerous optimization calculations and becomes a dead moderate sense of utilizing differential evolution (DE). The neural network model applied in this work is based on a training procedure mentioned in the next section of this article, although grammatical swarm optimization [24] can be applied to achieve a topology for the neural network. The author proposed an equalizer whose performance and execution outperform contemporary ANN-based [5,6,7] and neuro-fuzzy [14,15] equalizers available in the literature, which is the real essence of this work. Hybrid ANN was introduced by Panigrahi et al. [25] for the plummeting training time and delaying an assessment on equalization in the case of interference with the co-channel. The equalization of a communication channel with RBFs trained on GA has been reported by Mohapatra et al. [26]. The training scheme proposed by [27], using DSO-ANN, also gave good results in nonlinear channel equalization. The neural network model using FFA for channel equalization, introduced by Mohapatra et al. [28], provides some useful results. WNN, trained by a symbiotic organism search algorithm-based nonlinear equalizer, also provides a good result [29]. There are several kinds of neural network equalizers, including back-propagation (BP) algorithms and gradient descent algorithms [30,31]. Due to its slow convergence rate and the tendency to get trapped in local minima, this algorithm has limited performance. Several studies have indicated that evolutionary computing-based algorithms are capable of training neural networks for nonlinear channel equalization problems to overcome the limitations of gradient-based algorithms [32,33,34,35,36]. Shi et al. [37] proposed gated recycle unit neural networks for the equalization of QAM signals. The estimation of MIMO channels using feedback neural networks is performed by using three-layer neural networks by Zhang et al. [38] and has been well presented. In M-DPSK (M-ary differential phase shift keying), Baeza et al. [39] proposed a noncoherent massive single-output multiple-input system that is robust to the temporal correlation of the channels. Moreover, this SIMO-based M-DPSK uses a new constellation design that takes into account the interuser and intersymbol interferences for effective noncoherent detection in Rician channels [40]. Recently, fuzzy firefly-based ANNs, proposed by Mohapatra et al. [41] in nonlinear channel equalization, have been well reported. Fascinatingly, in these works, three modified forms of bat algorithms are applied for optimization purposes. An appropriate neuron’s weights, transfer functions, and topology were discovered through training the neural networks and, thus, with the successful application of these algorithms to optimize all network parameters.
In summary, this work has made the following contributions:
- Proposed a modified form of the bat algorithm trained with ANN in channel equalization.
- ANN-based nonlinear channel equalizers in wireless communication systems are trained using a modified version of the bat algorithm.
- Three nonlinear channels are tested to verify the superiority of the proposed work.
- Three nonlinearities were tested to prove how resilient the proposed scheme is, and the results revealed that the proposed work outperforms other methods in these situations.
The principal outlines of this article are as follows: The problem description is provided in Section 2, followed by a model of the nonlinear channel equalization in Section 3. The simulation study is conceded for performance evaluation and is discussed in Section 4. Lastly, Section 5 concludes the work.
2. Problem Description
Information that is to be transmitted is generated by the data source. In a digital communication system, there are some blocks, such as the data source, encoder, filter, modulator, etc., at the transmitter end, while the demodulator, filter, equalizer, decision device, etc., are placed at the receiver end. Between the transmitter and receiver, there is a channel. The channel is the medium through which information can be propagated from the transmitter to the receiver. At the receiver end, demodulation is first performed at the receiver to retrieve the transmitted signal. The receiver filters then process this demodulated signal, which must be matched to the transmitter filters and channels to provide optimal performance. In the receiver, the equalizer removes distortion caused by channel impairments [1,2]. By using the decision device, the encoded, transmitted signal is estimated. Figure 1 presents a model of nonlinear channel equalization. Based on co-channel and channel impulse responses, the following expression was identified. The linear channel is typically characterized by an FIR model, which is articulated as follows [5,32]:
and stands for the length and tap weights of the of the impulse response of the channel, respectively, as mentioned in Equation (1). We presume a parallel model that makes the study simple. The transmitted symbols are in the forms of self-regulating i.i.d data series’ of {±1} and are mutually independent.
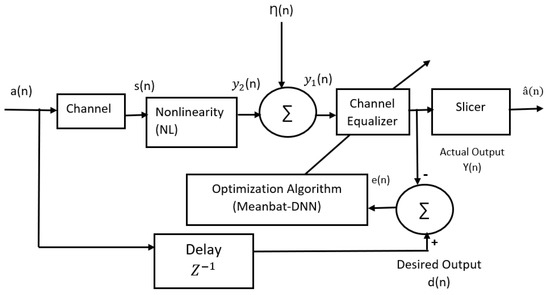
Figure 1.
Model of Nonlinear Channel Equalization.
Figure 1 illustrates a nonlinearity introduced in the channel output, identified as the NL block.
Based on the output from the NL block, we see the following:
This nonlinearity is defined by the NL block as .
Equation (3) shows the received signal as nothing more than a combination of the noisy signal caused by the nonlinearity of the channel, and the noise element should be Gaussian with variance
Equalizers reconstruct the original signal or delayed signal placed at the front end of the receivers.
Now,, is the channel observation vector, and the equalizers aim to approximate the transmitted sequences , when and are the equalizer order and delay factors, respectively.
Calculating the difference signal can be done by comparing the output of the equalizer with the desired signal which is shown in Equation (4)
A slicer provides an estimate of the transmitted symbol, as shown in the equation below:
Because of , the instantaneous power of the difference signal can be identified as a cost function, which is always positive, and it is replaced as . We will adopt an algorithm to update the weights iteratively so that: must be minimum and reduced to zero.
3. Proposed Model
In the literature, several ANNs have been suggested. In this work, a bat-inspired algorithm is proposed to optimize the ANN’s weights and structure. Each outcome in the populace of the bat algorithm requires both configuration and weight resolution. A fitness function is used to determine the number of layers, the number of nodes, and the weights of an ANN, all of which are parts of the proposed technique. By changing the parameters, such as velocity, frequency, and location, the diversification of each solution in this process is accomplished. The bat’s procedure’s diversity function can be added to the ANN configuration, and the biases and weights remain the same. In the following subsections, the specifics of the system are given.
3.1. Bat Algorithm
Initially proposed by Yang [42], this algorithm uses the echolocation behavior of bats to determine how fast they move. Bats emit an extremely noisy sound pulse and pay heed to the echo coming back from the substance. To hunt for prey, bats move randomly using frequency, velocity, and location. Each bat in the population is modified for further movement in the bat algorithm based on its frequency, velocity, and position. The algorithm is designed to mimic the ability of bats to find their prey. The bat algorithm follows a set of bat-action simplifications and idealization laws that Yang found and suggested. Rather than simply using a population-based algorithm, the bat algorithm makes use of local search capabilities. It requires a series of iterations, where a set of alternatives varies by arbitrarily changing the bandwidth of the signal, which is improved using harmonics. The pulse rate and loudness change only if the latest result is approved. Based on the following formulas, the frequency, velocity, and location of the results are estimated:
Upon initialization, each bat has a frequency associated with it, which is derived uniformly from [. A random vector resulting from a uniform distribution [0, 1] is.
For this purpose, to have a healthy mix of discovery and manipulation, the bat algorithm may be called a frequency tuning algorithm. In Equation (12), a new solution is created locally for each bat.
Here, ∈ is a random number that lies in [−1, 1] that attempts at the random walk power and direction, and identifies as the average loudness. The is the intensity of sound, termed loudness, and the pulse rate must be changed in each iteration. Usually, the sound reduces as a bat seeks its prey as the pulse rate escalates. The terms and are described in the following equations in which and are the same value, which is 0.9, as in [42].
Only if the proposed solution is approved will the loudness and pulse rate be improved. The flowchart of the bat algorithm is shown in Figure 2.
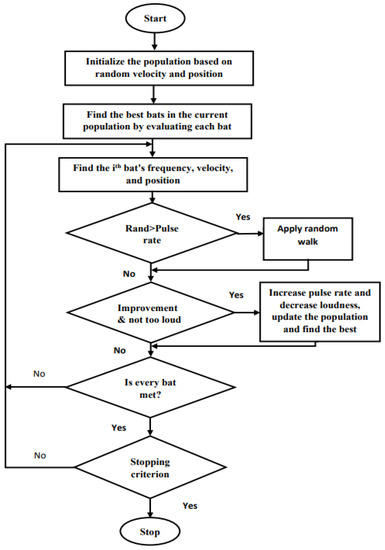
Figure 2.
Flowchart of bat algorithm.
BatDNN: The BatDNN [43] is simplified as a basic dynamic neural network. Figure 1 shows the flow chart of the algorithm for optimizing the ANN model implemented. Generally, it consists of two parts of the solution for the population. In the ANN structure, the first part represents the ANN configuration, and the next part represents the W&B configurations. In the original population, the solution configurations are randomly distributed, W&B is determined to match every arrangement, and the significance of W&B is determined at the end randomly. The adjustments in frequency, velocity, and position are likely to be applied to the configuration solution. In both instances, the likelihood is the same. As is obvious from Figure 1 and the related calculations, the progress of every bat in the quest space is into constantly appreciated positions in this bat algorithm. The search space is established as a binary sample when the configuration result can be changed by the original frequency, velocity, and position [44]. We used the sigmoid attribute to represent the location of the bat in the binary vector.
Modification can be achieved by applying Equation (15) to the output of Equation (11). The value of is set to 1 if the output of is within the range of (0,1), or it is 0.
Thus, we have simple values that comprise the binary for the configuration of every bat entrant chosen for the adaptation, with the assistance of the sigmoid function. Then, based on the current configuration, the weight bias approach is structured. The configuration result will remain the same as the earlier configuration if the algorithm’s adjustment practice is altered by the weight bias solution. A random walking technique is added to the results under some circumstances after producing a new solution. Additionally, the result is approved if the necessary circumstances are contented. When the solution is adopted, the intensity and the beat rate are modified. Until the stopping condition is satisfied, this method is sustained.
MBat-DNN [43]: In a manner similar to that in the PSO standard [45], the basic bat algorithm keeps track of every bat’s location as monitors the pace as well as its movement. It uses loudness and pulse rate modulation as part of its integration of the PSO and local quest. The basic algorithm is similar to PSO, but we were motivated to continue our research by introducing the dominance of best in adjusting the PSO speed by personal best and global best. Bats are moved to the gbest in the standard bat algorithm, which causes the algorithm to experiment, while the influence of pbest is considered to increase the algorithm’s utilization in the updated form. We have altered the Equation (8) into Equation (13).
Mean-BatDNN: In the velocity update equation, as a substitute for comparing gbest and pbest, the present location of every bat is contrasted utilizing the linear amalgamation of the positions of pbest and gbest. As follows, we recommend a new velocity update equation:
We used Equation (14) in this experiment in favor of Equation (7) to examine the result of this adaptation.
3.2. Modified Forms of Bat, Construction, and ANN Training
Bat and its different modified forms have applied many applications, such as feature extraction and feature selection for text categorization [46], optimal coordination of protection systems based on directional over-current relays [47], attribute selection [48], and so on. Based on a biological nervous system, ANN models have specific architecture formats. In ANN models, neurons are structured in a complex, nonlinear manner, similar to the structure of the human brain. An interconnected system of weighted links connects neurons. Network architecture is designed, the number of hidden layers is calculated, the ANN is simulated, as well as the trade-off between the weights and biases is determined through learning and training. Many scientific fields, from finance to hydrology, utilize ANNs to solve real-world problems, and these applications fall into three categories: pattern classification, prediction, and control and optimization. Different kinds of structures are used in the ANN models for clustering, classification, and simulation.
The main objective of this section is to give an overview of the ANN-based channel equalizations for readers’ convenience. A multilayer ANN was chosen in this study for channel equalization. To train the weights, MMSE was used as a criterion for the second layer of the ANN. Our proposed algorithm was used for training and to estimate the input symbols in the third layer. The equalization of the channel was then performed on the estimated symbol in the second layer. As a result, ANNs are more effective in predicting the input symbols. As part of the second layer, the ANN weights were computed, and as part of the third layer, the Mean-BatDNN was used to estimate the input and predict echolocation in one step. A channel equalization response was received from the second layer based on the estimation results.
This study is primarily concerned with training ANN on the three modified bat forms. An interactive network based on population will be built to accomplish this. In this study, a population of 30 networks performed well. The bat population was formed, and the bat community was initiated through this process. It is referred to as the system’s topology. Three modified forms of bats with ANN had the following training procedure:
- Count the number of network errors in the training samples for each network.
- Examine all errors to determine the optimal problem space network.
- The network that has achieved the minimum error should be identified, the program should be terminated, and the weights should be recorded.
- Otherwise, each network’s position and velocity vector can be changed.
- Step 1 should be repeated again.
The transition from being an employee to becoming a manager in ANN development occurs when a particle achieves a target fitness, which is when a result is obtained. It is difficult to equalize a communication network when many variables are in play. ANN has yet to prove itself exceptional in this regard. The purpose of the ANN is to calculate the channel state by constructing and training ANNs. As training data, [±1] is taken. These values were used as input to build the network. The network fitness Equation (15) shows how the MSE was calculated for the entire training collection using the network fitness equation.
The availability of a network is established after the network has satisfied any marginal execution requirements. In Equation (16), the coefficients of correlation were used as the measurable computation.
Here, in this work, the MeanBat_DNN train the entire network, which is built as a multilayer artificial neural network whose parameters, such as weight, topology, transfer function, etc., are suitably optimized.
3.3. The Training Procedure for the Proposed Algorithm with ANN
As shown in Algorithm 1, the author proposed a training algorithm that defines rules for the organizations that act as managers who provide assets (such as parameters to optimize) to a supervisor who gives guidelines to the employee. The equalization problem is then learned by ANNs. As such, the ANN acts as an employee and as a manager. The pseudo-code for the problem is shown in the flow chart below. With L and M, we can identify the number of particles as well as the number of hidden nodes. The following is a flowchart of this training algorithm.
| Algorithm 1. Training algorithm of the proposed equalizer. |
| Assign ANN to a manager For j = 1, 2, … … L Create Bat -as supervisor (j) for ANN-as worker k = 1, 2, … … L make ANN- as worker end end While no solution has been established Update evaluation Specify the maximum number of iterations for (Bat --as manager j = 1, 2, … … L) as (iterations<issuance) for (ANN-as worker k = 1, 2, … … M) test ANN-as worker (k) |
4. Simulations and Results
Modifying the bat algorithm aims to improve the trade-off between exploration and exploitation to achieve higher quality convergence. Additionally, we compared our best method with others in the literature to improve our evaluation. To compare our method with the latest and most similar approaches to ANNs, which optimize both weights and structure, we chose the most recent and most similar results in the literature, especially in the classification area. Table 1 and Table 2 represents the types of channel and non-linearity. Table 3, Table 4 and Table 5 list the results obtained in the simulation in terms of the MSEs and standard deviations. By comparing the PSO with three modified forms of the bat algorithm, the best values obtained are represented by bold letters. The pseudo-codes of all the algorithms are coded in MATLAB R2015a and are implemented on a 15.6-inch FHD Intel® HD Graphic with the memory of 16GB, 2x8GB, DDR4, 2666MHz. In the case of the PSO algorithm, the acceleration constants c1 and c2 were chosen as 0.7 for each. As part of the proposed algorithm, set the population size and number of iterations to 100, as well as the minimum and maximum frequency at 0 and 2, respectively. Loudness is selected as 0.25, the pulse rate is selected as 0.5, and W&B is 0.5. Here, the value of L is set at 30, and M is 5. The performance of the equalizer can be evaluated by using the following three nonlinear channels, as shown in Table 1, and the type of nonlinearity introduced, as shown in Table 2. Typically, the i.i.d sequences with a mean of zero are used as the channel input signals. Additive white Gaussians with a zero mean are introduced into the channel, and it is not dependent on the channel input. We have considered the following three examples for the performance evaluation of the channel equalizer. MSE and BER are the two most important parameters for the equalizer. Three different channels have been analyzed for the MSE and standard deviation statistically, as shown in Table 3, Table 4 and Table 5.

Table 1.
Types of channel.

Table 2.
Types of nonlinearity.

Table 3.
Comparing the mean square error (MSE) for channel-0 over 40 independent runs.

Table 4.
Comparing the mean square error (MSE) for channel-1 over 40 independent runs.

Table 5.
Comparing the mean square error (MSE) for channel-2 over 40 independent runs.
The evaluation of the mean square error and standard deviation for the channel equalization of channel-0 using the proposed algorithm when considering forty observations is seen in Table 3.
The evaluation of the mean square error and standard deviation for the channel equalization of channel-1 using the proposed algorithm when considering forty observations is seen in Table 4.
The evaluation of the mean square error and standard deviation for the channel equalization of channel-2 using the proposed algorithm when considering forty observations is seen in Table 5.
A summary of the results is presented in Table 3, Table 4 and Table 5, which include the best, worst, mean and standard deviation. Using 40 independent runs, ‘Best’ and ‘Worst’ identify the best and worst performances of the algorithms. An algorithm with a lower mean value will be more capable of finding a global optimum solution over 40 independent runs. As a result, the standard deviation can be used to determine the degree of dispersion of the results.
Scenario: 1
Consider the second-order nonlinear channel (CH0) model having a transfer function, as shown in the following Equation (17).
The nonlinearity of the above channel model is introduced in the following Equation (18) to exemplify the consequence on the equalizer performance.
We have compared three modified forms of bat algorithms by N.S. Jaddi et al. [43], with the PSO [18] and BP-ANN [9] having the same simulation parameter, which has already been defined. The bit error rate (BER) was plotted in Figure 3 and the corresponding mean square error (MSE) plotted in Figure 4 with a fixed SNR at 15 dB. A plot of the MSE for channel-0, with a severe nonlinearity as NL = 0, is shown in Figure 4. Using 300 iterations for each algorithm, the Mean-Bat and competing algorithms are compared for convergence performance. It is shown in Figure 4 that the proposed algorithm performed for channel-0 with a nonlinearity NL-0 represented a nonlinearity that occurs due to the saturation of the amplifiers used at the transmitter in a communication system.
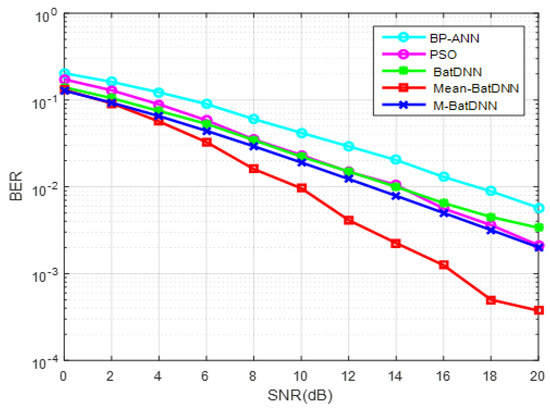
Figure 3.
BER performance for channel CH0.
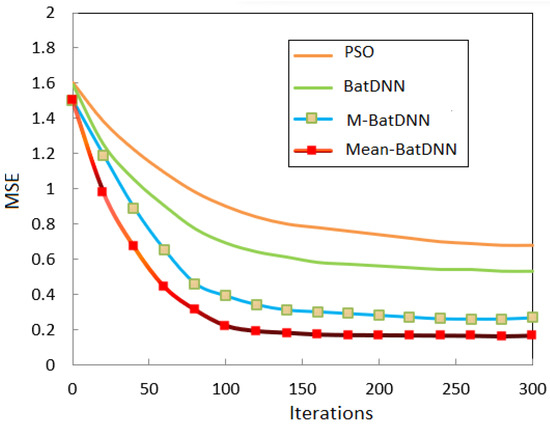
Figure 4.
MSE performance for CH0.
From Figure 4, it can be observed that the Mean-BatDNN showed a better performance than the other three equalizers. As far as the bit error rate is concerned, from Figure 4, it is clear that, up to 4 dB SNR, the performances of all the equalizers are comparable. After that, the Mean-BatDNN outperforms the other four equalizers.
Scenario: 2
In this scenario, the author used another popular nonlinear second-order channel model, as defined in Table 1, as CH1, and nonlinearity is introduced, as shown in Table 2, as NL1. An arbitrary nonlinearity encountered in a communication system is NL = 1 and is, in this case, for analyzing the BER performance. The bit error rate (BER) is plotted in Figure 5.
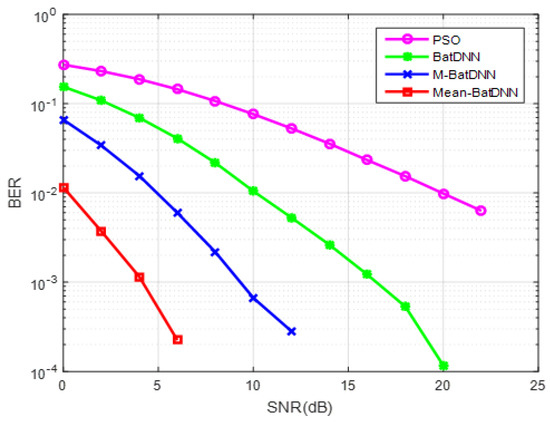
Figure 5.
BER performance for channel CH1.
As shown in Figure 5, the proposed algorithm has superior performance over the other three algorithms for channel-1 with nonlinearity 1. From Figure 5, it is observed that all SNR Mean-BatDNN equalizers demonstrated a better performance than the other three equalizers.
Scenario: 3
An evaluation of the performance of the proposed algorithm with nonlinearity 2 is carried out to explore whether the algorithm’s performance is consistent. It is calculated by transmitting 1,000,000 samples and adding the noise of different SNRs to the channel output to calculate the bit error rate. The equalizer estimates the transmitted sample based on the received samples. An increment of one is applied when the estimated sample does not match the transmitted sample. In this scenario, we have presented a widely used third-order nonlinear channel [49], as described in Table 1, as CH2, and the nonlinearity introduced as NL2 is shown in Table 2 for the simulations.
In this example, BER is plotted, which is shown in Figure 6. The simulation parameter is the same as in [32], which has already been mentioned in the above section. From this figure, it is clear that after 10 dB SNR, the Mean-BatDNN performs better than the other two equalizers.
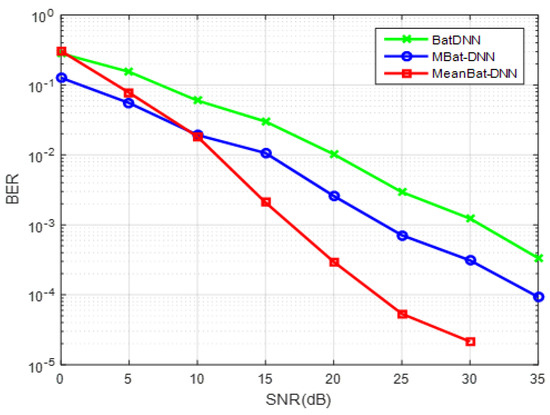
Figure 6.
BER performance for channel CH2.
5. Conclusions
In this work, an ANN-based nonlinear channel equalization problem is addressed using an efficient bat algorithm and its modified form. Using the proposed approach, we were able to identify promising areas of the solution space by avoiding local minima and performing exploration tasks.
Gradient algorithm-based equalizers struggle to accurately model the channel characteristics in the event of a burst error. The article presents a training strategy for an equalizer that we have proposed. The said equalizer trained modified forms of the algorithm with ANN in channel equalization. Simulations were conducted on three wireless communication channels with three different nonlinearities to evaluate the performance of the proposed algorithm. The interpretations of the algorithm were evaluated for their efficiency based on two parameters and correlated with each other, i.e., MSE and BER. It is observed that our equalizer executes better than the existing neural network-based equalizers in all noise circumstances. The main contribution can be focused on as follows:
- Develop a learning procedure for ANNs.
- Make use of this algorithm trained with neural networks in channel equalization.
- In this work, the nonlinearities are used to evaluate the performance of different channels.
In this paper, we explore efficient methods for equalization. This paper utilizes this algorithm for the said problem. The use of population-based algorithms, network topology, and transfer functions for ANN training is the essence of the contributions made in this paper. The approaches for the proposed equalizer used here in this paper provide thought-provoking results in the literature on equalizers, which are found to be better than the equalizers based on ANN as well as neuro-fuzzy equalizers. In addition, the MSE and BER of the proposed equalizers were found to perform better in all noise conditions without prior knowledge of SNR.
A future application of the proposed training method may include training other neural networks, including RBF, wavelet neural networks (WNN), and functional link artificial neural networks (FLAN) for nonlinear channel equalization.
Furthermore, the proposed method may also be used to solve a wide range of engineering problems, including node localization in wireless sensor networks, designing digital filters, MIMO communications, smart antenna design, and so on.
Author Contributions
Conceptualization, P.K.M., S.K.R. and S.K.B; writing—original draft preparation, P.K.M., S.K.R. and S.K.B.; data curation, P.K.M., S.K.R. and S.K.B.; funding acquisition, M.H.; investigation, S.K., M.H., M.B.J. and A.W.M.; methodology, S.K.B. and M.H.; project administration, resources, and supervision, M.H., M.B.J. and A.W.M.; writing—review and editing, S.K., M.H., M.B.J. and A.W.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the UMS publication grant scheme.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stearns, S.D. Adaptive Signal Processing; Pearson Education: London, UK, 2003. [Google Scholar] [CrossRef]
- Haykin, S. Adaptive Filter Theory, 5th ed.; Pearson Education: London, UK, 2008. [Google Scholar]
- Voulgaris, P.G.; Hadjicostics, C.N. Optimal processing strategies for perfect reconstruction of binarysignals under power-constrained transmission. In Proceedings of the IEEE Conference on Decision and Control, Atlantis, Bahamas, 14–17 December 2004; Volume 4, pp. 4040–4045. [Google Scholar]
- Touri, R.; Voulgaris, P.G.; Hadjicostis, C.N. Time varying power limited preprocessing for perfect reconstruction of binary signals. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 5722–5727. [Google Scholar]
- Patra, J.; Pal, R.; Baliarsingh, R.; Panda, G. Nonlinear channel equalization for QAM signal constellation using artificial neural networks. IEEE Trans. Syst. Man Cybern. Part B 1999, 29, 262–271. [Google Scholar] [CrossRef]
- Patra, J.C.; Poh, W.B.; Chaudhari, N.S.; Das, A. Nonlinear channel equalization with QAM signal using Chebyshev artificial neural network. In Proceedings of the International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; pp. 3214–3219. [Google Scholar]
- Zhao, H.; Zeng, X.; Zhang, J.; Liu, Y.; Wang, X.; Li, T. A novel joint-processing adaptive nonlinear equalizer using a modular recurrent neural network for chaotic communication systems. Neural Netw. 2011, 24, 12–18. [Google Scholar] [CrossRef]
- Zhao, H.; Zeng, X.; Zhang, X.; Zhang, J.; Liu, Y.; Wei, T. An adaptive decision feedback equalizer based on the combination of the FIR and FLNN. Digit. Signal Process. 2011, 21, 679–689. [Google Scholar] [CrossRef]
- Zhao, H.; Zeng, X.; Zhang, J.; Li, T.; Liu, Y.; Ruan, D. Pipelined functional link artificial recurrent neural network with the decision feedback structure for nonlinear channel equalization. Inf. Sci. 2011, 181, 3677–3692. [Google Scholar]
- Zhao, H.; Zhang, J. Adaptively combined FIR and functional link neural network equalizer for nonlinear communication channel. IEEE Trans. Neural Netw. 2009, 20, 665–674. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.Q.; Zeng, X.P.; He, Z.Y.; Jin, W.D.; Li, T.R. Complex-valued pipelined decision feedback recurrent neural network for nonlinear channel equalization. IET Commun. 2012, 6, 1082–1096. [Google Scholar] [CrossRef]
- Zhao, H.; Zeng, X.; Zhang, J. Adaptive reduced feedback FLNN nonlinear filter for active control of nonlinear noise processes. Signal Process. 2010, 90, 834–847. [Google Scholar] [CrossRef]
- Zhao, H.; Zeng, X.; Zhang, J.; Li, T. Nonlinear adaptive equalizer using a pipelined decision feedback recurrent neural network in communication systems. IEEE Trans. Commun. 2010, 58, 2193–2198. [Google Scholar] [CrossRef]
- Abiyev, R.H.; Kaynak, O.; Alshanableh, T.; Mamedov, F. A type-2 neuro-fuzzy system based on clustering and gradient techniques applied to system identification and channel equalization. Appl. Soft Comput. 2011, 11, 1396–1406. [Google Scholar] [CrossRef]
- Panigrahi, S.P.; Nayak, S.K.; Padhy, S.K. A genetic-based neuro-fuzzy controller for blind equalization of time-varying channels. Int. J. Adapt. Control Signal Process. 2008, 22, 705–716. [Google Scholar]
- Yogi, S.; Subhashini, K.; Satapathy, J. A PSO based Functional Link Artificial Neural Network training algorithm for equalization of digital communication channels. In Proceedings of the 5th International Conference on Industrial and Information Systems, Mangalore, India, 29 July–1 August 2010; pp. 107–112. [Google Scholar]
- Chau, K.W. Particle swarm optimization training algorithm for ANNs in stage prediction of Shing Mun River. J. Hydrol. 2006, 329, 363–367. [Google Scholar] [CrossRef]
- Das, G.; Pattnaik, P.K.; Padhy, S.K. Artificial Neural Network trained by Particle Swarm Optimization for non-linear channel equalization. Expert Syst. Appl. 2014, 41, 3491–3496. [Google Scholar] [CrossRef]
- Lee, C.-H.; Lee, Y.-C. Nonlinear systems design by a novel fuzzy neural system via hybridization of electromagnetism-like mechanism and particle swarm optimisation algorithms. Inf. Sci. 2012, 186, 59–72. [Google Scholar] [CrossRef]
- Lin, C.-J.; Liu, Y.-C. Image backlight compensation using neuro-fuzzy networks with immune particle swarm optimization. Expert Syst. Appl. 2009, 36, 5212–5220. [Google Scholar] [CrossRef]
- Lin, C.-J.; Chen, C.-H. Nonlinear system control using self-evolving neural fuzzy inference networks with reinforcement evolutionary learning. Appl. Soft Comput. 2011, 11, 5463–5476. [Google Scholar] [CrossRef]
- Hong, W.-C. Rainfall forecasting by technological machine learning models. Appl. Math. Comput. 2008, 200, 41–57. [Google Scholar] [CrossRef]
- Potter, C.; Venayagamoorthy, G.K.; Kosbar, K. RNN based MIMO channel prediction. Signal Process. 2010, 90, 440–450. [Google Scholar] [CrossRef]
- de Mingo López, L.F.; Blas, N.G.; Arteta, A. The optimal combination: Grammatical swarm, particle swarm optimization and neural networks. J. Comput. Sci. 2012, 3, 46–55. [Google Scholar] [CrossRef]
- Panigrahi, S.P.; Nayak, S.K.; Padhy, S.K. Hybrid ANN reducing training time requirements and decision delay for equalization in presence of co-channel interference. Appl. Soft Comput. 2008, 8, 1536–1538. [Google Scholar] [CrossRef]
- Mohapatra, P.; Samantara, T.; Panigrahi, S.P.; Nayak, S.K. Equalization of Communication Channels Using GA-Trained RBF Networks. In Progress in Advanced Computing and Intelligent Engineering; Springer: Singapore, 2018; pp. 491–499. [Google Scholar]
- Panda, S.; Mohapatra, P.K.; Panigrahi, S.P. A new training scheme for neural networks and application in non-linear channel equalization. Appl. Soft Comput. 2015, 27, 47–52. [Google Scholar] [CrossRef]
- Mohapatra, P.; Panda, S.; Panigrahi, S.P. Equalizer Modeling Using FFA Trained Neural Networks. In Soft Computing: Theories and Applications; Springer: Singapore, 2018; pp. 569–577. [Google Scholar]
- Nanda, S.J.; Jonwal, N. Robust nonlinear channel equalization using WNN trained by symbiotic organism search algorithm. Appl. Soft Comput. 2017, 57, 197–209. [Google Scholar]
- Patra, J.C.; Chin, W.C.; Meher, P.K.; Chakraborty, G. Legendre-FLANN-based nonlinear channel equalization in wireless communication system. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 1826–1831. [Google Scholar] [CrossRef]
- Patra, J.C.; Pal, R.N. Functional link artificial neural network-based adaptive channel equalization of nonlinear channels with QAM signal. In Proceedings of the 1995 IEEE International Conference on Systems, Man and Cybernetics. Intelligent Systems for the 21st Century, Vancouver, BC, Canada, 22–25 October 1995; pp. 2081–2086. [Google Scholar] [CrossRef]
- Patra, J.C.; Meher, P.K.; Chakraborty, G. Nonlinear channel equalization for wireless communication systems using Legendre neural networks. Signal Process. 2009, 89, 2251–2262. [Google Scholar] [CrossRef]
- Panda, S.; Sarangi, A.; Panigrahi, S.P. A new training strategy for neural network using shuffled frog-leaping algorithm and application to channel equalization. AEU Int. J. Electron. Commun. 2014, 68, 1031–1036. [Google Scholar] [CrossRef]
- Mohapatra, P.; Sahu, P.C.; Parvathi, K.; Panigrahi, S.P. Shuffled Frog-Leaping Algorithm trained RBFNN Equalizer. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2017, 9, 249–256. [Google Scholar]
- Ingle, K.K.; Jatoth, R.K. An Efficient JAYA Algorithm with Lévy Flight for Non-linear Channel Equalization. Expert Syst. Appl. 2019, 145, 112970. [Google Scholar] [CrossRef]
- Ingle, K.K.; Jatoth, R.K. A new training scheme for neural network based non-linear channel equalizers in wireless communication system using Cuckoo Search Algorithm. AEU Int. J. Electron. Commun. 2020, 138, 153371. [Google Scholar] [CrossRef]
- Shi, H.; Yan, T. Adaptive Equalization for QAM Signals Using Gated Recycle Unit Neural Network. In Proceedings of the 2021 3rd International Conference on Advances in Computer Technology, Information Science and Communication (CTISC), Shanghai, China, 23–25 April 2021; pp. 210–214. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X. MIMO channel estimation and equalization using three-layer neural networks with feedback. Tsinghua Sci. Technol. 2007, 12, 658–662. [Google Scholar] [CrossRef]
- Baeza, V.M.; Armada, A.G.; El-Hajjar, M.; Hanzo, L. Performance of a Non-Coherent Massive SIMO M-DPSK System. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Baeza, V.M.; Armada, A.G. Non-Coherent Massive SIMO System Based on M-DPSK for Rician Channels. IEEE Trans. Veh. Technol. 2019, 68, 2413–2426. [Google Scholar] [CrossRef]
- Mohapatra, P.K.; Rout, S.K.; Bisoy, S.K.; Sain, M. Training Strategy of Fuzzy-Firefly Based ANN in Non-Linear Channel Equalization. IEEE Access 2022, 10, 51229–51241. [Google Scholar] [CrossRef]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NISCO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Jaddi, N.S.; Abdullah, S.; Hamdan, A.R. Optimization of neural network model using modified bat-inspired algorithm. Appl. Soft Comput. 2015, 37, 71–86. [Google Scholar] [CrossRef]
- Nakamura, R.Y.M.; Pereira, L.A.M.; Costa, K.A.; Rodrigues, D.; Papa, J.P.; Yang, X.-S. BBA: A binary bat algorithm for feature selection. In Proceedings of the 25th SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Ouro Preto, Brazil, 22–25 August 2012; pp. 291–297. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Eligüzel, N.; Çetinkaya, C.; Dereli, T. A novel approach for text categorization by applying hybrid genetic bat algorithm through feature extraction and feature selection methods. Expert Syst. Appl. 2022, 202, 117433. [Google Scholar] [CrossRef]
- Sampaio, F.C.; Tofoli, F.L.; Melo, L.S.; Barroso, G.C.; Sampaio, R.F.; Leão, R.P.S. Adaptive fuzzy directional bat algorithm for the optimal coordination of protection systems based on directional overcurrent relays. Electr. Power Syst. Res. 2022, 211, 108619. [Google Scholar] [CrossRef]
- Akila, S.; Christe, S.A. A wrapper based binary bat algorithm with greedy crossover for attribute selection. Expert Syst. Appl. 2021, 187, 115828. [Google Scholar] [CrossRef]
- Liang, J.; Ding, Z. FIR channel estimation through generalized cumulant slice weighting. IEEE Trans. Signal Process. 2004, 52, 657–667. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).