Abstract
A high-throughput approach to determine the equilibrium shape of a crystal by brute force is impractical due to the vast number of density functional theory (DFT) calculations required along just a single crystallographic direction. We propose a screening method that allows the bypass of performing DFT calculations for each candidate surface. Using a series of physically-motivated simplifications, we are able to consider the relative surface energy of each of the large number of candidate surfaces required to solve the surface energy minimization problem in 3 dimensions. Application of this technique to calculate the surface energy landscapes of a set of well-known crystal structures demonstrates high accuracy in the prediction of stable planes and validates its potential as a valuable tool in ab initio determination of equilibrium crystal shapes.
1. Introduction
The surface energy landscape of a material drives many aspects of its behavior and properties. For instance, surface energies play an important role in determining (i) the microstructures arising during solidification [1] and precipitation from liquid phases [2] and (ii) colloidal nanocrystal shapes [3]. As a result, surface energies provide valuable inputs into the materials design and optimization processes in addition to furthering our understanding of morphologies observed in natural processes.
In recent decades, it has become possible to compute surface energies entirely from first principles, starting from quantum mechanics [4,5,6,7,8,9]. The computational infrastructure is well-equipped to solve the “forward problem”, namely: given a surface, what is its energy? However, truly predicting equilibrium crystal shapes would, in principle, involve calculating a very large number of candidate surface energies in search of those that are sufficiently low to actually form in thermodynamic equilibrium, a process that is computationally intensive. It is therefore of considerable benefit to develop simple screening methods to systematically identify candidate low-energy surfaces in order to selectively focus the expensive quantum mechanical calculation efforts. This is the aim of this paper.
2. Methods
2.1. A Simple Model of Surface Energy
The classical broken bond method, which relates the energy of a surface to the number of bonds broken to cut the surface out of a bulk, is simple yet generally accurate enough to reveal the relative stability of a set of planes [10]. A quantitative surface energy value can be estimated by assigning to each bond its appropriately-scaled, experimentally-determined heat of sublimation. Due to its simplicity, this method’s predictive power is best suited for crystals without strong directional bonds. Attempts to improve the accuracy of the broken bond method have explored added complexity to the bonds or the consideration of interactions beyond the first nearest neighbor. Examples have included the addition of atomic species labels to bonds [11], empirical potentials to describe bonds [12], neighbor distance weighting [13], and bonds beyond the nearest neighbor such as between sublattices [14,15].
Having reduced the surface energy screening problem to a purely geometric problem, we still face a challenge in enumerating all the possibilities:
- There are an infinite number of possible surface directions.
- For a given direction, there are an infinite number of possible locations at which to cut the crystal to make a surface.
Fortunately, simple considerations can reduce both sets of infinite possibilities to a manageable finite number. For direction, we can use the fact that it is empirically found that low-energy surfaces are typically associated with low-Miller index planes. In addition, integral Miller indices imply periodic surface termination and these are the only types of surfaces that can be computed using standard periodic-boundary-condition electronic structure codes. For cut plane location, we exploit the fact that different cut planes can be grouped into a finite number of sets, each containing cut planes that necessarily induce the same number of broken bonds. It is then sufficient to compute the number of broken bonds for one representative member of each of those sets, thus resulting in a finite number of possibilities.
These considerations suggest the following approach. First, standard algorithms exist to enumerate all nearest neighbor bonds in a crystal structure and have been implemented in open-source codes [16]. Essentially, one can construct a Voronoi tessellation [17] using atomic coordinates as input points and each face in the resulting tessellation will be associated with the nearest-neighbor bond intersecting it orthogonally. For a given surface orientation, we can also construct a supercell of the crystal’s unit cell consisting of (i) the two shortest non-colinear unit cell lattice vectors lying in the plane of the surface and (ii) the shortest third unit cell vector not lying the surface plane. The use of this supercell simplifies the calculation of the number of broken bonds per unit of surface area.
We then project all nearest neighbor bonds within the above supercell onto a one-dimensional space perpendicular to the surface to yield a set of (possibly overlapping) intervals, with each bond being now represented by an interval. Since nearest neighbor bonds may extend past the bounds of the supercell, some bonds need to be periodically repeated to properly represent their “wrap-around” in a system with periodic boundary conditions. Representing all nearest neighbor bonds entirely within one supercell in this fashion facilitates the determination of candidate cut planes for a given direction vector.
With this representation, it also becomes clear that, for a given direction vector, one only needs to consider a discrete set of representative candidate cut plane locations. This set consists of the locations between interval endpoints that originated from any interval. Indeed, the number of intervals that overlap in a region between two endpoints is always constant. Thus, without loss of generality, it is sufficient to only focus on the midpoints between all distinct consecutive endpoints. It is then straightforward to count the number of overlapping intervals at each of the candidate cut plane locations and determine the minimum in order to identify the candidate lowest-energy cut plane location. The resulting number of broken bonds is then normalized by the surface of the intersection of the unit cell with the surface plane to allow comparison with other surface directions.
Of course, this approach does exhibit some limitations. First, different types of chemical bonds may have different intrinsic energies, but it is easy to extend this method to allow for bonds with different bond-breaking energy penalties. More importantly, surfaces often re-construct to minimize the number of broken bonds. This limitation could be addressed by structure prediction algorithms [18,19,20,21]. Finally, at high temperature, modeling a surface structure by a single geometry is a significant approximation. A more realistic model, for instance based on molecular dynamics, should properly account for the fact that interface stability is also governed by entropic factors, due to structural fluctuations [22]. These improvements unfortunately entail significantly increased computational requirements, thus reducing their appeal as part of a simple screening step.
2.2. Wulff Construction
Given a set of surface orientations and associated surface energies, a well-established method to determine which surfaces are thermodynamically stable is the Wulff construction [23,24,25]. This construction yields a convex polyhedron consisting of all stable surfaces, which is called the Wulff shape. Here we recall how this construction can be easily implemented using standard convex hull calculations.
For a set of candidate facets indexed by , let denote facet i’s surface normal unit vector and let denote the associated surface energy, as determined in the previous section. As the number of candidate facets is finite in our setting, the Wulff shape will necessarily consist of flat surfaces. The case in which some parts of the Wulff shape consist of curved surfaces is obtained in the limiting case where .
We seek to determine:
- 1.
- The crystal’s Wulff shape , alternatively described by:
- (a)
- The set of facets of , encoded as vectors , (with K as small as possible) defining the convex hull . Note that gives the facet k’s unit normal and gives its surface energy.
- (b)
- The set of vertices of , denoted , .
- 2.
- The full orientation-dependence of the surface energy, encoded as a function of a normal unit vector u.
The algorithm to obtain from is as follows:
- 1.
- Construct the convex hull of the points and express it in terms of the minimal number of vectors such that .
- 2.
- Compute the convex hull of the points and express it in terms of the minimal number of vectors such that .
- 3.
- For any given unit vector u, compute .
Note that the resulting surface energy , when u is not parallel to one of the stable surface normals, has the interpretation of the surface energy of a microscopically faceted surface, where the facets are sufficiently small to be invisible at the macroscopic scale but are sufficiently large that edge energy contributions are negligible [26].
The above algorithm has been implemented as the command surfbond in the Alloy Theoretical Automated Toolkit (ATAT) [27].
3. Results
As an example, we predict the Wulff shape and calculate the associated surface energy anisotropy for selected crystal structures (see Figure 1). We first consider some simple structures, such as A1 (fcc) and A3 (hcp), where our results agree qualitatively with the Wulff shape determined in earlier DFT studies (e.g., [5]). The agreement is less impressive for elements with the A4 (diamond) structure, such Si or Ge, due to significant and well-documented surface reconstruction effects [28], which are neglected in our simple approach. As a forecasting exercise, we also predict possible Wulff shapes for metastable and high-temperature polymorphs, such the A15 (-W), A5 (-Sn) and A8 (grey Se) structures. These last three crystals are examples of more complex structures where the determination of low-energy orientations and cut plane positions would be extremely difficult to carry out without an automated software tool.
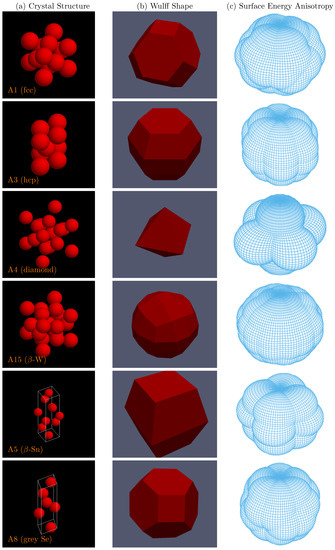
Figure 1.
(a) Left column: example crystal structures (conventional unit cell shown). (b) Center column: Wulff shapes derived from the calculated surface energy anisotropies to the right. (c) Right column: relative surface energy anisotropy surfaces determined by calculating the minimum energy plane over a mesh of plane vector orientations.
The surface energy results of this study are compared to those found in the literature in Figure 2. Plane surface energy ratios are used for comparison instead of absolute energies because the ratios are sufficient to determine the energy ranking of candidate surfaces and thus the Wulff shape. Within any given crystal and plane ratio entry, each point corresponds to results for a different chemical element. Red squares and black circles denote results from prior DFT surface energy calculations [5] obtained with and without surface reconstruction, respectively. We find that the surface energy ratios predicted by our method match well to those calculated using DFT methods. It is useful to note that the prediction error does not seem to be larger for data points that account for reconstruction effects.
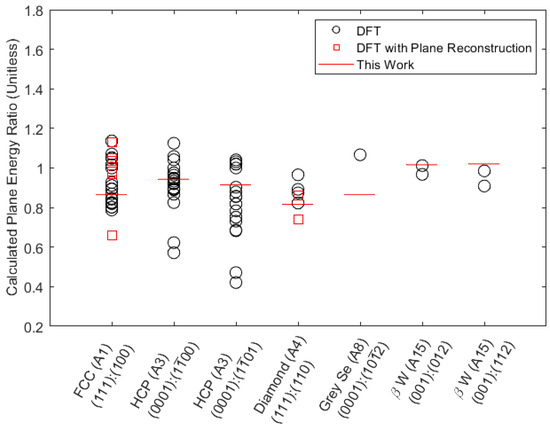
Figure 2.
Ratios of surface energies between two planes for various plane, crystal, and element combinations as found in the literature [5] and calculated in this study. Within each of the seven configurations labeled on the horizontal axis, each point that uses the same marker type represents a different chemical element.
Agreement with the DFT data suggests that our method accurately estimates surface energy ratios between different planes, which would imply that the surface energy rankings are correct. Rankings of surface energies can act as an initial screen to provide insight into planes relevant to several practical applications related to surface anisotropy, such as the calculation of stable crystal morphologies via the Wulff construction. These considerations are discussed further in the next section.
Both of the hcp ratio entries include two points lower than the rest of the group and in both cases correspond to the elements Cd and Zn. It is possible that Cd and Zn have particularly low energy ratios due to electronic structure effects characteristic of Group 12 elements.
4. Discussion
Although the method specifically models interfaces between a solid and the vacuum, the results naturally extend to gas-solid or liquid–solid interfaces. The orientation-dependence of such interfaces have the same symmetry since the non-solid phase is isotropic. In addition, the isotropic phase in these cases consist of random and dynamically fluctuating atomic configurations. As a result, the time-average of the variations in the number of bonds formed relative to a corresponding solid-vacuum interface is expected to, to first order, simply contribute an orientation-independent correction term to the energy. Of course, solid–solid interfaces would demand a different treatment, due to additional symmetry considerations.
Historically, computational high-throughput workflows have primarily focused on materials properties that can be easily and rapidly computed from first principles [29,30,31,32,33,34,35]. Unfortunately, surface energy calculations from first principles are notoriously expensive, in part because large supercells are needed and in part because a large number of candidate surfaces need to be considered in search of those with sufficiently low energies to contribute to the Wulff shape. More recently, high-throughput efforts to quantify a large number of surface energies have been undertaken [5,6] and these methods could benefit from our simple pre-screening scheme as more complex crystal structures are being considered.
Since our predicted surface energies are approximate, it is recommended, for screening purposes, to conservatively not limit oneself to merely the surfaces with lowest predicted energy. This consideration can be implemented by adding a random noise to each predicted energy whose magnitude reflects the uncertainty in the predicted energies. One would then repeat the Wulff construction for many random draws to identify a broader set of surfaces that may be stable.
Another potential application of our tool is to provide input to phase field modeling of microstructure evolution during solidification processes [36,37]. Due to sparsity of accurate surface energies data, the anisotropy in surface energy in these simulations is often specified only in a semi-quantitative fashion. Our approach provides an automated and objective way to assign these parameters. The fact that we obtain relative rather than absolute surface energies is inconsequential in this application because any multiplicative factor can be absorbed in the kinetic prefactor of the phase field equation of motion.
Author Contributions
Conceptualization: A.v.d.W.; Methodology: H.L. and A.v.d.W.; Writing: H.L. and A.v.d.W.; Funding acquisition: A.v.d.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the US Army Research Office under grant number W911NF-21-2-0161. Computational resources were provided by the Center for Computation and Visualization at Brown University and the Extreme Science and Engineering Discovery Environment (XSEDE) Stampede2 at the Texas Advanced Computing Center through allocation TG-DMR050013N, which is supported by National Science Foundation Grant No. ACI-1548562.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| DFT | Density Functional Theory |
| ATAT | Alloy Theoretic Automated Toolkit |
| FCC | Face-Centered Cubic |
| HCP | Hexagonal Close-Packed |
References
- Kurz, W.; Fisher, D. Fundamentals of Solidification; Trans. Tech.: Aedermannsdorf, Switzerland, 1989. [Google Scholar]
- Jamtveit, B.; Meakin, P. Growth, Dissolution and Pattern Formation in Geosystems; Kluwer: Dordrecht, Germany, 1999. [Google Scholar] [CrossRef]
- Yin, Y.; Alivisatos, A. Colloidal nanocrystal synthesis and the organic–inorganic interface. Nature 2005, 437, 664–670. [Google Scholar] [CrossRef]
- Methfessel, M.; Hennig, D.; Scheffler, M. Trends of the surface relaxations, surface energies, and work functions of the 4d transition metals. Phys. Rev. B 1992, 46, 4816–4829. [Google Scholar] [CrossRef] [PubMed]
- Tran, R.; Xu, Z.; Radhakrishnan, B.; Winston, D.; Sun, W.; Persson, K.A.; Ong, S.P. Surface energies of elemental crystals. Sci. Data 2016, 3, 160080. [Google Scholar] [CrossRef] [PubMed]
- Vitos, L.; Ruban, A.V.; Skriver, H.L.; Kollár, J. The surface energy of metals. Surf. Sci. 1998, 411, 186–202. [Google Scholar] [CrossRef]
- Beck, M.J.; van de Walle, A.; Asta, M.D. Surface energetics and structure of the Ge wetting layer on Si (100). Phys. Rev. B 2004, 70, 205337. [Google Scholar] [CrossRef]
- Lanier, C.H.; van de Walle, A.; Erdman, N.; Landree, E.; Warschkow, O.; Kazimirov, A.; Poeppelmeier, K.R.; Zegenhagen, J.; Asta, M.D.; Marks, L.D. The c(6×2) reconstruction on the SrTiO3 (001) Surface. Phys. Rev. B 2007, 76, 045421. [Google Scholar] [CrossRef]
- Chepulskii, R.V.; Butler, W.H.; van de Walle, A.; Curtarolo, S. Surface segregation in nanoparticles from first principles: The case of FePt. Scr. Mater. 2010, 62, 179. [Google Scholar] [CrossRef]
- Galanakis, I.; Bihlmayer, G.; Bellini, V.; Papanikolaou, N.; Zeller, R.; Blügel, S.; Dederichs, P.H. Broken-bond rule for the surface energies of noble metals. Europhys. Lett. (EPL) 2002, 58, 751–757. [Google Scholar] [CrossRef]
- Yang, Z.G.; Enomoto, M. Calculation of the interfacial energy of B1-type carbides and nitrides with austenite. Metall. Mater. Trans. A 2001, 32, 267–274. [Google Scholar] [CrossRef]
- Nicholas, J. Calculation of surface energy as a function of orientation for cubic crystals. Aust. J. Phys. 1968, 21, 21–34. [Google Scholar] [CrossRef]
- Sonderegger, B.; Kozeschnik, E. Generalized Nearest-Neighbor Broken-Bond Analysis of Randomly Oriented Coherent Interfaces in Multicomponent Fcc and Bcc Structures. Metall. Mater. Trans. A 1998, 40, 499–510. [Google Scholar] [CrossRef]
- Mackenzie, J.; Moore, A.; Nicholas, J. Bonds broken at atomically flat crystal surfaces—I: Face-centred and body-centred cubic crystals. J. Phys. Chem. Solids 1962, 23, 185–196. [Google Scholar] [CrossRef]
- Mackenzie, J.; Nicholas, J. Bonds broken at atomically flat crystal surfaces—II: Crystals containing many atoms in a primitive unit cell. J. Phys. Chem. Solids 1962, 23, 197–205. [Google Scholar] [CrossRef]
- van de Walle, A.; Ceder, G. Automating First-Principles Phase Diagram Calculations. J. Phase Equilib. 2002, 23, 348–359. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques: Deuxième Mémoire: Recherches sur les Paralleloèdres Primitifs. J. Reine Angew. Math. 1908, 134, 198. [Google Scholar] [CrossRef]
- Briggs, R.M.; Ciobanu, C.V. Evolutionary approach for finding the atomic structure of steps on stable crystal surfaces. Phys. Rev. B 2007, 75, 195415. [Google Scholar] [CrossRef]
- Chuang, F.; Ciobanu, C.V.; Shenoy, V.; Wang, C.Z.; Ho, K.M. Finding the reconstructions of semiconductor surfaces via a genetic algorithm. Surf. Sci. 2004, 573, L375–L381. [Google Scholar] [CrossRef][Green Version]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef] [PubMed]
- Hong, Q.J.; Yasi, J.; van de Walle, A. A Tetrahedron-tiling Method for Crystal Structure Prediction. Phys. Rev. Mater. Rapid Commun. 2017, 1, 020801. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Asta, M.; Karma, A. Method for computing the anisotropy of the solid–liquid interfacial free energy. Phys. Rev. Lett 2001, 86, 5530. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J.E. Crystalline Variational Problems. Bull. Am. Math. Soc. 1978, 84, 568–588. [Google Scholar] [CrossRef]
- Cahn, J.; Carter, W. Crystal shapes and phase equilibria: A common mathematical basis. Metall. Mater. Trans. A 1996, 27, 1431–1440. [Google Scholar] [CrossRef]
- Roosen, A.R.; McCormack, R.P.; Carter, W.C. Wulffman: A tool for the calculation and display of crystal shapes. Comput. Mater. Sci. 1998, 11, 16–26. [Google Scholar] [CrossRef]
- van de Walle, A.; Chirranjeevi, B.G.; Demers, S.; Hong, Q.J.; Kowalski, A.; Miljacic, L.; Pomrehn, G.S.; Tiwary, P. Ab initio calculation of anisotropic interfacial excess free energies. Phys. Rev. B 2014, 89, 184101. [Google Scholar] [CrossRef]
- van de Walle, A. Multicomponent multisublattice alloys, nonconfigurational entropy and other additions to the Alloy Theoretic Automated Toolkit. Calphad 2009, 33, 266–278. [Google Scholar] [CrossRef]
- Stekolnikov, A.A.; Furthmüller, J.; Bechstedt, F. Absolute surface energies of group-IV semiconductors: Dependence on orientation and reconstruction. Phys. Rev. B 2002, 65, 115318. [Google Scholar] [CrossRef]
- Jain, A.; Hautier, G.; Moore, C.J.; Ong, S.P.; Fischer, C.C.; Mueller, T.; Persson, K.A.; Ceder, G. A high-throughput infrastructure for density functional theory calculations. Comp. Mater. Sci. 2011, 50, 2295. [Google Scholar] [CrossRef]
- Curtarolo, S.; Hart, G.L.; Nardelli, M.B.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computational materials design. Nat. Mater. 2013, 12, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Talapatra, A.; Duong, T.; Son, W.; Gao, H.; Radovic, M.; Arróyave, R. High-throughput combinatorial study of the effect of M site alloying on the solid solution behavior of M2AlC MAX phases. Phys. Rev. B 2016, 94, 104106. [Google Scholar] [CrossRef]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Otis, R.; Liu, Z.K. High-Throughput Thermodynamic Modeling and Uncertainty Quantification for ICME. JOM 2017, 69, 886. [Google Scholar] [CrossRef]
- Curtarolo, S.; Oses, C.; Esters, M.; Hicks, D.; Divilov, S.; Eckert, H.; Friedrich, R.; Mehl, M.J.; Smolyanyuk, A.; Campilongo, X.; et al. Aflow++: A C++ framework for autonomous materials design. arXiv 2022, arXiv:2208.03052. [Google Scholar] [CrossRef]
- van de Walle, A.; Sun, R.; Hong, Q.J.; Kadkhodaei, S. Software tools for high-throughput CALPHAD from first-principles data. Calphad 2017, 58, 70. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Warren, J.A.; Beckermann, C.; Karma, A. Phase-Field Simulation of Solidification. Ann. Rev. Mater. Res. 2002, 32, 163–194. [Google Scholar] [CrossRef]
- Karma, A. Phase Field Methods; Elsevier: Oxford, UK, 2001; Volume 7, pp. 6873–6886. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).