1. Introduction
There exists in quantum optics a family of distinct so-called representations for phase space distributions (or quasi-probabilities), each connected to a different ordering of the underlying creation and destruction operators and . They are as follows.
From a historic viewpoint, the first is the Wigner quasi-probability distribution
W [
1], related to a symmetric operator ordering.
Since in quantum optics the particle number operator is naturally expressed in normal order, another representation ensues: the Glauber–Sudarshan
P one [
2].
Lastly, we confront an alternative representations [
3] called the Husimi
Q one [
4,
5,
6,
7], used when operators stand in anti-normal order.
It is important to note that the quasi probability distributions became a standard tool for analyzing quantum effects in theory and experiment, see Ref. [
8].
Our main idea here is to use the above representations in a Gibbs’ ensemble scenario at the temperature T, discussing and comparing the three representations.
The present article is designed as follows. The long
Section 2 is a review. We discuss the simple harmonic oscillator (HO) and continue with comments on its coherent states. Then, assuming that this HO is in equilibrium with a thermal bath at the temperature
T, we proceed to develop a Gibbs’ ensemble description involving the three representations mentioned in the Introduction.
Section 3 studies mean energies,
Section 4 entropies, and
Section 5 uncertainty relations. Finally, some conclusions are drawn regarding the degree of quantumness of the
P,
Q, and
W treatments in
Section 6.
2. Background Review
2.1. Simple Harmonic Oscillator
The quantized free electromagnetic field is usually regarded as an infinite collection of uncoupled HO of angular frequency
. Each HO has a Hamiltonian [
9]
where
ℏ is the Planck’s constant, and
is the particle-number Hermitian operator, with
and
standing for creation and annihilation operators, respectively. As
and
commute, we have
. Thus,
and
have the same eigenvectors that completely specify the state of the system [
9]. The pertinent set of eigenvectors of the number operator
is
. They constitute a basis in Hilbert’s space
, so that one has [
9]
with
the Kronecker delta, and the closure relation being
Therefore, the eigenvalue equation of the Hamiltonian is
where
is the energy-eigenvalue labeled by
n, with
[
9]. In addition, the following commutation relations hold
2.2. Gibbs-Ensemble
At temperature
T, the density operator in the canonical ensemble reads
being
, with
the Boltzmann constant [
10]. It is well known that the partition function per oscillator
has the form [
10]
that is [
10]
For the system’s mean energy, one writes [
10]
that, taking into account Equation (
8), leads to [
10]
Later, we will connect this quantity with their counterparts in alternative quasi-probability representations.
Further, from Equations (
6) and (
8), plus the definition (
1), we can write [
11,
12]
This special aspect of in terms of the creation and annihilation operators is rather convenient, as we will see below.
2.3. Coherent States
As most people know, the standard coherent states
of the HO are eigenstates of the annihilation operator
, with complex eigenvalues
, which verify [
2]
A coherent state
is a peculiar quantum state, the one that most resembles a classical one. It displays a maximal type of coherence and a classical sort of behavior. The states
are normalized, i.e.,
, and form an overcomplete basis resolution of the identity operator
which is a completeness relation states, with
and
being the coordinates in phase space [
2]. In terms of coherent states, the classical Hamiltonian is expressed as
. It deserves remembering that the phase space variables are related to the creation operator as
. Accordingly, the eigenvalue
is written as
with
and
, so that
[
9].
2.4. P-Representation
In this scenario, the most general density operator is a superposition of projection operators, known as the Glauber-Sudarshan
representation [
13]. One has
where the
function
plays the role of a probability density for the distribution of
values over the complex plane. Moreover,
P is a quasi-probability distribution function because it can display both negative values and strong singularities, especially when the density operator corresponds to a nonclassical state with sub-Poisson photon statistics (see Ref. [
14] and references therein). When this function tends to vary little over large ranges of the parameter
, the nonorthogonality of the coherent states will make little difference, and
P can be interpreted as a probability distribution [
2]. The normalization property of the density operator requires that the
function obey the normalization condition [
2]
Accordingly, the expectation value of an observable
is given by [
14]
In this context,
the average particle-number acquires a simple form that, according to Equation (
17) with
, can be cast in the fashion [
2]
indicating that the average photon number is the mean squared absolute value of the amplitude α. Note that
is the average with respect to
. Clearly, one has
.
For a thermal canonical ensemble state
P is given by Equation (
11) and it becomes [
11]
while the average particle-number is given by [
2]
We can reach the same conclusion in another way. As explained in Refs. [
11,
12], for all normal-ordered operator-averages, we have
so that for
one finds that
where
totally in agreement with Equation (
20).
Finally, according with Equation (
20), the
mean value for the of energy is
a temperature dependent expression, where the statistical average
, is regarded as the
semi classical contribution to the mean energy
U.
2.5. Function
Alternatively, we can take the diagonal matrix element of the density operator
an expression possessing all the properties of a classical probability distribution [
11]. For a thermal state, the
function is the Gaussian quantity [
11]
The
representation yields operator averages in antinormal order, so that
where
denotes the average with respect to
[
11]. Taking
, Equation (
27) reduces to
and we have
Finally, from Equation (
29) the mean energy in terms of the averages of
Q turns out to be
It coincides with the pertinent expression obtained via the
P-representation. Here, the mean value
, which is considered as the
semi classical contribution to the energy
U, was calculated using
with
given by Equation (
26).
2.6. Wigner Function W
The Wigner function
W can be obtained from the
function from the relation [
15]
such that for a thermal state one has
with
. The symmetric ordered operator used in this Wigner representation is, in this case
where
denotes the symmetric product of the creation and destruction operators and
indicates the average with respect to
[
11]. For
we find (the sub-index S means symmetrical)
yielding
From Equation (
36) we encounter the mean energy in the fashion
where we have expressed the mean value of
according to
with
a statistical wight function given by Equation (
33). Thus, in this case we name
.
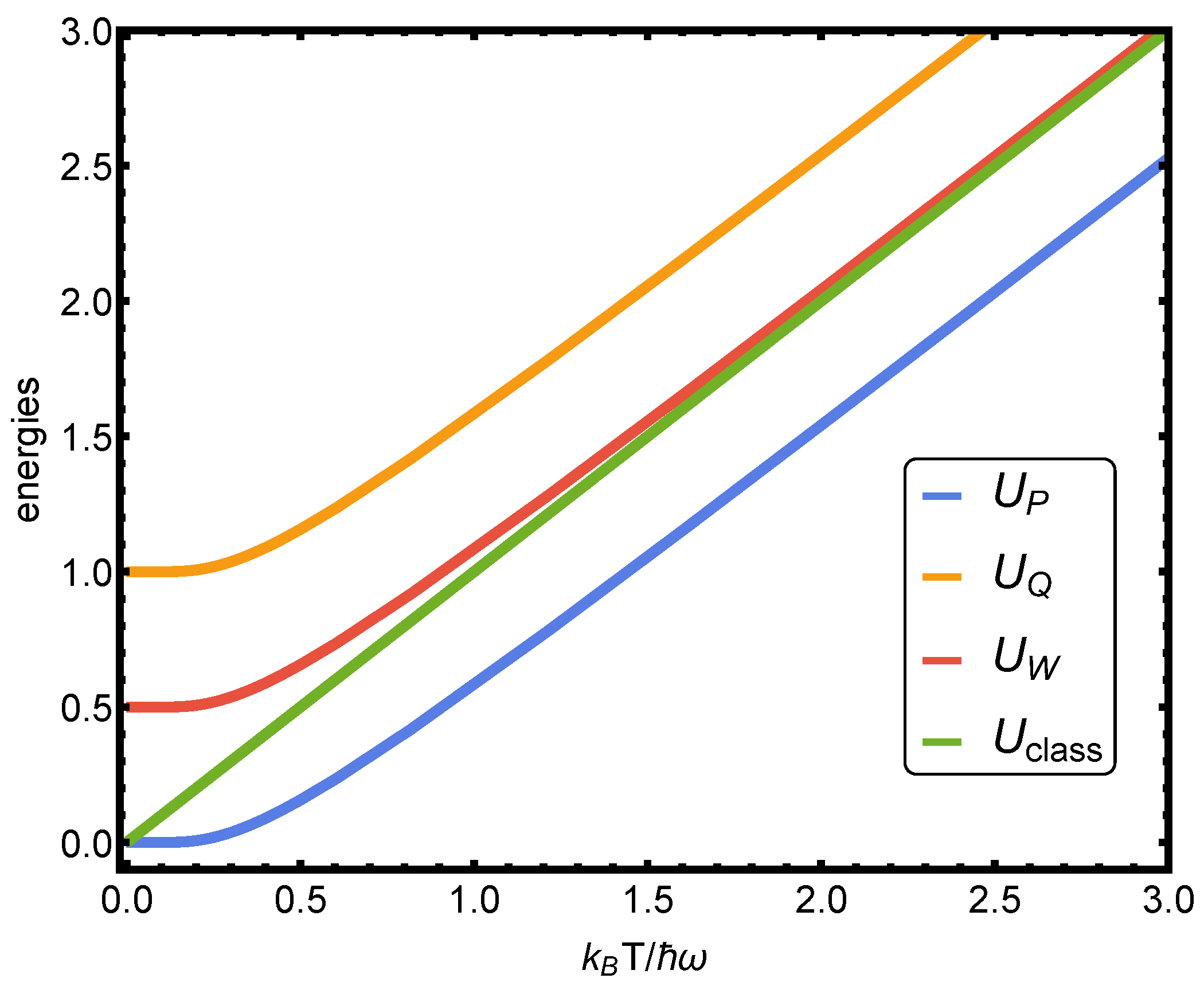
Not surprisingly, the mean value of energy U for a thermal state is the same in our three representations and equals that obtained from (harmonic oscillator in the canonical ensemble). However, and do not coincide with U, as does.
3. Three Semiclassical Ways of Expressing the Temperature Dependent Mean Energy U
As stated above, it is interesting to inspect Equations (
24), (
30) and (
37), because they tell us about the three possible ways of semi classically expressing the temperature dependent mean energy
of the quantum harmonic oscillator. The three ways correspond to the chosen representation. In the
representation, we have to express the mean energy
U in the form
, which reads
Using the
representation, we express
one as
and, finally, the
W way of expressing
is
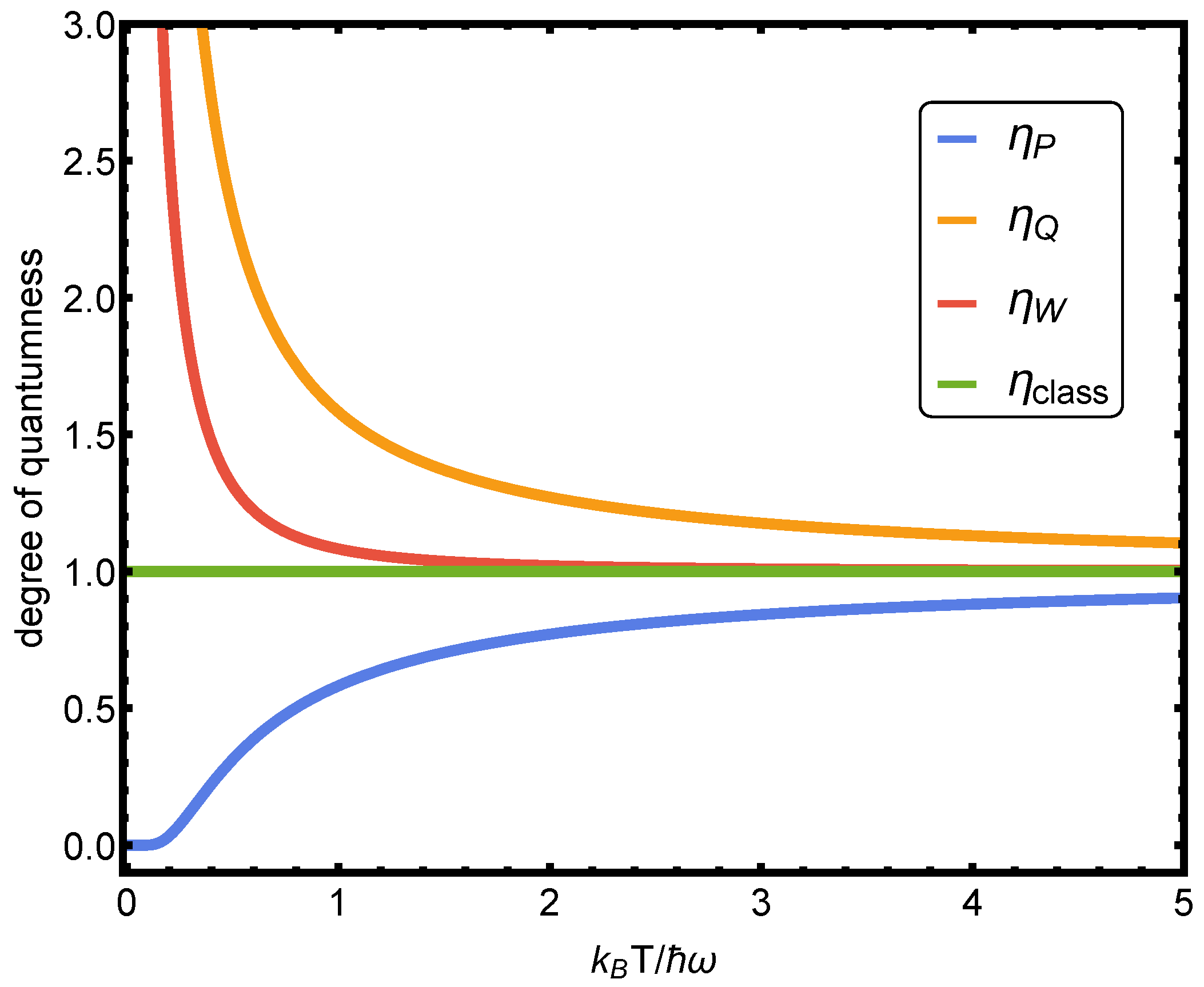
We will now compare these three semi classical mean energies to the classical one and ask how close each of the three is to the classical mean energy. We might then think that graphical closeness yields a kind of “degree of classicality”. Alternatively, of lack of “quantumness”. To repeat, we may associate graphical closeness with some degree of quantumness. This is just a suggestion, nor a firm commitment. A more tangible way of speaking of the classicality degree is to introduce the ratio between the semi classical mean value and the classical one
which we plot in
Figure 1.
Summarizing, we state that we have found the temperature-dependent relation
We plot our three representation of the mean energy in
Figure 2 together with the well-known classical energy
[
10].
From the right equality in Equation (
43), we obtain the
energy of the vacuum state as follows
an identity that we can also cast as
Replacing Equation (
44) into equality (
43), allows us to find
which is an expression that allows us to relate the three mean energies
,
, and
.
4. Comparing the Three Associated Entropies
In this Section, we start comparing the Boltzmann-Gibbs’ information measures (entropies) for our three quasi-distribution probabilities in phase space with the purpose to compare them and to ascertain their information content. In addition, we will incorporate their classical and quantum counterparts. First, for the
function, we have
that in view of Equation (
19), after performing the integral it becomes
We take the Boltzmann constant
equal to unity, hereafter. Considering the average-particle number
given by Equation (
20), we have that [
16]
Second, for the
function we define the entropy
Introducing Equation (
26) we obtain
so that taking into account Equation (
20), we obtain [
16]
Note this entropy
is the Wehrl entropy, i.e., the entropy of the Husimi distribution [
17,
18].
Third, for the Wigner function, we have
that considering Equation (
33), becomes
From Equation (
20), by means of algebraic manipulation, we obtain [
16]
In addition, the Shannon entropy is
that from Equation (
11) adopts the appearance [
10]
Now, from Equation (
20) we obtain
and we can replace this in
S, given by Equation (
57). Thus, one finds
Finally, the classical entropy, or Boltzmann-Gibbs entropy is [
10]
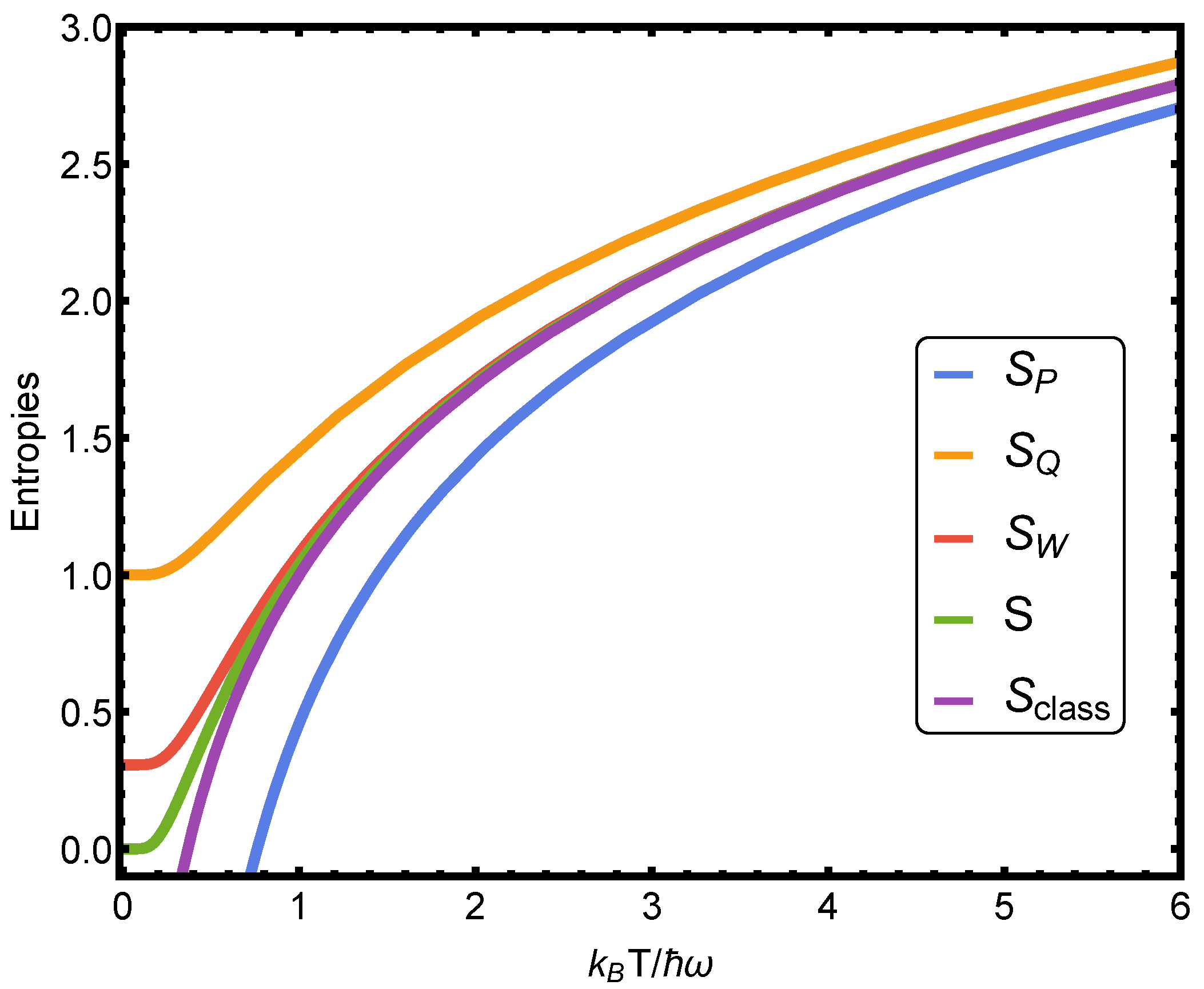
We compare the behaviors of all entropies in
Figure 3. We observe that, while
S,
, and
are positive definite,
and
can take negative values. Negative values indicate a failure of a classical entropy due to quantum effects.
and
entropies are not affected in this way. In particular,
if
, and
if
[
16].
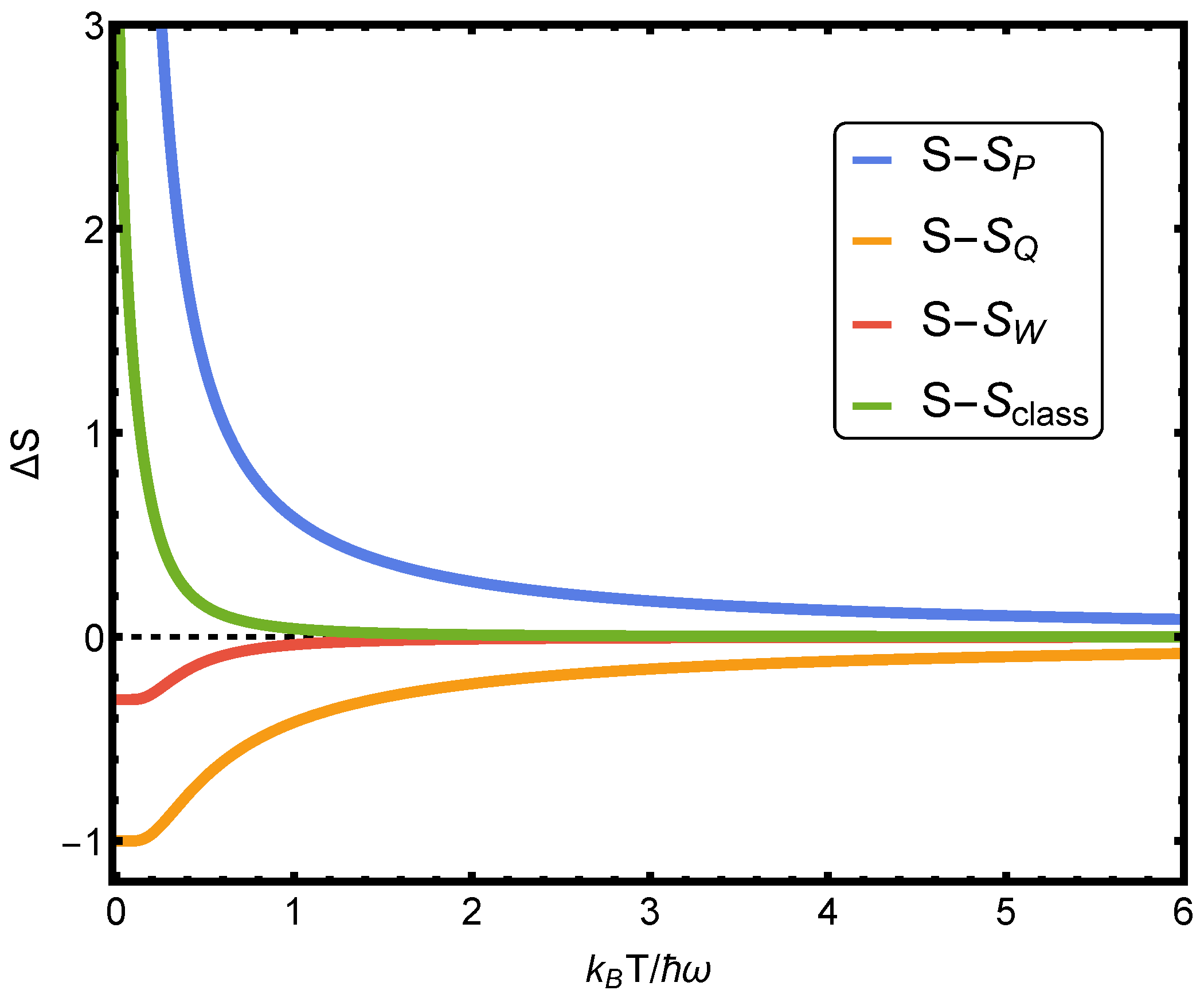
Figure 4 compares the entropic differences
(
, classic) to ascertain the type of information-content associated to each representation.
Remember that entropies measure ignorance or a lack of information [
19]. Thus, the
W and
Q distributions contain less information than the exact one. This is expected. Instead, the
P and the classical distributions appear to contain more information. This is expected for the classical entropy (no uncertainties involved) and we here discover that the same applies to the
instance, due to the classical contamination detected above.
5. Thermal Uncertainty Relations
5.1. Representation
We explore here interesting connections that involve the thermal uncertainty relations. Some details can be found in Ref. [
20]. First, let us consider the
representation. Since
, we calculate
that for Equation (
23) we obtain
Similarly,
and Equation (
23) yields
From Equations (
62) and (
64) we find the semi classical thermal uncertainty relation
Notice that, taking into account Equations (
23) and (
39), we can establish the following relation
where
. The connection (
66) shows that
and
are the canonically conjugate variables of
in a semiclassical context. It is the thermal uncertainty relation in the
representation.
5.2. Representation
We employ a similar procedure using the
representation. We start from
and equations
and
Using now Equation (
26) we immediately find the semiclassical thermal uncertainty relation
Considering subsequently Equations (
26) and (
40), we arrive at
with
. The semiclassical connection (
70) shows that
and
are the canonically conjugate variables of
.
5.3. Representation
For the
representation, we have
together with
and
Employing now Equation (
26), we obtain the semiclassical thermal uncertainty relation
Considering Equations (
33) and (
41) we arrive to
with
. The semiclassical connection (
74) shows that
and
are the canonically conjugate variables of
.
5.4. Joining Things
Accordingly, the three representations are associated to an amount of uncertainty that is two times the minimum quantum one.
6. Conclusions
We have studied in some detail the three usual quantum optics’ distribution-representations W, P, and Q. We discover that the W and Q distributions contain less information than the exact one, which is to be expected, since they are approximations. Instead, the P and the classical distributions appear to contain more information, which is again to be expected for the classical entropy (no uncertainties involved). In addition, we here find that the same applies to the instance, due to its classical contamination detected in the preceding section. One might assert that the P distribution is a better approximation to the classical entropy than to the quantum one. Finally, the three representations are characterized by uncertainties that are two times the minimum quantum one.
Our main conclusion is that some of them have either larger, or surprisingly smaller, entropies than the exact one. However, the three lead to uncertainties greater, by a factor two, than the minimum quantum one. Comparison of the mean energy teaches us that, looking at very low temperatures, the representation increasingly differs from the P one.