Abstract
Periodic high-utility sequential pattern mining (PHUSPM) is used to extract periodically occurring high-utility sequential patterns (HUSPs) from a quantitative sequence database according to a user-specified minimum utility threshold (minutil). A sequential pattern’s periodicity is determined by measuring when the frequency of its periods (the time between two consecutive happenings of the sequential pattern) exceed a user-specified maximum periodicity threshold (maxPer). However, due to the strict judgment threshold, the traditional PHUSPM method has the problem that some useful sequential patterns are discarded and the periodic values of some sequential patterns fluctuate greatly (i.e., are unstable). In frequent itemset mining (FIM), some researchers put forward some strategies to solve these problems. Because of the symmetry of frequent itemset pattern (FIPs), these strategies cannot be directly applied to PHUSPM. In order to address these issues, this work proposes the stable periodic high-utility sequential pattern mining (SPHUSPM) algorithm. The contributions made by this paper are as follows. First, we introduce the concept of stability to overcome the abovementioned problems, mine sequential patterns with stable periodic behavior, and propose the concept of stable periodic high-utility sequential patterns (SPHUSPs) for the first time. Secondly, we design a new data structure named the PUL-list to record the periodic information of sequential patterns, thereby improving the mining efficiency. Thirdly, we propose the maximum lability pruning strategy in sequential pattern (MLPS), which can prune a large number of unstable sequential patterns in advance. To assess the algorithm’s effectiveness, we perform many experiments. It turns out that the algorithm can not only mine patterns that are ignored by traditional algorithms, but also ensure that the discovered patterns have stable periodic behavior. In addition, after using the MLPS pruning strategy, the algorithm can prune 46.5% of candidates in advance on average in six datasets. Pruning a large number of candidates in advance not only speeds up the mining process, but also greatly reduces memory usage.
1. Introduction
High-utility sequential pattern mining (HUSPM) [1,2,3,4,5,6,7,8,9,10,11] is a significant area of knowledge discovery and data mining that has been the subject of a great deal of research. HUSPM has been applied in many applications, such as mining high-utility sequential patterns (HUSPs) in online dynamic log data [12], mobile commerce data [13], and gene regulation data [14]. Large numbers of HUSPs are mined, but some are redundant in some special scenarios. In the marketing example, the merchant needs to consider which product combinations are both highly profitable and can be sold regularly. However, some product combinations that are highly profitable but not frequently sold are considered HUSPs, in which case they are redundant. In recent years, some researchers have added the time constraint problem to HUSPM [15,16]. Considering the periodicity of HUSPs in the quantitative sequence database, some researchers proposed the periodic high-utility sequential pattern mining (PHUSPM) to mining periodic high-utility sequential patterns (PHUSPs) [15,16]. The PHUSPM is also widely used in pattern discovery and knowledge discovery-related fields, such as research on consumer habits, website click-through rate data, financial market analysis, biomedical applications, and mobile computing. The PHUSPM defines the interval of the same pattern in different sequences as a period. The maximum periods of a sequential pattern are generally used to define the pattern’s period. If a sequential pattern’s period is below the user-defined upper limit (), it will be regarded as periodic. However, is set too strictly, because if a sequential pattern exceeds the threshold for only one period, it will be discarded. For example, in the market basket analysis, is assumed to be one week and there are customers buying eggs and milk every weekend. This pattern will be periodic, but it will not be considered periodic if the customer skips a week. Therefore, traditional PHUSPM discards some useful and interesting PHUSPs. In addition, when the value of PHUSPM is set too large, the PHUSPs mined will also vary. Obviously, these sequential patterns are not suitable for most practical applications. To sum up, the traditional PHUSPM method suffers from problem that some useful sequential patterns are discarded and some sequential patterns have large periodic fluctuations.
These problems also exist in periodic frequency pattern mining (PFPM) [17,18,19]. In order to provide greater flexibility, Kiran et al. proposed the partial periodic frequency pattern mining (PPFPM) algorithm [20]. This algorithm relaxes the threshold constraint, allowing a specific amount of periods beyond it. In brief, if a pattern is considered periodic, it has no more than x (user-defined) periods that exceed the threshold. Obviously, PFPM is a special situation of . Although PPFPM is more adaptable than PFPM, there is still an important problem in that it only verifies whether each period exceeds the threshold. At the same time, PFPM and PPFPM ignore the amount by which each period exceeds the threshold. For example, if the threshold is set to a week, it makes no difference whether some products are discontinued by customers for two weeks or a year. Additionally, none of the models discussed above consider how closely spaced the values of the periods meeting the threshold are. As a result, a pattern can be considered periodic, even though this pattern’s several periods often alternate between values greater or smaller than the threshold. In order to solve the above problems, Fournier–Viger et al. proposed stable periodic frequent pattern mining (SPFPM) [21] and top-k stable periodic frequent pattern mining (TSPIN) [22]. SPFPM and TSPIN propose the concept of stability in PFPM, mining stable periodic patterns that satisfy periodicity while maintaining similar period lengths and thus are more predictable than unstable patterns. However, these algorithms are not suitable for PHUSPM, because they do not consider the utility of items, and PHUSPM has no symmetry compared to these algorithms. Briefly, an item could have several utility values in a sequence, and a corresponding sequence will also have multiple utility values.
This paper suggests the stable periodic high-utility sequential pattern mining (SPHUSPM) algorithm for mining stable periodic high-utility sequential patterns (SPHUSPs). The SPHUSPM has three important contributions.
- The SPHUSPM provides a brand-new stability method and utilizes the time period information to a greater extent to mine more useful patterns. In the HUSPM research field, the algorithm provides a new research strategy. The addition of multiple methods also makes the mined patterns more interesting and more in line with user requirements. At the same time, in the field of practical application, the algorithm considers the maximum profit and the time period information at the same time, giving decision makers more accurate and efficient decision-making methods.
- We design a new data structure named PUL-list and a maximum stability pruning strategy in HUSPM (MLPS) to increase the effectiveness of mining. Experiments show that these two methods greatly improve the efficiency of the algorithm.
- We perform some experiments on six different datasets, which are guaranteed to be able to mine the desired SPHUSPs, while also showing excellent performance in operational efficiency and memory usage efficiency.
The remainder of this paper is structured as follows. Section 2 discusses related work. The SPHUSPM’s preliminaries and problem definitions are introduced in Section 3. In Section 4 the suggested SPHUSPM algorithm is described. Comparative experiments are then presented in Section 5. Lastly, the conclusion of the paper is given.
2. Related Work
2.1. High-Utility Sequential Pattern Mining
High-utility itemset mining (HUIM) [23], which takes into account the quantity of items bought and unit profit, aims to find interesting patterns. Although a growing number of researchers have proposed several HUIM algorithms [24,25,26,27,28,29], they cannot be directly applied to the HUSPM because they did not consider the order of the itemsets.
HUSPM [2,3,4,5] is a research that combines HUIM and SPM, and its goal is to mine HUSPs in quantitative sequence databases. HUSPM was first proposed by Zhou et al., who added the concept of high utility to web log sequence pattern mining [1]. Ahmed et al. proposed a horizontal method called UL and a mode growth method called US [6]. Yin et al. proposed the concept of maximum utility value, the efficient USpan algorithm [3], which used a lexicographic sequence tree (LS-tree) structure to store sequence and utility information and used width and depth pruning strategies. On this basis, the top-k strategy was introduced, and the TUS algorithm [7] was proposed to mine HUSPs. The HUS-span algorithm [4], which made use of the same LS-tree structure as USpan, was put forth by Wang et al. In addition, pruning strategies such as the prefix extension utility (PEU) strategy and reduced sequence utility (RSU) strategy were also used in this algorithm. Lan et al. devised the PHUS algorithm [8], which used a sequential utility table structure to store sequential utility values, and employed a projection-based pruning strategy, and an indexing strategy to reduce search time. Alkan et al. proposed the HuspExt algorithm [9], which used a data matrix storage structure and a PBCG pruning strategy, which was based on a more compact overestimation strategy named CRoM, which could delete an abundance of unpromising candidates, greatly improving the mining efficiency. Recently, Gan et al. devised ProUM [10], an innovative projection-based mining algorithm. To increase mining speed, the algorithm makes use of the utility array structure and the sequence extended utility (SEU) pruning strategy. On this basis, Gan et al. devised the HUSP-ULL algorithm [11], which used a data structure called the utility-linked (UL)-list, which could efficiently record utility and location. To get strict upper constraints on the utility of candidate sequences, the algorithm also suggested the pruning methods irrelevant item pruning strategy (IPS) and look-ahead strategy (LAS).
Although the HUSPM could discover a large number of HUSPs, in some application scenarios, some of the sequential patterns were redundant and useless. The traditional HUSPM method ignored the time constraint problem, so some researchers proposed the PHUSPM algorithm. The next section will review the related work of PHUSPM.
2.2. Periodic High-Utility Sequential Pattern Mining
Some researchers have developed algorithms to mine periodic frequent patterns (PFPs) in transaction databases in the area of frequent pattern mining (FPM) [20,30,31,32,33]. Most of these algorithms relied on the excellent tree-based data structures to produce an entire collection of periodic–frequent patterns in a transactional database. Researchers have simultaneously suggested certain algorithms to exploit periodic–frequent sequential patterns (PFSPs) in sequence databases [34,35]. Because the above two types of algorithms used the support of the patterns to mine the corresponding patterns, ignoring the utility problem of the items, these algorithms could not find high-utility and periodic patterns.
In the field of HUIM, researchers have devised some methods for mining periodic high-utility itemsets (PHUIs) in the quantitative transaction database [36,37,38]. PHM [36] is an approach that Fournier–Viger et al. suggested for mining PHUIs in quantitative transaction datasets. The algorithm created a new class of pattern called as periodic high-utility itemsets by fusing the ideas of periodic itemsets and high-utility itemsets. They proposed the minimum periodicity and the average periodicity as two new measurements to more precisely assess periodic behavior. For finding short-period high-utility itemsets (SPHUIs) [37,38] in quantitative transaction databases, Lin et al. suggested two techniques.
In the field of HUSPM, there are currently only two algorithms to mine PHUSPs in the quantitative sequence database. Dinh et al. proposed an algorithm named PHUSPM [15] by adding the method of periodicity to HUSPM for the first time. However, this algorithm did not design the special data structure and pruning strategy, so the algorithm was not efficient. After that, Dinh et al. [16] suggested the PUSOM algorithm based on the original algorithm, which designed a data structure called PUSP and used the maximum periodic pruning (MPP) strategy. However, the maxPer threshold set by this algorithm was too strict, and some useful sequential patterns were discarded and some patterns had large periodic fluctuation (unstable) problems. These problems also exist in PFPM [18,19,20], and some researchers propose the concept of stability to solve this problem. The following sections will review related work on SPFPM.
2.3. Stable Periodic Frequent Pattern Mining
Most research about PFP mining has evaluated the periodic behavior of patterns by comparing them with a threshold, but ignored the extent to which these periods exceed [18,19,20,36]. In order to find patterns with stable periodic behavior, Fournier–Viger et al. [21] proposed to mine a novel class of periodic frequent patterns in transaction databases, named stable periodic frequent patterns (SPFPs). The algorithm was called stable periodic frequent pattern mining (SPFPM). On this basis, in order to address the issue that the minimum support threshold is difficult to set, Fournier–Viger et al. [22] suggested an algorithm named top-K stable periodic patterns (TSPIN). Although the above algorithms could mine patterns with stable periodic behavior in transaction databases, they could not be directly applied to HUSPM. Because they do not take into account the order of itemsets in a sequence, that is, asymmetry, nor the utility of patterns.
- In light of the above, we list the limitations of the previously proposed work.
- In the PHUSPM algorithm, it is difficult to set the threshold accurately. Some patterns have a few periodic fluctuations. However, this situation has little impact on the decision, and they are still useful patterns. If is set too small, these interesting patterns will be ignored. If is set too large, the mined patterns will have unstable periods.
- Because the SPFPM algorithm is designed specifically for FPM, it cannot be directly applied to HUSPM. In short, it did not take into account the order between itemsets and the utility values of the items.
To resolve the aforementioned issues, we suggest a new stabilization method to discover stable periodic high-utility sequential patterns (SPHUSPs). We will define the SPHUSPM problem definitions and provide its preliminary information in the next part.
3. Preliminaries and Problem Definitions
To help the reader better understand the topic, we summarized symbols that appear in the definition section into Table 1.

Table 1.
Symbols.
Let be a finite set containing M unique items. A q-item is denoted as , which represents the item and its purchase quantity (internal utility). Each item has a weight to represent importance or profit per unit, which is called external utility and is denoted by . A q-itemset is a set of q-items. Without loss of generality, the order of q-items in a q-itemset is in lexicographic order(≺). A q-sequence is an order list of itemsets. A quantitative sequence database is a set of q-sequences wherein each q-sequence has a unique identifier called . Table 2 is a quantitative sequence database. The external utility (profit) of each item in I is shown in Table 3. All the examples in this article are from this quantitative sequence database.

Table 2.
A quantitative sequence database.

Table 3.
A utility table.
Definition 1.
Let and be two q-itemsets, where and . If there exist positive integers 1 ≤ j≤ j≤…≤ j≤ m’, suchthat , ,…, , then X is said to contain X, whichis denoted as .
For example, the q-itemset in q-sequence contains q-itemsets , and .
Definition 2.
Let and be the two q-sequences, where are q-itemsets . If there exists positive integers , such that , then A is a q-subsequence of B and B is a q-supersequence of A, denoted as .
For example, the q-sequences and are two q-subsequences of .
Definition 3.
The utility of a q-item (i, q) in a q-sequence s is denoted and defined as
The utility of a q-itemset X in a q-sequence s is denoted and defined as
The utility of a q-sequence s is denoted and defined as
For example, the utility of the q-item c in q-sequence (e.g., ) is . The utility of the q-itemset in q-sequence is . The utility of the q-sequence is .
Definition 4.
Given a q-sequence and a sequence , s is said to match t if n = m and for , denoted as t ∼ s.
For example, .
Definition 5.
The sequence utility of a sequence in a q-sequence is denoted and defined as
The utility of t in a q-sequence database S is denoted as
For example, the utility of the sequence in the q-sequence is calculated as . The utility of t shown in Table 2 is .
Definition 6.
The maximum utility of a sequence t in a q-sequence s is denoted and defined as
The maximum utility of a sequence t in a q-sequence database S is denoted and defined as
For example, the maximum utility of the sequence in the sequence database S shown in Table 2 is .
Definition 7.
Given two q-sequences s and s′, if , the extension of s in s’ is said to be the rest of s’ after s, and is denoted as . Given a sequence t and a q-sequence s, if , the extension of t in s is the rest of s after , which is denoted as , where is the first match of t in s.
For example, given a sequence . There exist two matches of t in . The first one is . Thus, .
Definition 8.
The set of extension items of a sequence t in a quantitative sequential database D is denoted as and defined as
For example, .
Definition 9.
The remaining utility of a sequence t in a q-sequence s is denoted as and defined as
For example, given a sequence and a q-sequence in Table 2, the extension of t in is . The remaining utility is .
Definition 10.
A sequence t is said to be a high-utility sequential pattern if , where is a given a user-specified minimum utility threshold.
Definition 11.
Let there be a q-sequence database and a sequence t. The set of q-sequences containing t is denoted as
For example, Table 4 shows the occurrences of items in the q-sequence database S (Table 2). The list of q-sequences containing the sequences and are respectively and .

Table 4.
The occurrences of all items.
Definition 12.
Let there be two q-sequences , and a sequence t, such that and . and are said to be consecutive with respect to t if there is not a q-sequence , such that .
The period of two consecutive q-sequence and is denoted and defined as
In a word, is the number of q-sequences between and .
For example, The sequence appears in and . Hence, .
Definition 13.
Let there be a sequence t and The periods of a sequence t is a list of periods denoted and defined as
For example, the sequence has . The sequence has .
In PHUSPs, the mining algorithm PHUSPM and PUSOM proposed by Dinh et al. [15,16], three periodicity measures are used to assess the periodicity of HUSPs in sequence databases.
Definition 14.
The maximum periodicity, minimum periodicity, and average periodicity of a sequence t are denoted and defined respectively as
For example, the periods of are . Thus, , , and .
Definition 15.
Let there be five positive user-specified thresholds: , , and . A sequence t is a periodic high-utility sequential pattern if t is a HUSP (it satisfies Definition 8) and and .
Fournier–Viger et al. introduced a novel model based on the cumulative sum in order to find frequent patterns having a stable periodic behavior in PFP mining [21,22]. The main function of the model is to determine whether all periods of patterns are stable or not. Experiments on SPP [21] and TSPIN [22] algorithms show that this model is flexible and practical. However, this model is not designed for mining patterns on sequential databases. For the problem of this paper, we have modified this model to accommodate sequential databases. This model evaluates the stability of a pattern by calculating the cumulative sum of the difference between each period of the pattern and the . We define a method called lability to determine the periodic behavior of patterns.
Definition 16.
The lability of a sequence t is a list of values denoted as
The list contains values. In other words, . Each lability value in is no less than zero. The first lability value of t is defined as . Then, the i-th lability value of t for i > 0 is defined based on the the previous lability value as . Thus, lability values are calculated as a cumulative sum. Note that the above definition of lability can also be rewritten more concisely as follows:
For example, for the database of the running example and , the periods of are . Because the t has six periods, it also has six lability values. The first lability value of t is . Then, the following lability values are , and . Thus, the lability of itemset is .
For a sequence t, its corresponds one-to-one to the value in . If the value in is smaller, the calculated value in will also show a smaller value. Conversely, the calculated value in will also be relatively large. In addition, if a large value appears in , the value after that value may also become large. If the value of is 0 or tends to 0, it indicates that the sequence t has good periodic stability. Conversely, the sequence t has unstable periodic behaviors.
Definition 17.
The maximum lability of a sequence t is defined as
The maximum lability of a sequence t is also called the stability of t. For example, as the lability values of sequence is , then .
Definition 18.
Let there be a sequence database D, a sequence t, three user-defined thresholds minimum utility threshold (minutil or ξ) > 0, maximum periods (maxPer) > 0, and maximum lability threshold (maxLa) ≥ 0. The problem of mining the stable periodic high-utility sequential patterns in D consists of enumerating each sequence t in D such that and .
To better understand the above definitions, we will give a example. At the same time, the pattern in this example will provide a case that is ignored by other algorithms. Assume that and are the limiting conditions. Given a sequence , it appears in sequences and in the quantitative sequence database shown in Table 2. Consequently, . We get by Definition 13. So, . In the traditional PHUSPM algorithm, the sequence will not be considered periodic according to the constraint . Obviously, this pattern appears periodically in the first half of the database. Therefore, this pattern is useful for some applications. However, due to strict restrictions, this pattern is ignored by the traditional algorithm. In this article, we use the stability strategy that solves this problem. By Definition 16, we get that . According to , we get that is a useful pattern. It is clear from this example that this method can find interesting patterns that traditional methods miss.
4. Proposed Algorithms
4.1. The Data Structure
In 2019, Gan et al. [11] proposed the HUSP-ULL algorithm, which utilized a utility-linked (UL)-list structure and a lexicographic sequence (LS)-tree for mining HUSPs. This paper also uses LS-tree and designs a new data structure based on the UL-list, namely period utility-linked (PUL)-list structure. This structure can quickly access period and utility information, which greatly improves the operating efficiency of the algorithm.
4.1.1. Lexicographic Sequence Tree and Concatenations
Each node in the lexicographic sequence tree [39] represents a potential SPHUSP candidate. To identify an SPHUSP candidate, the utility value in the node can be evaluated to the minimal utility threshold and the stability value to the maximum lability threshold.
In the LS-tree nodes, all of the original database’s sequences are converted to UL-lists. The designed algorithm utilizes two common sequence mining operations named I-concatenation and S-concatenation to create new sequences (child nodes) in the LS-tree.
Definition 19.
Given a sequence t and an item , the I-concatenation of t with consists of appending to the last itemset of t, denoted as . The S-concatenation of t with an item consists of adding to a new itemset appended after the last itemset of t, denoted as .
For example, given a sequence and a item a, = and .
It is clear that after executing the I-concatenation operation, the sequence’s itemsets count stays the same; however, after doing the S-concatenation action, the itemsets count rises by one. All potential sequence patterns in the search space for SPHUSPM can be constructed based on these two methods.
The algorithm’s search procedure can be compared to the procedure of gradually constructing a LS-tree. The method first searches the database for a set of 1-sequences that meet the minimum utility and maximum lability thresholds. The LS-tree is then explored by using a depth-first search approach, starting from the 1-sequence. We use the I-concatenation and S-concatenation operations to obtain the child nodes of each node. Finally, the complete sequence database set is obtained.
4.1.2. The Period-Utility-Linked List Structure
The burden increases during the mining process because the program must repeatedly scan the original database. To solve this problem, this study uses the same UL-list structure as the HUSP-ULL algorithm [11] to store the relevant information of each q-sequence in the q-sequence database, and then constructs the PUL-list to discover SPHUSPs. The PUL-list contains the SID of each q-sequence where the candidate sequence is located and the suffix sequence information in the q-sequence. In order to facilitate candidate sequence expansion and utility calculation, the PUL-list also stores the first occurrence position of each different item of the suffix sequence in the q-sequence, that is, index information. In addition, in order to easily measure the stability of the candidate pattern, the order of the q-sequence (period information) where the candidate sequence is located in the original database is also included in the PUL-list.
In the UL-list, the utility and position (UP) information and header table of the q-sequence are included. Among them, the UP information records the item name, the utility of the item, the remaining utility of the item, and the position where the item appears next in the sequence. The heard table stores the name of each item in the q-sequence and the position where the item first appears in the sequence.
For example, Table 5 shows the UL-list of . In UP information, the first item in is a, the utility is 1, the remaining utility is 41, and the next position is empty, which means that it no longer appears in this sequence. In the heard table, the first occurrence location of the different items in is stored. The information indicates that the position where item a first appears in is the first position.

Table 5.
The utility-linked (UL)-list structure of .
The PUL-list is a projection database of candidate sequences in the mining process. It contains UP information, heard table and periodic information of candidate sequences of multiple sequences. Its purpose is to facilitate the calculation of periodicity and stability. The PUL-list takes as an example, as shown in Table 6. As indicated in Table 6, the PUL-list takes as an example. In the PUL-list of , the projection information of sequence in each q-sequence is stored; for example, the projection of sequence in is . The periodic information in this table records the index of the sequence containing the sequence in original databases (i.e., the quantitative sequence database), and means the sequence appears in the first, second, third, fifth and sixth sequences.

Table 6.
The period-utility-linked (PUL)-list structure of .
The SPHUSPM algorithm uses the PUL-list structure to simply access utility, location, and period information instead of repeatedly scanning the original database. The access efficiency and mining efficiency of the algorithm are both significantly increased by this structure.
4.2. Pruning Strategy
Numerous candidates are produced during the mining process. Therefore, this will increase the chance of combinatorial explosion, which in turn will cause the algorithm to run slower, so we need to introduce several pruning strategies to solve this problem.
4.2.1. The Downward Closure Property of Upper Bound
Definition 20.
The sequence-weighted utilization (SWU) [3] of a sequence t in a quantitative sequential database D is denoted as SWU(t) and defined as
For example, and .
Theorem 1.
Given a quantitative sequential database D and two sequences t and t’. If t ⊆ t’, then
Proof.
Because , . □
Theorem 2.
Given a quantitative sequential database D and a sequence t, it can be obtained that
Proof.
Because , we can obtain that . □
From the above SWU definition and theorems, the utility of sequence t must be less than the minimum utility threshold if the SWU value of t is less than that threshold. When this happens, the utility of any supersequence of t will also be below this threshold. SWU is able to eliminate many candidates that are unqualified as a result. In actuality, the utility of a sequence t is typically significantly smaller than its SWU value, so a tighter upper bound also needs to be introduced.
We introduce two strategies from the HUSP-ULL algorithm [11] to generate a stricter upper bound, which is built on the prefix extension utility (PEU) model.
Definition 21.
The PEU of a sequence t in a q-sequence s is denoted as and defined as
Definition 22.
The PEU of a sequence t in D is denoted as and defined as
Theorem 3.
Given a quantitative sequential database D, and two sequences t and t’. If t ⊆ t’, we obtain
Theorem 4.
Given a quantitative sequential database D and a sequence t, we can obtain
The proofs of Theorems 3 and 4 can be found in [11]. Theorems 3 and 4 demonstrate that if the sequence t’s PEU value is below the minimal utility threshold, then the supersequence of t’s PEU value is similarly below the minimum utility threshold. The utility of t and the utility of the supersequence of t are both less than the minimum utility threshold if the PEU value of the sequence t is less than the minimum utility threshold.
4.2.2. Pruning Strategies
The candidate sequence t can produce a lot of candidate sequences when doing I-concatenations and S-concatenations. In order to reduce a mount of candidate sequences, this research introduces the look-ahead strategy (LAS) and the irrelevant item pruning strategy (IPS) in the HUSP-ULL algorithm [11] to eliminate hopeless candidates in advance.
Theorem 5.
Given a sequence t and a quantitative sequential database D, two situations are considered to generate a supersequence.
(1) If is an I-concatenation candidate item of t, the maximal utility of is no more than .
(2) If is a S-concatenation candidate item of t, the maximal utility of is no more than .
The proof of Theorem 5 can be referred to [11].
Look-Ahead Strategy (LAS):
- (1)
- If is an I-concatenation candidate item of t andis less than the minimum utility threshold, should be removed from (the set of candidate items for I-concatenation with t).
- (2)
- If is a S-concatenation candidate item of t andis less than the minimum utility threshold, should be removed from (the set of candidate items for S-concatenation with t).
Theorem 6.
For any sequence t and item , the maximal utility of or is no more than .
Proof of Theorem 6 can be referred to [11].
Irrelevant Item Pruning Strategy (IPS):
Given a sequence t and an item , if is less than the minimum utility threshold, is called an irrelevant item of t and should be removed from the utility linked lists of t and t’s supersets.
This algorithm uses LAS and IPS pruning strategies to remove a large number of candidates, which greatly improves the running efficiency of the algorithm. The places where these two strategies are used will be marked in the algorithm section.
Because the pruning strategies mentioned above are all pruning in terms of utility, in order to further improve the mining speed of the algorithm, we introduced the maximum lability pruning (MLP) strategy in the TSPIN algorithm [22]. However, this strategy is only applicable to transactional databases, so we modified it to make it suitable for quantitative sequence databases.
Theorem 7.
For any two sequences , the relationship holds.
Proof.
Because , it follows that . In the case where, , the periods of t and are the same. Hence, and . In the case where , then for each sequence , the corresponding will have smaller numbers. Thus, . □
Theorem 8.
For a sequence database D, if for an sequence t, then t and its supersequences don’t have stability.
Hence, the part of the search space containing t and its supersets can be ignored.
Proof.
According to the definition of SPHUSPM, if , then t is not an SPHUSP. Then, any supersequence of t is also not a SPHUSPM based on Theorem 7. □
4.3. The SPHUSPM Algorithm
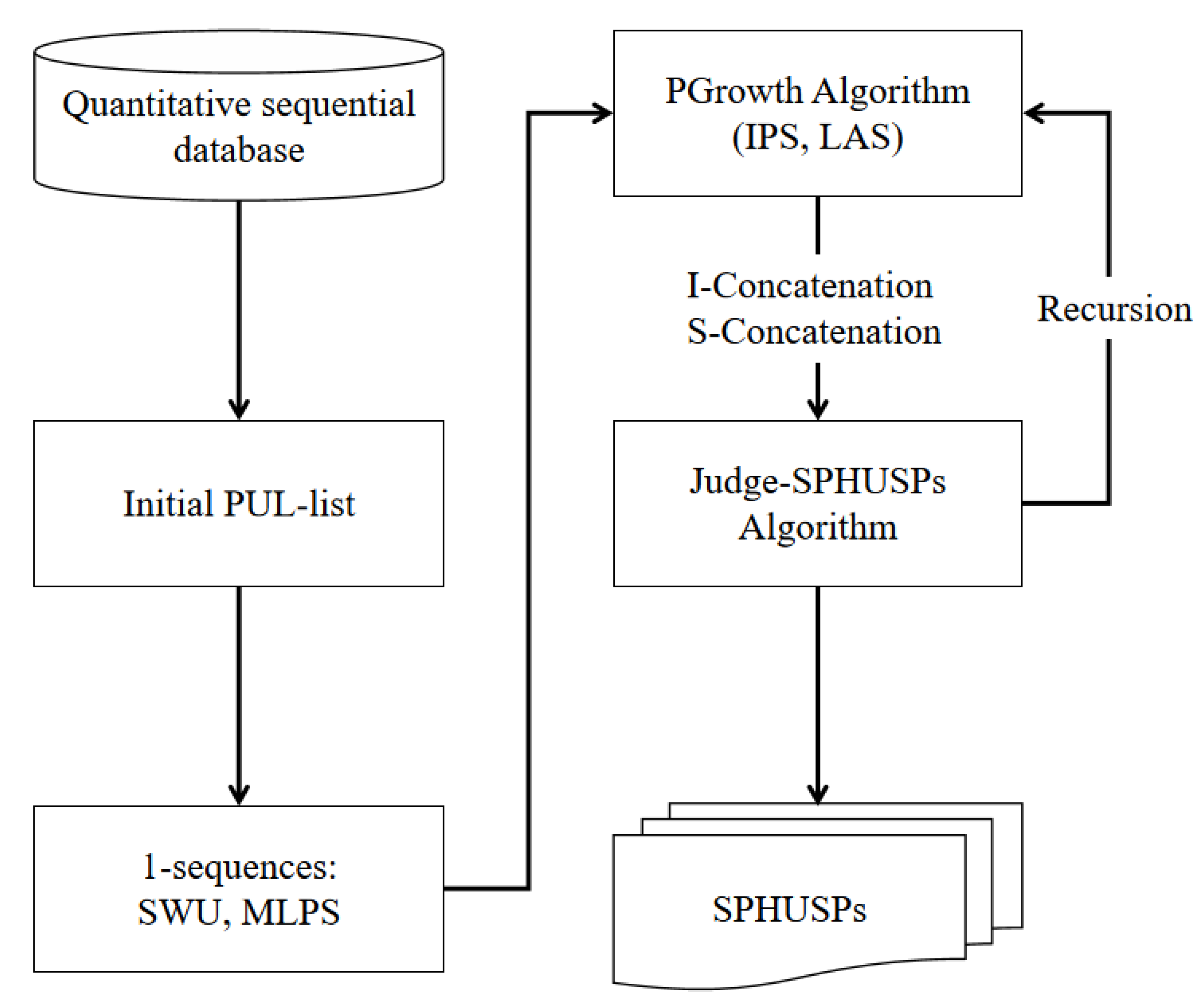
Based on the proposed problem definition, the PUL-list structure and SWU, LAS, IPS, and MLPS strategies, this section proposes the stable periodic high-utility sequential pattern mining (SPHUSPM) algorithm. The framework of the proposed SPHUSPM algorithm is shown in Figure 1, which shows the main parts of the method and their interworking. This algorithm is the first in the field of HUSPM to mine sequential patterns with stable periods. This work is challenging because SPHUSPs have not been defined before, and stability methods cannot be directly applied to quantitative sequence databases.
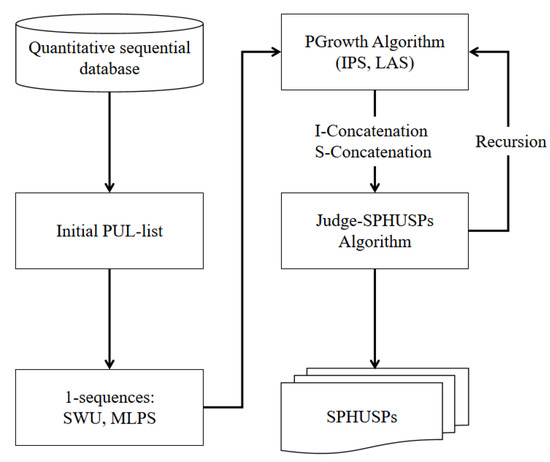
Figure 1.
Framework of the SPHUSPM algorithm.
The pseudo-code of the algorithm 1: SPHUSPM will be given below.
First, scan the quantitative sequence database D to calculate and , and construct the PUL-list for each q-sequence (Line 1). Initialize the set of SPHUSPs (Line 2). For each item , the algorithm builds a projection database to store the transformed PUL-list (Lines 3 to 4). The utility and values for each are computed by using the corresponding projection database (Line 5). A whose value is not less than the minimum utility threshold will be considered as the candidate SPHUSP (Lines 5 to 12). Therefore, those with lower values will be considered unpromising, and they will be deleted at this step. Then use the PUL-list of to calculate the set of and the set of . Then judge the stability of . If not satisfied, both it and its supersequence are considered not to be SPHUSPs, and the MLPS pruning strategy is applied here. The utility if not less than the minimum utility threshold will be output as SPHUSPs (Lines 6 to 10). Next, the PGrowth algorithm treats candidates as prefixes for mining more SPHUSPs (Line 12). The program is cited from [11]. In this part, we acquire the projection database of the and (candidate item set for I-concatenation), (candidate item set for S-concatenation) through IPS and LAS strategies, respectively. Then, we use the items in and to perform I-concatenation or S-concatenation with the respectively, and then enter the Judge-SPHUSPs program (Lines 13 to 18).
| Algorithm 1: SPHUSPM |
Input: D, a quantitative sequential database; , a utility table containing the unit profit of each item; , the minimum utility threshold; , the maximum periods; , the maximum lability threshold. Output: The complete set of SPHUSPs.  |
The judge-SPHUSPs process (Algorithm 2) first constructs the PUL-list of through the projection database of , and obtains the projection database of (Line 1). Then calculate the PEU value, utility value, the set of , and the set of of by (Line 2). If the utility of is not less than the minimum utility threshold and the value of is not greater than the value, is determined to be a SPHUSP (Lines 4 to 6). If the PEU value of is not less than the minimum utility threshold and the value of is not greater than the value, will enter the PGrowth process (Line 8). If no candidate sequence is generated, the process ends. Finally, the designed algorithm returns a list of mined SPHUSPs.
| Algorithm 2: Judge-SPHUSPs |
Input:  |
4.4. Total Computational Complexity
In order to further understand the proposed algorithm, we will analyze the time complexity of the algorithm in the following. is the number of sequences in the quantitative sequence database. is the average number of items in a sequence in the quantitative sequence database. is the number of all candidates produced by the algorithm. is the average number of occurrences of all candidates.
The SPHUSPM algorithm must scan the original database once when building the projection database and performing width pruning. Therefore, the time complexity of this operation is . This algorithm must build LS-tree by expanding the candidates, so the time complexity of this process is . All candidates must enter the judge-SPHUSPs algorithm to determine whether they are real SPHUSPs. Therefore, the time complexity of this operation is .
In summary, the time complexity of the SPHUSPM algorithm is .
5. Experimental Evaluation
The performance of SPHUSPM is not compared to that of other algorithms because it is the first algorithm for mining SPHUSPs. SPHUSPM is implemented in Java. To evaluate the SPHUSPM algorithm, extensive experiments have been done on a workstation running Windows 10, equipped with an Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz 3.41 GHz, and 32 GB of RAM.
5.1. Datasets
Six real datasets [40] are used in the experiment to evaluate the performance of the algorithm.
Sign. The National Center for Sign Language and Gesture Resources at Boston University developed Sign, a real-world dataset of sign language utterance sequences. Every utterance in the dataset corresponds to a video segment that has been meticulously transcribed.
Bible. By converting the Bible into a collection of item sequences, the Bible can be viewed as a real-world dataset.
Kosarak10k. Kosarak10k is a subset of the original Kosarak dataset. This is a real-world dataset made up of click-stream data from a news portal in Hungary.
Leviathan. Leviathan is a conversion of Thomas Hobbes’ Leviathan novel (1651) to a sequence of items (words).
yoochoose-buys. YOOCHOOSE GmbH created the yoochoose-buys commercial dataset to assist RecSys Challenge 20,151 participants.
MSNBC. The click-stream data from the MSNBC website has been transformed from the original data from the UCI repository to create the MSNBC dataset. Only 31,790 sequences remain after the smallest ones were eliminated.
Table 7 and Table 8, which show the parameters and properties of these datasets, respectively. The above datasets can be downloaded from [40].

Table 7.
Parameters of the datasets.

Table 8.
Characteristics of the datasets.
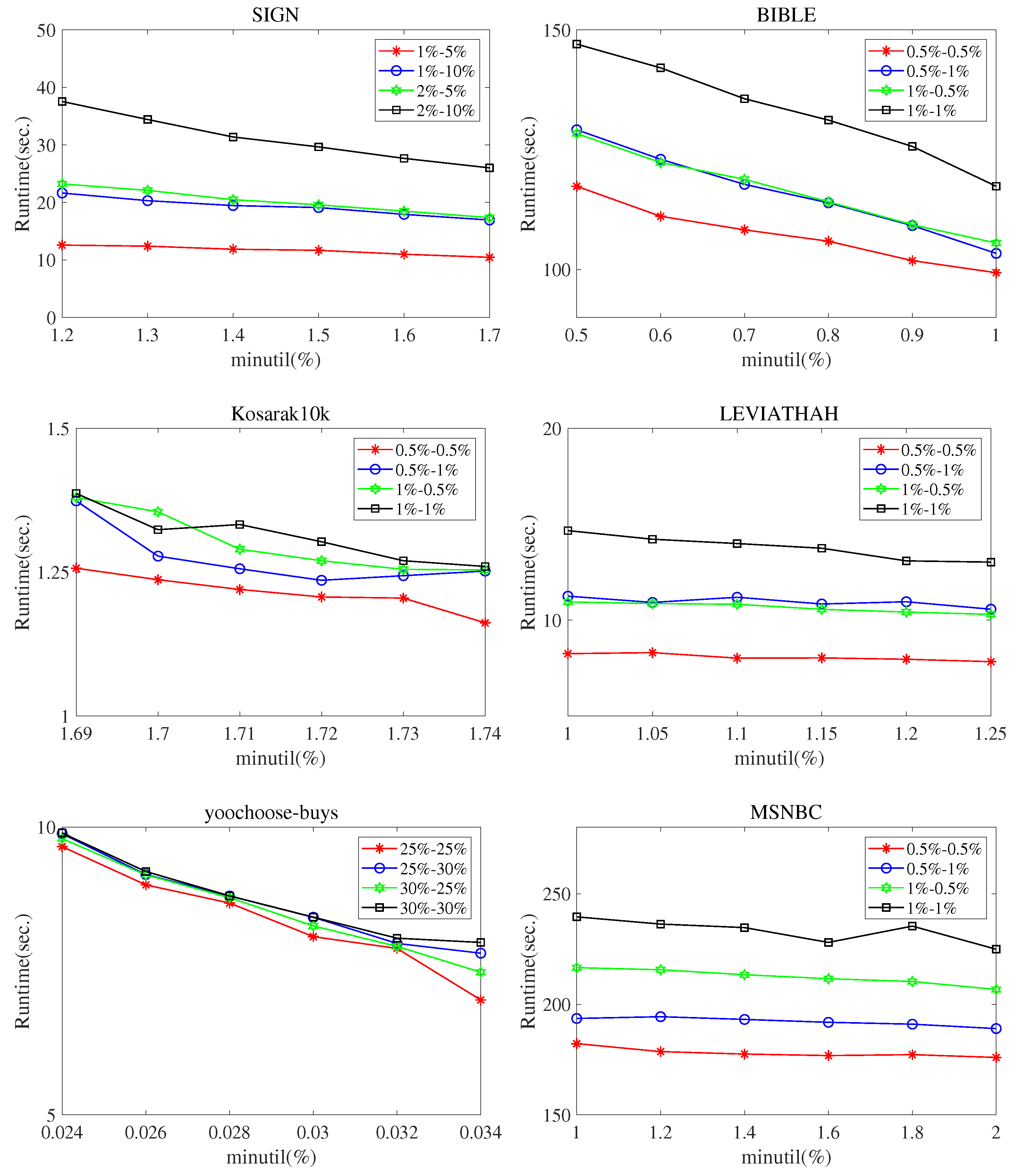
5.2. Execution Time
Figure 2 shows the experimental results of the execution time of the SPHUSPM algorithm. The experiment was conducted on the six real datasets mentioned above. We observe the performance of the algorithm on different datasets with different thresholds by setting the values of , , and . In Figure 2, the x axis represents and the y axis represents execution time. indicates and . The following observations can be drawn from Figure 2.
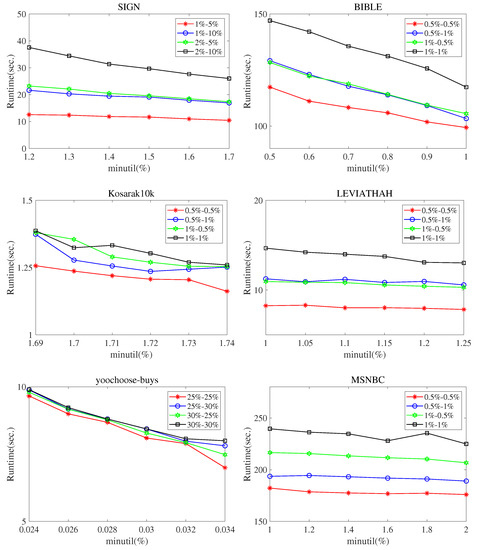
Figure 2.
Execution times for different parameter values. ().
When the execution time of the algorithm is high, the value of is usually set high. The reason is that with the increase of , the stability value of sequence patterns also decreases. In this case, SPHUSPM must consider more sequential patterns in mining.
At the same time, decreasing the value of and increasing the value of will relax the threshold. Therefore, in these cases, SPHUSPM must consider more sequence patterns and increase the execution time of the algorithm.
On the sparse dataset, the SPHUSPM method performs better than it does on the dense dataset. Because the occurrence probability of the same sequence pattern in sparse datasets is low, the sequence pattern stability is low. Thus, a large number of unstable patterns will not be considered.
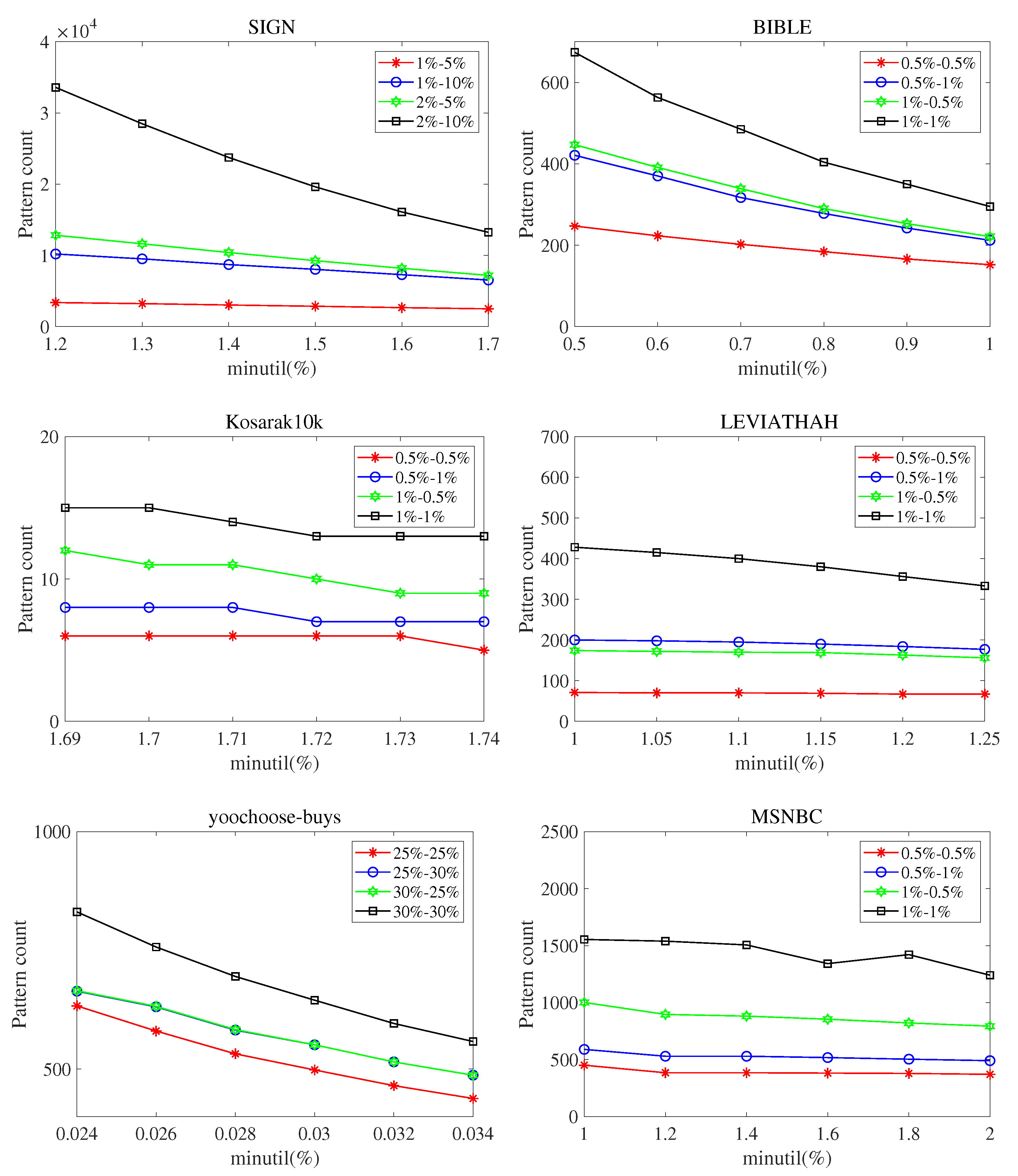
5.3. Pattern Count
Figure 3 shows the experimental results of the pattern count of SPHUSPM algorithm. The experiment was conducted on the six real datasets mentioned above. We observe the performance of the algorithm on different datasets with different thresholds by setting the values of , , and . In this figure, the x axis represents the minimum utility threshold (), and the y axis represents the number of SPHUSPs generated. means . The following observations can be drawn from Figure 3.
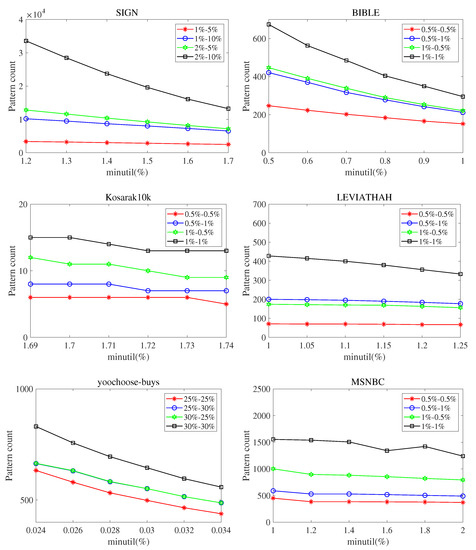
Figure 3.
Pattern count for different parameter values. ().
Fix the value and the value, and increase the value. Alternatively, fix the value and the value, and decrease the value. In both cases, the number of sequential patterns is reduced because the criteria for the threshold is increased.
When remains unchanged, the number of SPHUSPs increases with and , indicating a large number of potentially stable patterns in the HUSPs in datasets.
5.4. Memory Usage
Table 9 shows the memory usage of the SPHUSPM algorithm with different , , and values set on six datasets. The results show that the SPHUSPM algorithm uses less memory when the high value, the low value and the low value are set. This is reasonable because the algorithm can prune more sequential patterns in these cases.

Table 9.
Memory usage for different parameter values.
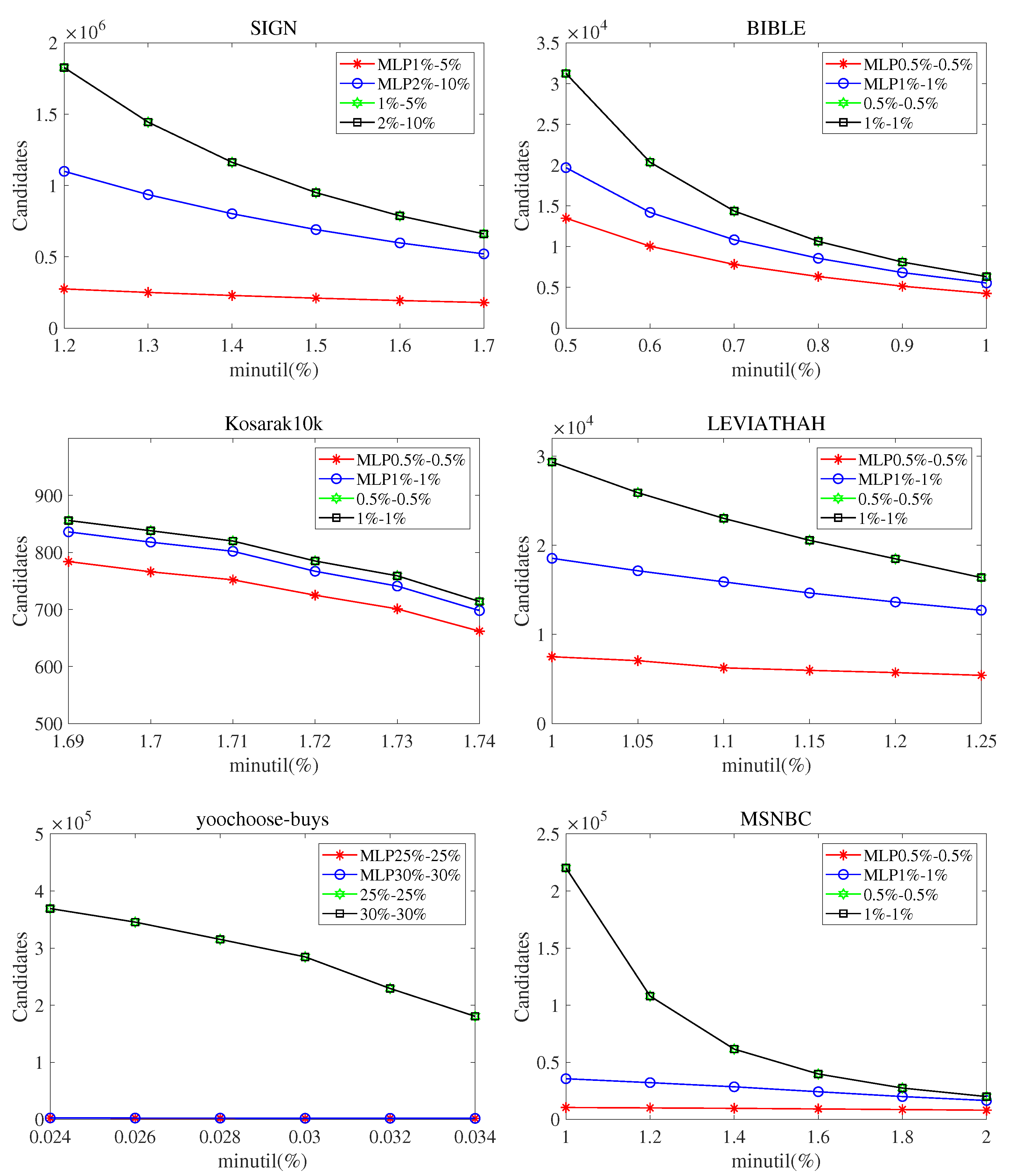
5.5. Effectiveness of Pruning Strategies
To test the performance of the improved maximum lability pruning strategy in sequential pattern mining (MLPS), we conduct experiments on six datasets. Figure 4 shows the number of candidates generated by the SPHUSPM when setting different values of , , and on six datasets. In this figure, the x axis represents the minimum utility threshold (), and the y axis represents the number of generated candidates. means , . In addition, indicates that the strategy is used. The following observations can be drawn from Figure 4.
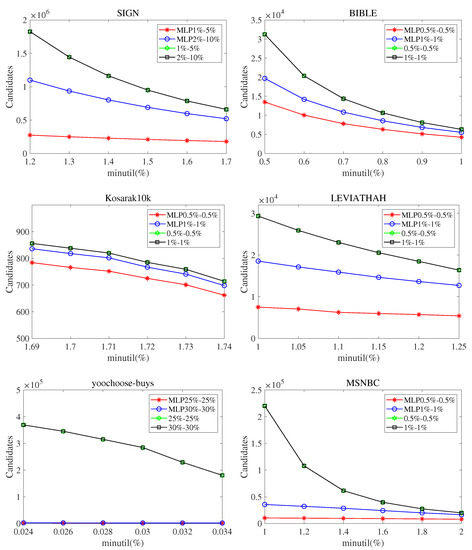
Figure 4.
Candidates for different parameter values. ().
MLPS can eliminate a large number of candidates in advance and show excellent performance on all datasets. The reduction of the number of candidates makes the execution time of the algorithm greatly reduced and the search space is greatly reduced. Moreover, with low and low , fewer candidates will be generated.
6. Conclusions
In this paper, the problem of mining stable periodic high-utility sequential patterns is defined, and the stability method is proposed for the first time in the mining of high-utility sequential patterns. In the HUSPM research area, this method provides a more flexible, precise decision-making mining strategy. In application areas, this method can be widely used in pattern discovery and knowledge discovery-related fields, such as research on consumer habits, website click-through rate data analysis, financial market analysis, biomedical applications, and mobile computing. To efficiently discover all SPHUSPs, an efficient SPHUSPM algorithm is designed. After experimental verification, the SPHUSPM algorithm can not only mine the sequence patterns ignored by the traditional algorithm, but also ensure that the mined sequence patterns show stable periodic characteristics in databases. At the same time, the addition of the PUL-list structure and the MLPS strategy accelerates the access speed and reduces the search space, so that the algorithm can ensure that the required sequence pattern can be mined, while also improving the mining efficiency and memory usage efficiency.
In future work, we will introduce the non-redundant strategy [17] and the negative utility strategy [41] based on this algorithm. These strategies are used to improve the accuracy of decision making and expand application scenarios.
Author Contributions
Conceptualization, S.X.; methodology, S.X.; software, S.X.; validation, L.Z.; formal analysis, L.Z.; investigation, L.Z.; resources, L.Z.; data curation, S.X.; writing—original draft preparation, S.X.; writing—review and editing, L.Z.; visualization, S.X.; supervision, L.Z.; project administration, L.Z.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was partly supported by the National Natural Science Foundation of China (61806105, 62076143, and 61906104) and the Natural Science Foundation of the Shandong Province (ZR2019BF018, ZR2021QF059).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PFPM | Periodic Frequency Pattern Mining |
| PPFPM | Partial Periodic Frequency Pattern Mining |
| SPFPM | Stable Periodic Frequent Pattern Mining |
| HUIM | High-Utility Itemset Mining |
| HUSPM | High-Utility Sequential Pattern Mining |
| HUSPs | High Utility Sequential Patterns |
| PHUSPM | Periodic High Utility Sequential Pattern Mining |
| PHUSPs | Periodic High Utility Sequential Patterns |
| SPHUSPM | Stable Periodic High Utility Sequential Pattern Mining |
| SPHUSPs | Stable Periodic High Utility Sequential Patterns |
| minimum utility threshold | |
| maximum periodicity threshold | |
| minimum periodicity threshold | |
| average periodicity threshold | |
| maximum lability threshold | |
| UL-list | utility-linked-list |
| PUL-list | period-utility-linked-list |
| LS-tree | Lexicographic Sequence Tree |
| SWU | Sequence Weighted Utilization |
| PEU | Prefix Extension Utility |
| RSU | Reduced Sequence Utility |
| SEU | Sequence Extended Utility |
| MPP | Maximum Periodic Pruning |
| MLP | Maximum Lability Pruning |
| MLPS | Maximum Lability Pruning in sequential pattern mining |
| IPS | Irrelevant Item Pruning Strategy |
| LAS | Look Ahead Strategy |
References
- Zhou, L.; Liu, Y.; Wang, J.; Shi, Y. Utility-based web path traversal pattern mining. In Proceedings of the Seventh IEEE International Conference on Data Mining Workshops (ICDMW 2007), Omaha, NE, USA, 28–31 October 2007; pp. 373–380. [Google Scholar]
- Truong-Chi, T.; Fournier-Viger, P. A survey of high utility sequential pattern mining. In High-Utility Pattern Mining; Springer: Berlin/Heidelberg, Germany, 2019; pp. 97–129. [Google Scholar]
- Yin, J.; Zheng, Z.; Cao, L. USpan: An efficient algorithm for mining high utility sequential patterns. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 660–668. [Google Scholar]
- Wang, J.Z.; Huang, J.L.; Chen, Y.C. On efficiently mining high utility sequential patterns. Knowl. Inf. Syst. 2016, 49, 597–627. [Google Scholar] [CrossRef]
- Ishita, S.Z.; Ahmed, C.F.; Leung, C.K. New approaches for mining regular high utility sequential patterns. Appl. Intell. 2022, 52, 3781–3806. [Google Scholar] [CrossRef]
- Ahmed, C.F.; Tanbeer, S.K.; Jeong, B.S. A Novel Approach for Mining High-Utility Sequential Patterns in Sequence Databases. ETRI J. 2010, 32, 676–686. [Google Scholar] [CrossRef]
- Yin, J.; Zheng, Z.; Cao, L.; Song, Y.; Wei, W. Efficiently mining top-k high utility sequential patterns. In Proceedings of the 2013 IEEE 13th international Conference on Data Mining, Dallas, TX, USA, 7–10 December 2013; pp. 1259–1264. [Google Scholar]
- Lan, G.C.; Hong, T.P.; Tseng, V.S.; Wang, S.L. Applying the maximum utility measure in high utility sequential pattern mining. Expert Syst. Appl. 2014, 41, 5071–5081. [Google Scholar] [CrossRef]
- Alkan, O.K.; Karagoz, P. CRoM and HuspExt: Improving efficiency of high utility sequential pattern extraction. IEEE Trans. Knowl. Data Eng. 2015, 27, 2645–2657. [Google Scholar] [CrossRef]
- Gan, W.; Lin, J.C.W.; Zhang, J.; Chao, H.C.; Fujita, H.; Philip, S.Y. ProUM: High utility sequential pattern mining. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 767–773. [Google Scholar]
- Gan, W.; Lin, J.C.W.; Zhang, J.; Fournier-Viger, P.; Chao, H.C.; Philip, S.Y. Fast utility mining on sequence data. IEEE Trans. Cybern. 2020, 51, 487–500. [Google Scholar] [CrossRef]
- Ahmed, C.F.; Tanbeer, S.K.; Jeong, B.S. Mining high utility web access sequences in dynamic web log data. In Proceedings of the 2010 11th ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing, London, UK, 9–11 June 2010; pp. 76–81. [Google Scholar]
- Shie, B.E.; Yu, P.S.; Tseng, V.S. Mining interesting user behavior patterns in mobile commerce environments. Appl. Intell. 2013, 38, 418–435. [Google Scholar] [CrossRef]
- Zihayat, M.; Davoudi, H.; An, A. Top-k utility-based gene regulation sequential pattern discovery. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shenzhen, China, 15–18 December 2016; pp. 266–273. [Google Scholar]
- Dinh, T.; Huynh, V.N.; Le, B. Mining periodic high utility sequential patterns. In Proceedings of the Asian Conference on Intelligent Information and Database Systems, Kanazawa, Japan, 3–5 April 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 545–555. [Google Scholar]
- Dinh, D.T.; Le, B.; Fournier-Viger, P.; Huynh, V.N. An efficient algorithm for mining periodic high-utility sequential patterns. Appl. Intell. 2018, 48, 4694–4714. [Google Scholar] [CrossRef]
- Afriyie, M.K.; Nofong, V.M.; Wondoh, J.; Abdel-Fatao, H. Mining non-redundant periodic frequent patterns. In Proceedings of the Asian Conference on Intelligent Information and Database Systems, Phuket, Thailand, 23–26 March 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 321–331. [Google Scholar]
- Amphawan, K.; Surarerks, A.; Lenca, P. Mining periodic-frequent itemsets with approximate periodicity using interval transaction-ids list tree. In Proceedings of the 2010 Third International Conference on Knowledge Discovery and Data Mining, Phuket, Thailand, 9–10 January 2010; pp. 245–248. [Google Scholar]
- Fournier-Viger, P.; Lin, C.W.; Duong, Q.H.; Dam, T.L.; Ševčík, L.; Uhrin, D.; Voznak, M. PFPM: Discovering periodic frequent patterns with novel periodicity measures. In Proceedings of the 2nd Czech-China Scientific Conference 2016, Ostrava, Czech Republic, 7 June 2016; IntechOpen: London, UK, 2017. [Google Scholar]
- Kiran, R.U.; Venkatesh, J.; Fournier-Viger, P.; Toyoda, M.; Reddy, P.K.; Kitsuregawa, M. Discovering periodic patterns in non-uniform temporal databases. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Chengdu, China, 16–19 May 2022; Springer: Berlin/Heidelberg, Germany, 2017; pp. 604–617. [Google Scholar]
- Fournier-Viger, P.; Yang, P.; Lin, J.C.W.; Kiran, R.U. Discovering stable periodic-frequent patterns in transactional data. In Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, Kitakyushu, Japan, 19–22 July; Springer: Berlin/Heidelberg, Germany, 2019; pp. 230–244. [Google Scholar]
- Fournier-Viger, P.; Wang, Y.; Yang, P.; Lin, J.C.W.; Yun, U.; Kiran, R.U. Tspin: Mining top-k stable periodic patterns. Appl. Intell. 2022, 52, 6917–6938. [Google Scholar] [CrossRef]
- Gan, W.; Lin, J.C.W.; Fournier-Viger, P.; Chao, H.C.; Hong, T.P.; Fujita, H. A survey of incremental high-utility itemset mining. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1242. [Google Scholar] [CrossRef]
- Fournier-Viger, P.; Wu, C.W.; Zida, S.; Tseng, V.S. FHM: Faster high-utility itemset mining using estimated utility co-occurrence pruning. In Proceedings of the International Symposium on Methodologies for Intelligent Systems, Limassol, Cyprus, 29–31 October 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 83–92. [Google Scholar]
- Lin, C.W.; Hong, T.P.; Lu, W.H. An effective tree structure for mining high utility itemsets. Expert Syst. Appl. 2011, 38, 7419–7424. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wu, C.W.; Tseng, V.S. Mining high utility itemsets in big data. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Chengdu, China, 16–19 May 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 649–661. [Google Scholar]
- Liu, M.; Qu, J. Mining high utility itemsets without candidate generation. In Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012; pp. 55–64. [Google Scholar]
- Yun, U.; Ryang, H.; Ryu, K.H. High utility itemset mining with techniques for reducing overestimated utilities and pruning candidates. Expert Syst. Appl. 2014, 41, 3861–3878. [Google Scholar] [CrossRef]
- Zida, S.; Fournier-Viger, P.; Lin, J.C.W.; Wu, C.W.; Tseng, V.S. EFIM: A highly efficient algorithm for high-utility itemset mining. In Proceedings of the Mexican International Conference on Artificial Intelligence, Mexico City, Mexico, 25–30 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 530–546. [Google Scholar]
- Amphawan, K.; Lenca, P.; Surarerks, A. Mining top-k periodic-frequent pattern from transactional databases without support threshold. In Proceedings of the International Conference on Advances in Information Technology, Bangkok, Thailand, 1–5 December 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 18–29. [Google Scholar]
- Kiran, R.U.; Kitsuregawa, M.; Reddy, P.K. Efficient discovery of periodic-frequent patterns in very large databases. J. Syst. Softw. 2016, 112, 110–121. [Google Scholar] [CrossRef]
- Surana, A.; Kiran, R.U.; Reddy, P.K. An efficient approach to mine periodic-frequent patterns in transactional databases. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Shenzhen, China, 24–27 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 254–266. [Google Scholar]
- Tanbeer, S.K.; Ahmed, C.F.; Jeong, B.S.; Lee, Y.K. Discovering periodic-frequent patterns in transactional databases. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Bangkok, Thailand, 27–30 April 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 242–253. [Google Scholar]
- Han, J.; Dong, G.; Yin, Y. Efficient mining of partial periodic patterns in time series database. In Proceedings of the 15th International Conference on Data Engineering (Cat. No. 99CB36337), Sydney, NSW, Australia, 23–26 March 1999; pp. 106–115. [Google Scholar]
- Yu, X.; Yu, H. An asynchronous periodic sequential patterns mining algorithm with multiple minimum item supports. In Proceedings of the 2014 Ninth International Conference on P2P, Parallel, Grid, Cloud and Internet Computing, Guangzhou, China, 8–11 November 2014; pp. 274–281. [Google Scholar]
- Fournier-Viger, P.; Lin, J.C.W.; Duong, Q.H.; Dam, T.L. PHM: Mining periodic high-utility itemsets. In Proceedings of the Industrial Conference on Data Mining, New York, NY, USA, 13–17 July 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 64–79. [Google Scholar]
- Lin, J.C.W.; Zhang, J.; Fournier-Viger, P. High-utility sequential pattern mining with multiple minimum utility thresholds. In Proceedings of the Asia-Pacific Web (APWeb) and Web-Age Information Management (WAIM) Joint Conference on Web and Big Data, Guangzhou, China, 23–25 August 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 215–229. [Google Scholar]
- Lin, J.C.W.; Zhang, J.; Fournier-Viger, P.; Hong, T.P.; Zhang, J. A two-phase approach to mine short-period high-utility itemsets in transactional databases. Adv. Eng. Inform. 2017, 33, 29–43. [Google Scholar] [CrossRef]
- Ayres, J.; Flannick, J.; Gehrke, J.; Yiu, T. Sequential pattern mining using a bitmap representation. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, Canada, 23–26 July 2002; pp. 429–435. [Google Scholar]
- Fournier-Viger, P.; Lin, J.C.W.; Gomariz, A.; Gueniche, T.; Soltani, A.; Deng, Z.; Lam, H.T. The SPMF open-source data mining library version 2. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Riva del Garda, Italy, 19–23 September 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 36–40. [Google Scholar]
- Dong, X.; Gong, Y.; Cao, L. e-RNSP: An efficient method for mining repetition negative sequential patterns. IEEE Trans. Cybern. 2018, 50, 2084–2096. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).