Abstract
The search for life outside Earth has been a popular topic for a long time in the scientific literature, but it gained more possibilities with the discovery of planets around other stars besides our Sun. In this sense, similarly to what happens in our Solar System, moons of planets sometimes offer good conditions for life if stable orbits for those moons exist. Thus, the present paper analyzes a system composed of a moon (with the mass of the Earth) orbiting a planet (with the mass of Jupiter), which is orbiting a double star system (whose total mass is equal to the mass of the Sun). It is an important topic because there is a large proportion of double stars in the universe. The initial conditions are given by a symmetric configuration of two circular orbits. Although this symmetry is broken due to the four body dynamics, the conditions in which the moon remains bound with the planet are investigated. The stability of the system is given by the survival of the orbit of the moon for an integration time of the order of 10,000 revolutions of the satellite around its mother planet. The regions of stable, unstable, and collision orbits are mapped, and empirical linear equations that separate those regions are obtained from the maps.
1. Introduction
An exoplanet is defined as a planet that orbits a star that is not the Sun. The study of the dynamics associated with those exoplanets is increasing in importance nowadays since systems of this type have been discovered very often with the increase of the capabilities to make observations of deep space objects. Exoplanets are very important because they help our understanding of the evolution of a solar system, as well as the possible evolution of life in the universe.
The possibility of the existence of exoplanets was in the mind of humans for a long time until the discovery of a planetary system around the pulsar PSR B1 257 + 1217 in [1]. The PSR B1620-26b was the first discovered circumbinary super-Jupiter planet [2], which means that it orbits a binary system. The discovery of a Jupiter-sized planet orbiting the Sun-like star 51 Pegasi by [3] led to the 2019 Nobel Prize in Physics. The Kepler-47 is a system composed of at least three planets orbiting a pair of stars [4,5]. More than 5 thousand exoplanets are known today. The investigation of systems composed of exoplanets orbiting binary stars is very important since about one-third of star systems are estimated to be composed of more than one star [6].
The knowledge about our own solar system shows the existence of a large number of moons, which calls our attention to the possibility of the existence of moons around exoplanets. As said before, a long list of exoplanets has been observed up to now. Each of them may be orbited by exomoons. This term was first used in [7], although habitable moons with the mass of the Earth orbiting a Jupiter-like planet have been investigated since [8]. Exomoons with a size and mass similar to the Earth are of particular interest to humankind for scientific purposes, to study and search for life. The major problem is that they are hard to observe. Thus, it is important to investigate their dynamics to facilitate the search. The habitability of moons around exoplanets were investigated through indirect (non-observational) methods in several papers. The influence of the flux due to the photons over the habitability was studied in [9]. The work shown in [10] provided a deep investigation, where the habitability of the moon is analyzed through its formation and its detectability from the Earth with the available technological instruments. The atmosphere of exomoons is analyzed for habitability in [11]. Note that the influence of the absorbed radiation over the atmosphere determines the possible presence of hydrogen and other elements essential to life [12]. Beyond the radiation, the tidal heating flux caused on the moon by the planet, and the star can also be taken into consideration [13,14,15,16,17]. Guimarães and Valio studied possible locations for an exomoon [18], considering the long term duration of the orbits and the Roche limit, which defines a minimum distance an exomoon should have to avoid being destroyed by the gravity of the planet. In that way, they found the limits in the semi-major axis for possible orbits, which guides observations that try to detect an exomoon.
Orbital stability has been studied using approximations of a Hill analytic model in [13]. The effects of general relativistic post-Newtonian and the J2 quadrupole mass moment of the moon over its obliquity for an Earth-like moon orbiting a Jupiter-like planet are investigated in [19]. The stability of satellites orbiting a planet that is orbiting a star using the elliptic restricted three-body problem is investigated in [20].
Note that a double star system is governed by the two-body dynamics, which show several symmetries, like periodic orbits. An initial circular orbit may emphasize such symmetric orbits. Furthermore, the motion of a moon orbiting a planet is locally governed by the two-body dynamics; hence, it also shows several symmetries. When all four bodies are taken into consideration, the more massive double star system perturbs the moon-planet system. It breaks the symmetry of their orbits around the barycenter of this last pair. It may cause a rupture of the bound between the moon and the planet—they become independent bodies—or the asymmetry of the orbits generated by the double star is not enough to break this bound, and the moon remains orbiting the planet locally.
As said before, the knowledge about the dynamics of the pair exomoon/exoplanet orbiting a binary star can be used to facilitate the search for habitable satellites. Research shows that Earth-like planets can be captured by exoplanets [21,22,23,24]. The stability of exomoons is investigated in [25] based on fitting expressions obtained from a statistical approach obtained from [26]. Linear expressions to the stability region in the parameters space given by the semi-major axis and the eccentricity were also obtained by [20] through statistical analysis. The stability of exomoons investigated in the literature shown above is based on the three-body problem [27]—a system composed of a star, an exoplanet, and an exomoon or two stars and a planet. There are works available in the literature which investigate the existence of satellites around exoplanets orbiting a double star system using a four-body problem approach [28,29], although the research presented in this paper shows a different approach based on a statistical analysis of the dynamics of such a system. The objective of the present paper is to extend the works mentioned above. In this research, a parameter survey approach is applied to a double star system instead. The main objective is to study the stability of the system through analyses of the space of the parameters and to obtain fitting expressions for several parameters based on the statistical analyzes of the data numerically generated. These data are obtained through numerical integrations of different initial conditions and for different values of the parameters involved. Note that the dynamics are much more complex due to the addition of the second star. A four-body model is used in the simulations. On the other side, several parameters will be fixed. At the same time, more attention will be given to the relation among the four following parameters: the semi-major axis, the eccentricity of the orbit, the distance of the exoplanet from the center of mass, and the separation distance between the stars. The problem is solved by performing numerical integrations of the whole system for several initial conditions to verify if the natural satellite stays in orbit around the planet for a time of the order of 10,000 revolutions of the satellite around its mother planet. The results will show the regions of stable orbits, the collision of the satellite with the planet, and where there are escapes of the satellite from the mother planet.
Note that methods for the determination of orbits for spacecraft in deep space are evolving nowadays [30], which increase the possibility of discovering exomoons. However, the resources are limited. In this sense, the results obtained by this paper can be used to improve the search for habitable exomoons in deep space by providing information regarding the regions where they may or may not exist.
2. Mathematical Model
The mathematical model uses the classical N-body problem [31] to solve this problem for the case where N = 4 (two stars, one planet, and one moon). The following assumptions are made for the system (see Figure 1 for more details):
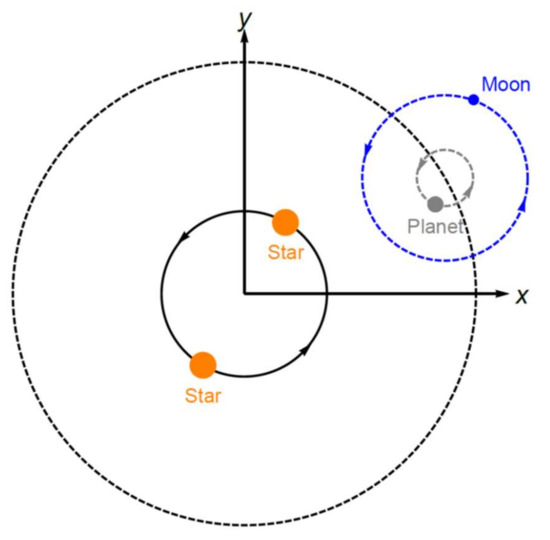
Figure 1.
The distribution of bodies for the problem under study.
- (I)
- There are two stars with 0.5 solar mass, each one in a circular orbit around their center of mass, which are the bodies that dominate the system;
- (II)
- A planet is orbiting this double star system at a variable distance from the center of mass of the system. This planet has the mass and size of Jupiter. Its initial orbit is circular, and the initial semi-major axis follows the values shown for each particular solution. After the initial time, its orbit follows the evolution given by the Four-Body dynamics;
- (III)
- A natural satellite (moon) with the mass of the Earth is in an elliptical orbit around the planet with a variable semi-major axis and eccentricity;
- (IV)
- Only planar motions are considered for all the bodies involved;
- (V)
- All the bodies are assumed to be mass points;
- (VI)
- Direct orbits are used for all bodies.
A system of reference is centered in the barycenter of the bodies. Assuming that this is an inertial system of reference, according to Newton’s laws of motion, the equation of motion of the bodies under their mutual gravitational attraction is given by [31]
where i = 1, 2, 3, 4 denotes the i-th body, and are the position and mass of the i-th body, respectively; and are the position and mass of the j-th body, respectively; and is the gravitational constant. Note that the left side of Equation (1) contains the constant mass of the i-th body times its acceleration in the inertial frame of reference, while the right side contains the sum of the total gravitational forces in which the i-th body is subject due to the presence of the other massive bodies.
The order is defined such that and represent the mass and position of the moon, and represent the mass and position of the planet, and and represent the mass and position of one of the stars, as well as and with respect to the other star. Thus, according to Equation (1), the equation of motion of the moon (for ) is given by
The relative positions vectors used in Equation (2) are shown in Figure 2 for a better visualization. The equations of motion of the other bodies are similarly obtained from Equation (1).
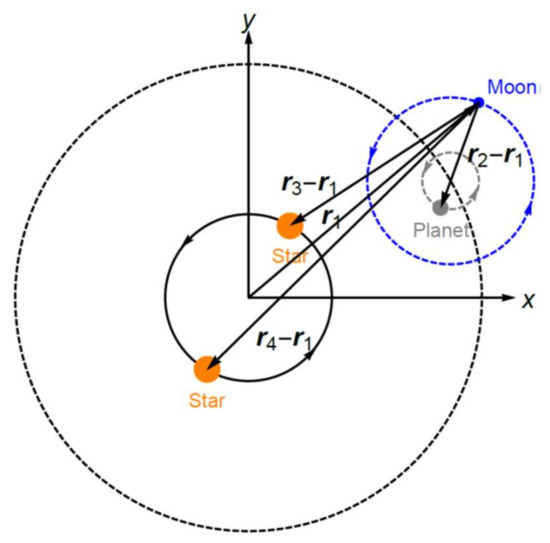
Figure 2.
The relative positions of the bodies with respect to the moon.
In order to perform the numerical integrations, a Runge–Kutta integrator was used, with variable step size control to adjust the numerical accuracy required. The mathematical numerical procedure was written in Fortran, and an Intel compiler was used to run the code. More than a week was required to collect the results for each grid related to the varied elements of the orbits.
Different times were used for the numerical integrations, from 10,000 revolutions of the primaries to 10,000 revolutions of the outer satellite, with little differences in the results, which means that if the system is unstable, the escapes or collisions happen at the beginning of the study. This is important because it shows that the approach used here gives trusted results, and very long integration times are not required.
3. Results
The results are expressed by plots that show the semi-major axis of the orbit of the moon around the planet (in a radius of the planet) in the horizontal axis and the eccentricity of the orbit of that moon in the vertical axis. Then, the region of stable orbits is colored in dark, with the regions of unstable orbits left in light gray. A cross marks the points of collisions between the moon and the planet. The distance separating the two stars had values of 0.1 AU (AU = Astronomical Unit, which is the mean Sun-Earth distance, equal to 1,496,000 km). Several values were also simulated for the distance of the planet from the center of the system. The results showed that values below 0.3 AU resulted in unstable orbits for the planet, ending in collisions with the star or escape from the system. Values above 1.0 AU are of little interest because the system planet-moon receives a gravitational force similar to a single point mass gravity field with the mass of the two stars since the distance is too large compared with the separations of the stars. After plotting the data, empirical equations based on statistical analysis are derived to relate the semi-major () axis and the eccentricity () of the orbit of the satellite for the main line that divides stable from unstable orbits. The regions of collisions do not follow a linear or other simple relation, so the results are available only in the drawings of Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, which give the more important results.
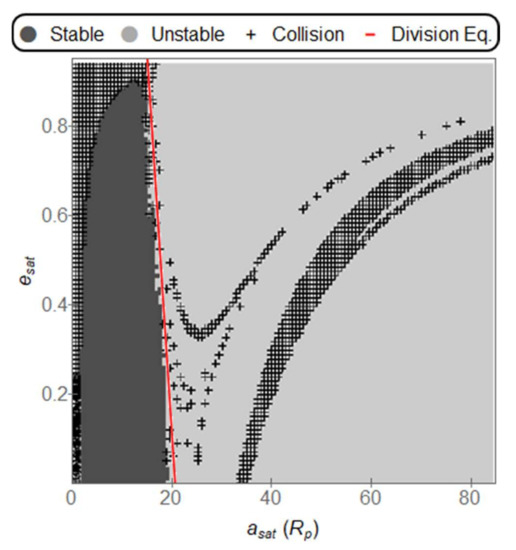
Figure 3.
Stable, Unstable, and Collision orbits for a Star separation of 0.1 AU, a planet distance from the center of 0.3 AU. The equation for the division between stable and unstable orbits is: = (−5.8601 ± 0.5711) + (20.6199 ± 0.3584). The values inside the parenthesis represent the error of the estimated variable.
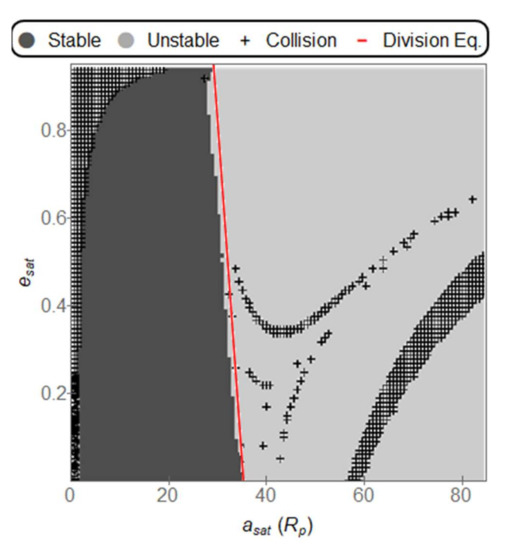
Figure 4.
Stable, Unstable and Collision orbits for a Star separation of 0.1 AU, a planet distance from the center of 0.4 AU. The equation for the division between stable and unstable orbits is: = (−6.4429 ± 0.4082) + (35.2454 ± 0.2087). The values inside the parenthesis represent the error of the estimated variable.
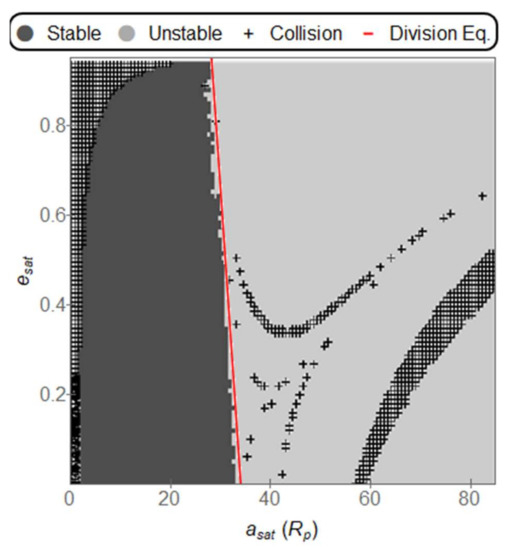
Figure 5.
Stable, Unstable, and Collision orbits for a Star separation of 0.1 AU, a planet distance from the center of 0.5 AU. The equation for the division between stable and unstable orbits is: = (−6.1369 ± 0.4857) + (34.0086 ± 0.3097). The values inside the parenthesis represent the error of the estimated variable.
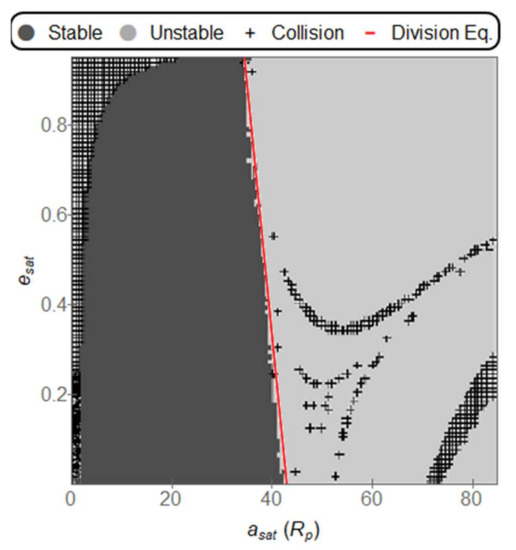
Figure 6.
Stable, Unstable, and Collision orbits for a Star separation of 0.1 AU, a planet distance from the center of 0.6 AU. The equation for the division between stable and unstable orbits is: = (−8.9012 ± 0.6133) + (42.8833 ± 0.2983). The values inside the parenthesis represent the error of the estimated variable.
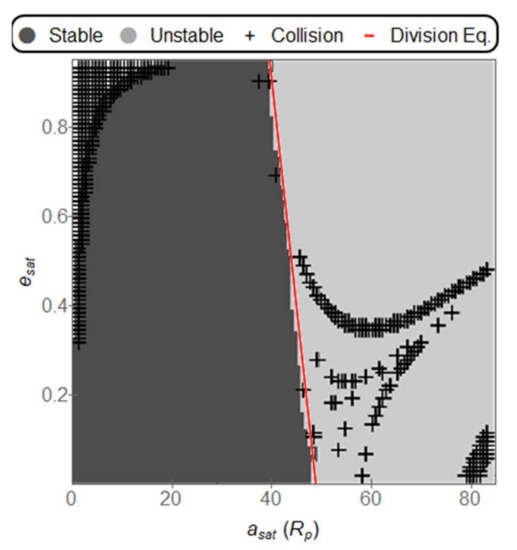
Figure 7.
Stable, Unstable, and Collision orbits for a Star separation of 0.1 AU, a planet distance from the center of 0.7 AU. The equation for the division between stable and unstable orbits is: = (−9.7735 ± 0.7104) + (48.8190 ± 0.4675). The values inside the parenthesis represent the error of the estimated variable.
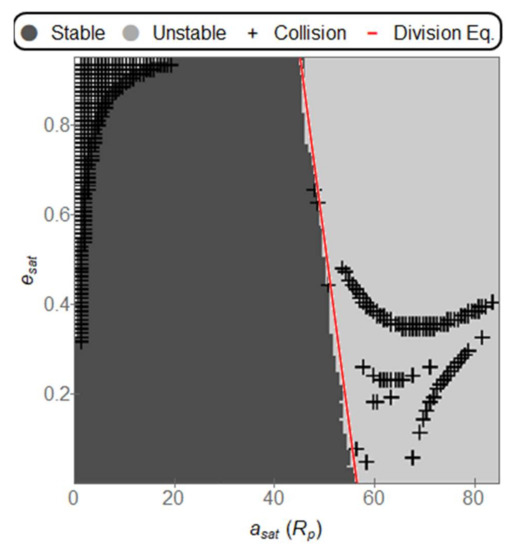
Figure 8.
Stable, Unstable, and Collision orbits for a Star separation of 0.1 AU, a planet distance from the center of 0.8 AU. The equation for the division between stable and unstable orbits is: = (−11.9669 ± 0.6077) + (56.4402 ± 0.3909). The values inside the parenthesis represent the error of the estimated variable.
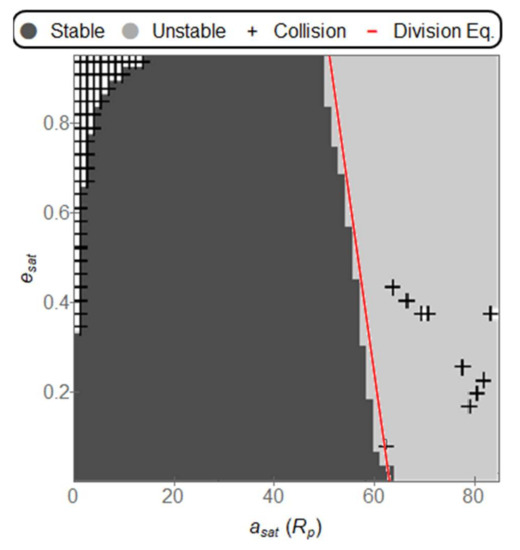
Figure 9.
Stable, Unstable, and Collision orbits for a Star separation of 0.1 AU, a planet distance from the center of 0.9 AU. The equation for the division between stable and unstable orbits is: = (−12.6449 ± 0.4462) + (62.9828 ± 0.2651). The values inside the parenthesis represent the error of the estimated variable.
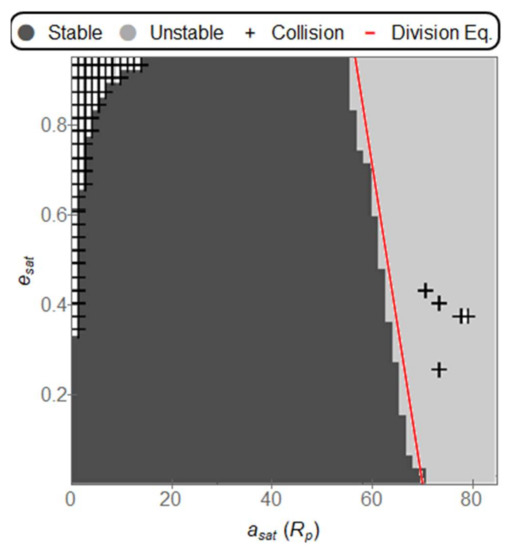
Figure 10.
Stable, Unstable, and Collision orbits for a Star separation of 0.1 AU, a planet distance from the center of 1.0 AU. The equation for the division between stable and unstable orbits is: = (−14.1659 ± 0.4077) + (69.9968 ± 0.2368). The values inside the parenthesis represent the error of the estimated variable.
Based on the statistical analysis, it is possible to find a general equation which relates the semi-major axis of the border line orbits (stable/unstable) as a function of the eccentricity of the orbit and/or other parameters, such as the distance of the planet to the center of the system () and the distance between the stars (). In order to have the statistical analysis done, the division points are defined such that their values are the average values between the last stable and the first unstable points for a varying parameter considering all other parameters at a constant (fixed) value. After that, a second parameter is varied, and the same procedure is done for the next value of this second parameter. After the second parameter is varied, the division points containing the two varied parameters can be used in a two-dimensional plot to show the border between the stable ad unstable regions. Such a border can be better described by a curve generated by the division points. Analyses of the two-dimensional plots suggest that linear curves can be used to separate the stable and unstable regions. Regression analysis is used in this paper to build this curve. A linear relation between the two varied variables is assumed, e.g., . Thus, a set of N equations is generated by applying this relation for each of the N elements of the division points. After that, a least square method is used to find the values of and that minimizes the sum of the squares of the residues generated by the application of the above linear relation over all the division points. The method explained above can be extended for linear relations between more than two variables.
An important relation is shown in Equation (3), which shows the semi-major axis of the border line orbits (stable/unstable) as a function of the eccentricity of the orbit and the distance of the planet to the center of the system (, in astronomical units). The numbers after the plus/minus signal () represent the statistical errors of the variables. This equation can be used to quickly find the regions of stable orbits. Hence, it is possible to predict the best regions to point to observational instruments to try to detect exomoons.
After that, a study is made to find the influence of the separation of the two stars that compose the main binary system. The plots have the same general behavior, so the figures are not repeated here, and only the new empirical equations are shown. Assuming a fixed distance for the planet of 0.3 AU and a variable star separation, the equations are shown below. Equation (4) shows the results for a star separation of 0.01 AU.
Equation (5) shows the results for a star separation of 0.05 AU.
Equation (6) shows the results for a star separation of 0.1 AU.
Some important points that need to be considered are made next. When the separation of the stars goes from 0.01 to 0.05 AU, there is a decrease of 1.21 radius of Jupiter in the stable region. Increasing this distance, there is an extra decrease of 0.34 radius of Jupiter when the separation goes to 0.1 AU.
Considering now a different distance for the planet around the stars, the study of the effects of the star separation is made again. The next equations are developed for a planet distance of 0.5 AU. Equation (7) shows the results for a star separation of 0.01 AU.
Equation (8) shows the results for a star separation of 0.05 AU.
Equation (9) shows the results for a star separation of 0.1 AU.
It can be observed that when the separation of the stars goes from 0.01 to 0.05 AU, there is a decrease of 0.48 radius of Jupiter in the stable region and that there is an extra decrease of 0.21 radius of Jupiter when the separation goes to 0.1 AU.
The next equations are developed for a planet distance of 0.6 AU. Equation (10) shows the results for a star separation of 0.01 AU.
Equation (11) shows the results for a star separation of 0.05 AU.
Equation (12) shows the results for a star separation of 0.1 AU.
Equation (13) shows the results for a star separation of 0.2 AU.
The results show that when the separation of the stars goes from 0.01 to 0.05 AU, there is a decrease of 0.88 radius of Jupiter in the stable region, and there is an extra decrease of 0.37 radius of Jupiter when the separation goes to 0.1 AU.
Considering simulations for different values of the distance between the stars (), a more general equation can be found, and it is shown in Equation (14) below. This equation has all the variables as independent and allows a fast estimation of the border limit between stable and unstable orbits for exomoons around the exoplanet. It can guide the locations where to point observational instruments to try to detect exomoons and can help in this important and difficult search.
In the case where the distance of the planet from the center of the system is AU and the distance between the stars is AU, an extrapolation of Equation (14) becomes
The four-body problem investigated in this paper coincides with the three-body problem in the case where there is no separation between the two stars. This is the case for a system composed of a Sun-like star, a Jupiter-like planet, and an Earth-like moon orbiting the Jupiter-like planet. This case was investigated by [20], where the following important equation was obtained for the separation of the stable/unstable regions
The conditions in which Equations (15) and (16) were obtained are similar, but they are not the same. For instance, the model adopted is different (4BP and 3BP to derive Equations (15) and (16), respectively) and Equation (16) was obtained for a mass ratio of , while the ratio between the mass of the Jupiter-like planet and the mass of both stars used in this paper is . Furthermore, the data collected to statistically derive Equation (15) was considered for in the range (in astronomical units). Hence, Equation (15) is an extrapolation of Equation (14) for AU. The difference between the semi-major axes given by Equations (15) and (16) is now defined as , which is shown in Figure 11 as a function of the eccentricity . Although the limit of the semi-major axis is about 3 larger in Equation (15) for very low eccentricities, it decreases more abruptly as the eccentricity is increased, and Equation (16) shows larger limits to the semi-major axis. The maximum absolute difference between Equations (15) and (16) is about 5 , and it occurs for larger values of the eccentricity. Equations (15) and (16) coincide for .
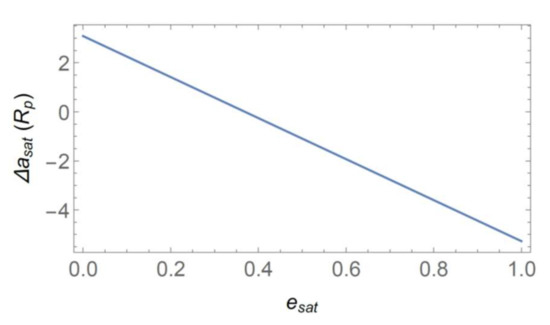
Figure 11.
The difference between Equations (15) and (16) as a function of the eccentricity .
Note that Equation (14) is derived for a wide range of several parameters, not only for the eccentricity. The simple (linear) equation given by Equation (14) separating the stable/unstable regions as a function of several parameters (eccentricity, distance of the planet from the center, and distance between the stars) can be useful as a guide to search for exomoons in the universe. They show the gravitational effect over the dynamics through the regions in which exomoons may or may not exist, for a double star system and also for a single star system through an extrapolation. The extra terms given by (64.6382 ± 0.6488) and (−7.2592 ± 0.2689) present in Equation (14) shown in this paper are very important since Equation (14) can be used in a much larger range of different systems, in comparison with Equation (16) available in the literature [20].
The Roche limit is the minimum distance a satellite must have from the planet it is orbiting such that its physical structure is not broken apart. In the case of a satellite orbiting the Jupiter-like planet investigated in this paper, the Roche limit is [32] , where and are specific masses of the planet and the satellite, respectively. The Roche limit for a satellite with the same specific mass as the Jupiter-like planet is radius of Jupiter. There are collisions for in most cases shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, but these figures show stable regions for low eccentricities in the cases where the distance of the planet from the center is above 0.7 AU (Figure 7, Figure 8, Figure 9 and Figure 10). Thus, it is important to note that although the dynamics of these small regions show stability, the physical structure of an exomoon would not be intact due to the tidal forces. An overlay of the data collected collect in this paper with the Roche limit may be useful to improve the searching for exomoons in some cases.
4. Conclusions
A study of the stability of orbits for exomoons around an exoplanet that is orbiting a double star system was studied. Numerical simulations of the full four-body problem were used to solve this problem, and it mapped the regions of stable, unstable, and collision orbits as a function of the main parameters of the system, which are the separation between the two stars that dominate the dynamics and the distance of the planet from the center of mass of the double stars.
The numerical simulations were used to build a large set of data, which was used to generate plots that identify the stable orbits of the moon, which are the ones that do not collide with the planet and that do not escape from its orbit around the planet. This data set was also used to generate empirical equations for the border lines between stable and unstable regions. They are nearly straight lines, so it is possible to obtain accurate equations representing those border lines. Those equations help in the observational search of exomoons, which are very difficult without some guidance from simulations such as the ones made here.
Comparisons of the equations obtained in this research with the literature show that the ones obtained here can be applied to a wider range of possibilities since four parameters are varied in this work and related to those equations. There is a small difference of zero up to 5 radii of the exoplanet between them. This difference is due to small differences in the values of the parameters, the different approaches, statistical approaches, the different model adopted, and mainly to an extrapolation done for the comparison purpose. This is a small price to pay since this work describes the relation of stability with four parameters in a simple linear equation, which is novel and can be useful for observational purposes.
The results also show that the distance between the planet and the stars plays an important role because the stable region increases with this distance, as expected. The only exception to this rule occurs for 0.5 AU. The dynamics are very complex, so it is not surprising to have some exceptions to general rules.
On the opposite side, the separation between the stars showed small differences in the results obtained, so it is not a key factor for the stability of the orbits.
Author Contributions
Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Validation, Visualization, Writing—original draft, and Writing—review & editing: A.K.d.A.J., V.M.G. and A.F.B.d.A.P. All authors have read and agreed to the published version of the manuscript.
Funding
The authors wish to express their appreciation for the support provided by grants 2016/24561-0 and 2018/07377-6, from São Paulo Research Foundation (FAPESP), the National Council for Scientific and Technological Development (CNPq), grants 309089/2021-2; and the financial support from the National Council for the Improvement of Higher Education (CAPES). This paper has been supported by the RUDN University Strategic Academic Leadership Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank the comments and suggestions of the referees.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wolszczan, A.; Frail, D.A. A planetary system around the millisecond pulsar PSR1257+12. Nature 1992, 355, 145–147. [Google Scholar] [CrossRef]
- Backer, D.C.; Foster, R.S.; Sallmen, S. A second companion of the millisecond pulsar 1620-26. Nature 1993, 365, 817–819. [Google Scholar] [CrossRef]
- Mayor, M.; Queloz, D. A Jupiter-mass companion to a solar-type star. Nature 1995, 378, 355–359. [Google Scholar] [CrossRef]
- Orosz, J.A.; Welsh, W.F.; Carter, J.A.; Fabrycky, D.C.; Cochran, W.D.; Endl, M.; Ford, E.B.; Haghighipour, N.; MacQueen, P.J.; Mazeh, T.; et al. Kepler-47: A Transiting Circumbinary Multiplanet System. Science 2012, 337, 1511–1514. [Google Scholar] [CrossRef] [PubMed]
- Orosz, J.A.; Welsh, W.F.; Haghighipour, N.; Quarles, B.; Short, D.R.; Mills, S.M.; Satyal, S.; Torres, G.; Agol, E.; Fabrycky, D.C.; et al. Discovery of a Third Transiting Planet in the Kepler-47 Circumbinary System. Astron. J. 2019, 157, 174. [Google Scholar] [CrossRef]
- Lada, C.J. Stellar Multiplicity and the Initial Mass Function: Most Stars Are Single. Astrophys. J. Lett. 2006, 640, L63–L66. [Google Scholar] [CrossRef]
- Szabó, G.M.; Szatmáry, K.; Divéki, Z.; Simon, A. Possibility of a photometric detection of “exomoons”. Astron. Astrophys. 2006, 450, 395–398. [Google Scholar] [CrossRef][Green Version]
- Williams, D.M.; Kasting, J.F.; Wade, R.A. Habitable moons around extrasolar giant planets. Nature 1997, 385, 234–236. [Google Scholar] [CrossRef] [PubMed]
- Hinkel, N.R.; Kane, S.R. Habitability of exomoons at the Hill or tidal locking radius. Astrophys. J. Lett. 2013, 774, 27. [Google Scholar] [CrossRef]
- Heller, R.; Williams, D.; Kipping, D.; Limbach, M.A.; Turner, E.; Greenberg, R.; Sasaki, T.; Bolmont, É.; Grasset, O.; Lewis, K.; et al. Formation, Habitability, and Detection of Extrasolar Moons. Astrobiology 2014, 14, 798–835. [Google Scholar] [CrossRef] [PubMed]
- Kaltenegger, L. Characterizing habitable exomoons. Astrophys. J. Lett. 2010, 712, L125. [Google Scholar] [CrossRef]
- Lammer, H.; Schiefer, S.-C.; Juvan, I.; Odert, P.; Erkaev, N.V.; Weber, C.; Kislyakova, K.G.; Güdel, M.; Kirchengast, G.; Hanslmeier, A. Origin and Stability of Exomoon Atmospheres: Implications for Habitability. Orig. Life Evol. Biosphere 2014, 44, 239–260. [Google Scholar] [CrossRef] [PubMed]
- Heller, R. Exomoon habitability constrained by energy flux and orbital stability. Astron. Astrophys. 2012, 545, L8. [Google Scholar] [CrossRef]
- Heller, R.; Barnes, R. Exomoon Habitability Constrained by Illumination and Tidal Heating. Astrobiology 2013, 13, 18–46. [Google Scholar] [CrossRef] [PubMed]
- Lingam, M.; Pryor, S.; Ginsburg, I. Tidal modulations and the habitability of exoplanetary systems. Mon. Not. R. Astron. Soc. 2022, 510, 4837–4843. [Google Scholar] [CrossRef]
- Dobos, V.; Heller, R.; Turner, E.L. The effect of multiple heat sources on exomoon habitable zones. Astron. Astrophys. 2017, 601, A91. [Google Scholar] [CrossRef]
- Dobos, V.; Haris, A.; Kamp, I.E.E.; van der Tak, F.F.S. A target list for searching for habitable exomoons. Mon. Not. R. Astron. Soc. 2022, 513, 5290–5298. [Google Scholar] [CrossRef]
- Guimarães, A.; Valio, A. The Best Planets to Harbor Detectable Exomoons. Astron. J. 2018, 156, 50. [Google Scholar] [CrossRef]
- Iorio, L. The Effect of Post-Newtonian Spin Precessions on the Evolution of Exomoons’ Obliquity. Astron. J. 2022, 163, 55. [Google Scholar] [CrossRef]
- Domingos, R.D.C.; Winter, O.; Yokoyama, T. Stable satellites around extrasolar giant planets. Mon. Not. R. Astron. Soc. 2006, 373, 1227–1234. [Google Scholar] [CrossRef]
- Kipping, D.M. Transit timing effects due to an exomoon. Mon. Not. R. Astron. Soc. 2009, 392, 181–189. [Google Scholar] [CrossRef]
- Kipping, D.M.; Bakos, G.Á.; Buchhave, L.; Nesvorný, D.; Schmitt, A. The hunt for exomoons with Kepler (HEK): I. Description of a new observational project. Astrophys. J. 2012, 750, 115. [Google Scholar] [CrossRef]
- Kipping, D.M.; Hartman, J.; Buchhave, L.A.; Schmitt, A.R.; Bakos, G.; Nesvorný, D. The hunt for exomoons with Kepler (HEK): II. Analysis of seven viable satellite-hosting planet candidates. Astrophys. J. Lett. 2013, 770, 101. [Google Scholar] [CrossRef]
- Kipping, D.M.; Forgan, D.; Hartman, J.; Nesvorny, D.; Bakos, G.; Schmitt, A.; Buchhave, L.A. The hunt for exomoons with Kepler (HEK): III. The first search for an exomoon around a habitable-zone planet. Astrophys. J. Lett. 2013, 777, 134. [Google Scholar] [CrossRef]
- Cuntz, M. S-type and P-type habitability in stellar binary systems: A comprehensive approach. I. Method and applications. Astrophys. J. 2014, 780, 14–33. [Google Scholar] [CrossRef]
- Holman, M.J.; Wiegert, P.A. Long-Term Stability of Planets in Binary Systems. Astron. J. 1999, 117, 621–628. [Google Scholar] [CrossRef]
- Musielak, Z.E.; Quarles, B. The three-body problem. Rep. Prog. Phys. 2014, 77, 065901. [Google Scholar] [CrossRef]
- Docobo, J.A.; Andrade, M. A Methodology for the Description of Multiple Stellar Systems with Spectroscopic Subcomponents. Astrophys. J. Lett. 2006, 652, 681–695. [Google Scholar] [CrossRef]
- Campo, P.P.; Docobo, J.A. Analytical study of a four-body configuration in exoplanet scenarios. Astron. Lett. 2014, 40, 737–748. [Google Scholar] [CrossRef]
- Takeuchi, H.; Yoshikawa, K.; Takei, Y.; Oki, Y.; Kikuchi, S.; Ikeda, H.; Soldini, S.; Ogawa, N.; Mimasu, Y.; Ono, G.; et al. The deep-space multi-object orbit determination system and its application to Hayabusa2′s asteroid proximity operations. Astrodynamics 2020, 4, 377–392. [Google Scholar] [CrossRef]
- Keith, S.R. Mechanics, 1st ed.; Addison-Wesley Inc.: Boston, MA, USA, 1953. [Google Scholar]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).