Nonconservative Unimodular Gravity: Gravitational Waves

Abstract

Unimodular gravity is characterized by an extra condition with respect to general relativity, i.e., the determinant of the metric is constant. This extra condition leads to a more restricted class of invariance by coordinate transformation: The symmetry properties of unimodular gravity are governed by the transverse diffeomorphisms. Nevertheless, if the conservation of the energy–momentum tensor is imposed in unimodular gravity, the general relativity theory is recovered with an additional integration constant which is associated to the cosmological term $\Lambda$. However, if the energy–momentum tensor is not conserved separately, a new geometric structure appears with potentially observational signatures. In this text, we consider the evolution of gravitational waves in a nonconservative unimodular gravity, showing how it differs from the usual signatures in the standard model. As our main result, we verify that gravitational waves in the nonconservative version of unimodular gravity are strongly amplified during the evolution of the universe.

1. Introduction

General relativity (GR) is considered as the modern theory of gravitation since its final formulation in 1915. However, soon after the GR theory was introduced, many other theories for the gravitational interaction were proposed. Unimodular gravity is one of the oldest alternative to GR, see for example [1] for a discussion of this alternative formulation of a gravity theory. Unimodular gravity is similar to GR in many respects. One important similarity is that both are geometric theories of gravity based on a Lagrangian containing the Ricci scalar. However, unimodular gravity has one special new ingredient: the determinant of the metric is imposed to be a constant which can be set equal to 1. In practice, this leads to equations that are traceless. Then, the source of the geometrical structure, i.e., the right-hand side of the field equations, must also correspond to a traceless structure.

In the GR theory, the Bianchi identities lead automatically to the conservation of the energy–momentum tensor. This is connected to the invariance of the theory by general diffeomorphisms. The unimodular gravity has a more restricted class of transformation due to the condition on the determinant of the metric, usually called transverse diffeomorphism. For a detailed discussion on the transverse diffeomorphism, see for example [2] and references therein. The invariance by this restricted class of transformations, with respect to the general diffeomorphism, in the unimodular gravity has one particular consequence for the divergence of the energy–momentum tensor: it can be zero, implying the usual conservation laws and the GR equations are recovered with an extra integration constant, which can be identified with the cosmological constant; or the energy–momentum tensor is not conserved, and a radical new structure appears. In this article, we want to explore the second option as described below.

The unimodular condition on the determinant of the metric implies that volumes must be preserved in a coordinate transformation. This property, together with the other aspects related to the notion of transverse diffeomorphism, has been explored in many studies related to quantum gravity [3,4,5,6,7,8,9,10,11]. See also [12], whose results are more relevant to our work.

The unimodular equations are traceless but not conformal invariant. Traceless equations in gravity theory have been evoked many times in the literature, see for example [13]. In [14,15], the mimetic gravity theory was proposed, which may be written also in a traceless form, and which has many interesting consequences for the early and late cosmological scenarios. Here, we restrict ourselves to the unimodular gravity. In general, in the investigations involving unimodular gravity, the conservation of the energy–momentum tensor is imposed. This imposition leads to some nice properties. One of them is that the theory becomes equivalent to GR in the presence of a cosmological term that appears as an integration constant. In some sense the diffeomorphism invariance may be recovered, see for example the discussion in [1].

However, the second option described above, the nonconservation of the energy–momentum tensor, may open many interesting possibilities. One of them is that the resulting cosmological model is equivalent, at the background level, to the cosmological model in GR, with only radiation and a cosmological constant. This can be seen as a bad feature, since in the standard cosmological model based in the GR theory, a matter-dominated phase is necessary in order to allow for a successful large structure formation process. However, in the unimodular gravity the perturbative features may allow structure formation even in a radiative universe. This problem is treated more in detail in a companion paper [16].

In the present paper we have a very specific goal: to study the evolution of gravitational waves in a cosmological model resulting from the unimodular gravity with non conservation of the energy–momentum tensor. We call it nonconservative unimodular gravity. We verify that gravitational waves in this nonconservative context have specific features that may allow for the testing of the model with future observational data on primordial gravitational waves. Our analysis is fundamentally qualitative for reasons to be discussed later in this article, but opens possibilities for a more quantitative study.

The paper is organized as follows. In the next section, we outline the main features of the unimodular gravity. In Section 3, we discuss the construction of the nonconservative unimodular gravity. In Section 4, we compute the evolution of cosmological gravitational waves in the nonconservative unimodular gravity and in Section 5, we compare it with known results from the standard cosmological model. In Section 6, we discuss our main results and present our conclusions.

2. Unimodular Gravity

In order to better evaluate the meaning of the unimodular condition, let us briefly first review aspects of the structure of the GR theory. Here we follow closely a similar exposition made in [17].

The equations of GR are obtained through variational principle from the Einstein–Hilbert action,

$$\begin{array}{c}\hfill \mathcal{S}=\int d^{4}x\sqrt{-g}\{R-2\Lambda +{\mathcal{L}}_m\},\end{array}$$

(1)

where ${\mathcal{L}}_m$ denotes the matter Lagrangian density, $\Lambda$ is the cosmological constant and R is the Ricci scalar. This is the simplest action allowed in four dimensions leading to second order differential equations. We have already introduced $\Lambda$ in the action since it is allowed by the Lovelock theorem. The presence of the cosmological term may also allow to implement later the standard cosmological model for the universe, the $\Lambda$CDM model.

The variation of action (1) with respect to the metric $g_{\mu \nu }$ leads to the GR equations in the presence of matter and a cosmological constant:

$$\begin{array}{c}\hfill R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R=8\pi G{T}_{\mu \nu }+g_{\mu \nu }\Lambda .\end{array}$$

(2)

Here, the energy–momentum tensor is defined as:

$$\begin{array}{c}\hfill T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta \sqrt{-g}{\mathcal{L}}_m}{\delta g^{\mu \nu }}.\end{array}$$

(3)

The use of the Bianchi identities lead the conservation of the energy–momentum tensor:

$$\begin{array}{c}\hfill {T^{\mu \nu }}_{;\mu }=0.\end{array}$$

(4)

This property is directly connected with the invariance of the GR theory with respect to diffeomorphism, see [18].

Now we turn to unimodular gravity. In principle, we must follow the same procedure used to obtain the GR equations, but implementing at the same time the unimodular condition, $g=$ constant (constant that may be equal to 1). In general, the introduction of a constraint in an action can be made with the help of Lagrange multipliers. In doing so, in the unimodular case, some details must be outlined. Let us consider, for example, the unimodular condition for a flat, isotropic and homogeneous universe, described by the metric,

$$\begin{array}{c}\hfill d{s}^2=N^{2}d{t}^2-a{\left(t\right)}^2(d{x}^2+d{y}^2+d{z}^2),\end{array}$$

(5)

where N is the lapse function and $a\left(t\right)$ is the scale factor. In this case, the unimodular condition, with the constant equal to one, implies,

$$\begin{array}{c}\hfill N{a}^3=1.\end{array}$$

(6)

Hence, the unimodular condition would fix the lapse function, $N=a^{-3}$. We see below how to circumvent this limitation.

In order to construct the unimodular equations, we use, as already stated, the Lagrangian multipliers in the action: The action becomes

$$\begin{array}{cc}\hfill \mathcal{S}=\int d^{4}x\{\sqrt{-g}& R-\chi (\sqrt{-g}-1)\}\hfill \\ \hfill & +\int d^{4}x\sqrt{-g}{\mathcal{L}}_m,\hfill \end{array}$$

(7)

where all the quantities are defined as in GR, and $\chi$ is the Lagrangian multiplier. To circumvent the restriction on the lapse function described above, we modify action (7), rewriting it as

$$\begin{array}{cc}\hfill \mathcal{S}=\int d^{4}x\{\sqrt{-g}& R-\chi (\sqrt{-g}-\xi )\}\hfill \\ \hfill & +\int d^{4}x\sqrt{-g}{\mathcal{L}}_m.\hfill \end{array}$$

(8)

where $\xi =\xi \left(t\right)$ is an arbitrary function of time which is not subjected to the variational principle: $\xi \left(t\right)$ may be considered as an external field since its functional form is not dynamically determined.

Varying action (8) with respect to the metric, it follows,

$$\begin{array}{c}\hfill R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R+\frac{\chi }{2}{g}_{\mu \nu }=8\pi G{T}_{\mu \nu }.\end{array}$$

(9)

Varying with respect to $\chi$ we obtain the unimodular constraint:

$$\begin{array}{c}\hfill \xi =\sqrt{-g}.\end{array}$$

(10)

Since, $\xi$ is an arbitrary function of time, now any choice for the lapse function is possible, as in GR. One can argue that this “external field” $\xi$ is not strictly speaking essential, since we can also work with a time coordinate such that $N=a^{-3}$, which corresponds to the case $\xi =1$. However, the generality of the function $\xi$ facilitates the interplay with the usual expressions obtained in GR.

From the trace of (9) we obtain

$$\begin{array}{c}\hfill \chi =\frac{R}{2}+8\pi G\frac{T}{2}.\end{array}$$

(11)

Inserting this result in (9) we obtain,

$$\begin{array}{c}\hfill R_{\mu \nu }-\frac{1}{4}{g}_{\mu \nu }R=8\pi G(T_{\mu \nu }-\frac{1}{4}{g}_{\mu \nu }T).\end{array}$$

(12)

These are the unimodular field equations. Remark that the equations are traceless.

Now we inspect the conservation laws. The use of the Bianchi identities lead to the following new conservation law:

$$\begin{array}{c}\hfill \frac{R^{;\nu }}{4}=8\pi G({T^{\mu \nu }}_{;\mu }-\frac{1}{4}{T}^{;\nu }).\end{array}$$

(13)

In principle, the GR conservation laws are not recovered. On one hand, this may be expected since the general diffeomorphism invariance is broken by the unimodular condition [2]. On the other hand, it can be imposed as a new choice. In fact, if the relation ${T^{\mu \nu }}_{;\mu }=0$ is imposed, we obtain the following expression:

$$\begin{array}{c}\hfill R^{;\nu }=-8\pi G{T}^{;\nu },\end{array}$$

(14)

which can be integrated, leading to

$$\begin{array}{c}\hfill R=8\pi GT-\Lambda ,\end{array}$$

(15)

where $\Lambda$ is an integration constant which is identified with the cosmological term. The choice that the energy–momentum tensor conserves separately leads to the GR equation with a cosmological term, that is, Equations (2) and (4). On the other hand, if the conservation of the energy–momentum tensor is not imposed, we have the field equations given by (12) with the generalized conservation law (13). It is these last sets of equations that we want to study here, considering the evolution of gravitational waves in a cosmological context.

3. A Cosmological Model

Our next step in analyzing the nonconservative unimodular gravity theory is to explore the evolution of gravitational waves in the cosmological context. Cosmological models in unimodular gravity with a conserved energy–momentum tensor has been discussed, for example, in [19]. The present work concentrates on this specific problem which may already give some insight on the consequences of using Equations (12) and (13). In these equations, we introduce the flat metric, with the lapse function given by $N=1$, a possibility allowed as discussed in the previous section. Hence, the line element is given by:

$$\begin{array}{c}\hfill d{s}^2=d{t}^2-a{\left(t\right)}^2(d{x}^2+d{y}^2+d{z}^2).\end{array}$$

(16)

What is remarkable is that the time–time and space–space components of (12) lead to the same equation:

$$\begin{array}{c}\hfill \dot{H}=-4\pi G(\rho +p),\end{array}$$

(17)

where we have noted $H=\dot{a}/a$. This fact indicates that the system of equations is underdetermined. It is worth noting that the above equation implies that the vacuum case corresponds to the de Sitter solution, in contrast to the GR case where it corresponds to the Minkowski solution [19].

However, we still have the conservation Equation (13), which we can explore in order to obtain a complete set of self-consistent equations. The conservation laws result in the following equation:

$$\begin{array}{ccc}\hfill \ddot{H}+4H\dot{H}& =& -4\pi G[\dot{\rho }+\dot{p}+4H(\rho +p)],\hfill \end{array}$$

(18)

Both Equations (17) and (18) surprisingly have the same content: inserting (17) into (18) we obtain $0=0$. Even with the use of the generalized conservation law, the system of equations remains underdetermined.

At this stage, two observations are in order: as already stated, the resulting system of equations in the cosmological context (with isotropy and homogeneity) is underdetermined, since there are two functions, $\rho$ and H, for just one equation, remembering that the pressure is connected to density by an equation of state; moreover, Equations (17) and (18) are sensitive only to the combination $\rho +p$, which is related to the enthalpy of the system, and does not depend on the equation of state, provided it is barotropic, $p=p\left(\rho \right)$.

Defining $\overline{\rho }=\rho +p$, the Equations (17,18) can be written as,

$$\begin{array}{ccc}\hfill \dot{H}& =& -4\pi G\overline{\rho },\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill \ddot{H}+4H\dot{H}& =& -4\pi G(\dot{\overline{\rho }}+4H\overline{\rho }),\hfill \end{array}$$

(20)

simplifying the notation.

An interesting aspect is that the usual radiative solution of GR

$$\begin{array}{c}\hfill H=\frac{1}{2t},\overline{\rho }={\overline{\rho }}_0{a}^{-4},\end{array}$$

(21)

is also a solution for (19) and (20), irrespective of the pressure p, except for the case where the pressure represents the vacuum energy or, alternatively, a cosmological term: $p\ne -\rho$.

The fact that the radiative solution is also a solution of the nonconservative unimodular equations may be related to the traceless property of the field equations. Remark, however, that these field equations are traceless but not conformal invariant. For $p=-\rho$, we find the usual de Sitter solution, $a\propto e^{\kappa t}$, where $\kappa$ is a constant (positive or negative). Is there any other solution? Since the system is underdetermined, we cannot obtain any other solution unless some additional hypothesis is introduced. We later provide more comments on this point.

To obtain a specific model, and taking into account the properties discussed above, we can impose that both sides of (20) conserves separately. This leads to,

$$\begin{array}{c}\hfill \ddot{H}+4H\dot{H}=0,\end{array}$$

(22)

$$\begin{array}{c}\hfill \dot{\overline{\rho }}+4H\overline{\rho }=0.\end{array}$$

(23)

Such an ansatz is equivalent to imposing the condition $R=$ constant, as it was done in [20]. The results obtained here do not depend strongly on this hypothesis, even if some details may change by choosing another ansatz. For the moment, it is just a working hypothesis.

Equation (23) has a simple solution:

$$\begin{array}{c}\hfill \overline{\rho }={\overline{\rho }}_0{a}^{-4}.\end{array}$$

(24)

This is typical of a radiative fluid. However, we recall that $\overline{\rho }=(\rho +p)$, hence the radiative behavior is independent of the fluid considered. This is a reflection of the traceless character of the field equations and the nonconservation of the energy–momentum tensor (otherwise we go back to the GR structure).

Besides the behavior for any fluid, which is always similar to a radiative fluid, independent of the corresponding pressure, there is another difference. In general relativity, the equations for a radiative fluid are given by,

$$\begin{array}{ccc}\hfill H^2& =& \frac{8\pi G}{3}\rho ,\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill 2\dot{H}+3H^2& =& -\frac{8\pi G}{3}\rho .\hfill \end{array}$$

(26)

These equations lead to

$$\begin{array}{c}\hfill \dot{H}+2H^2=0.\end{array}$$

(27)

We notice that Equation (22) can be written as

$$\begin{array}{c}\hfill \frac{d}{dt}(\dot{H}+2H^2)=0.\end{array}$$

(28)

This is equivalent to the ansatz used in [20]; $R=$ constant, which, in a similar context, has been introduced to complete the set of equations. The GR case corresponds to setting the constant equal to zero.

Following the reasoning exposed above, in the unimodular cosmology, without a separated conservation of the energy–momentum tensor, the equation for the Hubble function is given by,

$$\begin{array}{c}\hfill \dot{H}+2H^2=\frac{2}{3}{\Lambda }_{\mathrm{U}},{\Lambda }_{\mathrm{U}}=constant.\end{array}$$

(29)

The integration constant, which we call ${\Lambda }_{\mathrm{U}}$ to match with the cosmological term, makes the unimodular cosmological scenario similar to the GR radiative model in presence of a cosmological constant, even if no cosmological constant was present at the beginning. In fact, an integration constant similar to the cosmological constant is hidden in the structure of unimodular gravity.

From (29), we have three possibilities.

$$\begin{array}{ccc}\hfill {\Lambda }_{\mathrm{U}}<0& \to & a=a_0{sin}^{1/2}\sqrt{-\frac{4{\Lambda }_{\mathrm{U}}}{3}}t,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\Lambda }_{\mathrm{U}}=0& \to & a=a_0{t}^{1/2},\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill {\Lambda }_{\mathrm{U}}>0& \to & a=a_0{sinh}^{1/2}\sqrt{\frac{4{\Lambda }_{\mathrm{U}}}{3}}t.\hfill \end{array}$$

(32)

These are essentially the same solutions found in [20]. The case ${\Lambda }_{\mathrm{U}}=0$ is identical to the GR radiative model. If ${\Lambda }_{\mathrm{U}}\ne 0$, we formally obtain the cosmological solutions in GR for a mixture of radiation and cosmological constant. The solutions corresponding to ${\Lambda }_{\mathrm{U}}\ne 0$ could also be expressed in terms of cos and cosh functions, which represent a nonsingular universe. However, these possibilities would imply a negative energy density $\overline{\rho }$, which mounts to a violation of the null energy condition since $\overline{\rho }$ leads to $\rho +p<0$, and for this reason we avoid this possibility.

For all three values of $\Lambda$ the behavior for $t\to 0$ is similar, and coincides with the flat radiative case. Of particular interest is the case ${\Lambda }_{\mathrm{U}}>0$: it interpolates the initial radiative phase and a de Sitter phase. In the usual GR context, such possibility is generally not explored since structure formation requires a matter-dominated phase ($p=0$), which would be absent here. However, such restriction may be circumvented in the nonconservative unimodular scenario as it is discussed in [16]. The case ${\Lambda }_{\mathrm{U}}<0$ corresponds to an interpolation between a radiative phase and an anti-de Sitter phase, which in practice is not interesting from the observational point of view.

4. Gravitational Waves

We now perform the perturbative computation of the tensorial modes that represent the gravitational wave phenomena. The background gravitational waves in an expanding universe may be detected in future experiments. We refer the reader to [21,22] and references therein for some references on this important topic.

At a linear level, the computation of tensorial modes can be made by considering fluctuations around a given background solution, such that

$$\begin{array}{c}\hfill g_{\mu \nu }=g_{\mu \nu }^B+h_{\mu \nu },\end{array}$$

(33)

where the superscript B indicates the background metric and $|h_{\mu \nu }|<<|g_{\mu \nu }^B|$ such that we can use the linear approximation.

The tensorial modes are represented by the traceless, divergence-free spatial components of $h_{\mu \nu }$, which behaves as pure tensorial quantity on the three-dimensional spatial section. That is, the components $h_{ij}$ are such that $h_{kk}={\partial }_k{h}_{ki}=0$. The tensorial modes are invariant by any coordinate transformation. In this sense, in this study, we can impose any coordinate condition or use the gauge-invariant formalism. For simplicity, we use the synchronous coordinate condition, $h_{\mu 0}=0$. The perturbation of the unimodular condition implies,

$$\begin{array}{c}\hfill h_{kk}=0,\end{array}$$

(34)

which is already encoded in the condition to have pure tensorial modes.

Using the previous relation, i.e., the perturbation of the Ricci components, let us now perturb the Ricci scalar and the energy–momentum tensor. We restrict ourselves only to the tensorial modes. This implies that the only nonzero components are the ones with the form [23],

$$\begin{array}{ccc}\hfill \delta R_{ij}& =& -\frac{{\ddot{h}}_{ij}}{2}+\frac{H}{2}{\dot{h}}_{ij}-2H^2{h}_{ij},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill \delta T_{ij}& =& -p{h}_{ij}.\hfill \end{array}$$

(36)

With the help of the background equations and after performing a Fourier decomposition, we find that the gravitational radiative modes obey the equation,

$$\begin{array}{c}\hfill {\ddot{h}}_{ij}-H{\dot{h}}_{ij}-2(\dot{H}+H^2)h_{ij}+\frac{k^2}{a^2}{h}_{ij}=0.\end{array}$$

(37)

This is exactly the equation for gravitational waves in GR with a perfect fluid, see [23]. This is by itself a surprising feature taking into account the many differences between GR and the nonconservative unimodular gravity. However, the evolution of gravitational waves in the above-described unimodular cosmological scenario and in the standard cosmological scenario should be very different: the expressions for the background functions H and $\dot{H}$ are not the same, leading to special signatures in the evolution of gravitational waves.

Let us return for the moment to Equation (37) and review some of its property in the case where the universe is dominated by radiation and a cosmological constant $\Lambda$. An analytic solution can be obtained when ${\Lambda }_{\mathrm{U}}=0$. In this case, writing the scale factor in terms of the conformal time $\eta$ defined as $dt=ad\eta$, we obtain $a=a_0\eta$, and the equation becomes,

$$\begin{array}{c}\hfill h^{\prime \prime }-2\frac{h^{\prime }}{\eta }+\{k^2+\frac{2}{{\eta }^2}\}h=0,\end{array}$$

(38)

where we have, for simplicity, ignored the polarization indices after writing $h_{ij}={ϵ}_{ij}h\left(t\right)$, ${ϵ}_{ij}$ being the constant polarization tensor. As it is well known, in GR there are two polarization modes for gravitational waves that decouple at the linear level. The same occurs in the unimodular theory. Since we do not consider the interaction of these modes with matter, nor the mechanisms generating the waves, for our present purposes we can ignore specific features connected with the polarizations. This equation can be solved analytically for an equation of state $p=\omega \rho$. The solution reads [24]

$$\begin{array}{c}\hfill h={\eta }^{(5+3\omega )/\left[2\right(1+3\omega \left)\right]}\{A_1{J}_{\nu }\left(k\eta \right)+A_2{J}_{-\nu }\left(k\eta \right)\}.\end{array}$$

(39)

where $A_{1,2}$ are constants and $J_{\nu }\left(x\right)$ is the Bessel function of order $\nu$, with $\nu =3(1-\omega )/\left[2\right(1+3\omega \left)\right]$.

For a radiative universe ($\omega =1/3$), the solution is

$$\begin{array}{c}\hfill h={\eta }^{3/2}\{A_1{J}_{1/2}\left(k\eta \right)+A_2{J}_{-1/2}\left(k\eta \right)\}.\end{array}$$

(40)

The solution here is the same as in a cosmological model with only radiation in GR. Recall, however, that in the unimodular model, the solution is valid irrespective of the choice made for p.

The solutions (40) have two asymptotic behaviors:

$$\begin{array}{ccc}\hfill \eta \to 0& \Rightarrow & h\propto (A_1{\eta }^3+A_2\eta ),\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill \eta \to \infty & \Rightarrow & h\propto \eta cos(k\eta +\delta ),\hfill \end{array}$$

(42)

where $\delta$ is a phase. Hence, initially, the solutions exhibit growing modes, which, for large values of time, become a growing oscillatory mode.

We remark in passing that for the case of the de Sitter solution ($\omega =-1$, $\nu =3/2$), the conformal time range is $-\infty <\eta <0$. Initially there are growing oscillations that asymptotically become either growing or decreasing modes, with no oscillations.

For the other possible solutions for the background in unimodular gravity (with ${\Lambda }_{\mathrm{U}}>0$ or ${\Lambda }_{\mathrm{U}}<0$), it seems impossible to obtain a closed expression for h. However, we can integrate numerically. First, we do it in a qualitative way rewriting Equation (37) for the scale factor. The result is

$$\begin{array}{c}\hfill h^{\prime \prime }+\frac{\dot{H}}{H^2}\frac{h^{\prime }}{a}+\{\frac{k^2}{H^2{a}^4}-2[\frac{\dot{H}}{H^2}+1\left]\frac{1}{a^2}\right\}h=0.\end{array}$$

(43)

Now, we need the expressions for H and $\dot{H}$ in terms of the scale factor. In order to do so, we use (17), which already provides $\dot{H}$ in terms of a, since $\overline{\rho }\propto a^{-4}$. Then, we multiply that equation by H and integrate. The resulting set of equations is

$$\begin{array}{ccc}\hfill \frac{\dot{H}}{H_0^2}& =& -\frac{3}{2}\frac{{\overline{\Omega }}_0}{a^4},\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill \frac{H^2}{H_0^2}& =& \frac{3}{4}\frac{{\overline{\Omega }}_0}{a^4}+1-\frac{3}{4}{\overline{\Omega }}_0,\hfill \end{array}$$

(45)

where we have defined,

$$\begin{array}{c}\hfill {\overline{\Omega }}_0=\frac{8\pi G{\overline{\rho }}_0}{3H_0^2},\end{array}$$

(46)

and we have fixed $a(t=t_0)=1$, where $t_0$ is the present time. Remark that the density parameter (46) is perfectly logical in a GR cosmology. However, in unimodular gravity this definition may be seen as a choice, since $\overline{\rho }$ also contains the pressure.

We must now make a more detailed and realistic comparison with the standard $\Lambda$CDM model in GR. This is the object of the next section.

5. Comparing Unimodular Cosmology with the Standard Cosmological Model

Here, we make a more detailed comparison between the evolution of the gravitational wave in the unimodular gravity and in the standard $\Lambda$CDM model.

In the $\Lambda$CDM model the matter content is given by radiation, pressureless matter and the cosmological constant. In this case, the Friedmann equations read,

$$\begin{array}{ccc}\hfill \frac{H^2}{H_0^2}& =& \frac{{\Omega }_{r0}}{a^4}+\frac{{\Omega }_{m0}}{a^3}+{\Omega }_{\Lambda },\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill \frac{\dot{H}}{H_0^2}& =& -\frac{3}{2}\frac{{\Omega }_{m0}}{a^3}-2\frac{{\Omega }_{r0}}{a^4},\hfill \end{array}$$

(48)

where the subscript m indicates matter, the subscript r refers to radiation and the density parameter is defined as before. The subscript 0 indicates today’s values of the parameters. The matter component scales as $a^{-3}$ while the radiation component scales as $a^{-4}$. The constraint relation is now

$$\begin{array}{c}\hfill 1={\Omega }_{r0}+{\Omega }_{m0}+{\Omega }_{\Lambda }.\end{array}$$

(49)

Now, we go back to discuss the features of the nonconservative unimodular cosmological model. The main point, at this stage, is what we interpret as the matter parameter. The equations in unimodular gravity are sensitive only to the combination $\rho +p$. Moreover, the system of equations is underdetermined, hence an ansatz must be introduced. Our choice exposed above leads to expressions that are similar to the radiative case in GR with a cosmological constant. This property leads us to define,

$$\begin{array}{c}\hfill \overline{\rho }=\rho +p=\frac{{\overline{\rho }}_0}{a^4},\end{array}$$

(50)

with ${\overline{\rho }}_0$ indicating the value of the redefined density $\overline{\rho }$ today. Using the definitions for the density parameter already shown in the previous section, we obtain Equation (29) with solutions (30)–(32). The factor $3/4$ in these expressions is a consequence of our choices but allows us to represent the background expansion in a familiar form. Even if the unimodular equations are sensitiveonly to the combination $\rho +p$, if we fix $p=\rho /3$ and using the same definitions for the density parameter, we obtain exactly the equations for a cosmology with radiation and a cosmological constant, as we could expect. However, we keep ourselves within the context of the unimodular structure with a generalized conservation law.

With these definitions in mind, we plot the cosmological evolution of gravitational waves in two scenarios: the unimodular model and the concordance $\Lambda$CDM model. We remark that in both cases the evolution of gravitational waves is dictated by Equation (43), differing only on the background functions H and $\dot{H}$.

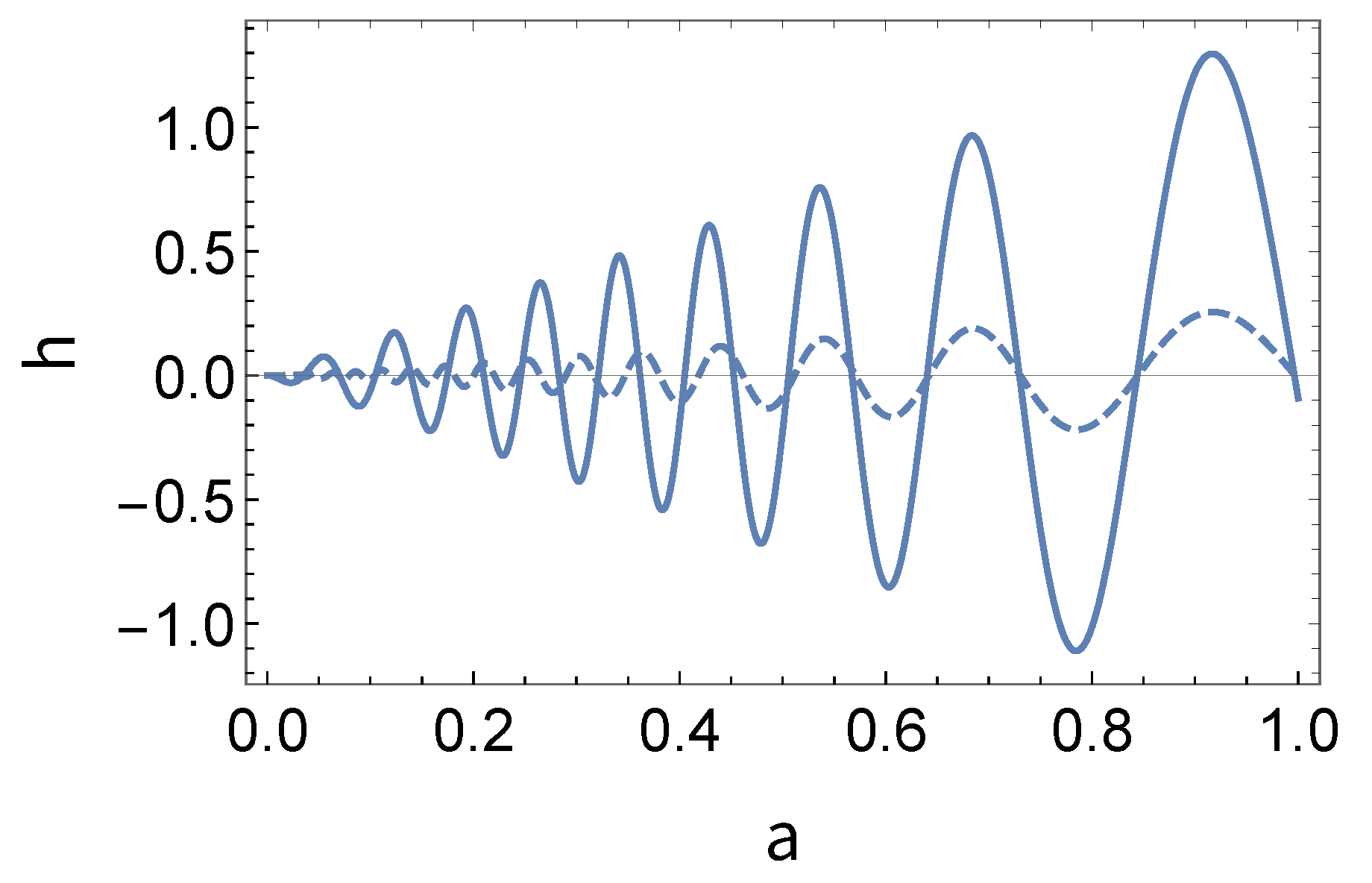
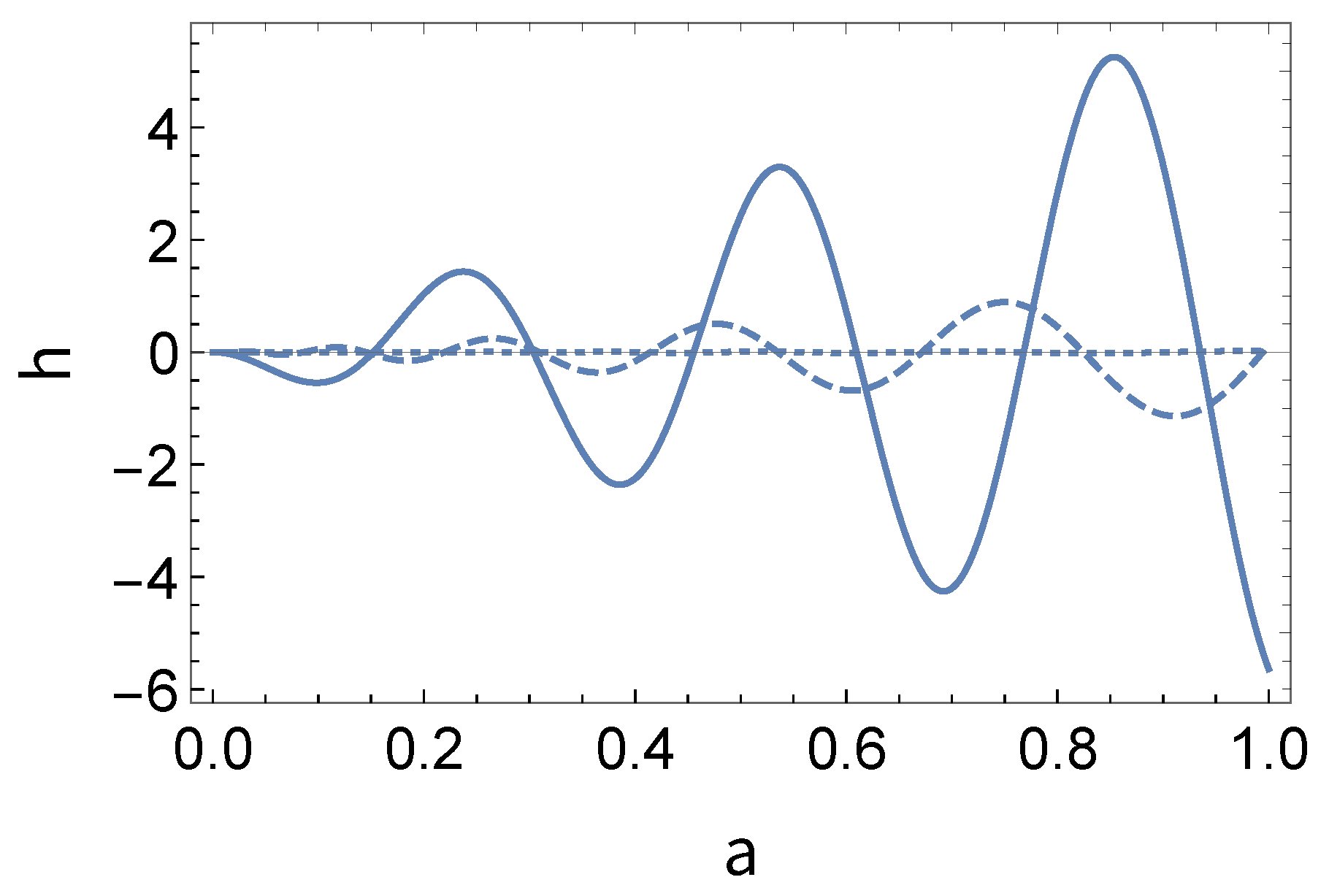
First, we fix ${\overline{\Omega }}_0=0.05$, corresponding to the total amount of baryonic matter, for the unimodular case. For the $\Lambda$CDM model, we fix ${\Omega }_{m0}=0.3$, and ${\Omega }_{r0}=5\times {10}^{-5}$ for the standard model. The result is displayed in Figure 1. In Figure 2, we repeat the computation, but imposing now ${\overline{\Omega }}_0=0.95$, keeping the same values for the $\Lambda$CDM model, in order to stress the difference between the models. We remark that the unimodular case presents a higher amplification of the gravitational waves compared with the standard cosmological model for any value of the parameter ${\Omega }_0$. Furthermore, the frequency of the waves differ significantly. This may have clear observational signatures.

6. Discussion and Conclusions

Unimodular gravity is a theory of gravity almost as old as GR. It is characterized by the condition $g=$ constant. One of the attractive aspects of unimodular gravity is that, imposing the usual conservation law for the energy–momentum tensor, the GR equations are recovered with an integration constant that can be identified with the cosmological term $\Lambda$. This fact brings a new perspective to the cosmological constant problem [1]. At a quantum level, unimodular gravity also has many interesting features discussed in [3].

In this paper, we investigated one variant of unimodular gravity not explored very much in the literature. As observed above, the conservation of the energy–momentum tensor is a free choice within the structure of the theory, since the general invariance on diffeomorphism is lost when we fix the determinant of the metric. The consequences of not imposing the usual conservation laws were stressed here. The first one is that, in the cosmological framework, the equations for the scale factor are sensitive only to the combination $\rho +p$, irrespective of the fluid. Moreover, the equations are underdetermined, and they can not be solved without an ansatz.

We showed that the typical solution of radiation with (and without) a cosmological constant was also consistently a solution of the nonconservative unimodular gravity. As a remark, from this result, we can speculate that the cosmological constant is always hidden in the unimodular gravity, irrespective of the conservation of the energy–momentum tensor.

In order to distinguish the unimodular cosmological model from the GR cosmological models, we investigated the evolution of gravitational waves in these different scenarios. The first obstacle was to identify the density parameters in unimodular gravity, since all equations are only sensitive to the combination $\rho +p$, the enthalpy of the system. This quantity scales as $a^{-4}$ as a legitimate radiative field. We identified this combination as the matter content of the model, and the density parameter was defined to correspond with the similar definitions in the standard cosmological model.

We then studied the evolution of gravitational waves in the different cosmological scenarios emerging from the unimodular gravity in comparison with the standard cosmological model, with radiation, matter and cosmological constant. The main feature is that unimodular gravity as well as the radiation plus cosmological constant scenario in GR provide a stronger amplification of gravitational waves amplitudes compared the $\Lambda$CDM model. Remark that if we choose a radiative equation of state, $p=\rho /3$, the unimodular scenario becomes identical to the radiative case with a cosmological constant in GR given the definition for the density parameter chosen.

Hence, it is possible in principle to distinguish the unimodular cosmological scenario from the $\Lambda$CDM model through the amplitude and the shape (frequency) of gravitational waves. However, in case future observations provide gravitational wave signals in agreement with the unimodular prediction, what could distinguish it from the radiative model with a cosmological constant, since the features are very similar, at least in what concerns the evolution of gravitational waves? To try to answer this question, we must remember that structure formation in a cosmological model based on GR can not take place without a matter-dominated phase, and we come back to the $\Lambda$CDM model. However, structure formation may take place in the unimodular scenario exhibited here, in spite of its radiative character, as some preliminary results indicate [16].

The results reported here are somehow qualitative, indicating the main characteristic features of the evolution of gravitational waves in unimodular gravity. A more detailed analysis of the observational signatures is necessary to clearly distinguish the different scenarios. Of course, the analysis of structure formation, which is currently under study, may be another powerful way to investigate the viability of the nonconservative version of unimodular cosmology.

However, the unimodular scenario discussed here seems to be incomplete, because it necessitates an additional condition to solve the equations. In the present work, we have imposed the same condition as in reference [20]. Perhaps the nonconservative unimodular gravity must be complemented by some version of the holographic principle, which we intend to perform in the future.

We remark that the gravitational waves are amplified as the universe expands. This surprising result may be related to the appearance of a cosmological term leading to an accelerated expansion of the universe and may be connected with the gravitational waves propagation in inflationary models, where such amplification also appears [21]. This result represents a challenging scenario for this approach. In order to keep an upper limit to the amplitude of cosmological gravitational waves today, as expected by current observations, this forces their initial conditions to be almost vanishing at early times. This can be considered a fine-tuning problem. Only a careful quantitative analysis, planned for a future communication, could clarify this issue.