Electromagnetic Form Factor of Doubly-Strange Hyperon

Abstract

The standard model of particle physics is a well-tested theoretical framework, but there are still some issues that deserve experimental and theoretical investigation. The $\mathrm{\Xi }$ resonances with strangeness $S=-2$, the so-called doubly-strange hyperon, can provide important information to further test the standard model by studying their electromagnetic form factors, such as probing the limitation of the quark models and spotting unrevealed aspects of the QCD description of the structure of hadron resonances. In this work, we review some recent studies of the electromagnetic form factors on doubly-strange hyperons in pair production from positron–electron annihilation experiment.

1. Introduction

Electromagnetic form factors (EMFFs) parameterizing the inner structure and dynamics of hadrons are fundamental observables of nucleons and hyperons to understand the QCD effects in hadronic resonances [1,2,3,4,5,6]. In the 1960s, Cabibbo et al. [7] first proposed that time-like EMFFs can be studied on $e^{+}{e}^{-}$ collider experiments by measuring the hadron pair production cross sections, such as the exclusive hyperon cross section. Figure 1 shows the lowest-order process for the hyperon-antihyperon ($H\overline{H}$) production in $e^{+}{e}^{-}$ annihilation.

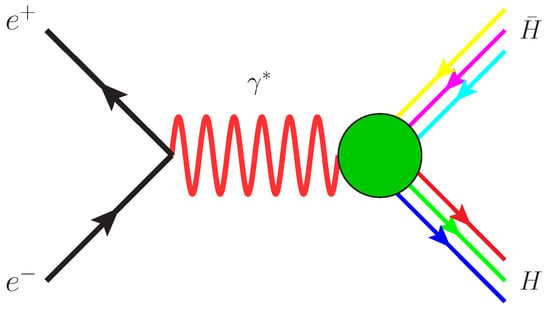
Figure 1. Lowest-order Feynman diagram for the $e^{+}{e}^{-}\to H\overline{H}$ process.

Assuming spin-1/2 hyperon pair production is dominated by one virtual photon exchange, the differential cross section for the $e^{+}{e}^{-}\to H\overline{H}$ process in the $e^{+}{e}^{-}$ center-of-mass (c.m.) frame can be expressed in terms of the EMFFs [7] $G_E\left(s\right)$ and $G_M\left(s\right)$ as:

$$\frac{d{\sigma }^B\left(s\right)}{d\Omega }=\frac{{\alpha }^2\beta C}{4s}\left[|G_M{\left(s\right)|}^2(1+{cos}^2\theta )+\frac{1}{\tau }|{G_E\left(s\right)|}^2{sin}^2\theta \right],$$

(1)

$$G_E\left(s\right)=F_1+\tau F_2,$$

(2)

$$G_M\left(s\right)=F_1+F_2,$$

(3)

where $F_1$ and $F_2$ are the Dirac’s and Pauli’s form factors [8], respectively, $\alpha$ is the fine-structure constant, s is the square of the c.m. energy, $\beta =\sqrt{1-4m_H^2{c}^4/s}$ is the velocity of the outgoing hyperon, and $m_H$ is the mass of the hyperon, $\tau =\frac{s}{4m_H^2{c}^4}$. The Coulomb factor $\mathcal{C}$ parameterizes the electromagnetic interaction of point-like fermions in the final state [9,10,11], and is unity for neutral hyperon, while for a charged one, $\mathcal{C}=y/(1-e^{-y})$ with $y=\pi \alpha \sqrt{1-{\beta }^2}/\beta$ [12,13,14]. In ref. [15], $\mathcal{C}$ is parameterized as a product of an enhancement factor $\mathcal{E}$ and a resummation factor $\mathcal{R}$, i.e., the so-called Sommerfeld–Schwinger–Sakharov rescattering formula: $\mathcal{C}=\mathcal{E}\times \mathcal{R}$ with $\mathcal{E}=\pi \alpha /\beta$. In the limit of $\beta \to 0$, and the factor $\beta$ due to the limitation of the phase space is canceled and results in a nonzero cross section at the production threshold. By integrating over a full solid angle for Equation (1), we can obtain the Born cross section as:

$${\sigma }^B\left(s\right)=\frac{4\pi {\alpha }^2\beta \mathcal{C}}{3s}\left[{\left|G_M\left(s\right)\right|}^2+\frac{1}{2\tau }{\left|G_E\left(s\right)\right|}^2\right],$$

(4)

and then, we can define the effective form factor (EFF) $G_{\mathrm{eff}}\left(s\right)$ [28] by:

$$\begin{array}{cc}\hfill |G_{\mathrm{eff}}\left(s\right)|=& \sqrt{\frac{2\tau |G_M{\left(s\right)|}^2+{\left|G_E\left(s\right)\right|}^2}{2\tau +1}},\hfill \end{array}$$

(5)

where the EMFFs $G_E\left(s\right)$ and $G_M\left(s\right)$ can be expressed by:

$$|G_M{\left(s\right)|}^2=\frac{2\tau +1}{2\tau +R^2}{\left|G_{eff}\left(s\right)\right|}^2,$$

(6)

$$|G_E{\left(s\right)|}^2=\frac{R^2(2\tau +1)}{2\tau +R^2}{\left|G_{eff}\left(s\right)\right|}^2,$$

(7)

with a definition of the ratio between $G_M\left(s\right)$ and $G_E\left(s\right)$ as:

$$R=|\frac{G_E\left(s\right)}{G_M\left(s\right)}|.$$

(8)

According to Equations (4) and (5), the EFF can be further written as:

$$\begin{array}{cc}\hfill |G_{eff}\left(s\right)|& =\sqrt{\frac{3s{\sigma }^B}{4\pi {\alpha }^2\beta \mathcal{C}(1+\frac{1}{2\tau })}}\hfill \\ & =\sqrt{\frac{3s{\sigma }^B}{4\pi {\alpha }^2\beta \mathcal{C}(1+2m_H^2{c}^4/s)}}.\hfill \end{array}$$

(9)

Additionally, Equation (1) can be written as:

$$\begin{array}{c}\hfill \frac{d{\sigma }^B\left(s\right)}{dcos\theta }\propto [(1+{cos}^2\theta )+\frac{R^2}{\tau }{sin}^2\theta ]\propto [1+\frac{\tau -R^2}{\tau +R^2}{cos}^2\theta ],\end{array}$$

(10)

and Equation (10) can be further expressed to be a simple form as:

$$\frac{d{\sigma }^B\left(s\right)}{dcos\theta }\propto 1+\eta {cos}^2\theta ,$$

(11)

with

$$\eta =\frac{\tau -R^2}{\tau +R^2},$$

(12)

where the ratio R can be further expressed to be

$$R=\sqrt{\frac{\tau (1-\eta )}{1+\eta }},$$

(13)

where $\eta$ is the angular distribution parameter and in principle it can be determined by studying angular distribution.

For time-like regions, the EMFFs can be complex, i.e.,

$$G_M\left(s\right)=\left|G_M\left(s\right)\right|e^{i{\mathrm{\Phi }}_M},$$

(14)

$$G_E\left(s\right)=\left|G_E\left(s\right)\right|e^{i{\mathrm{\Phi }}_E},$$

(15)

from which the relative phase can be defined: $\Delta \mathrm{\Phi }={\mathrm{\Phi }}_E-{\mathrm{\Phi }}_M$. Then, the electric form factor $G_E\left(s\right)$ can be expressed in terms of the magnetic form factor as:

$$G_E\left(s\right)=R{e}^{i\Delta \mathrm{\Phi }}\left|G_M\left(s\right)\right|.$$

(16)

Here, $\Delta \mathrm{\Phi }$ is the relative phase between $G_E\left(s\right)$ and $G_M\left(s\right)$, which corresponds to the hyperon polarization if a non-zero relative phase is observed. Thus, if we have enough statistics, the relative phase can be determined combined with the study of the hyperon polarization. Similarly, the EMFFs can be measured separately using the measured relative phase combined with Equation (5).

In the context of QCD and the quark–gluon structure of hadrons, it is particularly interesting to measure the EMFFs of nucleons and strange hyperons ($\mathrm{\Lambda }$, $\mathrm{\Sigma }$, $\mathrm{\Xi }$, $\mathrm{\Omega }$), which is expected to reveal the aspects of the QCD description of the hyperon structure. In experiments, a large amount of research has been carried out regarding nucleon and strange hyperon EMFFs in the time-like ($q^2>0$) momentum transfer regions [16]. Among them, the proton is a stable particle, and also can be available as a target to study its EMFFs by means of scattering experiments in the space-like ($q^2<0$) momentum transfer. Hyperons, which are slightly different from protons, are difficult to study in the space-like region since they are unstable. In other words, hyperon targets are unfeasible and the quality of hyperon beams is in general not sufficient. Time-like EMFFs therefore offer the best opportunity to study hyperon structure. The ${\mathrm{\Xi }}^0$ and ${\mathrm{\Xi }}^{-}$ hyperons are members of the SU(3) octet [17], similar to the nucleon, as shown in Figure 2. Understanding their structure is crucial to obtaining a complete picture of how quarks and gluons form hyperons.

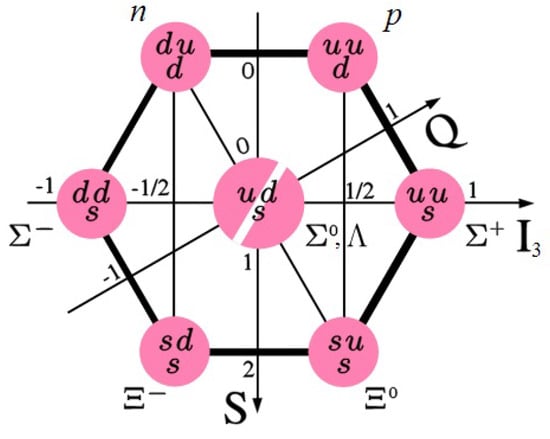
Figure 2. Baryon octet [4,17].

In this article, we review the recent studies of EMFFs on doubly-strange hyperons using the pair production near threshold and above open charm threshold reported by the BESIII experiment [18,19] and CLEO-c experiment [20,21]. These results provide useful and important information to understand the internal structure and production mechanism of doubly-strange hyperons, and even offer an extra dimension that probes the limitation of the quark models and spots unrevealed aspects of the QCD description of the structure of hadron resonances.

2. The $\mathrm{\Xi }$ EMFFs near Threshold

In the past decades, a few experiments have observed non-vanishing cross sections or enhancements near threshold in the production cross section of nucleon pairs at $e^{+}{e}^{-}$ colliders, which have attracted much interest and driven many theoretical studies. In the context of QCD and even our understanding of the quark–gluon structure of hadrons, the study of EMFFs near the hyperon pair production threshold is particularly interesting for probing these anomalous phenomena [22,23,24,25]. Recently, the BESIII collaboration performed measurements of Born cross sections and EFFs for the processes $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ based on a single hyperon tag method [26,27,28,29,30,31,32] using about 360 to 500 pb${}^{-1}$ data events collected at c.m. energies between 2.644 and 3.080 GeV [33,34]. Figure 3 shows the two-dimensional distribution of $M_{\pi \mathrm{\Lambda }}$ versus $M_{\pi \mathrm{\Lambda }}^{\mathrm{recoil}}$ for the sum of all energy points, where anti-hyperon candidates are extracted from the mass recoiling against the reconstructed $\pi \mathrm{\Lambda }$ system,

$$M_{\pi \mathrm{\Lambda }}^{\mathrm{recoil}}=\sqrt{{(\sqrt{s}-E_{\pi \mathrm{\Lambda }})}^2-{\left|{\overrightarrow{p}}_{\pi \mathrm{\Lambda }}\right|}^2}.$$

(17)

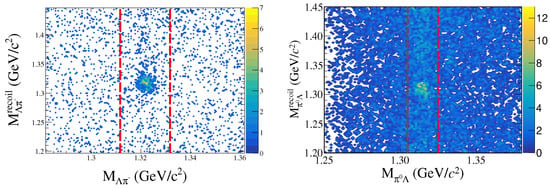
Figure 3. Distribution of $M_{\pi \mathrm{\Lambda }}$ versus $M_{\pi \mathrm{\Lambda }}^{\mathrm{recoil}}$ for all energy points from data [33,34]. The dashed lines denote the $\mathrm{\Xi }$ signal region.

Here $E_{\pi \mathrm{\Lambda }}$ and ${\overrightarrow{p}}_{\pi \mathrm{\Lambda }}$ are the energy and momentum of the selected $\pi \mathrm{\Lambda }$ candidate in the c.m. system. Clear signals for ${\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ productions can be seen around the $\mathrm{\Xi }$ nominal mass near threshold. Figure 4 shows the comparisons of the measured Born cross sections and EFFs between both modes from 2.6 to 3.1 GeV.

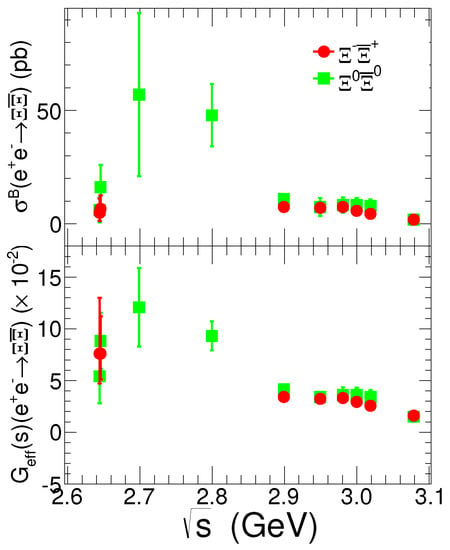
Figure 4. Comparisons of Born cross sections (top) and EFFs (bottom) between the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ mode and the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ mode from 2.6 to 3.1 GeV, where the uncertainties include both statistical and systematical contributions.

To understand well the doubly-strange hyperon production near threshold, a pQCD-driven energy power function [35] is used to describe the measured Born cross section as:

$${\sigma }^B=\frac{c_0·\beta }{{(\sqrt{s}-c_1)}^{10}},$$

(18)

where $c_0$ is the normalization factor, and $c_1$ is the mean effect of possible intermediate states. This model has also been applied successfully for the studies of other hyperon pair productions in $e^{+}{e}^{-}$ annihilation [24,36]. However, it is seen that the fit with the pQCD function only cannot describe the data points around 3.0 GeV well. To validate and accommodate a possible structure in this region, the other fit by assuming a coherent sum of a pQCD function plus a Breit–Wigner (BW) function as

$${\sigma }^B\left(\sqrt{s}\right)={\left|\sqrt{\frac{c_0·\beta }{{(\sqrt{s}-c_1)}^{10}}}+e^{i\mathrm{\Phi }}BW\left(\sqrt{s}\right)\sqrt{\frac{P\left(\sqrt{s}\right)}{P\left(M\right)}}\right|}^2,$$

(19)

is made, where $\mathrm{\Phi }$ is a relative phase between the pQCD function and the BW function

$$BW\left(\sqrt{s}\right)=\frac{\sqrt{12\pi {\mathrm{\Gamma }}_{ee}\mathcal{B}\mathrm{\Gamma }}}{s-M^2+iM\mathrm{\Gamma }},$$

(20)

where M is mass, $\mathrm{\Gamma }$ is width, ${\mathrm{\Gamma }}_{ee}$ is the di-electron partial width, $\mathcal{B}$ is the branching fraction for the possible resonance decaying into the ${\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ final states, and $P\left(\sqrt{s}\right)$ is the two-body phase space factor. The significance for this possible structure decaying into the ${\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ final state is estimated to be 2.4$\sigma$ including the systematical uncertainties. The mass and width of the resonance around 3.0 GeV in $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ process are fitted to be $M=$ (2993 ± 28) MeV/$c^2$ and $\mathrm{\Gamma }=$ (88 ± 79) MeV, respectively, with $\mathrm{\Phi }=2.4\pm 0.6$ rad and $(4.3\pm 0.3)$ rad for constructive and destructive interference conditions [37], with the statistical uncertainties only. While the mass and width of the resonance around 3.0 GeV in the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ process are fixed, according to the charged mode, the significance including the systematical uncertainty is found to be 2.0$\sigma$. Thus, the upper limits on the product of the electronic partial width and the branching fractions for this possible resonance decaying to the ${\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ final states are determined to be ${\mathrm{\Gamma }}_{ee}\mathcal{B}$< 0.1(1.0) and 0.3 eV at the 90% confidence level (C.L.) using a Bayesian approach [38,39], by taking into account the systematical uncertainties. In addition, the third model is also used to fit the Born cross section line shape of the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ process inspired by the production cross section of the nucleon pair [40] with the assumption of a near threshold plateau. It takes into account the strong interaction near the threshold instead of the Coulomb factor, and the Born cross section is expressed as:

$${\sigma }^B\left(\sqrt{s}\right)=\frac{e^{a_0}{\pi }^2{\alpha }^3}{s\left[1-e^{-\frac{\pi {\alpha }_s}{\beta }}\right]\left[1+{\left(\frac{\sqrt{s}-2m_{\mathrm{\Xi }}}{a_1}\right)}^{a_2}\right]},$$

(21)

where $a_0$ is the normalization constant, $a_1$ is the QCD parameter near threshold, $a_2$ is the power-law (PL) related to the number of valence quarks, and ${\alpha }_s$ is the running strong-coupling constant,

$${\alpha }_s={\left[\frac{1}{{\alpha }_s\left(m_Z^2\right)}+\frac{7}{4\pi }ln\left(\frac{s}{m_Z^2}\right)\right]}^{-1}.$$

(22)

Here $m_Z=91.1876$ GeV/c${}^2$ is the mass of the Z boson and ${\alpha }_s\left(m_Z^2\right)=0.11856$ is the strong coupling constant at the Z pole. The inflection point of the plateau is around 3.0 GeV, which is about 350 MeV far away from the threshold. Figure 5 shows the fitted Born cross sections for the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ processes. The last two assumptions are more consistent with the data than the simple perturbative QCD-driven energy power function.

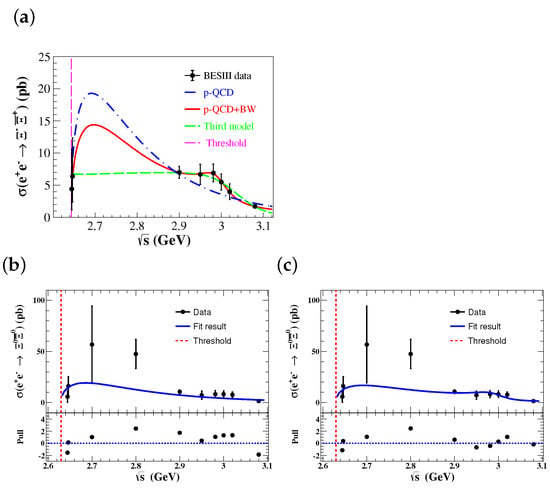
Figure 5. Fit to the Born cross sections of $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ with different assumptions [33,34]. In (a) the dots with the error bars are the measured Born cross sections at c.m. energies between 2.644 and 3.080 GeV, the blue dash-dotted line denotes the fit results using the pQCD function, the red solid line denotes the fit results using pQCD plus the BW function and the green dashed line denotes the fit results using the third model function. In (b,c) the blue solid line is the fit result using the pQCD function (b) and pQCD plus the BW function (c), and the bottom panel of each plot gives the pull distribution of the fit. The vertical dashed line denotes the production threshold for the $\mathrm{\Xi }$ hyperon pair.

The EFFs for $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ are determined at each energy point, but the samples are not large enough to allow separate measurements of EMFFs, $G_E\left(s\right)$ and $G_M\left(s\right)$. The ratio of Born cross sections and EFFs for both modes is within 1$\sigma$ of the expectation of isospin symmetry as shown in Figure 6. The measured Born cross sections tend to zero around the threshold of the $\mathrm{\Xi }$ hyperon pair production, 2.64 GeV, and show no obvious threshold enhancement. In theory, Haidenbauer et al. recently presented a phenomenological study for the EMFFs utilizing the model of the final state interaction [41]. Figure 7 shows the comparisons of Born cross section and EFF (bottom) between the experimental results of the BESIII collaboration and the theoretical calculation for the $e^{+}{e}^{-}\to \mathrm{\Xi }\overline{\mathrm{\Xi }}$ process near the threshold. It is indicated that the theoretical prediction is basically consistent with the experimental results for $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ under the current statistics [33], while it is not consistent with the experimental results between 2.64 and 2.90 GeV for the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ process [33,34]. Figure 8 shows the theoretical predictions for the EMFFs ratio $|G_E\left(s\right)/G_M\left(s\right)|$ and the relative phase $\mathrm{\Phi }=$ arg$(G_E\left(s\right)/G_{M\left(s\right)})$ for the $e^{+}{e}^{-}\to \mathrm{\Xi }\overline{\mathrm{\Xi }}$ process near the threshold, which could be tested in the future when the large data sample is available. These results provide useful and important information for constraining and improving the theoretical prediction, and even offer insight into the nature of hyperon pair production in $e^{+}{e}^{-}$ annihilation near the threshold.

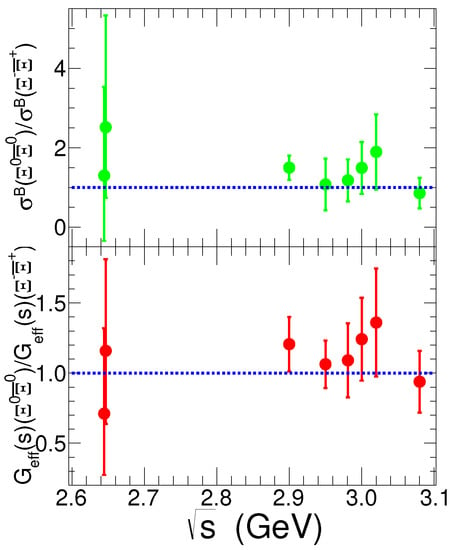
Figure 6. Ratios of Born cross sections (top) and EFFs (bottom) between the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ mode and the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ mode from 2.6 to 3.1 GeV [33,34], where the uncertainties include both statistical and systematical contributions.

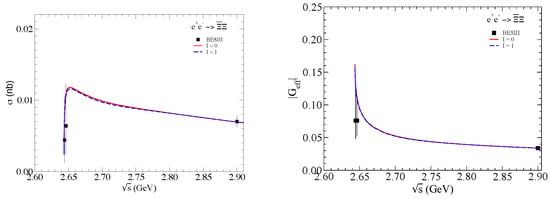
Figure 7. Comparisons of Born cross sections (left) and EFFs (right) between the experimental results of the BESIII collaboration and the theoretical study for the $e^{+}{e}^{-}\to \mathrm{\Xi }\overline{\mathrm{\Xi }}$ process near the threshold [41].

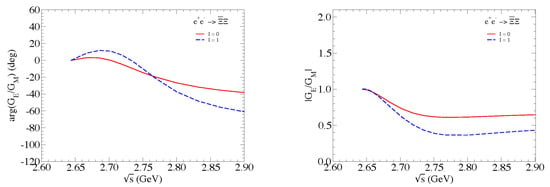
Figure 8. Theoretical predictions for the EMFFs ratio and $|G_E\left(s\right)/G_M\left(s\right)|$ and the relative phase $\mathrm{\Phi }=$ arg$(G_E\left(s\right)/G_M\left(s\right))$ for the $e^{+}{e}^{-}\to \mathrm{\Xi }\overline{\mathrm{\Xi }}$ process near the threshold [41].

3. The $\mathrm{\Xi }$ EMFFs above the Open Charm Threshold

The study of EMFFs above the open charm threshold in $e^{+}{e}^{-}$ annihilations provides important information for understanding the nature of charmonium-like states and testing the QCD calculation [42,43]. In the last decade, a series of charmonium-like states have been observed at positron–electron colliders [16]. According to potential models, as shown in Figure 9, there are more vector charmonium states between 3.77 and 4.7 GeV [42,44,45]. From experimental studies, beside the four well-established structures, i.e., $\psi \left(3770\right)$, $\psi \left(4040\right)$ $\psi \left(4160\right)$, and $\psi \left(4415\right)$, observed in the inclusive hadronic cross section [16,46], more new states, i.e., $Y\left(4220\right)$, $Y\left(4360\right)$, $Y\left(4634\right)$, and $Y\left(4660\right)$, have been reported in initial state radiation processes, i.e., $e^{+}{e}^{-}\to {\gamma }_{ISR}{\pi }^{+}{\pi }^{-}J/\psi$ or $e^{+}{e}^{-}\to {\gamma }_{ISR}{\pi }^{+}{\pi }^{-}\psi \left(3686\right)$ in the BABAR experiment [47,48,49,50] and Belle experiment [51,52,53,54,55], or in direct production processes in the CLEO [56] and BESIII experiments [57,58,59,60,61,62]. However, till now, no more experimental information for hyperon production above the open charm threshold associated with these states was found, with the exception of the $\psi \left(4634\right)$ resonance observed in ${\mathrm{\Lambda }}_c^{+}{\overline{\mathrm{\Lambda }}}_c^{-}$ by the Belle experiment [54]. The overpopulation of structures in this region and the mismatch of the properties between the experimental measurements and the potential model predictions make them good candidates for exotic states [63], such as hybrid states, tetra-quark states, or molecular states.

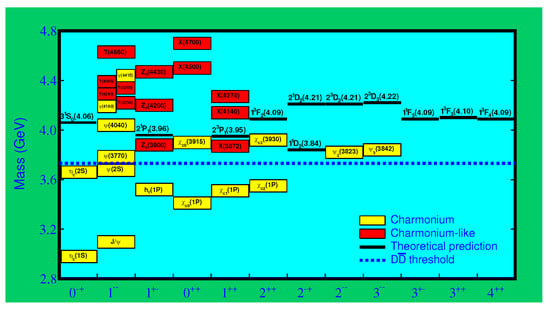
Figure 9. Charmonium(-like) family.

In 2013, the BESIII experiment performed a search for hyperonic pair production in $\psi \left(3770\right)$ and $\psi \left(4040\right)$ decays [64], including doubly-strange hyperon pair final states based on a full reconstruction method using data samples of 2.9 fb${}^{-1}$ collected at $\sqrt{s}=3.773$ GeV and 482 pb${}^{-1}$ collected at $\sqrt{s}=4.009$ GeV, and no significant signals were observed. Only the upper limits for the branching fractions of $\psi \left(3770\right)$ and $\psi \left(4040\right)$ decaying into ${\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ final states at the 90% C. L. were determined to be $\mathcal{B}[\psi \left(3770\right)\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}\left({\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0\right)]<1.5\left(1.4\right)\times {10}^{-4}$ and $\mathcal{B}[\psi \left(4040\right)\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}\left({\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0\right)]<1.6\left(1.8\right)\times {10}^{-4}$, and no EMFFs and EFF information was provided due to the limited statistics in this analysis. Subsequently, the CLEO-c experiment, by improving (by factors of 3–5) the efficiency of the hyperon identification, presented the measurements of the hyperon pair p (586) pb${}^{-1}$ of $e^{+}{e}^{-}$ annihilation data taken at $\sqrt{s}=3.77\left(4.17\right)$ GeV [65,66]. The Born cross sections and EFFs of $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ at c.m. energy of 3.77 and 4.17 GeV were determined as shown in Figure 10. Here, the Born cross sections for both modes are consistent with each other within 1$\sigma$ of the expectation of isospin symmetry, while the EFFs are not consistent with each other. Here the Coulomb factor $\mathcal{C}$ in Equation (9) for a neutral hyperon is different from the charged one, i.e., for a charged one, $\mathcal{C}=y/(1-e^{-y})$ with $y=\pi \alpha \sqrt{1-{\beta }^2}/\beta$ [12,13,14], while for neutral one, it is unity. The CLEO-c experiment also determined the time-like form factor with the assumption $|G_E/G_M|=0$, i.e., $G_M\left(s\right)(e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+})=1.28\pm 0.04\pm 0.03$, $G_M\left(s\right)(e^{+}{e}^{-}\to {\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0)=1.28\pm 0.07\pm 0.03$ at c.m. energy of 3.77 GeV, and $G_M\left(s\right)(e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+})=0.44\pm 0.06\pm 0.01$, $G_M\left(s\right)(e^{+}{e}^{-}\to {\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0)=0.40\pm 0.08\pm 0.04$ at c.m. energy of 4.17 GeV, as shown in Figure 11. These results achieved by the CLEO-c experiment could provide additional information to examine the features of di-quark correlations.

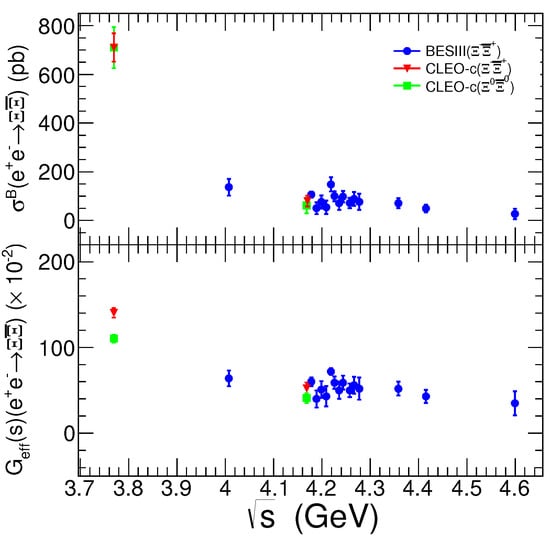
Figure 10. Comparisons of Born cross sections (top) and EFFs (bottom) between the CLEO-c experiment for the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ processes [65,66] and the BESIII experiment for the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ process from 3.7 to 4.6 GeV [32], where the uncertainties include both statistical and systematical contributions.

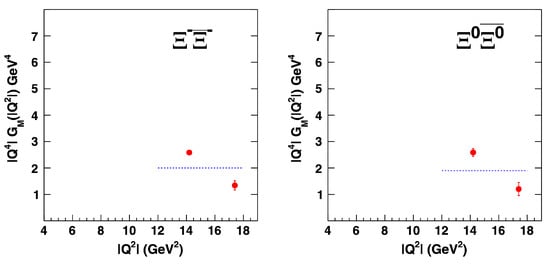
Figure 11. Illustration of $|Q^2|$ dependence on form factors for $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ at c.m. energies of 3.77 and 4.17 GeV [65,66].

Recently, BESIII collaboration also reported the measurements of Born cross sections and EFFs for the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ process [32] with a similar method to those described for the analysis of the near threshold [33,34]. The dataset used in this work corresponds to a total of 11.0 fb${}^{-1}$ of $e^{+}{e}^{-}$ collision data [32] collected at c.m. energies from 4.009 to 4.600 GeV with the BESIII detector at the BEPCII collider. Figure 12 shows the two-dimensional distribution of $M_{\pi \mathrm{\Lambda }}$ versus $M_{\pi \mathrm{\Lambda }}^{\mathrm{recoil}}$ for the sum of all energy points from 4.009 to 4.600 GeV. Clear signals for ${\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ production above the open charm threshold are observed for the first time.

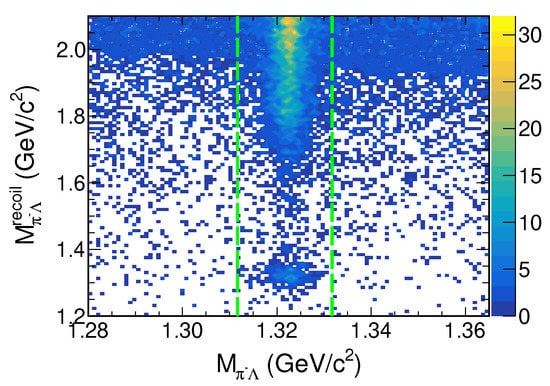
Figure 12. Distribution of $M_{\pi \mathrm{\Lambda }}$ versus $M_{\pi \mathrm{\Lambda }}^{\mathrm{recoil}}$ for all energy points from data from 4.009 to 4.600 GeV [32]. The dashed lines denote the $\mathrm{\Xi }$ signal region.

Figure 10 shows the comparisons of the measured Born cross sections and EFFs between the CLEO-c experiment and BESIII experiment from 4.009 to 4.600 GeV. The results for both experiments around 4.17 GeV are consistent with each other, and are well within the uncertainty of 1$\sigma$. It should be indicated that the line shape of the cross section for the $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ process around 4.26 GeV shows a complicated structure and could be due to the effect of some charmonium(-like) states although the uncertainties are large. In order to understand and probe the structures around 4.26 GeV well, a maximum likelihood method is employed to fit the dressed cross section ${\sigma }^{\mathrm{dressed}}={\sigma }^B/{|1-\Pi |}^2$ for the process $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ parameterized as the coherent sum of a PL function plus a BW function for $Y\left(4230\right)$ or $Y\left(4260\right)$,

$${\sigma }^{\mathrm{dressed}}\left(\sqrt{s}\right)={\left|c_0\frac{\sqrt{P\left(\sqrt{s}\right)}}{s^n}+e^{i\mathrm{\Phi }}\mathrm{BW}\left(\sqrt{s}\right)\sqrt{\frac{P\left(\sqrt{s}\right)}{P\left(M\right)}}\right|}^2,$$

(23)

where the mass M, and total width $\mathrm{\Gamma }$, are fixed to the $Y\left(4230\right)/Y\left(4260\right)$ resonance with PDG values [16], $\mathrm{\Phi }$ is the relative phase between the BW function (see Equation (20)) and PL, n is a free fit parameter, and $P\left(\sqrt{s}\right)$ is the two-body phase space factor. The significances of $Y\left(4230\right)$ and $Y\left(4260\right)$ resonances are found to be less than 3$\sigma$. Therefore, the upper limits on the products of the two-electron partial width and the branching fractions of $Y\left(4230\right)$ and $Y\left(4260\right)\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ at the 90% C.L. are determined using a Bayesian approach [38,39] to be ${\mathrm{\Gamma }}_{ee}{\mathcal{B}}_{Y\left(4230\right)}<0.33\times {10}^{-3}$ eV and ${\mathrm{\Gamma }}_{ee}{\mathcal{B}}_{Y\left(4260\right)}<0.27\times {10}^{-3}$ eV taking into account the systematical uncertainty, which may help understand the nature of $Y\left(4260\right)$ [67,68,69,70,71,72,73]. In particular, charmless decays of the $Y\left(4260\right)$ are predicted by the hybrid model [70]. Figure 13 shows the fit to the dressed cross section assuming a $Y\left(4230\right)$ or $Y\left(4260\right)$ resonance and without a resonance assumption.

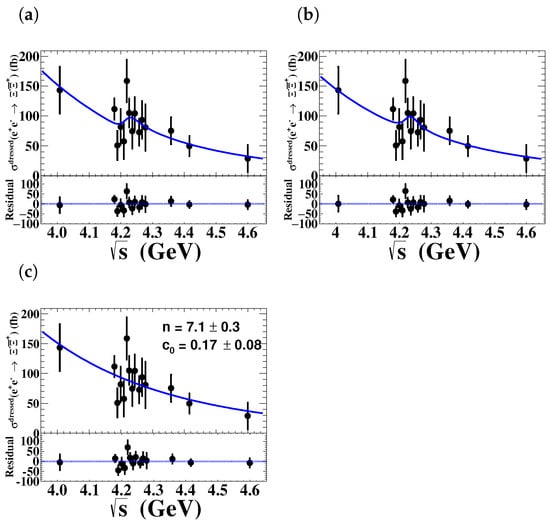
Figure 13. Fit to the dressed cross sections [32] at c.m. energies from 4.009 to 4.600 GeV with the assumptions of a PL function plus a $Y(4230/4260)$ resonance function (a,b) and without a resonance assumption (c), where the dots with error bars are the dressed cross sections and the solid lines show the fit results.

Additionally, an excited $\mathrm{\Xi }$ hyperon at 1820 MeV$c^2$ is observed by combining data of the 15 energy points in the range from 1.6 to 2.1 GeV/$c^2$ [32]. The significance is estimated to be more than 6.0$\sigma$. The mass and width are measured to be $M=(1825.5\pm 4.7\pm 4.7)$ MeV/$c^2$ and $\mathrm{\Gamma }=(17.0\pm 15.0\pm 7.9)$ MeV, which is consistent with the $\mathrm{\Xi }{\left(1820\right)}^{-}$ candidate from PDG [16] within 1$\sigma$ uncertainty, which sheds light on the structure of hyperon resonances with strangeness $S=-2$. These results also provide useful and important information for constraining and improving the theoretical prediction, and even offer insight into the nature of charmonium(-like) states and hyperon pair production in $e^{+}{e}^{-}$ annihilation above the open charm threshold.

4. Summary and Outlook

In summary, we reviewed the recent studies of EMFFs on doubly-strange hyperons using the pair production near threshold and above open charm threshold reported by the BESIII experiment and CLEO-c experiment. A possible structure near 3.0 GeV in the production cross section of $e^{+}{e}^{-}\to {\mathrm{\Xi }}^{-}{\overline{\mathrm{\Xi }}}^{+}$ and ${\mathrm{\Xi }}^0{\overline{\mathrm{\Xi }}}^0$ is considered but the current significance is less than 3 $\sigma$, which still needs be further checked when a large data sample is available. An excited $\mathrm{\Xi }$ baryon was observed; its mass and width are consistent with the $\mathrm{\Xi }\left(1820\right)$ baryon from PDG [16] but no quantum number was determined due to the limited statistics. These results on the ${\mathrm{\Xi }}^0$ and ${\mathrm{\Xi }}^{-}$ hyperon EMFFs provide useful and important information to test the standard model, such as probing the limitation of the quark models and to spot unrevealed aspects of the QCD description of the structure of hadron resonances. It is expected that more results and surprises from the studies of the hyperon EMFFs will be made with larger data sets in $e^{+}{e}^{-}$ annihilation in the BESIII experiment [19] and the proposed Super Tau-Charm Factory projects in China [74] and Russia [75], and the upcoming PANDA experiment in $p\overline{p}$ annihilation at FAIR [76].