Abstract
Solving equations of the form is one of the most faced problem in mathematics and in other science fields such as chemistry or physics. This kind of equations cannot be solved without the use of iterative methods. The Steffensen-type methods, defined using divided differences are derivative free, are usually considered to solve these problems when H is a non-differentiable operator due to its accuracy and efficiency. However, in general, the accessibility of these iterative methods is small. The main interest of this paper is to improve the accessibility of Steffensen-type methods, this is the set of starting points that converge to the roots applying those methods. So, by means of using a predictor–corrector iterative process we can improve this accessibility. For this, we use a predictor iterative process, using symmetric divided differences, with good accessibility and then, as corrector method, we consider the Center-Steffensen method with quadratic convergence. In addition, the dynamical studies presented show, in an experimental way, that this iterative process also improves the region of accessibility of Steffensen-type methods. Moreover, we analyze the semilocal convergence of the predictor–corrector iterative process proposed in two cases: when H is differentiable and H is non-differentiable. Summing up, we present an effective alternative for Newton’s method to non-differentiable operators, where this method cannot be applied. The theoretical results are illustrated with numerical experiments.
Keywords:
iterative method; local convergence; non-differentiable operator; dynamics; Steffensen’s method MSC:
47H99; 65H10
1. Introduction
One of the most studied problems in numerical mathematics is finding the solution of nonlinear systems of equations
where is a nonlinear operator, with , , and is a non-empty open convex domain. In this context, iterative methods are a powerful tool for solving these equations [1]. Many applied problems can be reduced to solving systems of nonlinear equations, which is one of the most basic problems in mathematics. These problems arise in all scientific areas. Both in mathematics, physics and especially in a diverse range of engineering applications. This task has applications in many scientific fields [2,3]. Applications in the geometric theory of the relativistic string can be found [4], also when solcing nonlinear equations in porous media problems [5,6], in solving nonlinear stochastic differential equations (by the first order finite difference method) [7], in solving nonlinear Volterra integral equations [8], an many others.
In general, there are two aspects that must be considered when we choose an iterative process to approximate a solution of Equation (1). The first one is related to the computational efficiency of the iterative process [9]. The other one, with the same importance, is known as the accessibility of the iterative process [10], which represents the possibility to locate starting points that ensure the convergence of the sequence generated by the iterative process to a solution of Equation (1). Newton’s method, due to its characteristics, it is usually considered as a reference in the measure of these two aspects. However, this method has a serious shortcoming: the derivative has to be computed and evaluated at each iteration. This makes it inapplicable when the equations involved presents non-differentiable operators and in situations when the evaluation of the derivative is too expensive in terms of computation and time. In these cases, one alternative commonly used is to approximate the derivatives by divided differences using a numerical derivation formula, where iterative processes free of derivatives are obtained. For this purpose, authors use first order divided differences [9,11]. First, we denote by the space of bounded linear operators from . An operator is called first order divided difference for the operator on the points x and y if it is satisfied that
In this paper, we consider derivative-free iterative processes using the previous ideas. But these methods have also a serious shortcoming: they have a region of reduced accessibility. In [10], the accessibility of an iterative process is increased by means of an analytical procedure, which consists of modifying the convergence conditions. However, in this work, we will increase accessibility by constructing an iterative predictor–corrector process. This iterative process has a first prediction phase and then a second accurate approximation phase. The first phase allows us, by applying the predictor method, to locate a starting point for the corrector method to ensure convergence to a solution of the equation.
Kung and Traub presented in [12] a class of iterative processes without derivatives. These iterative processes considered by Kung and Traub contain Steffensen-type methods as a special case. In [13], a generalized Steffensen-type is considered with the following algorithm:
As special cases of the previous algorithm, the three most well-known Steffesen-type methods: for and we obtain the original Steffensen method, the Backward-Steffensen method is obtained for and and the Center-Steffensen method is obtained for and
Notice that, if we consider the Newton’s method,
which is one of the most used iterative methods [14,15,16,17,18] to approximate a solution of , the Steffensen-type methods are obtained as a special case of this method, where the evaluation of in each step is approximated by the divided difference of first order . The Steffensen-type methods have been widely studied by many recognized researchers such as Alarcón, Amat, Busquier and López ([19]) who presented a study and applications of Steffensen method to boundary-value problems, Argyros ([20]) who gave an improved convergence theorem related to Steffensen method or Ezquerro, Hernández, Romero and Velasco ([21]) who studied the generalization of the Steffensen method to Banach spaces.
Symmetric divided differences generally perform better. This fact can be seen in the dynamical behavior of the Center-Steffensen method, see Section 2, which is the best one, in term of convergence, from the Steffensen-type methods given previously. Moreover, this method maintains the quadratic convergence of Newton’s method, by approximating the derivative through symmetric divided differences with respect to the , and the Center-Steffensen method also has the same computational efficiency as Newton’s method. However, to achieve the second order in practice, an iteration close enough to the solution is needed to have a good approximation of the first derivative of H used in Newton’s method. In other case, some extra iterations in comparison with Newton’s method are required. Basically, when the norm of is big, the approximation of the divided difference to the first derivative of H is bad. So, in general, the set of starting points of the Steffensen-type methods is poor. This reality can be observed experimentally by means of the basins of attraction shown in Section 2. This fact justifies that Steffensen-type methods are less used than Newton’s method to approximate solutions of equations for differentiable operators.
Thus, two are our main objectives in this work: on the one hand, in the case of differentiable operators, where Newton’s method can also be applied, our objective is to construct a predictor–corrector iterative process with an accessibility and efficiency such as Newton’s method. Secondly, the other objective is to ensure that this predictor–corrector iterative process considered have a behavior such as Newton’s method but considering the case of non-differentiable operators where Newton’s method cannot be applied.
Following this idea, in this paper we consider the derivative-free point-to-point iterative process given by
where for a real number . Thus, we use a symmetric divided difference to approximate the derivative that appear in Newton’s method. Furthermore, by varying the parameter , we can approach the value of . Notice that, in the differentiable case, for we obtain the Newton’s method. The dynamical behavior of this simple iterative process is like Newton’s method, with one varying the parameter .
However, although reducing the value of we can reach a speed of convergence like Newton’s method, its order of convergence is linear. That is why we will consider this method as a predictor, due to its good accessibility, and we will consider then the Center-Steffensen method:
as a corrector method, whose order of convergence is quadratic.
The paper is organized as follows. Section 2 contains the motivation of the paper. In Section 3, we present a semilocal convergence analysis of the new method when operator H is both differentiable and non-differentiable cases. Moreover, some numerical experiments are shown where the theoretical results are proven numerically. Next, Section 4 contains the study of dynamical behavior for the predictor–corrector method. Finally, in Section 5, we present the conclusions of the work carried out.
2. Motivation
When iterative processes defined by divided differences are applied to find the solutions of nonlinear equations, it is important to note that the region of accessibility is reduced with respect to Newton’s method. In practice, we can see this circumstance with the basins of attraction (the set of points of the plane such that initial conditions chosen in the set dynamically evolve to a particular attractor ([22,23]) of iterative methods when they are applied to solve a complex equation , where and .
First, in the differential case, we compare the dynamical behavior of the Newton’s method, the Steffensen-type methods (3) and the iterative process given in (5) for solving the complex equation . In the non-differentiable case, we compare the Steffensen-type methods (3) and the iterative process given in (5) for solving the complex equation . Our objective is to justify that the accessibility region of the iterative process (5) is comparable to the one associated to Newton’s method, in the differentiable case, and notably greater compared to Steffensen-type methods (3) in both cases, differentiable and non-differentiable. In each case, the favorable choice of the iterative process (5) as a predictor method is proven.
We will show the fractal pictures that are generated to approximate the three solutions of , , and and the ones generated to approximate the three solutions of , , and . We are interested in identifying the attraction basins of the three solutions , and [23]. These basins also allow us to compare the regions of accessibility of these methods.
In all the cases, the tolerance and a maximum of 100 iterations are used. If we have not obtained the desired tolerance after 100 iterations, we do not continue and decide that the iterative method starting at does not converge to any zero.
The regions of accessibility of the two iterative methods when they are applied to approximate the solutions , and of are shown in Figure 1 and Figure 2. The strategy used is the following: A color is assigned to each solution of the equation and if the iteration does not converge, color black is used. To obtain the pictures, red, yellow, and blue colors have been assigned for the attraction basins of the three zeros. The basins shown have been generated using Mathematica 10 [24].
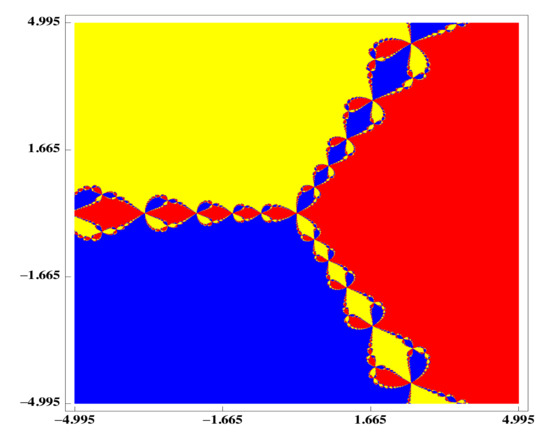
Figure 1.
Newton’s Method applied to .
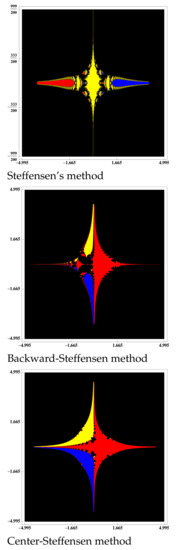
Figure 2.
Basins of attraction to polynomial .
If we observe the behavior of these methods, it is clear that methods (3) are stricter with respect to the starting point than Newton’s method (see the black zone). However, if we consider the iterative process (5), see in Figure 3, varying the parameter , a dynamical behavior similar to Newton’s method can be obtained.
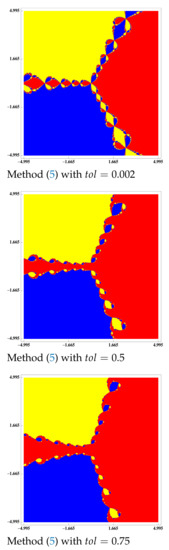
Figure 3.
Basins of attraction to polynomial .
In Figure 1 and Figure 2 are shown the dynamical behavior of Newton’s Method and the Steffensen, Backwards-Steffensen and Center-Steffensen method, where the predictor method (5) is better than the Steffensen-type methods (3).
Once the accessibility has been graphically analyzed, showing that method (5) is better than the Steffensen-type methods (3) and, like Newton’s method in terms of convergence, we want to prove it in a numerical way and, for that purpose, we compute the percentage of points that converges. This information is presented in Table 1.

Table 1.
Percentage of convergence points for .
Nevertheless, the use of derivative-free iterative methods is necessary when the operator H is non-differentiable. For this reason, one aim of this work is, from the predictor method (5), preserve, in some way, the good accessibility of Newton’s method.
Then, in non-differentiable case, if we use the Steffensen-type methods defined in (3) to solve the equation , the predictor method (5) improve the accessibility region of Steffensen-type methods (3), as we can see in Figure 4 and Figure 5, where the basins of attraction of the two solutions of this equation are drawn for the mentioned methods.
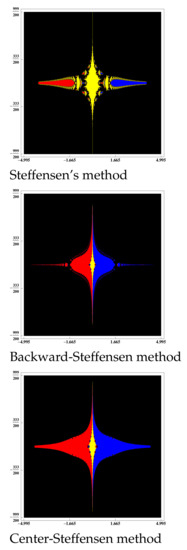
Figure 4.
Basins of attraction to equation .
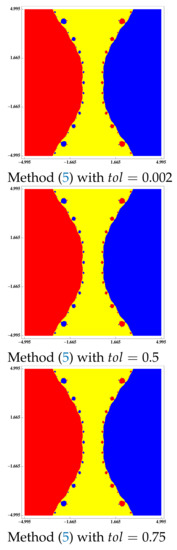
Figure 5.
Basins of attraction to equation .
Once the accessibility has been graphically analyzed, showing that method (5) is better than the other ones, we want to prove it in a numerical way and, for that purpose, we compute the percentage of points which converges. We get this information in Table 2.

Table 2.
Percentage of convergence points for .
As we have just seen, the iterative process predictor (5) has a significantly better dynamic behavior than the Steffensen-type methods, being like Newton’s method in the differentiable case. Therefore, we can say that the iterative process predictor has a good accessibility, improving the one of the Steffensen-type methods in both cases, differentiable and non-differentiable. This leads us to construct an iterative process predictor–corrector, using the Center-Steffensen method as the iterative correction process, which maintains its quadratic convergence. Consequently, we consider the predictor–corrector method:
where for a real number . Thus, this predictor–corrector method will be a Steffensen-type method with good accessibility and quadratic convergence from an iteration to be determined.
3. Semilocal Convergence
From the dynamic study carried out previously, it is evident that, if we denote by and given by (5), converges the accessibility domains of iterative processes (6) and (5), it will be verified that . That is, the set of starting points that ensure convergence for method (6) is less than the corresponding set for method (5). In this section we show that, starting from an element , we can locate a point such that . Therefore, we obtain a starting point that ensures the convergence of method (6). Thus, doing some iterations with the predictor method, we locate a point that ensures the convergence of method (6). Therefore, we increase the accessibility of Center-Steffensen method.
The semilocal study of the convergence is based on demanding conditions to the initial approximation , from certain conditions on the operator H, and provide conditions required to the initial approximation that guarantee the convergence of sequence (7) to the solution . In order to analyze the semilocal convergence of iterative processes that do not use derivatives in their algorithms, the conditions are usually required on the operator divided difference. Although in the case that the operator H is Fréchet differentiable, the divided difference operator can be defined from the Fréchet derivative of the operator H.
3.1. Differentiable Operators
Next, we establish the semilocal convergence of iterative process given in (7) for differentiable operators. So, we consider a Fréchet differentiable operator and there exists
for each pair of distinct points . Notice that, as H is Fréchet differentiable .
Now, we suppose the following initial conditions:
- (D1)
- Let such that exists with and .
- (D2)
- , , .
Firstly, we obtain some technical results.
Lemma 1.
The following items are verified.
- (i)
- Let with . If then, for each pair of distinct points , there exists such that
- (ii)
- If , for , then
- (iii)
- If , for , then
Proof.
To prove the item , from , we can write
Then, by the Banach Lemma for inverse operators [25] the item is proved.
Taking norms in the last equality obtained previously and, considering (8), the proof of item is evident.
Item is proved analogously to item , just considering the algorithm of the iterative process predictor–corrector (7). □
To simplify the notation, from now on, we denote
and the parameters and Other parameters which will be used are:
Moreover, notice that the polynomial equation where
has at least a positive real root since that and as Then, we denote by R the smallest positive root of the polynomial equation .
Finally, we denote by the integer part of the real number x.
Theorem 2.
Let a Fréchet differentiable operator defined on a nonempty open convex domain Ω. Suppose that conditions and are satisfied and there exists such that and If we consider
then the iterative process predictor–corrector (7), starting at , converges to a solution of Moreover, for and
Proof.
First, notice that it is easy to check that
Then, from the item , in the previous Lemma, , there exists such that Then, is well defined and with what we get that Now, obviously, and, again from the item in the previous Lemma, there exists such that Then, is well defined and, from (10), we have that
Moreover, from (13), we get
Therefore, we obtain that
And , since .
Consequently, it is easy to check that since that
Following a recursive procedure, it is easy to check the following relationships for
- (a)
- There exists such that
- (b)
- (c)
- (d)
- ,
- (e)
Now, from the algorithm of the iterative process predictor–corrector (7), we consider Then, from the hypothesis required to the parameter in (12), we have that Then So, from item of Lemma 1, there exists with
On the other hand, from item of Lemma 1, we obtain
Then,
And, as a direct consequence, we get that
and
Therefore, and, from item of Lemma 1, we have
So, we have that .
Then Now, from item of Lemma 1, there exists with
Moreover, we get
and
Now, following an inductive procedure, it is easy to check the recurrence relations defined for as:
- (a′)
- There exists such that
- (b′)
- (c′)
- (d′)
- ,
- (e′)
Now, using , for , we have
Hence, is a Cauchy sequence which converges to Since
thus, by using the continuity of □
Next, we present a uniqueness result for the iterative process predictor–corrector (7).
Theorem 3.
Under conditions of the previous Theorem, the solution of the equation is unique in .
Proof.
To prove the uniqueness part, suppose is another solution of (1) in If is invertible, then since But
Therefore, by the Banach Lemma of inverse operators, there exists and then □
3.2. Non-Differentiable Operators
In this section, we want to obtain a result of semilocal convergence for iterative process (7) when H is a non-differentiable operator. In order to obtain it, we must suppose that for each pair of distinct points , there exists a first-order divided difference of H at these points. As we consider an open convex domain of , this condition is satisfied ([9,26]). Moreover, it is also necessary to impose a condition on the first-order divided difference of the operator H. As it appears in [27,28], a Lipschitz-continuous condition or a Hölder-continuous can be considered, but in the above cases, it is known [29], that the Fréchet derivative of H exists in . Therefore, these conditions cannot be verified if the operator H is non-differentiable. Then, to establish the semilocal convergence of iterative process given in (7) for non-differentiable operator H, we suppose that the following conditions hold:
- [(ND1)] Let such that exists with and
- [(ND2)] , with
To simplify the notation, from now on, we denote
In these conditions, we start our study obtaining a technical result, the proof of which is evident from algorithm given in (7).
Lemma 4.
The following items can be easily verified.
- (i)
- If , for , then
- (ii)
- If , for , then
Theorem 5.
Under the conditions (ND1)-(ND2) if the real equation
has at least one positive root, the smallest positive root is denoted by R, and there exists such that satisfies
and If we consider
then the iterative process predictor–corrector (7), starting at , converges to a solution of Moreover, for and and is unique solution of in .
Proof.
Second, we prove that is well defined and for . From condition (ND1), is well defined and
Thus, and Using Lemma 4, we get
Now,
Hence, by using Banach Lemma for inverse operators, exists and
Thus, is well defined. Moreover,
and as
In a similar way, by using the principle of mathematical induction, we can establish the following recurrence relations. For
- (A1)
- (A2)
- (A3)
- (A4)
To study the convergence of the predictor of (7), we consider Using Lemma 4, we get
and, by the hypothesis required to the parameter in (19), we have
so, is well defined. Now, we consider
Hence, exists and
Hence, . Again, using Lemma 4 and condition (ND2), we have
and then
Then is well defined, therefore
Hence, exists and
Hence,
Using mathematical induction, we can establish the following recurrence relation for :
- (B1)
- (B2)
- (B3)
- (B4)
Now, using for
Hence, is a Cauchy sequence which converges to . Since,
and as thus by using the continuity of
□
Theorem 6.
Under conditions of the previous Theorem, the solution of the equation is unique in .
Proof.
To prove the uniqueness of , let be another solution of in . If is invertible, then . Since,
But, Hence, by the Banach Lemma for inverse operators, exists. Therefore, . □
3.3. Numerical Experiments
Now, we perform a numerical experience to show the applicability of the theoretical results previously obtained. So, we deal with nonlinear integral equations that are used in a great variety of applied problems in electrostatic, low frequency electromagnetic problems, electromagnetic scattering problems and propagation of acoustical and elastic waves ([30,31]). We focus on the nonlinear integral equation of Hammerstein type expressed as follows
where , G is the Green’s function, and M are known functions and x is the solution to be obtained.
We solve the equation , where by transforming the problem into a nonlinear system. First, we approximate the given integral by a quadrature formula with the corresponding weighs and nodes The discretization of the problem by using these nodes gives us the following nonlinear system:
where
We can formulate the system from into by using the following functions and matrices,
with
To illustrate the theoretical results in both differentiable and non-differentiable cases, we take for
with , and Specifically, we solve the following nonlinear system,
where
and
So, we are now in conditions of applying the theoretical development for both cases the differentiable and non-differentiable one.
3.3.1. H a Differentiable Operator
We consider in the above described nonlinear integral the following values and so we have a differentiable problem. Moreover, we work in the domain defined with the infinity norm. In these terms, for the associated operator H it is easy to characterize the Fréchet derivative so we have
Then, by applying the theoretical results obtained in previous sections we take as starting point and different values of . The values for the parameters than appear in the semilocal convergence study are and Other results such as and the value for the radii of the domains of existence and uniqueness for the solution can be find in Table 3. As can be seen in the results of this table when decreases also does the semilocal convergence radii, being the value of similar.

Table 3.
Radii of the semilocal convergence balls for different values of tol.
Finally, we obtain the approximated solution of the nonlinear integral Equation (31) by applying Newton’s method (4) and the new predictor–corrector Steffensen-type method, In (7). We run the corresponding algorithms with Matlab20 working in variable precision arithmetic with 100 digits, using as stopping criteria and with the starting point and values of used and obtained in the semilocal convergence study. The results in Table 4 show that the behavior of the new predictor–corrector Steffensen method is as good as Newton’s method. The approximated solution gives us following values if we round to 6 digits:

Table 4.
Numerical results with starting guess .
3.3.2. H a Non-Differentiable Operator
If, in (29) we work again in by considering , and , we obtain the non-differentiable system of nonlinear equations
In these terms, we characterize the divided difference operator by using the following formula:
having that
where with if but while with and . Furthermore, if we work in the domain we have the following bounds,
Now, by taking starting point and different values of we have the following bounds for the parameters involved in the semilocal convergence Theorem 5, , and Other results such as and the value for the radii of the domains of existence and uniqueness for the solution can be find in Table 5. We can corroborate a similar behavior than in the differentiable case, that is, for smaller values of the radii increases.

Table 5.
Radii of the semilocal convergence balls for different values of .
Finally, we obtain the approximated solution of the nonlinear integral equation (32) by applying center Steffesen method (3) and the new Steffesen method (7). We run the corresponding algorithms in Matlab20 working in variable precision arithmetic with 100 digits, using as stopping criteria and with the starting point and values of obtained in the semilocal convergence study. The results in Table 6 show that the behavior of the new predictor–corrector Steffensen method improves the Center-Steffensen method. The approximated solution gives us following values if we round to 6 digits:

Table 6.
Numerical results with starting guess .
4. Dynamical Behavior of Predictor–Corrector Method
In this section, we compare the behavior of predictor–corrector method (7) for functions and used in the motivation section for different values of and . In this case, we will have a greater demand to obtain the attraction basins. So, in all the cases, the tolerance and a maximum of 100 iterations are used. If we have not obtained the desired tolerance with 100 iterations, do not continue and decide that the iterative method starting at does not converge to any zero.
For the differentiable case, as we can see in Figure 6, Figure 7 and Figure 8, by increasing the value of we can achieve an accessibility such as that of Newton’s method. Once the accessibility has been graphically analyzed, showing that method (7) is better than the Steffensen-type methods (see Figure 2), we want to see its behavior in a numerical way and, for that purpose, we compute the percentage of points which converges. We get this information in Table 7.
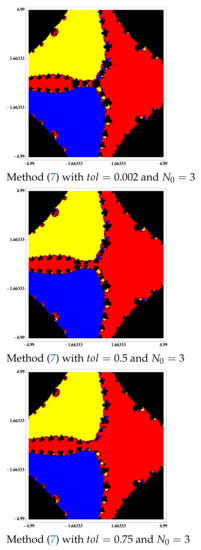
Figure 6.
Basins of attraction to polynomial .
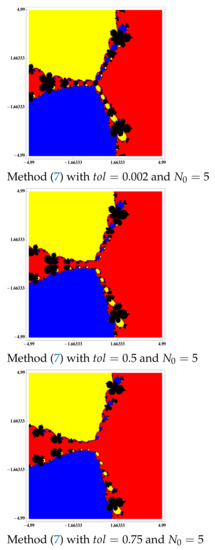
Figure 7.
Basins of attraction to polynomial .
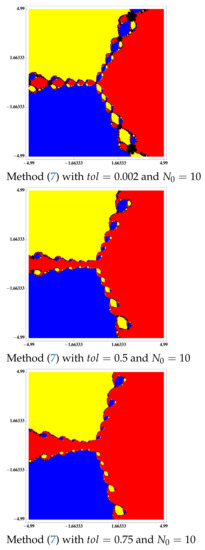
Figure 8.
Basins of attraction to polynomial .

Table 7.
Percentage of convergence points for .
Similarly, in the non-differentiable case, as it can be seen in Figure 9, Figure 10 and Figure 11, we verify that by increasing the value of , we can achieve an accessibility as presented by Newton’s method in the differentiable case.
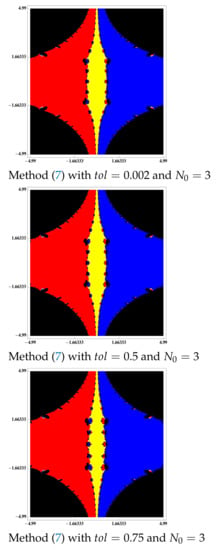
Figure 9.
Basins of attraction to equation .
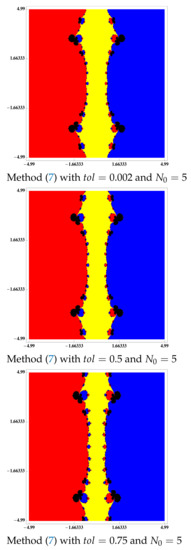
Figure 10.
Basins of attraction to equation .
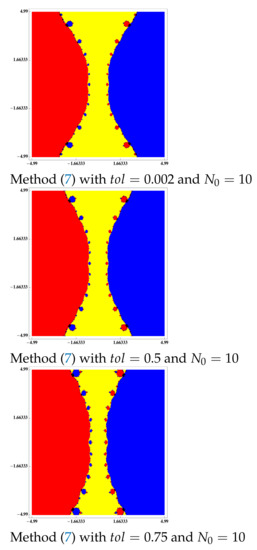
Figure 11.
Basins of attraction to equation .
Once the accessibility has been graphically analyzed, showing that method (7) is better than the Steffensen-type methods (see Figure 4), we want to see its behavior in a numerical way and, for that purpose, we compute the percentage of points which converges. We get this information in Table 8.

Table 8.
Percentage of convergence points for .
5. Concluding Remarks
Due to the inconvenience of applying Steffensen-type iterative processes in terms of their accessibility, we have built a predictor–corrector iterative process that, while maintaining the efficiency of Steffensen-type methods, improves the accessibility of these methods. Thus, it can be used as an efficient alternative to Newton’s method when applied to nonlinear systems of non-differentiable equations.
Author Contributions
Investigation, M.A.H.-V., S.Y., Á.A.M., E.M. and S.S.; Writing—original draft, M.A.H.-V., S.Y., Á.A.M., E.M. and S.S.; Writing—review and editing, M.A.H.-V., S.Y., Á.A.M., E.M. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the project PGC2018-095896-B-C21-C22 of Spanish Ministry of Economy and Competitiveness and by the project of Generalitat Valenciana Prometeo/2016/089.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Regmi, S. Optimized Iterative Methods with Applications in Diverse Disciplines; Nova Science Publisher: New York, NY, USA, 2021. [Google Scholar]
- Argyros, I.K.; Cho, Y.J.; Hilout, S. Numerical Methods for Equations and Its Applications; CRC Press/Taylor and Francis: Boca Raton, FL, USA, 2012. [Google Scholar]
- Argyros, I.K.; Hilout, S. Numerical Methods in Nonlinear Analysis; World Scientific Publishing Co.: Hackensack, NJ, USA, 2013. [Google Scholar]
- Barbashov, B.M.; Nesterenko, V.V.; Chervyakov, A.M. General solutions of nonlinear equations in the geometric theory of the relativistic string. Commun. Math. Phys. 1982, 84, 471–481. [Google Scholar] [CrossRef]
- Brugnano, L.; Casulli, V. Iterative Solution of Piecewise Linear Systems. SIAM J. Sci. Comput. 2008, 30, 463–472. [Google Scholar] [CrossRef]
- Difonzo, F.V.; Masciopinto, C.; Vurro, M.; Berardi, M. Shooting the Numerical Solution of Moisture Flow Equation with Root Water Uptake Models: A Python Tool. Water Resour. Manag. 2021, 35, 2553–2567. [Google Scholar] [CrossRef]
- Soheili, A.R.; Soleymani, F. Iterative methods for nonlinear systems associated with finite difference approach in stochastic differential equations. Numer. Algorithms 2016, 71, 89–102. [Google Scholar] [CrossRef]
- Gou, F.; Liu, J.; Liu, W.; Luo, L. A finite difference method for solving nonlinear Volterra integral equation. J. Univ. Chin. Acad. Sci. 2016, 33, 329–333. [Google Scholar]
- Grau-Sánchez, M.; Noguera, M.; Amat, S. On the approximation of derivatives using divided difference operators preserving the local convergence order of iterative methods. J. Comput. Appl. Math. 2013, 237, 363–372. [Google Scholar] [CrossRef]
- Argyros, I.K.; George, S. On the complexity of extending the convergence region for Traub’s method. J. Complex. 2020, 56, 101423. [Google Scholar] [CrossRef]
- Argyros, I.K. On the Secant method. Publ. Math. Debrecen 1993, 43, 223–238. [Google Scholar]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. ACM 1973, 21, 643–651. [Google Scholar] [CrossRef]
- Amat, S.; Ezquerro, J.A.; Hernández-Verón, M.A. On a Steffensen-like method for solving nonlinear equations. Calcolo 2016, 53, 171–188. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Asady, B. Newton’s method for solving fuzzy nonlinear equations. Appl. Math. Comput. 2004, 159, 349–356. [Google Scholar] [CrossRef]
- Chun, C. Iterative methods improving Newton’s method by the decomposition method. Comput. Math. Appl. 2005, 50, 1559–1568. [Google Scholar] [CrossRef]
- Galántai, A. The theory of Newton’s method. J. Comput. Appl. Math. 2000, 124, 25–44. [Google Scholar] [CrossRef]
- Kelley, C.T. Solving Nonlinear Equations with Newton’s Method; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Magreñán, Á.A.; Argyros, I.K. A Contemporary Study of Iterative Methods; Academic Press: Cambridge, MA, USA; Elsevier: Hoboken, NJ, USA, 2018. [Google Scholar]
- Alarcón, V.; Amat, S.; Busquier, S.; López, D.J. A Steffensen’s type method in Banach spaces with applications on boundary-value problems. J. Comput. Appl. Math. 2008, 216, 243–250. [Google Scholar] [CrossRef]
- Argyros, I.K. A new convergence theorem for Steffensen’s method on Banach spaces and applications. Southwest J. Pure Appl. Math. 1997, 1, 23–29. [Google Scholar]
- Ezquerro, J.A.; Hernández, M.A.; Romero, N.; Velasco, A.I. On Steffensen’s method on Banach spaces. J. Comput. Appl. Math. 2013, 249, 9–23. [Google Scholar] [CrossRef]
- Kneisl, K. Julia sets for the super-Newton method, Cauchy’s method, and Halley’s method. Chaos 2001, 11, 359–370. [Google Scholar] [CrossRef] [PubMed]
- Varona, J.L. Graphic and numerical comparison between iterative methods. Math. Intell. 2002, 24, 37–46. [Google Scholar] [CrossRef]
- Wolfram, S. The Mathematica Book, 5th ed.; Wolfram Media/Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Balazs, M.; Goldner, G. On existence of divided differences in linear spaces. Rev. Anal. Numer. Theor. Approx. 1973, 2, 3–6. [Google Scholar]
- Hilout, S. Convergence analysis of a family of Steffensen-type methods for generalized equations. J. Math. Anal. Appl. 2008, 329, 753–761. [Google Scholar] [CrossRef][Green Version]
- Moccari, M.; Lotfi, T. On a two-step optimal Steffensen-type method: Relaxed local and semi-local convergence analysis and dynamical stability. J. Math. Anal. Appl. 2018, 468, 240–269. [Google Scholar] [CrossRef]
- Hernández, M.A.; Rubio, M.J. A uniparametric family of iterative processes for solving non-differentiable equations. J. Math. Anal. Appl. 2002, 275, 821–834. [Google Scholar] [CrossRef]
- Bruns, D.D.; Bailey, J.E. Nonlinear feedback control for operating a nonisothermal CSTR near an unstable steady state. Chem. Eng. Sci. 1977, 32, 257–264. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Applications of Integral Equations; Linear and Nonlinear Integral Equations; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).