Symmetries and Geometries of Qubits, and Their Uses

Abstract

The symmetry SU(2) and its geometric Bloch Sphere rendering have been successfully applied to the study of a single qubit (spin-1/2); however, the extension of such symmetries and geometries to multiple qubits—even just two—has been investigated far less, despite the centrality of such systems for quantum information processes. In the last two decades, two different approaches, with independent starting points and motivations, have been combined for this purpose. One approach has been to develop the unitary time evolution of two or more qubits in order to study quantum correlations; by exploiting the relevant Lie algebras and, especially, sub-algebras of the Hamiltonians involved, researchers have arrived at connections to finite projective geometries and combinatorial designs. Independently, geometers, by studying projective ring lines and associated finite geometries, have come to parallel conclusions. This review brings together the Lie-algebraic/group-representation perspective of quantum physics and the geometric–algebraic one, as well as their connections to complex quaternions. Altogether, this may be seen as further development of Felix Klein’s Erlangen Program for symmetries and geometries. In particular, the fifteen generators of the continuous SU(4) Lie group for two qubits can be placed in one-to-one correspondence with finite projective geometries, combinatorial Steiner designs, and finite quaternionic groups. The very different perspectives that we consider may provide further insight into quantum information problems. Extensions are considered for multiple qubits, as well as higher-spin or higher-dimensional qudits.

1. Introduction

This article deals with the symmetry aspects of quantum information systems [1]. The unitary group SU(2) symmetry of a single two-level system, a “qubit”, is well-known and exploited widely; not just in quantum information, but throughout the field of physics. It is taught in the very first courses on quantum spin-1/2. The so-called Bloch sphere representation [2,3] has been used from the earliest days of nuclear magnetic resonance (NMR). Its mapping of the unitary transformations of complex wave functions onto the rotations of a classical unit vector attached to an ordinary sphere, $S^2$, pervades the very language of NMR and its applications in chemistry and medicine. It even provides the intuition for transformations between quantum states in terms of axes, and angles of rotation about them, to achieve a desired end. “Apply a $\pi$-rotation (’spin-flip’) about some axis followed by a different rotation around a second axis”; such phrases form the lore of the subject [4]. In contrast, the similar SU(4), that pertains to a two-qubit system, or higher-dimensional extensions and their corresponding geometrical pictures, have been little-used in the field of quantum information. This is in spite of such expectations, given the central role that two or more entangled spins play in quantum computing, quantum cryptography, and other sub-fields. It is even more surprising when we consider that quantum physics, as well as its various developments in atomic, nuclear, condensed matter, and particle physics, has repeatedly shown the importance, and even the necessity, of using symmetry—for understanding, insight, and as a technical aid to facilitate calculation. Furthermore, the rotations and associated symmetries of orthogonal groups, SO(d), had even already been studied in classical physics, before being used for quantum angular momentum (both orbital and spin). In addition, quantum physics introduced the unitary groups, SU(d), as natural objects for analyzing the time evolution of quantum states.

This review will examine the symmetry considerations that pertain to the operators and states of interest for entanglement [1], quantum discord [5,6], and a variety of other quantum correlations. Our examination will develop an understanding of, and provide convenient calculations for, these correlations. We will consider two or more qubits and also higher-dimensional “qudits” of dimension, d, larger than two. These require higher unitary groups, such as SU($2^q$) for q qubits or SU(d) for a single qudit. Whereas the SU(2) group, and the corresponding su(2) algebra (we follow the convention of using upper case for Lie groups and lower case for Lie algebras), involve three generators and parameters, the higher groups deal, of course, with many more. The SU(4), for two qubits, has fifteen generators; any general SU(d) has $(d^2-1)$ of them. In part, these larger numbers may have deterred the use of these groups. Their consideration nevertheless proves useful, especially since smaller sub-groups of them often come into play for the physics and symmetries of the system of interest. This will be a recurring theme of this review. As an example, many sub-groups of SU(4) have been shown to represent some of the logic gates and Hamiltonians that arise in coupled two-qubit systems (or in more general four-level systems of atomic and molecular physics and quantum optics [7,8]). One such sub-group, SU(2) × U(1) × SU(2), is also the symmetry of the seven-parameter X-states [9] that were previously defined and used for a variety of qubit-qubit problems, before this underlying symmetry was recognized [10].

A wider context for our discussion is provided by the famous 1872 Erlangen Program of Felix Klein [11,12]. Instead of the centuries-old view of geometry as a set of axioms that defined points, lines, triangles, and circles—as well as theorems relating to their properties—Klein reinterpreted geometry as the study of symmetries and their associated transformations; each such set then defined a particular geometry. Euclidean geometry is just one kind, which stems from Euclidean transformations in a plane. However, there is an infinite number of others, each of which depend upon the symmetries and transformations which are initially specified. This re-orientation and focus onto geometries in the plural, each associated with a set of symmetries, has had a profound effect on mathematics and physics ever since. Coupled with Emmy Noether’s theorem, which associates each symmetry with a conservation law (i.e., an invariant of that symmetry), the most fundamental laws of physics—namely, the conservation laws of linear and angular momentum, energy, charge, etc.—place symmetries at the heart of physics [2,3,13].

The influence on modern physics by Klein, as well as his contemporary colleague and friend Sophus Lie [14], who developed the subject of continuous symmetry groups such as SO(d) and SU(d), cannot be stressed enough. Havel and Doran [15] have produced a striking diagram which represents this historical influence. Reproduced here as Figure 1, they classify subsequent work into three separate ladders. The first is the study of invariants along with geometric relations, subsumed under a general study of algebraic curves and surfaces in the area of mathematics called algebraic geometry. A second ladder, initiated by Grassmann, which ties to quaternions (invented by Hamilton even before the advent of the Klein Program), has come to be known as geometric algebra. Closely linked to Clifford algebras, it is the study of tensors and spinors of various ranks, differential forms, etc. Its value has been recognized in recent times in the work of Baylis, Sobcyzk, Doran, Lasenby, Hestenes, and others. Hestenes, in particular, has shown how classical and quantum mechanics, both non-relativistic and relativistic, can be described by geometric algebra—to great advantage—throughout his works and textbooks. This even extends to a pedagogical benefit, when compared to alternative treatments that have otherwise become standard [16,17,18]. The third ladder is group representation theory; originated by Frobenius, it mainly became the work of Lie and Engel in the area of mathematics called Lie groups and Lie algebras [19]. Physics students are most familiar with this third ladder, as well as the matrix representation that it most commonly uses, because of the wide-ranging role for orthogonal SO and unitary SU groups.

Although symmetries and transformations are also important in classical physics, they became even more crucial from the very beginnings of quantum physics and its applications in atomic, condensed matter, nuclear, and particle physics. Most physicists are, therefore, familiar with SU(2), SU(3), SU(4), SO(3), SO(4), etc., while not as much with geometric algebra, quaternions, Grassmann manifolds, or similar areas. However, in the last 20 years, different lines of investigation in quantum information, and especially the study of pairs of qubits, has pointed to further inter-connections between the topics described in the previous paragraph; in particular, connections across the different ladders in Figure 1. These links between continuous Lie groups and algebras, the finite discrete groups of one or more quaternions, finite projective geometries (another field pioneered by Klein and contemporaries, notably Gino Fano), and balanced incomplete block designs [20,21] (in an area called design theory [22]) will be discussed in this review. It is remarkable that the fifteen generators of the qubit-qubit SU(4) symmetry connect these disparate fields. The same number of generators in re-arranged combinations describe SO(6), the group of six-dimensional rotations, as well as the closely allied non-compact groups SO(4,2) which describe the hydrogen atom in non-relativistic quantum mechanics [2,23]. In addition, there are fifteen Dirac matrices, which occur throughout relativistic field theories and particle physics [24], and fifteen points form the important finite projective geometry PG(3,2). The finite group of complex quaternions also has the same number of elements. Thus, our discussion of these disparate elements highlights the many cross-connections between the three ladders, providing additional insight into what seem to be widely different topics.

This review is, broadly, in two parts. Section 2 constitutes the first, which deals with the time-evolution operator of multiple qubits that is used in quantum information. This operator is derived on the basis of a particular Lie algebra of generators that close under commutation. The second part, contained in Section 3 and Section 4, concerns the various sub-algebras that may be involved, as well as other correspondences to the various elements of Figure 1, such as geometric algebra, discrete groups of quaternions, finite projective geometries, and combinatorial designs. Most of this is applied to multiple qubits, but easy extensions to higher-dimensional qubits are indicated in Section 5.

2. Unitary Evolution Operator

As more generally throughout quantum physics, the unitary operator, $U\left(t\right)$, of time evolution for a Hermitian Hamiltonian, $H\left(t\right)$, plays a central role. (Even more general extensions to non-Hermitian Hamiltonians and Lindblad-type master equations, for handling decoherence and dissipation, are possible. This would be through the embedding of the elements of an $n\times n$ density matrix in an $(n^2-1)$-dimensional space [25]; however, our discussion will be confined to Hermitian and unitary language.) The basic equations of motion, as well as the time development of wave functions, density matrices, and operators, are governed by this $U\left(t\right)$. The algebraic and geometric description of this unitary operator is, therefore, central to quantum physics and quantum information science. This review’s focus is on $U\left(t\right)$. This particular $U\left(t\right)$ took on greater importance for quantum information in the aftermath of a paper by Luo [26], which set the course for handling correlations such as the quantum discord of a composite system, AB, that call for all possible measurements on one of the sub-systems. The logic is that local measurements on A or B alone cannot change quantum correlations, but can provide all classical correlations. These can then be separated from the total correlations of AB, in order to leave behind what must be quantum correlations. Even though discord or other alternatives may have deficiencies as correlation measures [27], the importance of the unitary evolution operator is independent of, and more general than, any specific use of it.

To give concrete meaning to “all possible measurements”, either in a theoretical calculation or as an operational experimental procedure, Luo [26] considered, for a single qubit, the pair of Stern–Gerlach or von Neumann projections with respect to some z-axis, ${\mathsf{\Pi }}_{\pm }$. They were then subjected to a general unitary transformation,

$$A_i=U_i{\mathsf{\Pi }}_{\pm }{U}_i^{†}.$$

(1)

This provides a well-defined procedure to handle all possible measurements and resonates intuitively with the physics of a charged spin-1/2 particle. Its measurement is a Stern–Gerlach measurement with two possible outcomes: either of the antipodal points on the Bloch sphere. One then rotates that axis of orientation of the anisotropic magnet through all positions in three-dimensional space, thus exhausting all possibilities for measuring the qubit. This can, of course, be generalized to other spins, and also to qubits with a more general POVM (positive operator valued measure [28]) than a von Neumann projector of them but again using a general unitary $U\left(t\right)$ of the relevant dimension in Equation (1). This points to the requirement of such unitary evolution operators for multi-qubit systems, in order to understand correlations or to construct logic gates in quantum information systems.

For the SU(2) of a qubit, the general unitary transformation is unambiguous and well known:

$$U_i=tI+i\overrightarrow{y}·\overrightarrow{\sigma },t^2+{\overrightarrow{y}}^2=1,$$

(2)

in terms of the unit operator and the Pauli matrices $\overrightarrow{\sigma }$, with a scalar t and vector $\overrightarrow{y}$ coefficients. Three parameters then describe all the measurements on sub-system A. This basic procedure of Luo [26], initially for a very limited subset of qubit-qubit states, was later adapted [29,30] for a larger class of density matrices called X-states [9,10]. These are of the form,

$$\rho =\left(\begin{array}{cccc}{\rho }_{11}& 0& 0& {\rho }_{14}\\ 0& {\rho }_{22}& {\rho }_{23}& 0\\ 0& {\rho }_{32}& {\rho }_{33}& 0\\ {\rho }_{41}& 0& 0& {\rho }_{44}\end{array}\right).$$

(3)

They were, at first, named for their visual appearance, with non-zero entries standing only along the diagonal and anti-diagonal in a 4 × 4 matrix representation in the canonical basis. With three real diagonal elements and two complex off-diagonal ones, this is a seven-parameter set. (Local unitary transformations can reduce this to five real parameters, by removing the phase angles of the complex elements through unitary rotations [31].) While smaller than the full 15 parameters of the most general qubit-qubit density matrix, many calculations of entanglement and of other properties, as well as their evolution under unitary or dissipative processes, can be easily carried out for such states. This makes them appealing objects for study. Many specific states of interest, such as the maximally entangled Bell states [1] and ’Werner’ states [32], are a sub-class of X-states, lending further importance to their examination. The fact of fewer parameters in an X-state does not restrict the range of physical phenomena investigated; a large variety of qubit-qubit physics can be discussed using these states. At the same time, the restriction in the number of parameters simplifies calculation, which accounts for their popularity. The symmetry group and algebra of X-states will be discussed in detail in Section 3.1.

Even though SU(2) has three parameters, as does $U\left(t\right)$ in Equation (2), it turns out that only two are of interest, and can be identified with the two angles on the Bloch sphere. This reduction is clearest in the symmetry decomposition of SU(2) as the base $S^2$ and a one-dimensional “fiber” U(1), or pure phase. The latter element commutes past the projector in Equation (1) so as to cancel itself out in U and $U^{†}$, leaving only the two Bloch angles of $S^2$. This has been formalized as a simple prescription in [30], which is applicable to calculations, such as quantum discord, in a general density matrix of AB—for any dimension of B, so long as A is a qubit. This prescription also removes the restriction to X-states, as described in the previous paragraph, and can handle all qubit-qubit density matrices. The symmetry decomposition of the SU(2) $U\left(t\right)$ will be taken up in Section 2.1. It leads, suggestively, to a similar treatment of any SU(N) in Section 2.2, thereby providing a compact and simple procedure to construct $U\left(t\right)$ for any dimension. Furthermore, for X-states, the $\theta$ Bloch angle (latitude) describing $U\left(t\right)$ suffices; that is, $\varphi$ (longitude) is unnecessary. Studies [30,33] have found that, in over 99% of tens of thousands of randomly chosen density matrices, the extremum that produces quantum discord is reached at the extreme angle $\theta =\pi /2$. The initial prescription [29] seems to leave a very small worst case error [34] with regard to this conclusion.

2.1. Derivation of Evolution Operator for a Qubit

Solving the Schrödinger equation for the evolution operator, $idU\left(t\right)/dt=H\left(t\right)U\left(t\right)$, $U\left(0\right)=I$, is straightforward for a qubit. We will set $\hslash =1$. A non-zero trace of H can first be filtered out as a phase factor. Since the rest can be cast in terms of the three Pauli spin operators, $U\left(t\right)$ has three corresponding exponential factors, with each Pauli spinor multiplying a time-dependent coefficient in the exponent. Conventionally, one would use the three Cartesian Pauli spinors, the coefficients then being real Euler angles of rotation. They obey a system of coupled, first-order (in t) differential equations, familiar from Euler equations for rigid-body rotations in classical mechanics [35]. (This connection also points to differing terminologies—for many purposes, one could refer to so(3) instead of su(2) or SU(2), but we will use the unitary language in this review. Some of the mathematics literature uses so(3) instead.) However, these Euler equations are highly nonlinear, involving sines and cosines of the coefficients. Instead, and also conveniently for our later generalization to higher SU(N), we [36,37,38] use the step-up/down combinations ${\sigma }_{\pm }\equiv {\sigma }_x\pm i{\sigma }_y$ that lead to simpler equations and interpretations.

Along with ${\sigma }_z$, this alternative triplet choice of Pauli matrices spans the complete algebra, so that a full solution for $U\left(t\right)$ takes the form of a product of three exponential factors,

$$U\left(t\right)=e^{z\left(t\right){\sigma }_{+}/2}{e}^{w^{*}\left(t\right){\sigma }_{-}/2}{e}^{-i\mu \left(t\right){\sigma }_z/2}.$$

(4)

The complex quantities z, w, and $\mu$ are classical functions, vanishing at $t=0$. The solution is by construction [36]. Plugging Equation (4) into the evolution equation and re-arranging operators through the Baker–Campbell–Hausdorff identity (Equation 2.3.47 in [2]) is all that is required to acquire the defining equations for z, w, and $\mu$. We also acquire the relations between them that guarantee that the overall $U\left(t\right)$ is unitary, even if the individual factors in Equation (4) no longer are as in the Cartesian decomposition. Furthermore, those three relations reduce the three complex coefficients which are now involved, again, into three real independent parameters. With w essentially the complex conjugate of z, the three linearly independent quantities may be taken to be the real and imaginary parts of z and Re $\mu$. The last is determined by quadrature involving z, while z itself is solved using a self-contained Riccati equation [36,37,38].

The complex quantity z may then be inverse stereographically projected onto the “Bloch sphere” [2] by defining a unit three-dimensional vector $\overrightarrow{m}$[37]. The nonlinear Riccati equation for z then becomes the linear Bloch equation, $d\overrightarrow{m}/dt=-2\overrightarrow{B}\times \overrightarrow{m}$. However, z, $\overrightarrow{m}$, and the Bloch sphere account for only two of the three parameters of the full SU(2) problem, the third being the phase parameter Re $\mu$. Thus, the full (local) geometric description is a “spiked unit sphere”, as shown in Figure 2, with the spike at each point on the sphere representing a $U\left(1\right)$ phase. This is what mathematicians call the “fiber bundle” [SU(2)/U(1)] × U(1), with [SU(2)/U(1)] $\sim S^2$ the “base manifold” and the U(1) phase the one-dimensional “fiber” [39]. The evolution operator $U\left(t\right)$ in Equation (4) can be pictured schematically as in Figure 3. Its structure, with the first two factors in Equation (4) being triangular and the third being diagonal, suggests easy generalization, to be considered in Section 2.2.

This unitary integration procedure has as its its key feature, and as the only algebraic manipulation needed, the Baker–Campbell–Hausdorff identity (Equation 2.3.47 in [2]), which involves a sequence of successive commutators of the operators that occur in the problem. It is for this reason that Lie algebras and Lie groups arose and have fit naturally into quantum physics applications. It also means that unitary integration seems to have been introduced independently several times, even if not named as such. The earliest occurrence may be in [40], so that it may be referred to as the Wei–Norman method. It is related to, but different from and more convenient than, the Magnus expansion [41], and has had a revival since the mid-1980s for su(2), su(1,1), and also quantum spin-1 cases, among many different groups [42,43,44,45]. For problems involving two qubits and the algebra su(4), different applications were developed in the last twenty years, again independently, for Cartan decompositions of su(4) in quantum control [46,47] and more generally [48]. A decomposition of $U\left(t\right)$ for su(4), into factors of local unitaries of individual qubits and a 3-parameter diagonal unitary matrix, was produced independently in [47,49] and [50]. Related work on generating entanglement dynamics and the minimum number of unitaries required can be found in [51].

With 15 generators and their commutators involved (and eight for su(3) of a single spin-1), products which require so many exponentials, as in Equation (4), become unwieldy. Symmetries that restrict to a smaller number of generators of sub-algebras, especially in an NMR problem using just seven, help practical implementation [7]. In the next section, we consider a derivation of $U\left(t\right)$ that can handle this. Then, in Section 3, we consider some of the main sub-algebras of su(4) which are involved, as well as their associated physical systems.

2.2. Derivation of Evolution Operator for SU(N)

The above construction of $U\left(t\right)$ in the form of a three-term product, as in Equation (4) and Figure 3, can be carried over to any N-level or SU(N) problem. Thereby, the form and simplicity of the $N=2$ case can be extended to arbitrarily large N. The final result is very simply stated based on symmetry patterns alone. Consider the N-dimensional Hamiltonian ${\mathbf{H}}^{\left(N\right)}$ as $2\times 2$ blocks,

$${\mathbf{H}}^{\left(N\right)}=\left(\begin{array}{cc}{\mathbf{H}}^{(N-n)}& \mathbf{V}\\ {\mathbf{V}}^{†}& {\mathbf{H}}^{\left(n\right)}\end{array}\right),$$

(5)

with $n,1\le n<N$, an arbitrary choice. The diagonal blocks are square matrices, while the off-diagonal $\mathbf{V}$ is $(N-n)\times n$, and ${\mathbf{V}}^{†}$ is $n\times (N-n)$. These latter two are taken as Hermitian adjoints, and ${\mathbf{H}}^{\left(N\right)}$ is considered traceless; however, much of our construction applies more generally [25,37].

With a $2\times 2$ block view of the N-dimensional H, a solution for $U\left(t\right)$ can be written, in close analogy to Equation (4), as a product of three $2\times 2$ block matrices; the first two having one non-zero off-diagonal block while the last is block-diagonal. This structure, of two idempotent factors (the multiplication of two such matrices resulting in a similar matrix with a zero off-diagonal block) and a third that is block diagonal, was a result of our chosen step-up/down combination rather than Cartesian operators in Equation (4), and proves crucial. The rectangular matrices, $\mathbf{z}$ and ${\mathbf{w}}^{†}$, now stand in place of the complex numbers z and w, respectively, in Equation (4). This key step is illustrated in Figure 4, in direct analogy to Figure 3; now, however, the entries in the 2 × 2 structure are block matrices. First, one solves the equation satisfied by $\mathbf{z}$, now a matrix Riccati equation [52]. For unitary problems, the matrix $\mathbf{w}$ is simply related to $\mathbf{z}$, again as in the $N=2$ case [37]. Additionally from $\mathbf{z}$, effective Hamiltonians are constructed for the two diagonal blocks of the third factor in $U\left(t\right)$, for subsequent handling as smaller SU($N-n$) and SU(n) problems. We refer to [37] for details. For any N, and choice of n, the procedure can thus be iterated down to a final SU(2). One can describe this construction as following the spirit of Schwinger’s method of building higher angular momentum, j, representations of SU(2) as products of the “fundamental” $j=1/2$ [2,3]. However, instead of the different representations of the same SU(2) that are used in Schwinger’s method, we instead construct representations of different SU(N) in terms of a succession of three-factor products of block matrices, which are of the same form as the three Pauli factors in SU(2)’s Equation (4).

Typically, n will be chosen to be 1 or 2. In the former case, $\mathbf{z}$ is a vector of $(N-1)$ complex $z_i$. Furthermore, the lower diagonal block in the effective Hamiltonian is a single element, and its corresponding element in $U\left(t\right)$ is a phase. This generalizes the fiber bundle description for SU(2) to SU(N) with a base manifold SU(N)/[(SU($N-1$) × U(1)]. Iteratively, one can reduce from N to a lower value, extracting a U(1) phase at each step [37,38]. This is called the flag manifold. The construction for SU(3) is given in [53]. The case $n=2$ is also interesting and useful; here, the lower block in H is a $2\times 2$ matrix. Again, the Hamiltonians and unitary matrices at each step can be explicitly worked out [37] using Pauli algebra. We will return to this in Section 3.2 and Section 3.3, after considering sub-group symmetries that may apply in a high N case.

3. Sub-Group Symmetries and Sub-Algebras

The previous section constructed $U\left(t\right)$ for any SU(N) no matter how large N is. There is an explosive growth of N for multiple qubits, with $N=2^q$ for q qubits, and N even larger for multiple qubits of higher dimension. However, physical situations often introduce further symmetries, which limit us to a smaller number which can be handled more easily. As already noted, even for SU(4) of $q=2$ with fifteen operators and parameters in general, Hamiltonians and states may involve fewer operators and parameters, so that identifying a corresponding sub-group to which they belong can be useful. Many SU(2) and SU(2) × SU(2) are trivial examples of such sub-groups of SU(4). The latter would pertain to two completely independent spins with no coupling between them. In that case, $U\left(t\right)$ does not need to be written as a product of fifteen exponentials, but more simply as two factors of the form in Equation (4) for each qubit or SU(2). These six operators and the unit operator close under commutation, further dividing into two independent sets. The other nine need not be invoked at all. The unit operator is the only one that commutes with everything in this sub-group; the only “center” in the language of group theory.

A less trivial, but very important, example is the sub-group SU(2) × U(1) × SU(2), which involves seven operators and parameters in a Hamiltonian with this sub-group symmetry. The U(1) is a single, but non-trivial, operator, that also is a center, commuting with all six others which themselves can be arranged as two independent SU(2) or sets of three. In quantum error correction, it is referred to as the “stabilizer” [54]. In this case, again, $U\left(t\right)$ splits into two independent factors as in Equation (4), with an additional exponential in the U(1) element. Concrete examples occur in logic gates and Hamiltonians in quantum information theory [7]. Two independent spiked Bloch spheres, as in Figure 2 and the previous section, along with a U(1) fiber element linking them, provide a geometrical rendering of this kind of sub-group symmetry. The decomposition into the sub-algebra of the previous paragraph is referred to as so(3) ⊕ so(3) in Equations (45) and (46) of a general mathematical study [15], which also noted a seven-dimensional so(2) ⊕ so(3) ⊕ so(3) in its Section 5. Quantum physics applications have pointed to its importance in a variety of problems [7,37].

Other sub-groups of SU(4) include, of course, several SU(3) of sets of eight generators, as well as SO(5), the rotation or orthogonal group in five dimensions with 10 generators. Again, many instances occur in quantum optics, quantum information, atomic and molecular physics [37]. To identify all such sub-groups systematically, a table of commutators of all fifteen operators of SU(4), shown in

Table 1. Table of commutators displaying a closed algebra of fifteen operators $O_i$ of the SU(4) group for a pair of qubits. Each entry provides the commutator $[O_i,O_j]$. The seven zeroes in any row or column point to sub-groups SU(2) × U(1) × SU(2). Other sets of eight and ten that close under commutation give, similarly, SU(3) and SO(5) sub-groups, respectively. From [7,8,55].

$O_X$	$O_2$	$O_3$	$O_4$	$O_5$	$O_6$	$O_7$	$O_8$	$O_9$	$O_{10}$	$O_{11}$	$O_{12}$	$O_{13}$	$O_{14}$	$O_{15}$	$O_{16}$
$O_2$	0	0	0	$i{O}_6$	$-i{O}_5$	$i{O}_8$	$-i{O}_7$	0	0	0	0	$i{O}_{16}$	$-i{O}_{15}$	$i{O}_{14}$	$-i{O}_{13}$
$O_3$	0	0	0	0	0	0	0	$i{O}_{10}$	$-i{O}_9$	$i{O}_{12}$	$-i{O}_{11}$	$i{O}_{15}$	$-i{O}_{16}$	$-i{O}_{13}$	$i{O}_{14}$
$O_4$	0	0	0	$i{O}_8$	$-i{O}_7$	$\frac{i}{4}{O}_6$	$-\frac{i}{4}{O}_5$	$i{O}_{12}$	$-i{O}_{11}$	$\frac{i}{4}{O}_{10}$	$-\frac{i}{4}{O}_9$	0	0	0	0
$O_5$	$-i{O}_6$	0	$-i{O}_8$	0	$i{O}_2$	0	$i{O}_4$	0	0	$-i{O}_{16}$	$-i{O}_{14}$	0	$i{O}_{12}$	0	$i{O}_{11}$
$O_6$	$i{O}_5$	0	$i{O}_7$	$-i{O}_2$	0	$-i{O}_4$	0	0	0	$i{O}_{13}$	$i{O}_{15}$	$-i{O}_{11}$	0	$-i{O}_{12}$	0
$O_7$	$-i{O}_8$	0	$-\frac{i}{4}{O}_6$	0	$i{O}_4$	0	$\frac{i}{4}{O}_2$	$i{O}_{15}$	$-i{O}_{13}$	0	0	$\frac{i}{4}{O}_{10}$	0	$-\frac{i}{4}{O}_9$	0
$O_8$	$i{O}_7$	0	$\frac{i}{4}{O}_5$	$-i{O}_4$	0	$-\frac{i}{4}{O}_2$	0	$i{O}_{14}$	$-i{O}_{16}$	0	0	0	$-\frac{i}{4}{O}_9$	0	$\frac{i}{4}{O}_{10}$
$O_9$	0	$-i{O}_{10}$	$-i{O}_{12}$	0	0	$-i{O}_{15}$	$-i{O}_{14}$	0	$i{O}_3$	0	$i{O}_4$	0	$i{O}_8$	$i{O}_7$	0
$O_{10}$	0	$i{O}_9$	$i{O}_{11}$	0	0	$i{O}_{13}$	$i{O}_{16}$	$-i{O}_3$	0	$-i{O}_4$	0	$-i{O}_7$	0	0	$-i{O}_8$
$O_{11}$	0	$-i{O}_{12}$	$-\frac{i}{4}{O}_{10}$	$i{O}_{16}$	$-i{O}_{13}$	0	0	0	$i{O}_4$	0	$\frac{i}{4}{O}_3$	$\frac{i}{4}{O}_6$	0	0	$-\frac{i}{4}{O}_5$
$O_{12}$	0	$i{O}_{11}$	$\frac{i}{4}{O}_9$	$i{O}_{14}$	$-i{O}_{15}$	0	0	$-i{O}_4$	0	$-\frac{i}{4}{O}_3$	0	0	$-\frac{i}{4}{O}_5$	$\frac{i}{4}{O}_6$	0
$O_{13}$	$-i{O}_{16}$	$-i{O}_{15}$	0	0	$i{O}_{11}$	$-\frac{i}{4}{O}_{10}$	0	0	$i{O}_7$	$-\frac{i}{4}{O}_6$	0	0	0	$\frac{i}{4}{O}_3$	$\frac{i}{4}{O}_2$
$O_{14}$	$i{O}_{15}$	$i{O}_{16}$	0	$-i{O}_{12}$	0	0	$\frac{i}{4}{O}_9$	$-i{O}_8$	0	0	$\frac{i}{4}{O}_5$	0	0	$-\frac{i}{4}{O}_2$	$-\frac{i}{4}{O}_3$
$O_{15}$	$-i{O}_{14}$	$i{O}_{13}$	0	0	$i{O}_{12}$	$\frac{i}{4}{O}_9$	0	$-i{O}_7$	0	0	$-\frac{i}{4}{O}_6$	$-\frac{i}{4}{O}_3$	$\frac{i}{4}{O}_2$	0	0
$O_{16}$	$i{O}_{13}$	$-i{O}_{14}$	0	$-i{O}_{11}$	0	0	$-\frac{i}{4}{O}_{10}$	0	$i{O}_8$	$\frac{i}{4}{O}_5$	0	$-\frac{i}{4}{O}_2$	$\frac{i}{4}{O}_3$	0	0

, proves useful [8,37,55]. It follows immediately from inspection, for instance, that every row or column of this table has seven zeroes. This means that every one of the fifteen can play the role of the non-trivial center in an SU(2) × U(1) × SU(2) sub-group. (Other sets that close under commutation, of eight or ten, can also be seen in Table 1 to represent SU(3) and SO(5) symmetry, respectively; this is to be discussed in Section 3.2.)

Different notations have proved useful; a sequential set $O_i,i=1,2,\dots 16$[7,37,55] is applicable to any four-level system, or the direct products of two sets of Pauli operators when there is a two-qubit origin can be written as $(I,I\otimes {\sigma }_i,{\tau }_i\otimes I,{\tau }_i\otimes {\sigma }_j)$. Two different symbols, $\sigma$ and $\tau$, prove convenient for two independent spin-1/2 qubits; however, for easier generalization to more qubits, an upper index ${\overrightarrow{\sigma }}^{\left(i\right)}$ serves better [55]. When dealing with three components, the natural short-hand notation of $(X,Y,Z)$ proves convenient. Thus, $XZ$ denotes ${\tau }_x{\sigma }_z$, ${\sigma }_x^{\left(2\right)}{\sigma }_z^{\left(1\right)}$ or $O_{11}$, while $IX$ is ${\sigma }_x$ and $ZI$ is ${\tau }_z$, or $O_5$ and $O_3$, respectively.

Table 2. Dictionary for the fifteen operators $O_i$ of the two-qubit system [7,8,55] in alternative languages: as direct products of individual Pauli matrices of the two spins in the second row; the same in shorthand in the third row; in allied binary notation with square brackets in the fourth row; as Dirac gamma matrices in the sixth row; in other combinations of Dirac matrices in the seventh [13,24]; next as the bivectors $G_{ij}$ of [15]; and in complex quaternions $(i,j,k)$ with K an independent square root of $-1$ in the last row, along with an allied binary in round brackets in the fifth row.

$O_3$

$O_{10}$

$O_9$

$O_2$

$O_4$

$O_{12}$

$O_{11}$

$O_6$

$O_8$

$O_{14}$

$O_{16}$

$O_5$

$O_7$

$O_{15}$

$O_{13}$

$\frac{1}{2}{\tau }_z$

$\frac{1}{2}{\tau }_y$

$\frac{1}{2}{\tau }_x$

$\frac{1}{2}{\sigma }_z$

$\frac{1}{4}{\tau }_z{\sigma }_z$

$\frac{1}{4}{\tau }_y{\sigma }_z$

$\frac{1}{4}{\tau }_x{\sigma }_z$

$\frac{1}{2}{\sigma }_y$

$\frac{1}{4}{\tau }_z{\sigma }_y$

$\frac{1}{4}{\tau }_y{\sigma }_y$

$\frac{1}{4}{\tau }_x{\sigma }_y$

$\frac{1}{2}{\sigma }_x$

$\frac{1}{4}{\tau }_z{\sigma }_x$

$\frac{1}{4}{\tau }_y{\sigma }_x$

$\frac{1}{4}{\tau }_x{\sigma }_x$

ZI

YI

XI

IZ

ZZ

YZ

XZ

IY

ZY

-YY

XY

IX

ZX

YX

XX

[0100]

[1000]

[1100]

[0001]

[0101]

[1001]

[1101]

[0010]

[0110]

[1010]

[1110]

[0011]

[0111]

[1011]

[1111]

(0101)

(1110)

(1011)

(0010)

(0111)

(1100)

(1001)

(1010)

(1111)

(0100)

(0001)

(1000)

(1101)

(0110)

(0011)

$-\frac{i}{2}{\gamma }_1{\gamma }_2$

$-\frac{i}{2}{\gamma }_3{\gamma }_1$

$-\frac{i}{2}{\gamma }_2{\gamma }_3$

$\frac{1}{2}{\gamma }_4$

$\frac{i}{4}{\gamma }_5{\gamma }_3$

$\frac{i}{4}{\gamma }_5{\gamma }_2$

$\frac{i}{4}{\gamma }_5{\gamma }_1$

$-\frac{i}{2}{\gamma }_5{\gamma }_4$

$\frac{1}{4}{\gamma }_3$

$\frac{1}{4}{\gamma }_2$

$\frac{1}{4}{\gamma }_1$

$-\frac{1}{2}{\gamma }_5$

$-\frac{i}{4}{\gamma }_3{\gamma }_4$

$-\frac{i}{4}{\gamma }_2{\gamma }_4$

$-\frac{i}{4}{\gamma }_1{\gamma }_4$

${\mathsf{\Sigma }}_3$

${\mathsf{\Sigma }}_2$

${\mathsf{\Sigma }}_1$

${\gamma }_4$

$A_3$

$A_2$

$A_1$

${\alpha }_5$

${\gamma }_3$

${\gamma }_2$

${\gamma }_1$

${\gamma }_5$

${\alpha }_3$

${\alpha }_2$

${\alpha }_1$

$G_{03}$

$G_{02}$

$G_{01}$

$G_{30}$

$G_{33}$

$G_{32}$

$G_{31}$

$G_{20}$

$G_{23}$

$G_{22}$

$G_{21}$

$G_{10}$

$G_{13}$

$G_{12}$

$G_{11}$

$-i$

$-Kj$

$-Kk$

i

$\pm I$

$Kk$

$Kj$

$Ki$

$-K$

k

j

K

$-Ki$

$-j$

$-k$

gives the complete list, along with a correspondence to the Dirac gamma matrices [24] used in relativistic quantum field theories. Yet another notation is a convenient 4-binary labelling that we will take up in Section 3.5. In addition, a mapping onto complex quaternions and their finite groups, along with a different binary labelling, will be discussed in Section 3.6. Yet another labelling, in terms of bivectors $G_{ij}$ to be discussed in Section 4, is also shown. The Dirac gamma matrices constitute four four-vectors—${\gamma }_{\mu }$, $\mu =1-4$—denoted V and obeying anti-commutation relations. Six anti-symmetric products of two of them are denoted: T(ensor) as ${\sigma }_{\mu \nu }=-\frac{i}{2}{\gamma }_{\mu }{\gamma }_{\nu }$. One P(seudo-scalar) ${\gamma }_5$ is the product of all four gamma matrices, and four pseudo-vectors or A(xial vectors) are given by $i{\gamma }_5{\gamma }_{\mu }$ [24].

3.1. The SU(2) × U(1) × SU(2) “Fano Sub-Group” Symmetry and X-states

As mentioned above, an interesting sub-group, or sub-algebra, of the 15-generator SU(4) is provided by a subset of seven of them which plays a role in many physical systems. To identify them, Table 1 shows that each of the 15 operators $O_i$ can serve as a non-trivial center U(1), since it commutes with six others. Take as an example the operator $ZZ$, or $O_4$, which we will use as a running example in later sections—we emphasize, however, that any of fifteen choices can serve. Its six companions in such a sub-group are $(IZ,ZI,XX,YY,XY,YX)$; that is, $(O_2,O_3,O_{13-16})$. For charged spin-1/2 particles in an external magnetic field along the z-axis, the Hamiltonian, with scalar couplings $(XX,YY,ZZ)$ and what are termed cross-coherences $(XY,YX)$, is an example of a physical situation with this sub-symmetry [7]. It is realized in the CNOT quantum logic gate constructed out of two Josephson junctions [56]. Another example is to take $ZI$, or $O_3$, as a center. Now, the other six are $(IX,IY,IZ,ZX,ZY,ZZ)$ or $(O_5,O_6,O_2,O_7,O_8,O_4)$; or, more compactly, $(\overrightarrow{\sigma },{\tau }_z\overrightarrow{\sigma })$. That is, all three Pauli matrices of the first spin, along with their multiplication by (any) one of the matrices of the second, such as ${\tau }_z$, clearly provides six matrices that commute with this choice of center $ZI$. These two examples differ, however, in their quantum entanglement properties.

While they do not, as they stand, split into two sets of three that mutually commute with each other, the linear combinations $\frac{1}{2}(I\pm Z)\otimes (X,Y,Z)$—that is, the triplet $\frac{1}{2}(IX+ZX,IY+ZY,IZ+ZZ)$ and similar triplet with minus signs—indeed provide two sets of triplets that obey SU(2) commutation relations within themselves, while each member commutes with all three of the other set. The operators $\frac{1}{2}(II\pm ZI)$ behave like projection operators. The presence of a non-trivial center, along with the trivial unit center, leads immediately to such projection operators and a division of the space into two separate ones. These are termed, generically, P and Q; with $P+Q=1,P^2=P,Q^2=Q,PQ=QP=0$. For the purposes of unitary integration, since only commutation relations enter, the evolution $U\left(t\right)$ does indeed simplify into two independent factors, as in Equation (4), which may be termed pseudo-spin SU(2)s [7]. The prefix “pseudo-” is invoked because each member of the triplet no longer squares to unity, as with Pauli spinors, but into the overall commuting objects $\frac{1}{2}(II\pm ZI)$, involving both centers. Note that, in more general contexts beyond our currently considered multiple qubits, the presence of a non-trivial center that squares to unity leads to a similar decomposition into orthogonal P and Q spaces. While all fifteen $O_i$ lead to such a separation into two complementary projected spaces within a set of seven generators, only the nine involving both spins can accommodate quantum entanglement, as will be discussed further below. Explicitly, when $ZZ$ is the U(1) center, the two mutually commuting SU(2) triplets are $\frac{1}{2}(XX-YY,XY+YX,IZ+ZI)$ and $\frac{1}{2}(XX+YY,XY-YX,IZ-ZI)$. They square to $\frac{1}{2}(II\pm ZZ)$, and again behave similarly to pseudo-spins, but cannot be written in the same factorized form of ⊗ of the two spins (as at the beginning of this paragraph) for the center $ZI$ (or for any choice of center with only one of the spins).

The above discussion for operators and generators of a sub-group symmetry of SU(4) applies also to the states of a two-qubit system. In a matrix representation, they are again equivalent to 4 × 4 Hermitian matrices. The general $4\times 4$ density matrix of pure or mixed states is characterized by 15 parameters, three real ones along the diagonal and six complex off-diagonal elements in a Hermitian matrix. It was natural in the original heuristic definition [9] to denote those with only two non-zero off-diagonal entries, namely those on the anti-diagonal, as X-states, from visual appearance, as in Equation (3). There are now seven parameters in all, and this indeed provides an instance of the previous paragraph’s SU(2) × U(1) × SU(2) sub-group symmetry [7]. Depending on the center U(1), the density matrix may or may not look like the letter X, but this symmetry perspective shows their commonality [10]. In addition, under operations by members of that same set of seven operators, the X character of the physical system is preserved. This proves very convenient in many physical applications, by reducing the number of parameters and operators that we are required to handle. This accounts for the popularity of discussing the X-states of a two-qubit system. It also points toward a natural extension; to higher multiples of qubits and of higher-dimensional qudits. We will take this up in Section 3.4. We note that both the Lie-algebraic aspect—that the seven operators close under commutation—and their Clifford-algebraic structure—that they close under multiplication—are important [10]. A mathematical description of the occurrence of such sets, due to Clifford groups, is in [57,58].

Analytical handling is also simplified, reducing to merely evaluating traces. This is because all the $O_i$ are traceless and square to unity. With any such subset of seven $\left\{X_i\right\}$ out of the $O_i$, the density matrix that remains invariant under their operations can be rendered as a linear superposition of them,

$$\rho =(I+\sum _i{g}_i{X}_i)/4,$$

(6)

in analogy to that for a single spin, $(I+{\sum }_i{g}_i{\sigma }_i)/2$. The seven real coefficients $g_i$ in the sum in Equation (6) parametrize X-states, and are given by Tr[$\rho X_i$]. Eigenvalues, and entanglement or other correlation properties, can be expressed compactly in terms of these coefficients [10]. Furthermore, the triplet structure of the Lie–Clifford algebra is most conveniently captured geometrically, in Figure 5 [10,55,59,60].

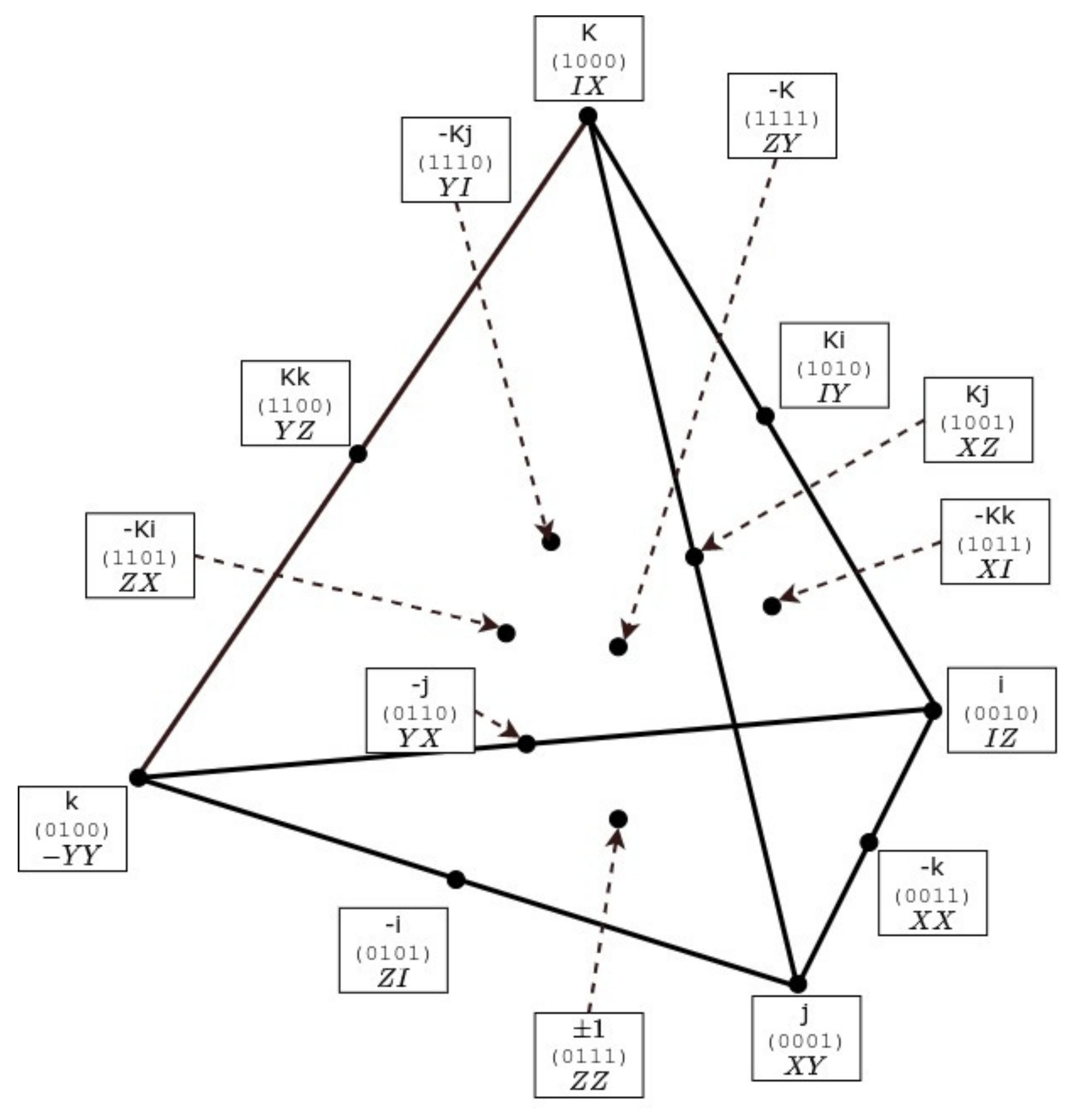
This figure, a beautifully symmetric pattern in its own right, occurs in projective geometry as the “Fano Plane” [22], where it is described as the finite projective geometry PG(2,2). Arranging the seven operators at the vertices, the mid-points of the sides, and in the center of an equilateral triangle, the seven lines shown (including the inscribed circle) each pass through three points, providing the multiplication rule for those $\left\{X_i\right\}$. The center U(1) element occupies the center of the triangle. On the three un-arrowed median lines, all three operators mutually commute, so that the product of two gives the third, regardless of order. On the four arrowed lines, the operators mutually anticommute, so that the product of two gives $(\pm i)$ times the third, with plus (minus) signs along (against) the line of the arrow [10,55]. They may be termed “cyclic”, to contrast with “commuting” (also called isotropic in [61] and orthogonal in [62]) for the other set of three medians. The central element commutes, of course, with all six of the others. Each of those six has one ’conjugate’ element with which it commutes, and four with which it anticommutes. All of this can be read off by merely glancing at Figure 5, which provides simple rules for their manipulation when calculating entanglement and discord [10]. Indeed, this figure may be regarded as a direct extension of the “$(i,j,k)$ cycle”, familiar from the multiplication or commutation of the Pauli operators for a single qubit. (Additionally, in vector product and quaternion multiplication rules.) It seems natural to call this Figure 5 the “Fano triangle”, after its Italian geometer originator Gino Fano, and the sub-group symmetry of two qubits as the “Fano sub-group”, in addition to its designation as the Fano Plane of finite projective geometry [22].

Besides the labels of the $X_i$ that are shown, Figure 5 also displays a binary and a quaternionic labelling to be discussed in subsequent sub-sections. For the purpose of this later discussion of quaternionic groups, note the placement of the $ijk$ cyclic triplet on four lines, with one minus sign on the three edges and three minus signs for the circle; the cyclicity arrow is used in opposite senses between them. The extension to octonions, that have seven independent square roots of $-1$ and all seven lines arrowed, will be taken up at the end of Section 3. In addition, the finite projective geometry PG( 2, 2), of seven points and seven lines, with a complete duality between these points and lines, differs interestingly from the finite Euclidean geometry EG(2, 2) of four points and six lines—this is obtained by dropping the midpoints in the diagram and terminating the median lines at the center. In finite geometries, only the points matter, and not the continuous lines connecting them. Furthermore, while two points define a line in Euclidean geometry, three do so in projective geometries. Another perspective is that the midpoints in Figure 5 are points “at infinity”, just as the circle is a line at infinity in Euclidean terms, but projective geometry makes no distinction between points at infinity and “regular” points at finite location.

In Dirac language, a sub-set of seven operators in a Fano sub-group —such as, for example, the one at the beginning of this section with $ZZ=O_4$ as the center—are one A, three V, and three T of three indices different to the ones chosen in A. Other possibilities are one V plus three each of T and A, or P plus the six T. Now, classify the Dirac matrices into five groups: three ${\gamma }_i$, three $A_i=i{\gamma }_5{\gamma }_i$, three ${\alpha }_i=-i{\gamma }_i{\gamma }_4$, three ${\mathsf{\Sigma }}_i=-i{\gamma }_j{\gamma }_k$ (cyclic), and the three singletons $A_4={\gamma }_4$, ${\gamma }_5$, ${\alpha }_5=-i{\gamma }_5{\gamma }_4$. In terms of these five classes, the 15 Fano sub-group sets are $({\gamma }_i;{\mathsf{\Sigma }}_i,{\alpha }_j,{\alpha }_k,A_j,A_k,{\alpha }_4),(A_i;{\mathsf{\Sigma }}_i,{\gamma }_j,{\gamma }_k,{\alpha }_j,{\alpha }_k,{\gamma }_4),({\alpha }_i;{\mathsf{\Sigma }}_i,{\gamma }_5,{\gamma }_j,{\gamma }_k,A_j,A_k)$, $({\mathsf{\Sigma }}_i;{\gamma }_4,{\gamma }_5,{\gamma }_i,{\alpha }_i,A_i,A_4),({\gamma }_4;A_{1-3},{\mathsf{\Sigma }}_{1-3}),({\gamma }_5;{\alpha }_{1-3},{\mathsf{\Sigma }}_{1-3}),({\alpha }_5;{\gamma }_{1-3},{\mathsf{\Sigma }}_{1-3})$. In each set of seven, the first entry, separated by a semi-colon, is the commuting U(1) element. A glance at the sets shows the involvement of the five classes in natural symmetric patterns. Interestingly, the division of 15 Dirac gamma matrices into five classes, four triplets or vector quantities and three scalar ones, parallels a geometric discussion where twelve are numbered numerically and three with alphabets a, b, and c [62], or an analogous division among the generators of the group symmetry of the hydrogen atom [23]. These connections between widely disparate problems may deserve further exploration.

While each $O_i$ acting as a center produces 15 different X-states, they differ in terms of their quantum entanglement which rests on the cross-correlation between the 1–2 and 3–4 sub-spaces of each spin of the two-qubit system in the canonical basis. When the $O_i$ is a single spin operator in Table 1, it does not mix these two spaces, and the projection operators provided by such a center do not describe entanglement. As an example, neither the $O_2=IZ$ nor the $O_3=ZI$ diagonal operators, with (1, 1, −1, −1) and (1, −1, 1, −1) entries along the diagonal, respectively, has entanglement, whereas for $O_4=ZZ$ with (1, −1, −1, 1), X-states may display entanglement for certain values of the parameters in the density matrix. The first of the three diagonal operators acts as a unit operator of opposite sign in the 1–2 and 3–4 spaces of the two qubits; the second, similarly, within 1–3 and 2–4, which are the spaces of same spin orientation—up or down. It is the third, with center $ZZ$ and grouping 1–4 and 2–3, that pairs a qubit with another of the opposite spin. This simultaneous involvement of both particle and spin seems necessary for quantum entanglement. There is a striking correspondence to Dirac theory, where the lower 3 and 4 components of negative-energy electron states are reinterpreted as positive-energy positron states, with a similar spin-flip involved; the 4 interpreted as up spin and the 3 as down spin of the positron (Section 3.10 of [24]). Thus, charge conjugation in that context is the analog of the entanglement of two qubits.

Such a sub-division of the 15 into 6 + 9, with single and double spin centers—the former always separable while the latter may admit entanglement—has also been discussed in detail from a finite geometric perspective [58]. Fifteen different Fano planes are listed in their Appendix A. A particular type of geometric hyperplane, called a perp-set, is identified as a symplectic polar space of rank 2 and order 2, called W(3, 2). Depending on a unique quadric $Q_0$ of this space, that involves only non-trivial Pauli matrices, and whether the perp-sets intersect that quadric tangentially or transversally, one can distinguish the groups of 9 and 6, respectively. An X-state set, such as $(ZZ,IZ,ZI,XX,YY,XY,YX)$ from the beginning of this section, is described in that language as one vector, $ZZ$, that is orthogonal to the other six [61] (in place of commuting in Lie-algebraic language). There will be further discussion in Section 4, but note that the simpler perspective is provided by spin/qubit language in terms of the nature of the center, whether it is a single or double spin operator. In terms of Dirac matrices, it is the nine $({\gamma }_i,A_i,{\alpha }_i)$ as centers that exhibit entanglement, not the other six of the ${\mathsf{\Sigma }}_i$ and the singletons enumerated above.

3.2. The SO(5) “Desargues Sub-Group” Symmetry

Identifying sub-group symmetries other than the Fano sub-group of the previous section proceeds, again, through the commutator Table 1 and by picking subsets that close under commutation as triplets. As mentioned, such a closed sub-algebra is all that is required for efficient construction of the evolution operator $U\left(t\right)$. Thus, $(O_2,O_3,O_{13-16},O_5,O_6,O_{11},O_{12})$ is such a set. Atomic and molecular four-level systems often have Hamiltonians that involve only ten parameters, because of the dipole selection rules for transitions between the four states. As a result, two parameters characterize energy positions along the diagonal, as in the case of two identical qubits when they share the same energy separation, and four complex off-diagonal dipole couplings display such a sub-group symmetry. Together then, ten real parameters define such a system [37]. It is the symmetry SO(5) of five-dimensional rotations. (Actually, it is the double covering group Spin(5), just as SU(2) is such a cover of SO(3); however, the distinction is unimportant for most of our discussion.)

As in the previous SU(2) × U(1) × SU(2) Fano sub-group, there are many such SO(5) that can be identified in Table 1. Indeed, the above set of ten operators, when compared with a similar set in Section 3.1, has the first six common, while the previous center of that Fano sub-group has been removed and replaced with the last four. This points to a systematic way of picking out the SO(5) examples, just as before for SU(2) × U(1) × SU(2). Again, for every $O_i$ in Table 1, pick the six other zeroes in that row or column and supplement by four others as required to close the sub-algebra. In terms of Dirac matrices, the above mentioned set of ten are four of the $\gamma$, with indices 1, 2, 4, and 5, and their pairwise combinations. That is, three each of V, A, and T plus P. There is no involvement of the ${\gamma }_3$. On the other hand, an alternative set of ten $(O_2,O_3,O_{13-16},O_7,O_8,O_9,O_{10})$, with the same initial six, but a different set of four (to replace the $O_4$ element) is V+T with no involvement of ${\gamma }_5$ or any pseudoscalar aspect. Yet another example is A+T, in the language of Dirac matrices.

The pleasing geometric figure of an equilateral triangle with an inscribed circle, as well as seven line triplets of seven operators (Figure 5), provided a rendering of the Fano sub-group in Section 3.1. Similarly, the well-known Desargues diagram of projective geometry [63,64], placing ten points on ten lines, produces a rendering of the SO(5) sub-group which may, therefore, be called the “Desargues sub-group”. Various renderings are in [55,59], as well as in [65], whose Figure 5 refers to it as the “Petersen” graph, dual to a five-point “ovoid”. These objects are to be discussed further in Section 4. Yet another geometric alternative, that follows the previous paragraph’s prescription of dropping the center in the set of seven and adding four others, is to remove the center and add a new vertex off the plane of the triangle, along with edges to the other three already-extant vertices and their corresponding three mid-points. This produces the next order simplex after the 2-simplex triangle, namely the 3-simplex tetrahedron, which represents the SO(5) Desargues sub-group. The ten lines are the six edges and four face circles of a tetrahedron, which will be shown and discussed in Section 3.3.

We turn now to the evolution $U\left(t\right)$, as per Equation (4); for such an SO(5), the Hamiltonian with $N=4$ is most naturally chosen as $n=N-n=2$, so that all handling is of 2 × 2 block matrices. For the ten-parameter H, a convenient representation [37] is $H\left(t\right)=F_{21}{\sigma }_z^{\left(2\right)}-F_{31}{\sigma }_y^{\left(2\right)}+F_{32}{\sigma }_x^{\left(2\right)}-F_{4i}{\sigma }_z^{\left(1\right)}{\sigma }_i^{\left(2\right)}+F_{5i}{\sigma }_x^{\left(1\right)}{\sigma }_i^{\left(2\right)}-F_{54}{\sigma }_y^{\left(1\right)}$, where the ten arbitrarily time-dependent coefficients $F_{\mu \nu }\left(t\right)$ form a $5\times 5$ antisymmetric real matrix, keeping with the aspect of five-dimensional rotations. (We will use $\mu ,\nu =1-5$ and $i,j,k=1-3$ with summation over repeated indices.) As noted, several quantum optics and multiphoton problems of four levels, driven by time-dependent electric fields, have such a Hamiltonian. It has also been considered extensively in coherent population transfer for many molecular and solid state systems [66]. Casting this Hamiltonian in the form of Equation (5), we have

$${\mathbf{H}}^{(1,2)}=(\mp F_{4k}-\frac{1}{2}{ϵ}_{ijk}{F}_{ij}){\sigma }_k,\mathbf{V}=i{F}_{54}{\mathbf{I}}^{\left(2\right)}+F_{5i}{\sigma }_i.$$

(7)

The 2 × 2 block matrix $\mathbf{z}$ in Figure 4 obeys a matrix Riccati equation, and the four entries ($\mu =1-4$) can be chosen as real: $z_{\mu }=z_4,z_i$; $\mathbf{z}=z_4{\mathbf{I}}^{\left(2\right)}-i{z}_i{\sigma }_i$. The equation for $z_{\mu }$ takes the form [37]

$$d{z}_{\mu }/dt=F_{5\mu }(1-z_{\nu }^2)+2F_{\mu \nu }{z}_{\nu }+2F_{5\nu }{z}_{\nu }{z}_{\mu }.$$

(8)

(As an alternative, $\mathbf{V}$ and $\mathbf{z}$ can also be rendered in terms of quaternions $(1,-i{\sigma }_i)$). We can now construct a five-dimensional unit vector $\overrightarrow{m}$ out of the four real z,

$$m_{\mu }=\frac{-2z_{\mu }}{(1+z_{\nu }^2)},m_5=\frac{(1-z_{\nu }^2)}{(1+z_{\nu }^2)},\mu ,\nu =1-4.$$

(9)

The nonlinear Equation (8) in z, takes on a simple, linear Bloch-like form,

$$d{m}_{\mu }/dt=2F_{\mu \nu }{m}_{\nu },\mu ,\nu =1-5,$$

(10)

which is the obvious analog of the Bloch equation of a single spin involving the cross product; that is, its higher-dimensional antisymmetric counterpart for rotations in five dimensions.

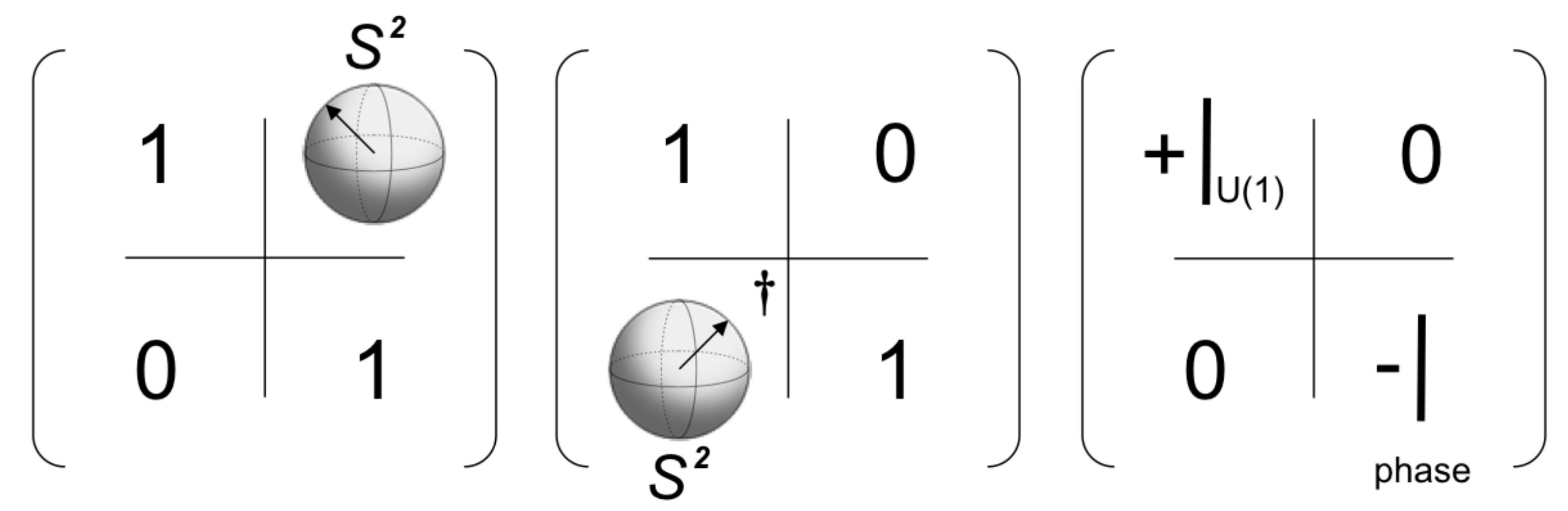
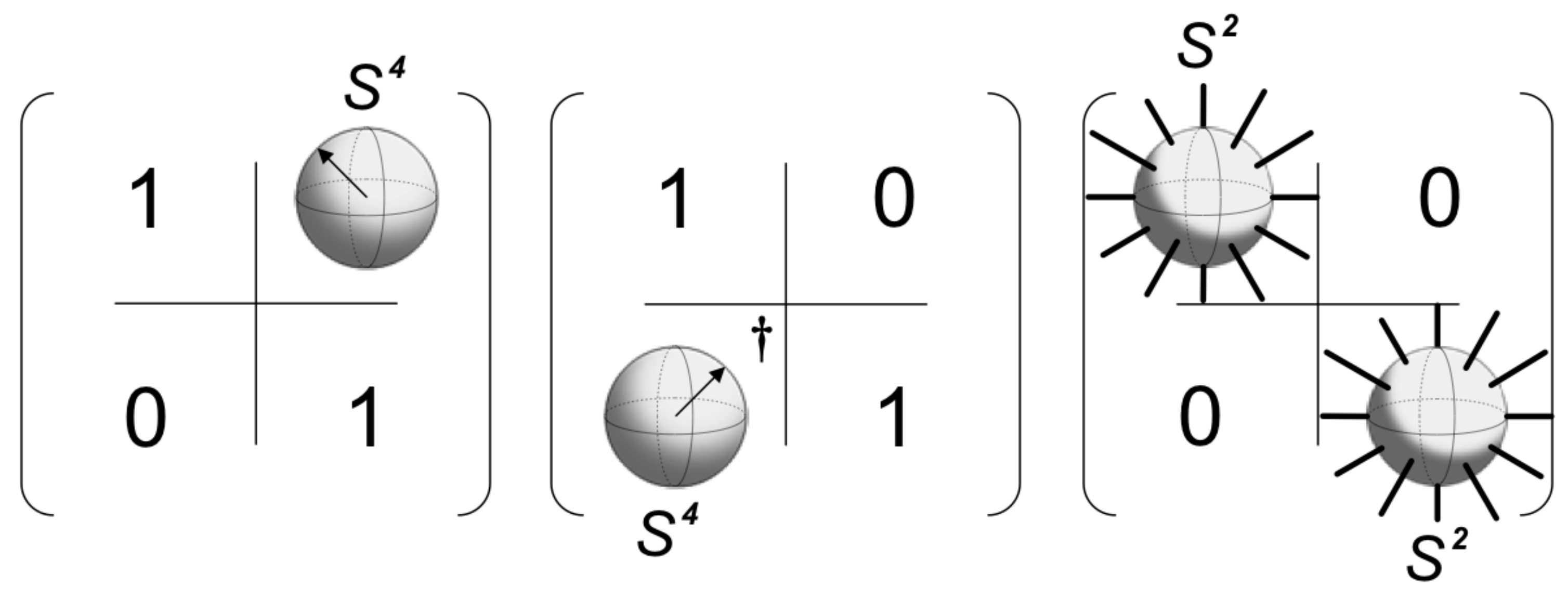
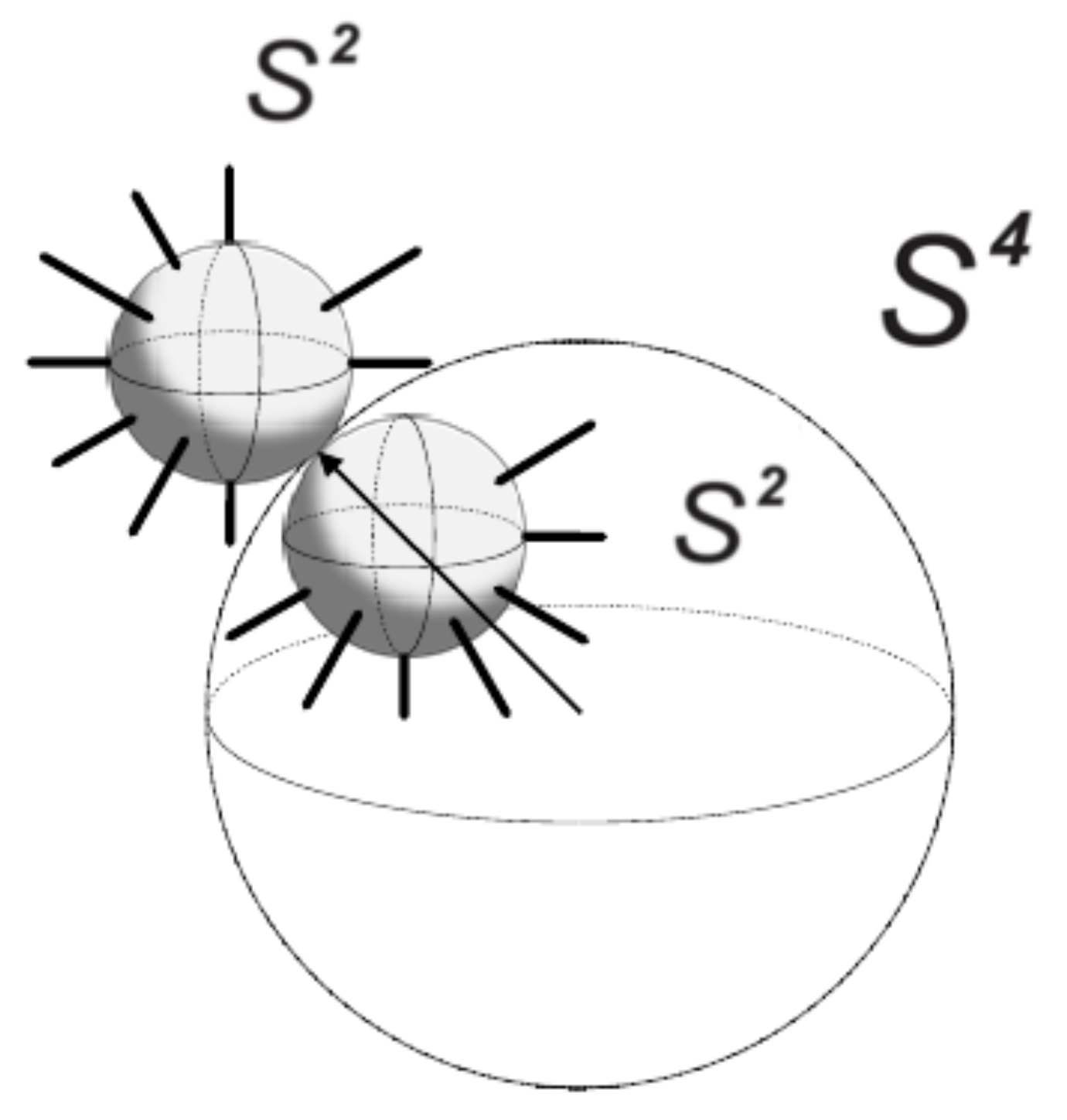
Solving this provides the first two factors in Figure 4, as well as the effective Hamiltonian for the two diagonal blocks of the third factor, which may in turn be analyzed as the spiked Bloch sphere of a single SU(2) [37]. As in the single-spin case, one can perform an inverse stereographic projection, now from the four-dimensional plane $z\in R^4$ to the four-sphere $S^4$. It provides a higher-dimensional polarization vector for describing two spin problems such as these. Hamiltonians possessing Spin(5) symmetry are, therefore, described by the geometrical picture of one $S^4$ and two $S^2$ spheres, along with two phases, as shown in Figure 6, and the unitary evolution operator depicted as in Figure 4. The former base manifold is similar, albeit of higher dimension than that of a single qubit, while the fiber is now a six-dimensional object and not a single phase. This can be pictured as two spiked Bloch spheres sitting on each point of the base manifold. Although a much larger, ten-dimensional, object than in the single-spin case, it is nevertheless an elegant and accessible generalization of Figure 2 [37].

3.3. SU(3) Sub-Groups and the Complete SU(4) Hamiltonian Involving all Fifteen Operators

Other sub-group symmetries of SU(4) include SU(3) with eight parameters; these can be thought of as two independent energy parameters along the Hamiltonian’s diagonal and three complex off-diagonal couplings. A general three-level system, embedded into four with the fourth level completely uncoupled, constitutes a trivial example of such an su(3) sub-algebra. However, less trivial examples can also occur. The $\mathbf{z}$ now contains two non-zero complex z for a total of four parameters. The description [53] of this four-dimensional manifold, as well as the remaining SU(2) and a U(1) phase, parallel the discussion of the general SU(4) that we now take up. Their manifolds are, however, more complex than spheres and one-dimensional fibers.

Moving beyond sub-groups to the full SU(4), consider an arbitrary $4\times 4$ Hamiltonian with its entire complement of 15 operators/matrices. This H is obtained by adding five additional terms to the previous Spin(5) Hamiltonian in Section 3.2: $F_{65}{\sigma }_z^{\left(1\right)}+F_{64}{\sigma }_x^{\left(1\right)}+F_{6i}{\sigma }_y^{\left(1\right)}{\sigma }_i^{\left(2\right)}$. This corresponds to the energy levels being arbitrarily positioned, as they would be in a general four-level (not necessarily two-qubit) system, and the two other couplings restored. Correspondingly, Equation (7) acquires an additional term, $\pm F_{65}{\mathbf{I}}^{\left(2\right)}$, in the diagonal ${\mathbf{H}}^{(1,2)}$. Meanwhile, in $\mathbf{V}$, the $F_{5\mu }$ are replaced by $F_{5\mu }-i{F}_{6\mu }$. Thus, the full SU(4) amounts to a simple modification to the previously considered Spin(5), executed by adding a term, which is proportional to the unit operator, to the diagonal blocks and making the four $F_{5\mu }$ complex; $F_{6\mu }$ is absorbed as their imaginary parts [37]. A full 6 × 6 antisymmetric collection of generators (see Appendix B of [37]) may then be viewed as the symmetry SO(6) to be discussed further below.

Combined with the tetrahedron introduced above for the ten-parameter SO(5), the full fifteen-parameter SU(4) completes that figure by adding the four face centers and the body center. In turn, there are now 35 triplet lines that have Lie–Clifford algebra. Besides the previous 6 edges and 4 face circles, there now are 12 medians, 4 altitudes, 3 lines that link the body center to two midpoints, and 6 that link two face centers to a midpoint. The full tetrahedron is shown in Figure 7 [55]. A similar description is provided in [67]. It is difficult to display all of the 35 lines, but Figure 8 of [62] makes a good attempt. Each of the four faces of the tetrahedron is now a Fano subgroup. A less immediately visual one is formed by the six midpoints and body centre of the tetrahedron; the seven lines now being the facial circles and the three lines connecting opposite midpoints to the body centre. The various Desargues sub-groups of 10 points and 10 triplet lines (6 edges and 4 face circles, as noted) with their labelling, and the ovoid consisting of five complementary points, are shown in [67].

In constructing $U\left(t\right)$, now for the full SU(4), the Riccati Equation (8), now for complex z, becomes

$$\begin{array}{ccc}\hfill d{z}_{\mu }/dt& =& F_{5\mu }(1-z_{\nu }^2)-i{F}_{6\mu }(1+z_{\nu }^2)+2F_{\mu \nu }{z}_{\nu }\hfill \\ \hfill & +& 2(F_{5\nu }+i{F}_{6\nu })z_{\nu }{z}_{\mu }-2i{F}_{65}{z}_{\mu },\mu ,\nu =1-4.\hfill \end{array}$$

(11)

Just as the structure of Equation (8) suggests that $z_{\mu }$ and $(1-z_{\nu }^2)$, with suitable normalization, define a five-dimensional unit vector $\overrightarrow{m}$ in Equation (9), we now have the same for a set of six complex quantities $\overrightarrow{m}$. The nonlinear Riccati equation for the four complex $z_{\mu }$ in Equation (11) becomes a linear Bloch-like equation, as before, but now in six dimensions,

$$d{m}_{\mu }/dt=2F_{\mu \nu }{m}_{\nu },\mu ,\nu =1-6.$$

(12)

Once again, the $m_{\mu }$ obey a first-order equation with an antisymmetric matrix which describes rotations in six dimensions. Since the 15 $F_{\mu \nu }$ are real, the real and imaginary parts of the six $m_{\mu }$ each obey a six-dimensional rotational transformation. The geometrical picture is of a Grassmannian manifold [37], with details as follows. The six complex $m_{\mu }$ obey three constraints, and thus describe a nine-dimensional Stiefel manifold St(6, 2, R) with SU(4)/[SU(2) × SU(2)] symmetry. This differs in a phase parameter from an eight-dimensional Grassmannian manifold Gr(4, 2, C), according to St(6, 2, R) ≃ Gr(4, 2, C) × U(1). Such a Gr manifold describes the four complex $z_{\mu }$. An alternative view, in terms of a five-sphere S${}^5$ that has two orthogonal six-dimensional unit vectors radiating from its origin, each of which rotated within that sphere, is given in [37]. Yet another description is to use what are called Plücker coordinates—six complex parameters which identify complex hyperplanes of Gr(4, 2, C), and are again discussed in [37]. They have been further discussed for pure states of three qubits, which is also a system with 15 real parameters, and used [68] for transforming between the so-called W and GHZ (Greenberger–Horne–Zeilinger) states that are familiar from quantum information theory [69]. Such a transformation has also been discussed using a SU(2) × SU(2) sub-group symmetry [70].

The occurrence of five- and six-dimensional antisymmetric equations in Equations (10) and (12) that are simple generalizations of the familiar vector Bloch equation for a single qubit, reflects the isomorphism between the groups SU(4) and SO(6) (more accurately, its covering group Spin(6): SU(4): SO(6) ∼ SU(4)$/Z_2$). They suggest a mapping between the 15 generators of these groups, as given in Equation (B1) of [37]. That mapping also extends to the full set of operators that describe the non-relativistic hydrogen atom and its transitions in quantum mechanics [23]. Interestingly, this correspondence between SU and SO symmetries is only present in the single- and two-qubit problems; it does not hold for any higher number of qubits. This fact rests on a curiosity in number theory called the Ramanujan–Nagell theorem, which states that the Diophantine equation which relates squares of integers and integer powers of two, $2^n=k^2+7$, has solutions for only five values of integer n and k [71].

3.4. Larger Numbers of Qubits and Their X-States

Recognizing the symmetry group and structure behind X-states permits simple generalization to a larger number of qubits. For this purpose, when we step back from two-qubits to a single qubit, any 2 × 2 density matrix looks necessarily like the letter X! It has, of course, SU(2) symmetry. The Fano sub-group symmetry of two-qubit X-states, SU(2) × U(1) × SU(2), may be regarded as repeating the previous one-qubit SU(2), along with attaching the center U(1) in between. This view also fits into a 4 × 4 density matrix, interpreted as two 2 × 2 ones of 1–4 and 2–3 spaces in the canonical basis, with a mutual phase between these spaces. This specific breakdown into 1–4 and 2–3, as in Equation (3) and the example in Figure 5, as opposed to other 2 × 2 breakdowns, will be discussed further below. The generalization to a higher number of q qubits is immediate. At each step, two copies of the previous step, with an added U(1) in between, provides the corresponding symmetry and set of X-states. Thus, for a system of three qubits, the SU(2) × U(1) × SU(2) × U(1) × SU(2) × U(1) × SU(2) group of 15 generators, a sub-group of the full SU(2${}^3$ = 8) of 63 generators, is the sub-group symmetry of the relevant three-qubit X-states. This corresponds to seven real diagonal and four complex anti-diagonal elements in an $8\times 8$ matrix. For any q, the full symmetry group is SU($2^q)$ with an explosively large number ($2^{2q}-1$) of generators; however, the smaller $2^{q+1}-1$ set provides the X-states and their operators. These q-qubit X-states constitute the finite projective geometry PG(q, 2) and, for $q=3$, can be geometrically represented by the same 3-simplex tetrahedron (in Figure 7) that was used for all two-qubit generators. When compared to general mixed states, pure states additionally form a subset with fewer parameters; that number coincides with the X-state values above, so that, again, the same figures can be used to represent them.

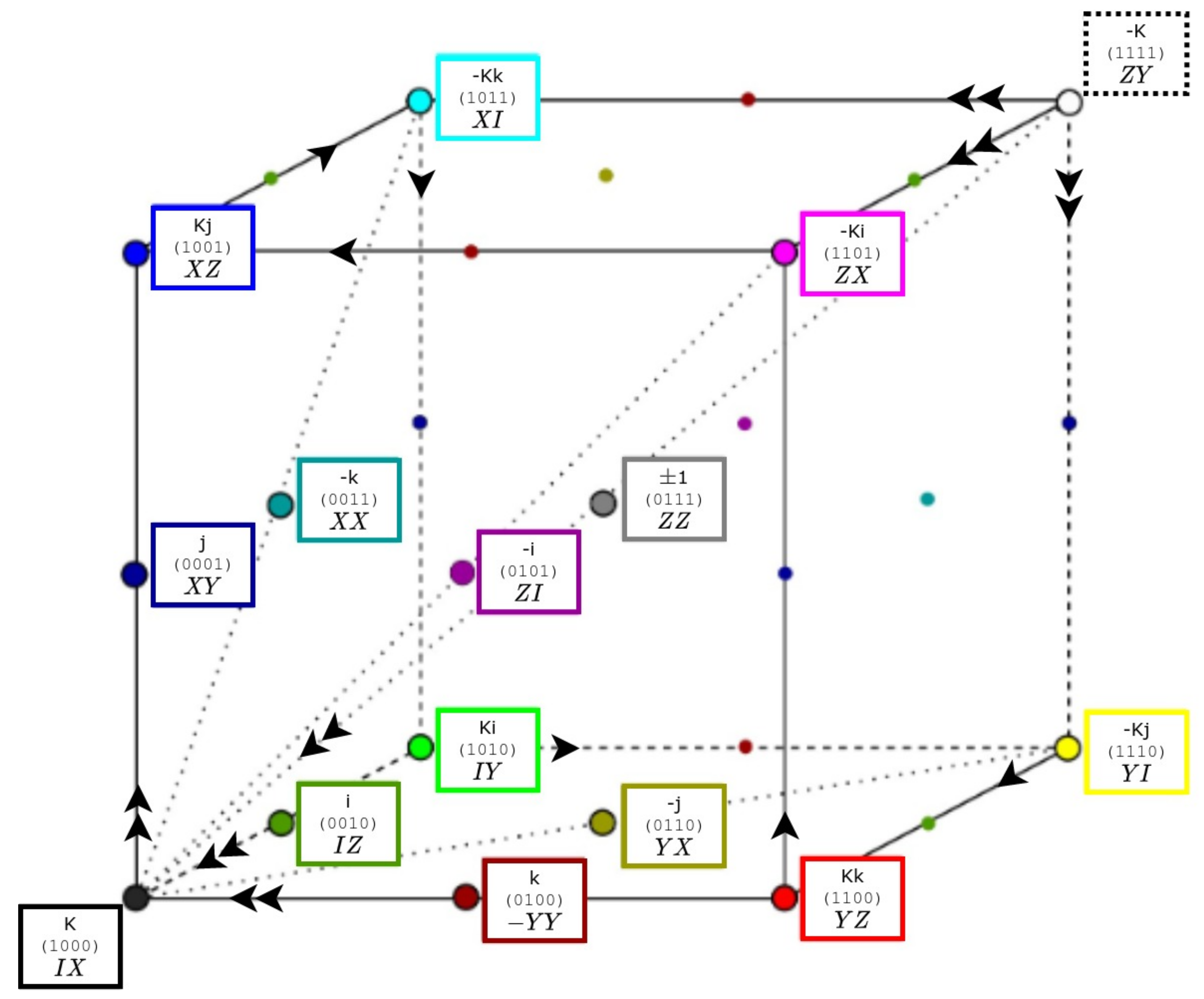
X-states of a two-qubit system entail seven parameters, whereas those with three qubits have fifteen; this latter value is also the number of generators or independent parameters of a full two-qubit system, suggesting an interesting nesting of projective geometries. PG(2, 2) of seven sits within PG(3, 2) of fifteen, with an additional eight members that may be seen as the vertices of a cube (Figure 8). This triangle-plus-cube provides an alternative to the tetrahedron in Figure 7, representing all fifteen operators and 35 triplet Lie–Clifford lines of the full SU(4), as discussed in Section 3.3. The Fano triangle’s seven vertices and seven triplet lines are supplemented by the eight vertices and 28 triplet lines (12 edges, 12 medians of faces, 4 body diagonals) of the Clifford cube, as shown in Figure 8. Such a cube has been used by computer scientists to represent a three-color (RGB) imaging scheme [72]. Generalizing to higher q, the PG(q, 2) of X-states has $2^{q+1}-1$ points running through the sequence $3,7,15,31,63,\dots$, each with the previous number of lines, triangles, tetrahedrons, etc., as supplemented by the hypercube of $(q+1)$ dimensions with $2^{q+1}$ vertices: 4, 8, 16, 32, …. On the other hand, the total number of parameters for a density matrix of q qubits is the sequence $3,15,63,255,\dots$ of PG(2q-1,2), which is the number of all generators of SU($2^q$) [73,74]. A binary labelling in the next sub-section provides another convenient addition to these algebraic and geometric perspectives of such sequences; for example, see Equation (13). The identification of Clifford algebras with PG(n, 2) over GF(2), the Galois field of order 2, for $n=2-4$ has also figured in the mathematics literature, although from a different approach. This was found in [75,76], and independently by another group [77,78], who have also investigated the connection of these projective geometries to qubits.

3.5. A Binary Labelling for Multiple Qubits

The four generators of unity and the Pauli $\overrightarrow{\sigma }$ of a single qubit have a natural 2-binary labelling that is widely used in quantum information: $I:00,{\sigma }_z:01,{\sigma }_y:10,{\sigma }_x:11$[1]. The extension to multiple qubits is immediate upon adding another such pair for each new qubit. Thus ${\tau }_x{\sigma }_x$ or, alternatively, ${\sigma }_x^{\left(2\right)}{\sigma }_x^{\left(1\right)}$ or $XX$, is assigned to [1111], and a three-qubit register [000010] would represent $I^{\left(3\right)}{I}^{\left(2\right)}{\sigma }_y^{\left(1\right)}$, while [110110] would be the operator ${\sigma }_x^{\left(3\right)}{\sigma }_z^{\left(2\right)}{\sigma }_y^{\left(1\right)}$. Corresponding base-10 values of these binary strings, ranging from 1 to $2^{2q}-1$, and the sequence $3,15,63,255,\dots$ noted in the last sub-section, would uniquely label states or operators of q qubits [55,67].

An alternative extension is more economical for the smaller number of X-states (also the number of pure states) noted in the previous paragraph. Note from the above four labels for a single qubit, the rule that an initial 0 reads the subsequent entries as $0:I,1:Z$, whereas an initial 1 reads instead $0:Y,1:X$, in what follows. In [73], they were named $D_i$ and $A_i$, respectively. This interpretation also contains the natural “duality” that is noted throughout this paper; that of $I\leftrightarrow Z,X\leftrightarrow Y$. Extending that rule to larger strings, the seven qubit-qubit X-states are rendered as 3-binary strings: $000:I,001:IZ,010:ZI,011:ZZ,100:YY,101:YX,110:XY,111:XX$. Generalizing to multiple (q) qubits, each step introduces an additional slot in the binary string, grouping all Z operators under $D_i$ and all $(X,Y)$ under $A_i$; for example, the 3-qubit X-states have $(Z_1,Z_2,Z_3,Z_1{Z}_2,Z_2{Z}_3,Z_3{Z}_1)$ in the first set and ($X_1{X}_2{X}_3,Y_1{X}_2{X}_3,X_1{Y}_2{X}_3,Y_1{Y}_2{X}_3$, $X_1{X}_2{Y}_3,Y_1{X}_2{Y}_3,X_1{Y}_2{Y}_3,Y_1{Y}_2{Y}_3$) in the second set for the total set of 15 operators involved [73]. A variant that is, aesthetically, a better fit to geometric pictures and to a quaternionic rendering was presented in [55]; it will be discussed below in Section 3.6.

This more economical $(q+1)$-binary, running from 1 to $2^{q+1}-1$, which applies both to X-states of q qubits and to pure states of $(q+1)$ qubits, has a natural connection to the geometric diagrams and finite projective geometry PG(q, 2) discussed in the previous sub-section. Each successive step in q introduces an initial 0 before the previous string, along with a new set having an initial 1. Thus, indeed, the sequence 3, 7, 15, … is the previous number plus the number of vertices of a hypercube. Geometrically, to each previous line, triangle, tetrahedron, etc., a new vertex is added in a new dimension, represented by the initial 1 which is connected to all the previous vertices. The new vertex, and its introduction of mid-points on the new connections to the ones of the previous q, matches the qubit-generator prescription referred to in the previous sub-section, wherein we duplicated the generators and added a single U(1) to move to the next step. The iteration can also be compactly rendered as

$$PG(q,2)=PG(q-1,2)+EG(q,2),$$

(13)

where iterating obviously results in PG(q, 2) = EG(q, 2) + EG($q-1$, 2) + …; a string of hypercubes. This is in conformity with a more general expression for PG($n,m$),

$$PG(n,m)=\frac{m^n-1}{m-1}=m^n+m^{n-1}+\dots =EG(n,m)+EG(n-1,m)+\dots .$$

(14)

3.6. A Quaternionic Correspondence

Hamilton’s quaternions, a four-dimensional division algebra, has long been regarded as an alternative to Pauli matrices for describing a single qubit with quantum spin-1/2 [17]. Similar correspondences for multiple qubits also bring out group-theoretic links between the discrete/finite groups of multiple quaternions and the continuous SU($2^q$) groups and generators of the qubit systems. As noted in the Introduction, quaternions are natural for geometric algebra, and Klein himself gives a nice description of three-dimensional rotations in terms of them [79]—see [80] for a pedagogical treatment. Maxwell too had advocated their use, although he himself wrote out his equations for electromagnetism in component form. However, subsequent developments in physics went in a different direction [59,64]. Vectors, and scalar and cross products of them, became the standard; geometric algebra and quaternions would not have separated a single product in this way. This would have had the merit of permitting division, which is not defined for two vectors in arbitrary directions. Many advantages would have accrued [16,79]. Interestingly, the consideration of SU symmetries in qubit systems, as discussed in this review, naturally highlighted connections [59] to finite projective geometries and geometric algebra, along with correspondences between continuous Lie groups and discrete finite groups. We will now discuss this. In addition, in Section 4, we will consider their development from the point of view of the purely geometric approach that is not motivated by quantum information. We will bring both views together on a common platform.

A variant of the more-economical binary labelling at the end of Section 3.5, which fits better with the geometric diagrams of simplexes and a consistent build-up of their labels, is the one adopted for the Fano Plane in Figure 5, the Clifford cube in Figure 8, and the tetrahedron in Figure 7. Consistently using round brackets for this binary (to distinguish from the earlier one with square brackets), start with the basic triplet of quaternions $(i,j,k)$ or the Pauli matrices $(X,Y,Z)$. With the correspondence $(i,j,k)\to -i({\sigma }_x,{\sigma }_y,{\sigma }_z)$ of the two triplets that obey the same cyclic multiplication rules, the 1-simplex of a single qubit or quaternion is a line of three points. With all seven lines of Figure 5 completely equivalent, including the inscribed circle, any of them can be the starting one. Choose the right edge, labelling the three points with a 2-binary of (01), (10) and (11), as shown. Again, for convenience of generalization, place $-k$ as the mid point, in assonance with the spin language convention that puts Z as the diagonal object in quantum physics. The minus sign is for later consistent generalization of every further simplex; these are, again, obtained by introducing a step into a new dimension, with a new k-like square root of minus 1 and its partner $(-k)$-like generalization of the mid-point of a line to a facial, space/body, etc., center. They will always carry a string of 1’s in the round bracket binary label. For these reasons, the correspondence to quaternions is $\left(xyz\right)\leftrightarrow \left(kij\right)$.

Next, the basic quaternion group Q${}_8$[81,82] of the set $\pm (1,i,j,k)$, with its Cayley table shown in

Table 3. Cayley multiplication table for quaternion group Q${}_8$ that can be characterized by two parameters: $a=k,b=i,a^2=b^2=-1$, with $ab=-ba=j$. Note the natural 2 × 2 block matrix structure with one of the C${}_4$ sub-groups in the diagonal blocks. With the mapping $(i,j,k)\to (-i{\sigma }_x,-i{\sigma }_y,-i{\sigma }_z)$, the two triplets share the same multiplication rules and the same structure applies to the SU(2) generators.

1	k	$-1$	$-k$	i	j	$-i$	$-j$
k	$-1$	$-k$	1	j	$-i$	$-j$	i
$-1$	$-k$	1	k	$-i$	$-j$	i	j
$-k$	1	k	$-1$	$-j$	i	j	$-i$
i	$-j$	$-i$	j	$-1$	k	1	$-k$
j	i	$-j$	$-i$	$-k$	$-1$	k	1
$-i$	j	i	$-j$	1	$-k$	$-1$	k
$-j$	$-i$	j	i	k	1	$-k$	$-1$

, can be set in correspondence with the Fano sub-group of seven operators and both placed on the Fano Plane’s equilateral triangle, as shown in Figure 5. This step to the 2-simplex introduces a new vertex, which may be denoted k and connected to the previous three points. It joins with the previous endpoints $(i,j)$, to provide the vertices of the Fano triangle. The center of the group, $\pm 1$, is the geometric center, and two new mid-points, “conjugate” negatives of the previous vertices $(i,j)$, arise at this step. Note the four cyclic lines (three edges and circle), shown arrowed, and three commuting median lines. As stated before, all lines are equivalent in a finite projective geometry. The circulation of the arrows is counter-clockwise around the edges and clockwise in the inscribed circle. Correspondingly, the extension from 2- to 3-binary labelling proceeds by adding an initial 0 to the points of the 1-simplex, and calling the new vertex (100). The other points then acquire labels by binary addition, with the commuting center as (111). In this manner, the Cayley table of Q${}_8$ is placed on the Fano Plane.

Such a 3-binary $\left(xyz\right)$ with round brackets labels the points in Figure 5 on purely geometric grounds: $x=0$ as the right edge, $y=0$ as the left edge, and $z=0$ as the base edge. The ascribing of quaternion $(i,j,k)$ to the points is, to some extent, arbitrary—all points and lines are equivalent, and are related by simple geometric transformations, such as rotations in the plane. However, it is natural to place $\pm 1$ and, equivalently (000)/(111), as the center of the triangle. Pairs of opposite signs then stand on opposite ends of the medians, which are conjugates under binary addition. As stated, it proves convenient for what follows to standardize the new vertex as k-like when proceeding to generalize to higher dimensions or a larger number of qubits. Another perspective, provided by geometric and Clifford algebra, is that 1 is a scalar and $(i,j,k)$ a vector, while $(-i,-j,-k)$, formed out of antisymmetric pairwise products, is a bi-vector, and $ijk=-1$ is a pseudoscalar. Together, they are placed on the Fano Plane in Figure 5.

With the equivalence of multiplication rules between quaternions and Pauli matrix generators of SU(2), a similar placement can be made of 1-qubit generators with $(I,-i{\sigma }_x,-i{\sigma }_y,-i{\sigma }_z)$ and $(i{\sigma }_x,i{\sigma }_y,i{\sigma }_z,-I)$ labelling points in Figure 5. Such an assignment also occurs in Figure 1 of [77]. However, a sign is irrelevant when dealing with generators of a continuous group. Instead, 2-qubit generators of the Fano sub-group provide an appropriate correspondence and natural identification with the 7-generator Fano sub-group and X-states of Section 3.1. Again, since any $O_i$ can serve as a center, the example shown in Figure 5 is for $ZZ$ as the center; the remaining six are commuting pairs at opposite ends of the medians. However, this match to 2-qubit generators is not to Q${}_8$ as such, but to another closely related order-8 “co-quaternion” group that is isomorphic to the dihedral group D${}_4$. This will be discussed further at the end of this sub-section. Note that the change in sign of a quaternion has, as its counterpart, the duality exchange $I\leftrightarrow Z,X\leftrightarrow Y$.

The same quaternion and spin generator labelling in Figure 5 is shown in Table 2, and it must again be noted that it is for the specific example chosen—other centers and choices of the seven generators yield other correspondences between quaternions and generators. As noted, the example chosen corresponds to a physical set up of two spins in a magnetic field along the z-axis, in addition to the four operators of magnetic interactions in the orthogonal $X-Y$ plane. Because any $O_i$ can serve as a center (and is thus placed as the geometric center), their square bracket and double spinor names cannot be universally related 1:1 to the geometric round bracket labels [55]. Furthermore, both sets of 4-binary can be rendered in base ten to run as a single number, so that points in Figure 7 and Figure 8 may be labelled from 1 to 15 as in [67], and the 2-qubit generators as in [55]; however, we have retained the $O_i$ names due to previous usage in [7,8,55].

The next step is to consider two independent quaternions (each commutes with all of the other set), which can be denoted by lower and upper case $(i,j,k)$ and $(I,J,K)$, along with the unit element and all bilinear products. Taking all sixteen with plus/minus signs forms the 32-element finite group Q${}_{32}$. A half-way step is to include just one of the upper case elements, say K, to acquire a group of order 16. This element could also be regarded as an ordinary complex square root of unity, so that we might call this the complex quaternion group. It has previously been referred to as a“bi-quaternion”, a term that Hamilton himself seems to have introduced [81,82]. (Bi-quaternion could more properly have been kept for the full order-32 group with all multiplicative combinations of two independent quaternions.) Its Cayley table is shown in

Table 4. Cayley multiplication table for the co-quaternion group or dihedral D${}_4$ that can be characterized by two parameters: $a=k,b=Ki,b^2=1,a^2=-1$, with $ab=-ba=Kj$. Contrast with Table 3.

1	k	$-1$	$-k$	$Ki$	$Kj$	$-Ki$	$-Kj$
k	$-1$	$-k$	1	$-Kj$	$-Ki$	$Kj$	$Ki$
$-1$	$-k$	1	k	$-Ki$	$-Kj$	$Ki$	$Kj$
$-k$	1	k	$-1$	$Kj$	$Ki$	$-Kj$	$-Ki$
$Ki$	$-Kj$	$-Ki$	$Kj$	1	$-k$	$-1$	k
$Kj$	$Ki$	$-Kj$	$-Ki$	k	1	$-k$	$-1$
$-Ki$	$Kj$	$Ki$	$-Kj$	$-1$	k	1	$-k$
$-Kj$	$-Ki$	$Kj$	$Ki$	$-k$	$-1$	k	1

, and its 15 elements have been placed in 1:1 correspondence with the Clifford cube and tetrahedron of Figure 7 and Figure 8. As a group, it is C${}_2\otimes$ Q${}_8$ or $(I,Kk)\otimes \pm (I,i,j,k)$. (The pair $(1,K)$ would also provide all 16 elements, but does not form a C${}_2$ group; the pair $(1,Kk)$ achieves this.)

In terms of the extension from the seven point/line triangle/2-simplex to this 8-vertex/28-line cube or 15-point/35-line tetrahedron/3-simplex, the previous 3-binary is extended to a 4-binary $\left(txyz\right)$ and, geometrically, a new vertex (1000) or K, in a new dimension is introduced. In the cube, that vertex is connected to the previous seven $\left(0xyz\right)$ as mid-points and extended to vertices $\left(1xyz\right)$ whereas in the tetrahedron, the seven lines from vertex to the base Fano triangle introduce seven new midpoints—three of them are face centers and one is a body center. Opposite vertices of the cube are of opposite sign: $\pm (K,Ki,Kj,Kk)$ and the center is the $\pm 1$ of quaternions and the $ZZ$ generator of the example chosen. With the quaternions placed at midpoints of the edges at the lower corner, their negatives stand at the midpoints of the orthogonal face in keeping with their bi-vector nature noted earlier. In the tetrahedron, the new vertex K introduces edge midpoints $(Ki,Kj,Kk)$, face centers the same triplet with minus signs, and its conjugate $-K$ is the body center, with $\pm 1$ and $ZZ$ the face center of the Fano triangle remaining in the base. Table 2 brings together all the alternative renderings of the 15 generators of the two-qubit system in terms of $O_i$, Pauli matrices, Dirac gamma matrices, binary, and quaternionic labels. Note the consistent pattern of each subsequent simplex having a $(-k)$-like center with a string of 1’s as its binary representation.

The 4-binary has a natural language in terms of space-time $\left(txyz\right)$ in physics, but could equally be rendered as alternatives, including four colors [72] or four acoustic notes, to describe similar constructs of 15 basic objects; it has even been used [55] in the context of a well-known combinatorics problem to be described below. In Table 2, the association of this round-bracket 4-binary with the bi-quaternions is fixed. That is, the latter read off the former with the simple 1:1 association introduced in an above paragraph: $\left(0xyz\right)\leftrightarrow \left(kij\right)$, i.e., $\left(0100\right)\leftrightarrow k$, etc. and conjugates such as $\left(0011\right)\leftrightarrow -k$. An initial 1 brings in $\pm K$: $\left(1000\right)\leftrightarrow K,\left(1111\right)\leftrightarrow -K,\left(1010\right)\leftrightarrow Ki$, etc. Multiplication of quaternions corresponds to binary addition. However, since any $O_i$ denoted by its spinor and square bracket binary can be chosen as the center, there is no one-to-one link of them, the correspondence shown being for the specific choice of $ZZ$ as center and $\pm 1$.

There are other order-8 sub-groups of the full order-16 complex quaternion group. One is the set, $\pm (I,k,Ki,Kj)$, forming the co-quaternion group D${}_4$ with a Cayley table as shown in Table 4. In a standard minimal notation [82] for D${}_4$, it can be rendered in terms of two parameters as $(a=k,b=Ki)$. With the same labelling as in Table 2, the set of seven generators are $(ZZ,XX,YY,IY,ZX,YI,XZ)$ with $YY$ as center. Correspondingly, the physical system is now of two spins in a magnetic field in the y-direction, with four magnetic coupling operators in the orthogonal $X-Z$ plane. Another is the set of eight elements $\pm (1,k,K,Kk)$ which is $(1,Kk)\otimes \pm (1,k)$ or C${}_2\otimes$ C${}_4$. It corresponds, for the example in Table 2, to the set $(ZZ,XX,YY,IX,ZY,XI,YZ)$ with $XX$ as center; that is, two spins in a magnetic field in the x-direction with coupling terms in the orthogonal $Y-Z$ plane. Differing only in a renaming of the magnetic field in terms of the $x,y,z$ directions, they share the same entanglement and other physics. All these sets show the same $I\leftrightarrow Z,X\leftrightarrow Y$ duality noted above. The full set of sixteen elements of a complex quaternion, or the generators of SU(4) in Table 2, have a Cayley table shown in

Table 5. Cayley table for group of complex quaternions $\pm (1,i,j,k,K,Ki,Kj,Kk)$, an order-16 group isomorphic to C${}_2\otimes$ Q${}_8$ and C${}_2\otimes$ D${}_4$ with C${}_2=(1,Kk)$. An eight-element sub-group in the diagonal blocks is another alternative to Table 3 and Table 4.

1

k

$-1$

$-k$

K

$-K$

$Kk$

$-Kk$

i

j

$-i$

$-j$

$Ki$

$-Ki$

$Kj$

$-Kj$

k

$-1$

$-k$

1

$Kk$

$-Kk$

$-K$

K

j

$-i$

$-j$

i

$Kj$

$-Kj$

$-Ki$

$Ki$

$-1$

$-k$

1

k

$-K$

K

$-Kk$

$Kk$

$-i$

$-j$

i

j

$-Ki$

$Ki$

$-Kj$

$Kj$

$-k$

1

k

$-1$

$-Kk$

$Kk$

K

$-K$

$-j$

i

j

$-i$

$-Kj$

$Kj$

$Ki$

$-Ki$

K

$Kk$

$-K$

$-Kk$

$-1$

1

$-k$

k

$Ki$

$Kj$

$-Ki$

$-Kj$

$-i$

i

$-j$

j

$-K$

$-Kk$

K

$Kk$

1

$-1$

k

$-k$

$-Ki$

$-Kj$

$Ki$

$Kj$

i

$-i$

j

$-j$

$Kk$

$-K$

$-Kk$

K

$-k$

k

1

$-1$

$Kj$

$-Ki$

$-Kj$

$Ki$

$-j$

j

i

$-i$

$-Kk$

K

$Kk$

$-K$

k

$-k$

$-1$

1

$-Kj$

$Ki$

$Kj$

$-Ki$

j

$-j$

$-i$

i

i

$-j$

$-i$

j

$Ki$

$-Ki$

$-Kj$

$Kj$

$-1$

k

1

$-k$

$-K$

K

$Kk$

$-Kk$

j

i

$-j$

$-i$

$Kj$

$-Kj$

$Ki$

$-Ki$

$-k$

$-1$

k

1

$-Kk$

$Kk$

$-K$

K

$-i$

j

i

$-j$

$-Ki$

$Ki$

$Kj$

$-Kj$

1

$-k$

$-1$

k

K

$-K$

$-Kk$

$Kk$

$-j$

$-i$

j

i

$-Kj$

$Kj$

$-Ki$

$Ki$

k

1

$-k$

$-1$

$Kk$

$-Kk$

K

$-K$

$Ki$

$-Kj$

$-Ki$

$Kj$

$-i$

i

j

$-j$

$-K$

$Kk$

K

$-Kk$

1

$-1$

$-k$

k

$-Ki$

$Kj$

$Ki$

$-Kj$

i

$-i$

$-j$

j

K

$-Kk$

$-K$

$Kk$

$-1$

1

k

$-k$

$Kj$

$Ki$

$-Kj$

$-Ki$

$-j$

j

$-i$

i

$-Kk$

$-K$

$Kk$

K

k

$-k$

1

$-1$

$-Kj$

$-Ki$

$Kj$

$Ki$

j

$-j$

i

$-i$

$Kk$

K

$-Kk$

$-K$

$-k$

k

$-1$

1

. They may be viewed as direct products of C${}_2$ with the order-8 groups, whether Q${}_8$ or D${}_4$.

As noted, the quaternion labels placed on the vertices in Figure 5 are arbitrary, given the natural geometric symmetries of the triangle such as rotations through multiples of $\pi /3$. The independent placement of the qubit generators is also arbitrary, as is their correspondence to the quaternions. Given that any of the 15 $O_i$ can serve as a center and define the X-states of the Fano sub-group, there are as many choices. However, entanglement properties differ; only the nine ${\tau }_i{\sigma }_j$ involving both qubits accommodate quantum entanglement. Their set of seven generators has two single spin generators, the ${\tau }_i$ and ${\sigma }_j$, and five two-spin operators. All square to unity. For the six single-spin centers, a similar set is composed of the three single operators of the other spin and the three products of them with the center. With these generators, a multiplicative sign or constant, such as $\pm i$, is irrelevant and, as observed, the $-i\overrightarrow{\sigma }$ satisfy all the multiplication rules of quaternions—including that they square to $-1$. Turning to the order-8 groups, the quaternion group Q${}_8$ has six $-1$ along the diagonal in its Cayley Table 3. Meanwhile, the co-quaternion group in Table 4, that is isomorphic to the dihedral D${}_4$, has two, and the C${}_2\times$ C${}_4$ has four (the upper left 8 × 8 block of Table 5). Thus, while all three of them can be associated with X-states, it is the co-quaternion which best matches the entangled class in having two of the seven square to −1. Those could be set to match in the set with center ${\tau }_i{\sigma }_j$; then, the two ${\tau }_i$ and ${\sigma }_j$, with $-i$ factors, would square to −1.

Thus, the choice made in Figure 5, Figure 7 and Figure 8, and Table 2 puts $\pm i$ as the two $IZ$ and $ZI$, with a corresponding co-quaternion $\pm (1,i,Kj,Kk)$. This set is trivially different from the one displayed in Table 4. For this choice, all rows of Table 2 can be retained unchanged, especially the binary and qubit generators; however, in the last row we must multiply entries involving $(j,k)$ by K with $K^2=-1$. In Figure 5, Figure 7 and Figure 8, we similarly have to multiply $(j,k)$ by K, and leave the other points unchanged. On the other hand, had we chosen the quaternion $\pm (1,k,Ki,Kj)$, the entries in Table 2 could be left unchanged, but this would correspond to the X-state set $(ZZ,XX,YY,IY,ZX,YI,XZ)$ with $YY$ as center. This would be at a slight conflict with the convention in physics of choosing z as the magnetic field direction or quantization axis. As stated, with no unique correspondence between the three labelling systems, binary, quaternion, and qubit generators, it is partly convention and partly aesthetics dictating the choice made in Table 2 and in our figures. The choice made in Table 2 is to tie the square-bracket 4-binary to qubit generators and the round bracket to bi-quaternions, with $ZZ$ as the center of the former matched to the $\pm 1$ center of quaternions.

An interesting connection can also be established with octonions, the only other division algebra besides reals, complex numbers, and quaternions [64]. With seven independent square roots of −1, they can also be laid on the seven points of Figure 5 but with crucial differences. With a cyclic triplet $\left(pqr\right)$ replacing $(-i,-j,-k)$ in order, and the seventh square root s placed at the center, these seven independent imaginaries $(i,j,k,p,q,r,s)$ have seven cyclic lines on the triangle $\left(irj\right),\left(jpk\right),\left(kqi\right),\left(psi\right),\left(qsj\right),\left(rsk\right),\left(pqr\right)$. All lines are now arrowed with the same circulation sense for the edges and the circle, unlike in Figure 5 which has them opposite, and medians are now also arrowed from midpoint to vertex. This turns out to be crucial, since octonionic multiplication is no longer associative, which was the case with the previous three division algebra. This means that opposite circulation is a necessary feature of the quaternions in Figure 5, in contrast to octonions. Interestingly, the seven quaternionic triplets can also be depicted on the cube in Figure 8, with the unit element at the lower left corner, $\left(ijk\right)$ on the three connected vertices to it, $\left(pqr\right)$ at their opposite corners, and s at the body center. An alternative placement of the seven at the seven corners of the cube is in [64].

This process of counting how many −1 occur along the diagonal of a Cayley table, that arises naturally in our discussion with qubit generators, also has a bearing on further extension. There are no more division algebras beyond octonions to place on all points after the 2-simplex of Figure 5. In the 3-simplex tetrahedron of Figure 7, $\pm (i,j,k,K,Ki,Kj,Kk)$, eight of them square to −1. Fifteen square roots of −1, placed at each of the points, represent what are called “sedenions” [83]. Products of pairs of them as 35 triplets can be specified and, as with octonions, the products are not commutative or associative. That loss of associativity in multiplication precludes, of course, matrix representation. Physics has seen little use of octonions or sedenions. (See, however, [84,85]. In addition, octonions do allow what is termed “limited associativity” [64]). However, from the 35 triplets we have discussed for the tetrahedron in either quaternionic or spinor language and a Cayley table such as Table 5, one can build a Cayley table for sedenions as in [83]. Indeed, a more symmetric arrangement than in [83] is to group the 35 triplets into seven columns of 5 rows each, with all 15 elements occurring once and only once in each column for the Kirkman arrangement of schoolgirls, as discussed below in Section 4. Note that a proper Cayley table requires the 15 square roots with both plus/minus signs, along with $\pm 1$, and is a group of order 32. As an alternative to the Cayley–Dickson construction in [83], the higher q-qubit simplexes provide another route to constructing these hypercomplex numbers, including sedenions and beyond, and associating them with finite projective geometries.

The correspondence to quaternions and higher string binaries for more than two qubits proceeds naturally. Each further qubit in a q-qubit sequence introduces a new initial entry of 1 in the string with a new independent K-like entry and new vertex in the next simplex—the previous simplex’s points are assigned an initial 0. $-K$ appears with $(111\dots )$ as the new simplex’s body center, just as the mid-point, face center, tetrahedron’s body center, did for 1-, 2-, 3-simplex of 1-, 2-, 3-qubit systems, respectively. This gives a geometric realization in simplexes of X-states of q-qubits. A somewhat different approach was adopted in [86], which followed the Cayley-Dickson $2^N$-dimensional algebra with imaginary units $e_a,1\le a\le 2^N-1$ encoded in PG($N-1$, 2), and triads of points with $e_a{e}_b=\pm e_c$ as lines. Binomial configurations $C_N$ are then identified with octonions for $N=3$, sedenions for $N=4$, and higher $2^N$–nions. Again, the PG($N-1$, 2) is a $(N-1)$-dimensional projective space over Galois field GF(2), as noted at the end of Section 3.4, and the $C_N$ are isomorphic to Grassmannian G${}_2(N+1)$. While [78] noted that there is no “neat picture” for these higher 2${}^N$-nions, the N-binary string and simplex schemes discussed above provide a unified picture of all of them and associate with the X-states (or, equivalently, pure states) of N-qubits. Additionally, in correspondence to quaternions, one new independent K-like imaginary unit is added at each step, in order to acquire the simplex of the next-highest dimension.

4. Geometric View

In the last twenty years, two lines of exploration, with very different starting points and motivations, have come together in studying symmetries of systems with a finite number of quantum spins. One that we have discussed already, in Section 3, started with a concrete physical problem relevant to NMR; that of two coupled spins [7]. The observation that sub-group symmetries in such a system simplify the construction of the evolution operator has led, in subsequent work, to generalization and systematic analysis of SU(2) × U(1) × SU(2) and other sub-groups of SU(4) [8,37,55]. These studies of continuous Lie groups and Lie algebras were later connected to quaternions and their discrete group symmetries, as well as to projective geometries (PG) that utilize pleasing geometric figures—triangles, tetrahedrons, and higher simplexes—to describe quantum states and operators, along with geometric manifolds that generalize the Bloch Sphere of a single spin [55,59]. At the same time and in the same period, geometers have investigated objects entirely within the field of geometric algebra, and have arrived at a similar picture [58,61,62,65]. This section will deal with this latter approach.

Three such early works [15,62,87] approached the “geometry of entanglement” for two qubits by considering a six-dimensional real metric vector space V with a non-degenerate quadratic form Q: V → R. Whereas earlier sections identifying SO(6) pointed to a corresponding six-dimensional space of real rotations, these geometers used a generalization of vector algebra to metric vector spaces in geometric algebra. An antisymmetric product in V is called an r-blade, and in the exterior algebra $\mathrm{\Lambda }$V, a geometric product of a vector and an r-blade is defined. The number of vectors, r, in an r-blade is called its grade. Spinors are defined as left-ideals in a three-dimensional vector space G(3), its even parity elements being the quaternions denoted G${}^{+}\left(3\right)$. Similarly, for two qubits, a space G(6) is defined with an orthonormal basis in R${}^6$ of two triplets ($e_i,f_i$) [15]. The bilinear combinations, i.e., bivectors of $\mathrm{\Lambda }$V are

$$G_{10}=e_2{e}_3,G_{01}=f_2{f}_3,G_{ij}=e_i{f}_j{(-1)}^{{\delta }_{ij}},$$

(15)

with other similar cyclic combinations. These 15 G’s can be placed in 1:1 correspondence with the $O_i$ introduced earlier, and are also shown in Table 2. They can also be conveniently depicted as a hexagon in Figure 9 [15]. When one of the subscripts of G is zero, they correspond to single-qubit operators within $e_i$ and $f_i$, and they stand on the left and right of the hexagon. Only the nine $G_{ij}$ with $i,j=1-3$–that is, the two-spin operators linking left and right–support entanglement when selected as centers, as per earlier remarks. It is these G’s that are the Dirac $({\gamma }_i,A_i,{\alpha }_i)$.

Pure states of two qubits, characterized by seven real parameters, are described in S${}^7$. The three-dimensional projective space P(V) = PG(3, 2) has an underlying vector space of dimension four. These are referred to as the boundary and bulk, respectively. Going back to the work of Plücker, Klein, and Grassmann, lines of the projective space can be parametrized in terms of points in four dimensions. There are 35 lines and 15 points of PG(3, 2), as described earlier in the tetrahedron of Figure 7. It is useful to fiber S${}^7$ over a one-dimensional quaternionic projective space HP${}^1\sim$ S${}^4$ by a second Hopf fibration $\pi$: S${}^7$→ S${}^4$ with an SU(2) ∼ S${}^3$ fiber. A natural metric, the Mannoury–Fubini–Study metric, is induced; this is the standard metric on S${}^4$ expressed in stereographically projected coordinates. The geodesic distance with respect to this metric provides a natural object for quantifying entanglement of the qubits, according to the prescription that entanglement is the geodesic distance to the nearest separable state [87,88]. Entanglement resides, therefore, in the twisting of the bundle between the base S${}^4$ and fiber S${}^3$. (This usage of S${}^4$ should not be confused with the one in Figure 6 for the Desargues sub-group in Section 3.2) Using this, geometric meaning is given to the standard Schmidt decomposition that is familiar in quantum information. The Schmidt states are the nearest and the furthest separable states lying on, or the ones obtained by parallel transport along, the geodesic passing through the entangled state [87]. That geodesic distance is expressible [87] in terms of the “concurrence” which quantifies entanglement in quantum information [89]. Another natural way of seeing this is through a connection on the bundle. Section IV of [87] identifies it as the instanton connection, familiar from quantum field theory, where it describes tunneling between different continua. Further, a Sp(1) ∼ SU(2) gauge degree of freedom of the second Hopf fibration gives an important geometric interpretation of local transformation in the second subsystem, and the fact that it does not change the entanglement properties of the whole. Those can only be affected by a global unitary U(4).

Other geometric objects are a generalized Klein quadratic, denoted as W${}_3$(2). It is a hyperbolic quadric in W(3, 2), the symplectic polar space of rank 2 and order 2, and the space of totally isotropic subspaces of PG(3, 2) with respect to a symplectic form. In PG(3, 2) with 15 points and 35 lines, 7 lines are incident on each point, three of them isotropic and 4 non-isotropic (commuting and cyclic, respectively, as referred to in the Lie-algebraic terminology of Section 3). W(3, 2) is a self-dual object of 15 points and 15 lines, called a “doily” or a Cremona–Richmond configuration [58,90] (Figure 1 of [61]). It is the smallest generalized quadrangle. A decomposition into a 10-point/line Petersen graph and five leftover points, none of them collinear, called an ovoid, is also shown. Furthermore, two distinct points of W(3, 2) are said to be orthogonal if joined by a line; this was what was termed “commuting” in our earlier Lie-algebra language. W(3, 2) has three kinds of hyperplanes: (1) called perp-set, which is a set of points collinear with a given point—there are 15 of these, and each has a Fano Plane (also called a pencil); (2) a grid of 9 points on 6 lines called a Pappus configuration, or a Mermin square in applications to quantum information theory, such as proofs of the Kochen–Specter theorem [91]—there are 10 of these; and (3) an ovoid, which is a set of 5 points with exactly one point in common with every line—there are six of these. The dual of an ovoid is called a “spread” [62]. A so-called Veldkamp space of the doily V(W(3, 2))—which is a parabolic quadric and isomorphic to PG(4, 2) with 31 points (and 155 lines), of which 15 are generated by single-point perp-sets, 10 by grids, and 6 by ovoids—has also been discussed [90]. Finally, a Mermin pentagram has been discussed in [92].

Besides entanglement, the quadric W(3, 2), as well as the correspondence between two-qubit observables on the boundary and three-qubit ones in the bulk, have been discussed for other purposes in quantum information, including the generation of error-correcting and stabilizer codes. The ovoid of five points represents five codewords encoding messages on the boundary [61]. It also provides a way of attaining the maximum number of MUBs (mutually unbiased bases) in a finite-dimensional Hilbert space, an otherwise-difficult problem that is, however, important in quantum information theory [65]. A group- and graph- theoretic approach to MUBs has also been considered in terms of Cayley graphs [93]. The basis group of a set of MUBs of a d-dimensional Hilbert space is defined by a sub-group of U(d), which is generated by unitary matrices associated with the bases. The edges of the Cayley graph that capture this structure form a completely connected subgraph called a “clique” [94]. This links the search for MUBs to the representation theory of finite groups [93].

The geometric literature has also extended beyond two qubits to q qubits. This discussion has again concerned pure states, rather than more general mixed states that are of greater interest in the field of quantum information. The starting manifold of q qubits is S${}^{2^{q+1}-1}$ and Hopf fibration $\pi$ : S${}^{2^{q+1}-1}\to$ S${}^{2^q}$, with fiber S${}^{2^q-1}$[95]. The projective geometry is now PG(2q − 1, 2) with Klein quadric W(2q − 1, 2). The role of W(5, 2) for three qubits and W(7, 2) for four has also been recently discussed [96]. There are now $2^{2q-1}$ points not orthogonal to a given point, instead of the eight non-zeroes in Table 1 of qubit commutators. Thus, PG(2q − 1, 2) is cut into $2^q+1$ disjoint fibers, each containing $2^q-1$ points. For three qubits, this amounts to 63 = 9 × 7, in place of 15 = 5 × 3 for a qubit-qubit system. An interesting connection to an old mathematical problem, called Kirkman’s Schoolgirls problem, which is associated with the latter decomposition, is worth noting [60], since it influenced several developments in finite projective geometries [97,98,99] and design theory [20,22,100,101,102].

This problem initiated another branch of mathematics within its area of combinatorics. Originating from a recreational problem from over 175 years ago [97], that has since been known as Kirkman’s Schoolgirls problem, mathematicians have studied it as “triple systems” within “design theory.” In particular, “balanced incomplete block (BIB)” designs and “Steiner triple systems” were related to finite projective geometries by mathematical statisticians, notably R. A. Fisher [20,22,60,101,103]. A number v of “varieties” are assigned to “blocks” b with incidence relations to provide $(v,b,r,k,\lambda )$ designs. The symbols v are assigned to blocks b with k in each, and each symbol is to occur in r different blocks, with every pair of symbols to occur together in $\lambda$ blocks. The case of $k=3$ is designated a triple system and $\lambda =1$ (with no repeats) is designated a Steiner system. The two conditions together define Steiner triple systems, which have been extensively studied and exist for all $v=1$, or 3 mod 6. Since BIBs must satisfy $vr=bk,\lambda (v-1)=r(k-1)$, such a Steiner triple is fixed by the single parameter v and denoted 2-(v, 3, 1). Apart from the trivial $v=3,b=1$, the next is $v=7,b=7$, an example of what is dubbed a “symmetric” design. The binomial configuration $C_3$, associated with octonions, that was discussed earlier has been recognized as isomorphic to a so-called “Pasch” configuration and used for classifying Steiner triple systems [85].

With v taken as points and b as lines, the incidence relation of projective geometry—that three points lie on every line—provides a connection to finite projective geometry. This recognition by Fisher and collaborators was very fruitful for the field of design theory, which was born from these origins [60,103]. Apart from the trivial single-line design 2-(3, 3, 1) of $v=3$ points and PG(1, 2), the next-simplest example of 2-(7, 3, 1) design is isomorphic to PG(2, 2) of the Fano Plane. Another design 2-(15, 3, 1) with $v=15,b=35$ is PG(3, 2), and it is this connection through the numbers 7 and 15 that led researchers to map two-qubit problems onto finite projective geometry and design theory [55,59,60]. With 7 points on 7 lines, we acquire the Fano triangle, and with 15 points on 35 lines, the tetrahedron—these are discussed in earlier sections. Kirkman’s schoolgirls problem was to have 15 schoolgirls march in a row of 3 to school for every day of a 7-day week, with no pairs of girls repeated in a row—the 35 required rows can be drawn from the tetrahedron to provide such a marching order [55,104].

The choice of three-in-a-row in the above recreational problem was a prescient and pleasing anticipation of three being the number of operators involved at a vertex (diagrams of Feynman, angular momentum coupling, many-body perturbation theory, etc.) and in a Lie commutator in quantum physics applications a century later. This ubiquitous appearance of three entities at a vertex in physics has been suggestive of connections to other areas of mathematics. Thus, quaternionic and octonionic symmetries for braids on three strands, their group structure, and triplets of half-odd integer labels have been discussed for the standard model of particle physics [105] and quantum gravity [106], as also the closely related study of knots [107]; see also [108]. A book on division algebras in particle physics is additionally helpful [109].

The connections apply to higher number (q) of qubits as well, with

$$v=2^{2q}-1,b=(2^{2q}-1)(2^{2q-1}-1)/3,r=2^{2q-1}-1,$$

(16)

and the geometry PG(2q − 1, 2) as illustrated in

Table 6. Triple system designs with v(arieties), b(locks), r(anks) and corresponding projective geometry PG. Integer values of q represent number of qubits in correspondence.

q	$n=2q-1$	v	b	r	-
$1/2$	0	1	0	0	PG(0, 2)
1	1	3	1	1	PG(1, 2)
$3/2$	2	7	7	3	PG(2, 2)
2	3	15	35	7	PG(3, 2)
$5/2$	4	31	155	15	PG(4, 2)
3	5	63	641	31	PG(5, 2)
$7/2$	6	127	2667	63	PG(6, 2)

. While $k=3$ triplets are directly related to projective geometries, as we have discussed, and to quantum commutators when two operators uniquely fix the third (physics abounds with triplets, such as vertices in angular momentum coupling or Feynman diagrams), the Kirkman problem can itself be generalized for other values and described in terms of PG($n,m$) with $m=k-1,n=2q-1$, and

$$v_n=m{v}_{n-1}+1=\frac{m^{n+1}-1}{m-1},b=\frac{(m^n-1)(m^{n+1}-1)}{{(m-1)}^2(m+1)},r=\frac{m^n-1}{m-1}.$$

(17)

Such generalizations have found application in recreational examples of golfers in rounds of four or more, which have followed Kirkman’s schoolgirl triplets [104]. The dimension of PG($n,m$) is shown in

Table 7. Dimension of PG($n,m$. )

$n/m$	1	2	3	4
-	Pairs	Triplets	Quartets	Quintets
0	1	1	1	1
1	2	3	4	5
2	3	7	13	21
3	4	15	40	85
4	5	31	121	341

for place values of m beyond the $m=k-1=2$ that has occurred throughout this paper as relevant to physics. For $m=1$, all entries being powers of 1, the column is simply $n+1$, and corresponds to pairs ($k=2$) instead of triplets. The $m=2$, $k=3$ column has the entries $1,3,7,\dots$ for the triplets discussed so far for PG($n,2$). The next column, for $m=3$, are quartet arrangements with dimension $(3^{n+1}-1)/2$. Along rows at fixed n are the sequences 1, 11, 111, etc., with place value m, and thus, $1,m+1,m^2+m+1,\dots ,[m^{n+1}-1]/(m-1),\dots$.

5. Higher Dimensional Spins

Increasingly, spins larger than 1/2 are being explored for applications in quantum information [110,111,112,113,114,115,116,117,118,119]. As is well known, entanglement measures, such as concurrence [89] and negativity of the partial transpose [120], fail when both d and D in a qudit-quDit system are larger than 2 [121]. A qutrit, with symmetry group SU(3) and symmetry algebra su(3), is characterized by 8 parameters, a general qudit of d-dimensions by su(d) with $(d^2-1)$ parameters. While various geometric extensions of the qubit Bloch sphere [122] have been advanced, with corresponding Bloch vectors for a qubit [123,124,125], it is still difficult to visualize a single qutrit [119,126], and there is no satisfactory way to view higher-d state space. A recent work put forward for this purpose projects state space onto measurements of observables, with illustrations for photonic qutrits that use three spatial modes of the electromagnetic field [119]. Another recent picture of qutrits is in [127]; see also [122,128]. In earlier quantum physics literature, a description of higher spin j in terms of observables can be found in [129,130]. One can also find a generalization of the Bloch equation, as in Equation (10) and Equation (12), in terms of multipoles for spin-j in Equation (7.37) of [2].

The 3 × 3 density matrix of a qutrit has two real parameters on the diagonal and three complex off-diagonal entries. An X-state of a qutrit, which may be denoted SU${}^{\left(X\right)}$(3), has only one off-diagonal for a total of four parameters. A central, real one-dimensional space is decoupled from the two-dimensional space surrounding it, thus making SU${}^{\left(X\right)}$(3) of SU(2) × U(1) symmetry. In extending to multiple qutrits, the symmetry structure generalizes the case of multiple qubits. The 9 × 9 matrix of a qutrit-qutrit system has, in general, 80 parameters which characterize it; this is discussed by [85] in terms of a two-qutrit Pauli group. However, X-states again involve a smaller number of parameters, only 16, consisting of 8 real diagonal entries and four off-diagonal complex elements. It can be seen in relation to the SU${}^{\left(X\right)}$(3) group of a single qutrit as three repeating copies (instead of two copies noted earlier for the similar qubit extension), with U(1)s in between and at the ends [74]. The 9-dimensional space has a central real one by itself, and is surrounded by four decoupled two-dimensional spaces. This structure of X-states says that, in any even dimension, the system’s density matrix may be viewed as $d/2$ independent U(2)s with one overall trace condition—whereas, in odd dimensions, there are $(d-1)/2$ such U(2)s and a central U(1), again with the trace condition. Similar and straightforward extensions to general qudit-quDit systems have been discussed in [74], with an enumeration of the parameter space involved. There remain many more connections to projective geometries and Clifford algebra to be explored.

6. Summary

The study of symmetries, Lie groups, and Lie algebras has a vast and rich history in physics. In the field of quantum information, SU($2^q$)—for q qubits—and SU($d^q$)—for higher-dimensional qudits—are of particular interest; as are their geometrical structures, which go beyond the single qubit’s Bloch sphere. To study evolution operators for their states, Hamiltonians, and logic gates, a compact procedure is given in Section 2.2 and capsuled by Figure 4. Furthermore, smaller sub-groups prove, often, very useful. We have discussed some of the important examples, such as SU(2) × U(1) × SU(2) for X-states of two-qubits. We have considered the frequently used Pauli spin operators for qubits, quaternions (and, to a lesser extent, octonions) and their groups, aspects of geometric algebra, finite projective geometries, and combinatorial designs; all of these can provide rich links and insights, as discussed in Section 3. This section includes a convenient binary labelling for states and operators, a rendering in terms of Dirac matrices and algebra, and a unified picture of these varied aspects. A parallel mathematical treatment is discussed in Section 4, and an immediate generalization to higher-dimensional qubits is indicated in Section 5—all of which are presented in terms accessible to a physics student. It is hoped that this paper may point towards further extensions and applications in the field of quantum information.