1. Introduction
Periodic bar-and-joint frameworks are mathematical models of crystalline materials, given by an infinite graph with vertices and edges, corresponding to atoms and bonds and subject to the action of a periodicity group. Precise definitions will be given in
Section 2. A framework may deform while maintaining the length of its edges.
With recent advances in additive manufacturing, efficient methods for recognizing and predicting the behavior along a deformation trajectory are gaining significance for the design of certain classes of metamaterials [
1,
2,
3,
4,
5].
The notion of auxetic behavior emerged from materials science and refers to lateral widening upon stretching [
6,
7,
8]. Usually, this type of structural deformation is discussed in terms of Poisson’s ratios [
9,
10,
11,
12], but for periodic frameworks, a strictly geometric theory of auxetics was introduced in [
13], leading to general structure and design theorems [
14].
Background. Mathematically, periodic frameworks may be considered in Euclidean spaces of arbitrary dimension
d. The periodicity group, represented by the rank
d lattice of translations of the framework structure, is fundamental in modern considerations [
15,
16]. It leads to a finite description (as a finite system of quadratic equations [
17,
18]) of the realization space of a
d-periodic framework, i.e., the space of all possible placements in
, for prescribed (squared) edge lengths and subject to the action of the abstract periodicity group. This positions the deformation theory of bar-and-joint periodic frameworks, from the very beginning, in the context of quadratically constrained structures. Feasibility and topology optimization problems arise quite naturally in this context [
19,
20,
21]. Spectrahedral cones, maxima and minima under quadratic constraints, are implicated in the larger picture of deciding the existence of infinitesimally auxetic deformations [
13,
14,
22], and a standard method for this purpose is semidefinite programming [
23,
24]. In [
25], we show that alternative algorithms are possible when more refined geometric information is employed.
Results. In this paper, we establish a correspondence between the infinitesimal deformations of a periodic bar-and-joint framework in a Euclidean space of dimension d and a system of quadrics in the same dimension. This leads to a simple method for detecting auxetic deformations, identified by a pattern of homothetic ellipsoids. Although not directly appealing to intuition, the correspondence provides new geometric insights on the relation between a framework configuration and its periodic deformations. For applications in dimension two or three, it gives a graphical tool for relating structure and functionality.
Overview. The main result is derived in
Section 2.
Section 3 presents specific examples related to planar periodic frameworks, commonly described as reentrant honeycombs. More involved arrangements of conics appear in
Section 4, where we apply the correspondence to uncover geometric characteristics of auxetic behavior. In
Section 5, we consider a structure endowed with higher crystallographic symmetry, introduced by T.-C. Lim, and determine the periodic arrangement of circles expressing its auxeticity.
2. From Infinitesimal Deformations to Quadrics
The general deformation theory of periodic frameworks is presented in [
17,
18], with summaries and various developments and applications available in [
13,
14,
26]. A periodic framework in dimension two is illustrated below in
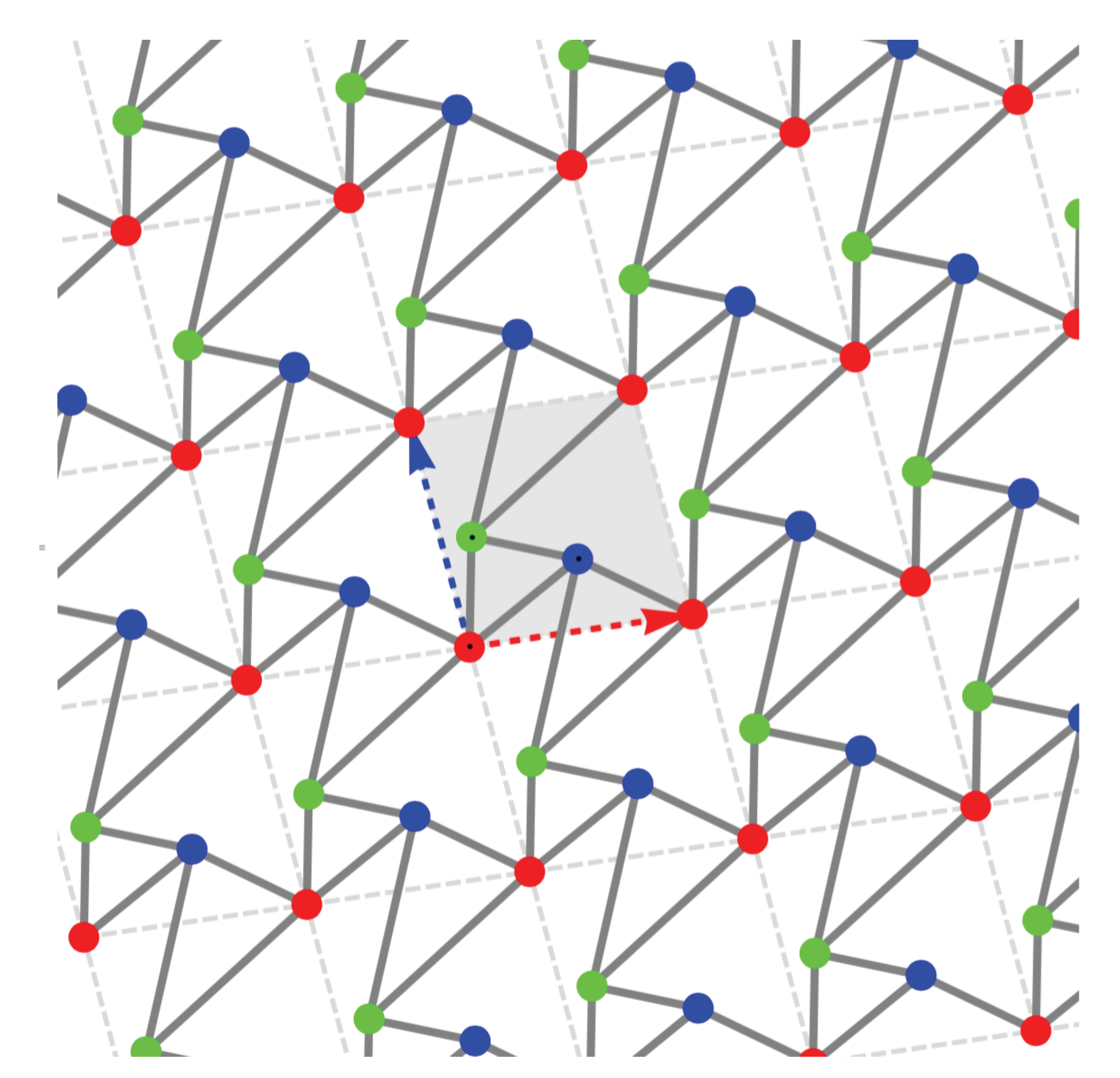
Figure 1.
Periodic frameworks. Let be a d-periodic graph, where is an infinite connected graph with vertex set V and edge set E and is a free Abelian group of rank d, which acts without fixed points on V and E, with finitely many vertex orbits and edge orbits .
A
d-periodic
framework is defined by a placement
of the vertices of
G in
and an injective group representation
of the periodicity group
in the translation group of
, with image
of maximal rank
d (when seen as an additive subgroup
). In addition, the following natural compatibility condition must be satisfied by the placement
p and periodicity representation
:
Frameworks obtained from one another by an isometry of are considered equivalent.
We assume non-degenerate placements, with all edges having distinct endpoints. We choose a complete set of representatives , … for vertex orbits and denote their placements as . We also choose a set of periodicity lattice generators , … and use the same notation for the matrix with column vectors .
In the example shown in
Figure 1, the red, blue and green points in the unit cell are the vertex representatives, and the two lattice generators are the red and blue dotted vectors defining the unit cell. All points in the same vertex orbit get the same color.
A
d-periodic framework
can thus be given by the placement of the vertex orbit representatives
…
and the periodicity matrix
. The edges of the framework are conceived as rigid bars, and in the given placement, they are represented by edge vectors of the form:
where
is an appropriate linear combination with integral coefficients of the generators
, i.e.,
where
is a column vector with integer entries. While we may have several edges between orbit
i and orbit
j, we keep the notation simple with the tacit understanding that all of these edges follow the same pattern in the linear systems implicated below. An explicit example will be given in
Section 3.
Deformations. The realization space of a
d-periodic framework, i.e., the space of all possible placements in
for prescribed (squared) edge lengths, is described by a system of quadratic equations:
Thus, the realization problem, asking for the existence of placements with
as assigned squared edge lengths, is cast as a feasibility problem with quadratic constraints [
19].
For a given periodic framework in , the configuration space is obtained from the realization space by factorization under Euclidean isometries, and the deformation space for is the connected component of the framework in this quotient space.
Infinitesimal deformations. In this paper, we are concerned primarily with infinitesimal periodic deformations, hence we will use a short route to the linear system defining them.
Note. By setting and keeping , we eliminate translations from the equivalence of frameworks and have only infinitesimal orthogonal transformations contributing trivial infinitesimal deformations.
The linear system for infinitesimal deformations is obtained from the condition that all edge vectors maintain their (squared) length, that is
in Equation (
2). This gives
, hence
where
…
and
denote infinitesimal displacements. Thus, infinitesimal deformations are solutions
of the system of
m equations of the form (
3) obtained from a complete set of representatives for edge orbits.
Correspondence with quadrics. Suppose now that
is a solution of the linear system (
3). To an edge vector
as above, we associate the following equation in
:
Lemma 1. For , the Equation (4) is just another form of Equation (3). Proof. Direct computation gives
□
Remark 1. This simple verification leads to the following considerations.
- (i)
In general, Equation (4) defines a quadric
in , passing through the origin. With the understanding that degenerate cases may occur, namely for skew-symmetric, we shall refer to (4) as a quadric. - (ii)
For an infinitesimal deformation, all edge vectors from to orbit j produce the same quadric (4). Thus, when the origin is translated to , the quadric passes through and all its connections in orbit j. - (iii)
Trivial infinitesimal deformations are given by some infinitesimal orthogonal transformation and have the form , . The corresponding equations (4) become tautological equations . Thus, trivial infinitesimal deformations do not contribute associated quadrics: infinitesimal deformations, which differ by trivial infinitesimal deformations, have the same associated quadrics. - (iv)
When we look from to connected vertices in orbit i and use the reverse edge vector to write the associated quadric, then, modulo periodicity, the quadrics traced through orbit i for turn into the quadrics traced through orbit j for by central symmetry in the midpoint of any edge representative for .
- (v)
the symmetric matrix does not depend on the choice of periodicity generators and is not affected by addition of a trivial infinitesimal deformation. This allows the definition of a signature of an infinitesimal deformation as the signature of the symmetric matrix (number of positive, null and negative eigenvalues).
A more formal way of expressing these results is the following.
Theorem 1. Let be a periodic framework in . Assume as above that describes the placement of the vertex representatives (with ) and the periodicity matrix (via d generators). Then infinitesimal deformations are described by solution vectors of the linear system (3). The linear map:associates to any oriented edge vector from vertex orbit i to vertex orbit j, one and the same polynomial in of total degree at most two and vanishing constant term , which satisfiesand is identically zero for trivial infinitesimal deformations. This provides an intrinsic correspondence from the infinitesimal deformation space at and a periodic arrangement of quadrics (or possibly lines) resulting from depicting, for each edge representative, the pair of quadrics passing through one end and associated to the edge vector going to the other end. When retaining only the quadratic part of i.e., the Hessian, we obtain the signature invariant of the infinitesimal deformation.
3. Arrangements of Conics
We illustrate the correspondence described above with a planar periodic framework commonly called a
re-entrant honeycomb. The framework has
orbits of vertices and
orbits of edges. In
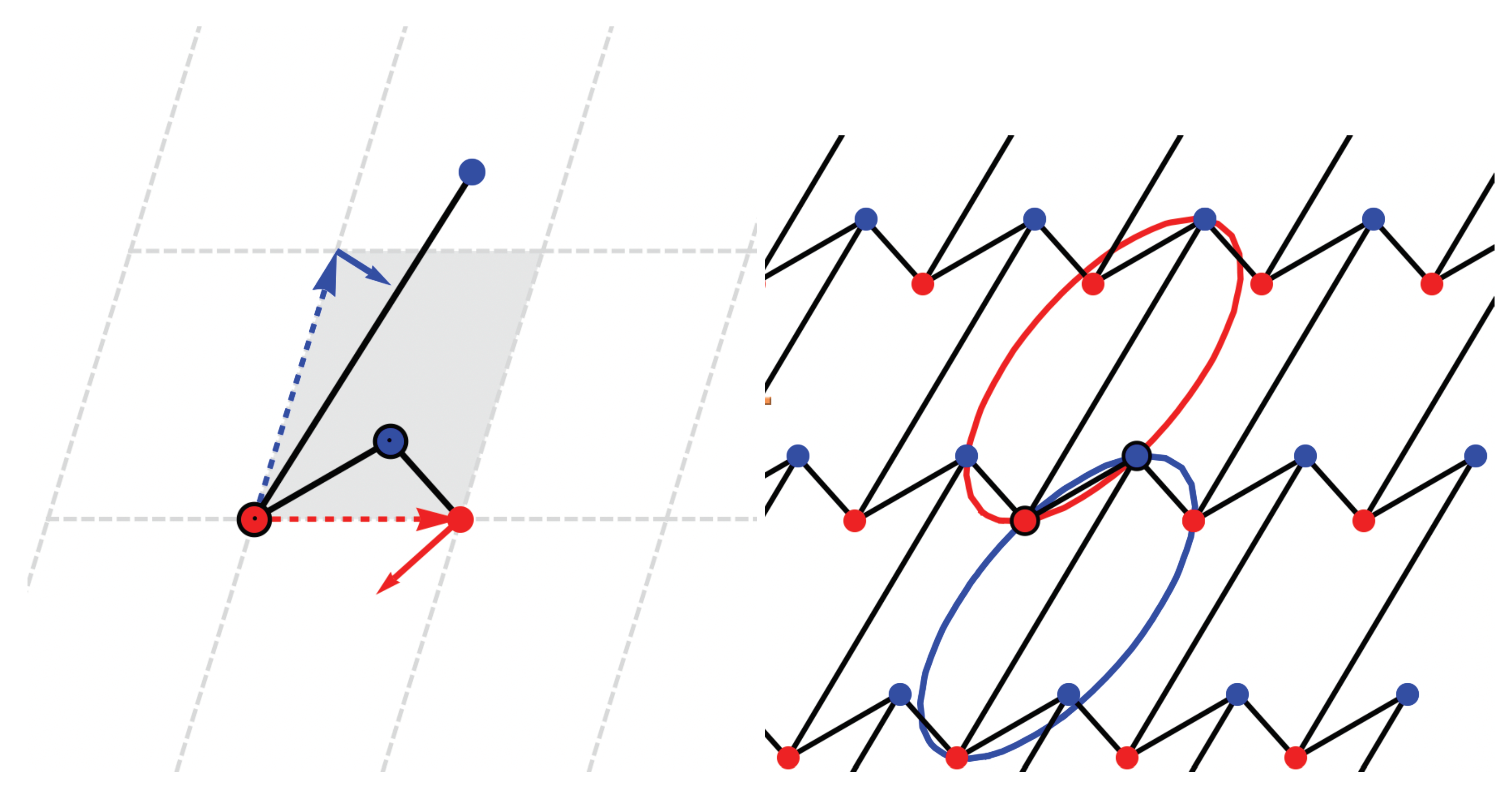
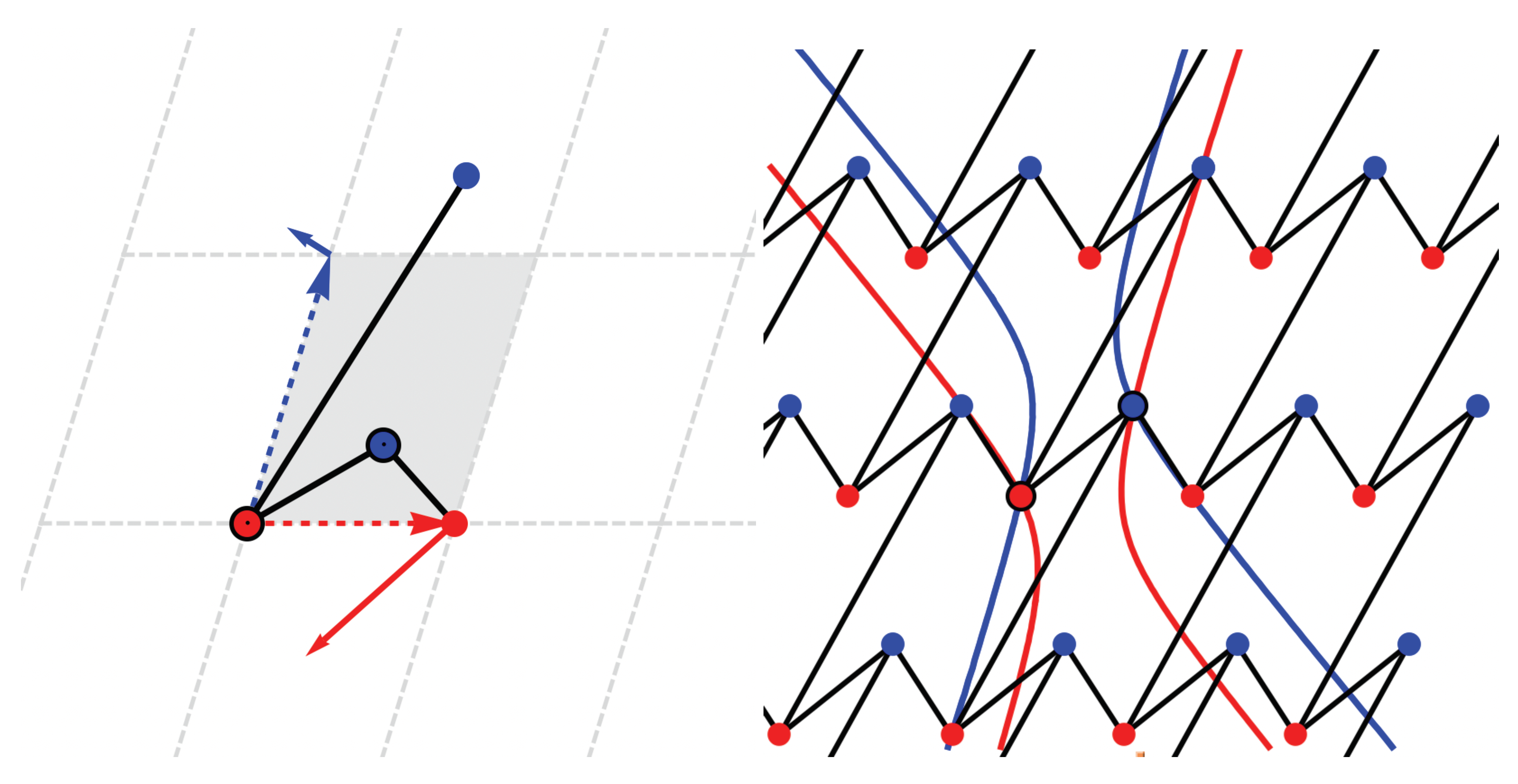
Figure 2 and
Figure 3, the two oversized red and blue points inside the unit cell are the vertex representatives. The red vertex at the origin is fixed. The two generators of the periodicity lattice are shown as dashed arrows, and the three edge representatives are solid segments. A unit cell is shaded. Thus, we have in a simple diagram all the information needed for generating the periodic framework.
The specific case used for
Figure 2 and
Figure 3 is obtained from the following data. The two vertex representatives
are at
(red, oversize), respectively,
(blue, oversize). The periodicity lattice generators are the vectors
and
. The three edge representatives, all three from
to orbit 1, are here denoted by
and have three different integer vectors
involved in the edge equations (
1):
,
and
. We have
and put
,
,
. System (
3) becomes:
The system has three independent equations, hence a three-dimensional solution space, with a one-dimensional subspace of trivial infinitesimal deformations produced by infinitesimal rotations. We factor out this subspace by assuming that both vertex representatives are fixed, hence . We are left with two independent equations for the four unknowns , and this shows that the space of infinitesimal deformations is two-dimensional.
In
Figure 2 and
Figure 3, we illustrate two instances of infinitesimal deformations through their effect on the periodicity generators. Next to them, on the right hand side, are the corresponding conics. To avoid overcrowding the image, we showed only two representative conics, modulo periodicity. The figure on the left is also widely simplified: it depicts only the periodicity lattice generators and the three edge representatives.
Remark 2. This case, in which we have just two vertex orbits and edges are from one orbit to the other, is the simplest possible illustration of a periodic framework, yet very revealing. Central symmetry with respect to the midpoint of any edge will exchange the two orbits, but take the image framework to itself. Modulo this transposition of the orbits, we have just one linear system of quadrics to consider, as given by the linear map (6). Geometrically, the linear system of quadrics passing through one vertex and all its connections in the other orbit is the expression of the projective infinitesimal deformation space. Thus, for the re-entrant honeycomb, we have an infinitesimal deformation space of dimension two, which gives a one-dimensional projective infinitesimal deformation space expressed as the pencil of conics passing through four points, e.g., a red vertex and its three blue connections, as can be seen in the figures.
4. Applications to Auxetic Behavior
Geometric auxetics. We review briefly the main elements of the geometric theory of auxetics introduced in [
13].
The
matrix of periodicity generators
, described in
Section 2, has an associated Gram matrix
and the map
, as a map from the deformation space of
to
, the vector space of symmetric
matrices, will be called the Gram map. The differential of this map at
gives a linear function from infinitesimal deformations of
to symmetric
matrices. A fundamental criterion, established in [
13], shows that infinitesimal auxetic deformations are exactly those mapping to positive semidefinite matrices. When the image is positive definite, we speak of strictly auxetic infinitesimal deformations.
A central problem in geometric auxetics is concerned with the existence of auxetic one-parameter deformations of a given periodic framework
. The infinitesimal version becomes a feasibility problem in semidefinite programming [
25].
This approach, further developed in [
14], shows that the correspondence exhibited in
Section 2 reveals more geometric structure on the vector space of infinitesimal periodic deformations of
. At the same time, it shows that, when auxetic capabilities are present, there is a cone of infinitesimal auxetic deformations and its image in
is a spectrahedral cone accessible via semidefinite programming [
23,
24].
Reformulation. The correspondence presented in
Section 2 permits a reformulation of the condition given in [
13] for the auxetic behavior of a framework, in terms of the signature of the infinitesimal deformations, namely: a deformation path is strictly auxetic when, at every instance, the corresponding infinitesimal deformation has top signature. This means that all associated quadrics are ellipsoids. We observe right away that all these ellipsoids must then be
homothetic, that is, any two of them differ at most by some translation and dilatation. This is not necessarily the case for other signatures, as shown below in our examination of two instances on the deformation trajectory of a Kagome framework.
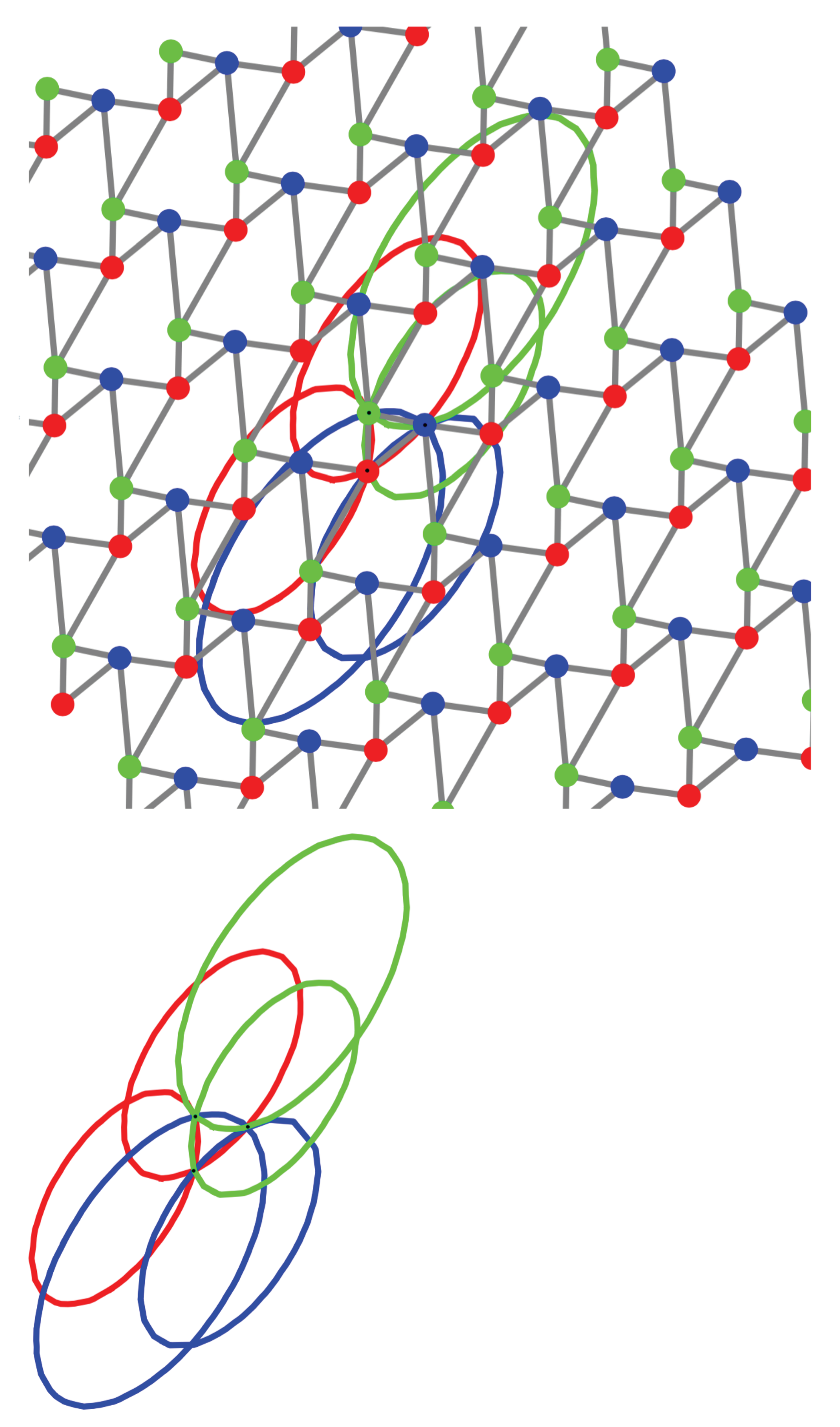
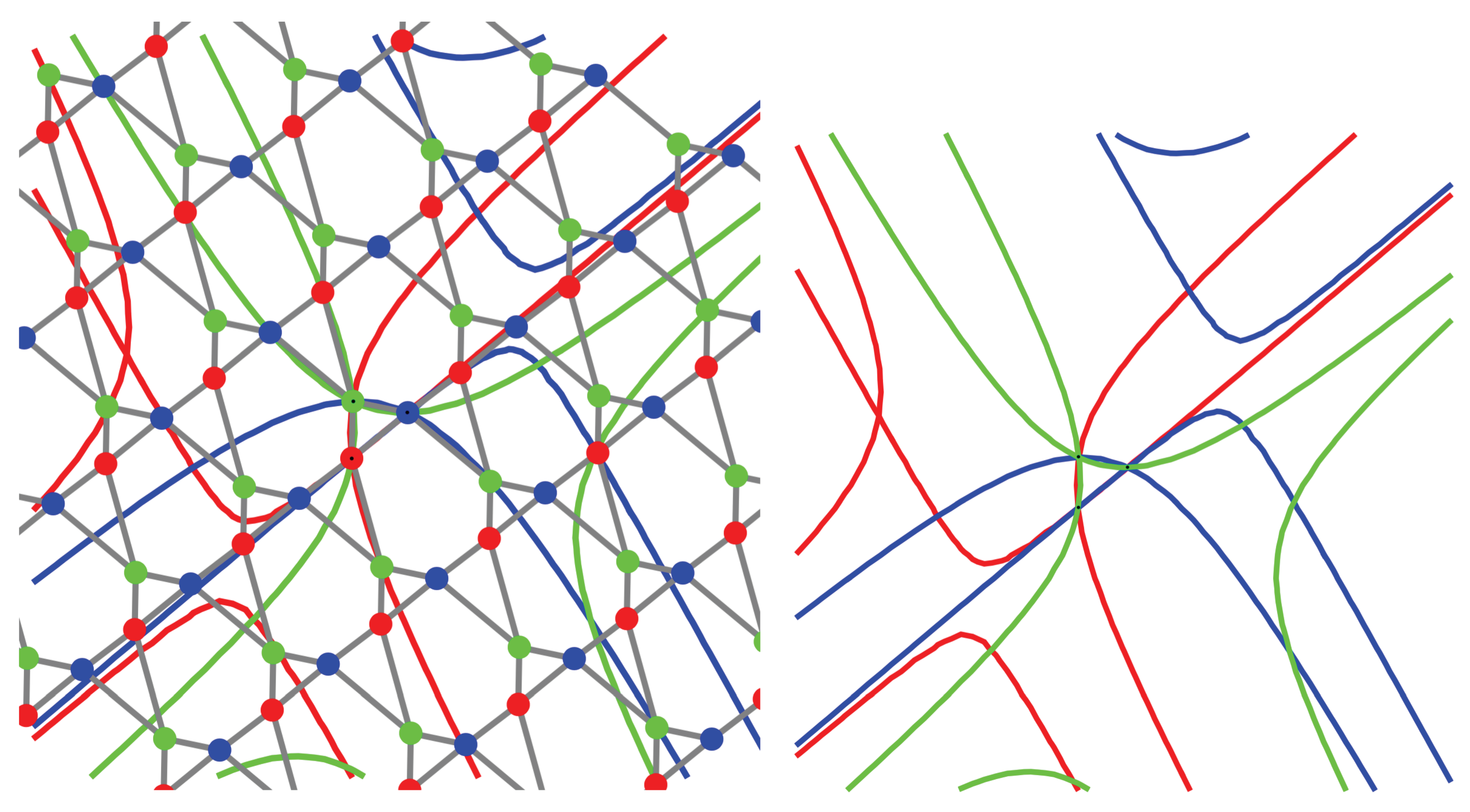
Example 1. We focus here on this type of planar periodic frameworks for graphical convenience and relevance in different areas [27,28]. A Kagome periodic framework has vertex orbits and edge orbits. The quotient multigraph is a triangle with doubled edges. The deformation space is one-dimensional and, for any given configuration, there is, up to proportionality, a single non-zero infinitesimal deformation. In
Figure 4 and
Figure 5, we illustrate six of the conics associated to a given configuration. For each of the three vertex orbits, there are two conics passing through that vertex representative and one of the two other remaining orbits. The coloring scheme respects the color of the first vertex representative.
In
Figure 4, we illustrate an arrangement where the associated quadrics are homothetic ellipses, and this indicates that the configuration is auxetic.
In
Figure 5, the conics are hyperbolas, hence the configuration is not auxetic. As mentioned earlier, when the signature of the infinitesimal deformation is mixed (with one positive eigenvalue and one negative eigenvalue in our case), the quadrics are not necessarily all homothetic. This is visibly happening in the illustrated arrangement of hyperbolas.
Algorithmic implications. The previous discussion shows that the correspondence between infinitesimal deformations and quadrics may be used for an effective recognition algorithm of auxetic capabilities in periodic frameworks (see also [
25]). Indeed, the presence of infinitesimal deformations of top signature can be determined by sampling the connected components in the complement of the vanishing locus of the Hessian of
, (cf. Theorem 1).
5. An Arrangement of Circles
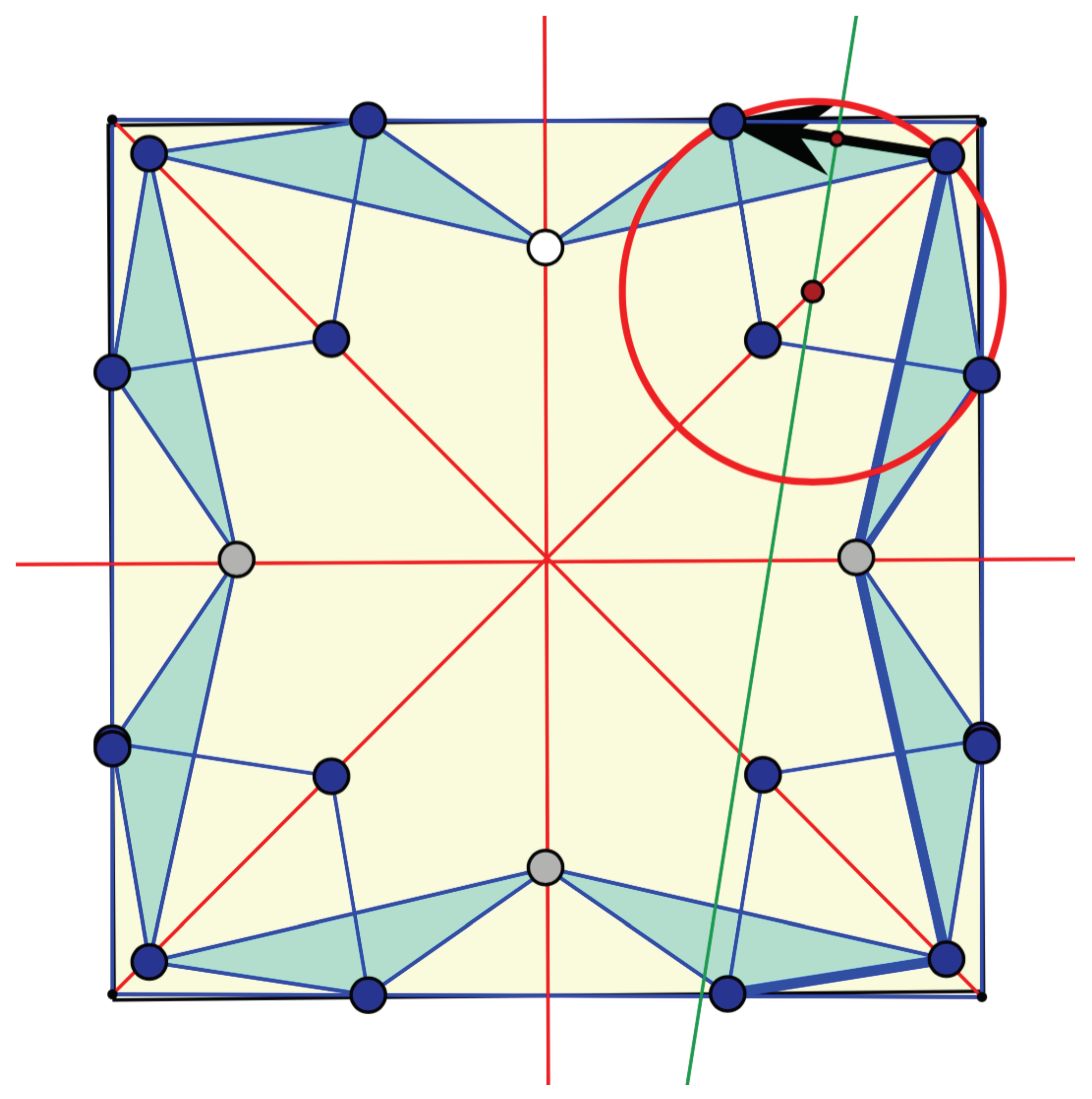
In this section, we illustrate the special case when the auxeticity criterion developed in the previous section yields circles for the homothetic ellipses. We use a planar periodic framework introduced by T.-C. Lim [
29], which has several distinctive features:
- (i)
it has one degree of freedom,
- (ii)
the deformation of the framework is auxetic and
- (iii)
throughout its deformation path, the framework maintains a planar crystallographic symmetry with point group , the dihedral group of order eight which describes the symmetries of a square.
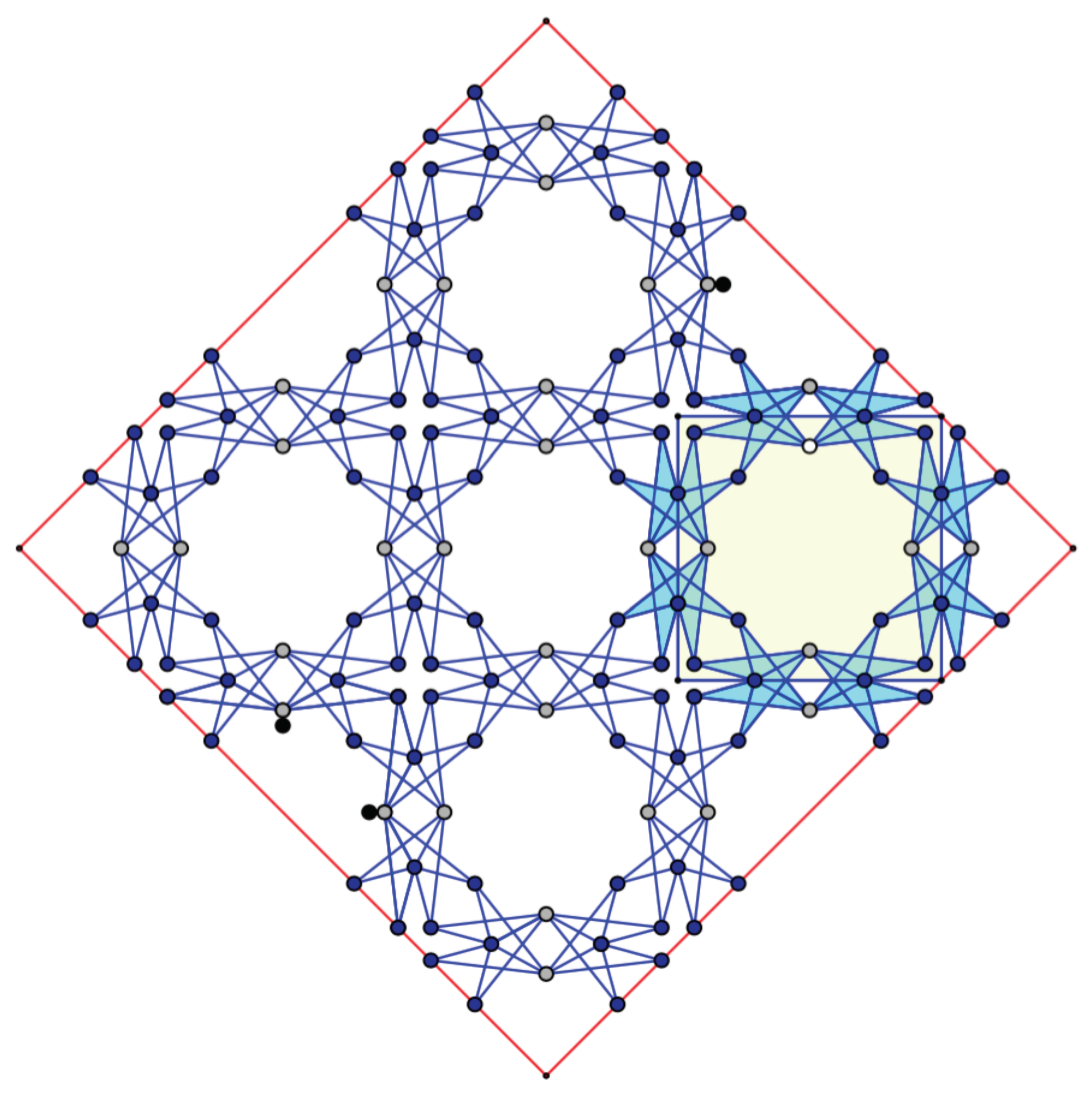
In
Figure 6 and
Figure 7, the structure is illustrated as a bar-and-joint periodic framework, after converting Lim’s Y-elements into equivalent five-bar rigid pieces consisting of two isosceles triangles with angles
, which share a short edge. With notations introduced above in
Section 2, we have
orbits of vertices and
orbits of edges under periodicity. Thus, the resulting quadratic system (
2) is over-constrained, but the linear dependence relations within the system (
3) describing the infinitesimal periodic deformations lead, ultimately, to a single degree of freedom. We do not insist here on computational details, since the resulting auxetic deformation mechanism and the preservation of the crystallographic symmetry along the deformation path are already covered in [
29].
Circles and crystallographic symmetry. Our present goal is to identify and depict the periodic system of conics associated to the framework. This task is considerably simplified by the presence of higher crystallographic symmetry [
16,
30]. More precisely, when we use the square unit cell shown in
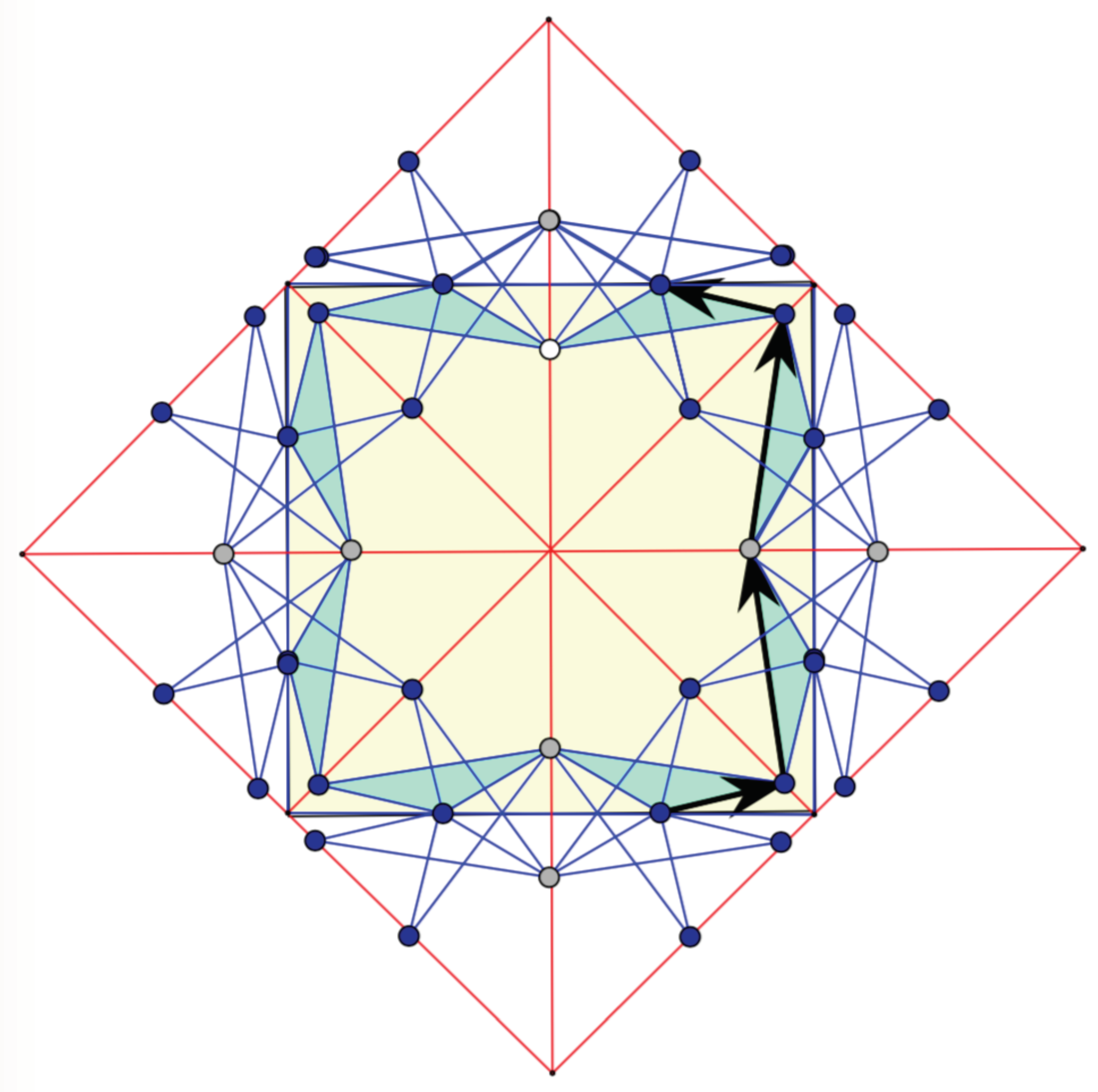
Figure 7, the point group
is represented by the symmetry group of this square (generated by reflections in midpoint axes and diagonals). Further crystallographic symmetries of the framework are provided by reflections in the sides of the unit cell.
Since the association described in Theorem 1 is intrinsic, the periodic arrangement of conics for (a non-zero infinitesimal deformation of) the framework under consideration will have the same crystallographic symmetries. Moreover, since the infinitesimal deformation is strictly auxetic, all conics must be homothetic ellipses. Given that has a rotation by , all ellipses must be circles.
The quotient graph
is a simple graph in our case, with an induced action of the point group
. Thus, it is enough to examine a single half-quadrant in
Figure 7.
Further reductions. We turn to additional relations in the family of homothetic ellipsoids associated to a strictly auxetic infinitesimal deformation. The following property was first established in [
14] and is a consequence of formulae (
4).
Proposition 1. Let a strictly auxetic infinitesimal deformation and its associated arrangement of homothetic ellipsoids be given. For any oriented cycle on the quotient graph, let be oriented edge representatives for the constituents of the cycle and let denote the vector from the origin of the edge to the center of the ellipsoid associated to that oriented edge (and passing through both its endpoints). Then, the sum of the vectors over the cycle vanishes.
We apply this proposition to the planar case under consideration, where all ellipses are circles. If the cycle comes from an oriented triangle in the framework, we have the following count of parameters. The centers for the three circles associated to the oriented edges must be on the corresponding perpendicular bisectors, hence there are three parameters to be determined. Proposition 1 gives a vector relation, i.e., two constraints between the parameters. This leaves a single parameter to be determined. In other words, one center determines the other two.
The five-bar linkage corresponding to a Y-element is made of two triangles with a common edge. Thus, the five centers for a given orientation require only the determination of a single center, on its perpendicular bisector. There are two such five-bar linkages in every half-quadrant of
Figure 7, one being the reflection of the other in the crossing cell-edge. By crystallographic symmetry, the centers for one linkage determine the centers for the reflected one. Hence, the configuration of centers in a half-quadrant requires the determination of a single parameter.
Summary of reductions. Based on crystallographic symmetry and Proposition 1, the configuration of centers for the arrangement of circles associated to our framework (deforming infinitesimally along its path) amounts to the determination of a single parameter, i.e., a single center determines the entire configuration of centers.
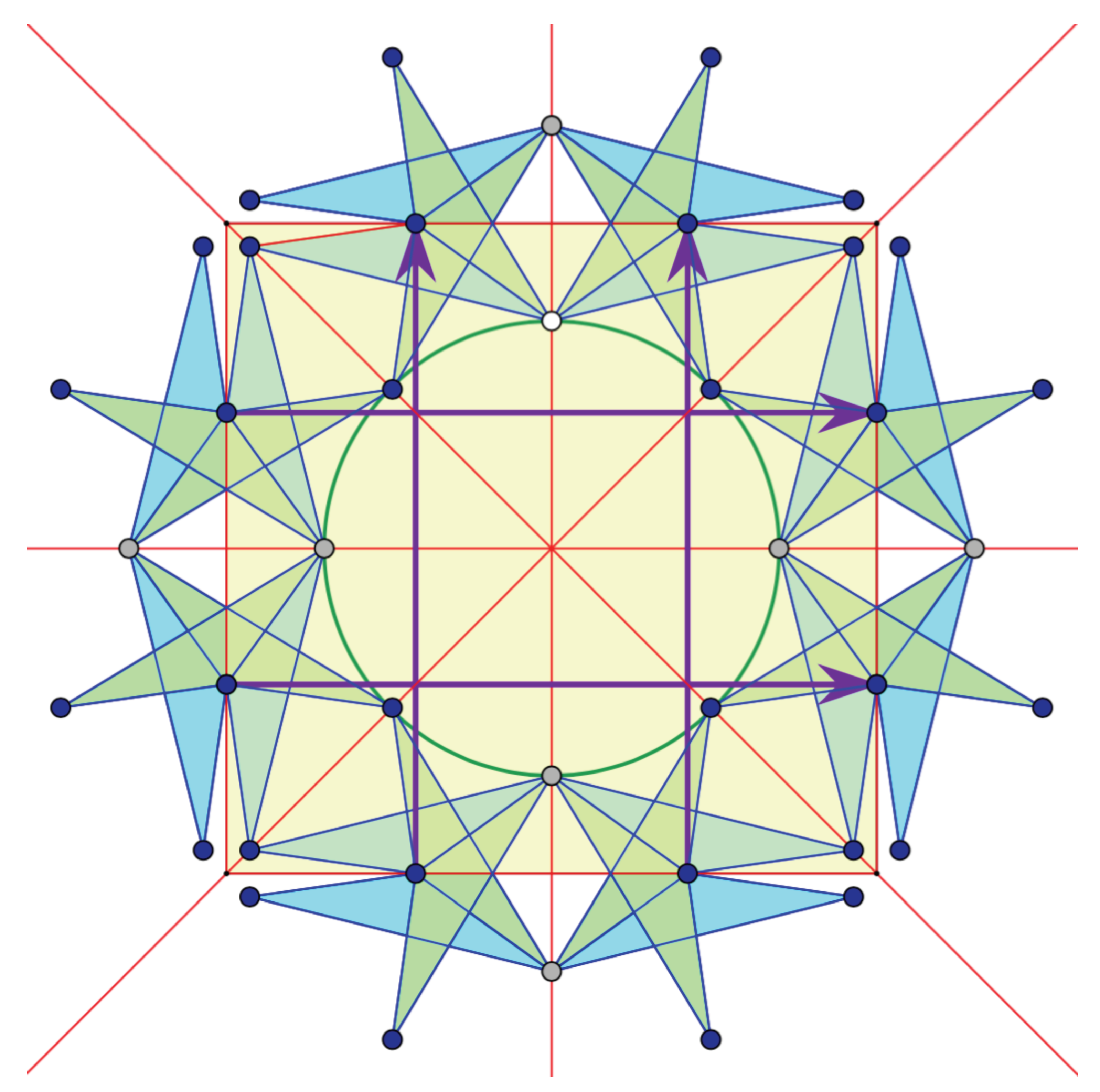
Our final step, which consists in finding the position of one center, will use Proposition 1 for a 4-cycle on the quotient graph. An oriented 4-path of the framework which produces this cycle is marked with black arrows in
Figure 8.
The next proposition and
Figure 9 describe the outcome of this last step.
Proposition 2. For the oriented edge shown in Figure 9, the associated circle has its center on the diagonal of the square unit cell passing through the origin of the edge. Remark 3. The identified circle passes through a third vertex of the framework, besides the endpoints of the oriented edge. This vertex is the reflection of the arrow marked endpoint of the edge in the diagonal. The three vertices are collinear for the configuration with maximal unit cell area, which must have degenerate associated conics. Indeed, at this limit of the auxetic deployment, the radius reaches infinity and the circle degenerates into a line.
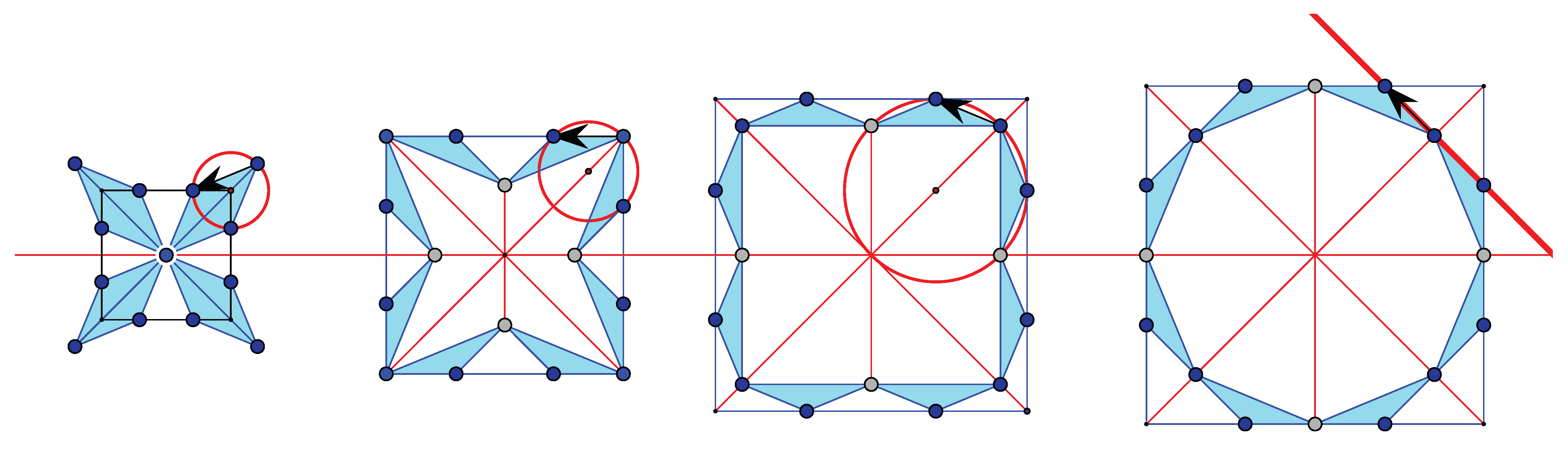
We illustrate in
Figure 10 the progress of the unit cell from a folded configuration of the 8-ring of triangles to the deployed configuration, which obtains the maximal unit cell area.
The unfolding process over this auxetic interval increases the unit cell area by a multiplicative factor of .