Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs
Abstract
:1. Introduction
2. Models and Methods
2.1. The Model
2.2. The Method
2.3. Simulation Details
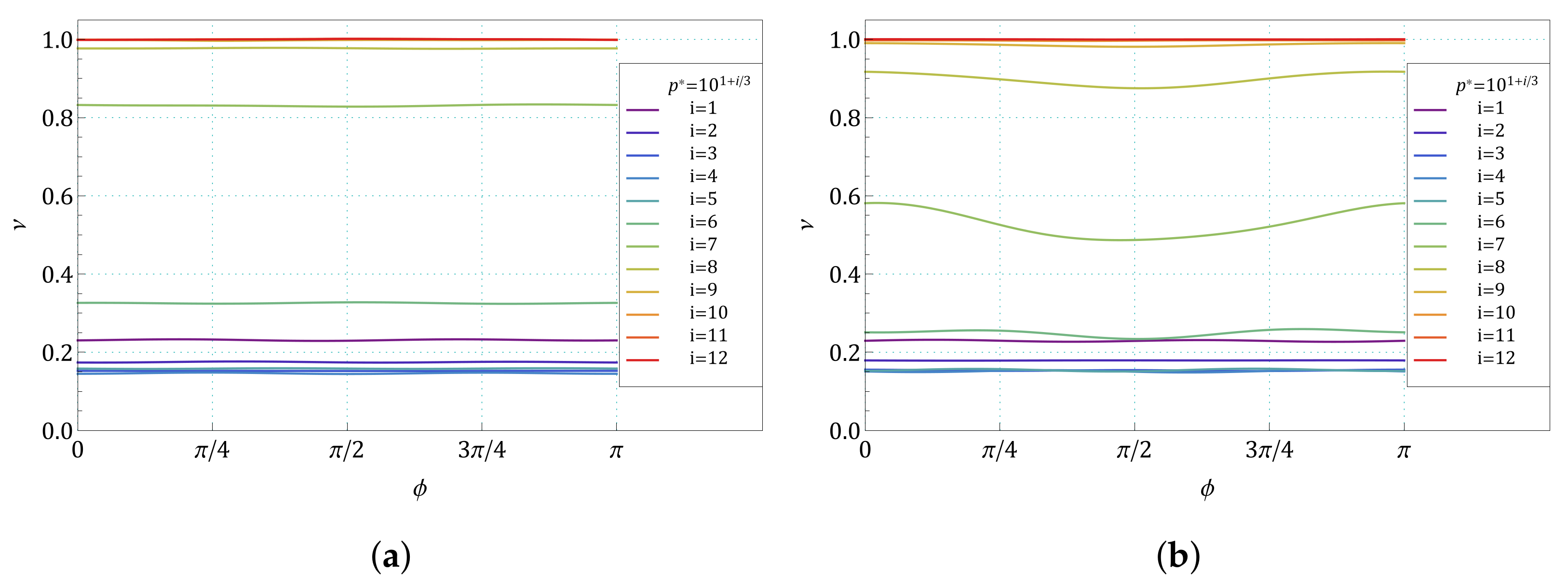
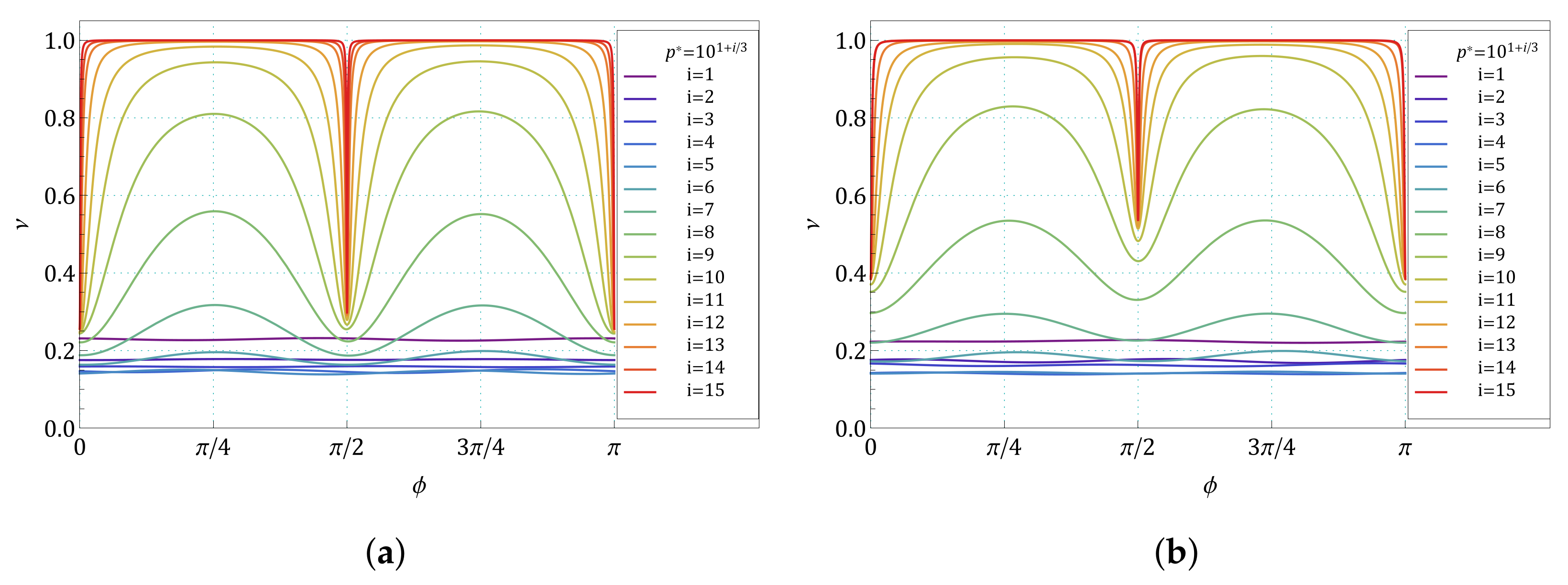
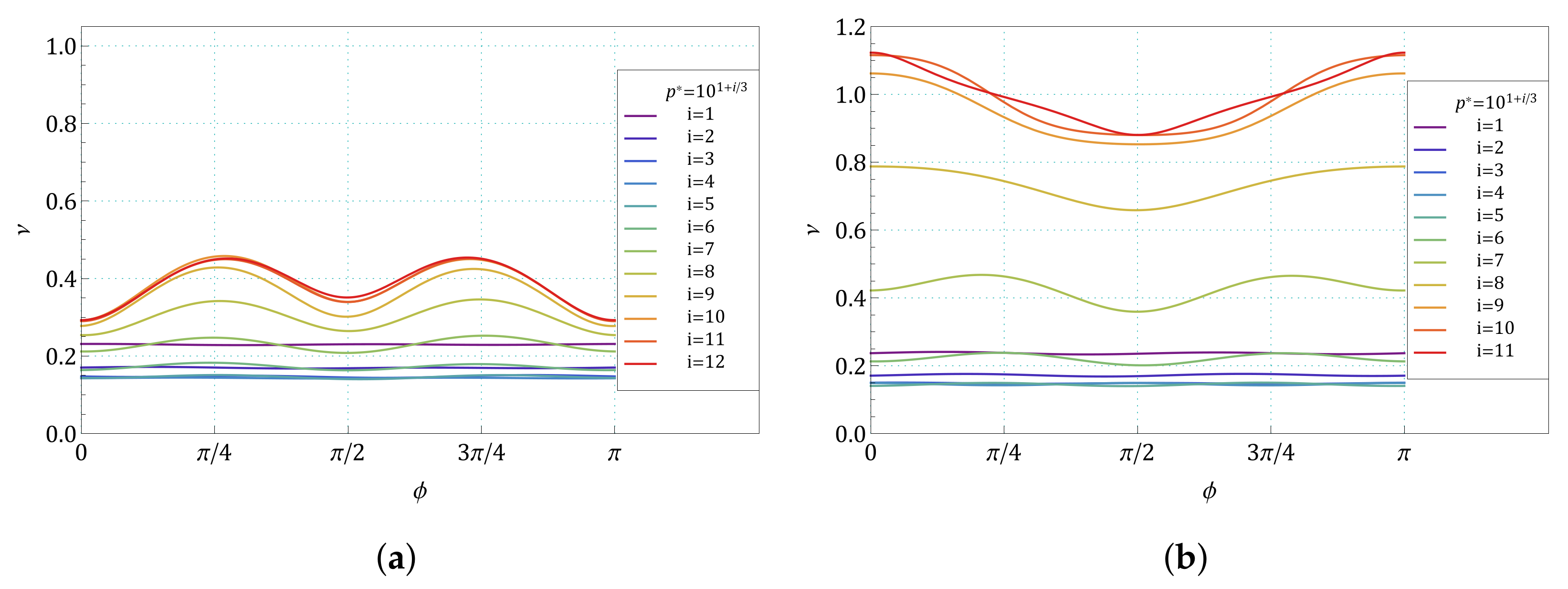
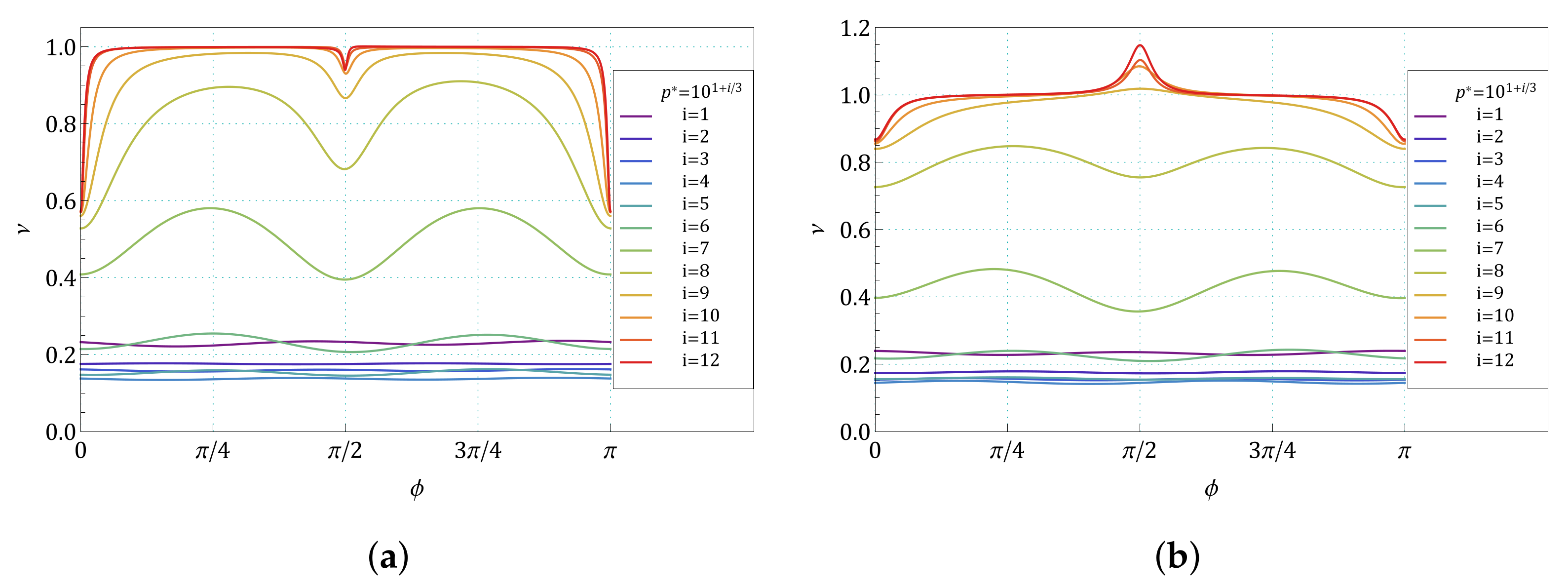
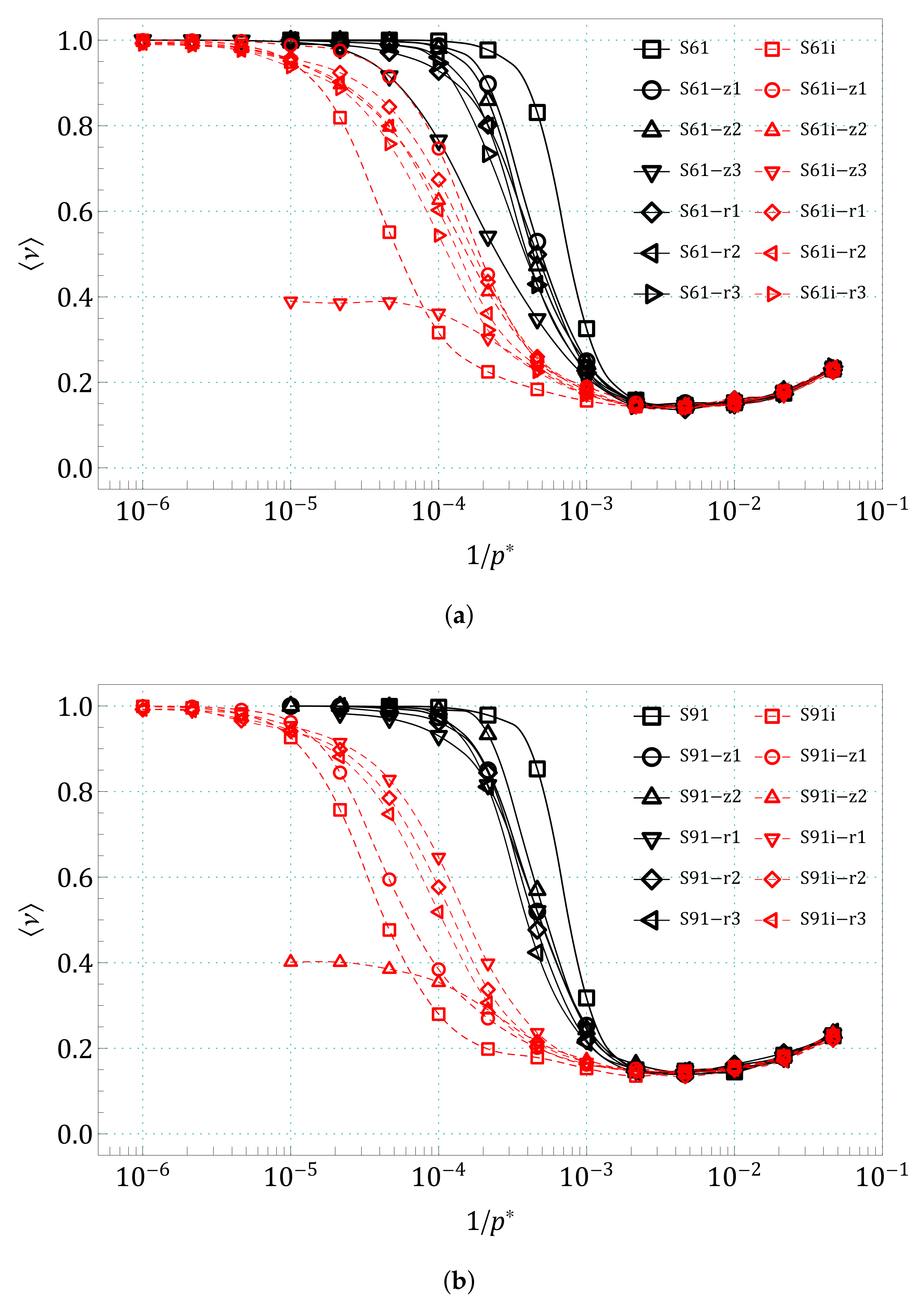
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PR | Poisson’s ratio |
| 2D | two-dimensional |
| 3D | three-dimensional |
| HD | hard disc |
| MC | Monte Carlo |
| isobaric-isothermal ensemble | |
| r | re-entrant |
| z | zigzag |
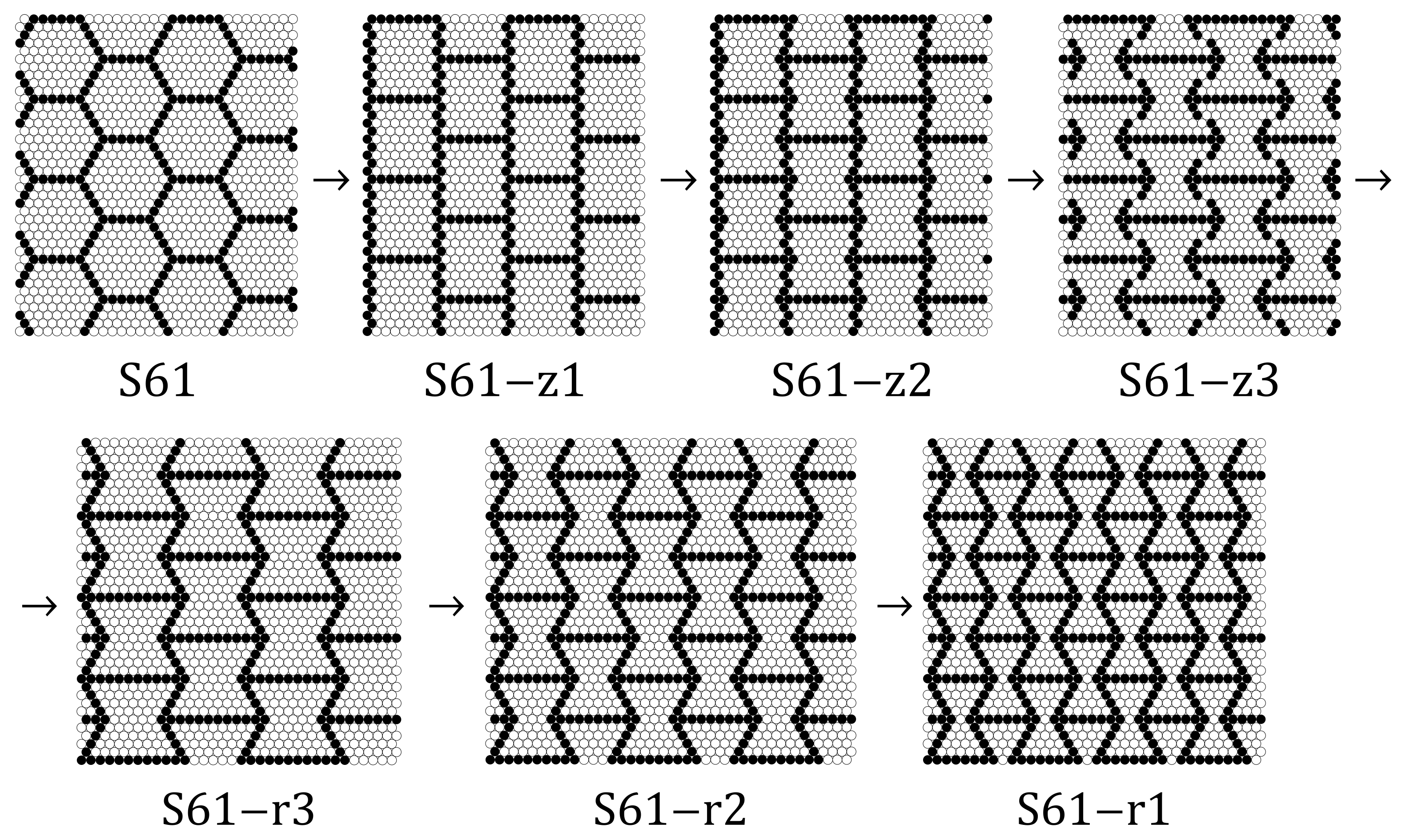
Appendix A. Images of Modified S61 and S91 Structures, Studied in the Work
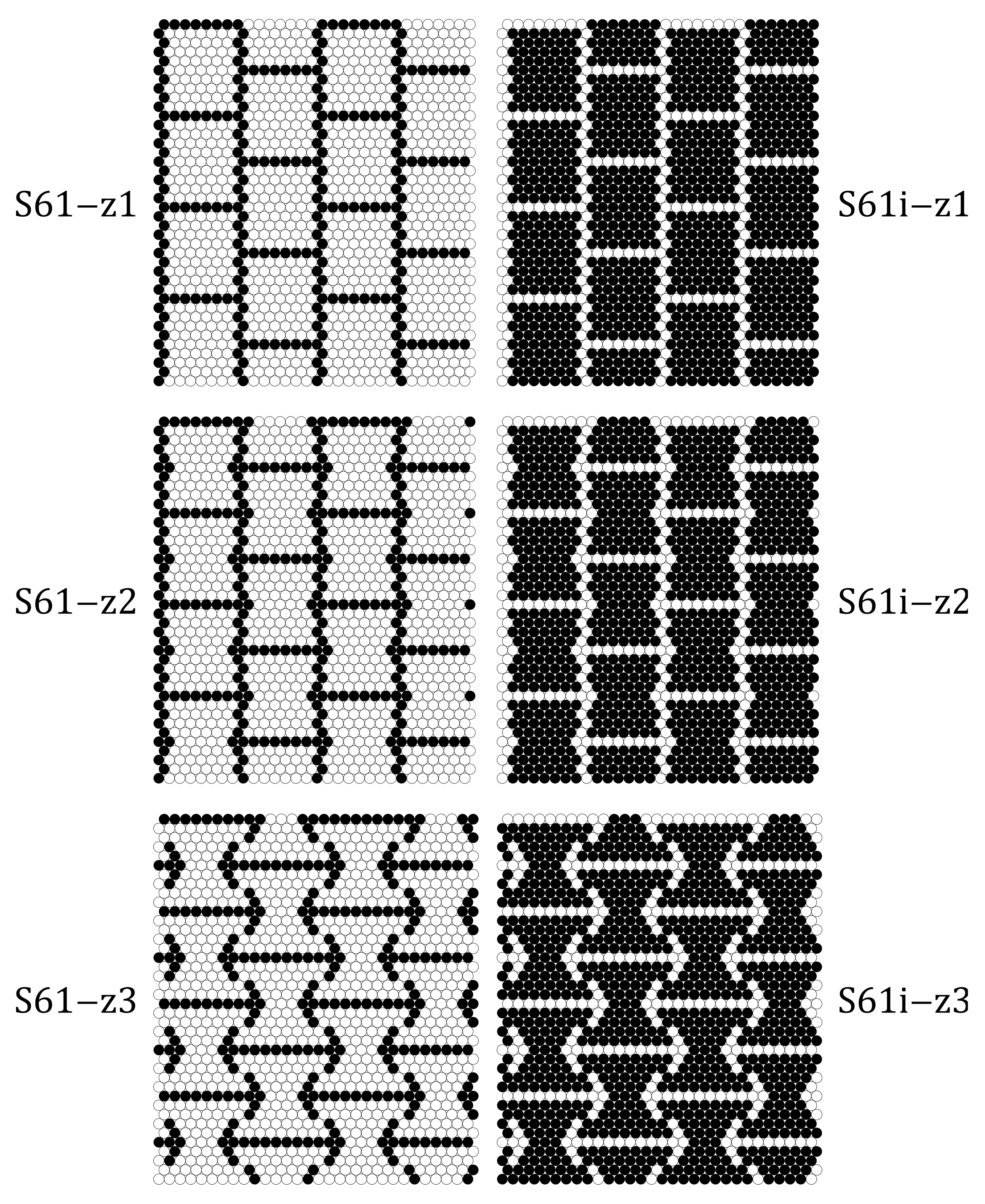



Appendix B. The Summary of Angle Dependence of Poisson’s Ratio, ν(ϕ), and Pressure Dependence of Average Value of Poisson’s Ratio, 〈ν(1/p*)〉, for All Pressures and for All the Structures Studied in the Work
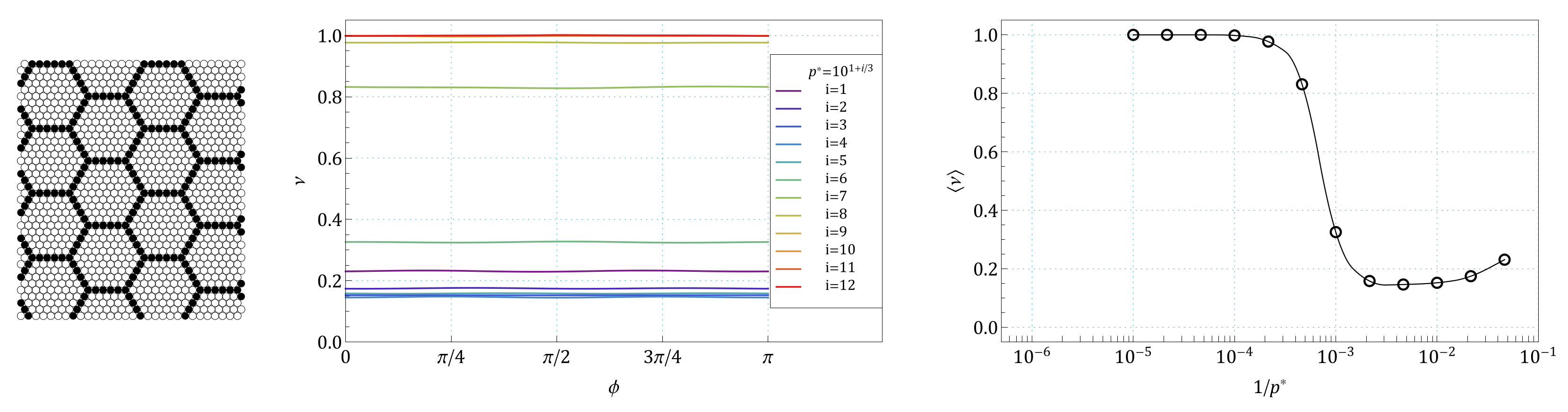
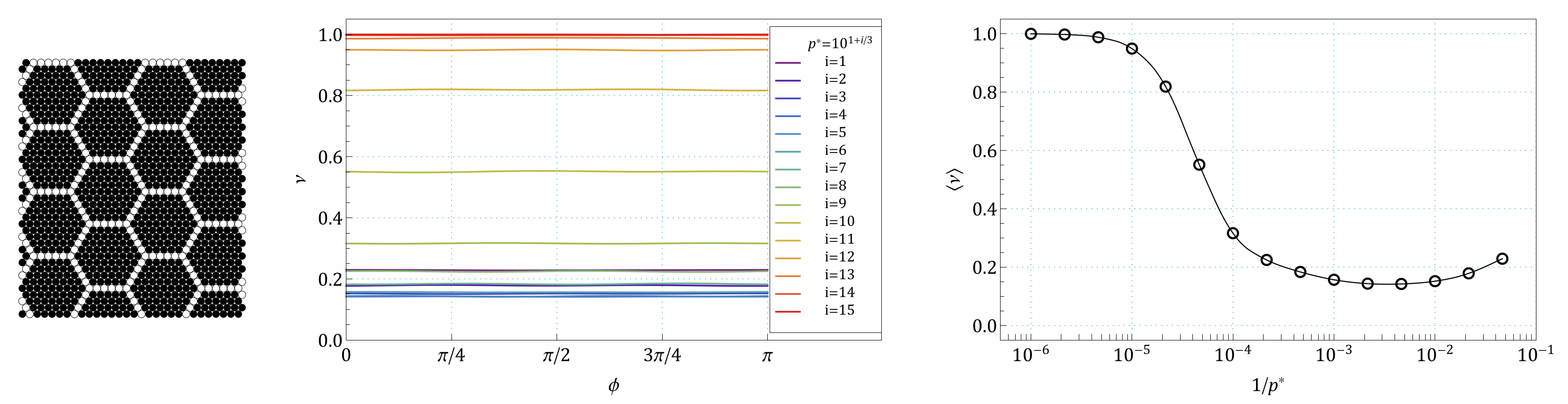
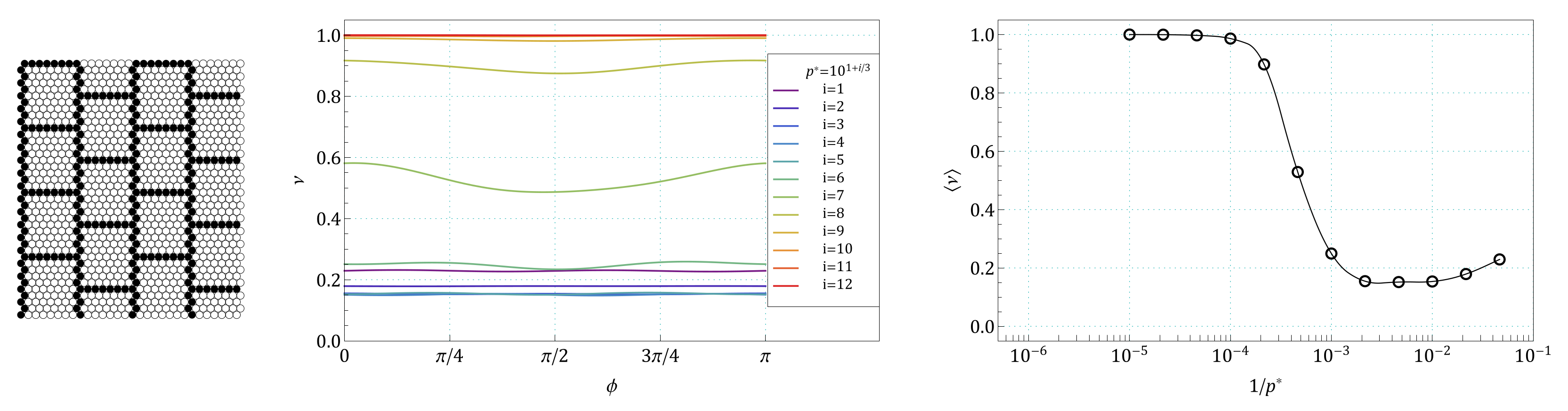

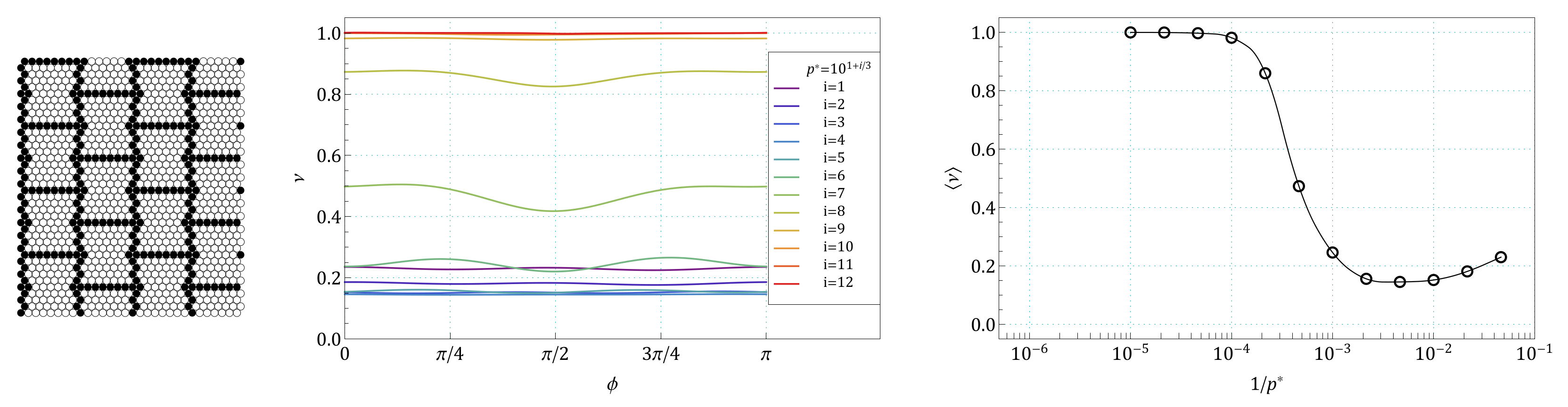
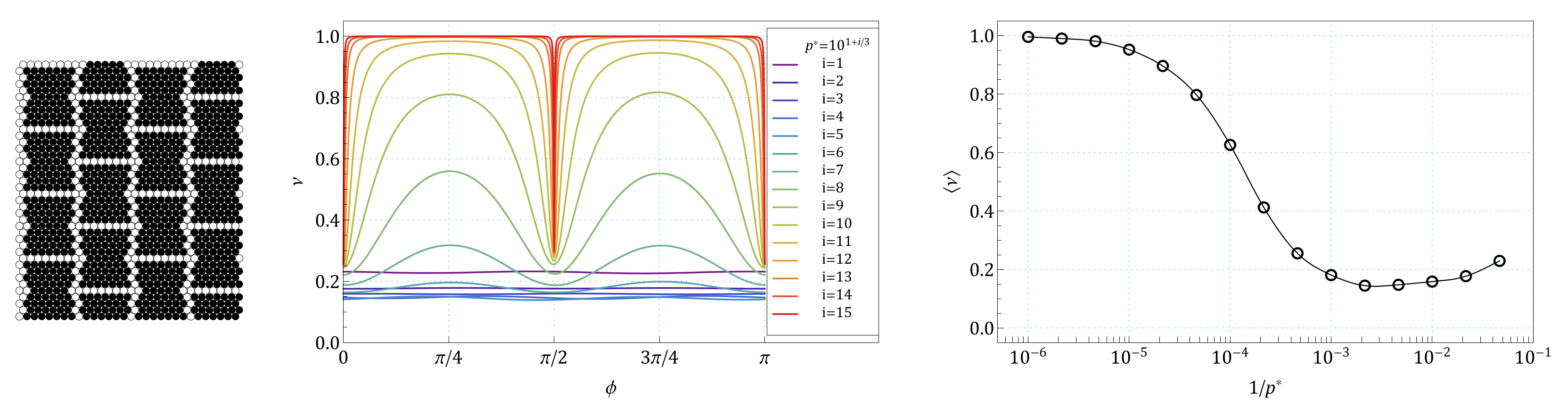



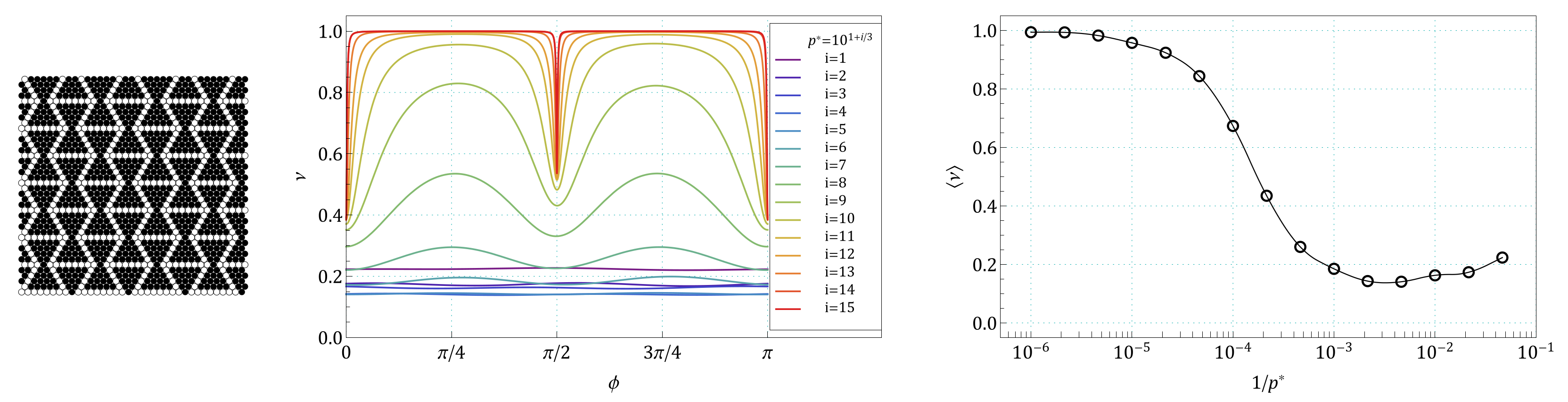
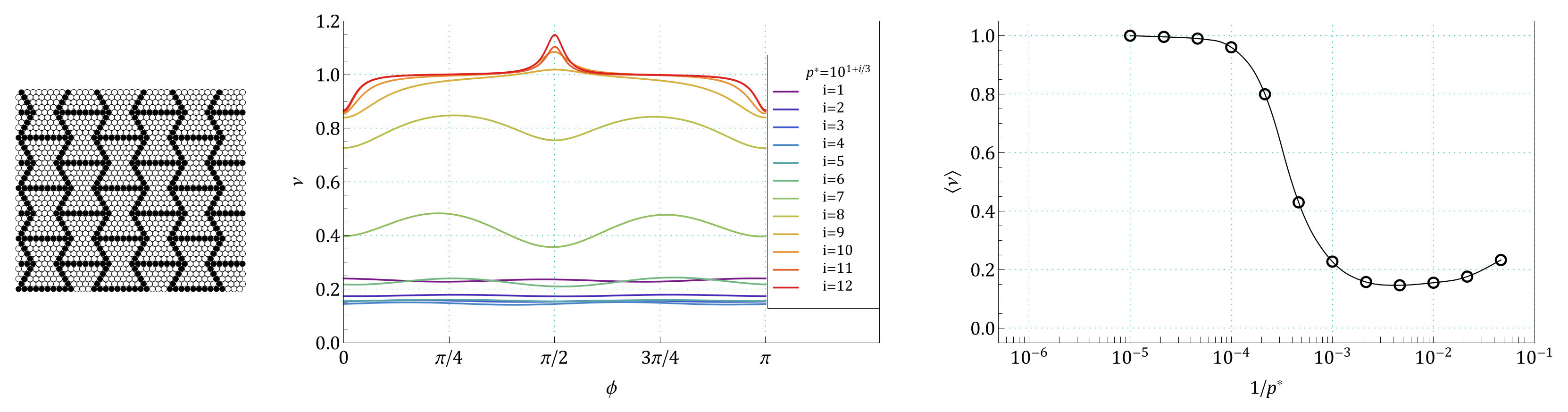
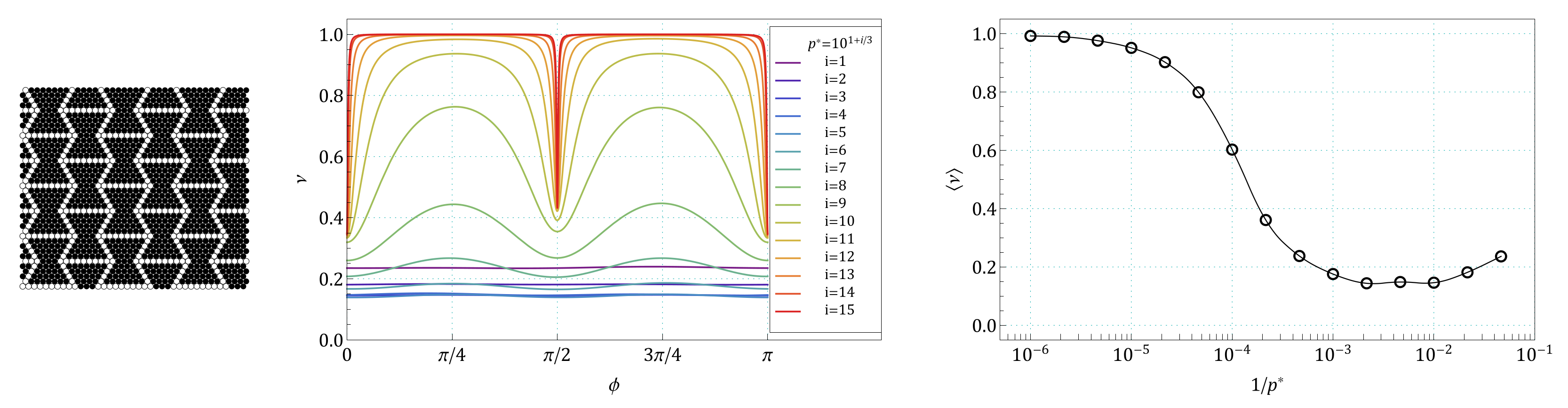
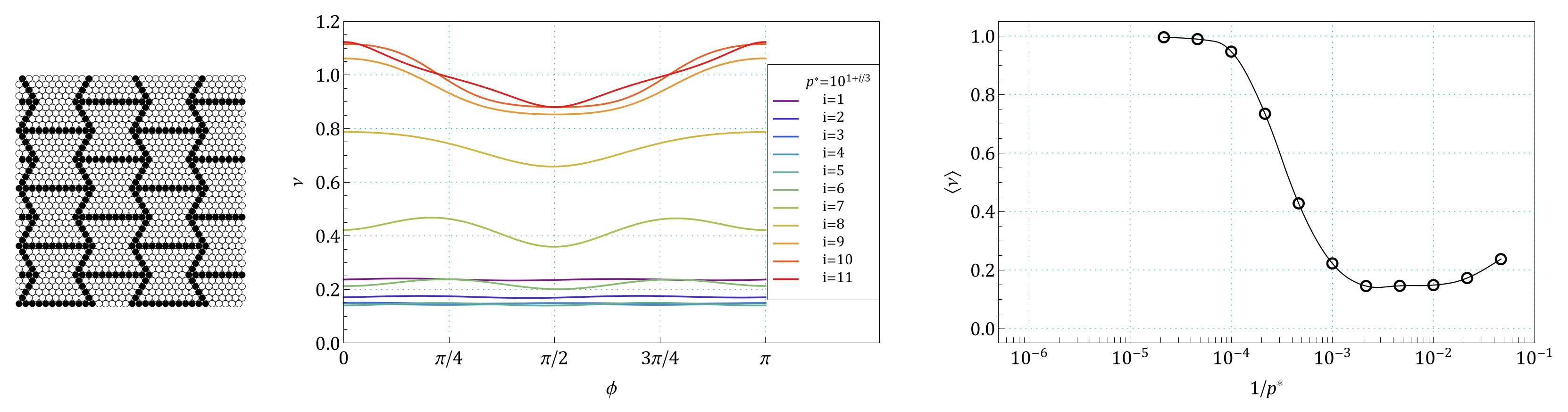
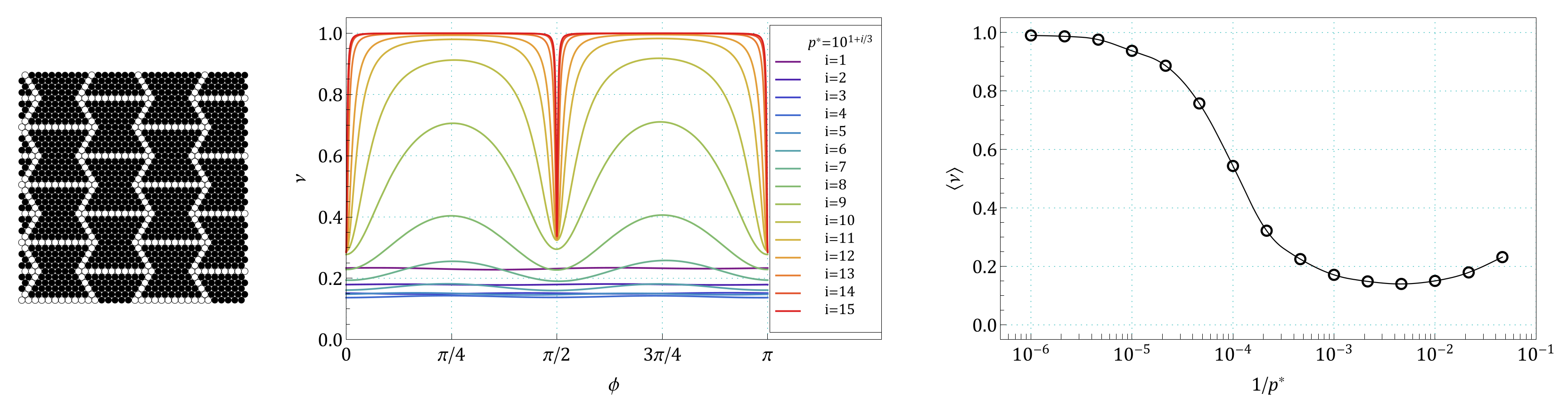
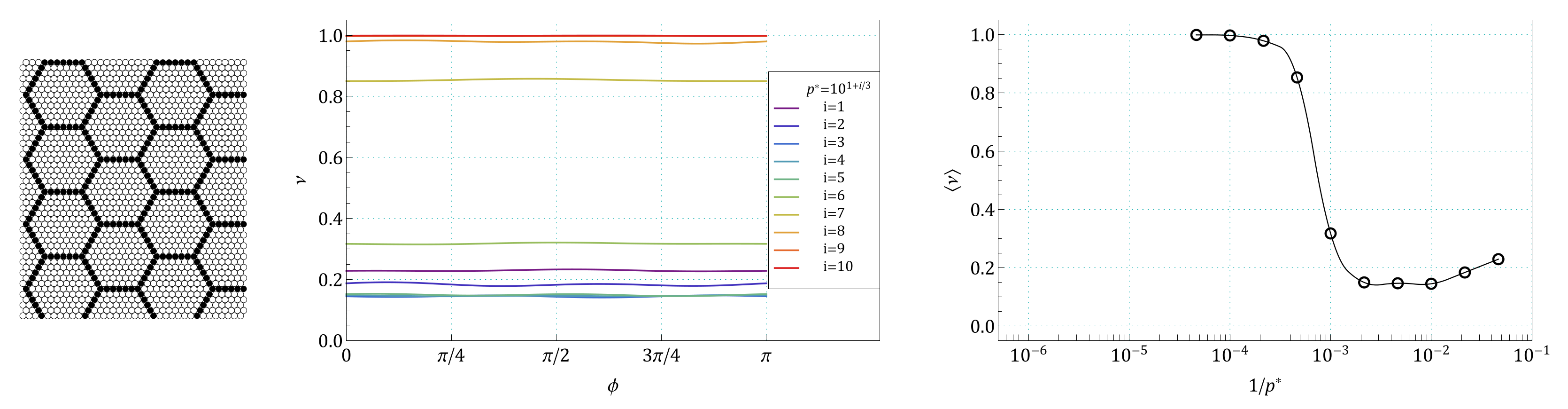
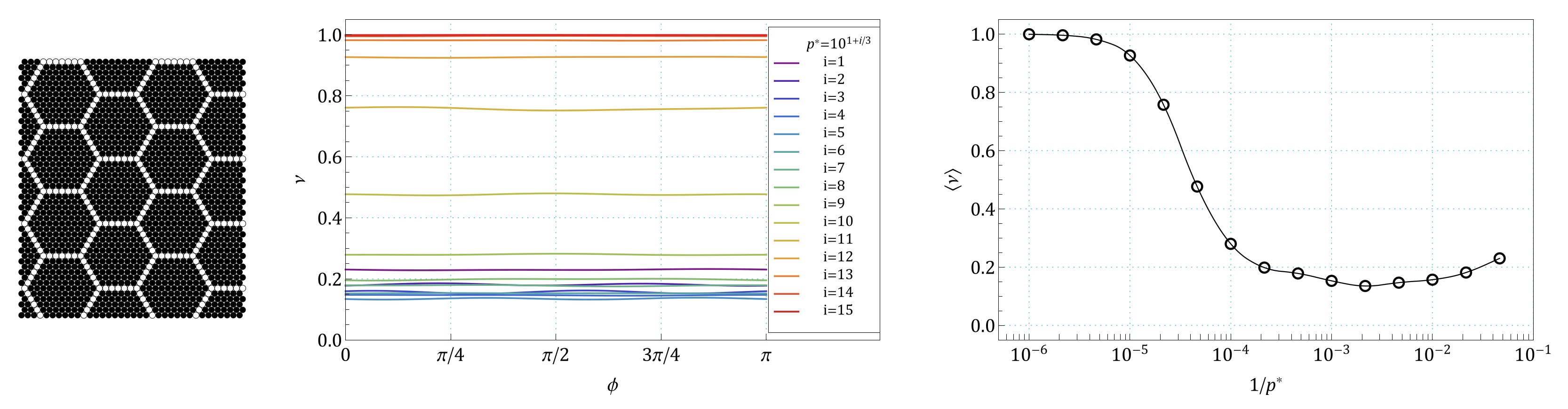



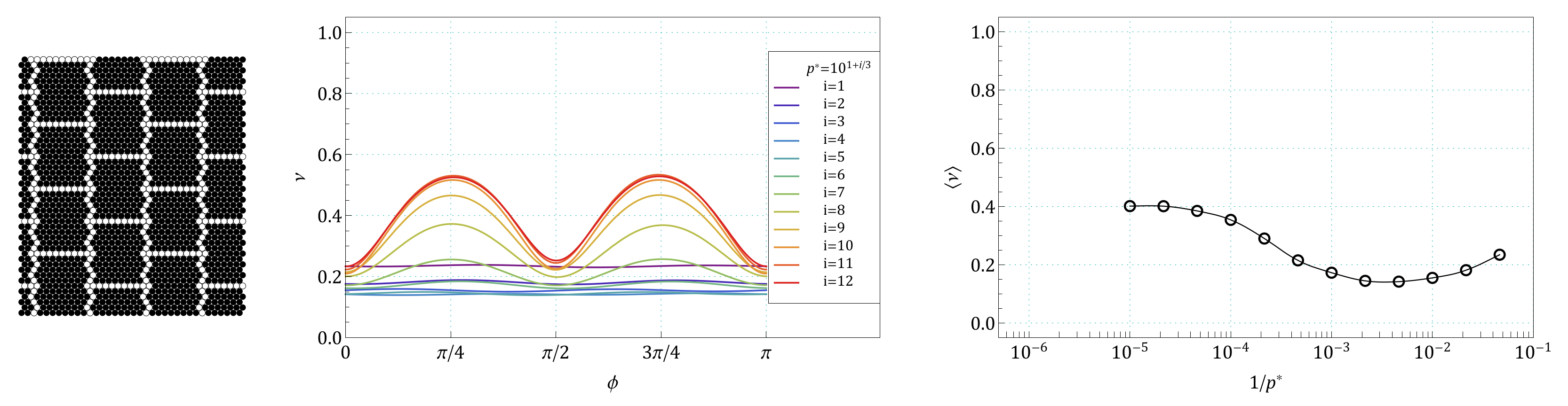
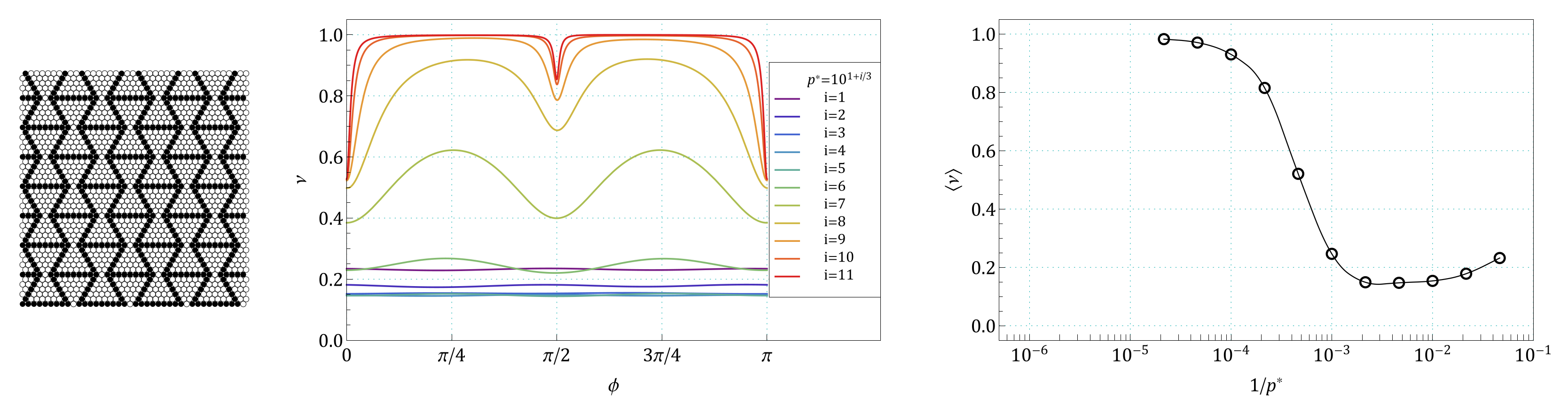
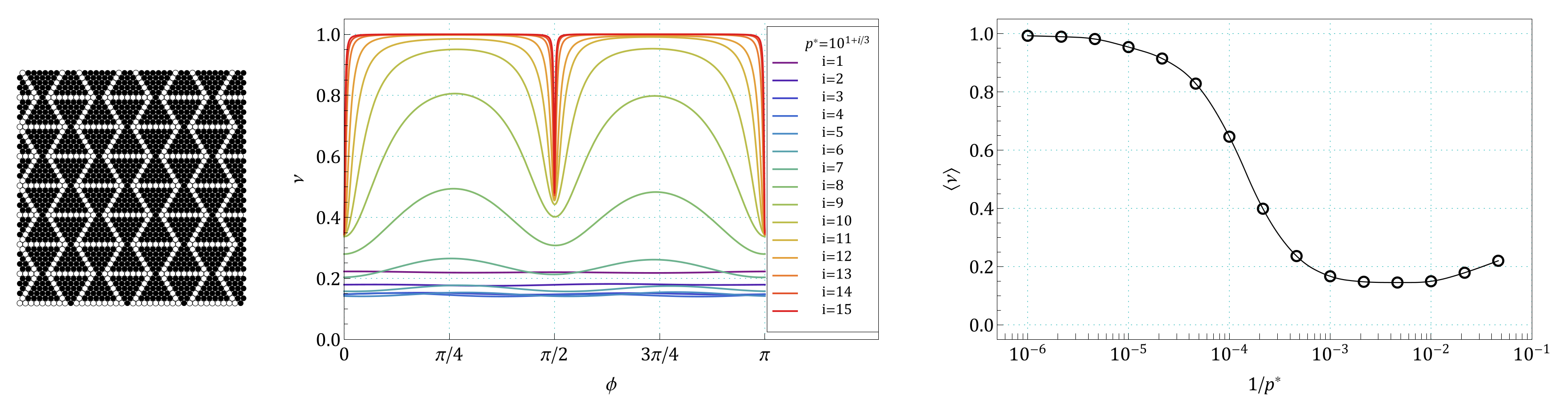
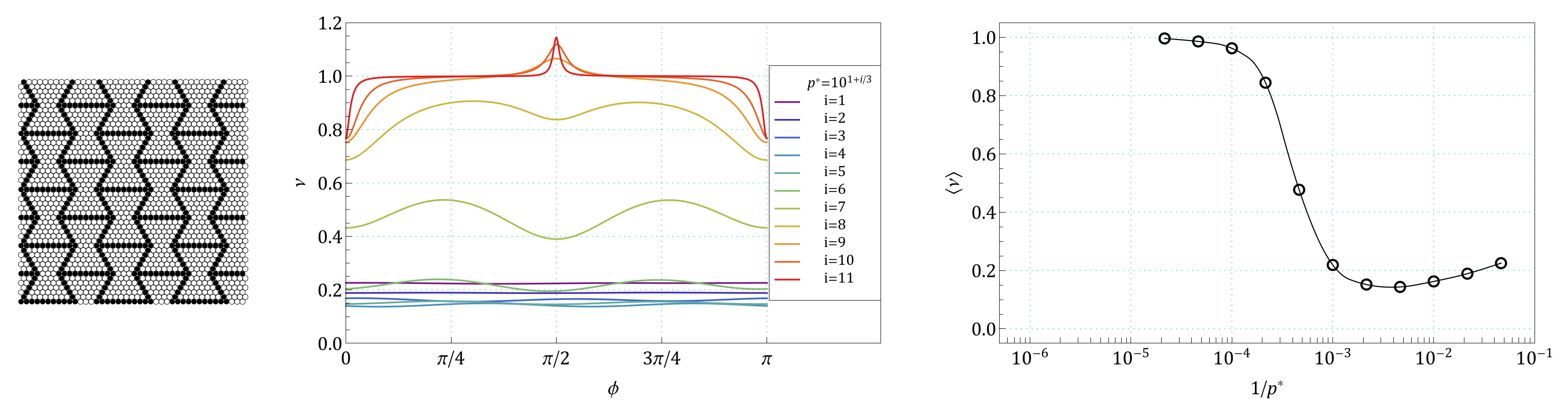
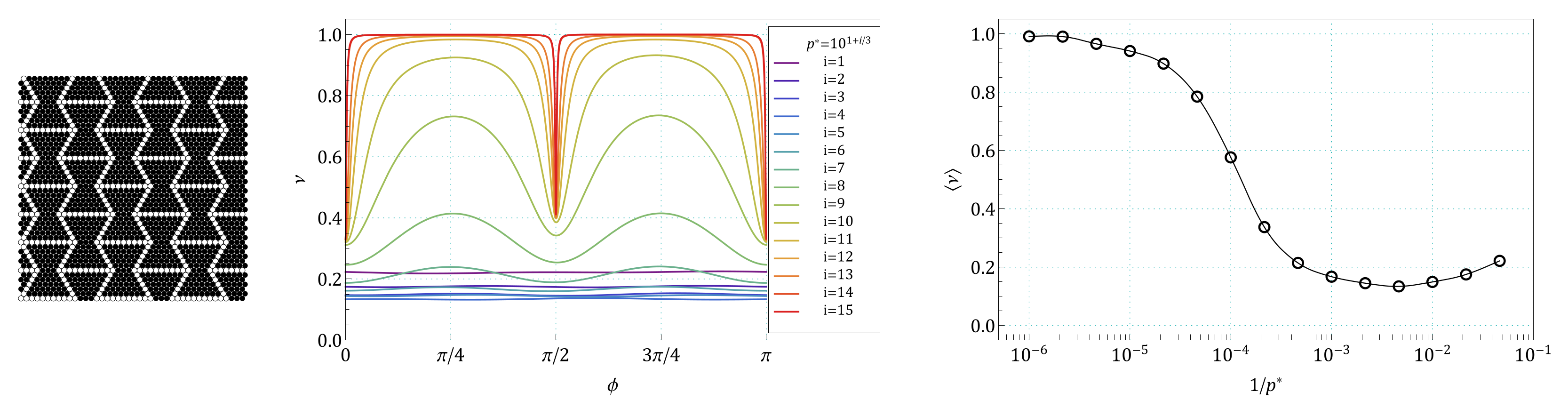
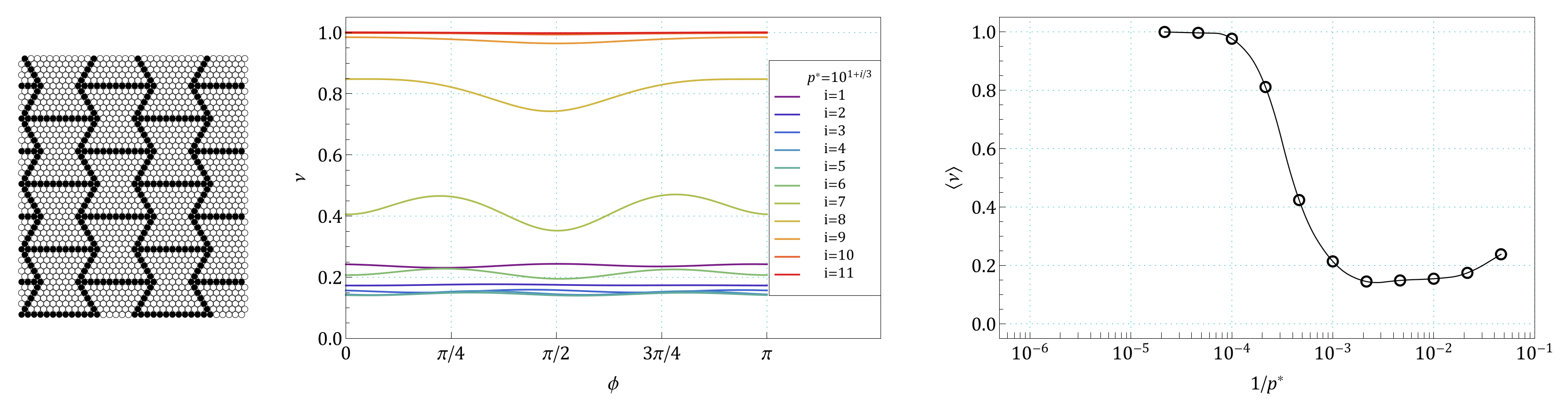
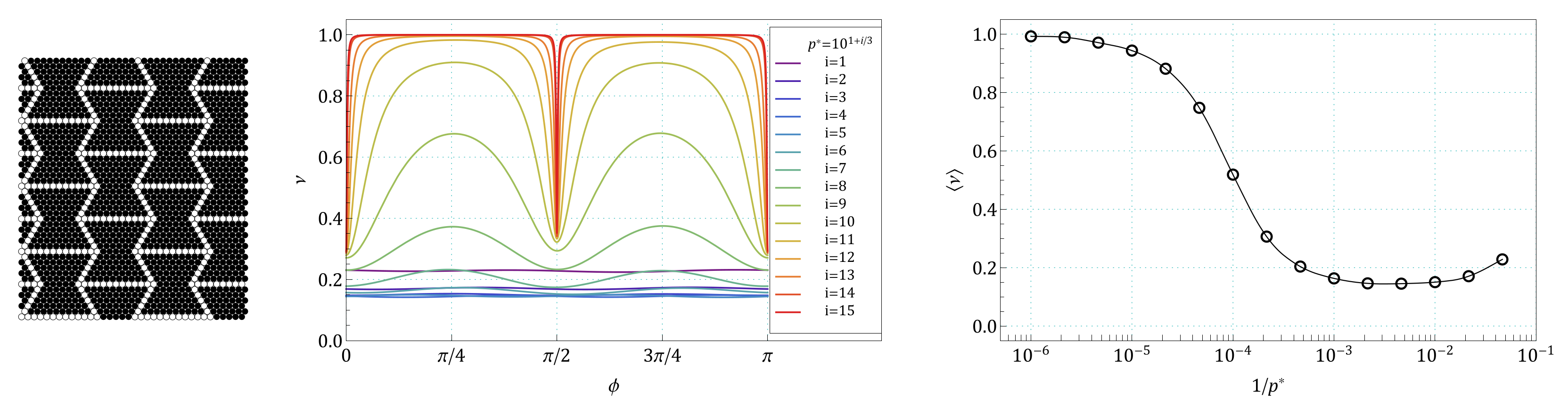
References
- Landau, L.; Lifshits, E. Theory of Elasticity, 3rd ed.; Pergamon Press: Oxford, UK, 1993. [Google Scholar]
- Wojciechowski, K.W. Negative Poisson ratios at negative pressures. Mol. Phys. Rep. 1995, 10, 129–136. [Google Scholar]
- Wojciechowski, K.W. Remarks on “Poisson Ratio beyond the Limits of the Elasticity Theory”. J. Phys. Soc. Jpn. 2003, 72, 1819–1820. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Bilski, M.; Wojciechowski, K.W. Maximum Poisson’s Ratios in Planar Isotropic Crystals of Binary Hard Discs at High Pressures. Phys. Status Solidi B 2017, 254, 1700543. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Nienartowicz, M. Dynamic response of sandwich panels with auxetic cores. Phys. Status Solidi B 2015, 252, 1540–1550. [Google Scholar] [CrossRef]
- Mizzi, L.; Grima, J.N.; Gatt, R.; Attard, D. Analysis of the Deformation Behavior and Mechanical Properties of Slit-Perforated Auxetic Metamaterials. Phys. Status Solidi B 2019, 256, 1800153. [Google Scholar] [CrossRef] [Green Version]
- Zulifqar, A.; Hu, H. Development of Bi-Stretch Auxetic Woven Fabrics Based on Re-Entrant Hexagonal Geometry. Phys. Status Solidi B 2019, 256, 1800172. [Google Scholar] [CrossRef] [Green Version]
- Almgren, R.F. An isotropic three-dimensional structure with Poisson’s ratio =−1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Lakes, R.S. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Pergamon Press: Oxford, UK, 1988. [Google Scholar]
- Wojciechowski, K.W. Two-dimensional Isotropic System with a Negative Poisson Ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Evans, K.E. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mat. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Tretiakov, K.V. Negative Poisson’s ratio of two-dimensional hard cyclic tetramers. J. Non-Cryst. Solids 2009, 355, 24–27. [Google Scholar] [CrossRef]
- Fowler, P.W.; Guest, S.D.; Tarnai, T. Symmetry Perspectives on Some Auxetic Body-Bar Frameworks. Symmetry 2014, 6, 368–382. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.C.; Lai, H.W.; Ren, X.J. Enhanced Auxetic and Viscoelastic Properties of Filled Reentrant Honeycomb. Phys. Status Solidi B 2020, 257, 1900184. [Google Scholar] [CrossRef]
- Lim, T.C. An Auxetic System Based on Interconnected Y-Elements Inspired by Islamic Geometric Patterns. Symmetry 2021, 13, 865. [Google Scholar] [CrossRef]
- Lakes, R. Advances in negative Poisson’s ratio materials. Adv. Mater. 1993, 5, 293–296. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comp. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Mizzi, L.; Attard, D.; Casha, A.; Grima, J.N.; Gatt, R. On the suitability of hexagonal honeycombs as stent geometries. Phys. Status Solidi B 2014, 251, 328–337. [Google Scholar] [CrossRef]
- Allen, T.; Hewage, T.; Newton-Mann, C.; Wang, W.; Duncan, O.; Alderson, A. Fabrication of auxetic foam sheets for sports applications. Phys. Status Solidi B 2017, 254, 1700596. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Wang, Y.B.; Sotzing, G.A.; Weiss, R.A. Conductive Polymer Foams as Sensors for Volatile Amines. Chem. Mater. 2003, 15, 375–377. [Google Scholar] [CrossRef]
- Chen, Y.J.; Li, Y.; Chu, B.T.T.; Kuo, I.T.; Yip, M.C.; Tai, N. Porous composites coated with hybrid nano carbon materials perform excellent electromagnetic interference shielding. Compos. Part B 2015, 70, 231–237. [Google Scholar] [CrossRef]
- Zhang, X.C.; Scarpa, F.; McHale, R.; Limmack, A.P.; Peng, H.X. Carbon nano-ink coated open cell polyurethane foam with micro-architectured multilayer skeleton for damping applications. RSC Adv. 2016, 6, 80334–80341. [Google Scholar] [CrossRef] [Green Version]
- Duncan, O.; Shepherd, T.; Moroney, C.; Foster, L.; Venkatraman, P.D.; Winwood, K.; Allen, T.; Alderson, A. Review of auxetic materials for sports applications: Expanding options in comfort and protection. Appl. Sci. Basel 2018, 8, 941. [Google Scholar] [CrossRef] [Green Version]
- Grima-Cornish, J.N.; Cauchi, R.; Attard, D.; Gatt, R.; Grima, J.N. Smart Honeycomb “Mechanical Metamaterials” with Tunable Poisson’s Ratios. Phys. Status Solidi B 2020, 257, 1900707. [Google Scholar] [CrossRef]
- Brańka, A.C.; Pierański, P.; Wojciechowski, K.W. Rotatory phase in a system of hard cyclic hexamers; an experimental modelling study. J. Phys. Chem. Solids 1982, 43, 817–818. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Monte Carlo simulations of highly anisotropic two-dimensional hard dumbbell-shaped molecules: Nonperiodic phase between fluid and dense solid. Phys. Rev. B 1992, 46, 26–39. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Evans, G.T.; Frenkel, D.; Mulder, B.M. Hard Convex Body Fluids. Adv. Chem. Phys. 1993, 86, 1–166. [Google Scholar]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Perturbation Theory of the Thermody-namic Properties of Simple Liquids. J. Chem. Phys. 1971, 55, 5422. [Google Scholar] [CrossRef]
- Frenkel, D. Order through entropy. Nat. Mater. 2015, 14, 9–12. [Google Scholar] [CrossRef]
- Aoki, K.M.; Ito, N. Effect of size polydispersity on granular materials. Phys. Rev. E 1996, 54, 1990–1996. [Google Scholar] [CrossRef]
- Both, J.A.; Hong, D.C. Variational Approach to Hard Sphere Segregation under Gravity. Phys. Rev. Lett. 2002, 88, 124301. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Strain fluctuations and elastic constants. J. Chem. Phys. 1982, 76, 2662–2666. [Google Scholar] [CrossRef]
- Ray, J.R.; Rahman, A. Statistical ensembles and molecular dynamics studies of anisotropic solids. J. Chem. Phys. 1984, 80, 4423–4426. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Tretiakov, K.V.; Kowalik, M. Elastic properties of dense solid phases of hard cyclic pentamers and heptamers in two dimensions. Phys. Rev. E 2003, 67, 036121. [Google Scholar] [CrossRef] [Green Version]
- Tokmakova, S.P. Stereographic projections of Poisson’s ratio in auxetic crystals. Phys. Status Solidi B 2005, 242, 721–729. [Google Scholar] [CrossRef]
- Bilski, M.; Wojciechowski, K.W. Tailoring Poisson’s ratio by introducing auxetic layers. Phys. Status Solidi B 2016, 253, 1318–1323. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Tretiakov, K.V.; Brańka, A.C.; Kowalik, M. Elastic properties of two-dimensional hard discs in the close-packing limit. J. Chem. Phys. 2003, 119, 939–946. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilski, M.; Pigłowski, P.M.; Wojciechowski, K.W. Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry 2021, 13, 1127. https://doi.org/10.3390/sym13071127
Bilski M, Pigłowski PM, Wojciechowski KW. Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry. 2021; 13(7):1127. https://doi.org/10.3390/sym13071127
Chicago/Turabian StyleBilski, Mikołaj, Paweł M. Pigłowski, and Krzysztof W. Wojciechowski. 2021. "Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs" Symmetry 13, no. 7: 1127. https://doi.org/10.3390/sym13071127
APA StyleBilski, M., Pigłowski, P. M., & Wojciechowski, K. W. (2021). Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry, 13(7), 1127. https://doi.org/10.3390/sym13071127





