Absorption of Light in Finite Semiconductor Nanowire Arrays and the Effect of Missing Nanowires
Abstract
:1. Introduction
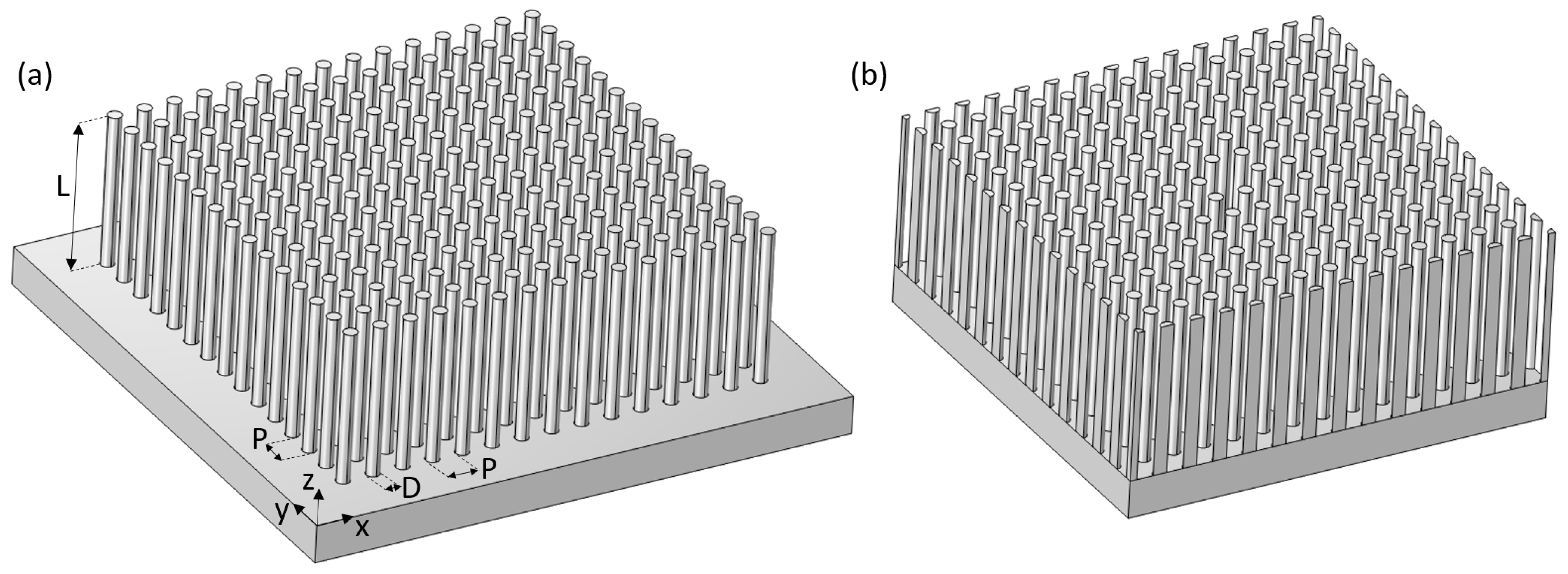
2. Materials and Methods
2.1. FEM Simulation Settings
2.2. Absorption Cross-Section and Short-Circuit Current
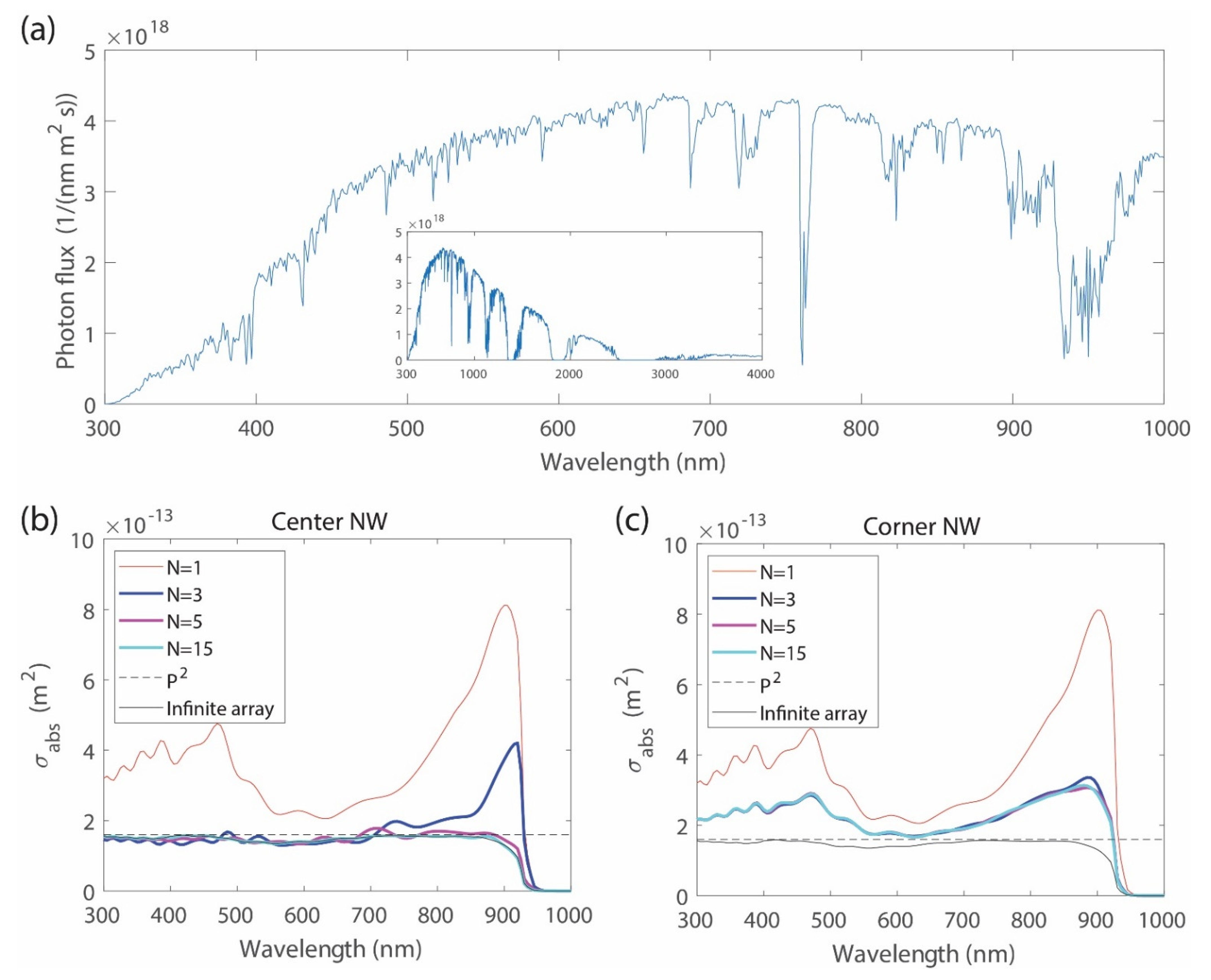
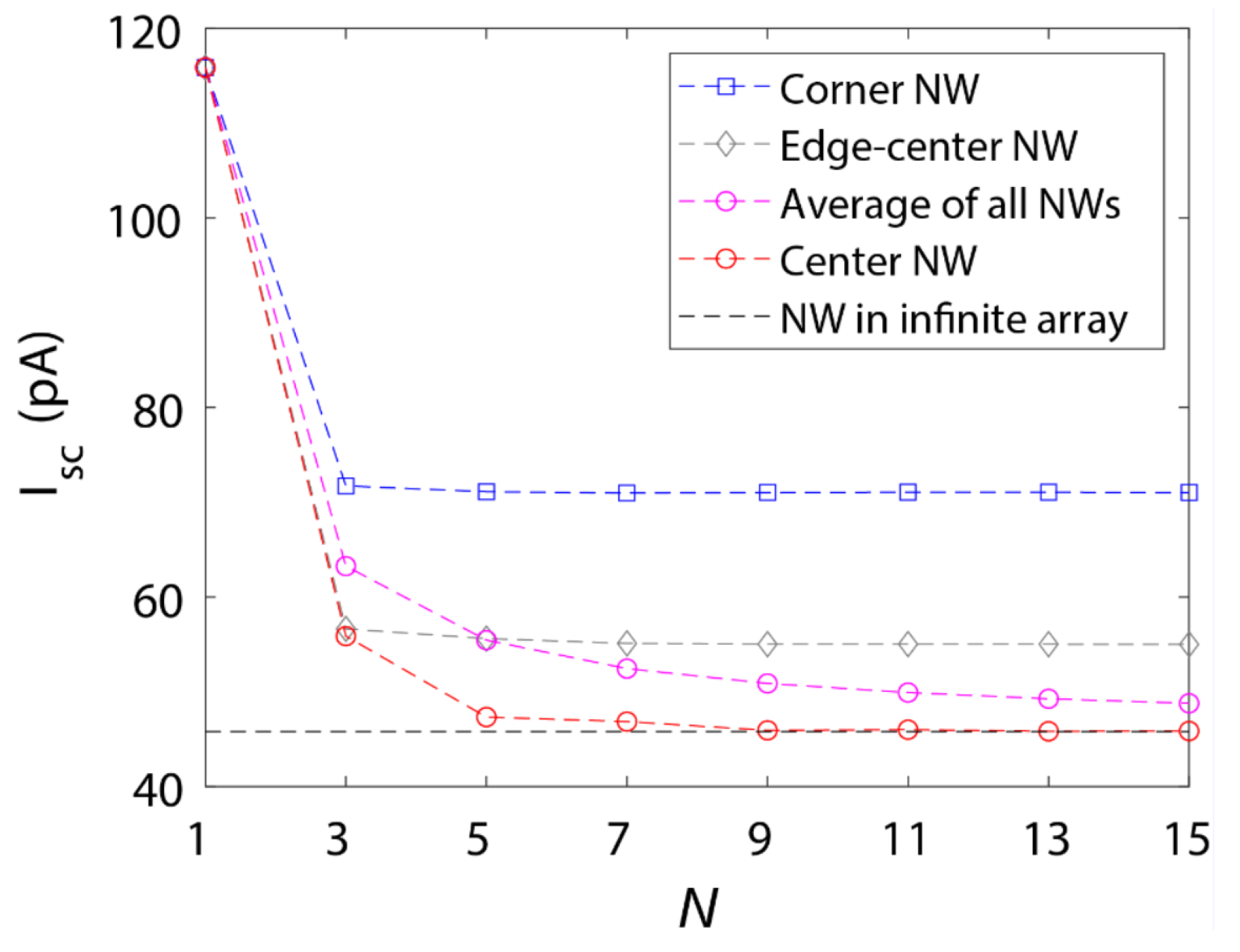
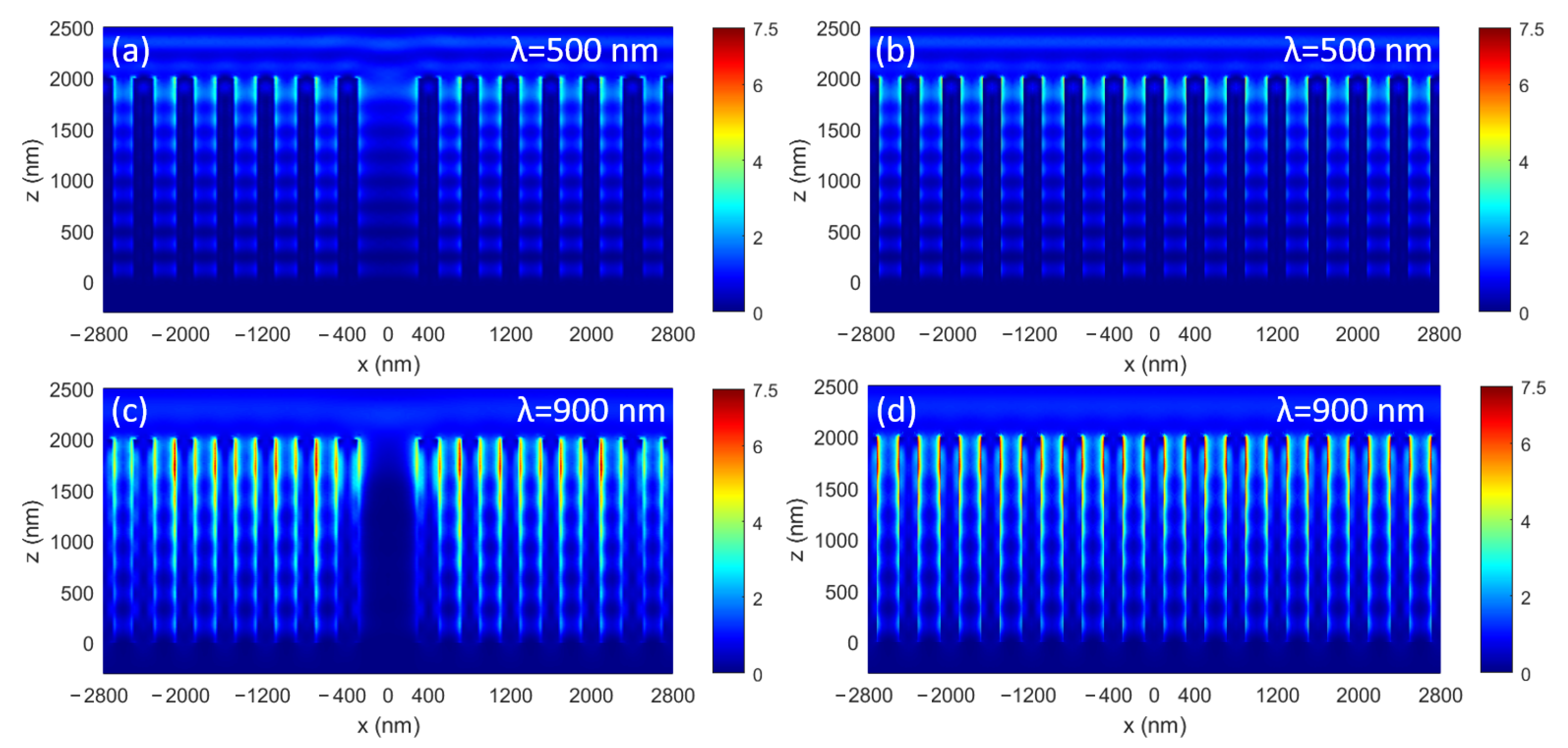
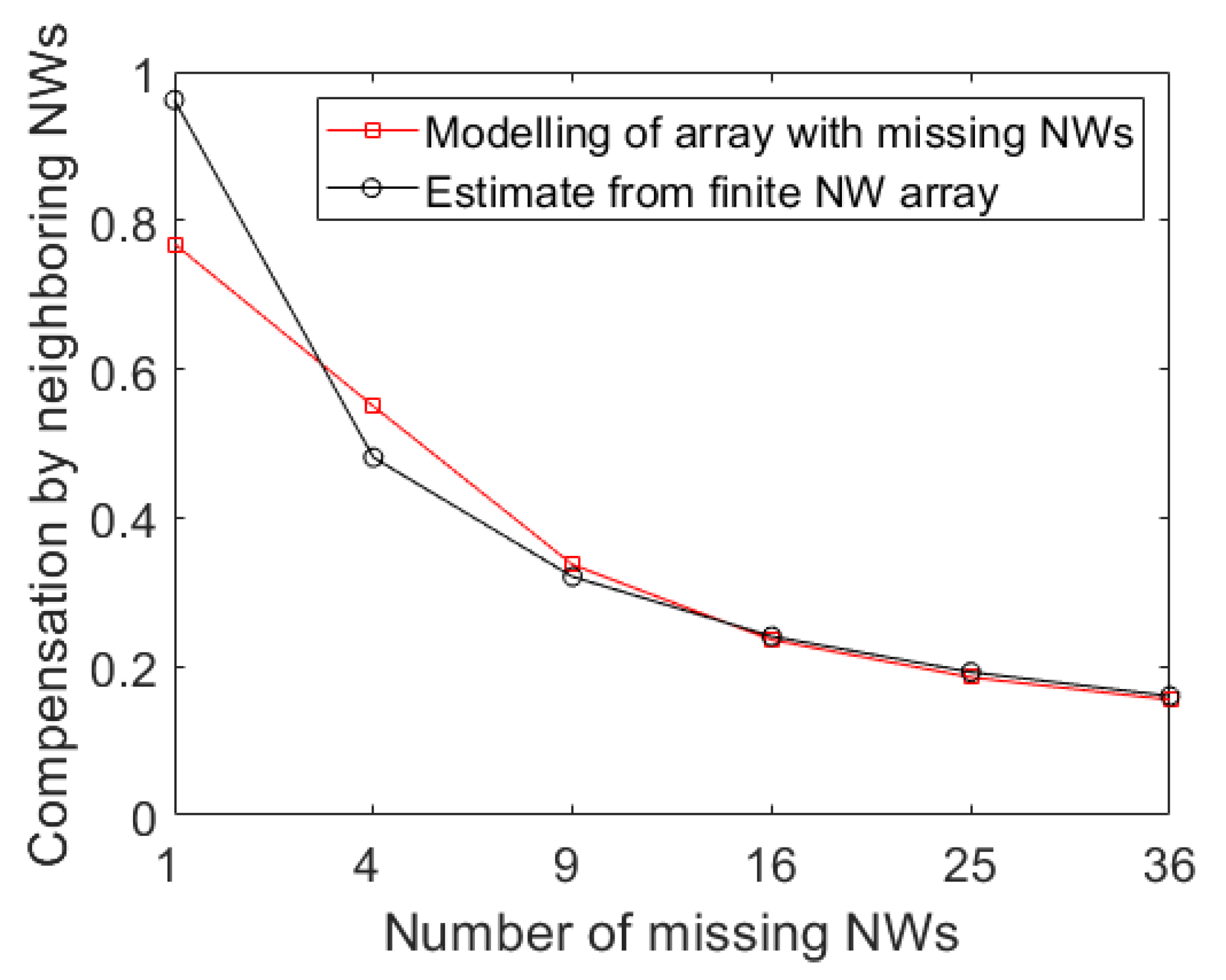
3. Results
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 71.7 | 56.6 | 71.7 |
| 56.6 | 55.9 | 56.6 |
| 71.7 | 56.6 | 71.7 |
| 71.1 | 55.6 | 55.6 | 55.6 | 71.1 |
| 55.6 | 49.4 | 47.4 | 49.4 | 55.6 |
| 55.6 | 47.4 | 47.3 | 47.4 | 55.6 |
| 55.6 | 49.4 | 47.4 | 49.4 | 55.6 |
| 71.1 | 55.6 | 55.6 | 55.6 | 71.1 |
| 71.0 | 55.5 | 55.3 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.3 | 55.5 | 71.0 |
| 55.5 | 48.9 | 46.9 | 47.2 | 47.0 | 47.0 | 47.0 | 47.0 | 47.0 | 47.0 | 47.0 | 47.2 | 46.9 | 48.9 | 55.5 |
| 55.3 | 46.9 | 46.2 | 46.2 | 46.0 | 46.1 | 46.0 | 46.0 | 46.0 | 46.1 | 46.0 | 46.2 | 46.2 | 46.9 | 55.3 |
| 55.0 | 47.2 | 46.2 | 46.2 | 46.0 | 46.0 | 46.0 | 46.0 | 46.0 | 46.0 | 46.0 | 46.2 | 46.2 | 47.2 | 55.0 |
| 55.0 | 47.0 | 46.0 | 46.0 | 45.8 | 45.9 | 45.8 | 45.9 | 45.8 | 45.9 | 45.8 | 46.0 | 46.0 | 47.0 | 55.0 |
| 55.0 | 47.0 | 46.1 | 46.0 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 46.0 | 46.1 | 47.0 | 55.0 |
| 55.0 | 47.0 | 46.0 | 46.0 | 45.8 | 45.9 | 45.8 | 45.9 | 45.8 | 45.9 | 45.8 | 46.0 | 46.0 | 47.0 | 55.0 |
| 55.0 | 47.0 | 46.0 | 46.0 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 46.0 | 46.0 | 47.0 | 55.0 |
| 55.0 | 47.0 | 46.0 | 46.0 | 45.8 | 45.9 | 45.8 | 45.9 | 45.8 | 45.9 | 45.8 | 46.0 | 46.0 | 47.0 | 55.0 |
| 55.0 | 47.0 | 46.1 | 46.0 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 45.9 | 46.0 | 46.1 | 47.0 | 55.0 |
| 55.0 | 47.0 | 46.0 | 46.0 | 45.8 | 45.9 | 45.8 | 45.9 | 45.8 | 45.9 | 45.8 | 46.0 | 46.0 | 47.0 | 55.0 |
| 55.0 | 47.2 | 46.2 | 46.2 | 46.0 | 46.0 | 46.0 | 46.0 | 46.0 | 46.0 | 46.0 | 46.2 | 46.2 | 47.2 | 55.0 |
| 55.3 | 46.9 | 46.2 | 46.2 | 46.0 | 46.1 | 46.0 | 46.0 | 46.0 | 46.1 | 46.0 | 46.2 | 46.2 | 46.9 | 55.3 |
| 55.5 | 48.9 | 46.9 | 47.2 | 47.0 | 47.0 | 47.0 | 47.0 | 47.0 | 47.0 | 47.0 | 47.2 | 46.9 | 48.9 | 55.5 |
| 71.0 | 55.5 | 55.3 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.0 | 55.3 | 55.5 | 71.0 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.9 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.9 | 45.9 | 45.9 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.9 | 46.0 | 46.5 | 46.0 | 45.9 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.9 | 46.0 | 46.9 | 52.7 | 46.9 | 46.0 | 45.9 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.9 | 45.9 | 46.5 | 52.7 | 0 | 52.7 | 46.5 | 45.9 | 45.9 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.9 | 46.0 | 46.9 | 52.7 | 46.9 | 46.0 | 45.9 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.9 | 46.0 | 46.5 | 46.0 | 45.9 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.9 | 45.9 | 45.9 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.9 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
| 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 | 45.8 |
References
- Czaban, J.A.; Thompson, D.A.; LaPierre, R.R. GaAs Core−Shell Nanowires for Photovoltaic Applications. Nano Lett. 2009, 9, 148–154. [Google Scholar] [CrossRef]
- Wallentin, J.; Anttu, N.; Asoli, D.; Huffman, M.; Åberg, I.; Magnusson, M.H.; Siefer, G.; Fuss-Kailuweit, P.; Dimroth, F.; Witzigmann, B.; et al. InP Nanowire Array Solar Cells Achieving 13.8% Efficiency by Exceeding the Ray Optics Limit. Science 2013, 339, 1057–1060. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Wang, J.; Plissard, S.R.; Cavalli, A.; Vu, T.T.T.; van Veldhoven, R.P.J.; Gao, L.; Trainor, M.; Verheijen, M.A.; Haverkort, J.E.M.; et al. Efficiency Enhancement of InP Nanowire Solar Cells by Surface Cleaning. Nano Lett. 2013, 13, 4113–4117. [Google Scholar] [CrossRef]
- Yao, M.; Huang, N.; Cong, S.; Chi, C.-Y.; Seyedi, M.A.; Lin, Y.-T.; Cao, Y.; Povinelli, M.L.; Dapkus, P.D.; Zhou, C. GaAs Nanowire Array Solar Cells with Axial p–i–n Junctions. Nano Lett. 2014, 14, 3293–3303. [Google Scholar] [CrossRef]
- LaPierre, R.R.; Robson, M.; Azizur-Rahman, K.M.; Kuyanov, P. A Review of III–V Nanowire Infrared Photodetectors and Sensors. J. Phys. D Appl. Phys. 2017, 50, 123001. [Google Scholar] [CrossRef]
- Kupec, J.; Witzigmann, B. Dispersion, Wave Propagation and Efficiency Analysis of Nanowire Solar Cells. Opt. Express 2009, 17, 10399–10410. [Google Scholar] [CrossRef] [PubMed]
- Diedenhofen, S.L.; Janssen, O.T.A.; Grzela, G.; Bakkers, E.P.A.M.; Gómez Rivas, J. Strong Geometrical Dependence of the Absorption of Light in Arrays of Semiconductor Nanowires. ACS Nano 2011, 5, 2316–2323. [Google Scholar] [CrossRef]
- Huang, N.; Lin, C.; Povinelli, M.L. Broadband Absorption of Semiconductor Nanowire Arrays for Photovoltaic Applications. J. Opt. 2012, 14, 024004. [Google Scholar] [CrossRef] [Green Version]
- Anttu, N.; Xu, H.Q. Efficient Light Management in Vertical Nanowire Arrays for Photovoltaics. Opt. Express 2013, 21, A558–A575. [Google Scholar] [CrossRef]
- Otnes, G.; Borgström, M.T. Towards High Efficiency Nanowire Solar Cells. Nano Today 2017, 12, 31–45. [Google Scholar] [CrossRef] [Green Version]
- Barrigón, E.; Heurlin, M.; Bi, Z.; Monemar, B.; Samuelson, L. Synthesis and Applications of III–V Nanowires. Chem. Rev. 2019, 119, 9170–9220. [Google Scholar] [CrossRef]
- Barrigón, E.; Zhang, Y.; Hrachowina, L.; Otnes, G.; Borgström, M.T. Unravelling Processing Issues of Nanowire-Based Solar Cell Arrays by Use of Electron Beam Induced Current Measurements. Nano Energy 2020, 71, 104575. [Google Scholar] [CrossRef]
- Glembocki, O.J.; Piller, H. Indium Phosphide (InP). In Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic Press: Burlington, VT, USA, 1997; pp. 503–516. ISBN 978-0-12-544415-6. [Google Scholar]
- Mäntynen, H.; Lipsanen, H.; Anttu, N. Symmetry Reduction in FEM Optics Modeling of Single and Periodic Nanostructures. Symmetry 2021, 13, 752. [Google Scholar] [CrossRef]
- Anttu, N. Absorption of Light in a Single Vertical Nanowire and a Nanowire Array. Nanotechnology 2019, 30, 104004. [Google Scholar] [CrossRef] [Green Version]
- ASTM G173-03(2020). Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37° Tilted Surface; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar]
- Vurgaftman, I.; Meyer, J.R.; Ram-Mohan, L.R. Band Parameters for III–V Compound Semiconductors and Their Alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef] [Green Version]
- Otnes, G.; Barrigón, E.; Sundvall, C.; Svensson, K.E.; Heurlin, M.; Siefer, G.; Samuelson, L.; Åberg, I.; Borgström, M.T. Understanding InP Nanowire Array Solar Cell Performance by Nanoprobe-Enabled Single Nanowire Measurements. Nano Lett. 2018, 18, 3038–3046. [Google Scholar] [CrossRef] [PubMed]
- Jain, V.; Nowzari, A.; Wallentin, J.; Borgström, M.T.; Messing, M.E.; Asoli, D.; Graczyk, M.; Witzigmann, B.; Capasso, F.; Samuelson, L.; et al. Study of Photocurrent Generation in InP Nanowire-Based P+-i-N+ Photodetectors. Nano Res. 2014, 7, 544–552. [Google Scholar] [CrossRef]
- Lin, C.; Povinelli, M.L. Optimal Design of Aperiodic, Vertical Silicon Nanowire Structures for Photovoltaics. Opt. Express 2011, 19, A1148–A1154. [Google Scholar] [CrossRef] [Green Version]
- Sturmberg, B.C.P.; Dossou, K.B.; Botten, L.C.; Asatryan, A.A.; Poulton, C.G.; McPhedran, R.C.; Sterke, C.M. de Absorption Enhancing Proximity Effects in Aperiodic Nanowire Arrays. Opt. Express OE 2013, 21, A964–A969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodriguez, S.R.K.; Schaafsma, M.C.; Berrier, A.; Gómez Rivas, J. Collective Resonances in Plasmonic Crystals: Size Matters. Phys. B Condens. Matter 2012, 407, 4081–4085. [Google Scholar] [CrossRef] [Green Version]
- Zundel, L.; Manjavacas, A. Finite-Size Effects on Periodic Arrays of Nanostructures. J. Phys. Photonics 2018, 1, 015004. [Google Scholar] [CrossRef] [Green Version]
- Dagytė, V.; Anttu, N. Modal Analysis of Resonant and Non-Resonant Optical Response in Semiconductor Nanowire Arrays. Nanotechnology 2018, 30, 025710. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anttu, N. Absorption of Light in Finite Semiconductor Nanowire Arrays and the Effect of Missing Nanowires. Symmetry 2021, 13, 1654. https://doi.org/10.3390/sym13091654
Anttu N. Absorption of Light in Finite Semiconductor Nanowire Arrays and the Effect of Missing Nanowires. Symmetry. 2021; 13(9):1654. https://doi.org/10.3390/sym13091654
Chicago/Turabian StyleAnttu, Nicklas. 2021. "Absorption of Light in Finite Semiconductor Nanowire Arrays and the Effect of Missing Nanowires" Symmetry 13, no. 9: 1654. https://doi.org/10.3390/sym13091654
APA StyleAnttu, N. (2021). Absorption of Light in Finite Semiconductor Nanowire Arrays and the Effect of Missing Nanowires. Symmetry, 13(9), 1654. https://doi.org/10.3390/sym13091654






