Unified Equation of State for Neutron Stars Based on the Gogny Interaction
Abstract
1. Introduction
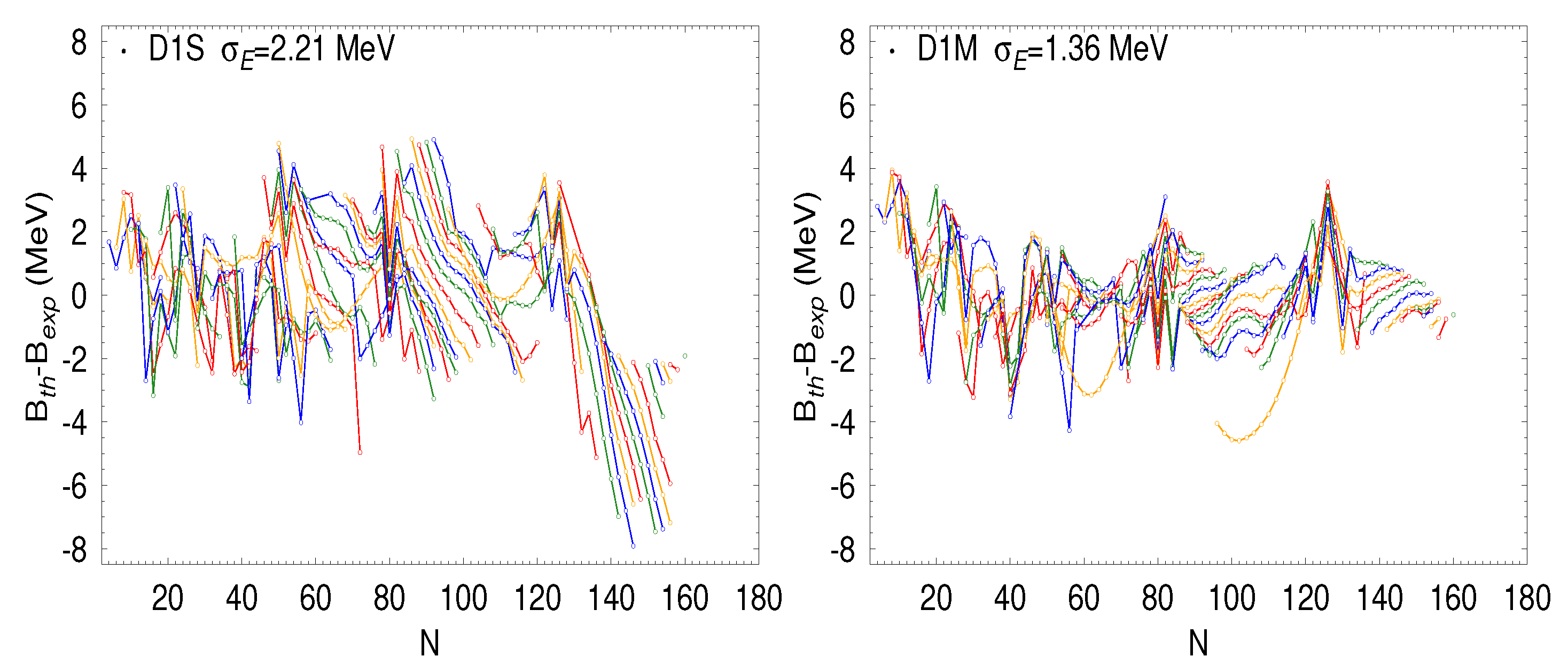
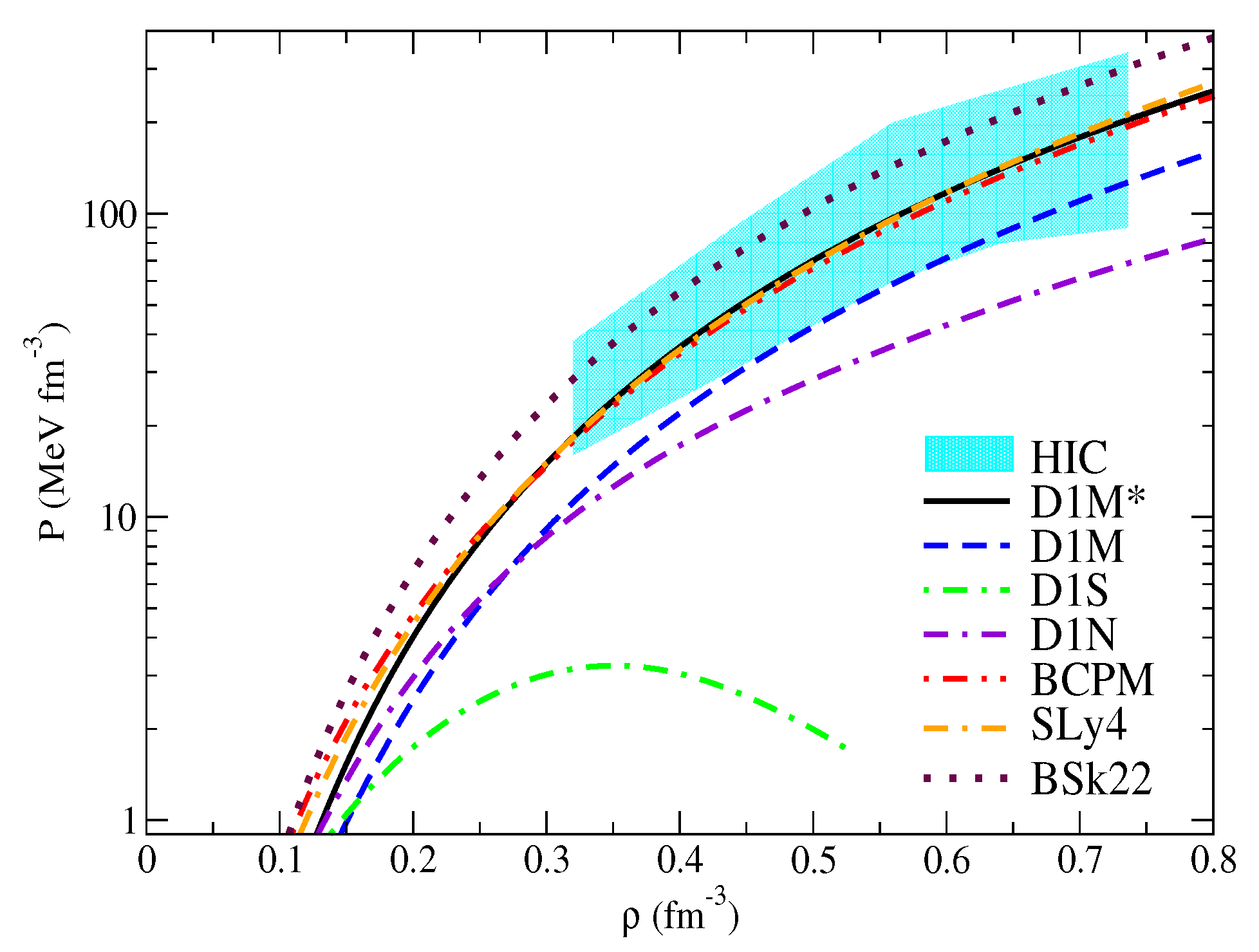
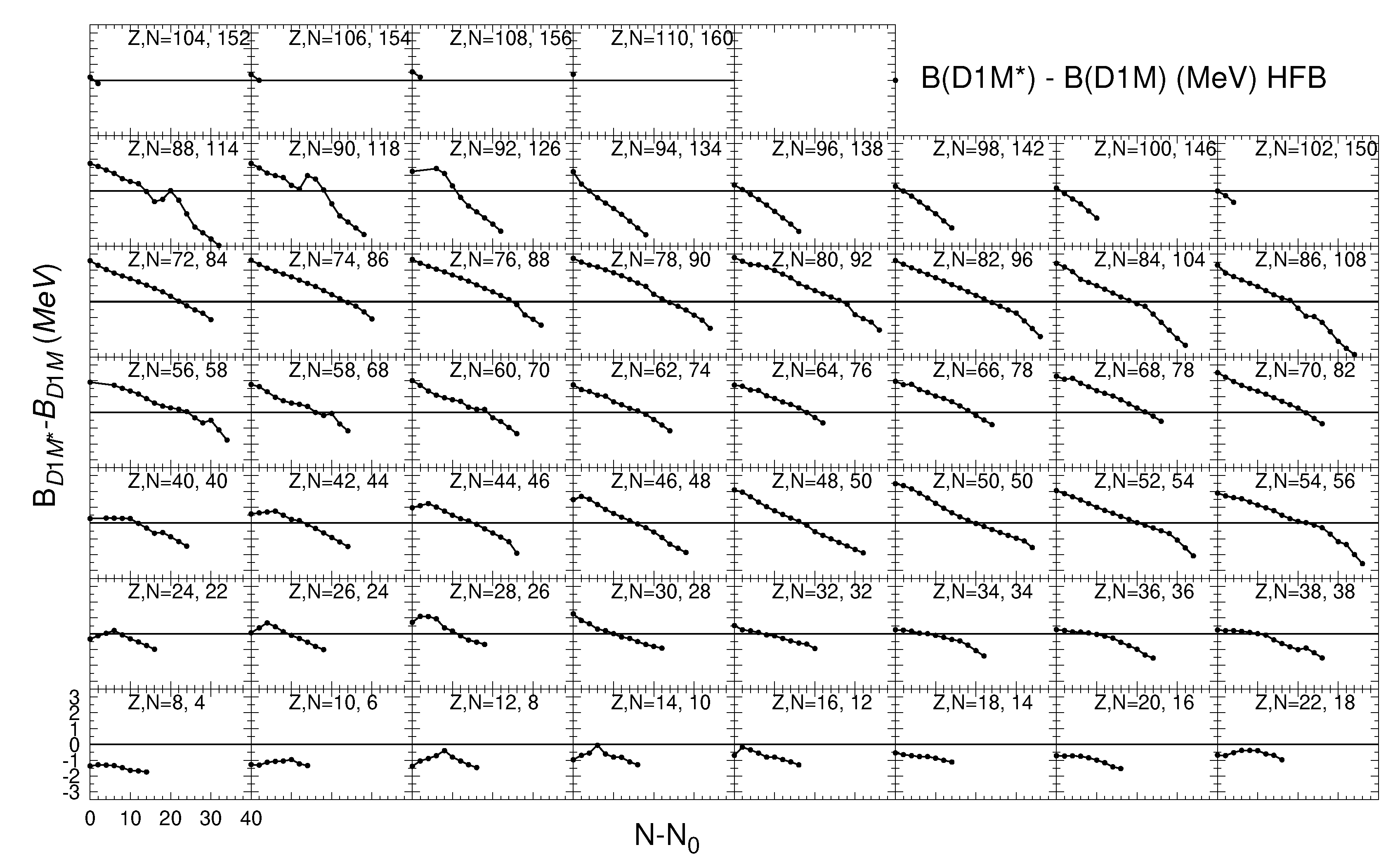
2. Gogny Interactions Adapted for Astrophysical Calculations
3. Neutron Star Crust with Gogny Forces
3.1. Variational Wigner-Kirkwood Method in Finite Nuclei
3.2. Shell and Pairing Effects
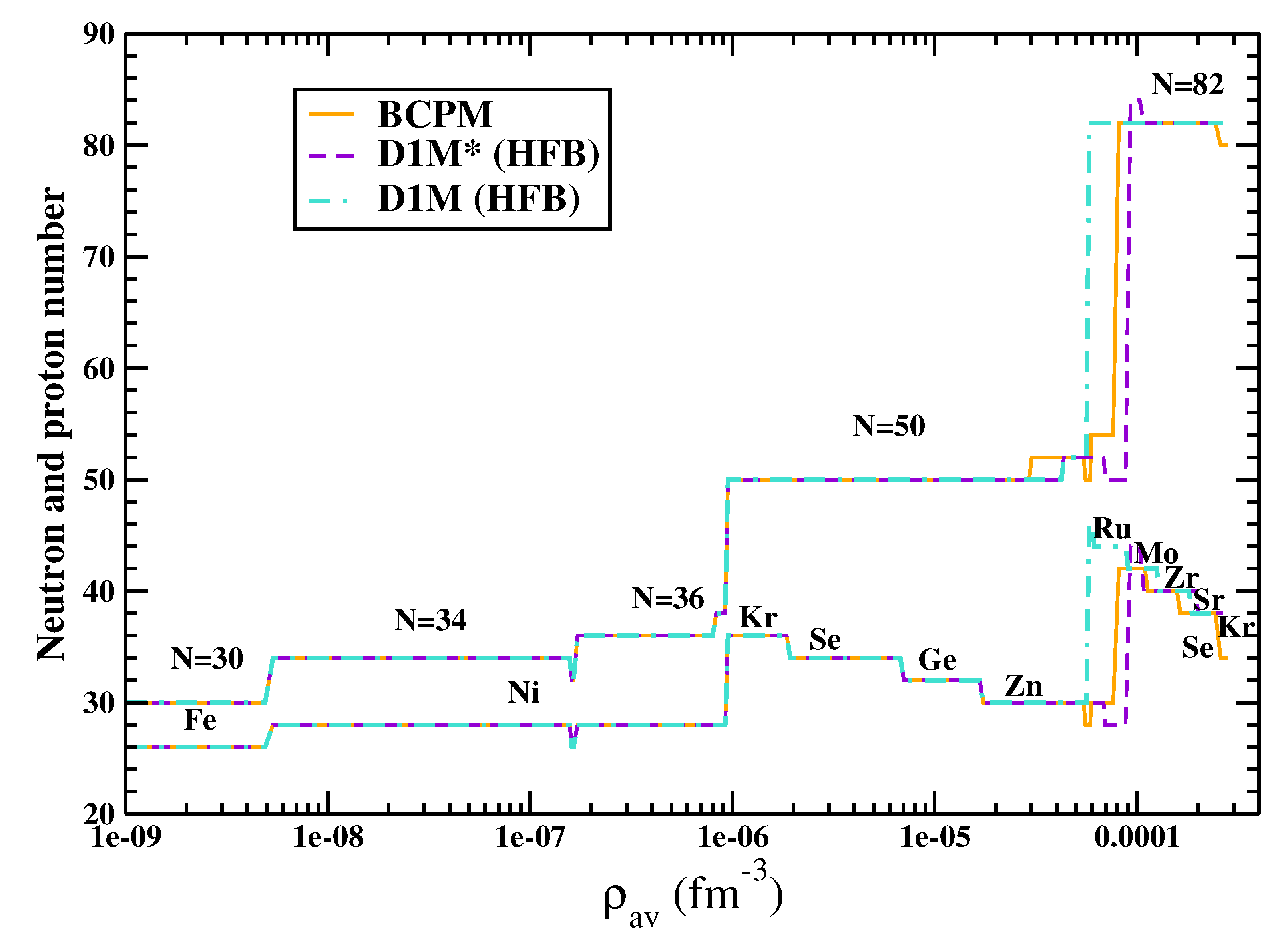
3.3. Outer Crust
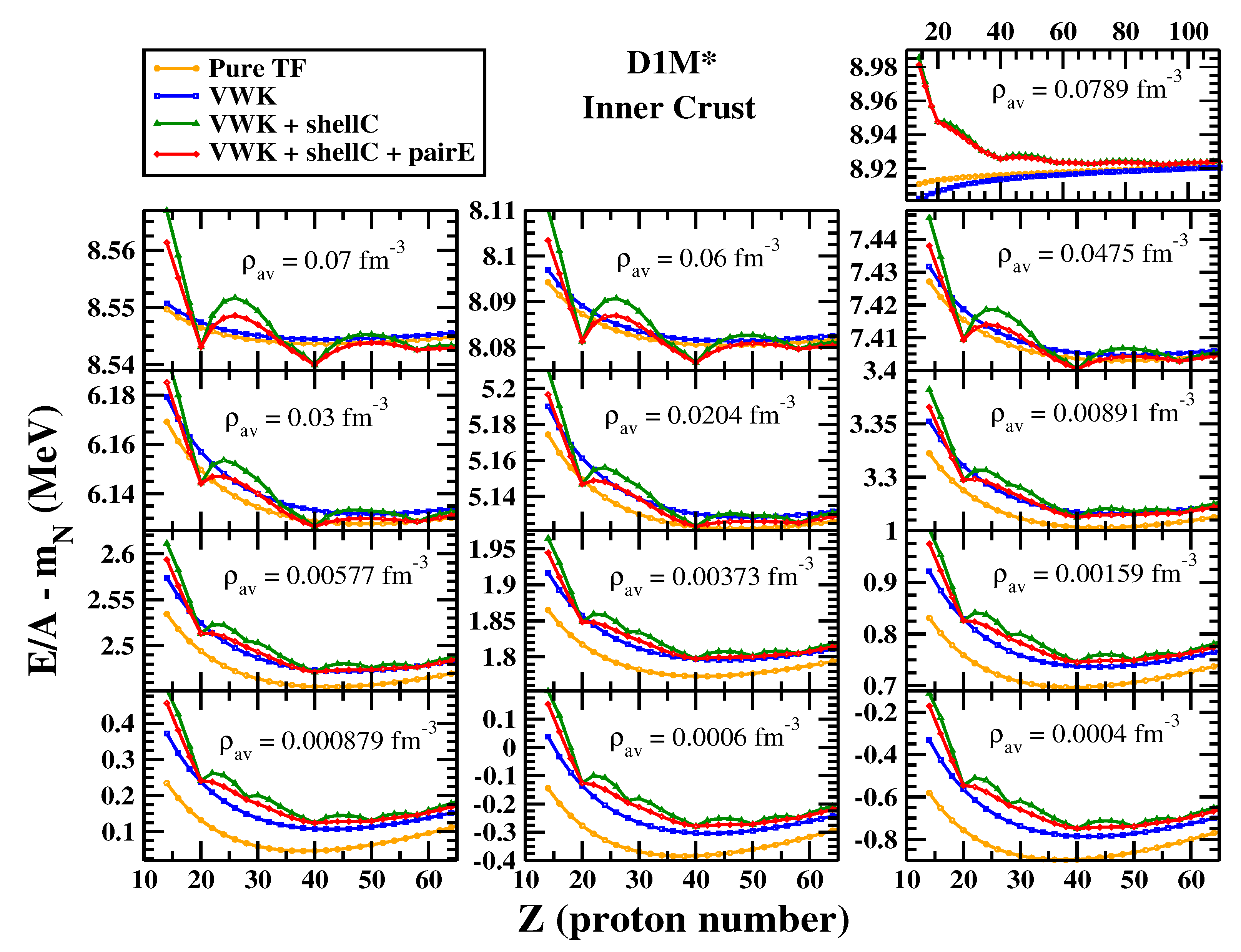
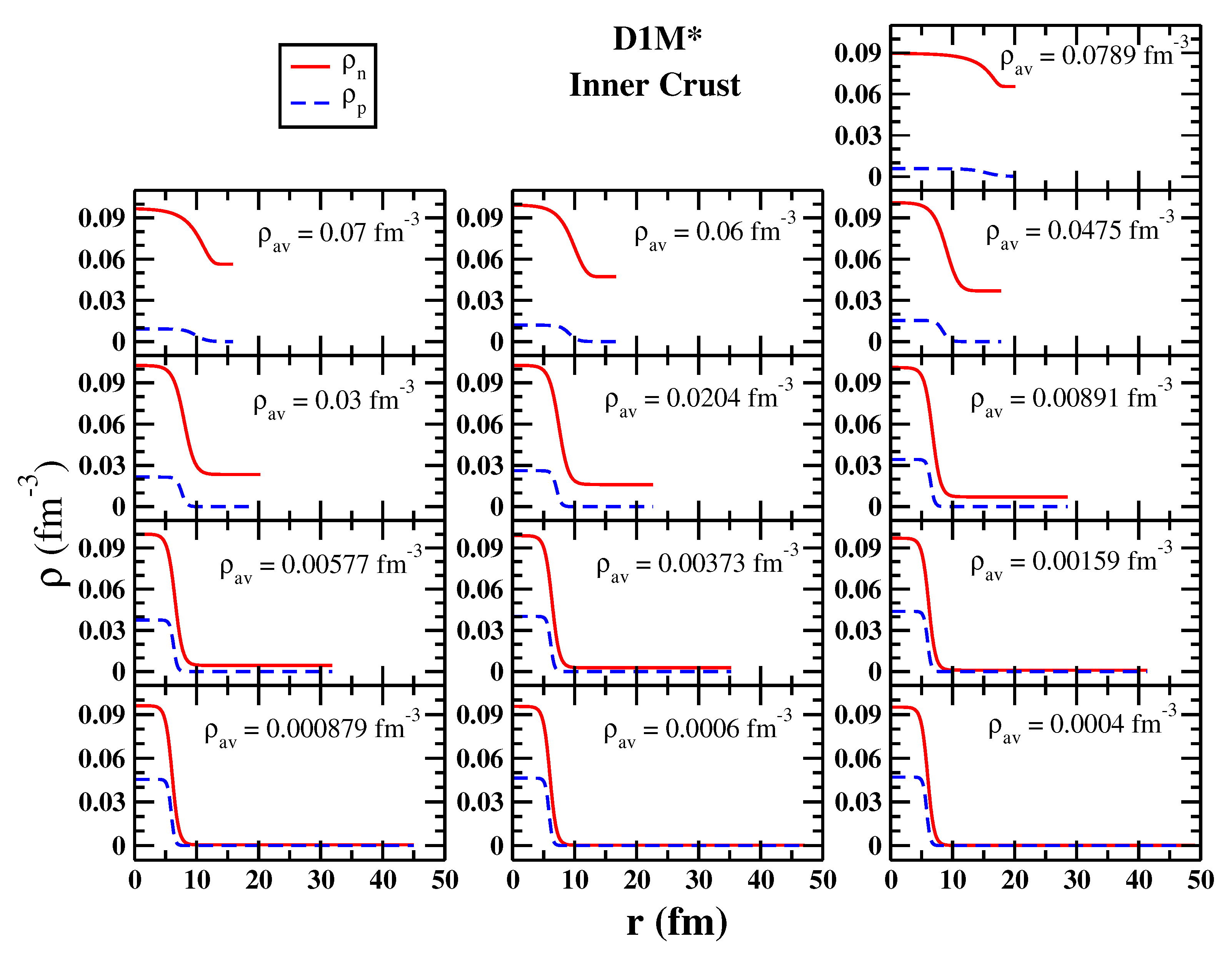
3.4. Inner Crust
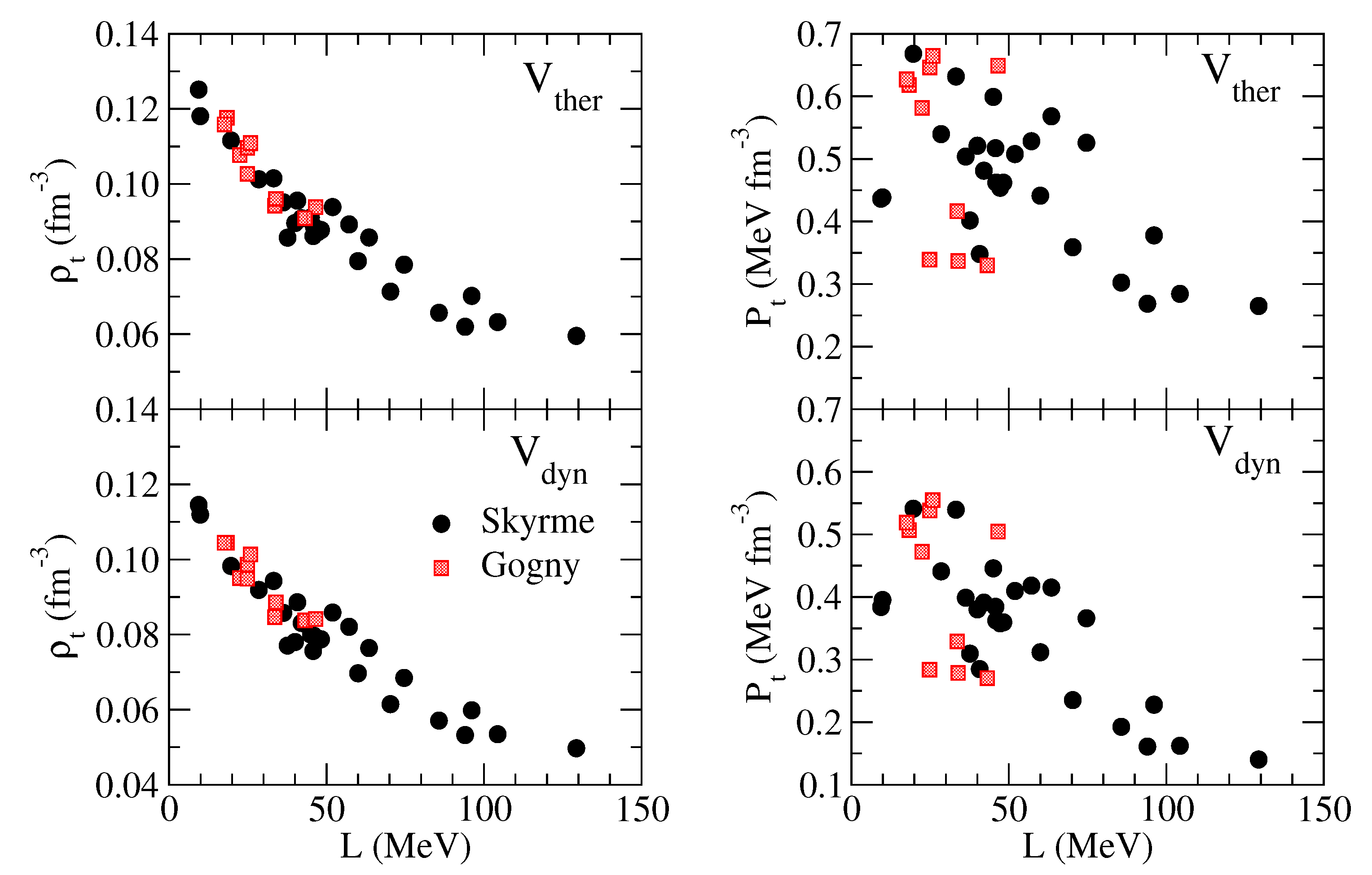
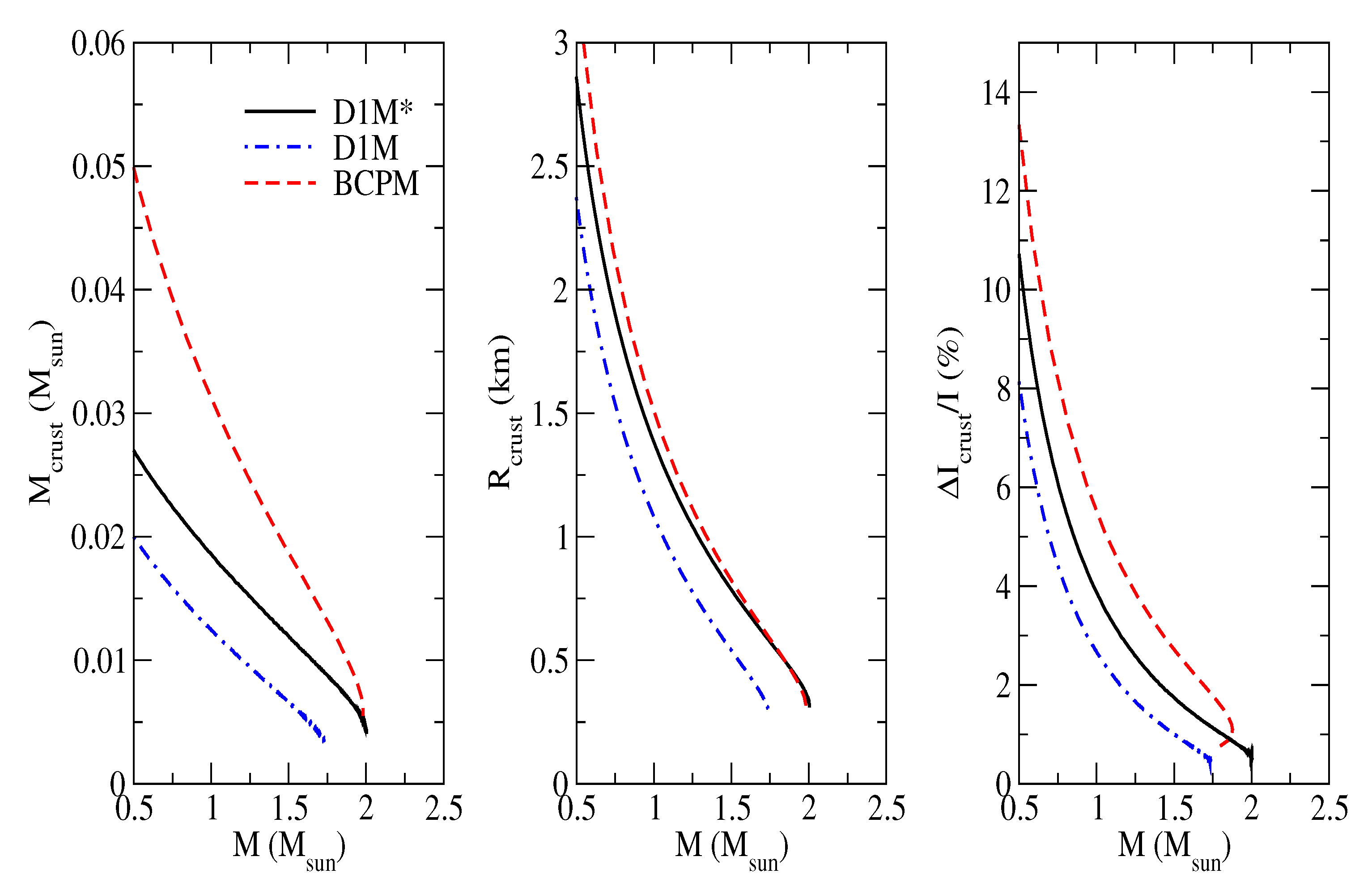
3.5. Core–Crust Transition
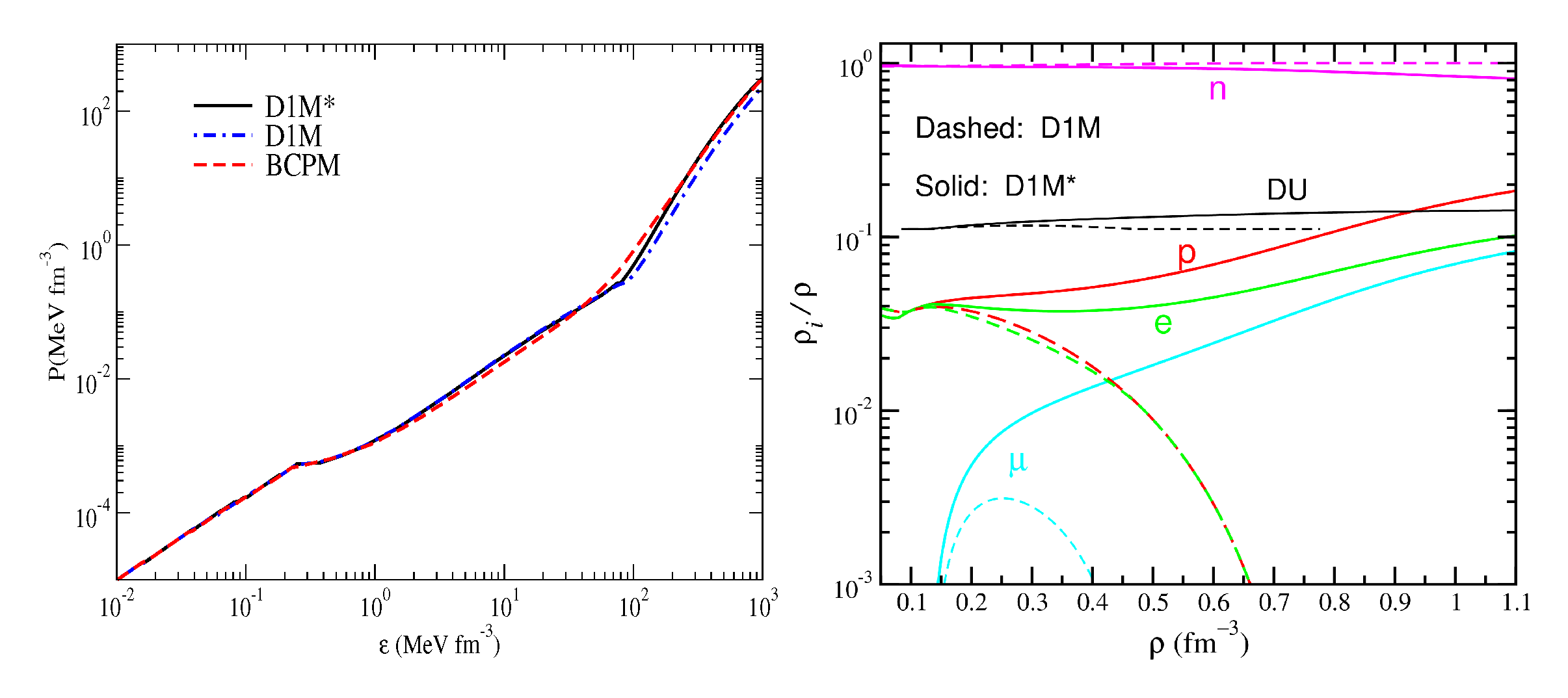
4. Global Properties of Neutron Stars Predicted by Gogny Forces
4.1. The Tolman–Oppenheimer–Volkov Equations
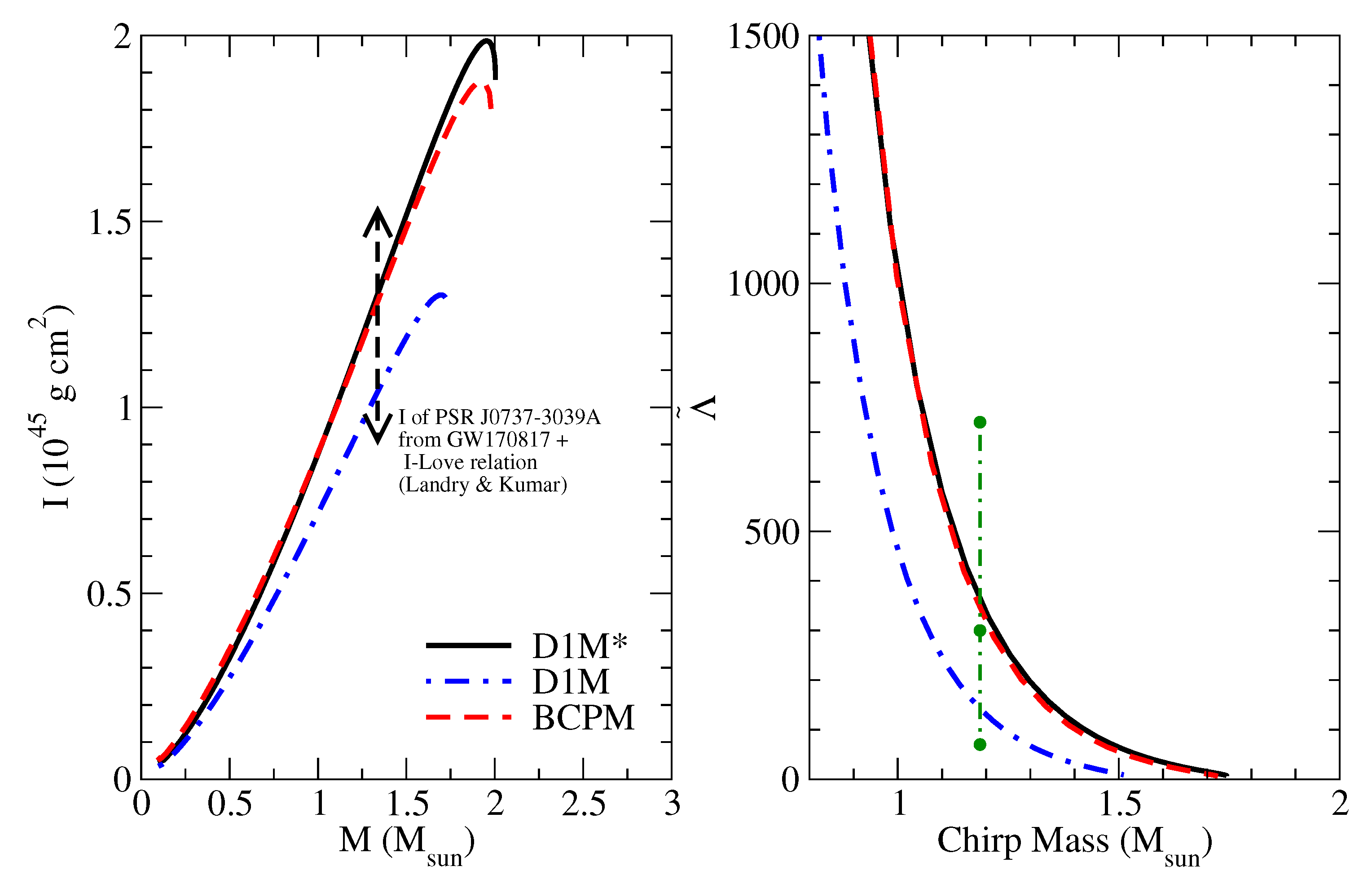
4.2. Moment of Inertia
4.3. Tidal Deformability
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dechargé, J.; Gogny, D. Hartree-Fock-Bogoliubov calculations with the D1 effective interaction on spherical nuclei. Phys. Rev. C 1980, 21, 1568. [Google Scholar] [CrossRef]
- Berger, J.-F.; Girod, M.; Gogny, D. Time-dependent quantum collective dynamics applied to nuclear fission. Comp. Phys. Comm. 1991, 63, 365. [Google Scholar] [CrossRef]
- Hilaire, S.; Girod, M. AMEDEE database, International Conference on Nuclear Data for Science and Technology. Nucl. Struct. Decay Data 2008. [Google Scholar] [CrossRef]
- Pillet, N.; Hilaire, S. Towards an extended Gogny force. Eur. Phys. J. A 2017, 53, 193. [Google Scholar] [CrossRef]
- Chappert, F.; Girod, M.; Hilaire, S. Towards a new Gogny force parametrization: Impact of the neutron matter equation of state. Phys. Lett. B 2008, 668, 420. [Google Scholar] [CrossRef]
- Goriely, S.; Hilaire, S.; Girod, M.; Péru, S. First Gogny-Hartree-Fock-Bogoliubov Nuclear Mass Model. Phys. Rev. Lett. 2009, 102, 242501. [Google Scholar] [CrossRef]
- Audi, G.; Waspra, A.H.; Thibault, C. The AME2003 atomic mass evaluation (II). Tables, graphs and references. Nucl. Phys. A 2003, 729, 337. [Google Scholar] [CrossRef]
- Friedman, B.; Pandharipande, V.R. Hot and cold, nuclear and neutron matter. Nucl. Phys. A 1981, 361, 502. [Google Scholar] [CrossRef]
- Robledo, L.M. HFBaxial Computer Code. 2002; unpublsihed. [Google Scholar]
- Robledo, L.M.; Bertsch, G.F. Application of the gradient method to Hartree-Fock-Bogoliubov theory. Phys. Rev. C 2011, 84, 014312. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Waspra, A.H.; Kondev, F.G.; MacCormick, M.; Xu, X.; Pfeifer, B. The AME2012 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2012, 36, 1603. [Google Scholar] [CrossRef]
- Sellahewa, R.; Rios, A. Isovector properties of the Gogny interaction. Phys. Rev. C 2014, 90, 054327. [Google Scholar] [CrossRef]
- Gonzalez-Boquera, C.; Centelles, M.; Viñas, X.; Rios, A. Higher-order symmetry energy and neutron star core-crust transition with Gogny forces. Phys. Rev. C 2017, 96, 065806. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ramson, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar mass neutron star measured using the Shapiro delay. Nature 2010, 467, 1081. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 448. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M. The NANOGrav nine-year data set: Mass and geometric measurements of binary millisecond pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S. The NANOGrav 11-year data set: High precision timing of 45 millisecond pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef]
- Chappert, F.; Pillet, N.; Girod, M.; Berger, J.-F. Gogny force with a finite-range density dependence. Phys. Rev. C 2015, 91, 034312. [Google Scholar] [CrossRef]
- Gonzalez-Boquera, C.; Centelles, M.; Viñas, X.; Robledo, L.M. New Gogny interaction suitable for astrophysical applications. Phys. Lett. B 2018, 779, 195. [Google Scholar] [CrossRef]
- Gonzalez-Boquera, C. Neutron-rich matter in atomic nuclei and neutron stars. arXiv 2019, arXiv:2003.00490. [Google Scholar]
- Sharma, B.K.; Centelles, M.; Viñas, X.; Baldo, M.; Burgio, G.F. Unified equation of state for neutron stars on a microscopic basis. Astron. Astrophys. 2015, A584, 103. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals–I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994. [Google Scholar] [CrossRef]
- Perot, L.; Chamel, N.; Sourie, A. Role of the symmetry energy and the neutron-matter stiffness on the tidal deformability of a neutron star with unified equations of state. Phys. Rev. C 2019, 100, 035801. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 1992, 922, 1. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, K.-W. Electric dipole polarizability in 208Pb as a probe of the symmetry energy and neutron matter around ρ0/3. Phys. Rev. C 2015, 92, 031301. [Google Scholar] [CrossRef]
- Tsang, M.B.; Zhang, Y.; Danielewicz, P.; Famiano, M.; Li, Z.; Lynch, W.G.; Steiner, A.W. Constraints on the density dependence of the symmetry energy. Phys. Rev. Lett. 2009, 102, 122701. [Google Scholar] [CrossRef] [PubMed]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.G.; olfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012, 86, 015803. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the symmetry parameters of the nuclear interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The equation of state of hot, dense matter and neutron stars. Phys. Rep. 2016, 621, 127. [Google Scholar] [CrossRef]
- Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Nuclear Symmetry Energy Probed by Neutron Skin Thickness of Nuclei. Phys. Rev. Lett. 2009, 102, 122502. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Centelles, M.; Viñas, X.; Warda, M. Neutron skin of 208Pb, Nuclear Symmetry Energy, and the Parity Radius Experiment. Phys. Rev. Lett. 2011, 106, 252501. [Google Scholar] [CrossRef]
- Viñas, X.; Centelles, M.; Roca-Maza, X.; Warda, M. Density dependence of the symmetry energy from neutron skin thickness in finite nuclei. Eur. Phys. J. A 2014, 50, 27. [Google Scholar] [CrossRef]
- Agrawal, B.K.; De, J.N.; Samaddar, S.K. Determining the density content of symmetry energy and neutron skin: An empirical approach. Phys. Rev. Lett. 2012, 109, 262501. [Google Scholar] [CrossRef] [PubMed]
- Li, B.-A.; Han, X. Constraining the neutron-proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Phys. Lett. B 2013, 727, 276. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Birkhan, J.; Miorelli, M.; Bacca, S.; Bassauer, S.; Bertulani, C.A.; Hagen, G.; Matsubara, H.; von Neumann-Cosel, P.; Papenbrock, T.; Pietralla, N.; et al. Electric Dipole Polarizability of 48Ca and implications for neutron stars. Phys. Rev. Lett. 2017, 118, 252501. [Google Scholar] [CrossRef]
- Holt, J.W.; Kaiser, N. Equation of state of nuclear and neutron matter at third order in perturbation theory from chiral effective field theory. Phys. Rev. C 2017, 95, 034326. [Google Scholar] [CrossRef]
- Drischler, C.; Hebeler, K.; Schwenk, N. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys. Rev. Lett. 2019, 122, 042501. [Google Scholar] [CrossRef] [PubMed]
- Roca-Maza, X.; Viñas, X.; Centelles, M.; Agrawal, B.K.; Colò, G.; Paar, N.; Piekarewicz, J.; Vretenar, D. Neutron skin thickness from the measured electric dipole polarizability in 68Ni, 120Sn, and 208Pb. Phys. Rev. C 2015, 92, 064304. [Google Scholar] [CrossRef]
- Hagen, G.; Ekström, A.; Forssén, C.; Jansen, G.R.; Nazarewicz, W.; Papenbrock, T.; Wendt, K.A.; Bacca, S.; Barnea, N.; Carlsson, B.; et al. Neutron and weak-charge distributions of the 48Ca nucleus. Nat. Phys. 2015, 12, 186. [Google Scholar] [CrossRef]
- Viñas, X.; Gonzalez-Boquera, C.; Centelles, M.; Robledo, L.M.; Mondal, C. Gogny forces in the astrophysical context. Bulg. J. Phys. 2018, 37, 68. [Google Scholar]
- Viñas, X.; Gonzalez-Boquera, C.; Centelles, M.; Mondal, C. The modified D1M interaction: New Gogny forces adapted for neutron star calculations. Acta Phys. Pol. B Proc. Suppl. 2019, 12, 705. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Brenna, M.; Agrawal, B.K.; Borington, P.F.; Colò, G.; Cao, L.G.; Paar, N.; Vretenar, D. Giant quadrupole resonances in 208Pb, the nuclear symmetry energy, and the neutron skin thickness. Phys. Rev. C 2013, 87, 034301. [Google Scholar] [CrossRef]
- Agrawal, B.K.; Shlomo, S.; Au, V.K. Determination of the parameters of a Skyrme type effective interaction using the simulated annealing approach. Phys. Rev. C 2005, 72, 014310. [Google Scholar] [CrossRef]
- Piekarewicz, J. Pygmy resonances and neutron skins. Phys. Rev. C 2011, 83, 034319. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Piekarewicz, J. Has a thick neutron skin in 208Pb been ruled out? Phys. Rev. Lett. 2013, 111, 162501. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Piekarewicz, J. Neutron star structure and the neutron radius of 208Pb. Phys. Rev. Lett. 2001, 86, 5647. [Google Scholar] [CrossRef]
- Hellemans, V.; Pastore, A.; Duguet, T.; Bennaceur, K.; Davesne, D.; Meyer, J.; Bender, M.; Heenen, P.-H. Spurious finite-size instabilities in nuclear energy density functionals. Phys. Rev. C 2013, 88, 064323. [Google Scholar] [CrossRef]
- Martini, M.; De Pace, A.; Bennaceur, K. Spurious finite-size instabilities with Gogny-type interactions. Eur. Phys. J. A 2019, 55, 150. [Google Scholar] [CrossRef]
- Gonzalez-Boquera, C.; Centelles, M.; Viñas, X.; Robledo, L.M. Finite-size instabilities in finite-range forces. Phys. Rev. C 2021, 103, 064314. [Google Scholar] [CrossRef]
- Mondal, C.; Viñas, X.; Centelles, M.; De, J.N. Structure and composition of the inner crust of neutron stars from Gogny interactions. Phys. Rev. C 2020, 102, 015802. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Springer-Verlag: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Chamel, N.; Haensel, P. Physics of neutron star crusts. Liv. Rev. Relat. 2008, 11, 10. [Google Scholar] [CrossRef]
- Grill, F.; Providência, C.; Avancini, S.S. Neutron star inner crust and symmetry energy. Phys. Rev. C 2012, 85, 055808. [Google Scholar] [CrossRef]
- Avancini, S.S.; Bertolino, B.P. Cold pasta phase in the extended Thomas-Fermi approximation. Int. J. Mod. Phys. E 2015, 24, 1550078. [Google Scholar] [CrossRef]
- Newton, W.G.; Gearheart, M.; Li, B.-A. A survey of the parameter space of the compressible liquid drop model as applied to the neutron star inner crust. Astrophys. J. Suppl. Ser. 2012, 204, 9. [Google Scholar] [CrossRef]
- Freiburghaus, C.; Rosswog, S.; Thielemann, F.K. r-process in neutron star mergers. Astrophys. J. 1999, 525, L121. [Google Scholar] [CrossRef]
- Goriely, S.; Demetriou, P.; Janka, H.-T.; Pearson, J.M.; Samyn, M. The r-process nucleosynthesis: A continued challenge for nuclear physics and astrophysics. Nucl. Phys. A 2005, 758, 587. [Google Scholar] [CrossRef]
- Baiotti, L.; Rezzolla, L. Binary neutron star mergers: A review of Einstein’s richest laboratory. Rep. Prog. Phys. 2017, 80, 096901. [Google Scholar] [CrossRef] [PubMed]
- von Weizsäcker, C.F. Zur theorie der kernmassen. Z. Phys. 1935, 96, 431. [Google Scholar] [CrossRef]
- Bethe, H.A.; Bacher, R.F. Nuclear Physics A. Stationary states of nuclei. Rev. Mod. Phys. 1936, 8, 82. [Google Scholar] [CrossRef]
- Strutinsky, V.M. Shell effects in nuclear masses and deformation energies. Nucl. Phys. A 1967, 95, 420. [Google Scholar] [CrossRef]
- Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Quantum statistics of almost classical assemblies. Phys. Rev. 1933, 44, 31. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Schuck, P.; Viñas, X. A variational Wigner-Kirkwood theory of finite nuclei. Phys. Lett. B 1993, 302, 1. [Google Scholar] [CrossRef]
- Brack, M.; Bhaduri, P.K. Semiclassical Physics; Adisson-Wesley: London, UK, 1997. [Google Scholar]
- Centelles, M.; Viñas, X.; Durand, M.; Schuck, P.; Von-Eiff, D. Variational Wigner-Kirkwood ℏ expansion. Ann. Phys. 1998, 266, 207. [Google Scholar] [CrossRef]
- Centelles, M.; Schuck, P.; Viñas, X. Thomas-Fermi theory for atomic nuclei revisited. Ann. Phys. 2007, 322, 363. [Google Scholar] [CrossRef]
- Soubbotin, V.B.; Viñas, X. Extended Thomas-Fermi approximation to the one-body density matrix. Nucl. Phys. A 2000, 665, 291. [Google Scholar] [CrossRef]
- Bhagwat, A.; Centelles, M.; Viñas, X.; Schuck, P. Woods-Saxon type of mean-field potentials with effective mass derived from the D1S Gogny force. Phys. Rev. C 2021, 103, 024320. [Google Scholar] [CrossRef]
- Centelles, M.; Pi, M.; Viñas, X.; Garcias, F.; Barranco, M. Self-consistent extended Thomas-Fermi calculations in nuclei. Nucl. Phys. A 1990, 510, 397. [Google Scholar] [CrossRef]
- Chu, Y.H.; Jennings, B.K.; Brack, M. Nuclear binding energies and liquid drop parameters in the Extended. Thomas-Fermi approximation Phys. Lett. B 1977, 68, 407. [Google Scholar]
- Pearson, J.M.; Chamel, N.; Goriely, S.; Ducoin, C. Inner crust of neutron stars with mass-fitted Skyrme functionals. Phys. Rev. C 2012, 85, 065803. [Google Scholar] [CrossRef]
- Del Estal, M.; Centelles, M.; Viñas, X.; Patra, S.K. Pairing properties in relativistic mean field models obtained from effective field theory. Phys. Rev. C 2001, 63, 044321. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.J.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Welker, A.; Althubiti, N.A.S.; Atanasov, D.; Blaum, K.; Cocolios, T.E.; Herfurth, F.; Kreim, S.; Lunney, D.; Manea, V.; Mougeot, M.; et al. Binding energy of 79Cu: Probing the structure of the doubly magic 78Ni from only one proton away. Phys. Rev. Lett. 2017, 119, 192502. [Google Scholar] [CrossRef] [PubMed]
- Pearson, J.M.; Goriely, S.; Chamel, N. Properties of the outer crust of neutron stars from Hartree-Fock-Bogoliubov mass models. Phys. Rev. C 2011, 83, 065810. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The ground state of matter at high densities: Equation of state and stellar models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Piekarewicz, J. Impact of the symmetry energy on the outer crust of non accreting neutron stars. Phys. Rev. C 2008, 78, 025807. [Google Scholar] [CrossRef]
- Chamel, N. Analytical determination of the structure of the outer crust of a cold nonaccreted neutron star. Phys. Rev. C 2020, 101, 032801. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Pastore, A.; Goriely, S. Role of proton pairing in a semimicroscopic treatment of the inner crust of neutron stars. Phys. Rev. C 2015, 91, 018801. [Google Scholar] [CrossRef]
- Shelley, M.; Pastore, A. Comparison between the Thomas-Fermi and Hartree-Fock-Bogolibov Methods in the Inner Crust of a Neutron Star: The role of Pairing Correlations. Universe 2020, 6, 206. [Google Scholar] [CrossRef]
- Shelley, M.; Pastore, A. Systematic analysis of the inner crust composition using the extended Thomas-Fermi approximation with pairing correlations. Phys. Rev. C 2021, 103, 035807. [Google Scholar] [CrossRef]
- Gonzalez-Boquera, C.; Centelles, M.; Viñas, X.; Routray, T.R. Core-crust transition in neutron stars with finite-range interactions: The dynamical method. Phys. Rev. C 2019, 100, 015806. [Google Scholar] [CrossRef]
- Xu, J.; Chen, L.-W.; Li, B.-A.; Ma, H.-R. Nuclear constraints on properties of neutron star crusts. Astrophys. J. 2009, 697, 1549. [Google Scholar] [CrossRef]
- Zhang, N.-B.; Li, B.-A. Constraints on the muon fraction and density profile in neutron stars. Astrophys. J. 2020, 893, 61. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Typel, S.; van Dalen, E.N.E.; Faessler, A.; Fuchs, C.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Nättilä, J.; Steiner, A.W.; Kajava, J.J.E.; Suleimanov, V.F.; Poutanen, J. Equation of state constraints for the cold dense matter inside neutron stars using the cooling tail method. Astron. Astrophys. 2016, 591, A25. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Constraints on the symmetry energy using the mass-radius relation of neutron stars. Eur. Phys. J. A 2014, 50, 40. [Google Scholar] [CrossRef]
- Abbott, B.; Jawahar, S.; Lockerbie, N.; Tokmakov, K. LIGO Scientific Collaboration and Virgo Collaboration. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER view of PSR J0030+0451: Millisecond pulsar parameter estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER view of the massive pulsar PSR J0740+6620 informed by radio timing and XMM-Newton spectroscopy. arXiv 2021, arXiv:2105.06980. [Google Scholar]
- Hartle, J.B. Slowly rotating relativistic stars. I. equations of structure. Astrophys. J. 1967, 150, 1005. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Piekarewicz, J. Sensitivity of the moment of inertia of neutron stars to the equation of state of neutron-rich matter. Phys. Rev. C 2010, 82, 025810. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J. Neutron star moments of inertia. Astrophys. J. 1994, 424, 846. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Schutz, B.F. Constraining the equation of state with moment of inertia measurements. Astrophys. J. 2005, 629, 979. [Google Scholar] [CrossRef]
- Link, B.; Epstein, R.I.; Lattimer, J.M. Pulsar constraints on neutron stars structure and equation of state. Phys. Rev. Lett. 1999, 83, 3362. [Google Scholar] [CrossRef]
- Anderson, N.; Glampedakis, K.; Ho, W.C.G.; Espinoza, C.M. Pulsar glitches: The crust is not enough. Phys. Rev. Lett. 2012, 109, 241103. [Google Scholar] [CrossRef]
- Chamel, N. Crustal Entrainment and Pulsar Glitches. Phys. Rev. Lett. 2013, 110, 011101. [Google Scholar] [CrossRef]
- Landry, P.; Kumar, B. Constraints on the moment of inertia of PSR J037-3039A from GW170817. Astrophys. J. 2018, 868, L22. [Google Scholar] [CrossRef]
- Breu, C.; Rezzolla, L. Maximum mass, moment of inertia and compactness of relativistic stars. Mon. Not. R. Astron. Soc. 2016, 459, 646. [Google Scholar] [CrossRef]
- Flanagan, É.É.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Abbott, B.; Jawahar, S.; Lockerbie, N.; Tokmakov, K. LIGO scientific collaboration and Virgo collaboration. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.; Jawahar, S.; Lockerbie, N.; Tokmakov, K. LIGO scientific collaboration and Virgo collaboration. Properties of the binary neutron star merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar]
- Lourenço, O.; Bhuyan, M.; Lenzi, C.H.; Dutra, M.; Gonzalez-Boquera, C.; Centelles, M.; Viñas, X. GW170817 constraints analyzed with Gogny forces and momentum-dependent interactions. Phys. Lett. B 2020, 803, 135306. [Google Scholar] [CrossRef]



| D1M | |||||
| i = 1 | −12,797.57 | 14,048.85 | −15,144.43 | 11,963.81 | 0.50 |
| i = 2 | 490.95 | −752.27 | 675.12 | −693.57 | 1.00 |
| 1562.22 | 1 | 1/3 | 115.36 | ||
| D1M | |||||
| i = 1 | −17,242.0144 | 19,604.4056 | −20,699.9856 | 16,408.3344 | 0.50 |
| i = 2 | 675.3860 | −982.8150 | 905.6650 | −878.0060 | 1.00 |
| 1561.22 | 1 | 1/3 | 115.36 | ||
| D1M | |||||
| i = 1 | −15,019.7922 | 16,826.6278 | −17,922.2078 | 14,186.1122 | 0.50 |
| i = 2 | 583.1680 | −867.5425 | 790.3925 | −785.7880 | 1.00 |
| 1562.22 | 1 | 1/3 | 115.36 |
| L | |||||||
|---|---|---|---|---|---|---|---|
| (fm) | (MeV) | (MeV) | (MeV) | (MeV) | (MeV) | ||
| D1M | 0.1647 | −16.02 | 224.98 | 0.746 | 28.55 | 23.80 | 24.83 |
| D1M | 0.1650 | −16.06 | 225.38 | 0.746 | 30.25 | 23.82 | 43.18 |
| D1M | 0.1647 | −16.02 | 224.98 | 0.746 | 29.37 | 23.80 | 33.91 |
| BCPM | 0.1600 | −16.00 | 213.75 | 1.000 | 31.92 | 24.20 | 52.96 |
| (fm) | (MeVfm) | ||
|---|---|---|---|
| D1M | |||
| 0.1027 | 0.3390 | 0.9241 | |
| 0.0949 | 0.2839 | 0.9257 | |
| D1M | |||
| 0.0909 | 0.3301 | 0.9275 | |
| 0.0838 | 0.2702 | 0.9300 | |
| D1M | |||
| 0.0960 | 0.3368 | 0.9257 | |
| 0.0886 | 0.2786 | 0.9279 | |
| BCPM | |||
| 0.0889 | 0.5137 | 0.9339 | |
| 0.0816 | 0.4132 | 0.9382 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viñas, X.; Gonzalez-Boquera, C.; Centelles, M.; Mondal, C.; Robledo, L.M. Unified Equation of State for Neutron Stars Based on the Gogny Interaction. Symmetry 2021, 13, 1613. https://doi.org/10.3390/sym13091613
Viñas X, Gonzalez-Boquera C, Centelles M, Mondal C, Robledo LM. Unified Equation of State for Neutron Stars Based on the Gogny Interaction. Symmetry. 2021; 13(9):1613. https://doi.org/10.3390/sym13091613
Chicago/Turabian StyleViñas, Xavier, Claudia Gonzalez-Boquera, Mario Centelles, Chiranjib Mondal, and Luis M. Robledo. 2021. "Unified Equation of State for Neutron Stars Based on the Gogny Interaction" Symmetry 13, no. 9: 1613. https://doi.org/10.3390/sym13091613
APA StyleViñas, X., Gonzalez-Boquera, C., Centelles, M., Mondal, C., & Robledo, L. M. (2021). Unified Equation of State for Neutron Stars Based on the Gogny Interaction. Symmetry, 13(9), 1613. https://doi.org/10.3390/sym13091613






