Abstract
In this paper, the dynamic characteristics of sandwich plates with external rigid layers and an upper layer with magnetorheological properties (MR) are investigated. An analysis of the effect of the magnetic field on frequency and loss factor is presented. Vibration can be controlled by a magnetic-rheological viscoelastomer (MRVE), when used in sandwich plates. During vibration, MRVE exhibits an inhomogeneous complex module, which is controlled by an applied magnetic field and depends on the oscillation frequency. Using the dynamic equilibrium conditions, physical and kinematic relationships, and the partial differential equations for the conjugate transverse and longitudinal oscillations of a sandwich plate, are derived. This paper presents a new method for stress analysis that provides accurate stress distributions for multilayer plates subject to cylindrical bending. It uses an adaptive method that does not make strict assumptions about the plate model. Based on the depicted theoretical model, the deformations of each layer of the plate are accounted for, including both transverse shear deformations and transverse normal deformations where the thickness is concerned, and nonlinear displacement changes. The magnetorheological (MR) identification of an inner layer is carried out using refined plate theory and sandwich bending tests. Using combined methods, the possibility of determining the MRVE parameters robustly, is examined.
1. Introduction
Magneto-rheological visco-elastomers (MRVE) are used in laminated plates to control vibration. It is necessary to explain the dynamic characteristics of such elements, in particular the amount of energy dissipation (damping), which is affected by the applied magnetic field. The magnetic elastomer is a smart, composite material composed of magnetically polarizable particles and nonmagnetic polymers, such as rubber, silicone oil, and iron particles. Interestingly, an elastomer’s time-invariant feature is the propensity of magnetic particles to settle to naught in magnetorheological fluids. With external magnetic fields applied in milliseconds, its dynamic characteristics, including rigidity and damping [1,2,3], can be changed reversibly.
MRVE usually consists of silicone rubber and carbonate iron particles. This composite continuum medium contains proportionally distributed iron particles. In the MRVE, such dynamics are available as controlled stiffness and the frequency-dependent damping of a magneto-rheological fluid combined with a viscoelastic polymer. Magnetic field changes can alter these characteristics in milliseconds.
Magnetorheological (MR) materials with dramatically changing rheological properties were first described in [1]. When a magnetic field is applied, both stiffness and damping properties are referred to [2]. The mechanical properties of composites consisting of ferroparticles in a polymer matrix are considered in [3]. The use of such materials and the study of their magneto-rheological properties is also analyzed in [4,5].
Usually, for calculations of layered structures with MR layers, classical models are used. In [6,7,8], three-layer constructions (sandwiches) with an internal magnetic layer are considered. In [9], a comparative description of the application of analytical methods is given. For the effective control of some dynamic objects, for example, dynamic oscillation dampers, MRVE are used in elastic elements [10,11,12].
There are a variety of numerical schemes for determining the characteristics of layered compositions, which correspond closely to known numerical models of layered plates. An evaluation of the theories of layered elements under various loads is presented in [13,14]. To study the dynamics of thin-walled elements, theories of ever-higher order are applied. An important task is to determine the damping properties of structural elements, in particular thin-walled laminated materials. This is due to the more common use of such elements in aerospace engineering, mechanical engineering, and construction. A generalized kinematic approximation method and the conventional Galerkin method are employed in this study to provide an adaptive algorithm to solve the system of equations on the linear theory of elasticity [15,16,17,18].
2. Materials and Methods
In the present study, the authors developed a numerical method using a semi-analytical approach in which an analytical field was applied in the longitudinal direction and a layer-wise power series displacement field was used in the transverse direction. In this approach, the authors aimed to explore the ability to decide the level of refinement needed in higher-order theory to conduct an efficient and accurate analysis. This method provided precise stress-distribution analyses for multilayer plates in reference to cylindrical bending. The approach employed an adaptive method, avoiding the use of strict assumptions applied to the plate model. Based on the depicted theoretical model, the deformations of each layer of the plate were accounted for, including both transverse shear deformations and transverse normal deformations where the thickness was concerned, and nonlinear displacement changes. Let us consider now such kinematic assumptions (U = Ue + Ud) for a symmetrical three-layered plate of thickness 2Hp (only cylindrical bending is considered):
where Ue, Ud, U were displacement vectors, respectively, of the core face sheet and the sandwich; H was thickness; z- was the set of optimization parameters; φk (x), γk (x) were a priori known coordinate functions (for all beam clamp conditions); and uike, wike, uikd, wikd were the unknown set of parameters representing the displacement and amplitude elements in x and z coordinates.
The following was achieved by substituting Equation (1) into the Hamilton variation equation presented in [18]:
where, σ is normal stress; ε is normal deformation; τ is shear stress; and P is the external force vector, and also assuming that from the single frequency vibration () we obtained the set of linear algebraic equations for the amplitudes:
where [A] was the system matrix and sub-matrices, and f was the eigenfrequencies. Using viscous damping, the following frequency equation could be written for the material:
where [M] was the mass matrix, [C] was the damping matrix, and [K] was the stiffness matrix. A frequency-domain method was typically used to investigate linear elastic systems. Due to the consideration of the first term in (1), we obtained the kinematic assumption for a TB. A more detailed approach to an explanation of this method may be found in [15,16,17,18].
3. Results
3.1. Modeling of Mechanical Properties of the MR Layer
The method of calculation of layered plates and model verification are given in [19]. Let us consider some numerical examples of the calculation of the vibrations of three-layer beams (sandwiches) with an inner MR layer (core). We first assume that its elastic moduli change corresponds to the change in the transverse magnetic field acting on it with the induction and vibration frequency. Then, the influence of the magnetic field on the MR layer can be considered through the complex core shear modulus of the sandwich:
where G is considered the real and assumed shear module.
Another form of recording is then possible:
where the real part of the module and the coefficient of the loss of viscoelastic damping is considered.
In future, for the calculations, we will use four types of material MR layers with the following dependencies of complex shear moduli:
- (1).
- The value of the modules are given in [19]:
- (2).
- The value of the modules are given in [9]:
- (3).
- The value of the modules are given in [20]:
Somewhat more complex dependencies of the modules, which rely not only on the magnetic field strength but also on the frequency of the fourth type of materials, (MRF122EG, MRF132DG) are given in [21] where the value of the coefficients for the material MRF132DG are: a0 = 192160.6, = a130663.56, a2 = 243.6247, a3 = 0.004080 and GI for a0 = 45524.40, a2 = 6757.977, = 6.4412, a3 = 0.007416 for GII. Figure 1 shows the real GI and imaginary part GII of the module G and the loss coefficient η0 for different types of material depending on the oscillation frequency and magnetic field strength.
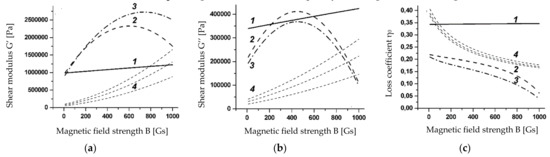
Figure 1.
Complex shear modulus (a,b) and loss coefficient (c) for different types of material: 1, 2, 3 and 4. Dashed lines correspond to the frequencies of 1 Hz, 100 Hz, 300 Hz.
3.2. Laminated Symmetric Beams with Inner MR Layer
Let us now consider the oscillations of a cantilever sandwich of length L = 0.3 m and equal thicknesses, Hc = Hf = 0.001 m, of layers with an inner MR layer for the first three types of material. The outer layers of the beam (cover) are made of aluminum with the following mechanical properties: EA = 70 GPA, GA = 30 GPA, VA = 0.3, and ρA = 2700 kg/m3.
Figure 2 and Figure 3 show the amplitude–frequency characteristic (AFC) and damping of the cantilever sandwich beam, depending on the magnetic field strength for different types of material of the MR layer.
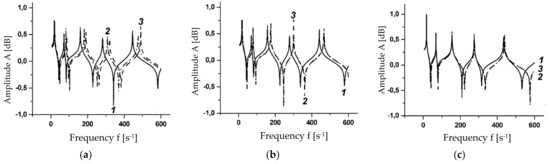
Figure 2.
Sandwich frequency response for different values of magnetic field strength (a–c) and for different types of material: 1, 2 and 3. B = 0 (a), B = 250 G (b), B = 800 G (c) and for different types of material: 1, 2 and 3.
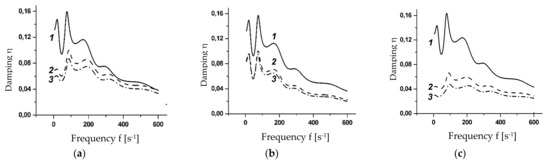
Figure 3.
Damping in sandwich frequency for different values of magnetic field strength: B = 0 (a), B = 250 G (b), B = 800 G (c) and for different types of material: 1, 2 and 3.
3.3. Five-Layered Beam
Let us now consider the oscillations of asymmetric five-layer freely supported centrally loaded beam with the following values of 0.3 m layer thicknesses: h1 = 0.001 m for a central rigid layer, h2 = 0.001 m for two inner symmetrically located MR layers, and h3 = 0.005 m for two outer layers of covers. A composite with the following mechanical properties is considered as a material of rigid layers: Cxx = 5400 MPa, Czz = 750 MPa, G = 200 MPa, Cxx = 375 MPa, ρA = 2400 kg/m3 and as a material of MR layers—MRF 132DG. Figure 4 shows the dynamic properties (damping) of a five-layer beam in comparison with a similar three-layer beam, the thickness of the inner MR layer of which was equal to 0.002 m, and the thickness of its composite covers were equal to −0.001 m. Here in Figure 4, solid lines correspond to a three-layer beam, and dotted lines correspond to a five-layer beam.
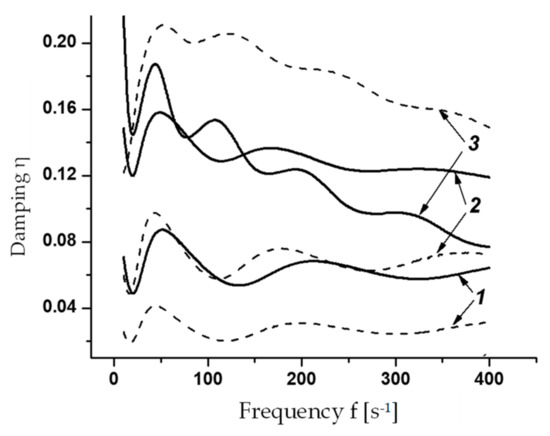
Figure 4.
Damping in three-layer and five-layer beams for different values of magnetic field strength B = 0 (1), B = 75 (2), B = 150 G (3).
3.4. Identification of MR Layer Modules
The identification of the shear modulus for the material of the second type (see relations (10)) according to the results of dynamic tests is implemented by minimizing the error function in the form of the total square deviation between the calculated and experimentally measured [22,23,24,25,26] Eigen frequency values:
Figure 5 and Figure 6 show the deviations of the shear modulus of the above freely sup-ported and cantilevered sandwich beams for three values of the magnetic field strength: 1’ – (7), 2’ – (8), 3’ – (9) (corresponding to materials given in [19,20,21]). The corresponding experimental values are marked with vertical dashed lines and with an index containg a dash. Figure 5 shows examples of the application of various kinematic approximations (1) for the average value of the magnetic field strength. If the approximations in thickness with the number of terms provide almost identical results, then the first-order approximation is unacceptable.
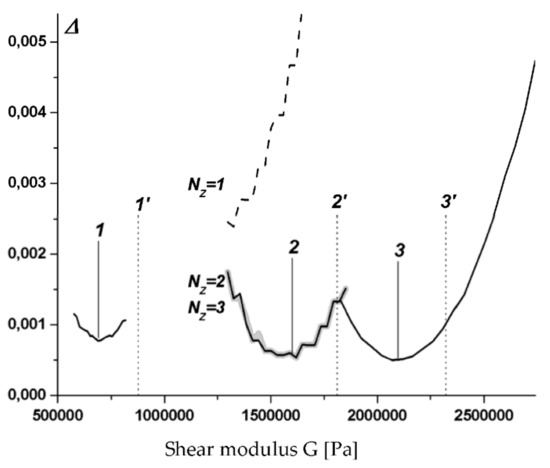
Figure 5.
Deviations of the shear modulus of a freely supported beam for three (1, 2, 3) values of the magnetic field strength and 1’, 2’, 3’ values derived from (7), (8) and (9) respectively.
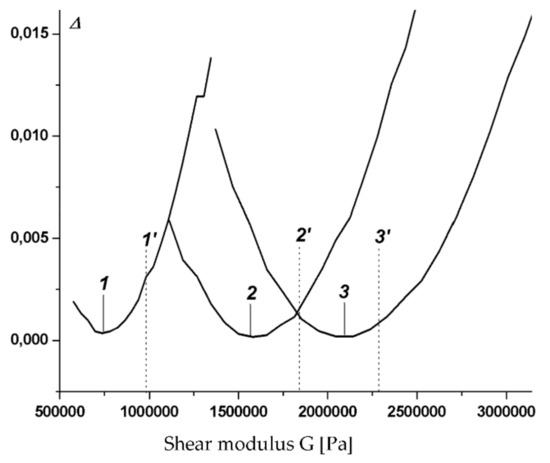
Figure 6.
Deviations of the cantilever beam shear modulus for three (1,2 3) values (1,2 3) of the magnetic field strength and 1’, 2’, 3’ values derived from (7), (8) and (9) respectively.
Figure 7 shows the deviation maps of the function (10) for the frequency-dependent shear modulus (9), where the point of intersection of the straight lines corresponds to their fixed values in (9).
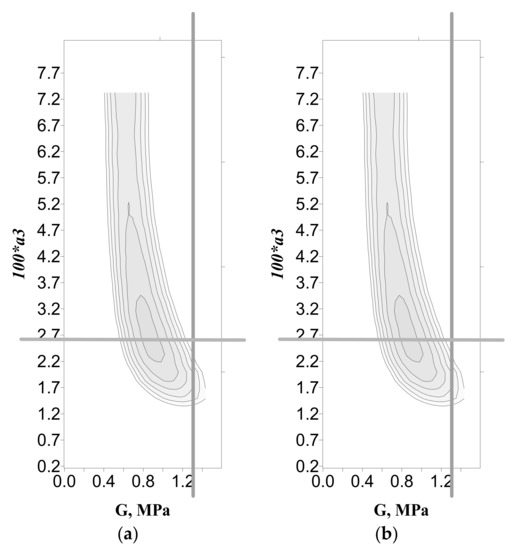
Figure 7.
Deviation maps depending on intensity: (a) B = 300 G; (b) = 500 G (the occluded ordinate in the figure is 2.7).
4. Conclusions
To determine the damping in layered structures, “unified” computational schemes have been proposed, in which the order of the equations is not limited (an arbitrary number of approximations in the thickness of each layer of the plate is considered). The validation of the presented model with FEM was performed by comparing the Eigen frequencies of a clamped-free uniform isotropic beam for the following geometrical parameters: length was chosen to be 0.3 m, thickness was chosen to be H = 0.0130 m. The reliable outcomes that have already been published in [18] allowed us to consider the model as empirically correct. Based on the refined computational schemes, the effect of the magnetic field in a laminated beam on its frequency spectrum and damping was determined. Several beams with various materials MP and rigid layers: aluminum, copper, composite and four types of material with MR layers were considered. The first three were materials with frequency-independent shear moduli of the MR layer, the fourth with modules dependent on frequency and magnetic field strength. As well as the console, the freely supported beams were considered in the research too. The material of the first type is the least rigid and has greater damping, especially at high frequencies. The materials of the second and third types were similar in mechanical properties and dynamic characteristics for all types of beams with different rigid layers. For the material of the fourth type (MRF 132DG), a comparison of the dynamic characteristics for three and five-layer beams were given. A five-layer beam had slightly more damping than a three-layer beam with a similar distribution of materials; the total thickness of the MR layers and the hard layers were the same) for magnetic fields of low intensity.
Author Contributions
I.K. and B.D.; methodology, O.H.; software, L.S.; validation, O.H., R.H. and P.O.; formal analysis, Y.S.; investigation, I.K.; resources, Y.S.; data curation, O.H.; writing—original draft preparation, I.K., O.H. and E.K.; writing—review and editing, P.O.; visualization, Y.S.; supervision, E.K.; project administration, I.K.; funding acquisition, I.K. and B.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jacob, R. Magnetic Fluid Torque and Force Transmitting Device. US Patent 2575360, 30 November 1951. [Google Scholar]
- Shiga, T.; Okadam, A.; Kurauchi, T. Magnetoviscoelastic behavior of composite gels. J. Appl. Polym. Sci. 1995, 58, 787–792. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Munoz, B.C.; Bullions, A. The magnetoviscoelastic response of elastomer composites consisting of ferrous particles embedded in a polymer matrix. J. Intell. Mater. Syst. Struct. 1996, 7, 613–722. [Google Scholar] [CrossRef]
- Yalcintas, M.; Dai, H. Magnetorheological and electrorheological materials in adaptive structures and their performance comparison. Smart Mater. Struct. 1999, 8, 560–573. [Google Scholar] [CrossRef]
- Bellan, C.; Bossis, G. Filed dependence of viscoelastic properties of magnetorheological elastomers. Inter. J. Mod. Phys. 2002, 16, 2447–2453. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Wang, Q. Study on the adjustable rigidity of magnetorheological-elastomer-based sandwich beams. Smart Mater. Struct. 2006, 15, 59–74. [Google Scholar] [CrossRef]
- Ying, Z.G.; Ni, Y.Q. Micro-vibration response of a stochastically excited sandwich beam with a magnetorheological elastomer core and mass. Smart Mater. Struct. 2009, 18, 095005. [Google Scholar] [CrossRef]
- Nayak, B.; Dwivedy, S.K.; Murthy, K.S. Dynamic analysis of magnetorheological elastomer-based sandwich beam with conductive skins under various boundary conditions. J. Sound Vibration 2011, 330, 1837–1859. [Google Scholar] [CrossRef]
- Rajamohan, V.; Sedaghati, R.; Rakheja, S. Vibration analysis of a multi-layer beam containing magnetorheological fluid. Smart Mater. Struct. 2010, 19, 015013. [Google Scholar] [CrossRef]
- Yalcintas, M.; Dai, H. Vibration suppression capabilities of magneto-rheological materials based adaptive structures. Smart Mater. Struct. 2004, 13, 1. [Google Scholar] [CrossRef]
- Sun, Q.; Zhou, J.X.; Zhang, L. An adaptive beam model and dynamic characteristics of magnetorheological materials. J. Sound Vibration 2003, 261, 465–481. [Google Scholar] [CrossRef]
- Yeh, Z.F.; Shih, Y.S. Dynamic characteristics and dynamic instability of magnetorheological based adaptive beams. J. Compos. Mater. 2006, 40, 1333–1359. [Google Scholar] [CrossRef]
- Carrera, E. Historical review of zig-zag theories for multilayered plates and shells. Appl. Mech. Rev. 2003, 56, 287–308. [Google Scholar] [CrossRef]
- Hu, H.; Belouettar, S.; Potier-Ferry, M.; Daya, E.M. Review and assessment of various theories for modeling sandwich composites. Compos. Struct. 2008, 84, 282–292. [Google Scholar] [CrossRef]
- Diveyev, B.; Butyter, I.; Shcherbyna, N. High order theories for elastic modules identification of composite plates. Part 1. Theoretical approach. Mech. Compos. Mater. 2008, 1, 25–36. [Google Scholar] [CrossRef]
- Diveyev, B.; Butyter, I.; Shcherbyna, N. High order theories for elastic modules identification of composite plates. Part 2. Theoretical-experimental approach. Mech. Compos. Mater. 2008, 2, 139–144. [Google Scholar] [CrossRef]
- Butyter, I.; Diveyev, B.; Kogut, I.; Marchuk, M.; Shcherbyna, N. Identification of elastic moduli of composite beams by using combined criteria. Mech. Compos. Mater. 2013, 6, 639–648. [Google Scholar] [CrossRef]
- Diveyev, B.; Konyk, S.; Crocker, M.J. Dynamic properties and damping predictions for laminated plates: High order theories—Timoshenko beam. J. Sound Vibration 2018, 413, 173–190. [Google Scholar] [CrossRef]
- Babu, V.R.; Vasudevan, R. Dynamic analysis of tapered laminated composite magnetorheological elastomer (MRE) sandwich plates. Smart Mater. Struct. 2016, 25, 035006. [Google Scholar] [CrossRef]
- Manoharan, R.; Vasudevan, R.; Jeevanantham, A.K. Dynamic characterization of a laminated composite magnetorheological fluid sandwich plate. Smart Mater. Struct. 2014, 23, 025022. [Google Scholar] [CrossRef]
- Eshaghi, M.; Rakheja, S.; Sedaghati, R. An accurate technique for pre-yield characterization of MR fluids. Smart Mater. Struct. 2015, 24, 065018. [Google Scholar] [CrossRef]
- Snitynskyy, V.; Kernytskyy, I.; Diveyev, B.; Horbay, O.; Koruniak, P.; Humenyuk, R.; Kokhana, T. Impact and particle vibration absorbers optimal design. Acta Sci. Pol. Arch. 2020, 19, 93–102. [Google Scholar] [CrossRef]
- Barretta, R.; Čanađija, M.; Sciarra, F.M.D. Nonlocal mechanical behavior of layered nanobeams. Symmetry 2020, 12, 717. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Wu, N.; Chu, F.; Luo, J. A finite element model for the vibration analysis of sandwich beam with frequency-dependent viscoelastic material core. Materials 2019, 12, 3390. [Google Scholar] [CrossRef] [PubMed]
- Pasik, T.; Chalecki, M.; Koda, E. Analysis of embedded retaining wall using the subgrade reaction method. Studia Geotech. Mech. 2015, 37, 59–73. [Google Scholar] [CrossRef][Green Version]
- Semenyuk, M.; Trach, V.; Zhukova, N. On the method of calculation of buckling and post-buckling behavior of laminated shells with small arbitrary imperfections. Acta Sci. Pol. Archit. 2021, 20, 17–25. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).