Rotational Diode: Clockwise/Counterclockwise Asymmetry in Conducting and Mechanical Properties of Rotating (semi)Conductors

Abstract

It is difficult to imagine an isolated classical object which possess different moments of inertia when it is uniformly rotated about the same axis with the same angular frequency in opposite, clockwise and counterclockwise, directions. We argue that due to quantum effects, certain (semi-) conductors should exhibit asymmetry in their mechanical and conducting properties with respect to the opposite rotations. We show that a cylinder made of a suitably chosen semiconductor, coated in a metallic film and placed in the magnetic-field background, can serve as a “rotational diode”, which conducts electricity only at a specific range of angular frequencies. The critical angular frequency and the direction of rotation can be tuned with the magnetic field’s strength. Mechanically, the rotational diode possesses different moments of inertia when rotated in clockwise and counterclockwise directions. These effects emerge as a particularity of the Fermi-Dirac statistics of electrons in rotating conductors.

1. Introduction

Our daily-life experience tells us that any physical body has the same moments of inertia with respect to rotations in clockwise and counterclockwise directions. In our paper, we show that this statement is no more correct at the quantum level if the statistical quantum effects of electronic systems are taken into account.

The effects of gravity, rotation, and acceleration on the electromagnetic and transport properties of physical systems have been a subject of intense interest throughout the decades [1]. The Einstein–de Haas [2] and Barnett [3] effects relate mechanical torque and magnetization in ferromagnets. In metals, the uniform rotation acts on electrons via a centrifugal force that produces a small, but experimentally observable radial gradient of electric potential [4]. The proposed rotational analogue of the classical Hall effect [5] highlights a well-known similarity between rotation and the magnetic field in non-relativistic systems. At the quantum level, rapidly rotating C${}_{60}$ fullerenes are suggested to exhibit Zeeman splitting in their energy levels in the absence of a true magnetic field [6].

Accelerating conductors generate intrinsic electric fields [7] while gravity exerts a force on the electrons that induces an electric field outside a metal surface [8]. Gravitational forces are expected to lead to various thermo-electromagnetic effects in (super) conductors [9]. At the same time, the quantum Hall conductance, as a true topological quantity, is insensitive to background gravity [10]. The inclusion of the spin degrees of freedom—and the ability to mechanically manipulate them in noninertial frames—is expected to play an important role in nano-electromechanical systems within the scope of the rapidly developing field of spintronics [11]. The emergence of synthetic gravitational fields in various condensed matter systems opens a new door for the discovery of novel quantum gravito-electromagnetic effects [12,13].

In our paper, we explore the mechanical and transport properties of rotating semiconductors and show that they break the equivalence of clockwise/counterclockwise rotations, which are naively expected for any isolated system. This purely quantum effect has its roots in a simple problem of classical electrodynamics which addresses the interplay between the rotation and the magnetism [14,15]. Before proceeding further, we mention that our discussion has no direct relation to the Einstein–de Haas effect [2] (which demonstrates the appearance of a mechanical torque exerted by an external magnetic field on a ferromagnet) and the Barnett effect [3] (which reveals a reciprocal phenomenon: a mechanical rotation changes the magnetization of a spinning ferromagnet). These phenomena appear naturally as a consequence of the conservation of angular momentum. They demonstrate a close relationship between the magnetism, induced by the spin and the orbital motion of the electrons, and the mechanical rotation. Both the Einstein–de Haas and Barnett effects are unusual under the time reversal transformation, thus maintaining the symmetry of the system under a clockwise/counterclockwise flip in the rotation sense (see, for example, the experimental work [16]). On the contrary, we consider an effect that breaks the clockwise/counterclockwise symmetry of rotation.

2. Rotating Conductor in Magnetic-Field Background in Classical Electrodynamics

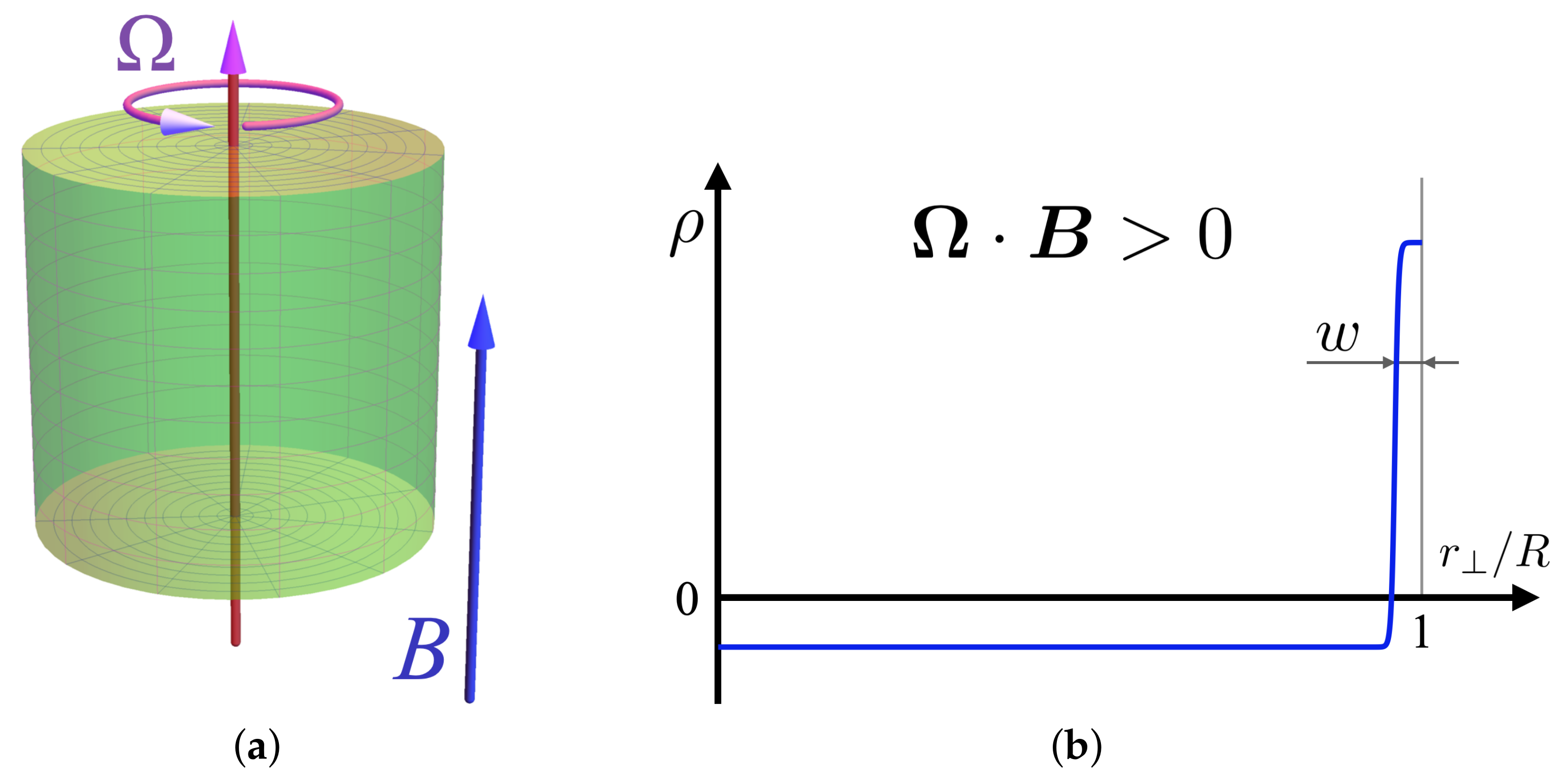
Let us consider an uncharged conducting cylinder of radius R and height L, which rotates rigidly with constant angular velocity $\mathrm{\Omega }=\mathrm{\Omega }{\mathbf{e}}_z$ about its symmetry axis z. We place the cylinder in the background of constant and uniform magnetic field $\mathit{B}=B{\mathbf{e}}_z$ directed along the axis of rotation as shown in Figure 1a. We set the relative permeability and permittivity of the material to unity $(ϵ=1,\mu =1)$ and use Gaussian units.

By treating the system in the scope of classical electrodynamics, one can show that the interior of the cylinder accumulates a uniformly distributed electric charge with bulk density [14]:

$${\rho }_{\mathrm{bulk}}=-\frac{\mathrm{\Omega }B}{2\pi c},$$

(1)

while the cylinder boundary (the part tangential to the axis z) acquires the uniform surface charge density:

$${\rho }_{\mathrm{surf}}=\frac{R\mathrm{\Omega }B}{4\pi c}.$$

(2)

Since the net electric charge of the isolated cylinder is zero, the bulk Equation (1) and surface Equation (2) charges compensate each other exactly: $\pi R^{2}L{\rho }_{\mathrm{bulk}}+2\pi RL{\rho }_{\mathrm{surf}}=0$. We do not restrict the mutual directions of $\mathrm{\Omega }$ and $\mathit{B}$ so that the excess of the charge density Equation (1) (and, respectively, Equation (2)) can take both positive and negative values.

The effect originates from the finite conductivity $\sigma \ne 0$ of the rotating cylinder. In an equilibrium state of an isolated physical body, the Joule losses should be absent. This property immediately implies the absence of any dissipative electric currents in the system. In turn, the Ohmic dissipation is generated by a local electric current with respect to the ionic crystal lattice of the conductor. Therefore, the current should vanish in the corotating frame in which the conductor appears to be static. If the axis of magnetic field and the angular velocity vector are aligned with each other, the local magnetic flux piercing the conductor is not affected by the uniform mechanical rotation. Consequently, the eddy (Foucault) currents and the associated energy losses are absent.

Denoting the quantities in the corotating (laboratory) frame by tilted (non-tilted) variables, the infinitesimal transformation between the coordinates in these frames is as follows:

$$d\tilde{\mathit{r}}=d\mathit{r}-\mathit{v}dt,d\tilde{t}=dt,\mathit{v}=\mathrm{\Omega }\times \mathit{r},$$

(3)

where $\mathit{v}$ is the local velocity of the fixed point $\mathit{r}$ of the cylinder with respect to the laboratory frame. We consider a non-relativistic rotation which guarantees the validity of the causality constraint, $\left|\mathrm{\Omega }\right|R\ll c$, where c is the speed of light.

The electromagnetic fields in the laboratory and corotating frames are related to each other as follows:

$$\tilde{\mathit{B}}=\mathit{B},\tilde{\mathit{E}}=\gamma \left(\mathit{E}+\frac{v}{c}\times \mathit{B}\right),$$

(4)

where $\gamma =1/\sqrt{1-v^2/c^2}$ is the relativistic Lorentz factor. Hereafter, we ignore all relativistic corrections because they are negligibly small in this system. The rotational motion of the bulk Equation (1) and surface Equation (2) electric charges produces, via the Ampère law, an additional magnetic field; however, this will be dropped out in the following as it makes a tiny correction to the existing magnetic-field background B. Aside from negligible relativistic effects, the densities (1) and (2) are the same in the laboratory and corotating frames, $\rho =\tilde{\rho }$.

The absence of current density in the corotating frame, $\tilde{\mathit{J}}=\sigma \tilde{\mathit{E}}=0$, implies that the rotating conductor produces a radial electric field in the laboratory frame:

$$\mathit{E}=-\frac{v}{c}\times \mathit{B}=-\frac{\mathrm{\Omega }B}{c}{{r}}_{\perp }.$$

(5)

In the last relation, we take into account the collinearity $\mathrm{\Omega }\parallel \mathit{B}\parallel {\mathbf{e}}_z$, Figure 1a, and denote by ${\mathit{r}}_{\perp }$ the radial component of the coordinate, ${\mathbf{e}}_z\perp {\mathit{r}}_{\perp }$, so that $\mathit{r}={\mathit{r}}_{\perp }+z{\mathbf{e}}_z$.

The rotation-induced electric field Equation (5) generates a uniform charge density in the interior of the cylinder, $\rho =\nabla ·\mathit{E}/\left(4\pi \right)$, providing us with the result Equation (1). The requirement of global charge neutrality leads, in turn, to the accumulation of a uniform surface charge density Equation (2) at the edge of the cylinder. The charge density is qualitatively shown in Figure 1b. In real metals, the width w of the surface layer is extremely small ($w\ll R$), of the order of a few nanometers.

3. Rotation and Band Filling

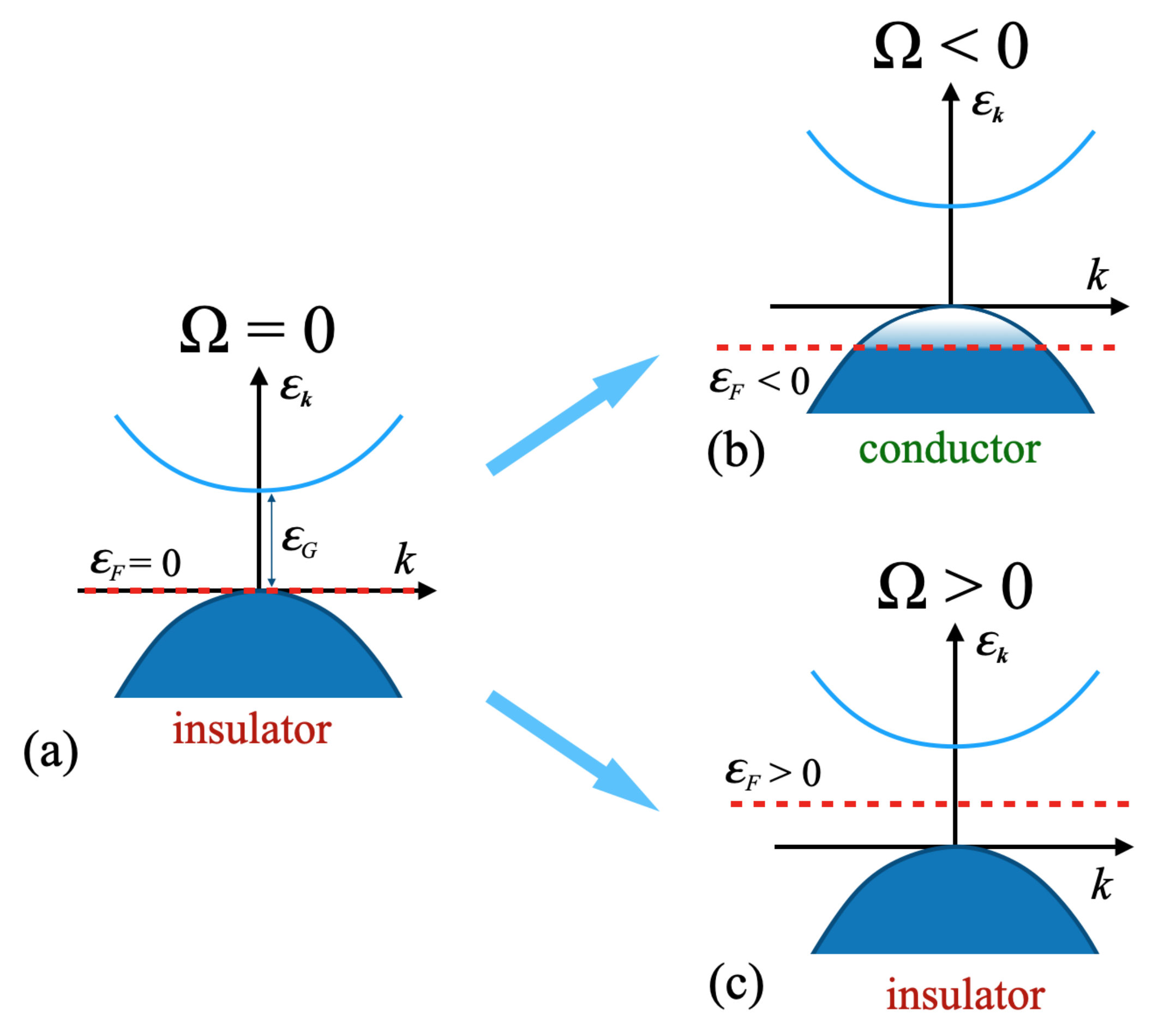
Our paper is based on the simple observation that a mechanical rotation in the background of the collinear magnetic field leads to a shift in the Fermi energy ${\epsilon }_F$ due to the uniform, coordinate-independent accumulation of electric charge density (1) in the bulk of the system. We analyze the situation that occurs when the rotation drives the Fermi energy across the edge of the conductance or valence band. We demonstrate that this crossing breaks the discrete clockwise/counterclockwise rotational symmetry $\mathrm{\Omega }\to -\mathrm{\Omega }$ for cylinders made of a semiconducting material. The effect impacts the mechanical and conducting properties of the system.

Given the generic nature of the effect, it is sufficient to consider a degenerate semiconductor with a simple parabolic form for conduction and valence energy bands, respectively [17]:

$${\epsilon }_k^{\left(\mathrm{e}\right)}={\epsilon }_G+\frac{k^2}{2m_e},{\epsilon }_k^{\left(\mathrm{h}\right)}=-\frac{k^2}{2m_h}.$$

(6)

Here, $m_e$ ($m_h$) is an effective mass of electrons (holes) and ${\epsilon }_G$ is the gap between valence and conduction bands. We neglect Zeeman and spin–orbit interactions, which do not play a significant role in the effect.

We consider a device made of an intrinsic (undoped) p-type semiconductor with a fully filled valence band. The Fermi energy lies in the gap close to the edge of the valence band, as shown in Figure 2a. In conventions leading to Equation (6), the Fermi energy ${\epsilon }_F=0$ corresponds to the upper edge of the valence band. We assume that the temperature is sufficiently low so that thermal energy is smaller than the energy gap between the bands, $k_{B}T\ll {\epsilon }_G$. We also coat the cylindrical semiconductor with a thin cylindrical shell (Figure 3) made of a metal with a wide enough conduction band that includes the Fermi energy level ${\epsilon }_F=0$. Therefore, the charge accumulation (1) happens inside the semiconducting bulk, while the boundary charge buildup Equation (2) occurs within the thin metallic layer. The electrodes are connected only to the bulk (semiconducting) part of the device and do not touch the metallic coating.

We apply a background magnetic field along the z axis, $\mathit{B}=B{\mathbf{e}}_z$ (with $B>0$) and assume that the magnetic field is sufficiently weak so that the semiconductor band spectrum Equation (6) serves as a good approximation of the problem.

4. Conductivity and Rotation

With the fully filled valence band, empty conduction band, and the wide energy gap between these two bands, the interior of the static (non-rotating) cylinder resides in an electrically insulating state, Figure 2a. The electrons cannot be thermally excited from the valence band to the conduction band.

The clockwise rotation ($\mathrm{\Omega }<0$) makes the bulk charge density (1) positive, implying that some of the electrons are relocated from the interior of the cylinder to its metallic boundary (2). The external metallic coating serves as a reservoir, which accommodates the electrons that were displaced from the interior of the system. The rotation lowers the Fermi level in the bulk of the cylinder, thus creating empty states near the Fermi level. The system enters the conducting regime; see Figure 2b.

The shift in the Fermi energy due to rotation,

$${\epsilon }_F\left(\mathrm{\Omega }\right)=-\frac{{\hslash }^2}{2m_h}{\left(\frac{3\pi \mathrm{\Omega }B}{2c}\right)}^{2/3}⩽0,\mathrm{\Omega }B⩾0,$$

(7)

is determined by a comparison of the bulk density (1) with the density of the degenerate fermionic gas (in our case, holes):

$$\rho =\frac{k_F^3}{3{\pi }^2{\hslash }^3},k_F=\sqrt{-2m_h{\epsilon }_F}.$$

(8)

Thus, the clockwise rotation ($\mathrm{\Omega }<0$) switches the interior of the cylinder from the insulator into a conductor phase. For a slow rotation with

$$|{\epsilon }_F\left(\mathrm{\Omega }\right)|\ll k_{B}T\ll {\epsilon }_G,$$

(9)

the thermally excited electrons from the Fermi sea will fill the hole pocket in the valence band. In other words, the rotation empties the energy levels in the hole pocket which can further be populated by a thermally excited electron from the Fermi sea. This process also creates a hole carrier. Thus, the electron and hole charge carriers have an equal density, $n=p={\rho }_{\mathrm{bulk}}/(-e)$. The conductivity of the system becomes:

$$\sigma =-\frac{({\mu }_e+{\mu }_h)\mathrm{\Omega }B}{2\pi c}>0,\mathrm{\Omega }B<0$$

(10)

where ${\mu }_e$ (${\mu }_h$) is the electron (hole) mobility. We used the expression (1) for the carrier concentration induced by the combined effect of magnetic field and rotation in the semiconducting bulk. Note that the effect Equation (10) has a universal character in the sense that it does not depend on the details of the band structure Equation (6), provided that the rotation does not shift the Fermi energy Equation (7) across the boundary of the band and the hierarchy Equation (9) holds.

The counterclockwise rotation ($\mathrm{\Omega }>0$) induces a radial electric field, which tends to make the bulk charge density (1) negative by displacing the electrons from the metallic coating to the semiconductor interior. However, the semiconducting bulk cannot accommodate them because the valence band is already filled; see Figure 2c. Therefore, the interior remains in the insulating state (An exceptionally fast rotation with the energy scale of the interband gap energy can produce a sufficiently strong radial electrochemical potential, $\varphi =-\mathrm{\Omega }B{r}_{\perp }/c$ which can gradually fill in the conduction band provided ${\epsilon }_G-\varphi \left(L\right)>0$.):

$$\sigma =0,\mathrm{\Omega }B⩾0.$$

(11)

The clockwise/counterclockwise asymmetry of the device is a purely quantum phenomenon based on the Pauli exclusion principle. Using symmetry arguments, one can show that the effect has its roots in the absence of definite symmetry with respect to the time-reversal transformation, $\mathrm{T}:t\to -t$. Indeed, the sign flip of the (T-odd) angular velocity $\mathrm{\Omega }$ does not bring the device to the same state because the magnetic field $\mathit{B}$ has a T-odd parity while the electric charge density $\rho$, accumulated due to the collective effect of magnetic field and rotation, has a T-even quantity:

$$\mathrm{T}:\mathit{B}\to -\mathit{B},\mathrm{\Omega }\to -\mathrm{\Omega },\rho \to \rho .$$

(12)

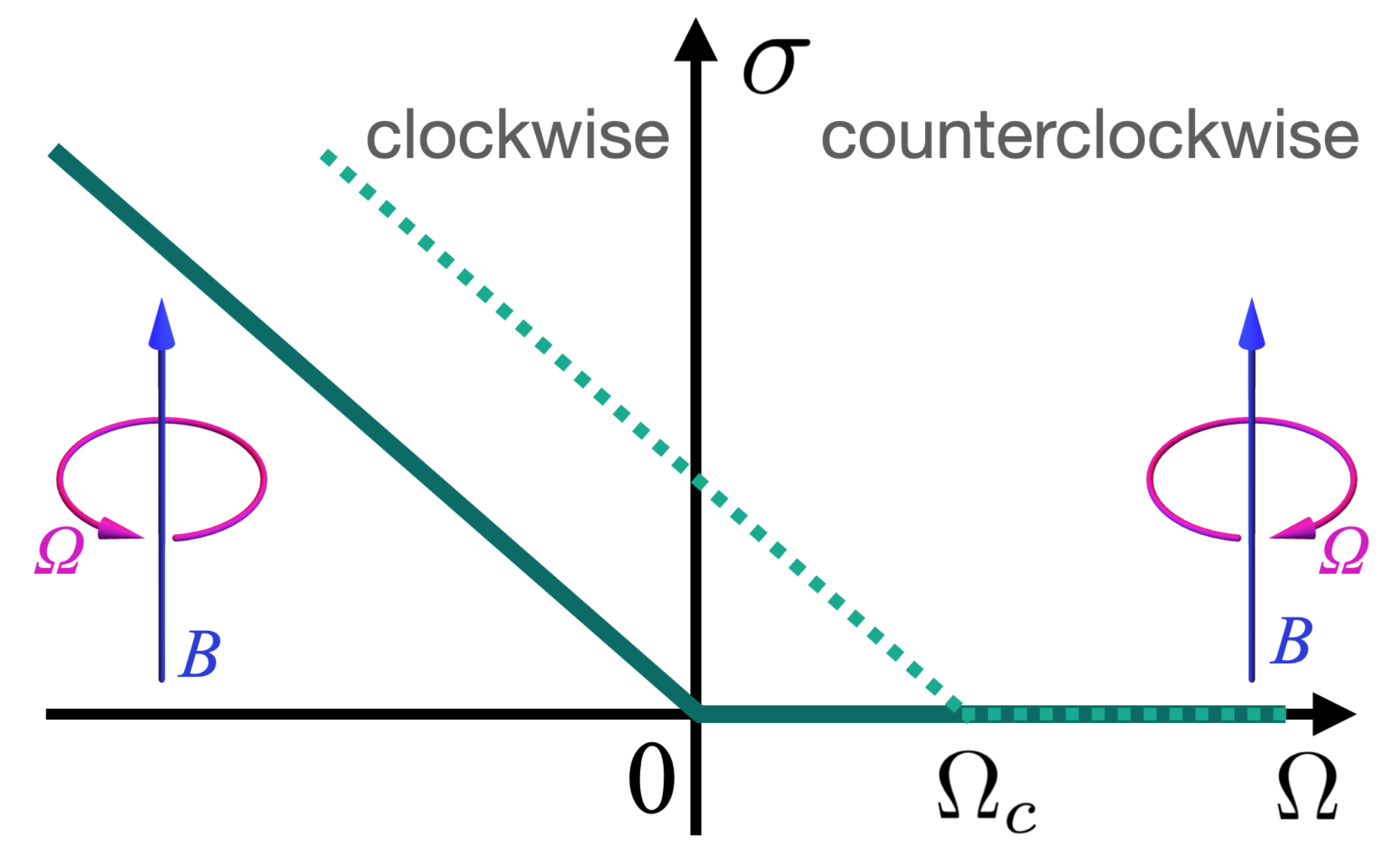
The dependence of the conductivity on the angular frequency, Equations (10) and (11), is shown in Figure 4: the cylinder made of a semiconductor material with the threshold chemical potential behaves as an insulator for the rotation in the counterclockwise sense ($\mathrm{\Omega }>0$) and a conductor when it turns in the counterclockwise direction ($\mathrm{\Omega }>0$). The directions are inverted with the flip of the sign of the magnetic field.

A similar effect appears in intrinsic n-type semiconductors, where the Fermi energy lies near the edge of the conduction band, ${\epsilon }_F={\epsilon }_G$. Its phase diagram is reverted with respect to the direction of rotation, $\mathrm{\Omega }\to -\mathrm{\Omega }$.

The idea behind our mechanism is simple: a background magnetic field tends to shift the Fermi energy (the chemical potential) in the bulk of the rotating system, thus affecting the conductivity of the latter. This can also be applied to semimetals with the Fermi energy lying in the vicinity of the upper edge of the hole pocket (the valence band), or above but close to the lower edge of the conduction band. The rotation shifts the Fermi energy across the edge of the corresponding band, and thus alters its conductivity. By denoting the gap ${\mathrm{\Delta }}_F=-{ϵ}_F>0$ and ${\mathrm{\Delta }}_F={ϵ}_F-{ϵ}_G>0$ in the former and latter cases, respectively, we obtain that the conductor–insulator transition takes place at the nonzero critical angular frequency with the magnitude:

$${\mathrm{\Omega }}_c=\frac{2{\left(2m{\mathrm{\Delta }}_F\right)}^{3/2}}{3\pi {\hslash }^{3}B},$$

(13)

where m is the mass of the appropriate carrier. The (hole) conductivity is shown in Figure 4 by the dashed line.

5. Mechanical Properties

The effect may also have interesting mechanical consequences. The reorganization of the electric charge density in rotating conductors produces a supplementary angular momentum $\delta L=L_{\mathrm{mech}}+L_{\mathrm{e}.\mathrm{m}.}$ which adds up to a purely mechanical quantity $L_0$ associated with the rotation of the ionic lattice together with the original electrons. There are two contributions: the mechanical part coming from the mass redistribution of the displaced electrons $L_{\mathrm{mech}}$ and a part originating from the angular momentum stored in the electromagnetic fields $L_{\mathrm{e}.\mathrm{m}.}$.

In typical metals, the surface charge density is concentrated within a thin surface skin of a few nanometers. For practical mechanical calculations in macroscopic, centimeter-sized systems, the surface charge Equation (2) can be treated as a $\delta$-functional distribution at the edge of the system, $r_{\perp }=R$. The same applies to semiconductors, where the screening length lies in the micrometer range. Thus, the electric charge density in the cylinder may be approximated by the following function:

$${\rho }_e\left(r\right)=\frac{\mathrm{\Omega }B}{4\pi c}\left[R\delta (r_{\perp }-R)-2\right],$$

(14)

using the convention ${\int }_0^R\delta (r_{\perp }-R)r_{\perp }d{r}_{\perp }=R$.

The mechanical excess of angular momentum,

$${\mathit{L}}_{\mathrm{mech}}={\int }_V{d}^{3}r{\rho }_m\left(r\right)r\times v\left(r\right)=\frac{m_{e}L{\mathrm{\Omega }}^2{R}^4}{4ce}\mathit{B},$$

(15)

is determined via the surplus of the mass density

$${\rho }_m\left(r\right)=\frac{m_e}{e}{\rho }_e\left(r\right),$$

(16)

where $e=+\left|e\right|$ is the elementary electric charge and $m_e$ is the mass of an electric charge carrier. Here, for simplicity, we assume the presence of a single carrier and we set its mass as the electron mass. The mechanical angular momentum (15) originates from the displacement of the electrons from the bulk to the boundary (or vice-versa, depending on the mutual orientation of the angular momentum $\mathrm{\Omega }$ and the background magnetic field $B$). Notice that, since the displaced mass is proportional to the angular frequency, Equations (14) and (16), the kinetic momentum (15) is an even function of $\mathrm{\Omega }$.

The local angular momentum carried by the electromagnetic field $L_{\mathrm{e}.\mathrm{m}.}\left(r\right)=r\times S$ can be expressed via the Poynting vector $S=E\times B$. This calculation, however, poses a practical inconvenience, as it requires the integration of the local momentum over the whole spatial volume and involves the calculation of the electric field $E=-\nabla \varphi$ (typically done via the electrostatic potential $\varphi =\varphi \left(r\right)$) in the exterior of the cylinder. An equivalent definition of the electromagnetic angular momentum for spatially finite systems is based on the Maxwell form:

$$L_{\mathrm{e}.\mathrm{m}.}=\frac{1}{c}\int d^{3}r{\rho }_e\left(r\right)r\times A=\frac{L{B}^2{R}^4}{8c^2}\mathrm{\Omega },$$

(17)

which involves the vector potential $A$ in the Coulomb gauge, $\nabla ·A=0$. In the evaluation of Equation (17), we set $B=\nabla \times A$ with $A=(B{r}_{\perp }/2){\mathrm{e}}_{\phi }$ where ${\mathrm{e}}_{\phi }={\mathrm{e}}_z\times {\mathrm{e}}_{\perp }$.

The energy stored in the induced electrostatic field inside the cylinder Equation (5), calculated in the laboratory frame,

$${\mathcal{E}}_{\mathrm{e}.\mathrm{m}.}\equiv {\mathcal{E}}_{\mathrm{e}.\mathrm{m}.}^{\left(E\right)}=\frac{1}{8\pi }{\int }_V{d}^{3}r{E}^2\left(r\right)=\frac{{\mathrm{\Omega }}^2{B}^2{R}^4}{16c^2},$$

(18)

is related to the angular momentum (17) via the thermodynamic relation $d{\mathcal{E}}_{\mathrm{e}.\mathrm{m}.}=\mathrm{\Omega }·d{\mathit{L}}_{\mathrm{e}.\mathrm{m}.}$, as expected. The energy in the corotating frame, ${\tilde{\mathcal{E}}}_{\mathrm{e}.\mathrm{m}.}={\mathcal{E}}_{\mathrm{e}.\mathrm{m}.}-\mathrm{\Omega }·{\mathit{L}}_{\mathrm{e}.\mathrm{m}.}$, satisfies the relation, $d{\tilde{\mathcal{E}}}_{\mathrm{e}.\mathrm{m}.}=-{\mathit{L}}_{\mathrm{e}.\mathrm{m}.}·d\mathrm{\Omega }$. Finally, the energy stored by the magnetic field is insensitive to rotation (up to a tiny correction due to an extra magnetic field generated via the Ampère circular current).

As we discuss later, the kinetic angular momentum (15) associated with the displaced mass Equation (16) in non-relativistic systems is much smaller than the angular momentum stored in the electromagnetic fields; see Equation (17). Therefore, we ignore the mechanical angular momentum in our discussion below and take the electromagnetic part only, $\delta L=L_{\mathrm{e}.\mathrm{m}.}$, as the excess of the angular momentum.

The electromagnetic moment of inertia ${\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}$ can be defined either via the angular momentum, ${\mathit{L}}_{\mathrm{e}.\mathrm{m}.}={\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}\mathrm{\Omega }$, or, equivalently, via the energy: ${\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}={\partial }^2{\mathcal{E}}_{\mathrm{e}.\mathrm{m}.}/\partial {\mathrm{\Omega }}^2$:

$${\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}=\frac{1}{8\pi }{\int }_V{d}^{3}r{B}^2\left(r\right)=\frac{L{R}^4}{8c^2}{B}^2.$$

(19)

In ordinary conductors, the extra angular momentum (17) is an odd function of the angular frequency $\mathrm{\Omega }$: the angular momentum changes its sign, $L_{\mathrm{e}.\mathrm{m}.}\to -L_{\mathrm{e}.\mathrm{m}.}$, under a flip of the direction of rotation, $\mathrm{\Omega }\to -\mathrm{\Omega }$. The reason for this symmetry is obvious: the rotations in opposite directions lead to the appearance of radial electric fields of equal magnitudes (but of opposite signs) due to the displacement of electrons, either from the bulk to the boundary or vice versa. The electric field emerges due to the depletion (or surplus) of the uniform electric charge density inside the bulk, depending on the direction of rotation.

At the threshold chemical potential $\mu =0$, the rotational diode generates an electric field for a particular rotational direction for which $\mathrm{\Omega }·B<0$. The rotation in opposite direction ($\mathrm{\Omega }·B>0$) does not produce the electric field in bulk. Therefore, the rotational energy and angular momentum stored in the induced electric field differs for rotations in the clockwise (CW) and counterclockwise (CCW) senses. For the device at the threshold value of the Fermi level, the difference between the angular momenta for the clockwise/counterclockwise rotations is given by Equation (19):

$$\Delta {\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}\equiv {\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}^{\mathrm{CW}}-{\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}^{\mathrm{CCW}}=-\frac{L{R}^4}{8c^2}{B}^2\mathrm{sign}\left(\mathrm{\Omega }·B\right).$$

(20)

Interestingly, this quantity has a universal character in the sense that it depends only on the geometry of the device and the background magnetic field.

While the odd nature of the effects and the simplicity of the device that hosts them may seem attractive, quantitative estimates, given below, challenge the suitability of these effects for an experimental detection since their magnitude is not exceptionally large. Notice that the mechanism cannot be realized for band insulators since these materials cannot exhibit charge displacement from bulk to the surface due to their insulating nature.

6. Electric Charge in the Bulk

In the background of the moderate magnetic field $B=1T$, the cylinder rotating with the angular frequency (It is of the order of the angular frequency of the consumer hard disk, $\mathrm{\Omega }=7200\mathrm{rpm}\sim {10}^2{\mathrm{s}}^{-1}$.) $\mathrm{\Omega }=100{\mathrm{s}}^{-1}$ accumulates in its interior the electric charge with the bulk density ${\rho }_{\mathrm{bulk}}=-8.8\times {10}^{3}e/{\mathrm{cm}}^3$. This is a small, but non-negligible number.

7. Conductivity

The rotation-induced conductivity Equation (10) depends substantially on the mobility $\mu$ of the charge carriers. For a typical semiconductor with mobility ${\mu }_e\sim {\mu }_e\sim {10}^3$ cm${}^2$/(V·s), an $\mathrm{\Omega }=100{\mathrm{s}}^{-1}$ rotation in the magnetic field background $B=1T$ induces conductivity $\sigma \simeq {10}^{-13}{\mathrm{\Omega }}^{-1}{\mathrm{cm}}^{-1}$, which makes the interior of the device as “good” a conductor as, for example, glass or rubber. This exceptionally bad conductivity can, however, be improved in systems with high-mobility charge carriers (possibly gated to achieve the correct position of the Fermi level at the upper/lower edge of a hole/electron band so that the non-rotating system resides at the border of an insulating state). For example, for AlGaAs/GaAs heterostructures featuring the high-mobility two-dimensional electron gas with [18] $\mu =3.5\times {10}^7$ cm${}^2$/(V·s), the rotation induces conductivity compared to the lowest value $\sigma \simeq {10}^{-8}{\mathrm{\Omega }}^{-1}{\mathrm{cm}}^{-1}$ achievable in a pure semi-insulating GaAs crystal [19].

8. Angular Momentum

The kinetic angular momentum associated with the radial displacement of electrons Equation (15) is much smaller than the angular momentum stored in the electromagnetic field (17): $L_{\mathrm{mech}}/L_{\mathrm{e}.\mathrm{m}.}\sim {10}^{-9}$. Therefore, the mechanical properties of the device are determined only by the electromagnetic fields generated by the rotation. The difference between the angular moments of inertia for clockwise and counterclockwise rotation Equation (20) of a centimeter-sized cylinder ($L=R=1\mathrm{cm}$) in the magnetic field $B=1T$ is $\Delta {\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}\simeq {10}^{-15}\mathrm{g}·{\mathrm{cm}}^2$. No matter how small this number may seem initially, it corresponds to a moment of inertia from a water droplet in a typical fine fog (with a size of about $10\mathsf{\mu }$m), which is already a macroscopic object. The latter example provides some hope that the change in the clockwise/counterclockwise moments of inertia may be within experimental reach, despite it constituting a negligible fraction of the total moment of inertia of the system, $\Delta {\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}/{\mathcal{I}}_{\mathrm{e}.\mathrm{m}.}^{\mathrm{tot}}\simeq {10}^{-16}$.

9. Summary

We demonstrated that the absence of a definite time-reversal state in a mechanically rotating semiconductor in the background magnetic field leads to asymmetry in its mechanical and transport properties with respect to rotations in clockwise and counterclockwise directions. A fine-tuned system becomes a “rotational diode” that possesses different moments of inertia and resides in different conductor/insulator phases when rotated in opposite directions. Although the effect has roots in classical electrodynamics of rotating conductors in the background magnetic field, the clockwise/counterclockwise rotational asymmetry appears as a purely quantum phenomenon based on the Pauli exclusion principle. The estimated magnitude of these effects is rather small for realistic materials.