Symmetries and Selection Rules of the Spectra of Photoelectrons and High-Order Harmonics Generated by Field-Driven Atoms and Molecules
Abstract
:1. Introduction
2. Theory
2.1. HHG Theory
2.2. HATI Theory
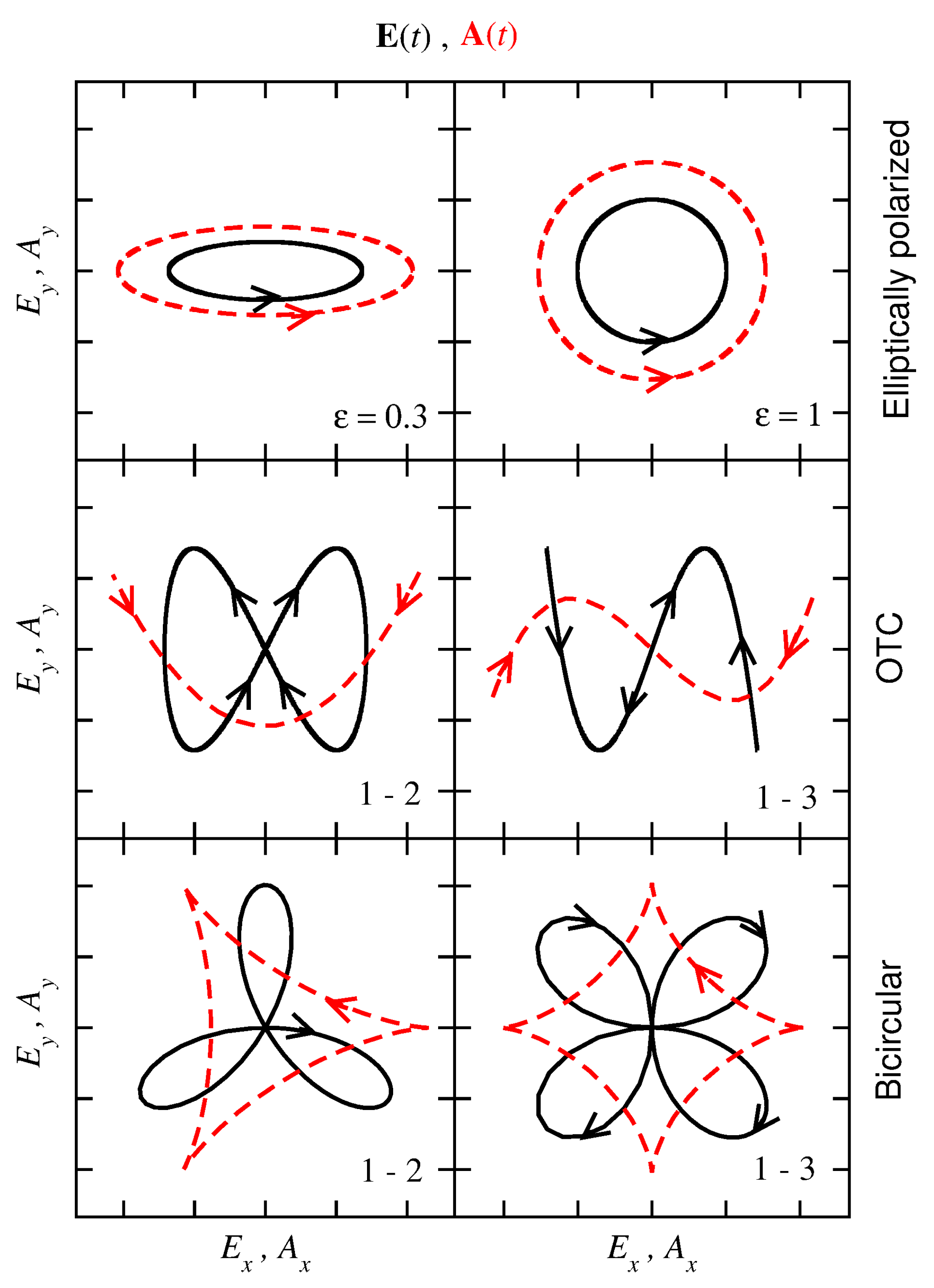
2.3. Laser Fields and Dynamical Symmetries
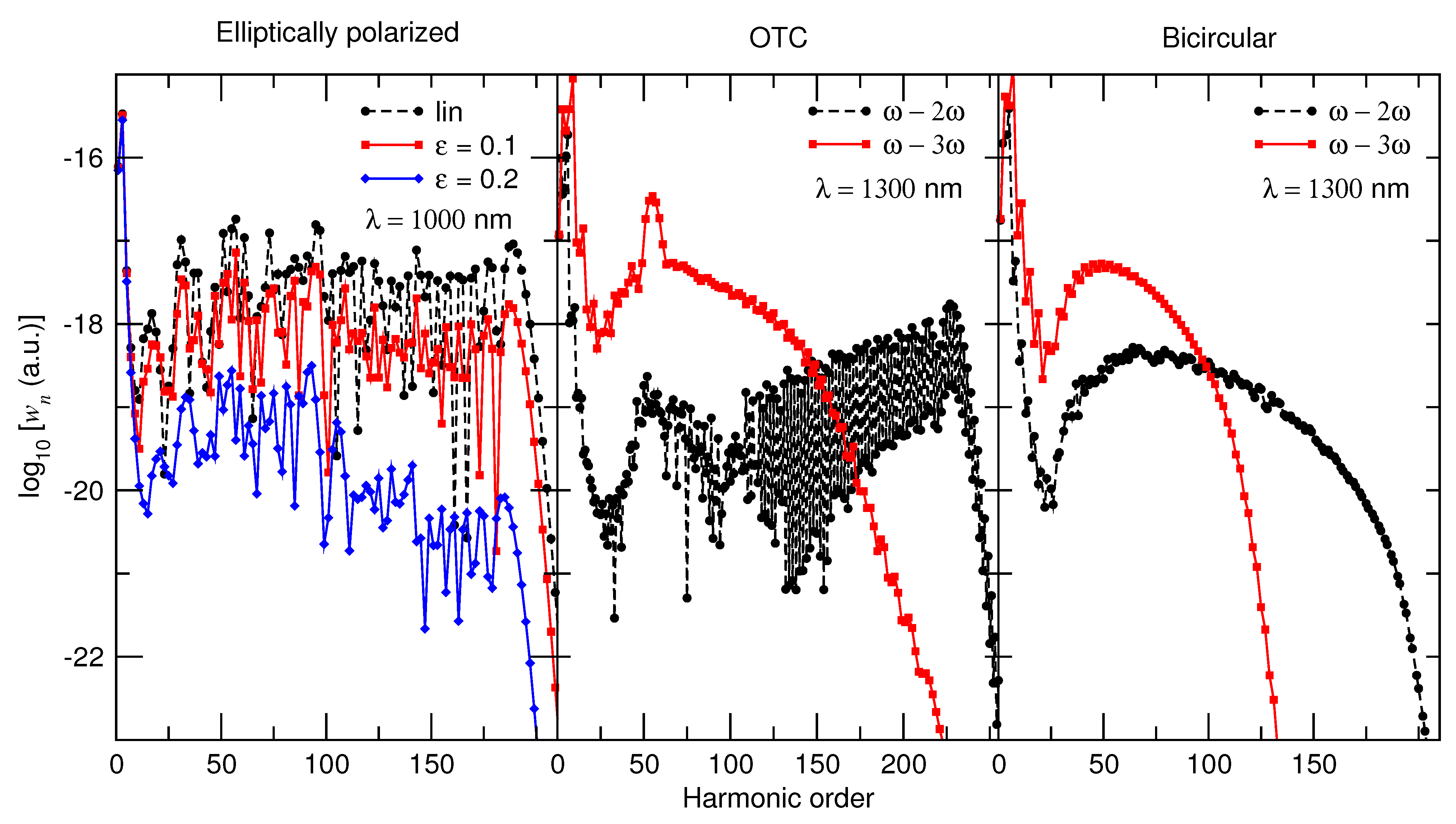
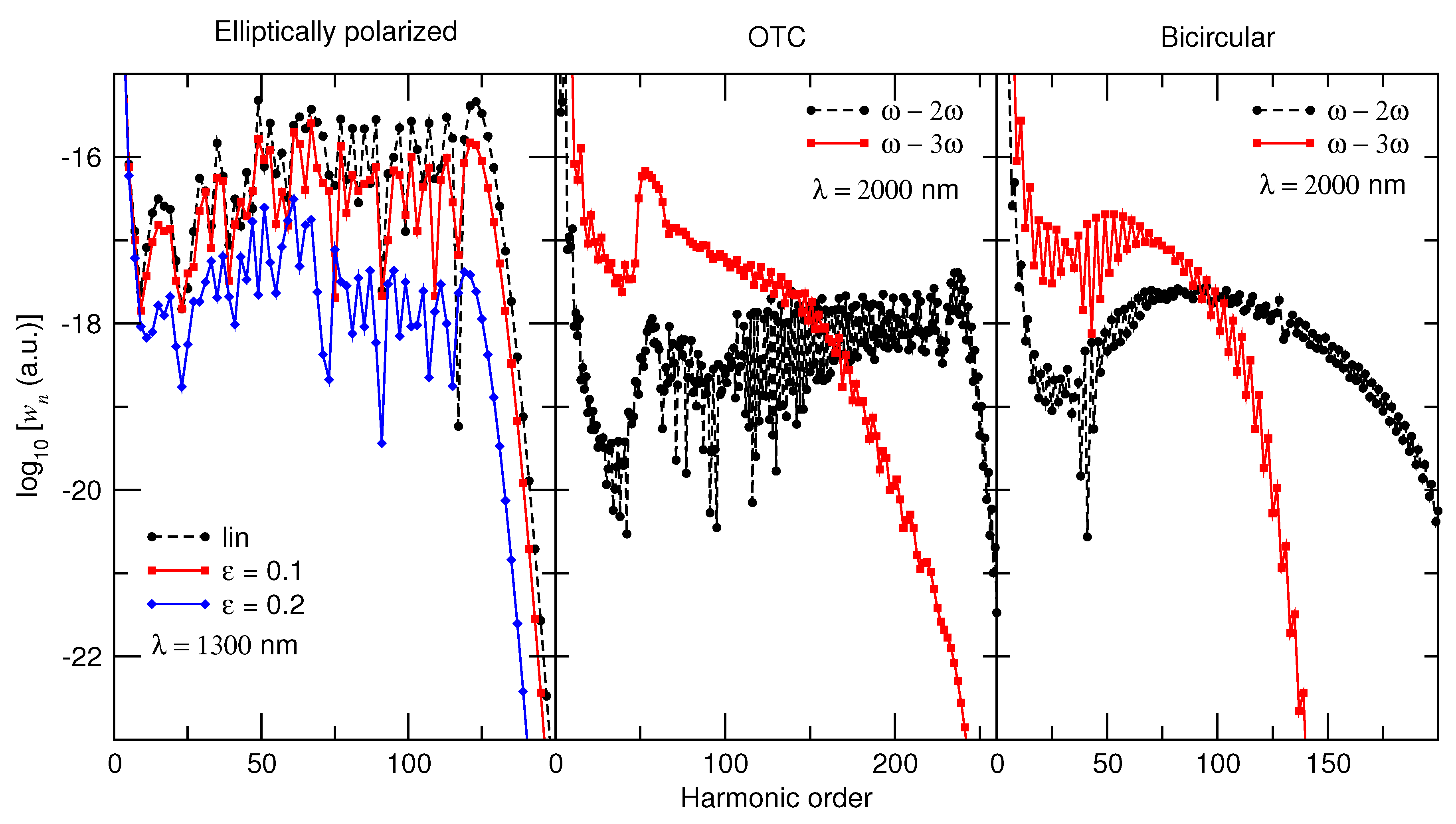
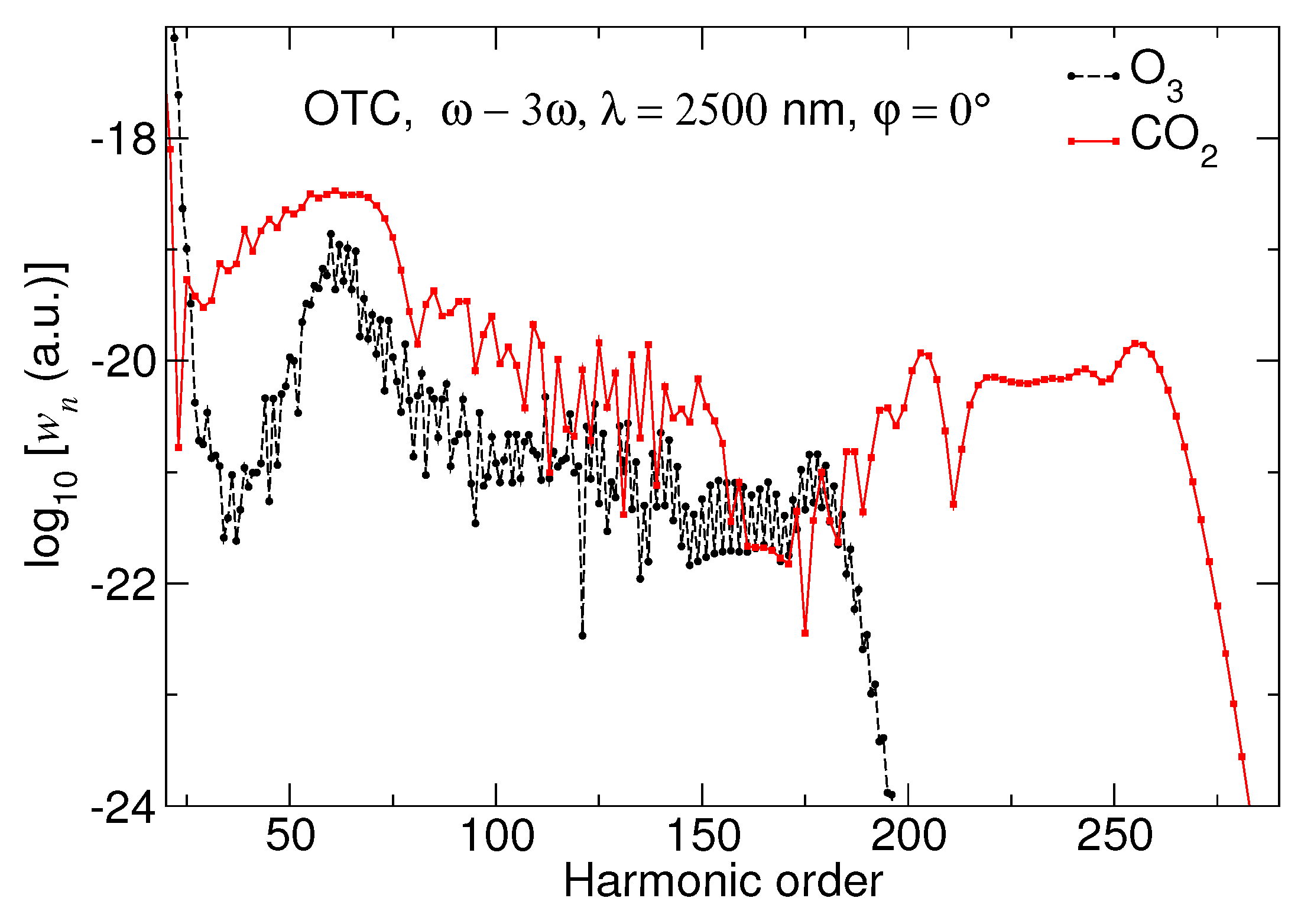
3. Selection Rules for HHG
3.1. Derivation of the Selection Rules
3.2. Illustration of the Selection Rules
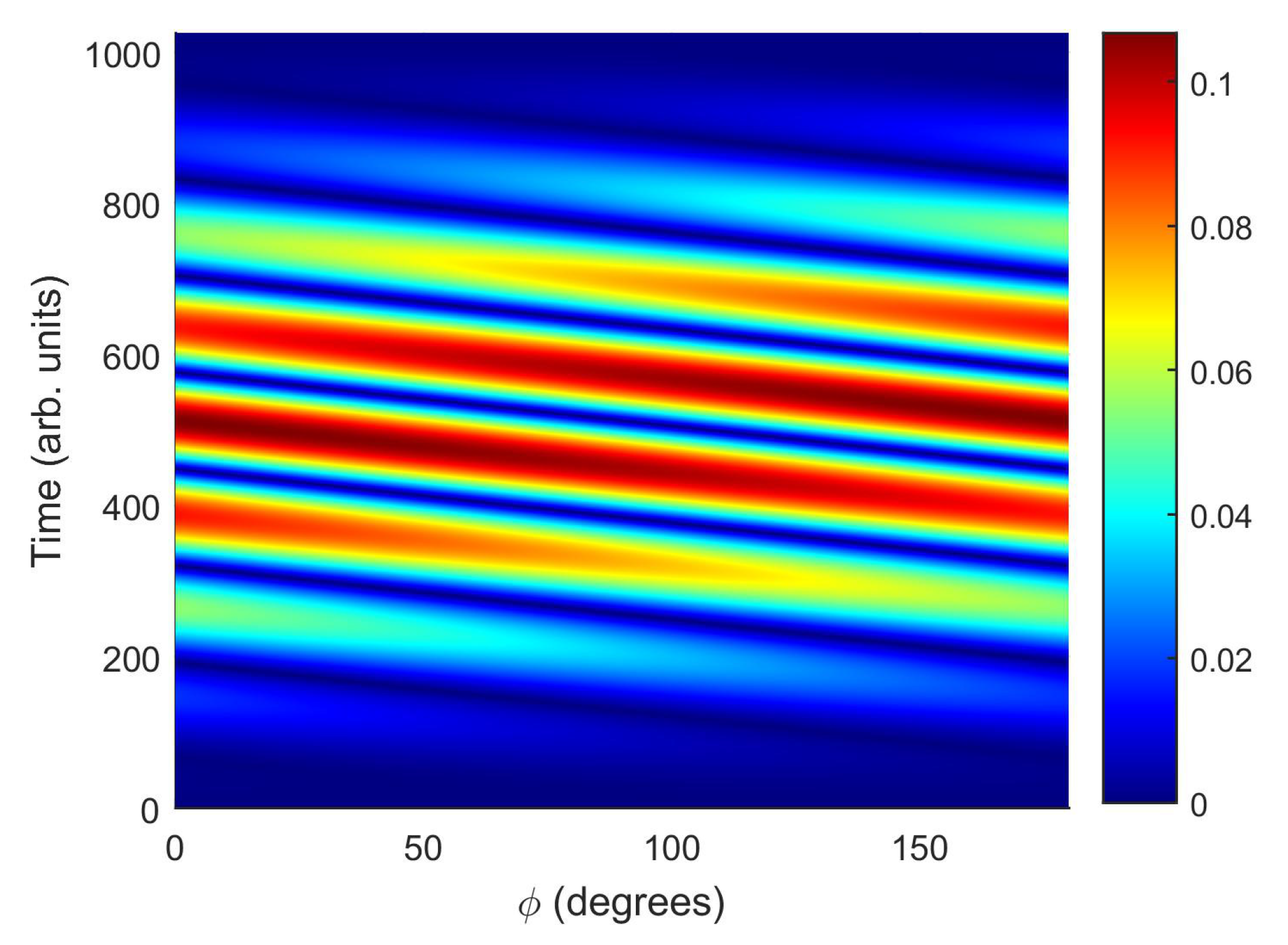
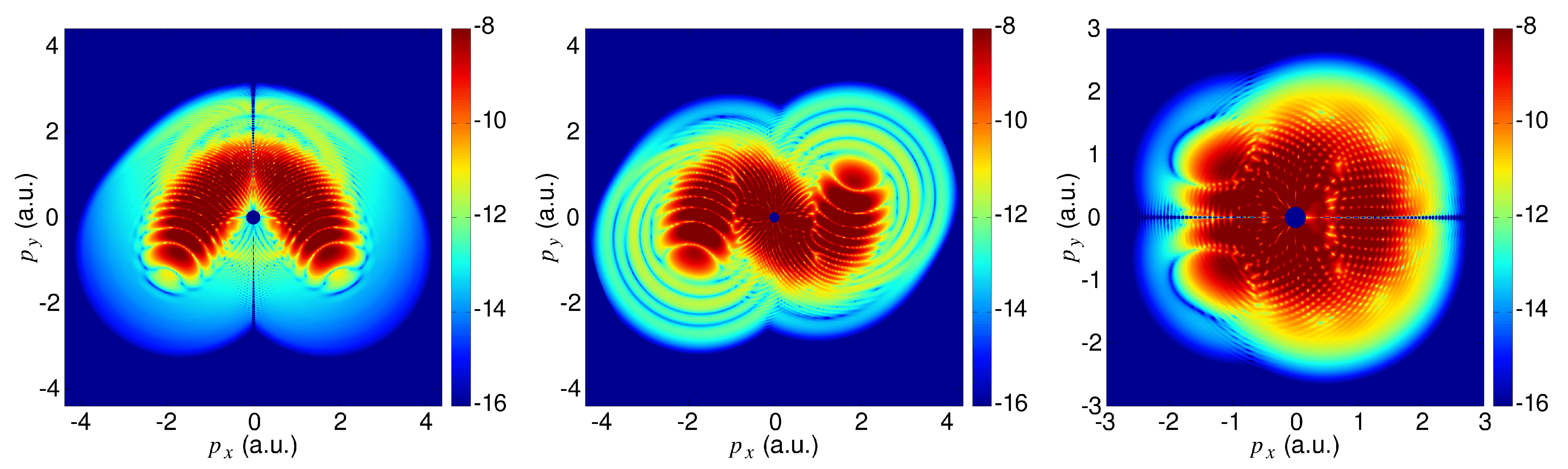
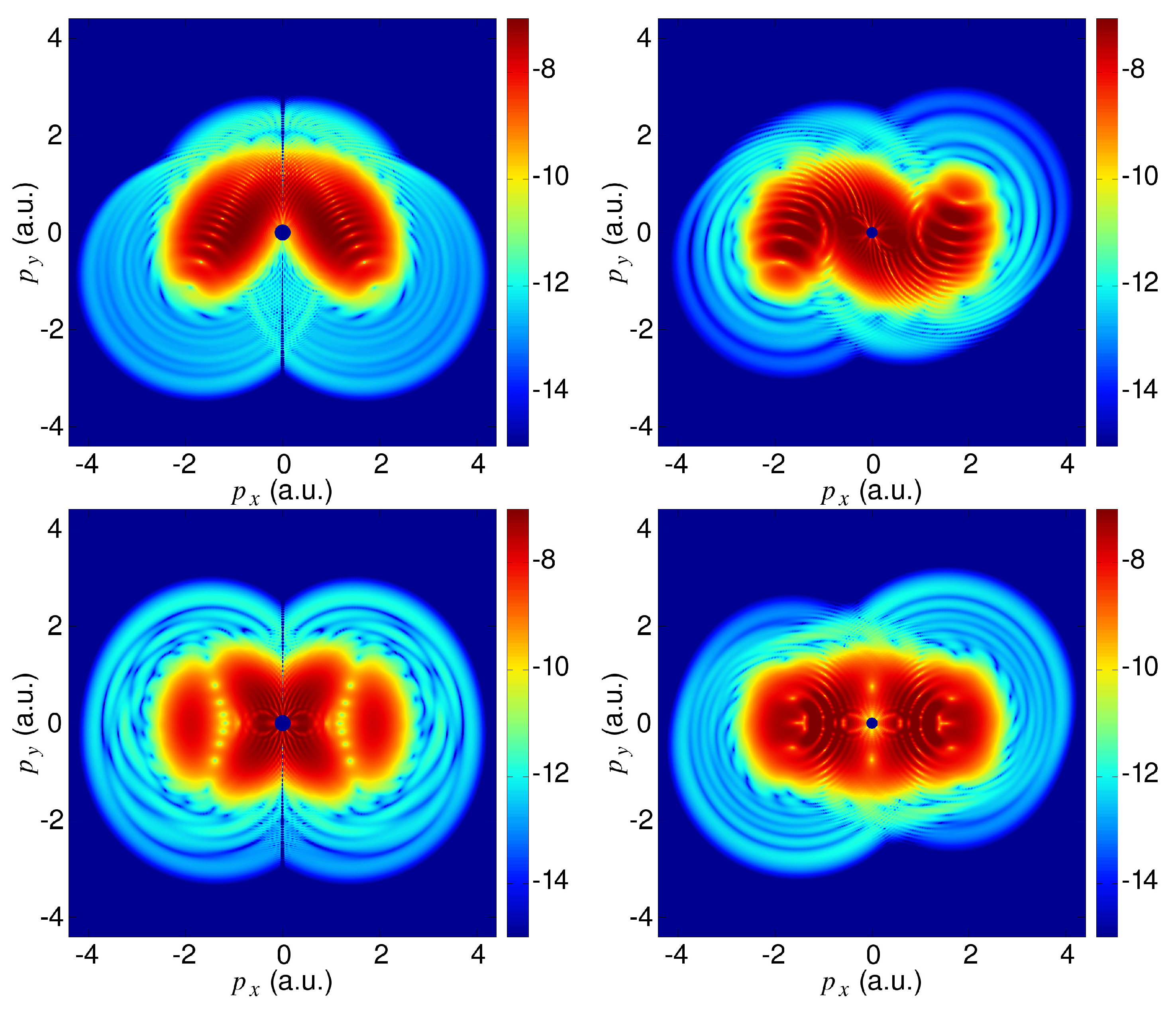
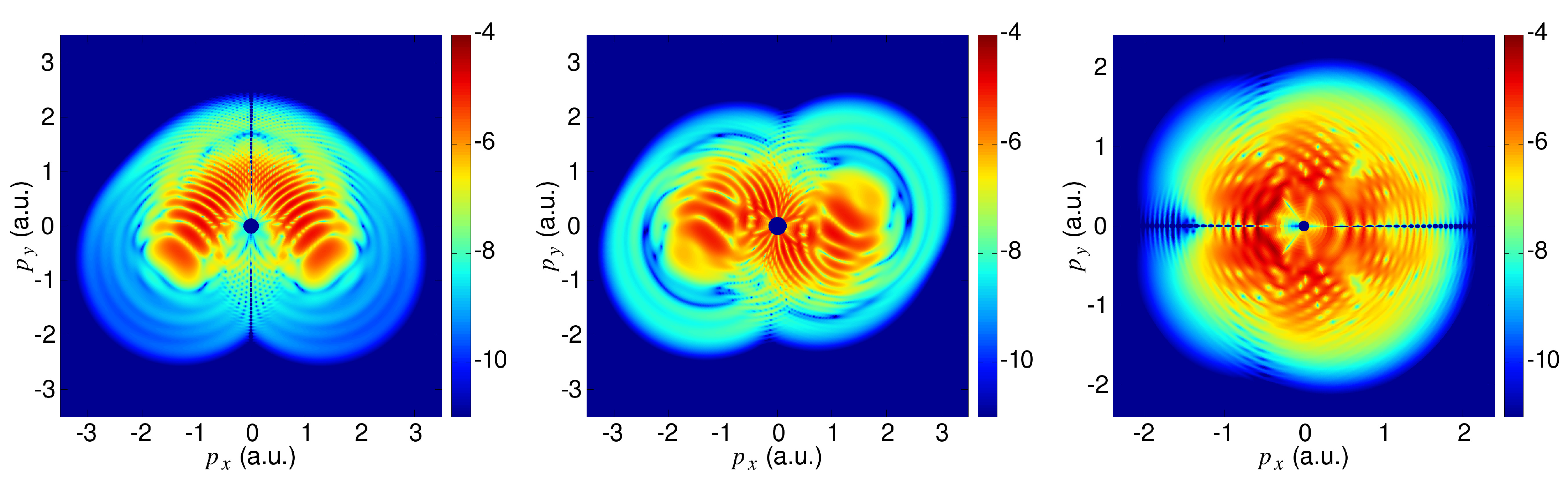
4. Symmetry Properties of the Photoelectron Momentum Distribution
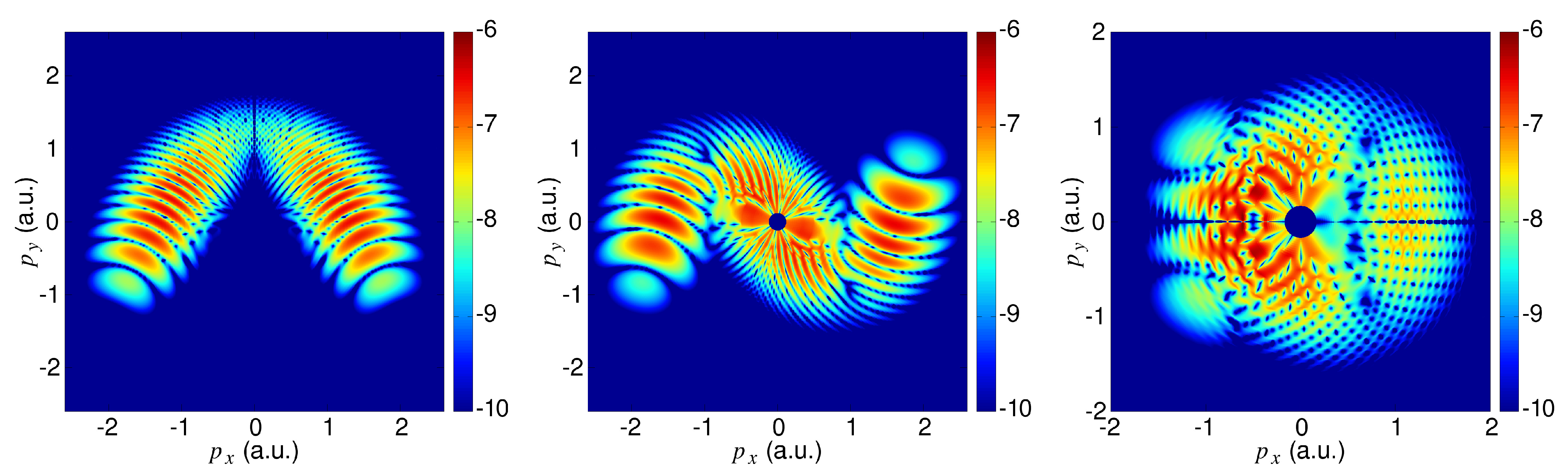
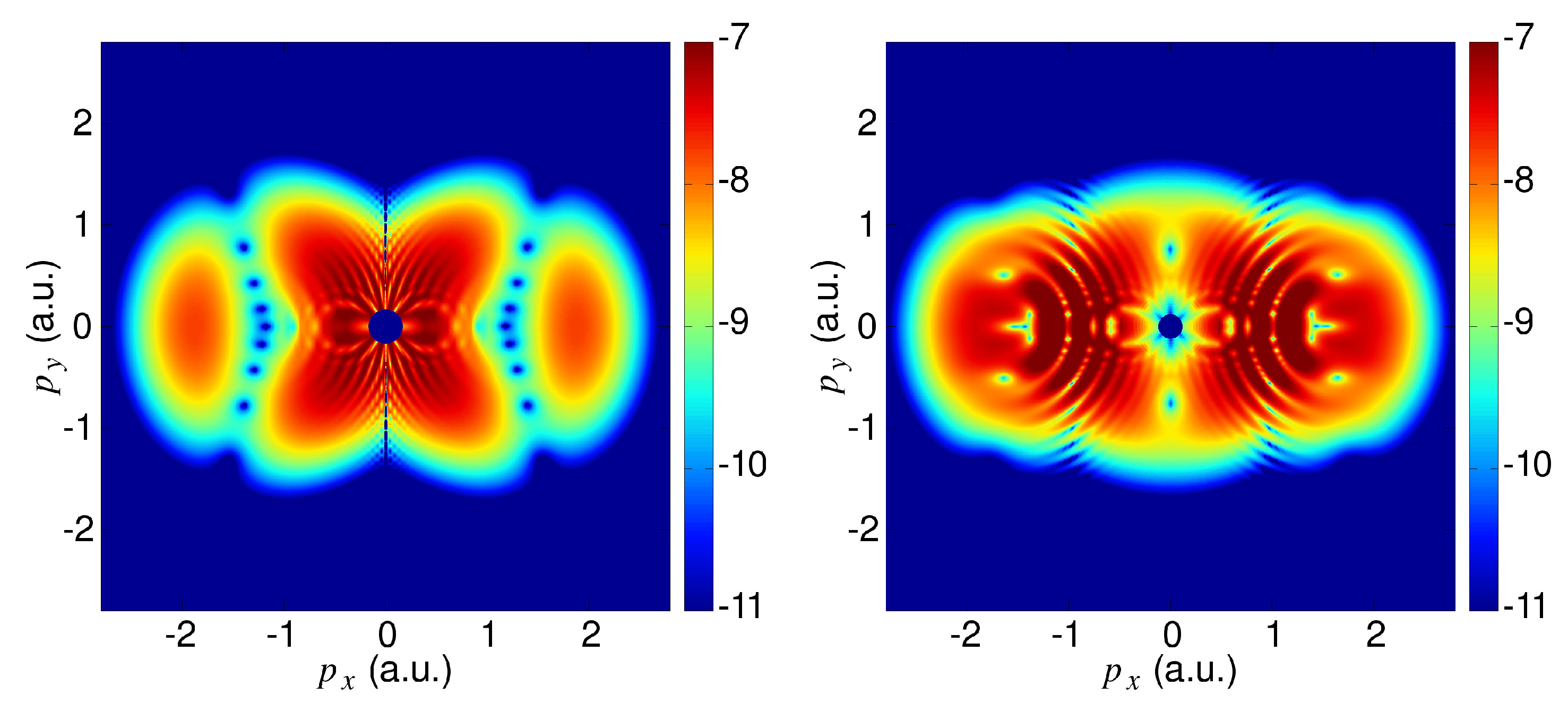
4.1. Symmetries of the Direct and Rescattered Photoelectron Momentum Spectra
4.2. Symmetries of the Direct Photoelectron Momentum Spectra
4.3. Influence of the Molecular Symmetry on the Photoelectron Momentum Distribution
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Symmetries of the Exact Ionization Amplitudes
References
- Weyl, H. Symmetry, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Noether, E. Invariant variation problems. Gött. Nachr. 1918, 1918, 235–257. [Google Scholar] [CrossRef] [Green Version]
- Becker, W.; Grasbon, F.; Kopold, R.; Milošević, D.B.; Paulus, G.G.; Walther, H. Above-threshold ionization: From classical features to quantum effects. Adv. At. Mol. Opt. Phys. 2002, 48, 35–98. [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F. Scattering and reaction processes in powerful laser fields. Adv. At. Mol. Opt. Phys. 2003, 49, 373–532. [Google Scholar] [CrossRef]
- Becker, A.; Faisal, F.H.M. Intense-field many-body S-matrix theory. J. Phys. B 2005, 38, R1–R56. [Google Scholar] [CrossRef] [Green Version]
- Milošević, D.B.; Paulus, G.G.; Bauer, D.; Becker, W. Above-threshold ionization by few-cycle pulses. J. Phys. B 2006, 39, R203–R262. [Google Scholar] [CrossRef]
- Lein, M. Molecular imaging using recolliding electrons. J. Phys. B 2007, 40, R135–R173. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef] [Green Version]
- Figueira de Morisson Faria, C.; Liu, X. Electron-electron correlation in strong laser fields. J. Mod. Opt. 2011, 58, 1076–1131. [Google Scholar] [CrossRef]
- Becker, W.; Liu, X.; Ho, P.J.; Eberly, J.H. Theories of photoelectron correlation in laser-driven multiple atomic ionization. Rev. Mod. Phys. 2012, 84, 1011–1043. [Google Scholar] [CrossRef]
- Popruzhenko, S.V. Keldysh theory of strong field ionization: History, applications, difficulties and perspectives. J. Phys. B 2014, 47, 204001. [Google Scholar] [CrossRef]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 2015, 87, 765–802. [Google Scholar] [CrossRef]
- Wolter, B.; Pullen, M.G.; Baudisch, M.; Sclafani, M.; Hemmer, M.; Senftleben, A.; Schröter, C.D.; Ullrich, J.; Moshammer, R.; Biegert, J. Strong-field physics with mid-IR fields. Phys. Rev. X 2015, 5, 021034. [Google Scholar] [CrossRef] [Green Version]
- Becker, W.; Goreslavski, S.P.; Milošević, D.B.; Paulus, G.G. The plateau in above-threshold ionization: The keystone of rescattering physics. J. Phys. B 2018, 51, 162002. [Google Scholar] [CrossRef]
- Ben-Tal, N.; Moiseyev, N.; Beswick, A. The effect of Hamiltonian symmetry on generation of odd and even harmonics. J. Phys. B 1993, 26, 3017–3024. [Google Scholar] [CrossRef]
- Long, S.; Becker, W.; McIver, J.K. Model calculations of polarization-dependent two-color high-harmonic generation. Phys. Rev. A 1995, 52, 2262–2278. [Google Scholar] [CrossRef] [PubMed]
- Alon, O.E.; Averbukh, V.; Moiseyev, N. Selection rules for the high harmonic generation spectra. Phys. Rev. Lett. 1998, 80, 3743–3746. [Google Scholar] [CrossRef]
- Ceccherini, F.; Bauer, D.; Cornolti, F. Dynamical symmetries and harmonic generation. J. Phys. B 2001, 34, 5017–5029. [Google Scholar] [CrossRef] [Green Version]
- Zuo, T.; Bandrauk, A.D. High-order harmonic generation in intense laser and magnetic fields. J. Nonlinear Opt. Phys. Mat. 1995, 4, 533–546. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W.; Kopold, R. Generation of circularly polarized high-order harmonics by two-color coplanar field mixing. Phys. Rev. A 2000, 61, 063403. [Google Scholar] [CrossRef]
- Yue, S.; Brennecke, S.; Du, H.; Lein, M. Probing dynamical symmetries by bicircular high-order harmonic spectroscopy beyond the Born-Oppenheimer approximation. Phys. Rev. A 2020, 101, 053438. [Google Scholar] [CrossRef]
- Tong, X.-M.; Chu, S.-I. Generation of circularly polarized multiple high-order harmonic emission from two-color crossed laser beams. Phys. Rev. A 1998, 58, R2656–R2659. [Google Scholar] [CrossRef] [Green Version]
- Fleischer, A.; Moiseyev, N. Attosecond laser pulse synthesis using bichromatic high-order harmonic generation. Phys. Rev. A 2006, 74, 053806. [Google Scholar] [CrossRef]
- Milošević, D.B. Circularly polarized high harmonics generated by a bicircular field from inert atomic gases in the p state: A tool for exploring chirality-sensitive processes. Phys. Rev. A 2015, 92, 043827. [Google Scholar] [CrossRef]
- Milošević, D.B. High-order harmonic generation by a bichromatic elliptically polarized field: Conservation of angular momentum. J. Phys. B 2015, 48, 171001. [Google Scholar] [CrossRef]
- Odžak, S.; Hasović, E.; Milošević, D.B. Strong-field-approximation theory of high-order harmonic generation by polyatomic molecules. Phys. Rev. A 2016, 93, 043413. [Google Scholar] [CrossRef]
- Hasović, E.; Odžak, S.; Becker, W.; Milošević, D.B. High-order harmonic generation in non-planar molecules driven by a bicircular field. Mol. Phys. 2017, 115, 1750–1757. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Li, L.; Li, Y.; Zhang, Q.; Lan, P.; Lu, P. Selection rules of high-order-harmonic generation: Symmetries of molecules and laser fields. Phys. Rev. A 2016, 94, 033410. [Google Scholar] [CrossRef] [Green Version]
- Habibović, D.; Becker, W.; Milošević, D.B. High-order harmonic generation by planar polyatomic molecules exposed to an orthogonally polarized two-color laser field. J. Phys. B 2021, 54, 134004. [Google Scholar] [CrossRef]
- Neufeld, O.; Podolsky, D.; Cohen, O. Floquet group theory and its application to selection rules in harmonic generation. Nat. Commun. 2019, 10, 405. [Google Scholar] [CrossRef] [Green Version]
- Ghimire, S.; DiChiara, A.D.; Sistrunk, E.; Agostini, P.; DiMauro, L.F.; Reis, D.A. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 2011, 7, 138–141. [Google Scholar] [CrossRef]
- Moiseyev, N. Selection rules for harmonic generation in solids. Phys. Rev. A 2015, 91, 053811. [Google Scholar] [CrossRef]
- Reiss, H.R. Effect of an intense electromagnetic field on a weakly bound system. Phys. Rev. A 1980, 22, 1786–1813. [Google Scholar] [CrossRef]
- Mittleman, M.H. Introduction to the Theory of Laser-Atom Interactions, 2nd ed.; Plenum Press: New York, NY, USA, 1993. [Google Scholar]
- Delone, N.B.; Krainov, V.P. Multiphoton Processes in Atoms, 2nd ed.; Springer: Berlin, Germany, 2000. [Google Scholar]
- DiMauro, L.F.; Agostini, P. Ionization dynamics in strong laser fields. Adv. At. Mol. Opt. Phys. 1995, 35, 79–120. [Google Scholar] [CrossRef]
- Muller, H.G.; Agostini, P.; Petite, G. Multiphoton ionization. In Atoms in Intense Laser Fields, 1st ed.; Gavrila, M., Ed.; Academic: New York, NY, USA, 1992; pp. 1–43. [Google Scholar]
- Milošević, D.B. Strong-field approximation for ionization of a diatomic molecule by a strong laser field. Phys. Rev. A 2006, 74, 063404. [Google Scholar] [CrossRef]
- Schafer, K.J.; Yang, B.; DiMauro, L.F.; Kulander, K.C. Above threshold ionization beyond the high harmonic cutoff. Phys. Rev. Lett. 1993, 70, 1599–1602. [Google Scholar] [CrossRef]
- Yang, B.; Schafer, K.J.; Walker, B.; Kulander, K.C.; Agostini, P.; DiMauro, L.F. Intensity-dependent scattering rings in high order above-threshold ionization. Phys. Rev. Lett. 1993, 71, 3770–3773. [Google Scholar] [CrossRef]
- Paulus, G.G.; Nicklich, W.; Xu, H.; Lambropoulos, P.; Walther, H. Plateau in above threshold ionization spectra. Phys. Rev. Lett. 1994, 72, 2851–2854. [Google Scholar] [CrossRef]
- Paulus, G.G.; Nicklich, W.; Walther, H. Investigation of above-threshold ionization with femtosecond pulses: Connection between plateau and angular distribution of the photoelectrons. Europhys. Lett. 1994, 27, 267–272. [Google Scholar] [CrossRef]
- Paulus, G.G.; Nicklich, W.; Zacher, F.; Lambropoulos, P.; Walther, H. High-order above-threshold ionization of atomic hydrogen using intense, ultrashort laser pulses. J. Phys. B 1996, 29, L249–L256. [Google Scholar] [CrossRef]
- Walker, B.; Sheehy, B.; Kulander, K.C.; DiMauro, L.F. Elastic rescattering in the strong field tunneling limit. Phys. Rev. Lett. 1996, 77, 5031–5034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becker, W.; Lohr, A.; Kleber, M. Effects of rescattering on above-threshold ionization. J. Phys. B 1994, 27, L325–L332, Erratum in J. Phys. B 1995, 28, 1931. [Google Scholar] [CrossRef]
- Lohr, A.; Kleber, M.; Kopold, R.; Becker, W. Above-threshold ionization in the tunneling regime. Phys. Rev. A 1996, 55, R4003–R4006. [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F. Coulomb and rescattering effects in above-threshold ionization. Phys. Rev. A 1998, 58, 3124–3127. [Google Scholar] [CrossRef]
- Milošević, D.B.; Ehlotzky, F. S-matrix theory of above-threshold ionization in a bichromatic laser field. J. Phys. B 1999, 32, 1585–1596. [Google Scholar] [CrossRef]
- Kopold, R.; Milošević, D.B.; Becker, W. Rescattering processes for elliptical polarization: A quantum trajectory analysis. Phys. Rev. Lett. 2000, 84, 3831–3834. [Google Scholar] [CrossRef] [PubMed]
- Salières, P.; Carré, B.; Le Déroff, L.; Grasbon, F.; Paulus, G.G.; Walther, H.; Kopold, R.; Becker, W.; Milošević, D.B.; Sanpera, A.; et al. Feynman’s path-integral approach for intense-laser-atom interactions. Science 2001, 292, 902–905. [Google Scholar] [CrossRef] [Green Version]
- Paulus, G.G.; Becker, W.; Walther, H. Classical rescattering effects in two-color above-threshold ionization. Phys. Rev. A 1995, 52, 4043–4053. [Google Scholar] [CrossRef]
- Ehlotzky, F. Atomic phenomena in bichromatic laser fields. Phys. Rep. 2001, 345, 176–264. [Google Scholar] [CrossRef]
- Hasović, E.; Milošević, D.B.; Becker, W. A method of carrier-envelope phase control for few-cycle laser pulses. Las. Phys. Lett. 2006, 3, 200–204. [Google Scholar] [CrossRef]
- Kramo, A.; Hasović, E.; Milošević, D.B.; Becker, W. Above-threshold detachment by a two-color bicircular laser field. Las. Phys. Lett. 2007, 4, 279–286. [Google Scholar] [CrossRef]
- Hasović, E.; Kramo, A.; Milošević, D.B. Energy- and angle-resolved photoelectron spectra of above-threshold ionization and detachment. Eur. Phys. J. D 2007, 160, 205–216. [Google Scholar] [CrossRef]
- Mancuso, C.A.; Hickstein, D.D.; Grychtol, P.; Knut, R.; Kfir, O.; Tong, X.-M.; Dollar, F.; Zusin, D.; Gopalakrishnan, M.; Gentry, C.; et al. Strong-field ionization with two- color circularly polarized laser fields. Phys. Rev. A 2015, 91, 031402(R). [Google Scholar] [CrossRef] [Green Version]
- Hasović, E.; Becker, W.; Milošević, D.B. Electron rescattering in a bicircular laser field. Opt. Express 2016, 24, 6413–6424. [Google Scholar] [CrossRef]
- Mancuso, C.A.; Hickstein, D.D.; Dorney, K.M.; Ellis, J.L.; Hasović, E.; Knut, R.; Grychtol, P.; Gentry, C.; Gopalakrishnan, M.; Zusin, D.; et al. Controlling electron-ion rescattering in two-color circularly polarized femtosecond laser fields. Phys. Rev. A 2016, 93, 053406. [Google Scholar] [CrossRef] [Green Version]
- Milošević, D.B.; Becker, W. Improved strong-field approximation and quantum-orbit theory: Application to ionization by a bicircular laser field. Phys. Rev. A 2016, 93, 063418. [Google Scholar] [CrossRef]
- Posthumus, J.H. The dynamics of small molecules in intense laser fields. Rep. Prog. Phys. 2004, 67, 623–665. [Google Scholar] [CrossRef]
- Stapelfeldt, H.; Seideman, M. Colloquium: Aligning molecules with strong laser pulses. Rev. Mod. Phys. 2005, 75, 543–557. [Google Scholar] [CrossRef] [Green Version]
- Talebpour, A.; Chien, C.-Y.; Chin, S.L. The effects of dissociative recombination in multiphoton ionization of O2. J. Phys. B 1996, 29, L677–L680. [Google Scholar] [CrossRef]
- Talebpour, A.; Larochelle, S.; Chin, S.L. Suppressed tunnelling ionization of the D2 molecule in an intense Ti:sapphire laser pulse. J. Phys. B 1998, 31, L49–L58. [Google Scholar] [CrossRef]
- Guo, C.; Li, M.; Nibarger, J.P.; Gibson, G.N. Single and double ionization of diatomic molecules in strong laser fields. Phys. Rev. A 1998, 58, R4271–R4274. [Google Scholar] [CrossRef] [Green Version]
- DeWitt, M.J.; Wells, E.; Jones, R.R. Ratiometric comparison of intense field ionization of atoms and diatomic molecules. Phys. Rev. Lett. 2001, 87, 153001. [Google Scholar] [CrossRef] [Green Version]
- Wells, E.; DeWitt, M.J.; Jones, R.R. Comparison of intense-field ionization of diatomic molecules and rare-gas atoms. Phys. Rev. A 2002, 66, 013409. [Google Scholar] [CrossRef]
- Grasbon, F.; Paulus, G.G.; Chin, S.L.; Walther, H.; Muth-Böhm, J.; Becker, A.; Faisal, F.H.M. Signatures of symmetry-induced quantum-interference effects observed in above-threshold-ionization spectra of molecules. Phys. Rev. A 2001, 63, 041402(R). [Google Scholar] [CrossRef] [Green Version]
- Litvinyuk, I.V.; Lee, K.F.; Dooley, P.W.; Rayner, D.M.; Villeneuve, D.M.; Corkum, P.B. Alignment-dependent strong field ionization of molecules. Phys. Rev. Lett. 2003, 90, 233003. [Google Scholar] [CrossRef] [Green Version]
- Eremina, E.; Liu, X.; Rottke, H.; Sandner, W.; Schätzel, M.G.; Dreischuh, A.; Paulus, G.G.; Walther, H.; Moshammer, R.; Ullrich, J. Influence of molecular structure on double ionization of N2 and O2 by high intensity ultrashort laser pulses. Phys. Rev. Lett. 2004, 92, 173001. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Zhang, J.; Liu, P.; Wang, Y.; Xu, Z. Photoelectron angular distributions of molecules in bichromatic laser fields of circular polarization. Phys. Lett. A 2009, 373, 227–230. [Google Scholar] [CrossRef]
- Fernández, J.; Madsen, B. Above-threshold ionization, energy-resolved photoelectron angular distributions, and momentum distributions of H2+ in intense femtosecond laser pulses. Phys. Rev. A 2009, 79, 063406. [Google Scholar] [CrossRef]
- Yuan, K.-J.; Bandrauk, A. Molecular above-threshold-ionization angular distributions with intense circularly polarized attosecond XUV laser pulses. Phys. Rev. A 2012, 85, 053419. [Google Scholar] [CrossRef]
- Fetić, B.; Milošević, D.B. High-order above-threshold ionization of the H2+ ion: The role of internuclear distance. Phys. Rev. A 2019, 99, 043426. [Google Scholar] [CrossRef]
- Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Angle-resolved high-order above-threshold ionization of a molecule: Sensitive tool for molecular characterization. Phys. Rev. Lett. 2008, 100, 203003. [Google Scholar] [CrossRef]
- Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Strong-field approximation for ionization of a diatomic molecule by a strong laser field. II. The role of electron rescattering off the molecular centers. Phys. Rev. A 2008, 78, 033412. [Google Scholar] [CrossRef]
- Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B. Strong-field approximation for ionization of a diatomic molecule by a strong laser field. III. High-order above-threshold ionization by an elliptically polarized field. Phys. Rev. A 2009, 80, 013420. [Google Scholar] [CrossRef]
- Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B. Strong-field ionization of homonuclear diatomic molecules by a bicircular laser field: Rotational and reflection symmetries. Phys. Rev. A 2017, 95, 033411. [Google Scholar] [CrossRef]
- Gazibegović-Busuladžić, A.; Busuladžić, M.; Hasović, E.; Becker, W.; Milošević, D.B. Strong-field ionization of linear molecules by a bicircular laser field: Symmetry considerations. Phys. Rev. A 2018, 97, 043432. [Google Scholar] [CrossRef]
- Gazibegović-Busuladžić, A.; Busuladžić, M.; Čerkić, A.; Hasović, E.; Becker, W.; Milošević, D.B. Strong-field ionization of linear molecules by a bichromatic elliptically polarized laser field with coplanar counterrotating or corotating components of different frequencies. J. Phys. Conf. Ser. 2019, 1206, 012003. [Google Scholar] [CrossRef]
- Busuladžić, M.; Čerkić, A.; Gazibegović-Busuladžić, A.; Hasović, E.; Milošević, D.B. Molecular-orientation-dependent interference and plateau structures in strong-field ionization of a diatomic molecule by a corotating bichromatic elliptically polarized laser field. Phys. Rev. A 2018, 98, 013413. [Google Scholar] [CrossRef]
- Habibović, D.; Gazibegović-Busuladžić, A.; Busuladžić, M.; Čerkić, A.; Milošević, D.B. Strong-field ionization of homonuclear diatomic molecules using orthogonally polarized two-color laser fields. Phys. Rev. A 2020, 102, 023111. [Google Scholar] [CrossRef]
- Habibović, D.; Gazibegović-Busuladžić, A.; Busuladžić, M.; Milošević, D.B. Strong-field ionization of heteronuclear diatomic molecules using an orthogonally polarized two-color laser field. Phys. Rev. A 2021, 103, 053101. [Google Scholar] [CrossRef]
- L’Huillier, A.; Schafer, K.J.; Kulander, K. Theoretical aspects of intense field harmonic generation. J. Phys. B 1991, 24, 3315–3341. [Google Scholar] [CrossRef]
- Bauer, D. (Ed.) Computational Strong-Field Quantum Dynamics: Intense Light-Matter Interactions; De Gruyter Textbook: Berlin, Germany, 2016. [Google Scholar]
- Fetić, B.; Milošević, D.B. Numerical solution of the time-dependent Schrödinger equation for H2+ ion with application to high-harmonic generation and above-threshold ionization. Phys. Rev. E 2017, 95, 053309. [Google Scholar] [CrossRef]
- Clarke, D.D.A.; Armstrong, G.S.J.; Brown, A.C.; van der Hart, H.W. R-matrix-with-time-dependence theory for ultrafast atomic processes in arbitrary light fields. Phys. Rev. A 2018, 98, 053442. [Google Scholar] [CrossRef] [Green Version]
- Odžak, S.; Hasović, E.; Milošević, D.B. High-order harmonic generation in polyatomic molecules induced by a bicircular laser field. Phys. Rev. A 2016, 94, 033419. [Google Scholar] [CrossRef] [Green Version]
- Odžak, S.; Milošević, D.B. Interference effects in high-order harmonic generation by homonuclear diatomic molecules. Phys. Rev. A 2009, 79, 023414. [Google Scholar] [CrossRef]
- Levine, I.N. Quantum Chemistry, 5th ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Hasović, E.; Milošević, D.B. Strong-field approximation for above-threshold ionization of polyatomic molecules. Phys. Rev. A 2012, 86, 043429. [Google Scholar] [CrossRef]
- Hasović, E.; Milošević, D.B. Strong-field approximation for above-threshold ionization of polyatomic molecules. II. The role of electron rescattering off the molecular centers. Phys. Rev. A 2014, 89, 053401. [Google Scholar] [CrossRef]
- Gallagher, T.F. Above-threshold ionization in the low-frequency limit. Phys. Rev. Lett. 1988, 61, 2304–2307. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B.; Burnett, N.H.; Brunel, F. Above-threshold ionization in the long-wavelength limit. Phys. Rev. Lett. 1989, 62, 1259–1262. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [Green Version]
- Milošević, D.B.; Becker, W. X-ray harmonic generation by orthogonally polarized two-color fields: Spectral shape and polarization. Phys. Rev. A 2019, 100, 031401(R). [Google Scholar] [CrossRef]
- Habibović, D.; Milošević, D.B. Ellipticity of high-order harmonics generated by aligned homonuclear diatomic molecules exposed to an orthogonal two-color laser field. Photonics 2020, 7, 110. [Google Scholar] [CrossRef]
- Smirnova, O.; Spanner, M.; Ivanov, M. Anatomy of strong field ionization II: To dress or not to dress? J. Mod. Opt. 2007, 54, 1019–1038. [Google Scholar] [CrossRef]
- Becker, W.; Chen, J.; Chen, S.G.; Milošević, D.B. Dressed-state strong-field approximation for laser-induced molecular ionization. Phys. Rev. A 2007, 76, 033403. [Google Scholar] [CrossRef]
- Okunishi, M.; Itaya, R.; Shimada, K.; Prümper, G.; Ueda, K.; Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Angle-resolved high-order above-threshold ionization spectra for N2 and O2: Measurements and the strong-field approximation. J. Phys. B 2008, 41, 201004. [Google Scholar] [CrossRef]
- Okunishi, M.; Itaya, R.; Shimada, K.; Prümper, G.; Ueda, K.; Busuladžić, M.; Gazibegović-Busuladžić, A.; Milošević, D.B.; Becker, W. Two-source double-slit interference in angle-resolved high-energy above-threshold ionization spectra of diatoms. Phys. Rev. Lett. 2009, 103, 043001. [Google Scholar] [CrossRef]
- Busuladžić, M.; Milošević, D.B. Simulation of the above-threshold-ionization experiment using the molecular strong-field approximation: The choice of gauge. Phys. Rev. A 2010, 82, 015401. [Google Scholar] [CrossRef]
- Gazibegović-Busuladžić, A.; Hasović, E.; Busuladžić, M.; Milošević, D.B.; Kelkensberg, F.; Siu, W.K.; Vrakking, M.J.J.; Lépine, F.; Sansone, G.; Nisoli, M.; et al. Above-threshold ionization of diatomic molecules by few-cycle laser pulses. Phys. Rev. A 2011, 84, 043426. [Google Scholar] [CrossRef]
- Quan, W.; Lai, X.Y.; Chen, Y.J.; Wang, C.L.; Hu, Z.L.; Liu, X.J.; Hao, X.L.; Chen, J.; Hasović, E.; Busuladžić, M.; et al. Resonancelike enhancement in high-order above-threshold ionization of molecules. Phys. Rev. A 2013, 88, 021401(R). [Google Scholar] [CrossRef]
- Milošević, D.B. Few-cycle-laser-pulse induced and assisted processes in atoms, molecules, and nanostructures. In Ultrafast Dynamics Driven by Intense Light Pulses: From Atoms to Solids, from Lasers to Intense X-rays, 1st ed.; Kitzler, M., Gräfe, S., Eds.; Springer: Berlin, Germany, 2016; Volume 86, pp. 27–48. [Google Scholar]
- Kübel, M.; Wustelt, P.; Zhang, Y.; Skruszewicz, S.; Hoff, D.; Würzler, D.; Kang, H.; Zille, D.; Adolph, D.; Paulus, G.G.; et al. High-order phase-dependent asymmetry in the above-threshold ionization plateau. Phys. Rev. Lett. 2021, 126, 113201. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.B.; Becker, W. High-order harmonic generation by bi-elliptical orthogonally polarized two-color fields. Phys. Rev. A 2020, 102, 023107. [Google Scholar] [CrossRef]
- Mauger, F.; Bandrauk, A.D.; Uzer, T. Circularly polarized molecular high harmonic generation using a bicircular laser. J. Phys. B 2016, 49, 10LT01. [Google Scholar] [CrossRef]
- Milošević, D.B. Cut-off law for high-harmonic generation by an elliptically polarized laser field. J. Phys. B 2000, 33, 2479–2488. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W.; Kopold, R. High-harmonic generation by two-color circularly polarized field mixing. In Atoms, Molecules and Quantum Dots in Laser Fields: Fundamental Processes; Bloembergen, N., Rahman, N., Rizzo, A., Eds.; Società Italiana di Fisica: Bologna, Italy, 2001; Volume 71, pp. 239–252. [Google Scholar]
- Milošević, D.B.; Becker, W. Generation of elliptically polarized soft x rays using high-order harmonic generation with orthogonal two-color laser fields. J. Phys. Conf. Ser. 2020, 1508, 012001. [Google Scholar] [CrossRef]
- Birkeland, T.; Førre, M.; Hansen, J.P.; Selstø, S. Dynamics of H(2p) ionization in ultrashort strong laser pulses. J. Phys. B 2004, 37, 4205–4219. [Google Scholar] [CrossRef]
- Habibović, D.; Becker, W.; Milošević, D.B. Attosecond-pulse-train generation using an orthogonally polarized two-color laser field. J. Opt. Soc. Am. B 2021, submitted. [Google Scholar]
- Milošević, D.B. Generation of elliptically polarized attosecond pulse trains. Opt. Lett. 2015, 40, 2381–2384. [Google Scholar] [CrossRef]
- Medišauskas, L.; Wragg, J.; van der Hart, H.W.; Ivanov, M.Y. Generating isolated elliptically polarized attosecond pulses using bichromatic counterrotating circularly polarized laser fields. Phys. Rev. Lett. 2015, 115, 153001. [Google Scholar] [CrossRef] [Green Version]
- De Bohan, A.; Antoine, P.; Milošević, D.B.; Piraux, B. Phase-dependent harmonic emission with ultrashort laser pulses. Phys. Rev. Lett. 1998, 81, 1837–1840. [Google Scholar] [CrossRef]
- Baltuška, A.; Udem, T.; Uiberacker, M.; Hentschel, M.; Goulielmakis, E.; Gohle, C.; Holzwarth, R.; Yakovlev, V.S.; Scrinzi, A.; Hänsch, T.W.; et al. Attosecond control of electronic processes by intense light fields. Nature 2003, 421, 611–615. [Google Scholar] [CrossRef]
- Möller, M.; Meyer, F.; Sayler, A.M.; Paulus, G.G.; Kling, M.F.; Schmidt, B.E.; Becker, W.; Milošević, D.B. Off-axis low-energy structures in above-threshold ionization. Phys. Rev. A 2014, 90, 023412. [Google Scholar] [CrossRef]
- Huismans, Y.; Rouzée, A.; Gijsbertsen, A.; Jungmann, J.H.; Smolkowska, A.S.; Logman, P.S.W.M.; Lépine, F.; Cauchy, C.; Zamith, S.; Marchenko, T.; et al. Time-resolved holography with photoelectrons. Science 2011, 331, 61–64. [Google Scholar] [CrossRef] [Green Version]
- Hickstein, D.D.; Ranitovic, P.; Witte, S.; Tong, X.-M.; Huismans, Y.; Arpin, P.; Zhou, X.; Keister, K.E.; Hogle, C.W.; Zhang, B.; et al. Direct visualization of laser-driven electron multiple scattering and tunneling distance in strong-field ionization. Phys. Rev. Lett. 2012, 109, 073004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Figueira de Morisson Faria, C.; Maxwell, A.S. It is all about phases: Ultrafast holographic photoelectron imaging. Rep. Prog. Phys. 2020, 83, 034401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Jiang, W.-C.; Xie, H.; Luo, S.; Zhou, Y.; Lu, P. Strong-field photoelectron holography of atoms by bicircular two-color laser pulses. Phys. Rev. A 2018, 97, 023415. [Google Scholar] [CrossRef]
- Lindner, F.; Schätzel, M.G.; Walther, H.; Baltuška, A.; Goulielmakis, E.; Krausz, F.; Milošević, D.B.; Bauer, D.; Becker, W.; Paulus, G.G. Attosecond double-slit experiment. Phys. Rev. Lett. 2005, 95, 040401. [Google Scholar] [CrossRef] [Green Version]
- Paulus, G.G.; Grasbon, F.; Walther, H.; Villoresi, P.; Nisoli, M.; Stagira, S.; Priori, E.; De Silvestri, S. Absolute-phase phenomena in photoionization with few-cycle laser pulses. Nature 2001, 414, 182–184. [Google Scholar] [CrossRef]
- Kling, M.F.; Rauschenberger, J.; Verhoef, A.J.; Hasović, E.; Uphues, T.; Milošević, D.B.; Muller, H.G.; Vrakking, M.J.J. Imaging of carrier-envelope phase effects in above-threshold ionization with intense few-cycle laser fields. New J. Phys. 2008, 10, 025024. [Google Scholar] [CrossRef] [Green Version]
- Milošević, D.B.; Paulus, G.G.; Becker, W. High-order above-threshold ionization with few-cycle pulse: A meter of the absolute phase. Opt. Express 2003, 11, 1418–1429. [Google Scholar] [CrossRef]
- Milošević, D.B.; Hasović, E.; Odžak, S.; Busuladžić, M.; Gazibegović-Busuladžić, A.; Becker, W. New results in above-threshold ionization and high-order harmonic generation of atomic and molecular systems. Las. Phys. 2009, 19, 185–190. [Google Scholar] [CrossRef]
- Hoang, V.-H.; Le, V.-H.; Lin, C.D.; Le, A.-T. Retrieval of target structure information from laser-induced photoelectrons by few-cycle bicircular laser fields. Phys. Rev. A 2017, 95, 031402. [Google Scholar] [CrossRef] [Green Version]
- Becker, W.; Kleber, M.; Lohr, A.; Paulus, G.G.; Walther, H.; Zacher, F. Electron spectra of above-threshold ionization in elliptically polarized laser fields. Las. Phys. 1998, 8, 56–68. [Google Scholar]
- Ostrovsky, V.N.; Greenwood, J.B. High harmonic generation by halogen anions and noble gas atoms in a laser field. J. Phys. B 2005, 38, 1867–1880. [Google Scholar] [CrossRef]
- Ostrovsky, V.N. High harmonic generation by anions and atoms: Effect of initial/final-state wavefunctions. J. Phys. B 2005, 38, 4399–4406. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habibović, D.; Becker, W.; Milošević, D.B. Symmetries and Selection Rules of the Spectra of Photoelectrons and High-Order Harmonics Generated by Field-Driven Atoms and Molecules. Symmetry 2021, 13, 1566. https://doi.org/10.3390/sym13091566
Habibović D, Becker W, Milošević DB. Symmetries and Selection Rules of the Spectra of Photoelectrons and High-Order Harmonics Generated by Field-Driven Atoms and Molecules. Symmetry. 2021; 13(9):1566. https://doi.org/10.3390/sym13091566
Chicago/Turabian StyleHabibović, Dino, Wilhelm Becker, and Dejan B. Milošević. 2021. "Symmetries and Selection Rules of the Spectra of Photoelectrons and High-Order Harmonics Generated by Field-Driven Atoms and Molecules" Symmetry 13, no. 9: 1566. https://doi.org/10.3390/sym13091566
APA StyleHabibović, D., Becker, W., & Milošević, D. B. (2021). Symmetries and Selection Rules of the Spectra of Photoelectrons and High-Order Harmonics Generated by Field-Driven Atoms and Molecules. Symmetry, 13(9), 1566. https://doi.org/10.3390/sym13091566





