Construction of an Approximate Analytical Solution for Multi-Dimensional Fractional Zakharov–Kuznetsov Equation via Aboodh Adomian Decomposition Method
Abstract
:1. Introduction
2. Prelude
3. Configuration for Aboodh Adomian Decomposition Method
4. Qualitative Aspects of Aboodh-Adomian Decomposition Method
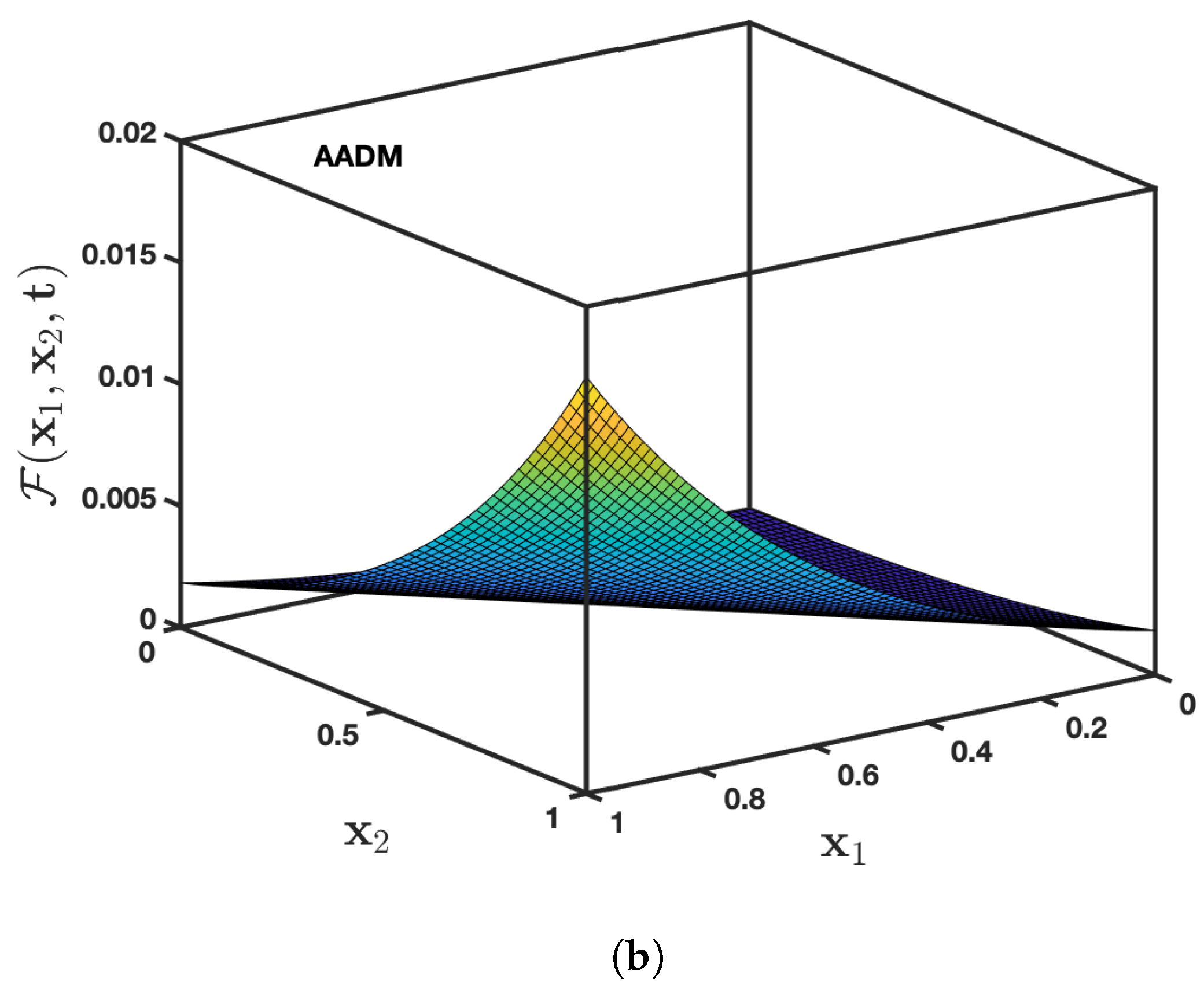
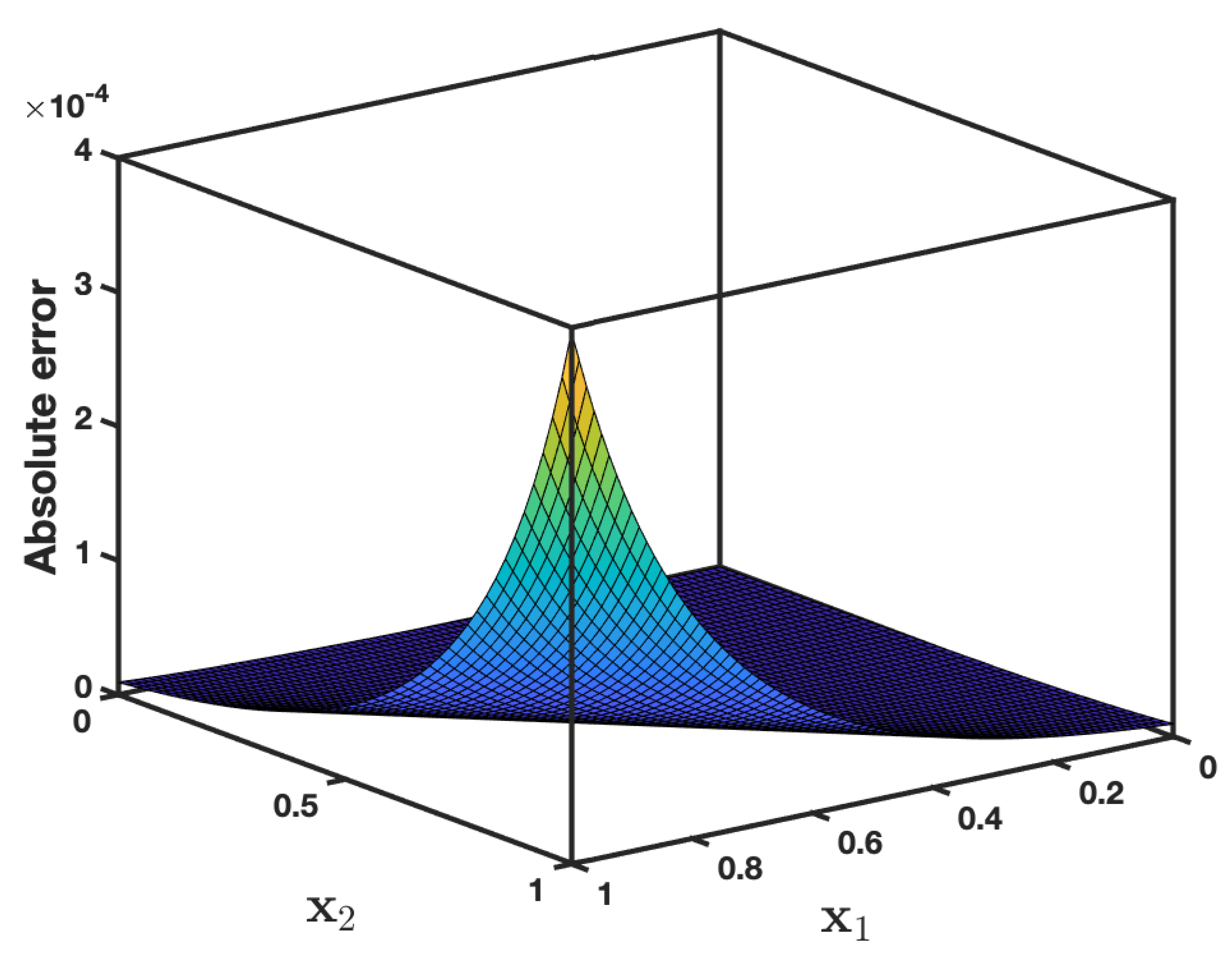
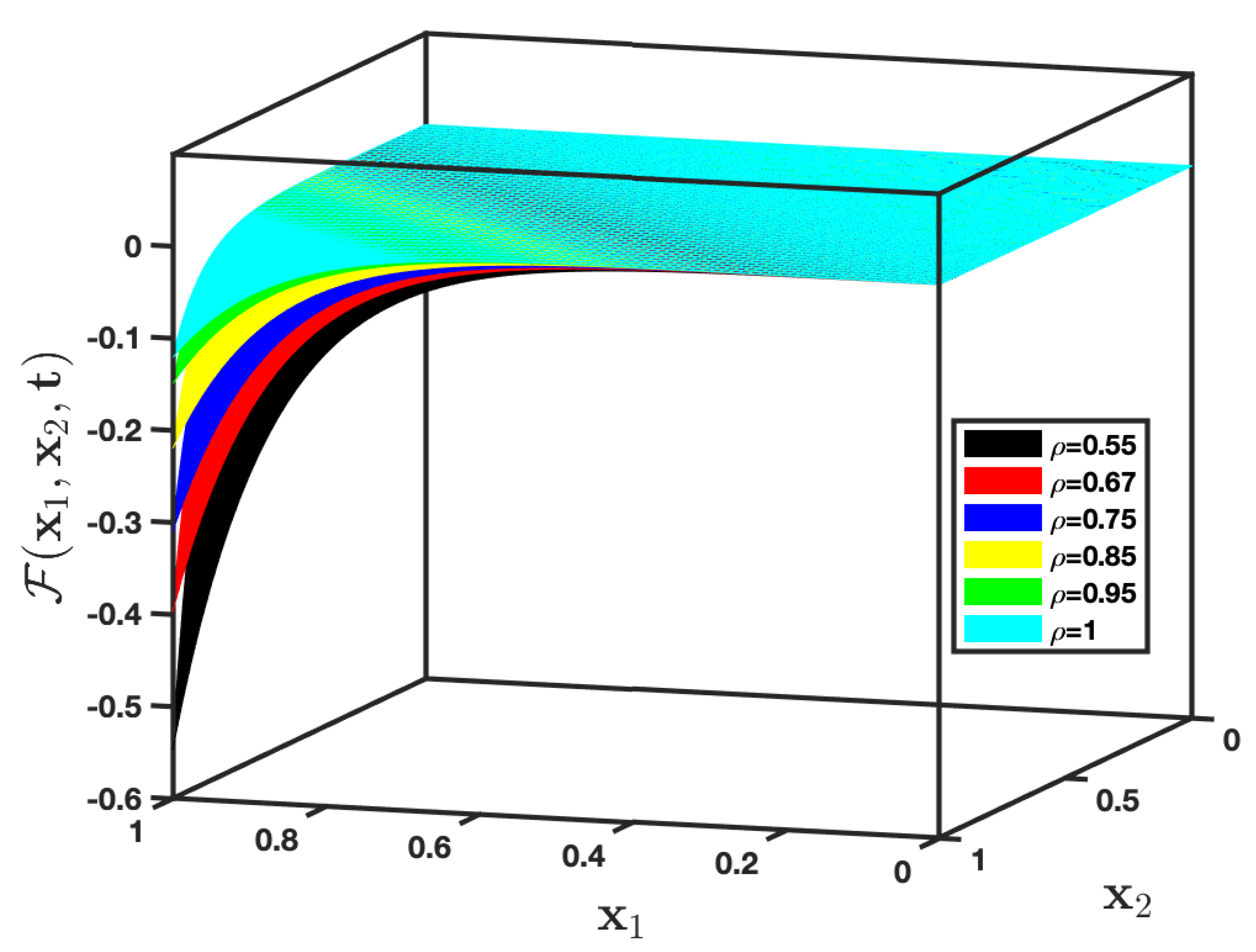
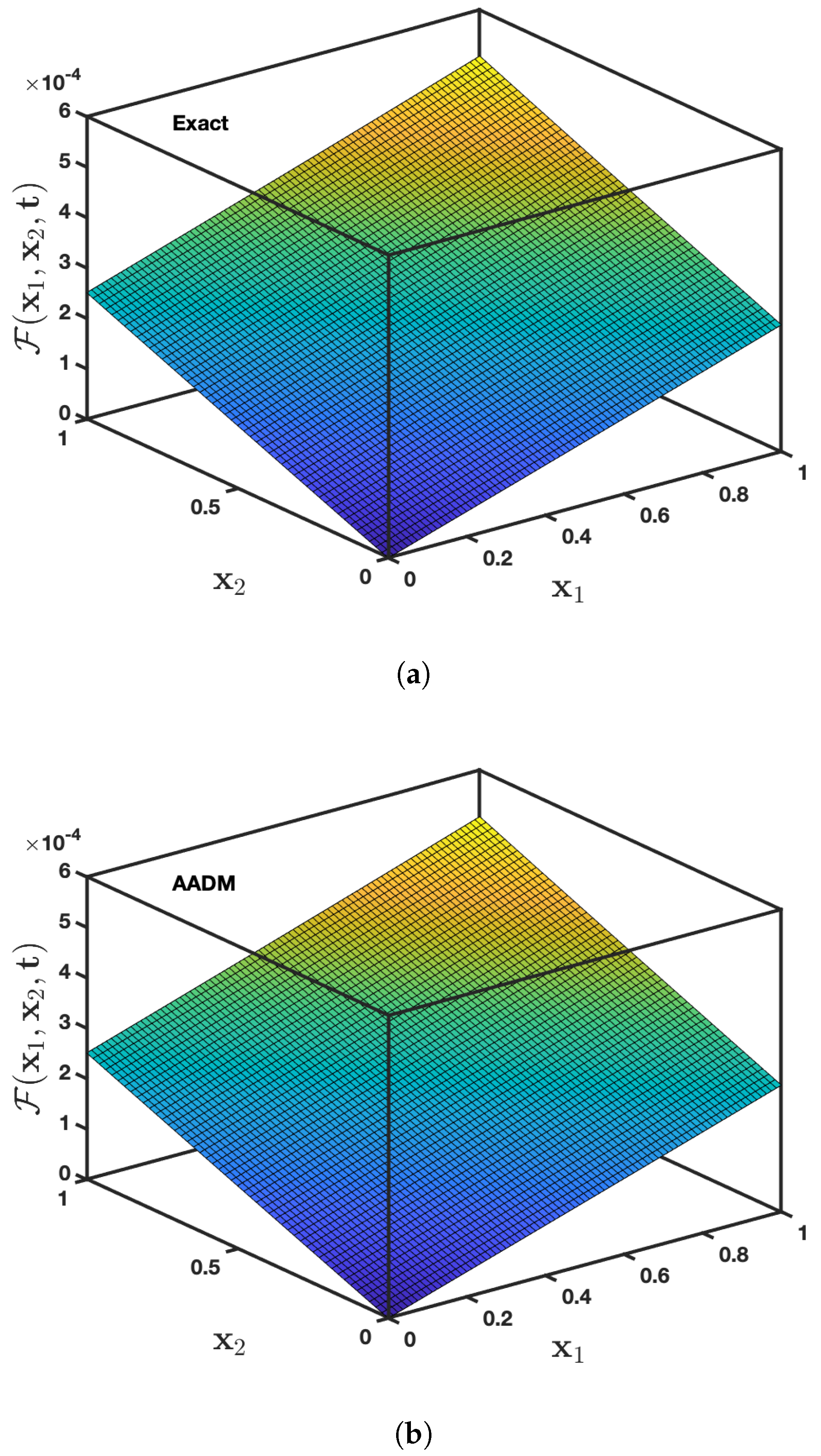
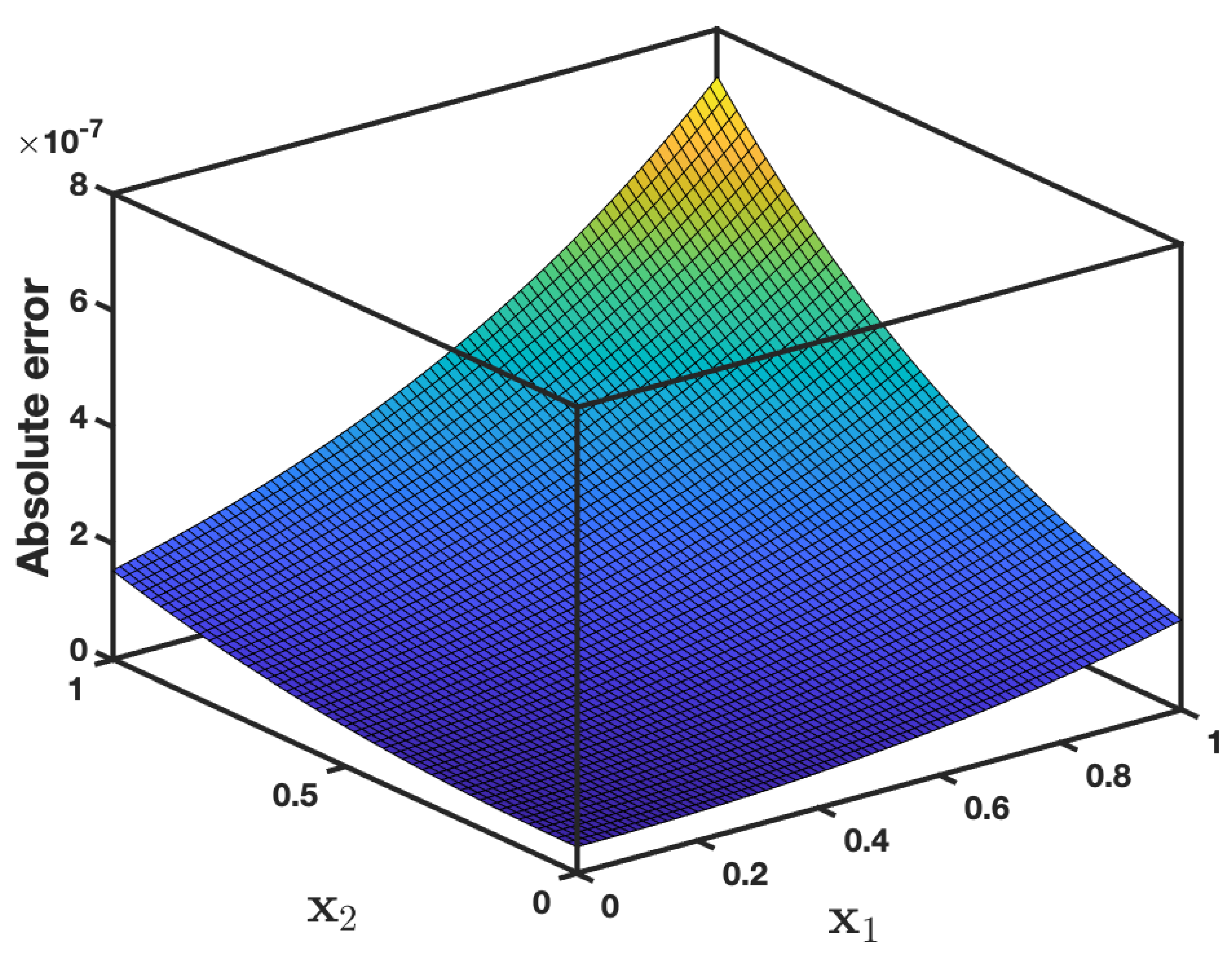
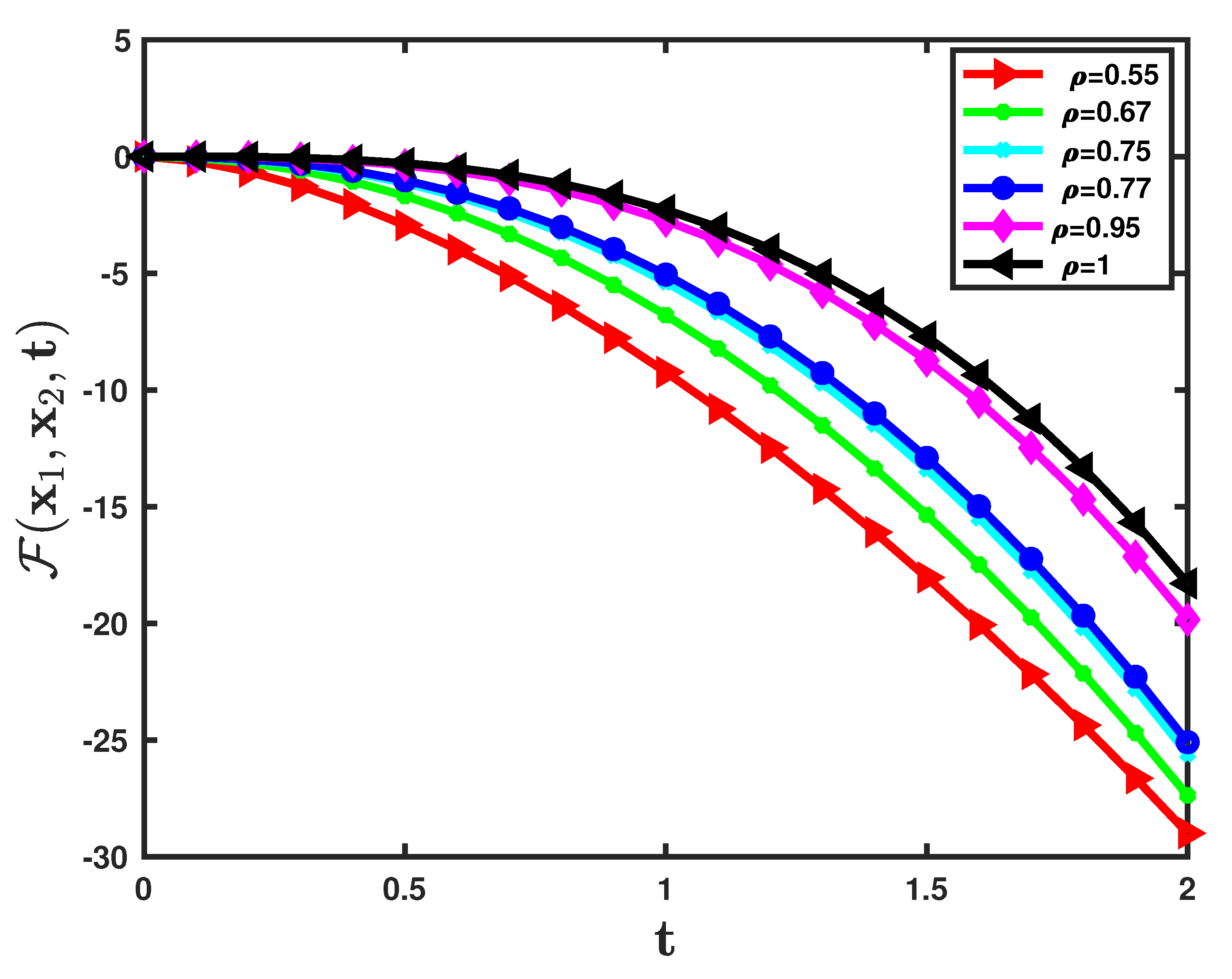
5. Numerical Illustrations
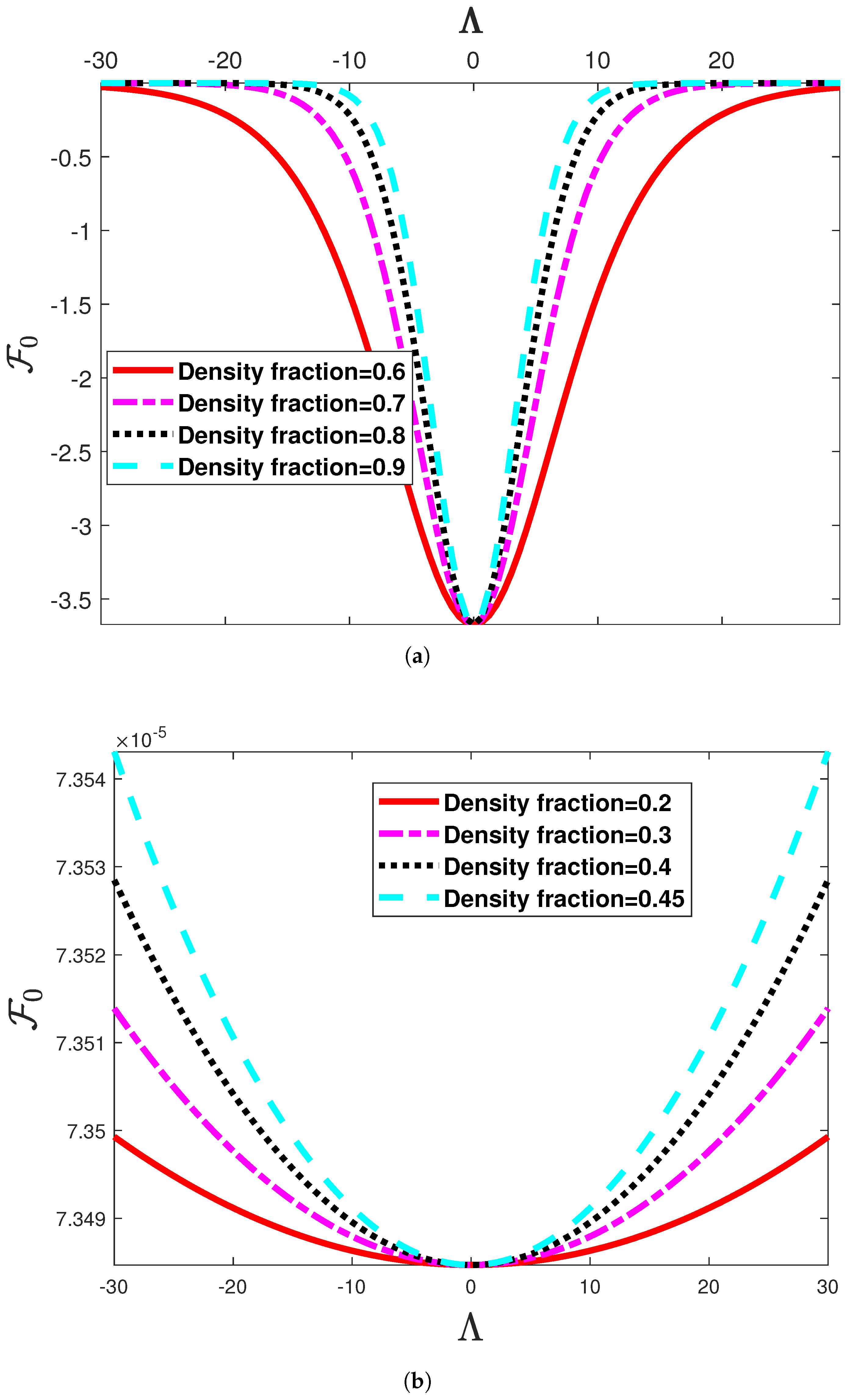
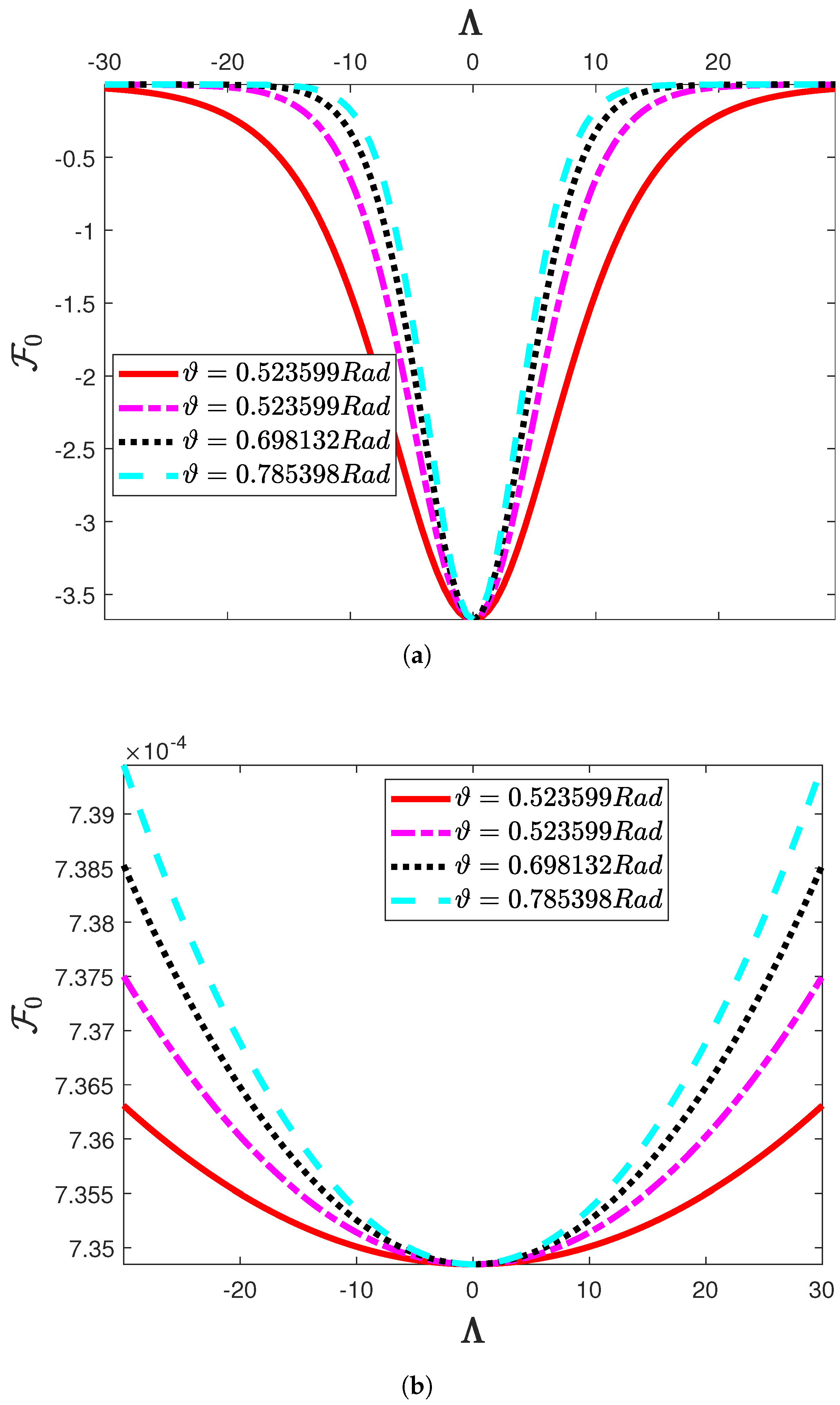
6. Other Aspects of ZKEs
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; Word Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Application of Fractional Differential Equations; North Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Rahaman, H.; Hasan, M.K.; Ali, A.; Alam, M.S. Implicit methods for numerical solution of singular initial value problems. Appl. Math. Nonliner Scis. 2020, 6, 1–8. [Google Scholar] [CrossRef]
- Aghili, A. Complete solution for the time fractional diffusion problem with mixed boundary conditions by operational method. Appl. Math. Nonliner Sci. 2020, 6, 9–20. [Google Scholar] [CrossRef] [Green Version]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Danbury, CT, USA, 2006. [Google Scholar]
- Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. On the exact solutions to some system of complex nonlinear models. Appl. Math. Nonliner Sci. 2020, 6, 29–42. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- El-Borhamy, M.; Mosalam, N. On the existence of periodic solution and the transition to chaos of Rayleigh-Duffing equation with application of gyro dynamic. Appl. Math. Nonliner Sci. 2020, 5, 93–108. [Google Scholar] [CrossRef]
- Günerhan, H.; Çelik, E. Analytical and approximate solutions of fractional partial differential-algebraic equations. Appl. Math. Nonlin. Sci. 2020, 5, 109–120. [Google Scholar] [CrossRef]
- Rashid, S.; Khalid, A.; Sultana, S.; Hammouch, Z.; Shah, R.; Alsharif, A.M. A novel analytical view of time-fractional Korteweg–De Vries equations via a new integral transform. Symmetry 2021, 13, 1254. [Google Scholar] [CrossRef]
- Rashid, S.; Kubra, K.T.; Lehre, S.U. Fractional spatial diffusion of a biological population model via a new integral transform in the settings of power and Mittag-Leffler nonsingular kernel. Phy. Scr. 2021, 96. [Google Scholar] [CrossRef]
- Rashid, S.; Kubra, K.T.; Rauf, A.; Chu, Y.-M.; Hamed, Y.S. New numerical approach for time-fractional partial differential equations arising in physical system involving natural decomposition method. Phys. Scr. 2021, 96. [Google Scholar] [CrossRef]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Aboodh, K.S. The new integral transform Aboodh transform. Glob. J. Pure Appl. Math. 2013, 9, 35–43. [Google Scholar]
- Evirgen, F.; Uçar, S.; Özdemir, N. System analysis of HIV infection model with CD4+T under non-singular kernel derivative. Appl. Math. Nonliner Sci. 2020, 5, 139–146. [Google Scholar] [CrossRef] [Green Version]
- Elzaki, T.M.; Elzaki, S.M. On the ELzaki transform and systems of ordinary differential equations. Glob. J. Pure. Appl. Math. 2011, 7, 113–119. [Google Scholar]
- Watugula, G.K. A new integral transform to solve differential equations and control engineering problems. Int. J. Math. Edu. Sci. Technol. 1993, 24, 409–421. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A. Natural transform-properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Maitama, S.; Weidong, Z. New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. Int. J. Anal. Appl. 2019, 17, 167–190. [Google Scholar]
- Saadeh, R.; Ahmad, Q.; Aliaa, B. A new integral transform: ARA transform and its properties and applications. Symmetry 2020, 12, 925. [Google Scholar] [CrossRef]
- Sharifi, M.; Raesi, B. Vortex theory for two dimensional Boussinesq equations. Appl. Math. Nonliner Sci. 2020, 5, 67–84. [Google Scholar] [CrossRef]
- Rajesh Kanna, M.R.; Pradeep Kumar, R.; Nandappa, S.; Cangul, I.N. On solutions of fractional order telegraph partial differential equation by Crank-Nicholson finite difference method. Appl. Math. Nonliner Sci. 2020, 5, 85–98. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef] [Green Version]
- Daftardar-Gejji, V.; Bhalekar, S. Solving multi-term linear and non-linear diffusion-wave equations of fractional order by Adomian decomposition method. Appl. Math. Comput. 2008, 202, 113. [Google Scholar] [CrossRef]
- Modanli, M.; Akgül, A. On solutions of fractional order Telegraph partial differential equation by Crank-Nicholson finite difference method. Appl. Math. Nonliner Sci. 2020, 5, 163–170. [Google Scholar] [CrossRef] [Green Version]
- Topsakal, M.; Taşcan, F. Exact travelling wave solutions for space-time fractional Klein-Gordon equation and (2+1)-Dimensional time-fractional Zoomeron equation via auxiliary equation method. Appl. Math. Nonliner Sci. 2020, 5, 437–446. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Abdelkawy, M.A.; Kumar, S.; Johnson, S.; Biswas, A. Solitons and other solutions to quantum Zakharov–Kuznetsov equation in quantum magneto-plasmas. Indian J. Phys. 2013, 87, 455–463. [Google Scholar] [CrossRef]
- Khater, A.H.; Malfliet, W.; Callebaut, D.K.; Kamela, E.S. The tanh method, a simple transformation and exact analytical solutions for nonlinear reaction–diffusion equations. Chaos Solitons Fract. 2002, 14, 513–522. [Google Scholar] [CrossRef]
- Ray, S.S.; Bera, R. Analytical solution of a fractional diffusion equation by Adomian decomposition method. Appl. Math. Comp. 2006, 174, 329–336. [Google Scholar]
- Momani, S.; Odibat, Z. Numerical approach to differential equations of fractional order. J. Comput. Appl. Math. 2007, 207, 96–110. [Google Scholar] [CrossRef] [Green Version]
- Yousef, F.; Alquran, M.; Jaradat, T.; Momani, S.; Baleanu, D. Ternary-fractional differential transform schema: Theory and application. Adv. Differ. Equ. 2019, 2019, 197. [Google Scholar] [CrossRef]
- Hemeda, A.A. Homotopy perturbation method for solving systems of nonlinear coupled equations. Appl. Math. Sci. 2012, 6, 4787–4800. [Google Scholar]
- Marinca, V.; Herisanu, N. The optimal homotopy asymptotic method for solving Blasius equation. Appl. Math. Comput. 2014, 231, 134–139. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Aljoudi, S. On using the G/G′-expansion method for solving nonlinear partial differential equations in mathematical physics. Commun. Appl. Nonliner Anal. 2010, 17, 49–64. [Google Scholar]
- Li, C.; Zhang, J. Lie symmetry analysis and exact solutions of generalized fractional Zakharov-Kuznetsov equations. Symmetry 2019, 11, 601. [Google Scholar] [CrossRef] [Green Version]
- Şenol, M.; Alquran, M.; Kasmaei, H.D. On the comparison of perturbation-iteration algorithm and residual power series method to solve fractional Zakharov-Kuznetsov equation. Res. Phys. 2018, 9, 321–327. [Google Scholar] [CrossRef]
- Zakharov, V.; Kuznetsov, E. On three-dimensional solitons. Sov. Phys. 1974, 39, 285–288. [Google Scholar]
- Monro, S.; Parkes, E.J. The derivation of a modified Zakharov-Kuznetsov equation and the stability of its solutions. J. Plasma Phys. 1999, 62, 305–317. [Google Scholar] [CrossRef]
- Monro, S.; Parkes, E.J. Stability of solitary-wave solutions to a modified Zakharov-Kuznetsov equation. J. Plasma Phys. 2000, 64, 41126. [Google Scholar] [CrossRef]
- Molliq, R.Y.; Noorani, M.S.M.; Hashim, I.; Ahmad, R.R. Approximate solutions of fractional Zakharov-Kuznetsov equations by VIM. J. Comput. Appl. Math. 2009, 233, 103–108. [Google Scholar] [CrossRef] [Green Version]
- Yildirim, A.; Gulkanat, Y. Analytical approach to fractional Zakharov-Kuznetsov equations by He’s homotopy perturbation method. Commun. Theor. Phys. 2010, 53, 1005. [Google Scholar] [CrossRef]
- Aruldoss, R.; Devi, R.A. Aboodh transform for solving fractional differential equations. Glob. J. Pure Appl. Math. 2020, 16, 145–153. [Google Scholar]
- Aggarwal, S.; Sharma, N.; Chauhan, R. Application of Aboodh transform for solving linear Volterra integro-differential equations of second kind. Int. J. Res. Adv. Technol. 2018, 6, 1186–1190. [Google Scholar]
- Cherif, M.H.; Ziane, D. A new numerical technique for solving systems of nonlinear fractional partial differential equations. Int. J. Anal. Appl. 2017, 15, 188–197. [Google Scholar]
- El-Kalla, I. Convergence of the Adomian method applied to a class of nonlinear integral equations. Appl. Math. Lett. 2008, 21, 372–376. [Google Scholar] [CrossRef] [Green Version]



| t | AADM Solution | Exact Solution | PIA [37] Error | RPSM [37] Error | AADM Error | ||
|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.2 | 5.3966 × | 5.39388 × | 3.85217 × | 3.85217 × | 2.71884 × |
| 0.1 | 0.1 | 0.3 | 5.39248 × | 5.38841 × | 5.75911 × | 5.75912 × | 4.07394 × |
| 0.1 | 0.1 | 0.4 | 5.38837 × | 5.38294 × | 7.65359 × | 7.65352 × | 5.42615 × |
| 0.6 | 0.6 | 0.2 | 3.02967 × | 3.03651 × | 4.66337 × | 4.66389 × | 6.83433 × |
| 0.6 | 0.6 | 0.3 | 3.02553 × | 3.03578 × | 6.86056 × | 6.86314 × | 1.02517 × |
| 0.6 | 0.6 | 0.4 | 3.02138 × | 3.03505 × | 8.98263 × | 8.99046 × | 1.36692 × |
| 0.9 | 0.9 | 0.2 | 1.14455 × | 1.15370 × | 5.12131 × | 5.14241 × | 9.14704 × |
| 0.9 | 0. 9 | 0.3 | 1.13973 × | 1.15345 × | 7.38186 × | 7.48450 × | 1.37206 × |
| 0.9 | 0.9 | 0.4 | 1.13492 × | 1.15321 × | 9.57942 × | 9.89139 × | 1.82943 × |
| t | AADM Solution | PIA [37] | RPSM [37] | AADM Solution | PIA [37] | RPSM [37] | |
|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 5.39424 × | 5.31854 × | 5.31244 × | 5.3953 × | 5.32747 × | 5.32479 × |
| 0.1 | 0.3 | 5.39094 × | 5.28631 × | 5.28410 × | 5.39191 × | 5.29757 × | 5.29675 × |
| 0.1 | 0.4 | 5.38798 × | 5.25777 × | 5.25897 × | 5.38881 × | 5.27039 × | 5.27119 × |
| 0.6 | 0.2 | 3.02730 × | 2.95493 × | 2.95185 × | 3.02837 × | 2.96356 × | 2.96251 × |
| 0.6 | 0.3 | 3.02397 × | 2.92662 × | 2.92709 × | 3.02496 × | 2.93717 × | 2.93780 × |
| 0.6 | 0.4 | 3.02099 × | 2.90307 × | 2.90522 × | 3.02182 × | 2.91448 × | 2.91561 × |
| 0.9 | 0.2 | 1.14179 × | 1.06822 × | 1.05522 × | 1.14303 × | 1.07716 × | 2.91561 × |
| 0.9 | 0.3 | 1.13792 × | 1.04487 × | 1.01199 × | 1.13907 × | 1.05488 × | 1.03695 × |
| 0.9 | 0.4 | 1.13447 × | 9.02777 × | 9.60606 × | 1.13543 × | 1.03736 × | 9.96743 × |
| t | AADM Solution | Exact Solution | VIM [41] Error | AADM Error | ||
|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.2 | 5.00092 × | 4.99592 × | 5.00091 × | 4.99519 × |
| 0.1 | 0.1 | 0.3 | 5.00091 × | 4.99342 × | 5.00091 × | 7.49278 × |
| 0.1 | 0.1 | 0.4 | 5.00091 × | 4.99092 × | 5.00091 × | 9.99037 × |
| 0.6 | 0.6 | 0.2 | 3.02004 × | 3.01953 × | 3.02003 × | 5.08987 × |
| 0.6 | 0.6 | 0.3 | 3.02004 × | 3.01927 × | 3.02003 × | 7.63479 × |
| 0.6 | 0.6 | 0.4 | 3.02004 × | 3.01902 × | 3.02003 × | 1.01797 × |
| 0.9 | 0.9 | 0.2 | 4.5678 × | 4.56728 × | 4.56780 × | 5.21227 × |
| 0.9 | 0. 9 | 0.3 | 4.5678 × | 4.56702 × | 4.56780 × | 7.81839 × |
| 0.9 | 0.9 | 0.4 | 4.5678 × | 4.56676 × | 4.56780 × | 1.04245 × |
| t | AADM for | VIM [41] for | AADM for | VIM [41] for | |
|---|---|---|---|---|---|
| 0.1 | 0.2 | 5.00091 × | 5.00091 × | 5.00091 × | 5.00091 × |
| 0.1 | 0.3 | 5.00091 × | 5.00090 × | 5.00091 × | 5.00090 × |
| 0.1 | 0.4 | 5.0009 × | 5.00090 × | 5.00091 × | 5.00090 × |
| 0.6 | 0.2 | 3.02004 × | 3.02003 × | 3.02004 × | 3.02003 × |
| 0.6 | 0.3 | 3.02004 × | 3.02003 × | 3.02004 × | 3.02003 × |
| 0.6 | 0.4 | 3.02004 × | 3.02003 × | 3.02004 × | 3.02003 × |
| 0.9 | 0.2 | 4.5678 × | 4.56780 × | 4.5678 × | 4.5678 × |
| 0. 9 | 0.3 | 4.5678 × | 4.56780 × | 4.5678 × | 4.5678 × |
| 0.9 | 0.4 | 4.5678 × | 4.56780 × | 4.5678 × | 4.5678 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, S.; Kubra, K.T.; Guirao, J.L.G. Construction of an Approximate Analytical Solution for Multi-Dimensional Fractional Zakharov–Kuznetsov Equation via Aboodh Adomian Decomposition Method. Symmetry 2021, 13, 1542. https://doi.org/10.3390/sym13081542
Rashid S, Kubra KT, Guirao JLG. Construction of an Approximate Analytical Solution for Multi-Dimensional Fractional Zakharov–Kuznetsov Equation via Aboodh Adomian Decomposition Method. Symmetry. 2021; 13(8):1542. https://doi.org/10.3390/sym13081542
Chicago/Turabian StyleRashid, Saima, Khadija Tul Kubra, and Juan Luis García Guirao. 2021. "Construction of an Approximate Analytical Solution for Multi-Dimensional Fractional Zakharov–Kuznetsov Equation via Aboodh Adomian Decomposition Method" Symmetry 13, no. 8: 1542. https://doi.org/10.3390/sym13081542
APA StyleRashid, S., Kubra, K. T., & Guirao, J. L. G. (2021). Construction of an Approximate Analytical Solution for Multi-Dimensional Fractional Zakharov–Kuznetsov Equation via Aboodh Adomian Decomposition Method. Symmetry, 13(8), 1542. https://doi.org/10.3390/sym13081542







