Abstract
The eigenvalues of the characteristic polynomial of a graph are sensitive to its symmetry-related characteristics. Within this study, we have examined three eigenvalue–based molecular descriptors. These topological molecular descriptors, among others, are gathering information on the symmetry of a molecular graph. Furthermore, they are being ordinarily employed for predicting physico–chemical properties and/or biological activities of molecules. It has been shown that these indices describe well molecular features that are depending on fine structural details. Therefore, revealing the impact of structural details on the values of the eigenvalue–based topological indices should give a hunch how physico–chemical properties depend on them as well. Here, an effect of a ring in a molecule on the values of the graph energy, Estrada index and the resolvent energy of a graph is examined.
MSC:
05C09; 05C92
1. Introduction
Molecular descriptors are quantities that may be regarded as numerical representations of a molecule. They are carriers of information about some parts or the whole structure of a molecule and, therefore, implicitly about its physico–chemical properties. Because of their success in predicting the behavior of molecules, investigations of molecular descriptors have been intensive over the years. Such an activity resulted in introducing thousands of molecular descriptors [1]. Among them, a salient place is reserved for topological indices [2,3]. Reasons for this will not be detailed here, but, in a nutshell, the topological indices represent a good balance between the amount of information they are harvesting from a molecular structure and the computational complexity of their algorithms. The main applications of topological indices represent construction of mathematical predictive models (QSPR/QSAR) and in virtual screening [4]. In addition, some of them have proved to be useful in molecular design and in drug discovery [5]. They can be roughly classified into three major groups: degree–based [6], distance–based [7], and eigenvalue–based topological indices [8].
The eigenvalue–based topological molecular descriptors emerged in the seventies of the last century when a linkage between one of them and the total -electron energy of conjugated molecules was established [9]. Nowadays, there are hundreds of these indices [10], but only a couple of them originate from the eigenvalues obtained from the adjacency matrix of a graph. These particular indices are mainly used in modeling the physico–chemical properties of molecules. In the rest of the text, we shall refer to them as the eigenvalue–based indices.
Probably the oldest eigenvalue–based topological index is the graph energy. Its roots can be traced to the Hückel molecular orbital theory, and in the majority of cases, it coincides with the total -electron energy. The graph energy is defined as follows [9]:
where is the ith eigenvalue obtained from the adjacency matrix.
Hundreds of papers are written about graph energy and several books. Such a vivid interest in this descriptor is not waning even today (e.g., see [10,11,12,13,14,15] and the references cited therein).
The second representative of this class of topological molecular descriptors that attracted much attention is the Estrada index. It was introduced at the beginning of the XXI century, aiming to model the folding of polypeptide chains. The Estrada index is defined as follows [16]:
The is the ith eigenvalue obtained from the adjacency matrix.
This index gained considerable popularity, resulting in numerous papers [15,17,18,19]. Such success of Estrada index may be attributed to the fact that this index found applications beyond chemistry. Namely, the authors of [20] have applied this graph invariant as a measure of subgraph centrality to study some real–world networks. In addition, the Estrada index was applied to quantify robustness of weighted networks [21].
The last member of the eigenvalue–based topological indices that will be treated here is the resolvent energy of a graph (). The resolvent energy,
was introduced recently [22]. Despite its juvenility, this index has attracted the attention of scientists thanks to its specific features and a noticeable predictive potential [13,17,23,24,25,26,27,28,29]. For example, it has been shown that discriminating power of resolvent energy outperforms such feature of graph energy and Estrada index [30]. This makes resolvent energy a proper candidate for isomers-distinguishing calculations. In addition, this topological descriptor exhibited good performance in modeling physico–chemical properties, such as boiling point, heat of formation, and logP of hydrocarbons [24].
Lately, several articles have appeared in which the comparative analysis of the above–mentioned topological indices has been exhibited [13,17,23,24,25]. A similar type of analysis is performed here, aiming to investigate the influence of a ring in a molecule on the values of the eigenvalue–based topological indices.
Molecules containing rings are of a great importance in chemistry and biology. The presence of a ring significantly influences many molecular properties. For instance, cyclic structures in saturated hydrocarbons are related with an additional instability, also known as ring strain. On the other hand, in the case of conjugated polycyclic molecules, the size of the rings determines whether cyclic electron delocalization will cause either stabilization (in aromatic compounds) or destabilization effects (in antiaromatic compounds). A method for assessing the effect of a ring on the value of the graph energy has been introduced already in 1977 [31]. In the present work, it will be shown how this methodology can be generalized so to be applicable to other eigenvalue–based topological descriptors.
2. Preparations
The method for measuring the effect of a ring on the value of the graph energy is long-time known [31,32,33,34]. It is based on the relation between the values of coefficients of the characteristic polynomial of a molecular graph and some of its structural details. This relation was established by H. Sachs (e.g., [35], pp. 35–38), showing that the bonds, rings, and their specific combinations determine the values of the coefficients of the . The effect of a cycle on the graph energy has been widely applied to study energetic aspects of cyclic electron delocalization in polycyclic conjugated molecules (see [33] and references cited therein).
In [31], the authors derived a polynomial similar to the , but in which the effects of a ring R were excluded. This polynomial has the following form
where and are the characteristic polynomials of a graph G and a ring R, respectively.
Then the energy effect of a ring R could be seen as
where and are the energies obtained by summing the absolute values of the roots of polynomials and , respectively [33,36,37].
Due to the complex conjugate root theorem () [38] the is always the real number, despite complex roots that may occur in the polynomial . Thence, the energy effect is also a real quantity.
This elegant approach for assessing the effect of a ring on the value of the graph energy can be applied also to some other eigenvalue–based descriptors. The only requirement is that the mathematical function used in the definition of the descriptor has the property . This provides that the value of the effect of a ring is in the realm of real numbers. Then, by generalizing the Equation (5) we get
where and are topological indices that are obtained from the roots of and , respectively.
The Estrada index and the resolvent energy of a graph are molecular topological descriptors for which the effect of a ring, using Equation (6), can be calculated.
The enables us (by using simple algebraic manipulations) to extend the domain of the Formula (2) onto complex numbers:
where and are the real and complex part of the complex eigenvalue (root) .
The effect of ring on the value of the Estrada index is being calculated by applying the Equation (7) in the Equation (6):
The effect of a ring on the value of the resolvent energy of a graph can be calculated in a more direct way. Using the result given in [22], [Theorem 8], we get
where n is total number of vertices in a molecular graph G.
3. Results and Discussion
Previous investigations of the energy effect of a ring detected an influence of the size of a ring, the size of a molecule, and the ring annelation on its value. Hence, three in-silico experiments were designed, aiming to investigate an impact of these features on the values of and . Obtained results were compared with those calculated for .
The first experiment is directed toward assessing the influence of the size of a ring on the ring-effects , , and . To examine this factor, but at the same time to eliminate the influence of the size of a molecule, the 20-sized ring has been used as a starting point. Then, the edge, always starting from the same vertex, but changing the end-vertex in each new iteration, is inserted (see Figure 1). That is how we get the rings whose size varies from 3 up to 20 vertices.
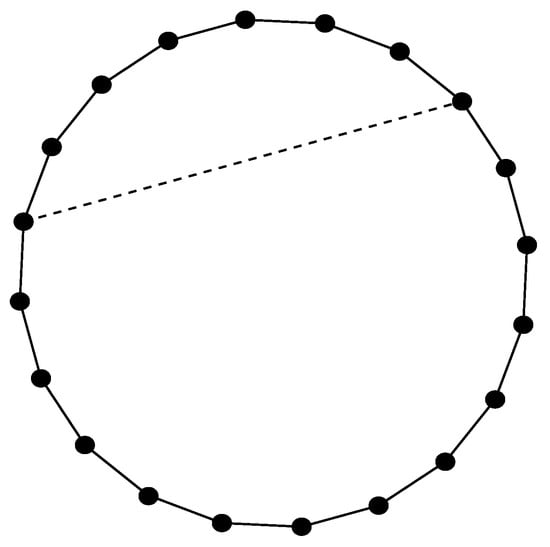
Figure 1.
Reducing the ring size by inserting dashed line as an edge.
The Python script (as a Jupyter notebook) was coded for the calculation of the ring-effects. The NumPy [39] module was used for easier handling of the polynomials, the NetworkX [40] for the manipulation of molecular graphs, and the mpmath [41] module for enhancing the precision of the calculation. The results are given in Table 1.

Table 1.
The values of the effects of a ring on the values of the resolvent energy, Estrada index, and the energy of a graph for rings of size varying from 3 up to 20 vertices.
Presented results clearly indicate a trend of the exponential decreasing of the values of and with an increase in the size of the ring. The pictorial representations are given in Figure 2 and Figure 3.

Figure 2.
Impact of the size of a ring on the values of the ring-effect of the resolvent energy of a graph.

Figure 3.
Impact of the size of a ring on the values of the ring-effect of the Estrada index.
From the data given in Table 1, it can be deduced that the ring-effects of the resolvent energy of a graph and the Estrada index are negligible for rings with a size greater than 6 vertices. Moreover, it is interesting that the ring-effect of the resolvent energy of a graph does not exist when the size of a ring is greater than or equal to 13 vertices. This finding was double-checked by increasing the precision of the calculations up to 50 decimals.
The effect of a ring on the value of the energy (a.k.a., energy effect) shows a rather different relationship to the size of a ring (see Figure 4).
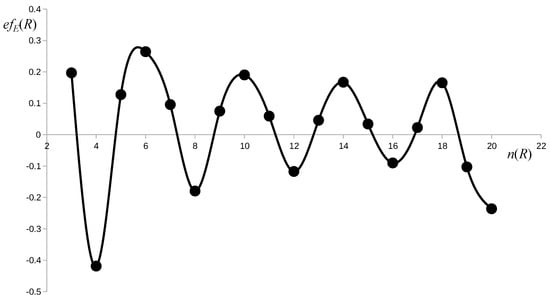
Figure 4.
Impact of the size of a ring on the values of the energy effect.
Its values are negative for all -rings and positive for all -rings. This follows the extended Hückel rule of ring influence on the stability of a molecule. At this point, it should be noted that there is a detailed mathematical analysis showing that the –values generally follow the extended () rule [33]. Such a physico-chemical meaning of varying the values of and cannot be noticed.
The second experiment is checking the influence of the size of a molecule on the values of , , and . In this experiment, the size of a ring was kept constant, while the molecule was being enlarged in each iteration. To check the influence of this factor, the homologous series of acenes starting with benzene and ending with dodecacene were used (see Figure 5). The values of , , and of a terminal benzene ring were being tracked and recorded.

Figure 5.
An acene.
The results are obtained by the Python script, coded in the form of the Jupyter notebook, and gathered in Table 2.

Table 2.
The effect of the terminal benzene-ring on the values of the resolvent energy, the Estrada index, and the energy of a graph in the class of acenes up to 50 carbon atoms.
The records show that the effect of a ring on the value of the Estrada index is almost insensitive to the size of a molecule. The Estrada ring effect rises with increasing the size of a molecule from 6 to 10 carbon atoms. Further enlarging of a molecule does not affect the value of the , as is evident from Table 2. The ring effects on the value of the energy and the resolvent energy, in contrast to the Estrada ring effect, are exponentially decreasing with the number of atoms in the acene. The value of the is decreasing in each iteration, while the is reaching the minimum for acene having 22 carbon atoms, and it slightly increases afterward. Figure 6, Figure 7 and Figure 8 illustrate the way of changing the , , and with the increasing size of a molecule.
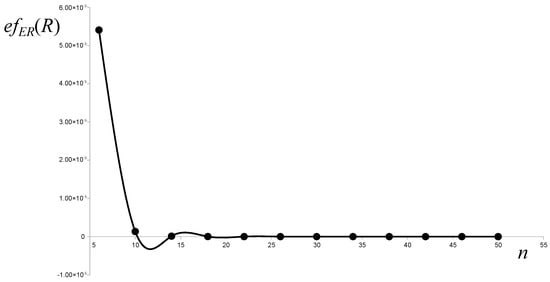
Figure 6.
Distribution of the resolvent energy ring-effects with the size of a molecule.
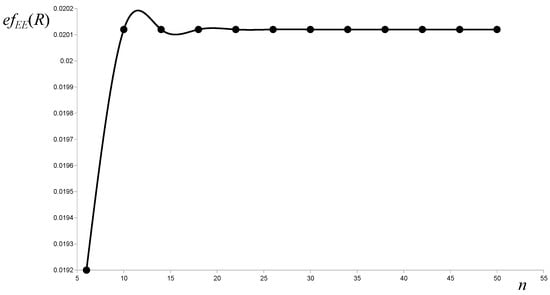
Figure 7.
Distribution of the Estrada ring-effects with the size of a molecule.
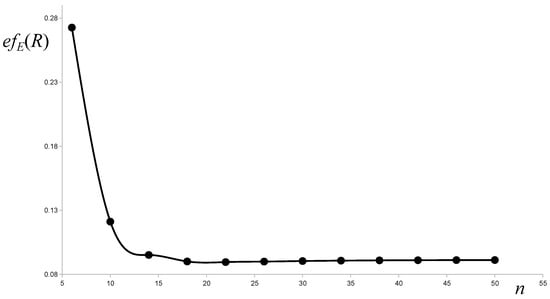
Figure 8.
Distribution of the energy ring-effects with the size of a molecule.
The third in-silico experiment is designed to evaluate the influence of the annelation of a ring on the values of , , and , but in the same time to keep the size of a ring and of a molecule constant. The energy effects of a benzene ring were calculated. There are 12 types of benzene annelations in a polycylic aromatic compounds, that are depicted in the Figure 9.
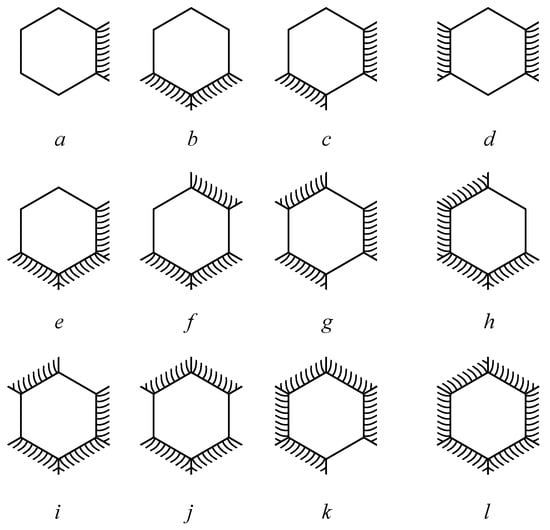
Figure 9.
Benzene annelations.
The idea was to use a benzenoid molecule that has all types of benzene annelations, shown in Figure 9, for assessing the influence of this factor on the values of , , and . In the Figure 10, the benzenoid hydrocarbon is depicted that is used for the evaluation of the influence of benzene annelation on the above-mentioned ring-effects. The rings on which the calculation was performed are denoted by letters that correspond to the notification given in Figure 9. Results are summarized in Table 3.
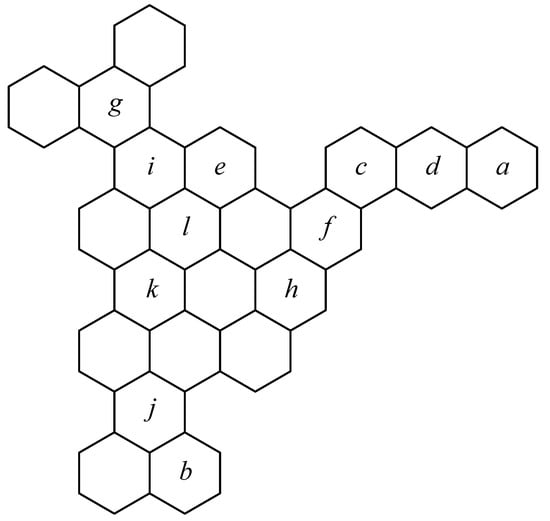
Figure 10.
Benzenoid hydrocarbon having benzene rings with all types of annelations.

Table 3.
Values of , , and for all types of benzene annelations. Values of the are multiplied by .
The results show that the effect of a ring on the values of the resolvent energy and the Estrada index does not experience any impact from the ring annelation. On the other hand, the energy effect significantly varies with the type of benzene annelation. These variations of may be explained by the Clar structures of the investigated benzenoid hydrocarbon. Namely, Clar aromatic sextet theory [42] describes distribution of -electrons in benzenoid hydrocarbons. Within this approach hexagons containing aromatic sextet are described as “full”, while other hexagons are marked as “empty”. In most cases, the agreement between Clar structures and the energy effect values are excellent. Roughly speaking, benzene annelations that contain more -electron sextets in the Clar structures should have the greater value of the energy effect and vice versa.
4. Conclusions
The comparative analysis of the effects of a ring on the values of the resolvent energy, Estrada index, and the energy of a graph is performed here. Three in-silico experiments that assess the impact of ring size, molecule size, and ring annelations were performed and the following conclusions have been derived:
- Enlarging the size of a ring decreases the values of the and . Rings with a size exceeding 12 non-hydrogen atoms do not have . The energy effect varies with the ring size in accordance with the extending Hückel rule.
- The size of acene does not affect the . Interestingly, the effect of a ring on the value of the Estrada index is rising from benzene to the first member in acene series (naphthalene). The values of are exponentially decreasing with the size of an acene. The is decreasing for acenes up to 22 carbon atoms, and the negligible rise in its value is detected afterward.
- The third experiment shows that the benzene annelation does not influence the values of and . The results indicate a considerable impact of the benzene annelation on the values of the energy effect.
The and , juxtaposed to the , are showing significantly different behavior. This implies that in comparison with the energy of a graph, the resolvent energy, and the Estrada index are gathering completely different structural details. Although the previous investigations detected similar behavior of the resolvent energy and the Estrada index [17,23,24,25,30], the effect of a ring detected differences that certainly contribute to the observed fine variations in the predictive potential of the Estrada index and the resolvent energy of a graph.
Author Contributions
Conceptualization, B.F.; data curation, I.R., S.R. and B.F.; investigation, I.R., S.R. and B.F.; software, I.R. and B.F.; writing—original draft, B.F.; writing—review and editing, S.R. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are supported by the Serbian Ministry of Education, Science and Technological Development (Grant No. 451-03-9/2021-14/200122).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; Wiley–VCH: Wheinheim, Germany, 2009. [Google Scholar]
- Dearden, J.C. The use of topological indices in QSAR and QSPR modeling. In Advances in QSAR Modeling–Applications in Pharmaceutical, Chemical, Food, Agricultural and Environmental Sciences; Roy, K., Ed.; Springer: Cham, Switzerland, 2017; pp. 57–88. [Google Scholar] [CrossRef]
- Gálvez, J.; Gálvez-Llompart, M.; García-Domenech, R. Basic concepts and applications of molecular topology to drug design. In Advances in Mathematical Chemistry and Applications; Basak, S.C., Restrepo, G., Villaveces, J.L., Eds.; Bentham Science Pub.: Sharjah, United Arab Emirates, 2014; Volume 1, Chapter 8; pp. 161–195. [Google Scholar]
- Roy, K.; Kar, S.; Das, R.N. A Primer on QSAR/QSPR Modeling: Fundamental Concepts; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Estrada, E.; Uriarte, E. Recent advances on the role of topological indices in drug discovery research. Curr. Med. Chem. 2001, 8, 1573–1588. [Google Scholar] [CrossRef]
- Ma, Y.; Cao, S.; Shi, Y.; Gutman, I.; Dehmer, M.; Furtula, B. From the connectivity index to various Randić–type descriptors. MATCH Commun. Math. Comput. Chem. 2018, 80, 85–106. [Google Scholar]
- Xu, K.; Liu, M.; Das, K.C.; Gutman, I.; Furtula, B. A survey on graphs extremal with respect to distance–based topological indices. MATCH Commun. Math. Comput. Chem. 2014, 71, 461–508. [Google Scholar]
- Gutman, I.; Ramane, H.S. Research on graph energies in 2019. MATCH Commun. Math. Comput. Chem. 2020, 84, 277–292. [Google Scholar]
- Gutman, I. The energy of graph. Ber. Math. Stat. Sekt. Forschungsz. Graz 1978, 103, 1–22. [Google Scholar]
- Gutman, I.; Furtula, B. Energies of Graphs: Survey, Census, Bibliography; Center Res. SANU & Univ. Kragujevac: Kragujevac, Serbia, 2019. [Google Scholar]
- Li, X.; Shi, Y.; Gutman, I. Graph Energy; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Gutman, I.; Li, X. Energies of Graphs: Theory and Applications; Univ. Kragujevac: Kragujevac, Serbia, 2016. [Google Scholar]
- Redžepović, I.; Furtula, B.; Gutman, I. Relating total π-electron energy of benzenoid hydrocarbons with HOMO and LOMO energies. MATCH Commun. Math. Comput. Chem. 2020, 84, 229–237. [Google Scholar]
- Oboudi, M.R. Bounds for energy of matrices and energy of graphs. MATCH Commun. Math. Comput. Chem. 2020, 84, 377–384. [Google Scholar]
- Hayat, S.; Khan, S. Quality testing of spectrum-based valency descriptors for polycyclic aromatic hydrocarbons with applications. J. Mol. Struct. 2021, 1228, 129789. [Google Scholar] [CrossRef]
- Estrada, E. Characterization of 3D molecular structure. Chem. Phys. Lett. 2000, 319, 713–718. [Google Scholar] [CrossRef]
- Redžepović, I.; Furtula, B. Resolvent energy and Estrada index of benzenoid hydrocarbons. J. Serb. Soc. Comput. Mech. 2020, 2020, 37–44. [Google Scholar] [CrossRef]
- Jahanbani, A.; Karimi, A.T.; Rodriguez, J. Results on the Estrada indices of benzenoid hydrocarbons. Polycyc. Arom. Comp. 2020, 1–18. [Google Scholar] [CrossRef]
- Gutman, I.; Deng, H.; Radenković, S. The Estrada index: An updated survey. In Selected Topics on Applications of Graph Spectra; Cvetković, D., Gutman, I., Eds.; Math. Inst. SASA: Belgrade, Serbia, 2011; pp. 155–174. [Google Scholar]
- Estrada, E.; Rodriguez-Velazquez, J.A. Subgraph centrality in complex networks. Phys. Rev. E 2005, 71, 056103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shang, Y. Perturbation results for the Estrada index in weighted networks. J. Phys. A Math. Theor. 2011, 44, 075003. [Google Scholar] [CrossRef]
- Gutman, I.; Furtula, B.; Zogić, E.; Glogić, E. Resolvent energy of graphs. MATCH Commun. Math. Comput. Chem. 2016, 75, 279–290. [Google Scholar]
- Redžepović, I.; Furtula, B. On relationships of eigenvalue–based topological molecular descriptors. Acta Chim. Slov. 2020, 67, 312–318. [Google Scholar] [CrossRef] [PubMed]
- Redžepović, I.; Furtula, B. Predictive potential of eigenvalue–based topological molecular descriptors. J. Comput. Aided Mol. Des. 2020, 34, 975–982. [Google Scholar] [CrossRef] [PubMed]
- Redžepović, I.; Furtula, B. Comparative study on structural sensitivity of eigenvalue–based molecular descriptors. J. Math. Chem. 2021, 59, 476–487. [Google Scholar] [CrossRef]
- Das, K.C. Conjectures on resolvent energy of graphs. MATCH Commun. Math. Comput. Chem. 2019, 81, 453–464. [Google Scholar]
- Ghebleh, M.; Kanso, A.; Stevanović, D. On trees with smallest resolvent energy. MATCH Commun. Math. Comput. Chem. 2017, 77, 635–654. [Google Scholar]
- Gök, G.K.; Ashrafi, A.R. Some bounds for the resolvent energy. Appl. Math. Comput. 2021, 397, 125958. [Google Scholar] [CrossRef]
- Zhu, Z. Some extremal properties of the resolvent energy, Estrada and resolvent Estrada indices of graphs. J. Math. Anal. Appl. 2017, 447, 957–970. [Google Scholar] [CrossRef]
- Redžepović, I.; Furtula, B. On degeneracy of A-eigenvalue–based molecular descriptors and r-equienergetic. MATCH Commun. Math. Comput. Chem. 2020, 84, 385–397. [Google Scholar]
- Bosanac, S.; Gutman, I. Effect of a ring on the stability of polycyclic conjugated molecules. Z. Naturforsch. 1977, 32a, 10–12. [Google Scholar] [CrossRef]
- Gutman, I.; Bosanac, S. Quantitative approach to Hückel rule the relations between the cycles of a molecular graph and the thermodynamic stability of a conjugated molecule. Tetrahedron 1977, 33, 1809–1812. [Google Scholar] [CrossRef]
- Gutman, I. Cyclic conjugation energy effects in polycyclic π-electron systems. Monats. Chem. 2005, 136, 1055–1069. [Google Scholar] [CrossRef]
- Gutman, I. Mathematical modeling of chemical phenomena. In Advances in Nonlinear Sciences II–Sciences and Applications; Stevanović Hedrih, K.R., Ed.; Academy of Nonlinear Sciences: Belgrade, Serbia, 2008; pp. 110–136. [Google Scholar]
- Gutman, I.; Polansky, O.E. Mathematical Concepts in Organic Chemistry; Springer: Berlin, Germany, 1986. [Google Scholar] [CrossRef]
- Gutman, I. Cyclic conjugation in dianions: Effect of cycles on the thermodynamic stability of polycyclic conjugated dianions. J. Mol. Struct. (Theochem) 1998, 428, 241–246. [Google Scholar] [CrossRef]
- Fatoorehchi, H.; Gutman, I.; Abolghasemi, H. A combined technique for computation of energy-effect of cycles in conjugated molecules. J. Math. Chem. 2015, 53, 1113–1125. [Google Scholar] [CrossRef]
- Friedman, B. Complex Roots of Polynomial Equations; HardPress Publishing: Houston, TX, USA, 2013. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 21 August 2008; Varoquaux, G., Vaught, T., Millman, J., Eds.; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2008; pp. 11–15. Available online: http://conference.scipy.org/proceedings/SciPy2008/paper_2/full_text.pdf (accessed on 16 June 2021).
- Mpmath: A Python Library for Arbitrary-Precision Floating-Point Arithmetic (Version 0.18). 2013. Available online: http://mpmath.org/ (accessed on 16 June 2021).
- Clar, E. The Aromatic Sextet; Wiley: London, UK, 1972. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).