A Multiple Comprehensive Analysis of scATAC-seq Based on Auto-Encoder and Matrix Decomposition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Feature Representation
2.3. Auto-Encoders
2.3.1. General Autoencoder
2.3.2. Sparse Autoencoder
2.3.3. Stacked Autoencoder
- Use the input data to train the autoencoder and obtain the learning data.
- Take the learning data of the previous hidden layer as the input of the next hidden layer until the end of training.
- After training all hidden layers, the backpropagation algorithm is used to minimize the cost function, and the training set is used to update the weights to achieve fine-tuning.
2.3.4. Variational Autoencoder
2.4. Matrix Factorization
2.4.1. Non-Negative Matrix Factorization (NMF)
2.4.2. Alternating Non-Negative Least Squares Matrix Factorization (Lsnmf)
2.5. Clustering
2.6. Performance Evaluation of Clustering
2.6.1. Adjusted Rand Index (ARI)
2.6.2. Normalized Mutual Information (NMI)
2.6.3. F1 Score
2.6.4. Silhouette_Score
3. Results
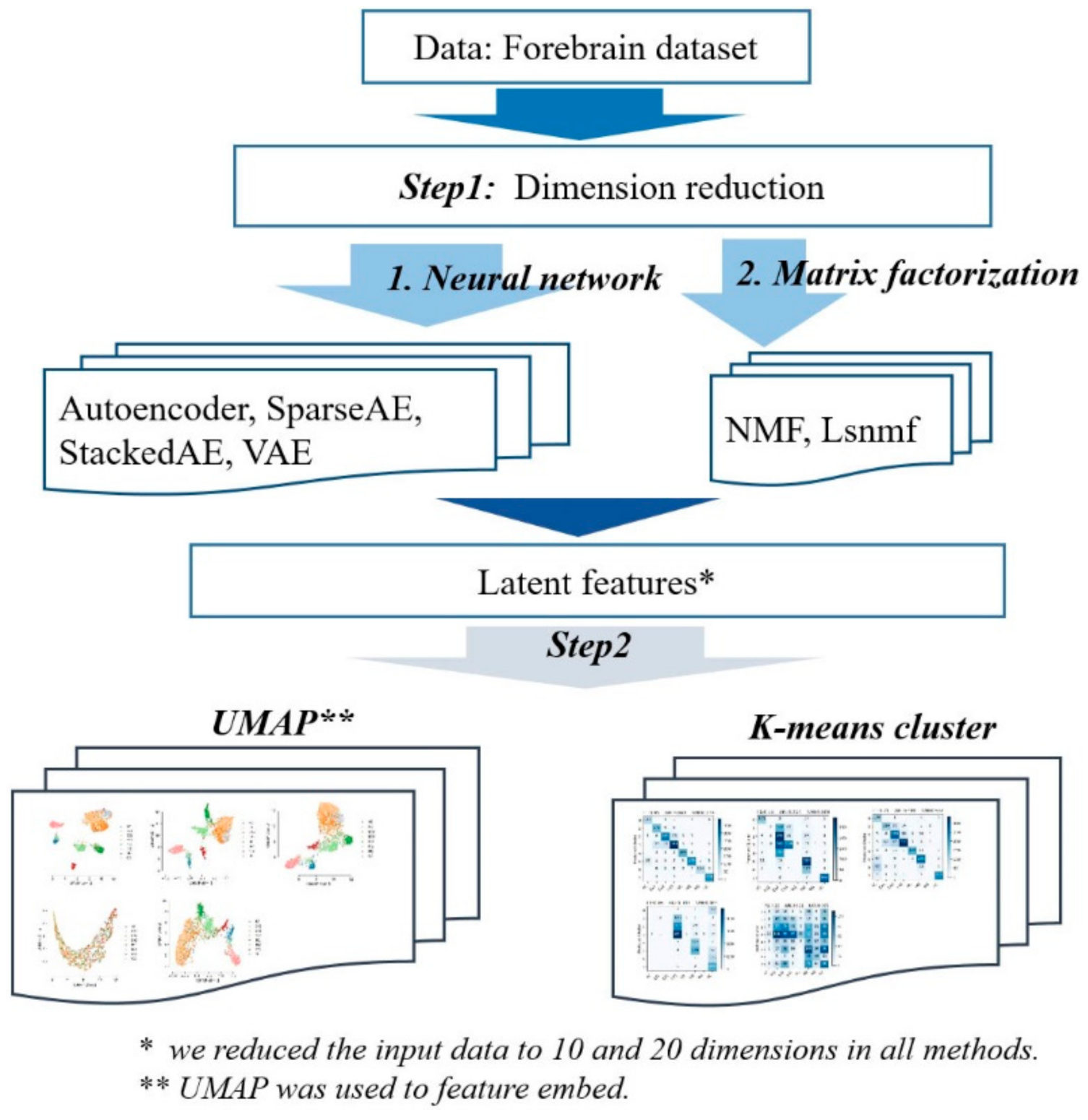
- The General autoencoder was used for dimensionality reduction of scATAC-seq and the K-means clustering was applied on the extracted latent features to obtain cluster assignments, and the cluster assignments were used to assess the clustering accuracy. Then, the extracted features were visualized with UMAP.
- The Sparse autoencoder (SparseAE), an autoencoder whose training criterion involves a sparsity penalty on the code layer, was used for dimensionality reduction of scATAC-seq. K-means clustering was applied on the extracted latent features to obtain cluster assignments. The cluster assignments were used to assess the clustering accuracy. In the end, the extracted features were visualized with UMAP.
- Stacked autoencoder (StackedAE) is a neural network which consists of several layers of autoencoders where the output of each hidden layer is connected to the input of the successive hidden layer. It was used for dimensionality reduction of scATAC-seq. K-means clustering was applied on the extracted latent features to obtain cluster assignments and the extracted features were visualized with UMAP.
- Variational autoencoders (VAEs) are generative models similar to generative adversarial networks. In this work, they were used for dimensionality reduction of scATAC-seq. K-means clustering was applied on the extracted latent features to obtain cluster assignments and the extracted features were visualized with UMAP.
- Non-negative Matrix Factorization (NMF), a traditional machine learning method, was also used for the dimensionality reduction of scATAC-seq. K-means and UMAP were used in the same way as above.
- Alternating Non-negative Least Squares Matrix Factorization (Lsnmf)—the calculation flow of Lsnmf is the same as that of NMF.
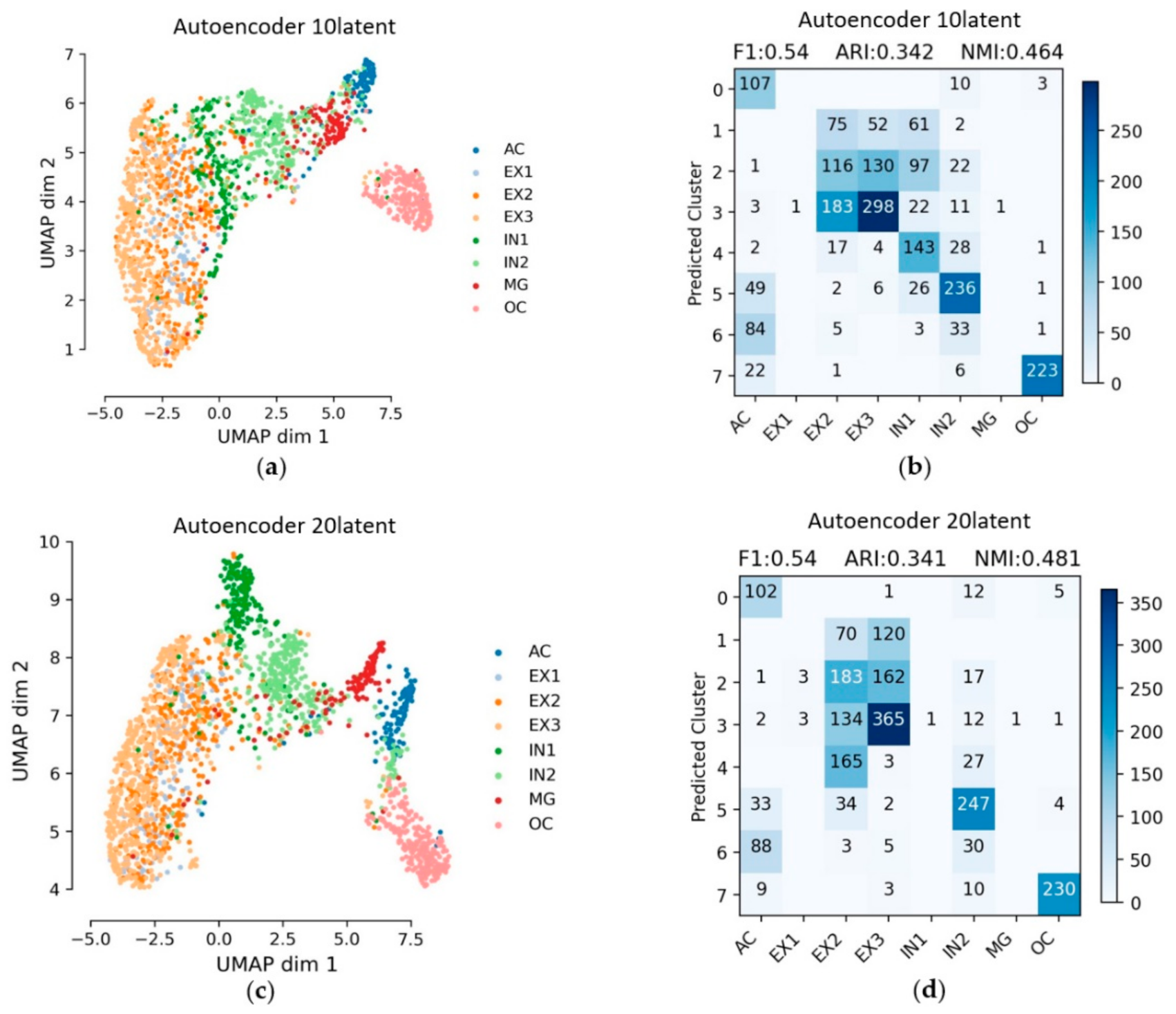
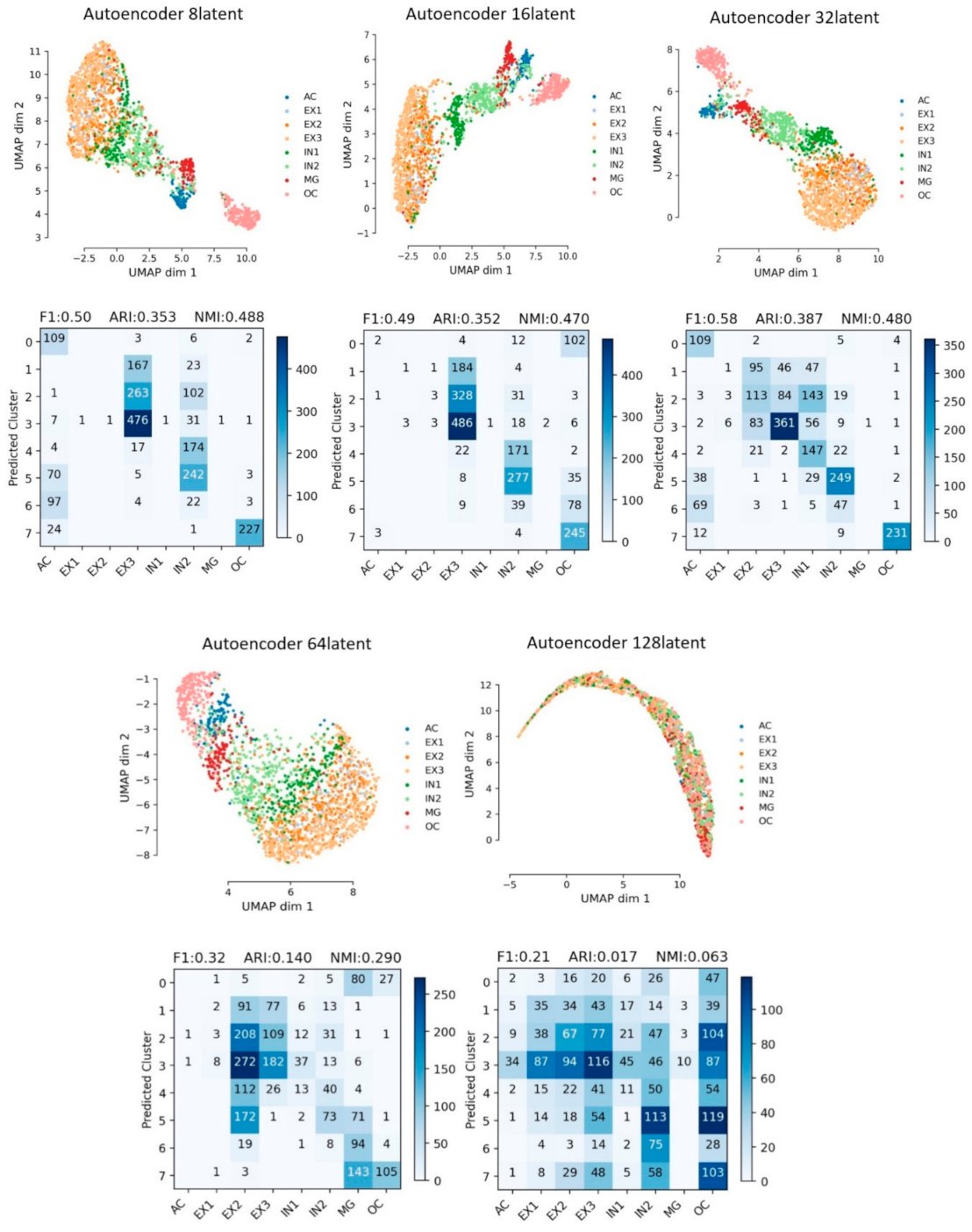
3.1. General Autoencoder
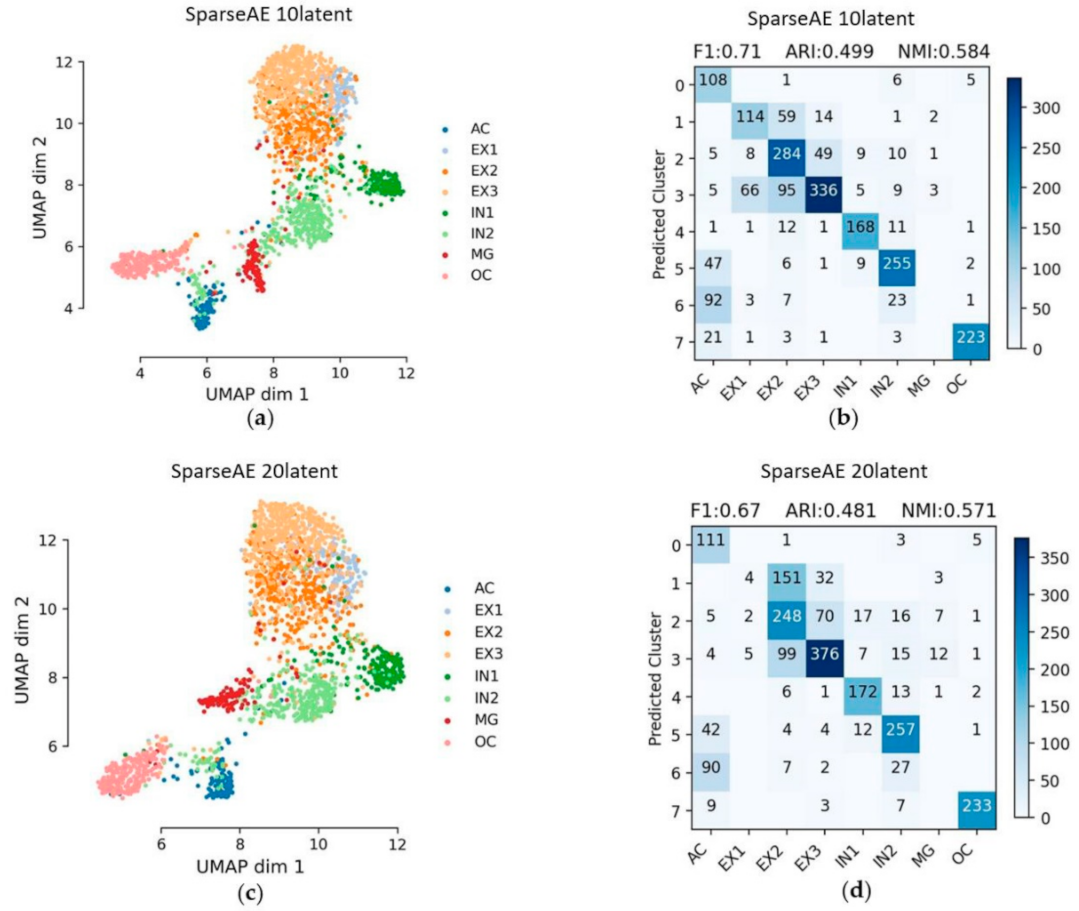
3.2. Sparse Autoencoder (SparseAE)
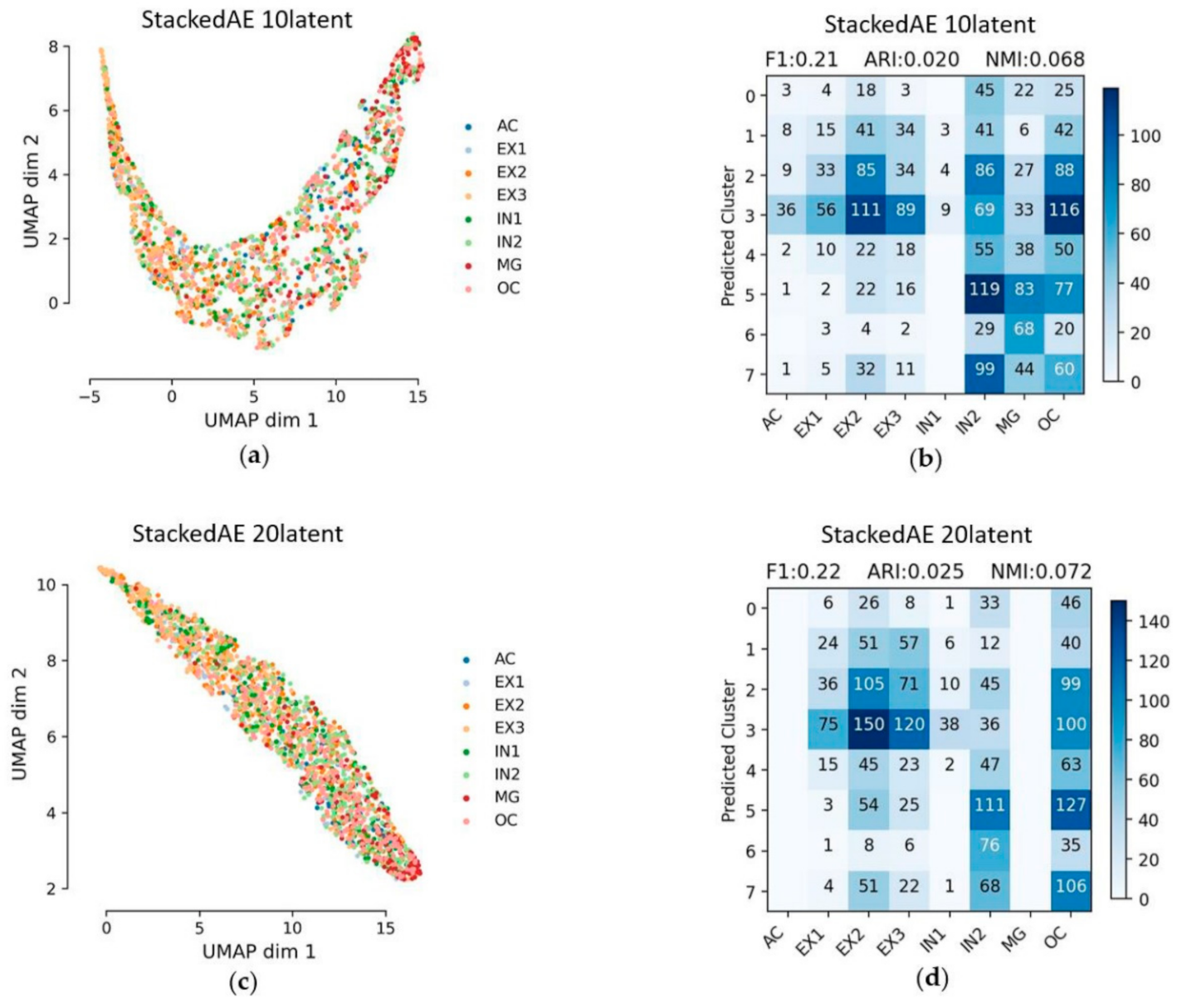
3.3. Stacked Autoencoder (StackedAE)
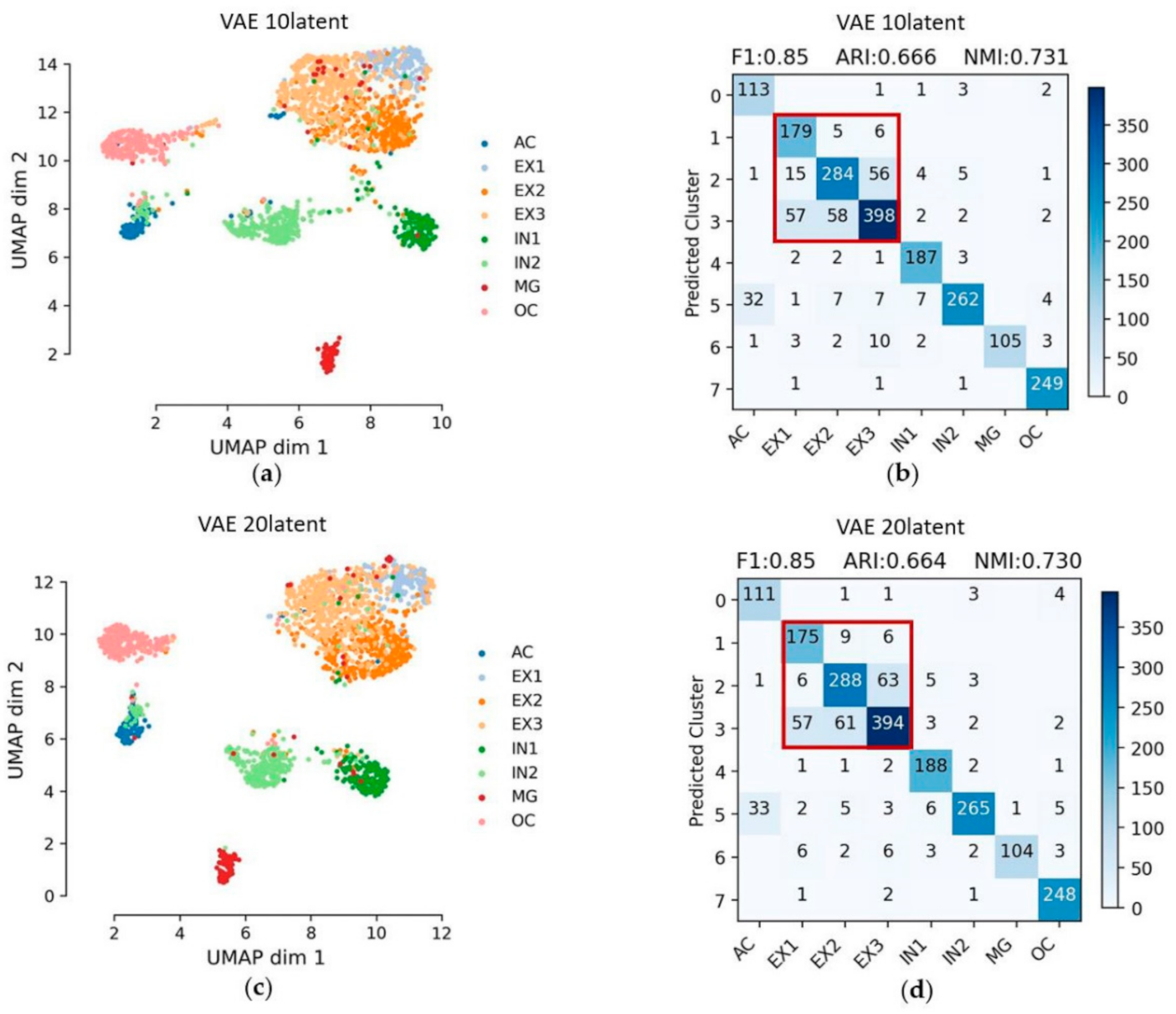
3.4. Variational Autoencoder (VAE)
3.5. Non-Negative Matrix Factorization (NMF)
3.6. Alternating Non-Negative Least Squares Matrix Factorization (Lsnmf)
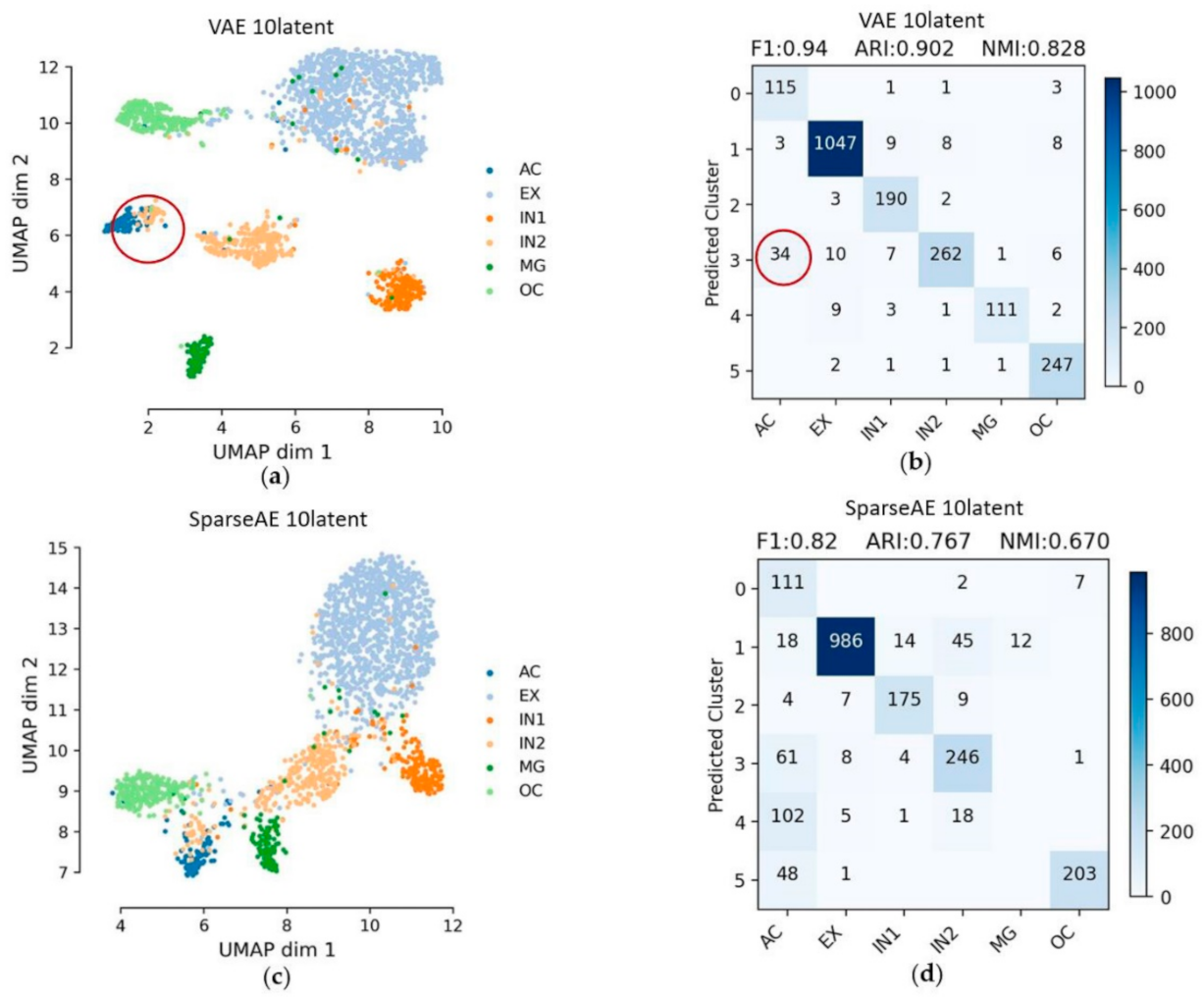
3.7. An Additional Test by Merging the Label of EX Cells
4. Discussion
4.1. The Globally Outperformed Methods
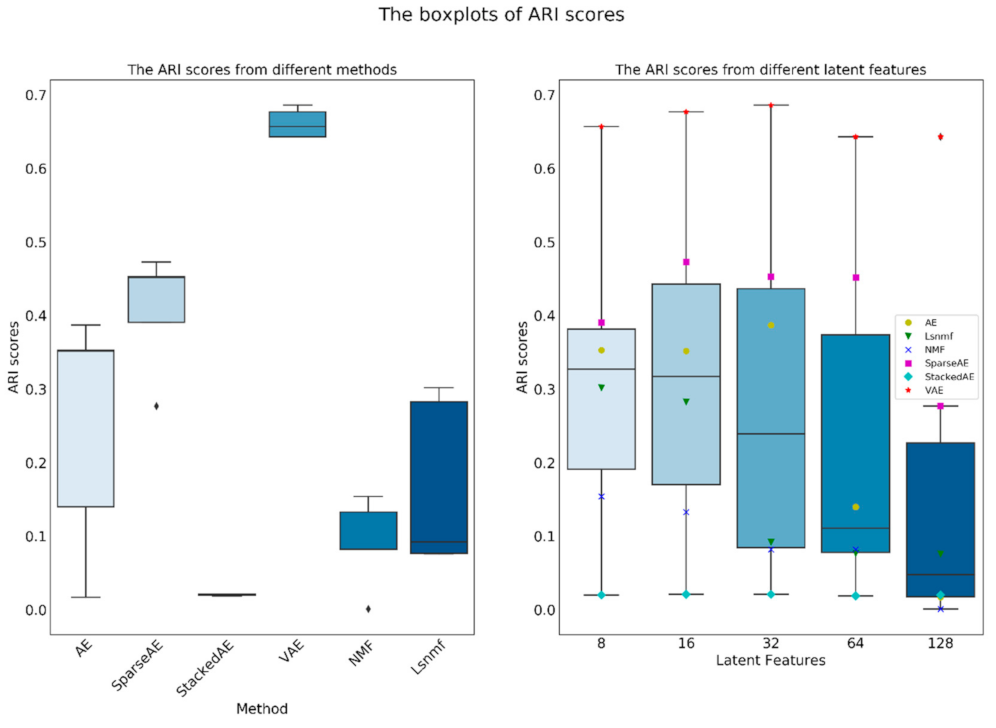
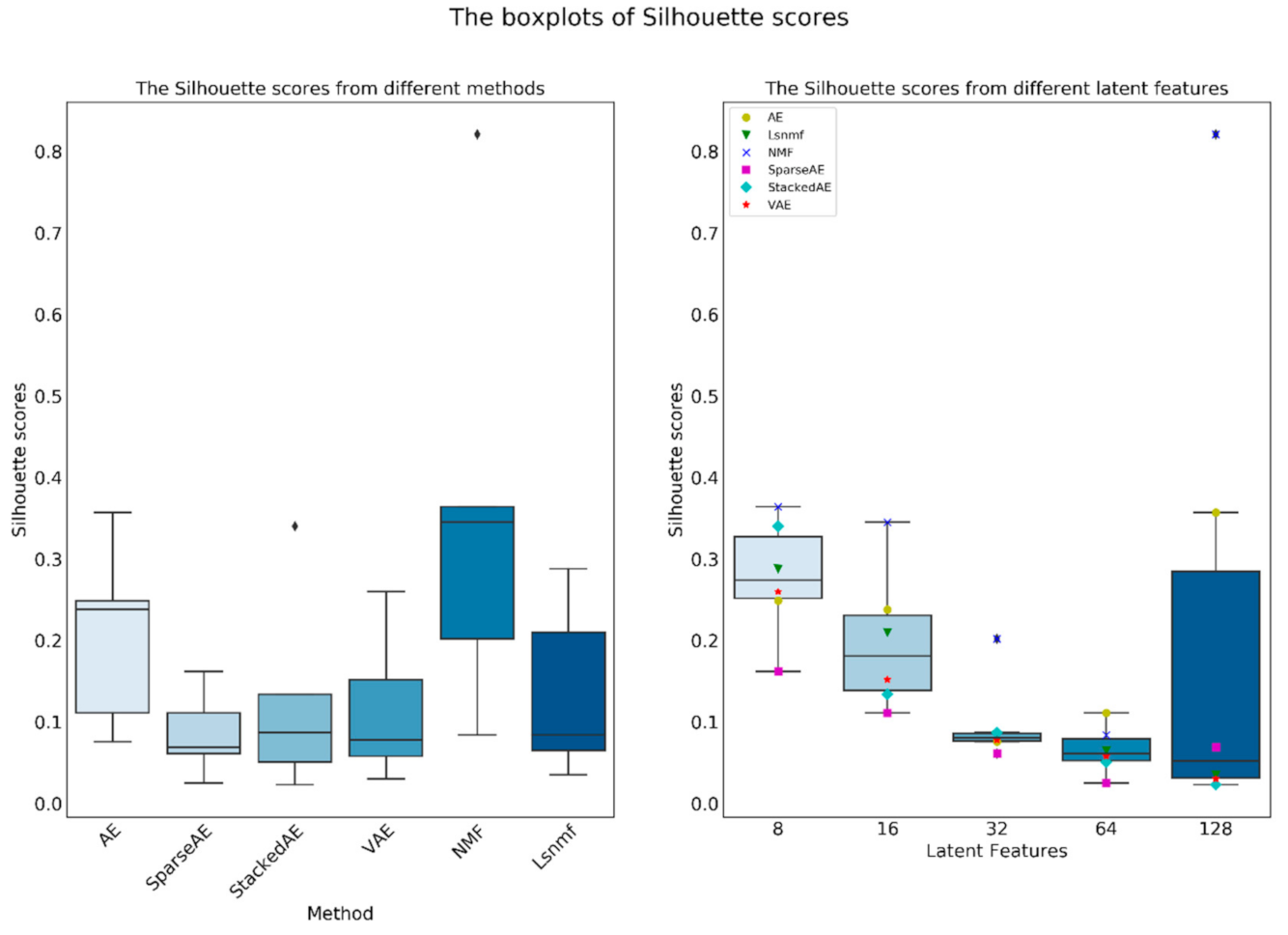
4.2. The Statistics from the Methods and the Size of Latten Variables
4.3. The Separation of EX Cells
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SparseAE | Sparse autoencoder |
| StackedAE | Stacked autoencoder |
| VAE | Variational autoencoder |
| NMF | Nonnegative Matrix Factorization |
| Lsnmf | Alternating Nonnegative Least Squares Matrix Factorization |
| ARI | Adjusted Rand Index |
| NMI | Normalized mutual information |
| UMAP | Uniform Manifold Approximation and Projection |
References
- Buenrostro, J.D.; Giresi, P.G.; Zaba, L.C.; Chang, H.Y.; Greenleaf, W.J. Transposition of native chromatin for fast and sensitive epigenomic profiling of open chromatin, DNA-binding proteins and nucleosome position. Nat. Methods 2013, 10, 1213–1218. [Google Scholar] [CrossRef]
- Buenrostro, J.D.; Wu, B.; Litzenburger, U.M.; Ruff, D.; Gonzales, M.L.; Snyder, M.P.; Chang, H.Y.; Greenleaf, W.J. Single-cell chromatin accessibility reveals principles of regulatory variation. Nature 2015, 523, 486–490. [Google Scholar] [CrossRef] [PubMed]
- Cusanovich, D.A.; Daza, R.; Adey, A.; Pliner, H.A.; Christiansen, L.; Gunderson, K.L.; Steemers, F.J.; Trapnell, C.; Shendure, J. Multiplex single-cell profiling of chromatin accessibility by combinatorial cellular indexing. Science 2015, 348, 910–914. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Granja, J.M.; Corces, M.R.; Pierce, S.E.; Bagdatli, S.T.; Choudhry, H.; Chang, H.Y.; Greenleaf, W.J. ArchR is a scalable software package for integrative single-cell chromatin accessibility analysis. Nat. Genet. 2021, 53, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Stuart, T.; Butler, A.; Hoffman, P.; Hafemeister, C.; Satija, R. Comprehensive Integration of Single-Cell Data. Cell 2019, 177, 1888–1902. [Google Scholar] [CrossRef]
- Wolf, F.A.; Angerer, P.; Theis, F.J. SCANPY: Large-scale single-cell gene expression data analysis. Genome Biol. 2018, 19, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trapnell, C.; Cacchiarelli, D.; Grimsby, J.; Pokharel, P.; Li, S.; Morse, M.; Lennon, N.J.; Livak, K.J.; Mikkelsen, T.S.; Rinn, J.L. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 2014, 32, 381–386. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Preissl, S.; Hou, X.; Lucero, J.; Ren, B. Fast and Accurate Clustering of Single Cell Epigenomes Reveals Cis-Regulatory Elements in Rare Cell Types. bioRxiv 2019. [Google Scholar] [CrossRef] [Green Version]
- Murtuza, B.S.; Connor, R.; Andrew, H.; Sharrocks, A.D.; Magnus, R. Classifying cells with Scasat, a single-cell ATAC-seq analysis tool. Nuclc Acids Res. 2019, 47, e10. [Google Scholar]
- González-Blas, C.B.; Minnoye, L.; Papasokrati, D.; Aibar, S.; Hulselmans, G.; Christiaens, V.; Davie, K.; Wouters, J.; Aerts, S. cisTopic: Cis-regulatory topic modeling on single-cell ATAC-seq data. Nat. Methods 2019, 16, 397–400. [Google Scholar] [CrossRef]
- Mahdi, Z.; Lin, Z.; Timothy, D.; Chen, X.; Zhana, D.; Alicia, S.; Greenleaf, W.J.; Hung, W.W. Unsupervised clustering and epigenetic classification of single cells. Nat. Commun. 2018, 9, 2410. [Google Scholar]
- Yu, W.; Uzun, Y.; Zhu, Q.; Chen, C.; Tan, K. ScATAC-pro: A comprehensive workbench for single-cell chromatin accessibility sequencing data. Genome Biol. 2020, 21, 94. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Lopez, R.; Regier, J.; Cole, M.B.; Jordan, M.I.; Yosef, N. Deep generative modeling for single-cell transcriptomics. Nat. Methods 2018, 15, 1053–1058. [Google Scholar] [CrossRef]
- Xiong, L.; Xu, K.; Tian, K.; Shao, Y.; Tang, L.; Gao, G.; Zhang, M.; Jiang, T.; Zhang, Q.C. SCALE method for single-cell ATAC-seq analysis via latent feature extraction. Nat. Commun. 2019, 10, 4576. [Google Scholar] [CrossRef]
- Grnbech, C.H.; Vording, M.F.; Timshel, P.; Snderby, C.K.; Winther, O. scVAE: Variational auto-encoders for single-cell gene expression data. Bioinformatics 2020, 36, 4415–4422. [Google Scholar] [CrossRef]
- Cao, Y.; Fu, L.; Wu, J.; Peng, Q.; Xie, X. SAILER: Scalable and Accurate Invariant Representation Learning for Single-Cell ATAC-Seq Processing and Integration. bioRxiv 2021. [Google Scholar] [CrossRef]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Makhzani, A.; Frey, B. k-Sparse Autoencoders. arXiv 2013, arXiv:1312.5663. [Google Scholar]
- Ng, A. Sparse autoencoder. CS294A Lect. Notes 2011, 72, 1–19. [Google Scholar]
- Bengio, Y.; Lecun, Y. Scaling Learning Algorithms Towards AI. In Large-Scale Kernel, Machines; Bottou, L., Chapelle, O., DeCoste, D., Weston, J., Eds.; MIT Press: Cambridge, UK, 2007. [Google Scholar]
- Shao, C.; Höfer, T. Robust classification of single-cell transcriptome data by nonnegative matrix factorization. Bioinformatics 2017, 33, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Preissl, S.; Fang, R.; Huang, H.; Zhao, Y.; Raviram, R.; Gorkin, D.U.; Zhang, Y.; Sos, B.C.; Afzal, V.; Dickel, D.E. Single-nucleus analysis of accessible chromatin in developing mouse forebrain reveals cell-type-specific transcriptional regulation. Nat. Neurosci. 2018, 21, 432–439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mcinnes, L.; Healy, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. J. Open Source Softw. 2018, 3, 861. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G.E. Visualizing High-Dimensional Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Chintala, S. PyTorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Hinton, G.E.; Krizhevsky, A.; Wang, S.D. Transforming Auto-Encoders; Springer: Berlin/Heidelberg, Germany, 2011; pp. 44–51. [Google Scholar]
- Liou, C.Y.; Cheng, W.C.; Liou, J.W.; Liou, D.R. Autoencoder for words. Neurocomputing 2014, 139, 84–96. [Google Scholar] [CrossRef]
- Liu, G.; Bao, H.; Han, B. A Stacked Autoencoder-Based Deep Neural Network for Achieving Gearbox Fault Diagnosis. Math. Probl. Eng. 2018, 2018, 5105709. [Google Scholar] [CrossRef] [Green Version]
- Doersch, C. Tutorial on Variational Autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Adv. Neural Inf. Process. Syst. 2014, 3, 2672–2680. [Google Scholar] [CrossRef]
- Dilokthanakul, N.; Mediano, P.; Garnelo, M.; Lee, M.; Salimbeni, H.; Arulkumaran, K.; Shanahan, M. Deep Unsupervised Clustering with Gaussian Mixture Variational Autoencoders. arXiv 2016, arXiv:1611.02648. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Dhillon, I.; Sra, S. Generalized Nonnegative Matrix Approximations with Bregman Divergences. In Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada, 2005; pp. 283–290. [Google Scholar]
- Ren, B.; Pueyo, L.; Chen, C.; Choquet, É.; Debes, J.H.; Duchêne, G.; Ménard, F.; Perrin, M.D. Using Data Imputation for Signal Separation in High Contrast Imaging. Astrophys. J. 2020, 892, 74. [Google Scholar] [CrossRef]
- Ben, M.; Thomas, W.; Jan, B.; Robert, K.; Sasha, M.; Gerdus, B.; Du, B.L.; Daniel, K.; Tristan, H.; Konrad, S. Non-Negative Matrix Factorization for Learning Alignment-Specific Models of Protein Evolution. PLoS ONE 2011, 6, e28898. [Google Scholar]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Hoyer, P.O. Nonnegative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar]
- Zitnik, M.; Zupan, B. NIMFA: A Python Library for Nonnegative Matrix Factorization. J. Mach. Learn. Res. 2012, 13, 849–853. [Google Scholar]
- Lin, C. Projected Gradient Methods for Nonnegative Matrix Factorization. Neural Comput. 2014, 19, 2756–2779. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Kossenkov, A.V.; Ochs, M.F. LS-NMF: A modified non-negative matrix factorization algorithm utilizing uncertainty estimates. BMC Bioinform. 2006, 7, 175. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]


| Auto-Encoders | Encoder Layer | Encoder 1 | Decoder Layer | Decoder 1 | Optimizer |
|---|---|---|---|---|---|
| General autoencoder | (1024-128) | ReLU | Nan 2 | Sigmoid | Adam |
| Sparse autoencoder | (30) | ReLU | Nan 2 | Sigmoid | Adam |
| Stacked autoencoder | (8192-2048-256) | ReLU | (256-2048-8192) | ReLU | SGD |
| Variational autoencoder | (1024-128) | ReLU | Nan 2 | Sigmoid | Adam |
| Methods | Latent Feature Number | F1 Score | ARI | NMI | Silhouette_Score |
|---|---|---|---|---|---|
| Autoencoder | 10 | 0.54 | 0.342 | 0.464 | 0.198 |
| 20 | 0.54 | 0.341 | 0.481 | 0.188 | |
| SparseAE | 10 | 0.71 | 0.499 | 0.584 | 0.065 |
| 20 | 0.67 | 0.481 | 0.571 | 0.056 | |
| StackedAE | 10 | 0.21 | 0.020 | 0.068 | 0.340 |
| 20 | 0.22 | 0.025 | 0.072 | 0.199 | |
| VAE | 10 | 0.85 | 0.666 | 0.731 | 0.223 |
| 20 | 0.85 | 0.664 | 0.730 | 0.236 | |
| NMF | 10 | 0.45 | 0.158 | 0.364 | 0.339 |
| 20 | 0.36 | 0.082 | 0.255 | 0.298 | |
| Lsnmf | 10 | 0.55 | 0.314 | 0.504 | 0.283 |
| 20 | 0.46 | 0.343 | 0.483 | 0.168 |
| Methods | F1 Score | ARI | NMI | Silhouette_Score |
|---|---|---|---|---|
| VAE | 0.94 | 0.902 | 0.828 | 0.259 |
| SparseAE | 0.82 | 0.767 | 0.670 | 0.065 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Li, Y.; Liu, Y.; Jing, R.; Li, M. A Multiple Comprehensive Analysis of scATAC-seq Based on Auto-Encoder and Matrix Decomposition. Symmetry 2021, 13, 1467. https://doi.org/10.3390/sym13081467
Huang Y, Li Y, Liu Y, Jing R, Li M. A Multiple Comprehensive Analysis of scATAC-seq Based on Auto-Encoder and Matrix Decomposition. Symmetry. 2021; 13(8):1467. https://doi.org/10.3390/sym13081467
Chicago/Turabian StyleHuang, Yuyao, Yizhou Li, Yuan Liu, Runyu Jing, and Menglong Li. 2021. "A Multiple Comprehensive Analysis of scATAC-seq Based on Auto-Encoder and Matrix Decomposition" Symmetry 13, no. 8: 1467. https://doi.org/10.3390/sym13081467
APA StyleHuang, Y., Li, Y., Liu, Y., Jing, R., & Li, M. (2021). A Multiple Comprehensive Analysis of scATAC-seq Based on Auto-Encoder and Matrix Decomposition. Symmetry, 13(8), 1467. https://doi.org/10.3390/sym13081467





