1. Introduction
In this paper, an interesting difference between Euclidean geometry and Lorentz geometry is studied. In particular, it appears that a very natural geometric symmetry in Euclidean geometry seems to be broken in the Lorentz case. The central object of study in this discussion is scalar curvature.
Minimizing curvature is a general mathematical problem with many facets, both in pure and applied mathematics. Metrics which minimize curvature can, in a sense, be said to be the simplest ones, and they are of special interest in very much the same way as configurations in classical mechanics, which minimize the energy, are interesting. To a large extent, this is because they are in a natural sense stable. In this paper, I will take the integral,
of the square of the scalar curvature as the most natural measure of the total curvature of a manifold. Other choices are of course possible, but will not be discussed here. For a physical motivation for using this measure, see [
1].
Of special interest is the question of what happens with the curvature when the geometry is rotating: what happens with a metric on when we add a time-direction and let it rotate around some axis? In particular, what happens to the curvature of the four-dimensional manifold that emerges? In this case, it is very natural (in analogy with mechanics) to say that the metric is stable with respect to rotation if the least curvature is obtained for the non-rotating metric (at least among all nearby metrics) and unstable if the non-rotating metric is not minimizing in this sense.
Formulated in this way, the problem is far too complicated to be solved in a single paper, so I will mainly restrict myself to the case of metrics, which are close to being invariant under rotation and close to the flat metric (and in fact coincides with it outside some sphere around the origin).
In the case when the metric is four-dimensional and Euclidean (i.e., positive definite), it seems very natural to conjecture that non-rotating metrics should be stable. After all, the rotation in itself does somehow bend the geometry, which should generate additional curvature. This also seems to be exactly what happens, although the general case will not be treated here (see, however,
Section 2). What is, however, remarkable is that this will not be the case if Euclidean geometry is replaced by Lorentz geometry. In the latter case, it turns out that non-rotating metrics can be unstable, and in fact this seems to be the most common situation (see
Section 3). In other words, rotating geometries tend to be less curved than non-rotating ones. Continuing the above analogy with classical mechanics, this would very much be like saying that the energy minimizing configuration of a system of particles in a problem in mechanics is not the one where all particles are at rest, but one where they are moving. This certainly is counter to our usual intuition, but I will not continue this discussion here. Rather, I will concentrate on the purely mathematical aspects of these questions.
Direct computations of curvature can be very lengthy, even for simple manifolds. In this paper, the symbolic computations have mainly been carried out by Mathematica using brute force, and the author is indebted to [
2] for this method of computing curvature (see the
accompanying Mathematica file in Supplementarty Materials). This is enough to obtain the theorems, but in view of the enormous complexity of the output, it is very hard to gain intuition for the underlying mechanism. The author recently learned about the methods in [
3] for calculating the scalar curvature of twisted products, which seem to have the potential to simplify the calculations considerably, and hence also to offer an explanation of the strange phenomena in this paper, although further research is still required.
2. Rotations in Euclidean Geometry
In traditional locally Euclidean geometry, where space and time are, so to speak, different concepts and can be separated in a natural way, a rotation of a perturbation of the flat metric can, at least to start with, be viewed as a rigid motion around a given axis. Thus, given a smooth metric,
on
at time
(where the
:s are functions of
), the natural metric
on
, corresponding to rotating
around, for example, the
z-axis with speed
b, will be
where
is the metric on
, given by pull-back of
under the rotation map
. To make the main point of this paper, it will be enough to consider perturbations of the standard metric
of the form
where
is a small number and
is a smooth function with compact support. In fact, for the purposes here we can, without loss of generality, assume that the support is contained in the unit ball,
. The corresponding rotating metric in (
3) then becomes simply
where
It is obvious that, for a rotationally invariant choice of
, the above metric
, and hence the curvature, will be independent of
b. The question to be investigated in this paper is what happens when such a metric is slightly perturbed so as to become non-invariant under rotation. Although more general classes of perturbations can of course be studied, the main features of concern here can already be seen for the simple choice,
where
is a linear transformation close to the identity. In fact, for the moment it will be enough to consider the particularly simple map
(where
is a small number), which turns the spherical level surfaces of
f into ellipsoids. The particular rotating metric as in (
3) for the corresponding function,
will be denoted
, that is,
where now
With this setup, we can finally start to do computations. In particular, we can study the curvature integral in (
1) as a function of the speed of rotation
b,
where the dependence of
I on everything except
b has temporarily been suppressed from the notation. To be more precise, what will actually be discussed is the integral of the square of the scalar curvature per unit of time. In fact, the integrand as defined above is independent of
t so we may as well just put
and replace the four-dimensional volume measure
by the three-dimensional volume measure
, which, in view of the simple form of the metric, works out to be
Thus, we can write
In
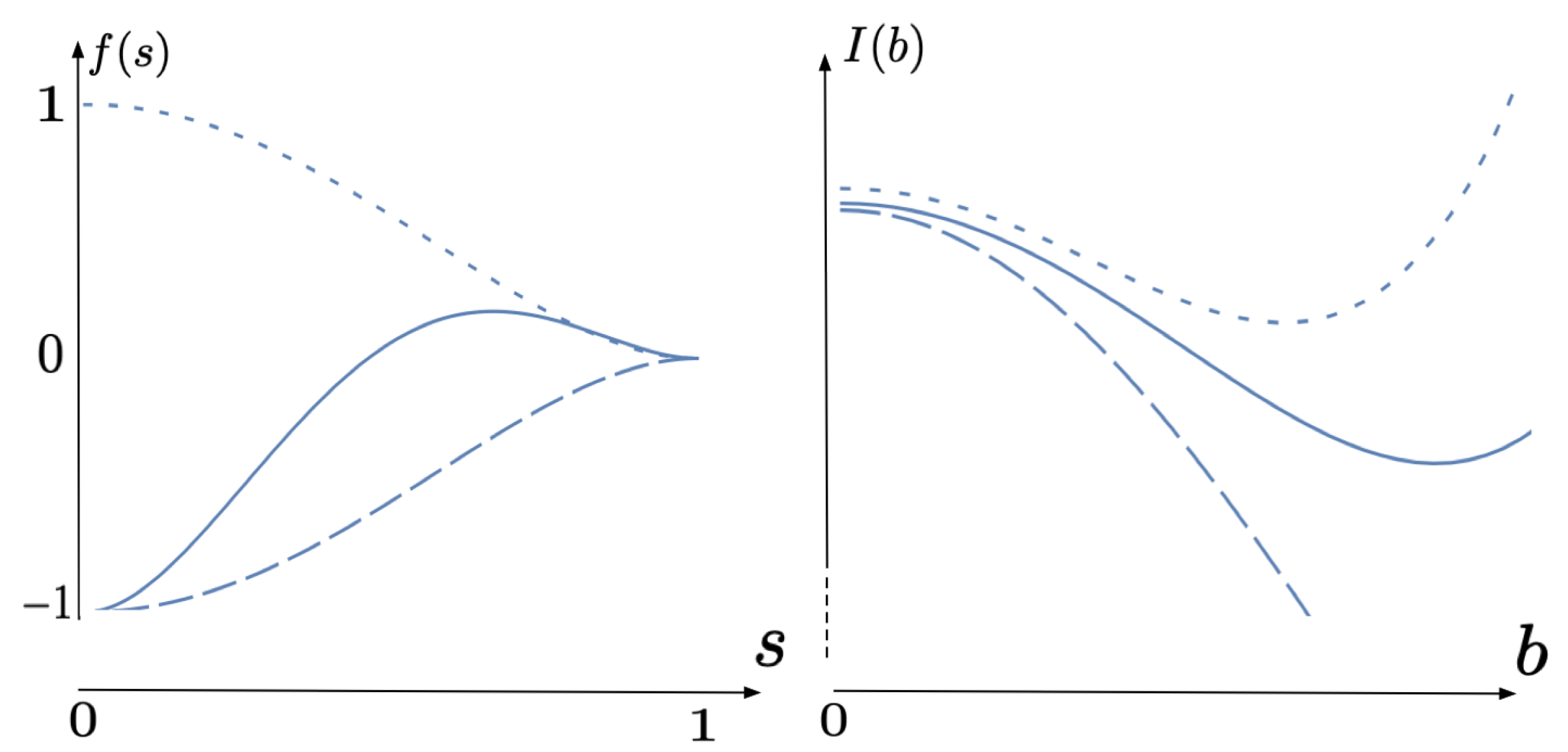
Figure 1, using Mathematica, I have displayed the graph of
for three explicit choices of the function
f. They all indicate that
is an increasing function of the speed, quite independently of whether the perturbation function
f is positive, negative or a mixture of these.
Remark 1. For completeness, the functions used in Figure 1 are on the interval and zero outside. These functions have been chosen because they seem to illustrate the general situation, but still give computations which are within reach. It should be noted that these functions have discontinuous second derivatives at , but this does not give any singular contributions to the curvature. The magnitudes of ϵ and δ are of the order , but the graphs have been scaled and translated so as to make them fit together into the same figure. Thus, only the forms of the corresponding graphs are correct in Figure 1, not their sizes and their relative positions. For the numerically correct graphs, see the accompanying Mathematica file in Supplementarty Materials. The behavior in
Figure 1 is hardly surprising and, as has already been pointed out, one might conjecture that the same should hold true under very general circumstances. However, it may not be so easy to prove this for large values of
b, and in this paper I will restrict myself to the case when
b is small. In fact, in this case we can use Taylor expansion of the function
. Since it is trivial to check that the first derivative of
with respect to
b is zero (because the complete symmetry between the two directions of rotation implies that
is an even function). Thus,
To prove that a metric is stable (with respect to this special kind of perturbation) in the sense of
Section 1, it is hence enough to prove that the second derivative of
is strictly positive. This is essentially the content of the following:
Theorem 1. For any sufficiently smooth function f and the metric as in (8) above, is a smooth function and the second derivative is given byIn particular, for any fixed (non-zero) ratio between δ and ϵ, and if their magnitudes are sufficiently small, the second derivative will be positive. The proof of this theorem will be given in
Section 4, together with the corresponding parallel result for Lorentz geometry, which is the main concern of this paper.
3. Rotations in Lorentz Geometry
The results of the previous section correspond very well to what our intuition would predict, although it may of course be questioned whether or not this has anything deep to say about the geometry when time and space are strictly separated. However, if we now instead turn to the case of an indefinite metric, where time and space are inseparable, the situation changes completely.
First of all, it must be said that rotation is a much more complicated concept in Lorentz geometry than in the Euclidean case. In fact, the idea of rigid motion here loses most of its meaning. For example, rotating a body will, in general, inevitably deform it. Still, rotation is a much studied topic in general relativity (see e.g., Kerr [
4]) and, at least when the curvature is small and the rotation is slow, the intuitive meaning is quite close to our usual idea of rotation in Euclidean space.
Since in this paper, mainly an infinitesimal (or very low) speed of rotation will be considered, it thus makes sense to start the investigation by replacing the metric in (
8) by
This may not be the only possible extension to four dimensions, but on the other hand it may also be argued that there is no completely natural such extension. I will come back to this point in
Section 5.
In analogy with the Euclidean case, we can now write
where again the dependence on everything except
b has been suppressed. If we start to compute
, then the first observation is that if
, the value of
will be exactly the same as in the Euclidean case. In fact, when the spacial part is independent of
t, it does not matter for the scalar curvature whether there is a plus or a minus sign in front of
. However, for
, this will no longer be true: when the coefficients of the metric depend on
t, their partial derivatives with respect to t will complicate the expression for R tremendously, and it becomes difficult to see what is happening.
However, the result of computing the function
on a computer for the metric
, with essentially the same three choices of the function
f and
as in
Figure 1, is shown in
Figure 2.
Clearly, these graphs seem to indicate that, in the case of Lorentz geometry, the corresponding metrics are in fact unstable in the sense of
Section 1.
This is certainly no coincidence. In fact, we can now prove the following theorem, which is analogous to Theorem 1:
Theorem 2. For any sufficiently smooth function f and the metric as in (15) above, is a smooth function and the second derivative is given by In particular, for any fixed (non-zero) ratio between δ and ϵ, and if their magnitudes are sufficiently small, the second derivative will be negative.
4. Proofs of the Main Theorems
The proofs of Theorems 1 and 2 are based on enormous symbolic calculations, which have in fact been carried out on a computer using Mathematica (see the
accompanying Mathematica file in Supplementarty Materials). As it turns out, the two proofs are more or less identical except for a sign, so rather than presenting two proofs I will just give one, but instead point out where this sign appears. The first step is to observe that the resulting curvature integrals are functions of class
, of the three variables
, for any even function
with compact support in the interval
. This is most easily seen after rewriting the integrals by noting that the support of the function
lies within the ellipsoid
, hence the scalar curvature integrals can, after a trivial change of variables by
, be written as integrals over the ordinary unit ball
B:
where we have also made use of the three-dimensional volume element as in (
11). It has already been observed that the first derivative of this function with respect to
b is zero. With this in mind, we can write the Taylor expansion in
b as
where
To compute
as in the theorems, we make a Taylor expansion of the integrand up to order four around the origin in the
-plane. Although the resulting expression is complicated (see the
accompanying Mathematica file in Supplementarty Materials), only a few terms will be different from 0, namely the
,
and
terms. This is because of the various symmetries involved, and in particular because
, which is obviously true since in these cases the metric will not be asymmetric with respect to rotation. We obtain by Taylor’s theorem:
Integrating this expression (with Mathematica) over the sphere
now gives (noting on the way that the integrals of the terms which are first order with respect to
vanish)
in the Euclidean case, and
in the Lorentz case. In order to ease presentation and also to emphasize the similarities, the two cases will simultaneously be written as:
where the minus sign refers to the Euclidean case and the plus sign to the Lorentz case. Putting
turns this integral into
which, after a trivial integration by parts where the boundary term drops out in view of the conditions on
f, becomes
Noting the switch of signs in the last step, we have now arrived at the conclusions of Theorems 1 and 2.
5. How Common Is Lack of Stability in Lorentz Geometry?
In the Euclidean case, it seems natural to conjecture that, in fact, all sufficiently regular metrics on , which agree with the standard metric outside some compact set, are rotationally stable.
However, in the case of Lorentz geometry, things are more complicated. This is partly due to the fact that in this case it is no longer natural to treat space and time as completely different concepts. In particular, one can ask what happens when the metric is also modified in the time direction.
Formulated in this way, the problem seems to be a very complex one. Here, I will only consider an example, which indicates that if the geometry considered is sufficiently general, then both stable and unstable metrics can occur.
Theorem 3. For any sufficiently smooth function f, sufficiently small and the metric as in (27) above, the second derivative at the origin is given by As with the previous theorems, we conclude that the above metric is unstable for . The theorem also strongly suggests that the metric should be stable for , but a complete proof of this may require more sophisticated methods.