1. Introduction
Statistical models for dealing with the issue of random variables with limited or censored responses have been approached by different authors, standing out among others, the censored normal (CN) model, widely known in the literature as the Tobit model, Tobin [
1]. The CN or normal Tobit (NT) model is defined from the considering the random variable
, with
, for
, where
is a
unknown parameter vector,
is a
vector of known independent variables, and the error term
. This can be written as:
The model (
1) has been used in applications in various areas of knowledge, often in situations with excess of zeros in the censoring value; however, the probability of censoring is not well estimated by the Tobit model since the tails of the data distribution are heavier than the normal distribution and other assumptions of the error distribution are not satisfied. A similar situation is presented in the case of data with non-negative support, where usually log-normal Tobit model (LNT) is used.
In some situations, the degrees of asymmetry and kurtosis of the distribution of the errors in the model can not be captured by the normal or the log-normal models. In this case it is not advisable to fit the CN or censored log-normal (CLN) models. To consider more flexible models, such as the skew-normal (SN) model by Azzalini [
2] or the power-normal (PN) model of Durrans [
3] is another solution. In the case of non-negative data, it can be considered the log-skew-normal alpha-power model by Martínez-Flórez et al. [
4] or the log-power-normal model of Martínez-Flórez et al. [
5].
The Tobit model extension for censored data with high degree of kurtosis was proposed by Arellano-Valle et al. [
6], while the case of censored data with high or low degree of asymmetry was studied by Martínez-Flórez et al. [
7], the latter is known as the Tobit power-normal model (TPN). When the censored part does not fit well with the Tobit model, mixture of distributions can be used, in this situation as in the usual censored distribution, the mean and the variance of the response variable is associated with the linear predictor. In addition, the proportion of censored data can be explained by using the binomial model with the logit or probit link function. This type of model has been used in many areas of knowledge such as economics, biology, agriculture, medicine, among others. Cragg [
8], Moulton and Halsey [
9], Moulton and Halsey [
10] and Chai and Bailey [
11], for example, use a mixture of distribution (which is denoted by “/”) between a Bernoulli distribution and other continuous distribution.
The probability density function (PDF) of the random variable
proposed by Cragg [
8], which is often called “two-part model”, is given by
where
is the probability that determines the relative contribution made by the point mass distribution to the overall mixture distribution,
f is a density function with positive support and
is an indicator variable given by
if
and
if
. The model (
2) is more informative than the Tobit model because the two components are determined by different stochastic processes, see Chai and Bailey [
11].
The two-part model of Cragg [
8] was generalized by Moulton and Halsey [
9], by introducing a new model in which the response limit can result from a censorship interval of the PDF
f, that is, a zero point can result in mass or may be a value of
f in the censorship interval
, where
T is constant. Specifically, the model proposed by [
9] is represented by the PDF given by
where
is the cumulative distribution function (CDF) associated to the PDF
. In particular, a Bernoulli variable can be used with the logit or probit link functions, see Cragg [
8]. Moulton and Halsey [
9] consider asymmetric log-normal and log-gamma data, while the log-skew-normal model (LSN) and log-power-normal model (LPN) with limited response are studied by Chai and Bailey [
11] and Martínez-Flórez et al. [
5], respectively.
2. Models for Asymmetric Data
Important proposals to modelling data with high/low degree of asymmetry and/or kurtosis in relation to the normal model have arisen in recent decades. Two of these proposals widely discussed in the statistical literature are the SN model of Azzalini [
2] and PN model by Durrans [
3]. The SN model, with asymmetry parameter
, which is denoted by
has PDF given by
where
and,
and
represent the PDF and CDF of the standard normal distribution, respectively. The
parameter controls the asymmetry in the model. The associated CDF to the PDF in (
4) is given by
where
is the Owen’s function, see [
12]. The PN model is denoted by
and has the PDF given by
where
is a shape parameter. The model (
6) was introduced by Durrans [
3] and it has had multiple applications in the situations where the data distribution presents high or low asymmetry and/or kurtosis, which can not be fitted by the normal distribution.
The extension to the location and scale version of the SN model is obtained by applying the transformation , where is a location parameter, is a scale parameter, and This is denoted by In a similar way, the extension of the location and scale version of the PN model is obtained, which is denoted by
A special feature of the SN and PN models is that both containing the normal model as special case when
and
, respectively, highlighting that the SN model has a range of asymmetry higher than the PN model, and at the same time, the PN model has a higher range of kurtosis than the SN model, see Pewsey et al. [
13]. Therefore, it is natural to expect that respective extensions for positive data have similar characteristics. Martínez-Flórez et al. [
5] studied the extension of the PN model to the case of positive data and they denoted it the log-power-normal (LPN) model, while the extension of the SN distribution for positive data was studied by Azzalini et al. [
14], which is denominated the log-skew-normal (LSN) model.
The main difficult with the SN model, which does not present the PN model is that, for
the Fisher information matrix for the parameters vector
is singular, see Azzalini [
2]. Hence, the regularity conditions are not satisfied in general and the usual
-property for the maximum likelihood estimator is kept only for
. The information matrix problem for the case
has been addressed by using the methodology proposed by Rotnitzky et al. [
15], who devised an iterative algorithm that under certain conditions leads to a non-singular information matrix for
.
The singularity of the Fisher information matrix has been found in multiple extensions of SN model, such as the LSN model, the skew-exponential power distribution, DiCiccio and Monti [
16] and the skew-flexible-normal model, Gómez et al. [
17], to name some of these cases. The log-skew-normal alpha-power (LSNAP) distribution is an extension of LPN model, which is obtained by replacing in the LPN model, the PDF and the CDF of the normal distribution for the PDF and the CDF of the SN distribution. This proposal is based on the non-singularity property of the information matrix of the PN model, Pewsey et al. [
13], and the flexibility in terms of asymmetry in the SN model, Azzalini [
2]. So, it is natural that a new model based on these two distributions can fit the distributions with higher or lower asymmetry than the fitted by the LSN model and/or higher or lower kurtosis than the fitted by the LPN model.
The PDF of the location and scale version of a random variable with LSNAP distribution is given by
where
, with
being the location parameter and,
the scale parameter. The functions
and
are the PDF and CDF of the SN distribution given in (
4) and (
5), respectively. The LSPN distribution is represented by the notation
. One can see that, the model in (
7) contains as special cases, the log-normal (LN) model when
and
; the LSN model when
, and the LPN model when
. Thus, the LSPN model is more flexible in terms of asymmetry and kurtosis than the LN, LSN and LPN models.
The Centred Parametrization of the Skew-Normal Model
Facing the problem of the singularity of the information matrix of the SN model and the consequences in the estimation process of the parameters when
, Arellano-Valle and Azzalini [
18] proposed an alternative parametrization to the SN model of Azzalini [
2]. This new parametrization starts from the definition of the variable
where
and
are parameters of the random variable
Y, and
. This representation is called centred parametrization, since
and
. The centred parametrization of the SN model is denoted by
, where the parameters
,
and
, represent the mean, standard deviation and coefficient of asymmetry of
Y, respectively. One can see that, if
, then
and
, where
and
.
Thus, we have that the random variable
Y is allowed to be written in the form
, which follows a SN distribution of location and scale version denoted by
, where
with
.
Under the centred parametrization of the SN model, the Fisher information matrix can be written as , where is a matrix representing the derivative of the parameters , and of the standard representation, regarding to the new parameters , and . In addition, when , the information matrix converges to the diagonal matrix , which guarantees the existence and uniqueness of the maximum likelihood estimator (MLE) of the parameters and , for each fixed value of .
Given the properties of the LSN and LPN models, the Bernoulli/log-skew-normal (BLSN) and the Bernoulli/log-power-normal (BLPN) mixture models are alternatives to the Bernoulli/log-normal (BLN) model for the case of positive data when the distribution of the continuous part presents greater or lower asymmetry and/or kurtosis than the LN model. Thus, the BLSN and BLPN mixture models are more flexible than the BLN mixture model. Details of the inferential properties of the MLE for the BSLN mixture model when
are not presented by Chai and Bailey [
11], since it is expected that the same difficulties are arisen in relation to the continuous part that is fitted through the LSN model.
In this paper, we introduced a new model to fit asymmetric data, more flexible than LN, LSN and LPN models, and with non-singular Fisher information matrix. This model is obtained by replacing in the LPN model, the normal distribution by the
distribution. From the introduced model, a new regression model for censored data is proposed, which is a mixture of the proposed asymmetric model and a random variable with logit link function. The new model is more flexible in terms of asymmetry and kurtosis than the proposed by Moulton and Halsey [
9], Chai and Bailey [
11] and Martínez-Flórez et al. [
5]. Data from a safety and immunogenicity study of measles vaccine conducted in Haiti during 1987–1990, see Job et al. [
19] are used as an illustration. Here, the goal of the study was to demonstrate that the higher titer vaccines could effectively immunize infants as young as 12 months of age.
The rest of the paper is organized as follows. In
Section 3, the centred exponentiated log-skew-normal distribution for censored data is presented. A small simulation study to evaluate the asymptotic properties of the parameter estimators is presented. In
Section 4, the Bernoulli/centred log-skew-normal alpha-power mixture model is introduced. The inference process is carried out by using the maximum likelihood method. In
Section 5, an application with measles vaccine data is presented to illustrate the proposed model.
3. The Centred Exponentiated Log-Skew-Normal Family of Distribution for Censored Data
Based on the flexibility and the non-singularity of the Fisher information matrix of the
model, the LPN model is extended to the case of the
model. This extension is denominated the centred exponentiated log-skew-normal (
) distribution. The PDF of the
distribution, with parameters
,
,
and
is given by
where
and
and
defined as in (
8). This model is denoted by
. It is important to note that
with
and
defined in (
8), that is, the
model can be assumed as a reparametrization of LSNAP model, which corrects the problem of singularity in the Fisher information matrix. In addition, if
, the
model is obtained and, when
, the centred log-skew-normal model follows, which is denoted by
. Some forms of the PDF of the ELSN
distribution are presented in the
Figure 1. One can shown that, LSN
model has non-singular information matrix. Finally, if
and
, the log-normal model is obtained,
. This shows that the
model is more flexible in terms the asymmetry and kurtosis than LN, LSN and LPN models.
The importance of the proposed extension is that the information matrix of the model is non-singular, since for the parameter vector
, the information matrix is given by
, where
is the information matrix of the model (
7) given in Martínez-Flórez et al. [
5] with
, and
therefore, when
and
it follows from Azzalini [
2] and Pewsey et al. [
13] that the information matrix of the
model converges to
where
represents the vector of mixed second derivatives of
and the rests of the parameters
. This turns out to be non-singular matrix, since its columns (or rows) are linearly independent. Hence, the regularity conditions are satisfied in general and the usual
-property for the MLE
of
is satisfied for all
and
. This result guarantees the asymptotic distribution of the MLE for large samples, allowing to make inferences for the parameters of the
model, which is an advantage against to the LSN model whose information matrix is singular for
.
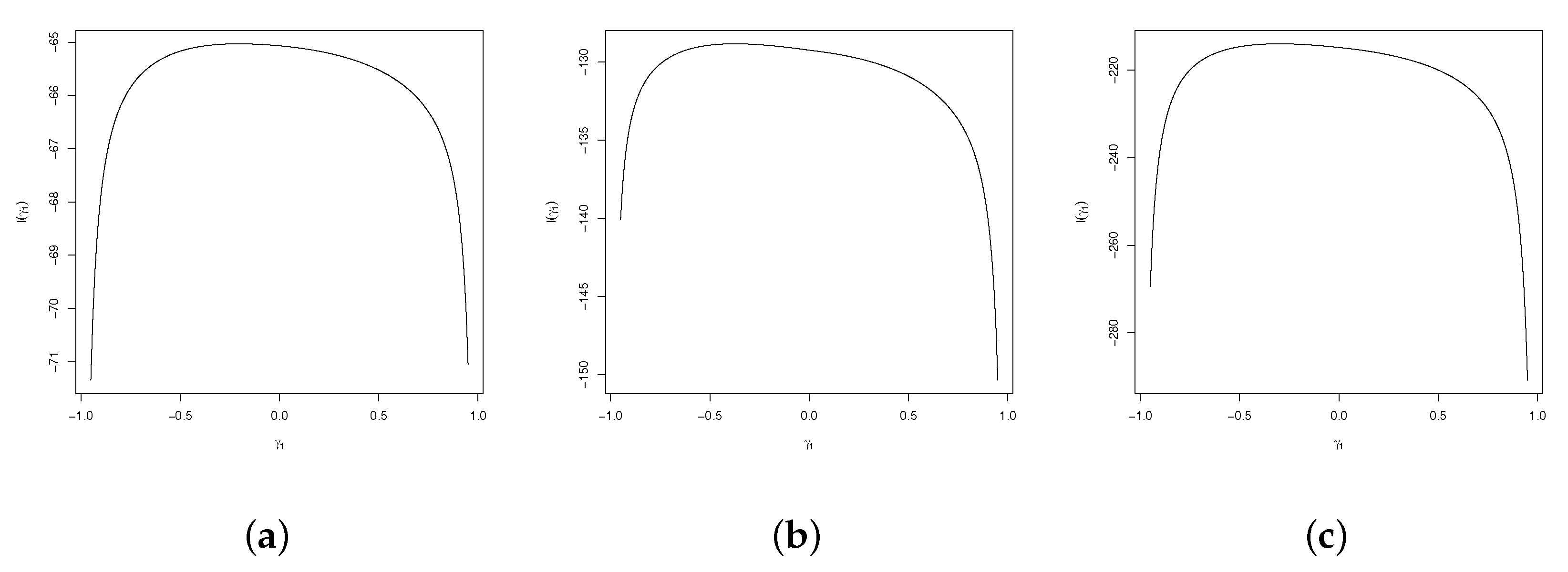
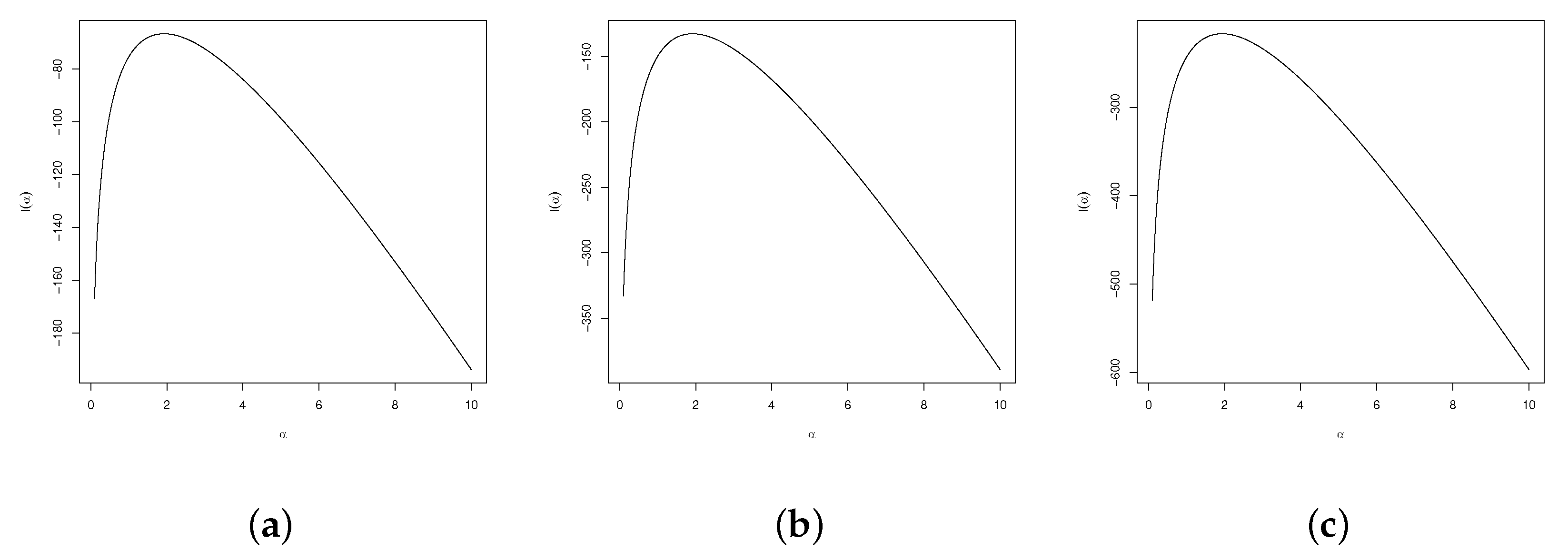
The
Figure 2 and
Figure 3 represent of the log-likelihood profiled of the
distribution for samples sizes 50, 100 and 150. The graphics show a regularity in the behaviour of the log-likelihood function, which gives strong evidence for the existence and uniqueness of the MLE.
3.1. The ELSN Regression Models
Azzalini [
2] ensures that the properties of existence and uniqueness of the MLE model
can be extended to the more general models case such as
,
, where
is a
vector of covariates,
is an unknown vector of regression coefficients and
are independent and identically distributed random variables
.
In this section, the location and scale version of the
model, is extended to situations of the regression models, that is, we consider the regression model
where
. The model (
10) is denominated the centred exponentiated log-skew-normal regression (ELSNR
) model and is denoted by
. Estimates for the components of the parameters vector
of the ELSNR
model can be obtained by using the maximum likelihood method.
To analyse the behaviour of the estimators of the parameters in the ELSNR
model, we carried out a small Monte Carlo simulation study, so, we analysed the behaviour of the estimators in the model (
10). Since the coefficients
, for
, have no restrictions on the values that can be assumed, without loss of generality we took
and the particular values
. Furthermore, without loss of generality, we took the value of the scale parameter equal to
; however, the following results can be obtained for any value of the scale parameter from the simple transformation
with
. The values of shape parameter were taken as
to take into account different configurations in the form of the pdf of the random variable
. Finally, we took values for the asymmetry parameter
, to take into account different degrees of asymmetry in the distribution of the data.
To analyse some statistical measures of the MLE, we considered small, moderate and large sample sizes:
and 500, and 1000 iterations were performed for each sample size. The studied characteristics were the bias and the root of the mean square error (RMSE) of the MLEs of the parameters. All calculations and estimates were obtained by using optim function of R Development Core Team [
20].
Table 1 presents the results of the simulation study, where it can be observed that the bias (in absolute value) and the RMSE of the MLEs tend to decrease when the sample size increases, which guarantees the asymptotic convergence of the MLEs. Another important fact, is the good estimation of the regression coefficients for all sample sizes considered, with a strong evidence that the model achieves to fit the high levels of skewness and kurtosis present in the response variable. On the other hand, the near zero values of the bias for the parameters
and
for large sample sizes (
), the values indicate that average iterations fences were true parameter value and therefore, there are no problems of identifiability in the estimation process.
3.2. The Censored ELSN Distribution
In this section, the centred ELSN
model for censored positive data is introduced. Suppose that random variable
follows a
model, and let
a random sample of size
n, where only those values of
greater than constant
T are recorded; and for values
only the value
T is recorded. The observed values, which we denote by
can be written as
The PDF of
is
where
with
y
defined in
. This model is represented by the notation
. One can see that, if
, the
distribution is identical to the log-normal Tobit model, see Moulton and Halsey [
9]. This shows that the
model is much more flexible than the log-normal Tobit model. Furthermore, for
, the centred LSN model for censored data follows, while for
the censored LPN model of Martínez-Flórez et al. [
5] is obtained.
Extensions of the
model to the case of regression models are defined in the same way, by assuming
, and defining
with
defined as in (
8).
5. An Application to Antibody Response to Vaccine
Data from a safety and immunogenicity study of measles vaccine conducted in Haiti during 1987–1990 are used as an illustration, see Job et al. [
19]. In this case, the goal of the study was to demonstrate that the higher titer vaccines could effectively immunize infants as young as 12 months of age. The response variable was neutralization antibody and the covariates involved in the study were:
EZ (vaccine type;
Schwarz,
Edmonston-Zagreb),
HI (vaccine dose;
medium,
high) and
FEM (gender;
male,
female). The sample size was 330 children, of which 86 were at or below the lower detection limit, (LDL). The number of expected zeros by considering the usual Tobit model was four. The response variable was the neutralization antibody, with LDL equal to 0.1 international units (UI), and the covariates involved in the study were encoded as
,
and
.
The high asymmetry degree for values above
indicated by the sample asymmetry coefficient
reveals that it seems worthwhile trying to fit an asymmetric model for this data set, so we fit the Moulton and Halsey [
9], Martínez-Flórez et al. [
4] and the centred version of the Chai and Bailey [
11] models, with
, and the results are presented in
Table 2. The parameter estimates of the fitted models were obtained by using the optim function of R Development Core Team [
20]. The source codes of the fitted models can be obtained by requesting them by email to the authors.
We also fit the
model, initially only with covariates in the continuous part and subsequently with covariates in the two components. The fitted models are shown in
Table 3. To compare the fitted models, we computed the Akaike information criterion [
21], namely
, where
p is the number of parameters for the considered model. The best model is the one with the smallest AIC value.
According to the AIC criterion, the best fit is presented by the model. To corroborate the good performance of the model, the proportion of the data set coming from units with low response was estimated. For the model without covariates the estimator of the Bernoulli intercept is 1.106, so that the estimator of the proportion of observations at or below the detection limit is which, compared to the observed , indicates good agreement with the proposed model.
We also consider the problem of testing the null hypothesis of no difference between the
model and the censored log-normal (CLN) model, i.e.,
We use the likelihood ratio statistic
where
is the likelihood function under model
F. Numerical evaluations indicate that
which is greater than the 5% chi-square critical value with two degree of freedom,
. Hence, the null hypothesis is rejected and we conclude that the
fits the data better than the logit/LN model.
Hypothesis testing for the Logit/LPN (CLPN) and Logit/LSN
(CLSN
) models against the
model are also conducted. Formally the hypotheses
can be tested by using the statistics
After numerical evaluations, we obtained
which are greater than the 5% chi-square critical value with one degree of freedom,
. The null hypothesis are rejected and we conclude that the
model fits the data better than the Logit/LPN and Logit/LSN
models.
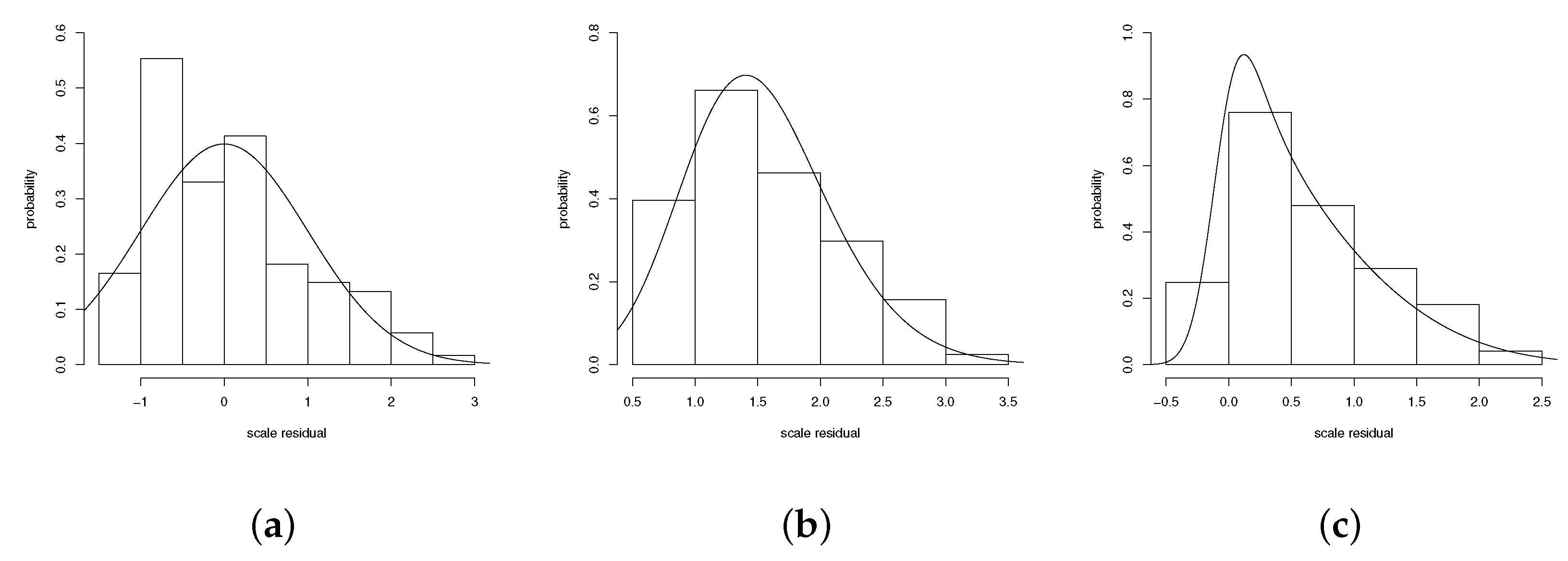
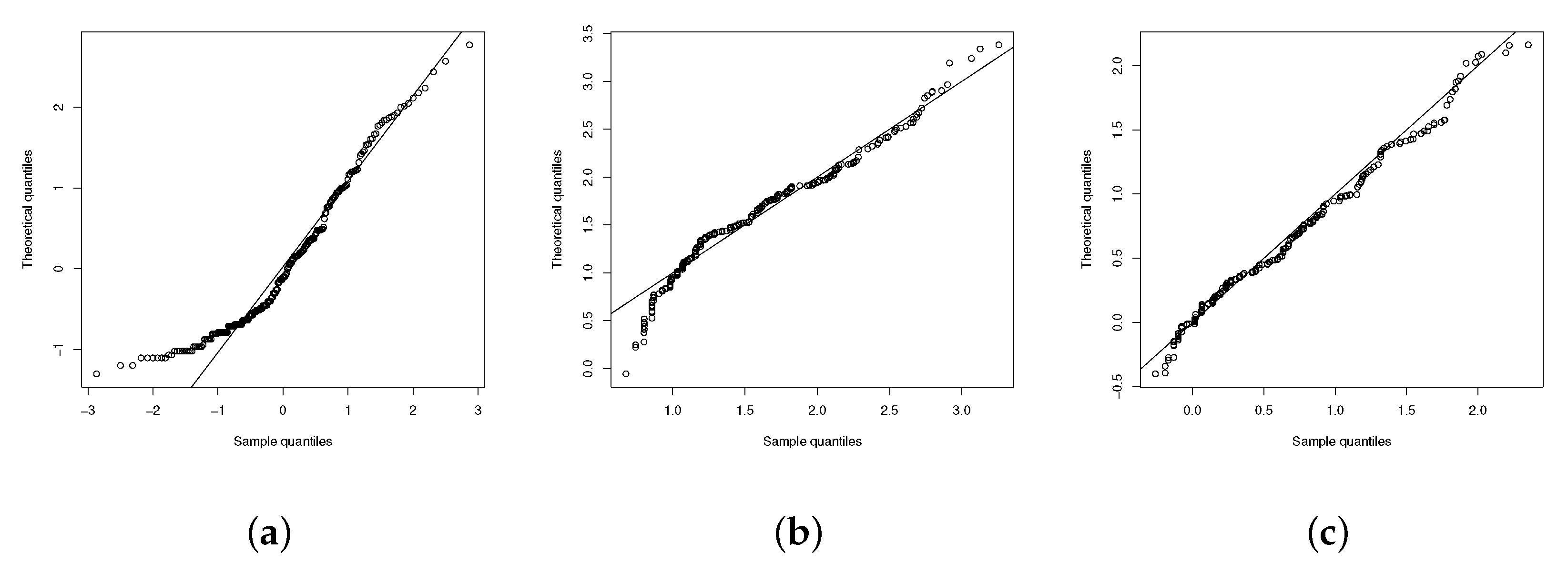
Using distributions LN, LPN and
for the continuous part, the scaled residuals
are evaluated and presented in the
Figure 4 and
Figure 5.
The figures reveal good performance of the distribution, further indicating that it is a viable alternative for asymmetric data with censored responses.
6. Final Discussion
In this paper, a more flexible model than the Logit/LN, Logit/LSN and Logit/LPN distributions is proposed. The new model is able to fit data with greater degree asymmetry and kurtosis than the Moulton and Halsey [
9], Chai and Bailey [
11] and Martínez-Flórez et al. [
5] models. The score function and the maximum likelihood estimator (MLE) of the model parameters are presented. A small Monte Carlo simulation study carried out showed a good performance of the MLE. An illustration with safety and immunogenicity data was presented in which the
model makes a better fit with respect to the Logit/LN, Logit/LSN and Logit/LPN models.
Among the main advantages that can be seen from the proposed models, there is greater flexibility with respect to the log-normal (log-Tobit), log-SN and log-PN models. On the other hand, the logit link function allows us to estimate the point mass probability with greater precision compared to the Tobit and log-Tobit models. As a disadvantage, the number of parameters in the model—although making it more flexible—also make it less parsimonious. However, even though the model is less parsimonious, it continues to be a good proposal, especially in cases where the asymmetry and kurtosis indices are high.