An Advised Indirect-Utility Ranking of Opportunity Sets

Abstract

There is a substantial strand of literature about ranking the subsets of a set of alternatives, usually referred to as opportunity sets. We investigate a model that is dependent on the preference of a grand set of alternatives. In this framework, the indirect-utility criterion ranks the opportunity sets by the following rule: a subset A is weakly preferred to another subset B if and only if A contains at least one preference maximizing element from $A\cup B$. This criterion leads to the indifference of each subset of alternatives to a singleton; symmetry appears at this stage, as the property holds true for any one of the maximizers in A. Conversely, suppose that a ranking of opportunity sets satisfies the property that each opportunity set is indifferent to a singleton contained within it. Then, we prove that such a ranking must use a generalized form of the indirect-utility criterion, where maximization is applied to a selection of the alternatives. Altogether, these results produce a characterization of the advised indirect-utility criterion for ranking opportunity sets.

1. Introduction

Making decisions is a problem that we face everyday, and decisions often take the form of multiobjective optimization problems [1]. Frequently, in our daily lives, prior to making a final decision, we select a smaller set of alternatives from the set of all available possibilities in order to reduce the complexity of the structure of the problem. This might correspond to the sequential application of criteria in a multiobjective setting. Kreps [2] cites a simple example consisting of ranking menus (or restaurants): before selecting a meal, the decision maker has to choose a menu or restaurant from the many available choices. The selection of a committee, coalition building, or hiring workers are situations of this kind, to mention but a few from different areas.

These sort of experiences raise the problem of ranking the subsets of a fixed set of alternatives, which, in the social choice literature, are also named ‘opportunity sets’ or ‘menus’. This issue has been considered in different contexts and it has given rise to various interesting formulations. Contrary to the case of mathematical analysis, which focuses on numerical valuations, the fundamental tool in mathematical economics is typically a binary relation that captures the preferences of the agents. The mathematical argument is that binary relations have allowed to extend the scope of application of the Weierstrass Extreme Value Theorem to economics and the social sciences quite efficiently (cf., Bergstrom [3], Walker [4], Alcantud [5]). The recent Quartieri [6] gives an updated account of concepts, results and techniques that take advantage of this classical approach. Nevertheless, numerical assessments and binary relations are strongly linked by the idea of a utility function (cf., Aleskerov, Bouyssou and Monjardet [7]).

Fishburn [8] was the first to investigate the preferences of agents over sets of alternatives or ‘opportunity sets’. Other authors have characterized different criteria based on principles of independence and continuity (Nehring and Puppe [9]), or in a framework of choice under complete uncertainty (for example, Bossert et al. [10] or Arlegi [11]). Some scholars have extended this analysis to incorporate the value of freedom of choice (see, for example, Bossert et al. [12] and Puppe [13], among others). Many competing models have contributed to understanding these problems and the choice behavior that they induce. An extensive, although outdated, survey of these approaches can be found in Barbera et al. [14].

From a more general standpoint, both individual and collective decision making may be based on either simultaneous or sequential multiple criteria. Pre-screening can be applied in more than one stage, and then each stage can utilize a specific criterion. For example, when a family decides on a place for their holiday, budget restrictions might produce a first reduction of the set of resorts under consideration; subsequently, other factors, such as the tastes of parents and children or weather forecasts are applied until a final choice is reached by a multi-stage decision process. A more technical recent example is Wu et al. [15], who use a screening tool for selecting criteria prior to the application of the TOPSIS (or Technique for Order Preference by Similarity to Ideal Solution) technique.

Our approach in this work belongs to the strand of literature that investigates choices under the fundamental model that determines the ranking of the subsets by the examination of a part of the alternatives. In this sense, the model responds to the principle of limited rationality, so that the agent concentrates on some focal alternatives, and more concretely, to the subset formed by the best elements, according to a criterion. Such a model is the germ of the indirect-utility (IU) approach for which Kreps [2] provides a characterization. The difference in the model that we propose here is that prior to the application of the IU criterion to rank the subsets of alternatives, in each subset, some of the options are rejected. We do not attach special semantics to this process, which we model by the fictitious figure of an ‘adviser’. The reduction of the opportunity sets may be achieved either by a real external adviser, by another criterion that precedes the IU criterion (e.g., gender regulations in the selection of a committee), by a search engine that provides some alternatives (maybe those in the first page only), or simply by drawing a lottery in order to focus on a lower number of options. We call the ranking defined under these characteristics “advised IU ranking” and we investigate when a given ranking (a complete preorder) of subsets ≽ of a finite set X is an advised IU ranking. Theorem 1 answers this question: one single behavioral property of choice serves us to test whether it belongs to this class or not.

Prior attempts to extend the logic of the IU criterion include Lahiri [16] and Ryan [17]. More precisely, Lahiri [16] obtains a necessary and sufficient condition for the existence of a preference R on the set of alternatives that explains both the transitive and quasi transitive preferences over opportunity sets in the sense of selecting the best elements of each set of alternatives. Ryan [17] generalizes the IU criterion to encompass decision makers who choose alternatives, according to a path-independent choice function. Relatedly, the sequential application of different criteria has been studied by Manzini and Mariotti [18], Apesteguía and Ballester [19], García-Sanz and Alcantud [20], García-Sanz and Alcantud [21], Kops [22], Cuhadaroglu [23] or Cantone et al. [24], among others.

The rest of the paper is organized as follows. In Section 2, we introduce some notation and preliminaries about binary relations. Moreover the IU criterion is defined, and one of its properties (the indifference of each subset to a singleton) is highlighted since it is essential for the main result. Section 3 contains the definition of a ranking of opportunity sets in two steps. In the first one, some alternatives are selected from each subset (for an external expert, because of a budget restriction, …) and then, the IU criterion is applied. This section ends with the main result: the characterization of the advised IU rankings. We summarize our conclusions in Section 4. Here, we highlight the fact that we have not dealt with the popular indirect-utility criterion for ranking subsets, but that rather we have approached a particular form of it.

2. Notation and Preliminaries

We denote by $X=\{x_1,\dots ,x_n\}$ a finite set of n objects or alternatives, and by ${\mathcal{P}}^{*}\left(X\right)$ the set of nonempty subsets of $X,$ also named opportunity sets. A binary relation on $X,$ $R\subseteq X\times X,$ is interpreted as a preference relation of an agent, that is to say, we claim $xRy$ (a convenient shorthand for $(x,y)\in R$) if and only if the element $x\in X$ is at least as good as the element $y\in X.$

Any binary relation R on X produces two associated relations in a natural way, namely the following:

(i)

A strict relation P defined by the expression $xPy\iff \left\{xRy\mathrm{and}\mathrm{not}yRx\right\}$, for each $x,y\in X$.

(ii)

An indifference relation I defined by the expression $xIy\iff \left\{xRy\mathrm{and}yRx\right\}$, for each $x,y\in X$.

Irrespective of the properties of R, strict relations are asymmetric, whereas indifference is obviously symmetric.

A binary relation R is transitive if for any $x,y,z\in X$, when $xRy$ and $yRz$ we have $xRz$. R is complete if for any $x,y\in X$ it must be the case that either $xRy$ or $yRx$ or both hold true. When R satisfies transitivity and completeness, we say that R is a complete or total preorder.

Definition 1.

Given a total preorder R on a finite set $X,$ a best element of a subset $A\subseteq X$ for R is an element $x\in A$ such that $xR{x}^{\prime }forall{x}^{\prime }\in A.$ In particular, a best element for R is $x\in X$ such that $xR{x}^{\prime }forall{x}^{\prime }\in X$ (cf., [25]).

According to Definition 1, best elements must exist due to the finiteness assumption on X. However, they are not necessarily unique. When R is a linear preorder, which means that R satisfies the antisymmetry property, then the best elements are forcefully unique.

2.1. Opportunity Sets: Criteria for Comparisons

In order to deal with rankings of opportunity sets, notice that any complete preorder R over a set X can be extended to a complete preorder over ${\mathcal{P}}^{\ast }\left(X\right)$ in the following fashion:

$$A\succcurlyeq B\iff max\left(A\right)Rmax\left(B\right),\mathrm{for}\mathrm{any}A,B\in {\mathcal{P}}^{\ast }\left(X\right)$$

(1)

where $max\left(C\right)$ denotes a best element of a subset $C\subseteq X$ for the complete preorder R. Since best elements are not necessarily unique, it is important to emphasize that the properties of R ensure that the definition of ≽ is independent of the choice of the best elements in A and B.

Definition 2.

The criterion defined by Equation (1), which resorts to the ordering among a selection of best elements for each set of alternatives, is called the “indirect-utility criterion” (also IU criterion for brevity): cf., [14].

Henceforth, we refer to a “ranking” (over X) in order to denote any complete preorder ≽ over ${\mathcal{P}}^{\ast }\left(X\right)$. With this convention, Equation (1) defines the IU ranking, as one can readily check that the IU criterion satisfies the properties of transitivity and completeness, and thus, it is a complete preorder.

The strict relation associated with ≽ is denoted by ≻, and ∼ denotes its indifference relation.

Conversely, when ≽ is a ranking over X, it produces a complete preorder $R^{\succcurlyeq }$ on X in the following natural manner:

$$x{R}^{\succcurlyeq }y\iff \left\{x\right\}\succcurlyeq \left\{y\right\},\mathrm{for}\mathrm{any}x,y\in X.$$

(2)

An alternative x is considered at least as good as another alternative y if and only if their corresponding singletons satisfy this relationship (i.e., when $\left\{x\right\}$ is at least as good as $\left\{y\right\}$ in terms of the ranking).

2.2. Ranking Opportunity Sets: Axiomatic Approches

It is well known that the IU criterion is characterized by Kreps’ property (see [2]) that establishes $A\succcurlyeq B\Rightarrow A\sim A\cup B$ for any $A,B\in {\mathcal{P}}^{\ast }\left(X\right)$. Whenever a ranking of opportunity sets ≽ satisfies this property, it must be the case that any subset of alternatives is indifferent to a singleton formed by any one of the best elements in the subset (by the relation $R^{\succcurlyeq }$ trivially induced by ≽). Indeed, for any $A=\{a_1,\dots ,a_p\}$, we can suppose without loss of generality that the following holds:

$$\left\{a_1\right\}\succcurlyeq \left\{a_2\right\}\succcurlyeq \dots \succcurlyeq \left\{a_p\right\}$$

which entails $a_1{R}^{\succcurlyeq }{a}_2{R}^{\succcurlyeq }\dots R^{\succcurlyeq }{a}_p$ by (2). Now, Kreps’ property and transitivity lead to the successive indifferences as follows:

$$\left\{a_1\right\}\sim \{a_1,a_2\}\sim \dots \sim \{a_1,\dots ,a_p\}$$

hence $\left\{a_1\right\}\sim \{a_1,\dots ,a_p\}=A$.

Motivated by this characteristic of the IU criterion, we pose the problem of investigating the rankings over X for which any opportunity set is indifferent to one of its singletons. Therefore we consider the following property:

Indifference to singletons (IS): A ranking ≽ of the opportunity sets of a finite set of alternatives X satisfies IS if for any subset $S\subseteq X$, there exists $x\in S$ such that $S\sim \left\{x\right\}$.

When for each $S\subseteq X$ the element in this singleton is one of the best elements in S by the relation $aRb\iff \left\{a\right\}\succcurlyeq \left\{b\right\}$, the IU criterion associated with R is applied.

This property can be understood as a case of choosing alternatives in which the final choice is an only element. When the ranking is observed and each opportunity set is identified with one of its singletons, we can think of this element as the chosen alternative. The ranking of the singletons leads to the ranking of all the opportunity sets.

We have argued that Kreps’ property implies IS. In order to prove that IS is strictly weaker than the Kreps’ property, Example 1 below shows a case in which IS is satisfied, but not the Kreps’ property. In this way, we are assured that there does not exist a complete and transitive binary relation R over X such that ≽ is the IU ranking associated with Example 1.

In fact, we shall prove that a stronger conclusion is true. Example 1 below considers the property $A\succcurlyeq B\Rightarrow A\succcurlyeq A\cup B$. This is a relaxed version of Kreps’ property that is used in [16] for characterizing (jointly with a monotonicity property) “justifiable” transitive preferences over opportunity sets, that is, transitive preferences ≽ for which there exists a complete and reflexive binary relation R over the set of alternatives such that for any subsets of alternatives $A,B$, the comparison $A\succcurlyeq B$ holds true if and only if $\{x\in A\cup B:xRy,\forall y\in A\cup B\}\cap A\ne \varnothing$. Example 1 below does not satisfy this property, so it cannot be justified in Lahiri’s sense either.

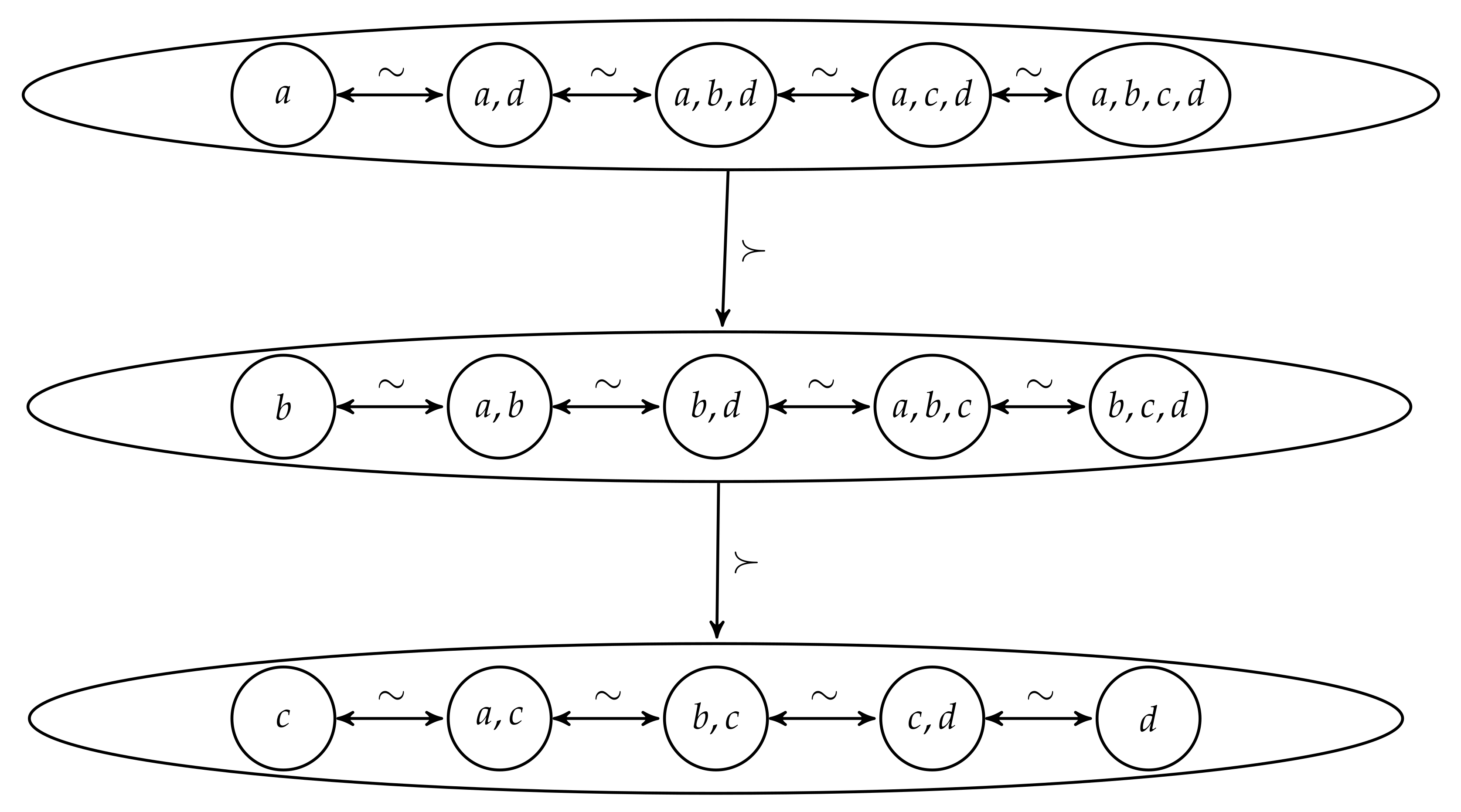
Example 1.

Let $X=\{a,b,c,d\}$, and consider a ranking ≽ over X which is represented in Figure 1 below. Subsets in the same ellipses are indifferent among them, and subsets in higher ellipses are strictly preferred to those in lower ellipses.

The ranking ≽ does not satisfy Kreps’ property because of the following:

$$\left\{a\right\}\succ \left\{b\right\}\mathrm{but}\left\{a\right\}\nsim \{a,b\}$$

The ranking ≽ does not satisfy $A\succcurlyeq B\Rightarrow A\succcurlyeq A\cup B$ because of the following:

$$A=\{a,c\}\succcurlyeq B=\left\{d\right\},\mathrm{but}A\cup B=\{a,c,d\}\succ A=\{a,c\}$$

Nevertheless, ≽ clearly satisfies IS.

Figure 1. Example of a ranking of opportunity sets satisfying IS but not Kreps’ property.

Figure 1. Example of a ranking of opportunity sets satisfying IS but not Kreps’ property.

2.3. The Research Question

The IU criterion satisfies IS as explained above. The following question arises: what is the exact class of rankings that satisfies IS?

To solve this problem, we define a generalization of the IU criterion with the help of the concept of a choice correspondence.

Definition 3.

Let X be a set and $\mathcal{D}$ a nonempty domain of nonempty subsets of $X.$ A choice correspondence of X is an application $\mathcal{C}:\mathcal{D}\to \mathcal{P}\left(X\right)$ such that $\mathcal{C}\left(S\right)\subseteq S$ and $\mathcal{C}\left(S\right)\ne ⌀$ for all $S\in \mathcal{D}.$

The next section defines the concept that characterizes the exact class of rankings of opportunity sets that satisfy IS.

3. An Advised Indirect-Utility Ranking

This section is devoted to defining a new procedure for ranking opportunity sets, and then proving that this is the exact solution to the problem posed in Section 2. We call it the class of advised IU rankings.

The intuitive construction of advised IU rankings proceeds in two steps. For any subset of alternatives, it applies the indirect-utility criterion to some of them that are previously selected. The interpretation of this selection is external to the model. It may be given by an expert who uses their expertise to prune the initial set of feasible alternatives, or it may be the result of some constraint, as in the case of the budget restriction that eliminates some alternatives from a travel agency. We use a choice correspondence to model this preliminary shortlist of options. It is important to bear in mind that the two steps are independent: the choice correspondence that shrinks the subset of options is not necessarily linked to the preference over the grand set of alternatives.

Definition 4 below formalizes this idea:

Definition 4.

Let X be a finite set of alternatives. Suppose that R is a complete preorder over X and $\mathcal{C}$ is a choice correspondence on $X.$ The advised IU ranking associated with R and $\mathcal{C}$, ${\succcurlyeq }_{\mathcal{C}}$, is defined as follows:

$$\forall A,B\subseteq X,A{\succcurlyeq }_{\mathcal{C}}B\iff max\left(\mathcal{C}\left(A\right)\right)Rmax\left(\mathcal{C}\left(B\right)\right)$$

(3)

As in the case of Equation (1), here, $max\left(C\right)$ denotes a best element of $C\subseteq X$ for R. Equation (3) produces a well-defined expression of a complete preorder on ${\mathcal{P}}^{\ast }\left(X\right)$, so it is a ranking over X.

Remark 1.

The IU ranking (cf., Definition 2) is a special case of advised IU ranking where the choice correspondence that shrinks the initial set of alternatives is trivial in the sense that it does not reduce the offer. In other words, when $\mathcal{C}\left(A\right)=A$ for all $A\subseteq X$, Definition 4 becomes Definition 2.

The next example proves that not any complete preorder on ${\mathcal{P}}^{\ast }\left(X\right)$ can be represented as an advised IU ranking.

Example 2.

Let $X=\{a,b\}.$ We consider the complete preorder over ${\mathcal{P}}^{\ast }\left(X\right)$ defined by $\{a,b\}\succ \left\{a\right\}\sim \left\{b\right\}.$

Then the complete preorder R on X induced by ≽ is $aRbandbRa.$

A choice correspondence $\mathcal{C}$ on ${\mathcal{P}}^{\ast }\left(X\right)$ is determined by one of the following alternative selections:

$$\begin{array}{ccc}\left(1\right)\mathcal{C}\left(\right\{a,b\left\}\right)=\left\{a\right\},\hfill & \left(2\right)\mathcal{C}\left(\right\{a,b\left\}\right)=\left\{b\right\},\hfill & \left(3\right)\mathcal{C}\left(\right\{a,b\left\}\right)=\{a,b\}.\hfill \end{array}$$

All three conditions lead to $\{a,b\}{\sim }_{\mathcal{C}}\left\{a\right\}$, thus proving that $\succcurlyeq \ne {\succcurlyeq }_{\mathcal{C}}$ for any choice correspondence $\mathcal{C}$ on ${\mathcal{P}}^{\ast }\left(X\right)$.

It is easy to check that the advised IU ranking in Definition 4, as a generalized form of the IU ranking, also satisfies Property IS. In fact, for each $S\subseteq X$, it must be the case that $S{\sim }_{\mathcal{C}}\left\{s\right\}$ when s is a best element of the subset $max\left(\mathcal{C}\right(S\left)\right)$.

Now, we proceed to show that the converse of this statement is true. By doing so, we establish that IS is the exact property that characterizes the class of advised IU rankings.

For illustration, the next example presents a situation where a ranking that satisfies IS is explicitly shown to be an advised IU ranking.

Example 3.

In continuation of Example 1, observe that the choice correspondence on $X=\{a,b,c,d\}$ defined as

$$\mathcal{C}\left(\right\{a,d\left\}\right)=\mathcal{C}\left(\right\{a,b,d\left\}\right)=\mathcal{C}\left(\right\{a,c,d\left\}\right)=\mathcal{C}\left(\right\{a,b,c,d\left\}\right)=\left\{a\right\},$$

$$\mathcal{C}\left(\right\{a,b\left\}\right)=\mathcal{C}\left(\right\{b,d\left\}\right)=\mathcal{C}\left(\right\{a,b,c\left\}\right)=\mathcal{C}\left(\right\{b,c,d\left\}\right)=\left\{b\right\},\mathrm{and}$$

$$\mathcal{C}\left(\right\{a,c\left\}\right)=\mathcal{C}\left(\right\{b,c\left\}\right)=\mathcal{C}\left(\right\{c,d\left\}\right)=\left\{c\right\}$$

allows us to prove that $\succcurlyeq ={\succcurlyeq }_{\mathcal{C}}$.

Observe also that the choice correspondence justifying that the IS ranking in Example 1 is an advised IU ranking is not unique. To prove it, we point out that, if in the definition of $\mathcal{C}$ given above, we modify $\mathcal{C}\left(\right\{a,b,c\left\}\right)$ so that we use $\mathcal{C}\left(\right\{a,b,c\left\}\right)=\{b,c\}$ instead, the argument proceeds exactly in the same fashion.

3.1. Defining a Choice Correspondence $\mathcal{C}$ from a Ranking ≽ That Satisfies IS

In order to prove our main result, it is convenient to set some additional notation. Hence, along this section, ≽ denotes a ranking over X satisfying IS.

We proceed to establish a way to construct a choice correspondence associated with ≽. The process is inspired by a recent development in a related context (v. Bernardi et al. [26]).

As we have assumed that ≽ is complete, its restriction to the singletons produces a strict chain as follows:

$$\left\{x_{i_1}\right\}\succ \left\{x_{i_2}\right\}\succ \dots \succ \left\{x_{i_l}\right\}$$

such that any $x_j\in X$ satisfies that $\left\{x_j\right\}\sim \left\{x_{i_k}\right\}$ for some $k=1,\dots ,l$.

The whole set of opportunity sets of X has $2^{\left|X\right|}$ elements so that, leaving the empty set aside, we have the subsets of alternatives $S_1,S_2,\dots ,S_{2^n-1}$. Because ≽ is a ranking, we can suppose, without loss of generality, the following:

$$S_1\succcurlyeq S_2\succcurlyeq \cdots \succcurlyeq S_{2^n-1}.$$

Then, we can distribute these subsets in indifference classes ${\Sigma }_k$ generated by the indifference or symmetric part of ≽:

$$\stackrel{{\Sigma }_1}{\overbrace{S_1^1\sim S_2^1\sim \dots \sim S_{p_1}^1}}\succ \stackrel{{\Sigma }_2}{\overbrace{S_1^2\sim S_2^2\sim \dots \sim S_{p_2}^1}}\succ \dots \succ \stackrel{{\Sigma }_l}{\overbrace{S_1^l\sim S_2^l\sim \dots \sim S_{p_l}^l}}.$$

So, we have split ${\mathcal{P}}^{\ast }\left(X\right)$ into ${\Sigma }_1=\{S_1^1,\dots ,S_{p_1}^1\},\dots ,{\Sigma }_l=\{S_1^l,\dots ,S_{p_l}^l\}$. Observe that the number of equivalence classes is exactly l because the ranking satisfies IS. This property ensures that for each ${\Sigma }_k$, there exists $x_{i_k}\in X$ such that $\left\{x_{i_k}\right\}\in {\Sigma }_k$. The number of classes ${\Sigma }_k$ must coincide with the number of singletons in the strict chain produced by the restriction of ≽ to such subsets (which is, therefore, a maximal chain of ≽).

For each $k=1,\dots ,l$, let $X_k$ be the subset formed by all the elements of X which as singletons, belong to the indifference class ${\Sigma }_k$. Then, for each $S\subseteq X$ we have that $S\in {\Sigma }_k$ for some $k=1,\dots ,l$ and then $S\cap X_k\ne \varnothing$ (otherwise it would be $S\sim \left\{x_r\right\}\not\subset X_k$ which leads to $S\nsim \left\{x_{i_k}\right\}$ and then $S\notin {\Sigma }_k$, against the hypothesis).

Now, we are prepared to define the choice correspondence of X with the required properties:

Definition 5.

Let ≽ be a ranking over the opportunity sets of X that satisfies IS. For any $S\subseteq X$, we define the choice correspondence associated with ≽ by the following:

$${\mathcal{C}}^{\succcurlyeq }\left(S\right)=S\cap X_{i_k}$$

(4)

where $X_{i_k}$ is such that $S\in {\Sigma }_k$.

The next example illustrates this definition:

Example 4.

In continuation of Example 1, the choice correspondence associated with ≽ by the process described above (cf., Definition 5) is as follows:

$$\mathcal{C}\left(\right\{a,d\left\}\right)=\mathcal{C}\left(\right\{a,b,d\left\}\right)=\mathcal{C}\left(\right\{a,c,d\left\}\right)=\mathcal{C}\left(\right\{a,b,c,d\left\}\right)=\left\{a\right\},$$

$$\mathcal{C}\left(\right\{a,b\left\}\right)=\mathcal{C}\left(\right\{b,d\left\}\right)=\mathcal{C}\left(\right\{a,b,c\left\}\right)=\mathcal{C}\left(\right\{b,c,d\left\}\right)=\left\{b\right\},$$

$$\mathcal{C}\left(\right\{a,c\left\}\right)=\mathcal{C}\left(\right\{b,c\left\}\right)=\left\{c\right\},\mathrm{and}\mathcal{C}\left(\right\{c,d\left\}\right)=\{c,d\}.$$

The reader can compare this output with the two choice correspondences on X utilized in Example 3 to justify that ≽ is an advised IU ranking.

3.2. Main Result

We are ready to prove our main result, namely, the characterization of the advised IU rankings by IS:

Theorem 1.

Let X be a finite set of alternatives and let ≽ be a ranking over $X.$ Then, there exist a complete preorder R over X and a choice correspondence $\mathcal{C}:{\mathcal{P}}^{\ast }\left(X\right)\to {\mathcal{P}}^{\ast }\left(X\right)$ such that ≽ is the advised IU ranking associated with R and $\mathcal{C}$ (i.e., $\succcurlyeq ={\succcurlyeq }_{\mathcal{C}})$, if and only if $\succcurlyeq$ satisfiesIS.

Proof. (⇒)

We have already mentioned that the ranking ${\succcurlyeq }_{\mathcal{C}}$ given by (3) satisfies IS because for each $S\subseteq X$, one has $S{\sim }_{\mathcal{C}}\left\{s\right\}$ when s is a best element of $\mathcal{C}\left(S\right)$ for R.

$(\Leftarrow )$ Let us suppose that we have a ranking ≽ over X. Then, $R^{\succcurlyeq }$ defined by Equation (2) is a complete preorder on X. As ≽ satisfies IS, we can proceed as in Section 3.1, and define ${\mathcal{C}}^{\succcurlyeq }$ by the expression in (4). Finally, we check that the complete preorder $R^{\succcurlyeq }$ and the choice correspondence ${\mathcal{C}}^{\succcurlyeq }$ satisfy the consequent, that is to say, $\succcurlyeq ={\succcurlyeq }_{{\mathcal{C}}^{\succcurlyeq }}$, or in other words, that ≽ is the advised IU ranking associated with $R^{\succcurlyeq }$ and ${\mathcal{C}}^{\succcurlyeq }$. We proceed in two steps.

First, suppose that $A\succcurlyeq B$. Let us prove that $A{\succcurlyeq }_{{\mathcal{C}}^{\succcurlyeq }}B$.

The assumption $A\succcurlyeq B$ leads to $A\in {\Sigma }_k$ and $B\in {\Sigma }_r$ for any $k,r\in 1,\dots ,l$ and $k⩽r$. Then, ${\mathcal{C}}^{\succcurlyeq }\left(A\right)=A\cap X_k$ and ${\mathcal{C}}^{\succcurlyeq }\left(B\right)=B\cap X_r$ and for all $a\in {\mathcal{C}}^{\succcurlyeq }\left(A\right)$ and all $b\in {\mathcal{C}}^{\succcurlyeq }\left(B\right)$, $\left\{a\right\}\succcurlyeq \left\{b\right\}$ is satisfied. Therefore, $max\left({\mathcal{C}}^{\succcurlyeq }\left(A\right)\right)Rmax\left({\mathcal{C}}^{\succcurlyeq }\left(B\right)\right)$ and $A{\succcurlyeq }_{{\mathcal{C}}^{\succcurlyeq }}B$.

It remains to be proven that whenever $A{\succcurlyeq }_{{\mathcal{C}}^{\succcurlyeq }}B,$ it must be the case that $A\succcurlyeq B$. By contradiction, suppose $B\succ A$ with $B\in {\Sigma }_k$ and $A\in {\Sigma }_r$ and $k<r.$ Then, $max\left({\mathcal{C}}^{\succcurlyeq }\left(B\right)\right){\succ }_{{\mathcal{C}}^{\succcurlyeq }}max\left(\mathcal{C}\left(A\right)\right)\iff B{\succ }_{\mathcal{C}}A$, against the hypothesis. □

Remark 2.

Example 3 above (see also Example 4) explains that the choice correspondence $\mathcal{C}$ that justifies that a ranking ≽ satisfying IS is an advised IU ranking, is not unique. For the sake of simplicity, we have defined the choice correspondence associated with ≽ by Equation (4). In fact, for any $S^{\prime }\subseteq S\cap X_{i_k}$ (being $S\in {\Sigma }_k$), we can define ${\mathcal{C}}^{\succcurlyeq }\left(S\right)=S^{\prime }$, and it will also satisfy the required conditions.

We finish by making some further remarks about the choice correspondence we have defined to prove Theorem 1. First and foremost, we are not restricting our model to rational choices. This should not restrict the applicability of the model, as we can observe plenty of real cases in which rationality seems not to exist. For example, everybody is familiar with working with search engines; however, the way that they select and present the results in the first page or in the first places is irrelevant to the user, who often finds different alternatives ranked first when they use different search engines. There is a large amount of literature about when correspondences can be classified as “rational choice correspondences” (in a classical way, we cite Suzumura [25] as a good survey of the characterization of the classical concept of rational choice correspondences). Rationality when the choice is made in different steps is examined in [18] or [20,21] among others.

In this regard, notice that the choice correspondence $\mathcal{C}$ defined in Example 4 does not satisfy any of the classical properties of rationality, such as the Chernoff condition or the binariness property. However, this inconvenience does not mean that the choice cannot be justified. In fact, Dogan and Yildiz [27] (Proposition 1) prove that any choice correspondence can be rationalized by a plurality-wins election. In our context, this justification implies that a set of (fictitious) voters exist that order the alternatives so that for each subset, we first select the plurality winners, and then we apply the IU criterion to it.

4. Conclusions

The extension of preference on a set of elements to a ranking of its subsets is widely studied in the literature (see Barbera et al. [14] for a complete survey). One popular ranking of subsets is the indirect-utility criterion, which ranks subsets of alternatives on the basis of its best elements with respect to an underlying preference on the original set. From another point of view, individual and collective decision making based on multiple criteria (either applied simultaneously or in a sequential way) is also a frequent research target. We have investigated rankings that combine both dimensions: the decision maker applies the indirect utility-criterion, not directly to the given subset of alternatives, but to the result of a pre-screened subset. This selection was done by another criterion, perhaps representing an external adviser. Put differently, we face a sequential decision. First, some alternatives are discarded and afterward, the indirect-utility criterion is applied to make the final choice. We call these kinds of criteria “advised IU rankings”. We formalize the “adviser” acting at the first step by a choice correspondence $\mathcal{C}$ in such a way that for any $S\subseteq X,\mathcal{C}\left(S\right)\subseteq S$ and $\mathcal{C}\left(S\right)\ne \varnothing .$ However, we are not bound by any particular semantics for it and the term “adviser” is just a convenient label. The ranking defined in this way establishes that $A\succcurlyeq B\iff max\left(\mathcal{C}\right(A\left)\right)Rmax\left(\mathcal{C}\right(B\left)\right)$, and we characterize it by one simple property: each subset of alternatives is indifferent to one of its singletons. This can ex-post be understood as a final choice of a single element for each opportunity set.

Although the literature about choice correspondences often works with the idea or “rational choice”, we have not imposed any rationality property to the “adviser”. The possibility that a rational adviser (for specific realizations of this concept) justifies the ranking is an interesting question for future work. In this regard, Dogan and Yildiz [27] have already proven that any choice correspondence can be rationalized by a plurality-wins election, so it admits a “rational” ex-post justification. Similar sequential choices in which the indirect-utility criterion is replaced by another one may become an interesting topic to consider in future work.