A Note on Decomposable and Reducible Integer Matrices

Abstract

We propose necessary and sufficient conditions for an integer matrix to be decomposable in terms of its Hermite normal form. Specifically, to each integer matrix, we associate a symmetric integer matrix whose reducibility can be efficiently determined by elementary linear algebra techniques, and which completely determines the decomposability of the first one.

1. Introduction

For integer valued matrices, the notion of decomposability can be stated analogously to the real case (see Definition 1). The main difference here is that unimodularity is required for the transformation matrices. This is necessary to preserve the $\mathbb{Z}$-module structure generated by the columns of the matrix. Thus, if one wants to keep the group structure unchanged, pure linear algebra techniques cannot be applied to study the decomposability of an integer matrix.

Let $m\le n$ be two positive integers. Given an $m\times n$ integer matrix A, we can consider the submonoid S of ${\mathbb{Z}}^m$ generated by the non-negative combinations of the columns of A. A decomposition of A yields a decomposition of S, and vice versa. In [1], the authors deal with the computation of the decompositions of S, if possible, using the (integer) Hermite normal form as the main tool. Following this idea, we relate the decomposition of any integer matrix and the decomposition of its Hermite normal form (Proposition 1). This leads to our main result (Theorem 1) which states that if H is the Hermite normal form of an integer matrix A, the necessary and sufficient condition for A to be decomposable is that a certain symmetric matrix is reducible in the usual sense (see Definition 3). Now, we can adapt the combinatorial and linear algebra machinery to determine if A is decomposable: note that, for a symmetric real matrix, it is possible to decide if it can be decomposed into a direct sum of smaller symmetric real matrices by analyzing the connectivity of a certain associated graph, which is closely related to the spectral properties of the graph. All this allows us to propose an algorithm (Algorithm 1) for the computation of the decomposition of the matrix A, if possible.

Apart from practical computational considerations, we emphasize that, given an integer matrix A, we propose a new approach by associating A with a simple graph whose connectivity determines its decomposition. Consequently, this can be used to determine the decomposition of any finitely generated commutative submonoid of ${\mathbb{Z}}^m$, as an alternative method to [1]. Recall that the study of finitely generated commutative submonoids of ${\mathbb{Z}}^m$ is of great interest due to its close relation with Toric Geometry (see [2,3] or [4], and the references therein). Moreover, in this context, integer decomposable matrices have their own importance; to mention a couple of illustrative examples we observe that decomposable graphical models have associated integer decomposable matrices, as can be deduced from [5] (Theorem 4.2), and that decomposable semi-groups correspond to direct products of certain algebraic (toric, in a wide sense) varieties.

Algorithm 1: HNF-decomposition.

Input: An $m\times n$ integer matrix A.    Output: A unimodular matrix P and a permutation matrix Q such that    $P^{-1}AQ=H_1\oplus \dots \oplus H_t$ with $H_i$ into Hermite normal form for every i.    1. Set $H=HNF\left(A\right)$ and let $P_0$ be a unimodular matrix, such that $P_0^{-1}A=H$;    2. Define the square matrix $tim\left(H\right)$ and set $B=tim\left(H\right)+tim{\left(H\right)}^{\top }$;    3. Let D be the diagonal matrix whose elements in the main diagonal are entries of $B{(11\dots 1)}^{\top }$ and define $L=D-B$. If $n-rank\left(L\right)=1,$ then return $P=P_0$ and Q equal to the identity matrix;    4. Let R be the reduced row echelon form of L and let $k=0$;    5. For $j=1$ to n do     If the j-th column, ${\mathbf{v}}_j$, of R is a non-pivot column; then      i.  Set $k=k+1$ and ${\ell }_k$ equal to the cardinality of $supp\left({\mathbf{v}}_j\right)$;      ii. Let $Q_k$ be the $n\times ({\ell }_k+1)$-matrix whose columns are $\left\{{\mathbf{e}}_j\right\}\cup \{{\mathbf{e}}_i\mid i\in supp\left({\mathbf{v}}_j\right)\},$ where ${\mathbf{e}}_i$ denotes the n-dimensional vector that has the i-th coordinate equal to 1 and all the other coordinates equal to 0.    6. Set $Q=\left(Q_1\right|\dots \left|Q_t\right)$;    7. Let $P_1$ be the unimodular matrix such that $P_1^{-1}\left(HQ\right)=HNF\left(HQ\right)$;    8. Return $P=P_0{P}_1$ and Q.

2. On Decomposable and Reducible Integer Matrices

Let $m\le n$ be two positive integers.

Definition 1.

Let $A\in {\mathbb{Z}}^{m\times n}$. We say that A is decomposable if there exist a unimodular matrix P and a permutation matrix Q such that $P^{-1}AQ$ decomposes into a direct sum of matrices.

As mentioned in the introduction, the main purpose of this note is to study decomposable matrices in terms of their Hermite normal form. Let us recall the notion of Hermite normal form of an integer matrix.

Definition 2.

Let $A\in {\mathbb{Z}}^{m\times n}$ of rank r. The Hermite normal form of $A,HNF\left(A\right)$, is the unique matrix $H=\left(h_{ij}\right)\in {\mathbb{Z}}^{m\times n}$, such that $A=PH$, for a unimodular matrix P, satisfying the following three conditions:

(a)

there exists a sequence of integers $j_1,\dots ,j_r$ such that $1\le j_1<\dots <j_r\le n$, and for each $1\le i\le r$ we have $h_{ij}=0$ for all $j<j_i$ (row echelon form);

(b)

for $1\le k<i\le r$ we have $0\le h_{k{j}_i}<h_{i{j}_i}$ (the pivot element is the greatest along its column and the coefficients above are non-negative);

(c)

the last $m-r$ rows of H are zero.

We say that A is in Hermite normal form when $A=HNF\left(A\right)$.

There are well-known efficient algorithms for the computation of the Hermite normal form of an integer matrix (see, e.g., [6]). They are implemented in the usual computer algebra systems; for example, in GAP ([7]) and Mathematica ([8]), the commands HermiteNormalFormIntegerMat and HermiteDecomposition, respectively, compute the Hermite normal form of an integer matrix.

Example 1.

The Hermite normal form of

$$A=\left(\begin{array}{ccccc}2& -4& 2& 5& -6\\ 2& -2& 2& 5& -3\\ 0& -2& 1& 2& -3\end{array}\right)$$

is

$$HNF\left(A\right)=\left(\begin{array}{ccc}\hfill 1& \hfill 0& \hfill -2\\ \hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 1& \hfill 1\end{array}\right)A=\left(\begin{array}{ccccc}2& 0& 0& 1& 0\\ 0& 2& 0& 0& 3\\ 0& 0& 1& 2& 0\end{array}\right),$$

where the matrix $\left(\begin{array}{ccc}\hfill 1& \hfill 0& \hfill -2\\ \hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 1& \hfill 1\end{array}\right)$ is the product of the elementary matrices transforming the matrix A into its reduced row echelon form as above, in such a way that the unimodular matrix in Definition 2 is

$$P={\left(\begin{array}{ccc}\hfill 1& \hfill 0& \hfill -2\\ \hfill -1& \hfill 1& \hfill 0\\ \hfill -1& \hfill 1& \hfill 1\end{array}\right)}^{-1}=\left(\begin{array}{ccc}\hfill 1& \hfill -2& \hfill 2\\ \hfill 1& \hfill -1& \hfill 2\\ \hfill 0& \hfill -1& \hfill 1\end{array}\right).$$

The next propositions provide necessary and sufficient conditions for an integer matrix to be decomposable in terms of its Hermite normal form.

Proposition 1.

Let $A\in {\mathbb{Z}}^{m\times n}$ and let $H=HNF\left(A\right)$. Then, A is decomposable if and only if H is decomposable.

Proof. 

Let $P_1$ be a unimodular matrix such that $P_1^{-1}A=H$. If A is decomposable, then $A_1\oplus \dots \oplus A_t=P_2^{-1}AQ=P_2^{-1}{P}_{1}HQ={\left(P_1^{-1}{P}_2\right)}^{-1}HQ$, for a unimodular matrix $P_2$ and a permutation matrix Q. Now, since $P_1^{-1}{P}_2$ is unimodular, we have that H is decomposable. Conversely, assume that H is decomposable, so there exist a unimodular matrix $P_3$ and a permutation matrix $Q_1$, such that $P_3^{-1}H{Q}_1=H_1\oplus \dots \oplus H_s$. Thus, $H_1\oplus \dots \oplus H_s=P_3^{-1}{P}_1^{-1}A{Q}_1={\left(P_1{P}_3\right)}^{-1}A{Q}_1$ and we are done. □

In the following, we use the symbol ⊤ to denote the transpose operation.

Proposition 2.

Let H be an $m\times n$ integer matrix in Hermite normal form. Then, H is decomposable if and only if there exist permutation matrices P and Q, such that $P^{\top }HQ$ decomposes into a direct sum of matrices.

Proof. 

First, we observe that if the rank of H is $r<m$, then the last $m-r$ rows of H are zero. As these rows do not affect the condition of H to be decomposable, we assume that H has rank m.

The sufficiency part is obvious since the permutation matrix P is unimodular and $P^{\top }=P^{-1}$. Conversely, if H is decomposable, there exist a unimodular matrix R and a permutation matrix Q such that $R^{-1}HQ=A_1\oplus \dots \oplus A_t.$ For simplicity, we assume that $t=2$. Let $P_1$ and $P_2$ be unimodular matrices, such that $H_1:=P_1^{-1}\left(A_1\right|0)Q^{\top }$ and $H_2:=P_2^{-1}\left(0\right|A_2)Q^{\top }$ are in Hermite normal form, and define the following matrix

$$B:=\left(\begin{array}{c}{H}_1\\ 1-1H_2\end{array}\right)={(P_1\oplus P_2)}^{-1}(A_1\oplus A_2)Q^{\top }=(P_1^{-1}{A}_1\oplus P_2^{-1}{A}_2)Q^{\top }.$$

Since the rank of B is m, each row of B contains a pivot element of $H_1$ or $H_2$. If we move the row containing the first (leftmost) pivot element to the first place, the row containing the second pivot element to the second place and so forth, the resulting matrix is necessarily in Hermite normal form. Thus, there exists a permutation matrix P such that $PB=H$, by the uniqueness of the Hermite normal form. Therefore, $H=PB=P(P_1^{-1}{A}_1\oplus P_2^{-1}{A}_2)Q^{\top }$ and we conclude that $P^{\top }HQ$ decomposes into $P_1^{-1}{A}_1\oplus P_2^{-1}{A}_2$. □

Example 2.

By Proposition 2, we can easily see that the matrix A in Example 1 is decomposable. Indeed,

$$\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right)HNF\left(A\right)\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1\end{array}\right)=\left(\begin{array}{ccccc}2& 0& 1& 0& 0\\ 0& 1& 2& 0& 0\\ 0& 0& 0& 2& 3\end{array}\right).$$

For symmetric matrices, decomposability can be refined to the more restrictive notion of reducibility. This notion has a rich combinatorial nature, because of its relationship with graph theory, as we will see later on.

Definition 3.

A symmetric matrix $B\in {\mathbb{Z}}^{n\times n}$ is reducible if there exists a permutation matrix Q such that $Q^{\top }BQ$ decomposes into a direct sum of square matrices. Otherwise B is said to be irreducible.

The following result gives a necessary and sufficient condition for an integer matrix to be decomposable in terms of the reducibility of a certain related symmetric matrix. To state our result we need a piece of notation.

Notation 1.

Let H be an $m\times n$ integer matrix in Hermite normal form. With the same notation as in Definition 2, we write $tim\left(H\right)$ for the $n\times n$ triangular integer matrix whose $j_i$-th row is the i-row of $H,i=1,\dots ,m$, and zeros elsewhere.

The following example illustrates the above notation.

Example 3.

If

$$H=\left(\begin{array}{ccccc}\hfill 1& \hfill 1& \hfill -2& \hfill 0& \hfill 0\\ \hfill 0& \hfill 2& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 3& \hfill 2\end{array}\right),$$

then

$$tim\left(H\right)=\left(\begin{array}{ccccc}\hfill 1& \hfill 1& \hfill -2& \hfill 0& \hfill 0\\ \hfill 0& \hfill 2& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 3& \hfill 2\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right).$$

Observe that the matrix $tim\left(H\right)$ is not necessarily in Hermite normal form.

Lemma 1.

Let H be an $m\times n$ integer matrix in Hermite normal form. If H is decomposable, then there exists a permutation matrix Q such that $Q^{T}tim\left(H\right)Q$ decomposes into a direct sum of triangular matrices; in particular, $tim\left(H\right)$ is decomposable.

Proof. 

By Proposition 2, there exist permutation matrices $P_0$ and Q, such that $P_0^{\top }HQ$ decomposes into a direct sum of matrices. Clearly, adding rows and columns to $P_0$ conveniently, we may construct an $n\times n$ permutation matrix $P_1$ such that $P_1^{\top }tim\left(H\right)Q=H_1^{\prime }\oplus \dots \oplus H_t^{\prime }$. Matrices $H_i^{\prime },i=1,\dots ,t$ are not necessarily triangular. However, since $tim\left(H\right)$ is triangular, there exists a permutation matrix $P_2$ such

$${\left(P_1{P}_2\right)}^{\top }tim\left(H\right)Q=P_2^{\top }(P_1^{\top }tim\left(H\right)Q)=H_1\oplus \dots \oplus H_t$$

where $H_i$ is triangular for every $i\in \{1,\dots ,t\}$. Now, since ${\left(P_1{P}_2\right)}^{\top }tim\left(H\right)Q$ and $tim\left(H\right)$ are both triangular, we conclude that $P_1{P}_2$ and Q are identical up to permutation of the zero rows of ${\left(P_1{P}_2\right)}^{\top }tim\left(H\right)Q$. □

Theorem 1.

Let A be an $m\times n$ integer matrix. If $H=HNF\left(A\right)$, then A is decomposable if and only if

$$tim\left(H\right)+tim{\left(H\right)}^{\top }$$

is reducible.

Proof. 

By Proposition 1, we may assume that $A=H$. Now, if H is decomposable, by Lemma 1, there exists a permutation matrix Q, such that $Q^{\top }tim\left(H\right)Q=H_1\oplus \dots \oplus H_t$, with $H_i,i=1,\dots ,t,$ triangular. Therefore,

$$\begin{array}{cc}\hfill Q^{\top }(tim\left(H\right)+tim{\left(H\right)}^{\top })Q& =Q^{\top }tim\left(H\right)Q+Q^{\top }tim{\left(H\right)}^{\top }Q=\hfill \\ & =Q^{\top }tim\left(H\right)Q+{(Q^{\top }tim\left(H\right)Q)}^{\top }=\hfill \\ \hfill & =H_1\oplus \dots \oplus H_t+{(H_1\oplus \dots \oplus H_t)}^{\top }=\hfill \\ & =H_1\oplus \dots \oplus H_t+H_1^{\top }\oplus \dots \oplus H_t^{\top }=\hfill \\ & =(H_1+H_1^{\top })\oplus +\dots +\oplus (H_1+H_t^{\top }),\hfill \end{array}$$

and we conclude that $tim\left(H\right)+tim{\left(H\right)}^{\top }$ is reducible.

Conversely, if $tim\left(H\right)+tim{\left(H\right)}^{\top }$ is reducible, then there exists a permutation matrix Q, such that $Q^{\top }(tim\left(H\right)+tim{\left(H\right)}^{\top })Q=H_1\oplus \dots \oplus H_t$. Now, since $tim\left(H\right)$ is triangular, we have that $Q^{\top }(tim\left(H\right)-tim{\left(H\right)}^{\top })Q=H_1^{\prime }\oplus \dots \oplus H_t^{\prime }$, with $H_i^{\prime }$ having the same order than $H_i$, for each $i\in \{1,\dots ,t\}$, respectively. So, it follows that

$$\begin{array}{cc}\hfill Q^{\top }tim\left(H\right)Q& =Q^{\top }\left(\frac{1}{2}\left(tim\left(H\right)+tim{\left(H\right)}^{\top }\right)+\frac{1}{2}\left(tim\left(H\right)-tim{\left(H\right)}^{\top }\right)\right)Q=\hfill \\ \hfill & -\frac{1}{2}\left((H_1+H_1^{\prime })\oplus \dots \oplus (H_t+H_t^{\prime })\right),\hfill \end{array}$$

and we conclude that $tim\left(H\right)$ is decomposable. □

Example 4.

We already know that the matrix A in Example 1 is decomposable. Thus, in the light of Theorem 1, the symmetric matrix $B:=tim(HNF\left(A\right))+tim{(HNF\left(A\right))}^{\top }$ must be reducible. Indeed,

$$B=\left(\begin{array}{ccccc}4& 0& 0& 1& 0\\ 0& 4& 0& 0& 3\\ 0& 0& 2& 2& 0\\ 1& 0& 2& 0& 0\\ 0& 3& 0& 0& 0\end{array}\right),$$

and

$$Q^{\top }BQ=\left(\begin{array}{ccccc}4& 0& 1& 0& 0\\ 0& 2& 2& 0& 0\\ 1& 2& 0& 0& 0\\ 0& 0& 0& 4& 3\\ 0& 0& 0& 3& 0\end{array}\right),\mathit{with}Q=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1\end{array}\right).$$

3. The Simple Graph of a Integer Matrix. HNF-Decomposition Algorithm

An important advantage of dealing with symmetric matrices is their strong combinatorial meaning: any symmetric matrix $B=\left(b_{ij}\right)\in {\mathbb{Z}}^{n\times n}$ can be considered as the adjacency matrix of an undirected graph ${\mathcal{G}}_B$ with n vertices $\{1,\dots ,n\}$, such that $\{i,j\}$ is an edge of ${\mathcal{G}}_B$ if and only if $i\ne j$ and $b_{ij}\ne 0$.

Note that we are not concerned with diagonal elements and magnitudes of B to construct ${\mathcal{G}}_B$.

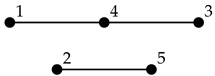
Example 5.

The graph ${\mathcal{G}}_B$ corresponding to the matrix B in Example 4 is

Notice that ${\mathcal{G}}_B$ is not connected in this case.

Clearly, a symmetric matrix B is reducible if and only if the graph ${\mathcal{G}}_B$ is not connected. Thus, by Theorem 1, we can study the reducibility of an integer matrix A by means of the graph ${\mathcal{G}}_B$ for $B=tim(HNF\left(A\right))+tim{(HNF\left(A\right))}^{\top }$ as follows.

Corollary 1.

Let $A\in {\mathbb{Z}}^{m\times n}$ and set $B=tim(HNF\left(A\right))+tim{(HNF\left(A\right))}^{\top }.$ Then A is decomposable if and only if ${\mathcal{G}}_B$ is not connected.

Note 1. 

Given $A\in {\mathbb{Z}}^{m\times n}$, the graph ${\mathcal{G}}_B$, with $B=tim(HNF\left(A\right))+tim{(HNF\left(A\right))}^{\top }$, can be constructed directly from $H=HNF\left(A\right)$. Indeed, with the notation of Definition 2, it suffices to observe that $\{i,j\}\in {\mathcal{G}}_B$ if, and only if, $h_{j_{i}j}\ne 0$. Therefore, all the information concerning the decomposability of A is encoded in H.

We finalize this note by giving an algorithm for the computation (if possible) of the decomposition of an $m\times n$ integer matrix into the direct sum matrices in Hermite normal form.

Let G be the adjacency matrix of an undirected simple graph $\mathcal{G}$. Recall that the degree of the i-vertex of $\mathcal{G}$ is

$$d_i:=\sum _{\{i,j\}\in \mathcal{G}}1,$$

and the Laplacian matrix of $\mathcal{G}$ is $D-G$, where D is the diagonal matrix with diagonal entries $(d_1,\dots ,d_n)$.

The second part of the following result is well-known; however, for lack of a reference we sketch a proof.

Proposition 3.

Let $\mathcal{G}$ be an undirected simple graph on n vertices. Then, $\mathcal{G}$ has t connected components if and only if the Laplacian matrix of $\mathcal{G}$ has rank $n-t$. In this case, the connected components of $\mathcal{G}$ are completely determined by the reduced row echelon form of the Laplacian matrix of $\mathcal{G}$.

Proof. 

The first statement follows from the well-known matrix-tree theorem (see, e.g., [9] (Section 1) and the references therein). Let us analyze the second statement with a little more detail. First, we observe that the Laplacian matrix of a connected graph on n vertices is an order n symmetric matrix of rank $n-1$ whose columns sum to zero. So, its reduced row echelon form is equal to

$$\left(\begin{array}{ccccc}\hfill 1& \hfill 0& \hfill \dots & \hfill 0& \hfill -1\\ \hfill 0& \hfill 1& \hfill \dots & \hfill 0& \hfill -1\\ \hfill ⋮& \hfill ⋮& \hfill \ddots & \hfill ⋮& \hfill ⋮\\ \hfill 0& \hfill 0& \hfill \dots & \hfill 1& \hfill -1\\ \hfill 0& \hfill 0& \hfill \dots & \hfill 0& \hfill 0\end{array}\right).$$

Thus, if V is the reduced row echelon of the Laplacian matrix of a (non-necessarily connected) undirected simple graph on n vertices, then if the j-th column, ${\mathbf{v}}_j$, of V is not a pivot column, the set of vertices of the connected component containing the vertex j is $\left\{j\right\}\cup supp\left({\mathbf{v}}_j\right)$, where $\mathrm{supp}\left({\mathbf{v}}_j\right):=\{i\mid v_{ij}\ne 0\}$ denotes the support of ${\mathbf{v}}_j.$ □

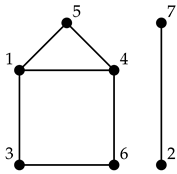
Example 6.

Consider the graph $\mathcal{G}$ with vertex-set $\{1,2,3,4,5\}$ and edges $\{1,4\},\{2,5\},\{3,4\}$. The Laplacian matrix of $\mathcal{G}$ is

$$\left(\begin{array}{ccccc}\hfill 1& \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0\\ \hfill -1& \hfill 0& \hfill -1& \hfill 2& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0& \hfill 1\end{array}\right)$$

and its reduced row echelon form is

$$R:=\left(\begin{array}{ccccc}\hfill 1& \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right).$$

Now, we can read from R that $\mathcal{G}$ has the following two connected components: the subgraph with vertices $\{\mathit{4},1,3\}$ and the subgraph with vertices $\{\mathit{5},2\}$.

The previos proposition is the last piece needed to ensure the correctness of Algorithm 1. We discuss below some aspects of Algorithm 1.

Comments to Algorithm 1:

• Steps (1)–(6) provide unimodular matrices $P_0$ and Q, such that $P_0^{-1}AQ=\tilde{P}(A_1\oplus \dots \oplus A_t)$, for some permutation matrix $\tilde{P}$;
• Clearly $t=n-rank\left(L\right)$; moreover, we have that $rank\left(L\right)={\sum }_{k=1}^t{\ell }_k$;
• If $n-rank\left(L\right)=1$ then A is not decomposable. In this case $A_1=HNF\left(A\right)$ and Q is the identity matrix. Otherwise, if A is decomposable, we cannot guarantee that $\tilde{P}=I_m$ and that the matrices $A_i,i=1,\dots ,t$, are in Hermite normal form. However, since $HNF\left(A_1\right)\oplus \dots \oplus HNF\left(A_t\right)=HNF(A_1\oplus \dots \oplus A_t)$, by the uniqueness of the Hermite normal form, step (7) provides the matrix $P_1$ such that $P_1^{-1}{P}_0^{-1}AQ$ is in Hermite normal form as desired;
• By Note Section 3, we may replace the Step (2) by

  (2)

  Let B be the adjacency matrix of the graph $\mathcal{G}$ with vertices $\{1,\dots ,n\}$ such that $\{i,j\}\in \mathcal{G}$ if and only if $h_{j_{i}j}\ne 0$.

  This is advantageous for small n.
• An HNF-decomposition, if it exists, is not unique. It depends on the choice of the order of the columns of the matrices $Q_i,i=1,\dots ,t$ and the order in which these matrices are placed.

Example 7.

The matrix

$$H=\left(\begin{array}{ccccccc}1& 0& 1& 1& 2& 0& 0\\ 0& 1& 0& 0& 0& 0& 3\\ 0& 0& 3& 0& 0& 3& 0\\ 0& 0& 0& 2& 1& 2& 0\end{array}\right)$$

is in Hermite normal form and its associated graph $\mathcal{G}$ (see Note 1) is

Therefore, H is a decomposable matrix. Of course, we do not need to construct the graph $\mathcal{G}$ to compute an HNF-decomposition of H.

In order to compute effectively two matrices P and Q such that $P^{-1}HQ$ is in HNF-decomposed form, we compute the reduced row echelon form, R, of the Laplacian matrix of ${\mathcal{G}}_B,$ for $B=tim\left(H\right)+tim{\left(H\right)}^{\top }$,

$$R=\left(\begin{array}{ccccccc}\hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 1& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right).$$

Now, following Steps (5)–(7) in Algorithm 1, we may take the matrix Q equal to $\left({\mathbf{e}}_6\right|{\mathbf{e}}_1\left|{\mathbf{e}}_3\right|{\mathbf{e}}_4\left|{\mathbf{e}}_5\right|{\mathbf{e}}_7\left|{\mathbf{e}}_2\right),$ in this case, the corresponding matrix P is

$$\left(\begin{array}{cccc}\hfill 0& \hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\\ \hfill 3& \hfill 0& \hfill -1& \hfill 0\\ \hfill 2& \hfill 0& \hfill -1& \hfill 0\end{array}\right).$$

Now, we can check that

$$P^{-1}HQ=\left(\begin{array}{ccccccc}\hfill 1& \hfill 0& \hfill 3& \hfill -2& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 1& \hfill 1& \hfill 2& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 6& \hfill -6& \hfill -3& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 0& \hfill 3& \hfill 1\end{array}\right).$$

As mentioned above, other choices of Q determine a different P and, consequently, another HNF-decomposition, equivalent to the one given.

4. Conclusions and Future Work

Using the Hermite normal form as the main tool, we have obtained a theoretical criterion to determine whether a given integer matrix decomposes into a direct sum of lower order integer matrices.

This criterion allows us to associate a simple graph to the integer matrix whose connectedness determines the decomposition of the integer matrix and facilitates the formulation of an algorithm to decompose an integer matrix into a direct sum of matrices in Hermite normal form, provided such decomposition exists.

Our results have immediate applications to the study of affine semi-groups and semi-group algebras; in fact, this was our original motivation for tackling this problem. However, we believe that our results can be generalized to matrices with entries in any Euclidean ring further than $\mathbb{Z}$.

Since we were only interested in decomposition issues, we underestimated a lot of information from B when constructing the graph ${\mathcal{G}}_B$. Alternatively, B can be considered as the adjacency matrix of an (undirected) weighted graph ${\mathcal{G}}_B$ with n vertices $\{v_1,\dots ,v_n\}$, where the weight of the edge $\{v_i,v_j\}$ is $b_{ij}$. This alternative graph is sensitive to all the information recorded in the entries of B. One might wonder if this alternative graph can be used to provide information for integer matrices, beyond decomposability and reducibility.