Abstract
Fault-crossing tunnels are often severely damaged under seismic dynamics. Study of the dynamic response characteristics of tunnels crossing faults is thus of great engineering significance. Here, the Xianglushan Tunnel of the Central Yunnan Water Diversion Project was studied. A shaking table experimental device was used, and four sets of dynamic model tests of deep-buried tunnels with different fault inclination angles were conducted. Test schemes of model similarity ratio, similar material selection, model box design, and sine wave loading were introduced. The acceleration and strain data of the tunnel lining were monitored. Analysis of the acceleration data showed that when the input PGA was 0.6 g, compared with the ordinary tunnel, the acceleration increases by 117% when the inclination angle was 75°, 127% when the inclination angle was 45°, and 144% when the inclination angle was 30°. This indicates that the dynamic response of the cross-fault tunnel structure was stronger than that of the ordinary tunnel, and the effect was more obvious as the fault dip angle decreased. Analysis of the strain data showed that the strain response of the fault-crossing tunnels was more sensitive to the fault dip. The peak strain and increase in fault-crossing tunnels were much larger than those of ordinary tunnels, and smaller fault dips led to larger increases in the strain peak; consequently, the tunnel would reach the ultimate strain and break down when the input PGA was smaller. Generally, the influence of fault inclination on the dynamic response of the tunnel lining should receive increased consideration in the seismic design of tunnels.
1. Introduction
Tunnel structures are restrained by surrounding rocks. It has long been thought that tunnel structures have better seismic resistance and sustain less damage compared with above–ground structures [1,2]. However, in many earthquake disasters, such as the 1999 Chi-Chi earthquake in Taiwan, China, and the 2008 Wenchuan earthquake in China, tunnels displayed varying degrees of damage. Fault–crossing tunnel structures were easily affected by the earthquake fault zone, the structure shear deformation of the lining structure was large, and the surrounding rock quality was poor [3,4,5,6]. With the continuous advancement of China’s western development strategy, tunnels often inevitably cross-fault fracture zones and weak interlayers, and the western region features frequent seismic activities. Therefore, study of the dynamic response law and failure mechanism of cross-fault tunnels is critically important for ensuring tunnel safety.
Tunnels crossing faults and fracture zones are the weak links of tunnel seismic resistance. Even if effort is made to avoid potentially problematic areas, high-intensity seismic zones and fracture zones cannot be completely avoided [7,8,9,10]. Consequently, much research has focused on the seismic dynamic response and anti-seismic problems of tunnels crossing faults, and several insightful conclusions have been made. Kun et al. [11] investigated the dangerous area around a shallow subway tunnel in weak fault rock and found that the deformation of the tunnel causes surface settlement and greater damage to the surface structure. Corigliano et al. [12] used a pseudo–static method combined with a kinematics method to analyze the seismic dynamic response of deep-buried tunnels across faults. Yang et al. [13] used the three–dimensional discrete element model to describe the nonlinear dynamic failure process of the tunnel fault system under the action of strong earthquakes. Based on the viscous–spring artificial boundary finite element method, Huang et al. [14] revealed that the most serious plastic damage occurred at the point where the tunnel crosses the fault under seismic dynamics, followed by the fault hanging wall. Guan et al. [15] conducted a shaking table model test of a tunnel crossing a large section, studied the seismic response and seismic performance of a large section mountain tunnel, and concluded that the existence of a large section significantly changed the seismic performance of the tunnel. Baziar et al. [16] conducted centrifugal model tests of tunnels with different buried depths through faults and characterized the interaction effects of tunnels with different depths. Shen and Yan et al. [17,18] found that the tunnel structure at the fault sustains more serious damage and that the lining of the hanging wall of the fault is more likely to be damaged than the lining of the footwall, respectively.
The research described above has mainly focused on the influence of the fault zone on the dynamic response characteristics of the tunnel. However, the location, thickness, and dip of the fault zone also have a major effect on the tunnel. Jeon et al. [19,20] studied the influence of fault location on tunnel stability and concluded that when the fault was located on the upper part of the tunnel, the displacement of the top of the tunnel was greater than that when the fault was located on the left side of the tunnel. Jeon [21] conducted a comparative study including a scale model test and numerical simulation and found that the deformation amount and the size of the plastic zone increase as the distance between the fault and tunnel decreases. Based on the finite element method, Zhang et al. [22] studied the influence of fault location and fault thickness on the deformation, stress, and plastic zone of the tunnel surrounding rock. Ardeshiri–Lajimi et al. [23] established a numerical model of the fault-underground cavern system under seismic excitation and obtained the influence law of the fault dip and location on the underground cavern. Liu et al. [24] considered the influence of the normal fault inclination on the dynamic response of the tunnel lining and conducted multiple sets of shaking table model tests. They found that the range of the fracture shear zone increases as the fault dip decreases and proposed corresponding reinforcement measures.
Most previous research has focused on the influence of fault location and thickness on tunnels; by contrast, the fault dip angle has been seldom studied. Similarly, the fault dip is a significant factor affecting the stability of the tunnel. The dip of the fault affects the propagation path of the dynamic load, resulting in different dynamic responses at different positions of the tunnel lining, and at the same position of the tunnel lining, the dynamic response will be different due to the different fault dip. Therefore, it is worth paying attention to exploring the dynamic response law of tunnels with different fault inclination angles.
Here, the Xianglushan Tunnel was studied, and four sets of tunnel model shaking table tests (three sets of fault–crossing tunnels and one set of ordinary tunnels) were carried out. In Section 2, the test device of the tunnel shaking table is introduced. In Section 3, the model design of fault–crossing tunnels and ordinary tunnel is introduced. According to the acceleration and strain data, the dynamic response difference of tunnel lining under different fault inclination angles was compared and analyzed in Section 4. Finally, the dynamic response and failure mechanism of tunnels crossing different fault dips were briefly summarized in Section 5 to provide a reference for the seismic fortification of tunnels crossing faults.
2. Experimental Equipment
2.1. Shaking Table
The shaking table device of the experimental base of Nanjing Institute of Hydraulic Research was used in this experiment. The electric vibration test system model was an electric vibration test system with horizontal sliding table (DLS), which was composed of a DL–3000 electric vibration table body, SA–40 power amplifier, and vibration control instrument. The size of the small shaking table is 1.1 × 1.1 m2. Because the focus of this model test was to reveal the dynamic response law of tunnel linings under different fault inclination angles, the small-scale shaking table test is low in cost, rapid and can be tested multiple times. The specific parameters of the vibration table are shown in Table 1.

Table 1.
Parameters of vibration table.
2.2. Model Box
The rigid model box was used in the model test. As shown in Figure 1a, the size of the test model box was 1000 mm × 950 mm × 850 mm (length × width × height) (inner dimensions). It was welded by 20 mm plexiglass plates and ribbed around, which ensured that the entire model test system was stiff and strong. A drill was used to make holes in the bottom glass plate, and 34 high-strength bolts were used to fix the box on the shaking table. The reliability of the box moving with the shaking table during the vibration process was guaranteed. For the boundary processing of the model box, 10 cm-thick polystyrene foam was used as the boundary condition around the model box, and the outer layer of the foam board was covered with a layer of polyethylene plastic. This way, the contact friction between the surrounding rock and the foam board was reduced [25,26]. At the bottom of the model box, a layer of gravel was bonded by solid glue. The relative slip between the surrounding rock and the bottom plexiglass plate could be effectively prevented, and the boundary conditions of the tunnel prototype could be better reproduced (Figure 1b).

Figure 1.
Model box. (a) Model box; (b) boundary effect mitigation measures for model box.
3. Shaking Table Test
3.1. Tunnel Prototype
Xianglushan Tunnel is a controlling project in the Central Yunnan Water Diversion Project in Yunnan Province, China. The regional geological conditions are complex: many fault fracture zones with different dip angles are crossed by tunnels, and the fault fracture zone is characterized by poor surrounding rock geological conditions as well as stratum transition from soft rock to hard rock or from hard rock to soft rock. These areas were the places where the tunnel seismic damage was concentrated.
According to the geological conditions of the prototype tunnel, the model test tunnel had a circular cross-section with a diameter of 8.4 m, grade V surrounding rock, and fault angles of 30°, 45°, and 75°. Three sets of cross-fault dip angle tunnel model tests were carried out, in addition to a set of ordinary tunnel model tests (not crossing the fault). The length of the model tunnel is 80 cm, the outer diameter of the lining is 9.4 cm, and the thickness of the lining is 1 cm. The surrounding rock conditions for ordinary tunnels were the same as those for fault-crossing tunnels. The ordinary tunnel model test was used as the control group, and the influence of the cross-fault dip on the tunnel response characteristics was revealed.
3.2. Design of the Similitude Relation
The shaking table model test was a dynamic test. The physical and mechanical similarities of the static model and the dynamic model should both be satisfied. According to the law of similarity, the equation analysis method and dimensional analysis method were employed [27,28], and related physical similarity parameters could be obtained by derivation. The influence of the inclination of the fault on the tunnel under the action of an earthquake was studied in the test. Therefore, the model test and the prototype needed to be in the same gravity field. Combined with the relevant parameters of the shaking table test instrument, the length, density, and acceleration were used as the control variables. According to the prototype size of the tunnel and the size of the shaker device, the geometric similarity ratio, density similarity ratio, and acceleration similarity ratio were determined. According to the Buckingham theorem, the similarity relations and similarity ratios of other physical quantities were derived (Table 2).

Table 2.
Similarity relations and ratios of the shaking table test.
3.3. Model Materials
According to the results of the on-site rock core drilling test, metamorphic rocks (schist sandwiched mainly by shallow metamorphic limestone), magmatic rocks (mainly basalt and andesite), and sedimentary rocks (carbonate and sand-mudstone) crossed by the tunnel. The surrounding rock was mainly grade V. According to the engineering rock mass test method, a batch of 50 100 mm surrounding rock test blocks were made, and the RMT150 testing machine was used to perform uniaxial compression tests on the core drilling test. The mechanical parameters are shown in Table 3. With the similarity relationship and similarity ratio of the shaking table model test in the previous section, the similar material of the tunnel surrounding rock was determined. Quartz sand, cement, and detergent were used as similar materials for the surrounding rock in the test [15]. Through several indoor uniaxial compression tests, the mass ratio of similar materials of grade V surrounding rock was determined as m (quartz sand):m (cement):m (washing detergent) = 5.6:2.8:1 (Table 3).

Table 3.
Surrounding rock parameters of the prototype and model.
The lining material was gypsum-based material with similar properties to the original model C25 concrete lining. Gypsum, quartz sand, barite powder, and water prepared in a certain proportion were used as lining model materials. Standard cylindrical specimens of 50 100 mm were used, and the above-mentioned materials in different proportions were poured into prefabricated molds. After the specimens achieved a certain strength, the molds were removed and placed in an incubator for curing. A uniaxial compression test was conducted on an RMT150 testing machine. Finally, the mass ratio of gypsum, quartz sand, barite powder, and water was 1.0:1.0:1.6:1.2. Cement, fine sand, and sawdust were used as materials of the crushing belt, and the volume ratio was 1:1:1 (Table 4). The setting of the inclination of the fault was based on the previously marked partition position, the calculated position was placed in parallel, and the partition was tilted to the angle required for the test. For the fault layout, the inclination angle, position and thickness of the fault were determined by two parallel diaphragms, and then the broken belt material was poured in layers and compacted by layers.

Table 4.
Lining parameters of the prototype and model.
3.4. Sensor Layout
Accelerometer sensors and resistance strain sensors were used for every test condition. Seven accelerometers (model JY901) with the measuring range of ±16 m/s2, sensitivity of 2000 mv/g, and dimensions of 20 mm × 20 mm × 5 mm were used. Forty-eight resistance strain sensors (model BF350) with a resistance value of 120 ± 0.2 Ω, dimensions of 40 mm × 8 mm, sensitivity of 2.0 ± 1%, and accuracy class of A were used. The strain gauge was connected with the special copper wire by the connector.
The sensor layout is shown in Figure 2. The layout scheme of the acceleration of the transverse section of the tunnel is shown in Figure 2a. Figure 2a shows the layout plan of the transverse section acceleration of the tunnel. The layout plan of the cross-section of the four test conditions was the same. A0 was the measuring point on the shaking table, and A1–A6 were the monitoring points on different sections, which were arranged on the vault and the inverted arch. Figure 2b,c show the longitudinal section acceleration and strain sensor arrangement schemes of ordinary tunnels and fault-crossing tunnels. Three cross-sections—B–B, C–C and D–D—were monitored at the fault and 200 mm from the left and right of the fault (Figure 2) to examine the seismic response of the lining in the axial direction. Figure 2d shows the layout of the strain gauges on the three monitoring surfaces. A symmetrical layout of the inside and outside was used.
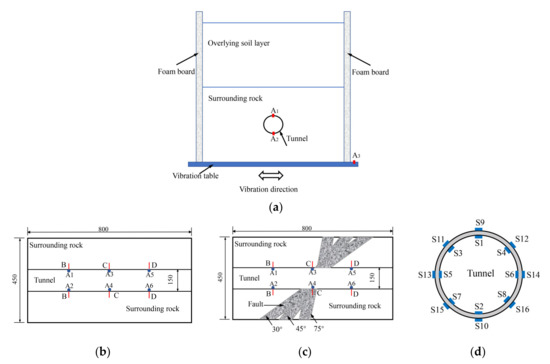
Figure 2.
Test arrangement. (a) Accelerometer sensors in cross–section; (b) accelerometer sensors in longitudinal cross–section for an ordinary tunnel; (c) accelerometer sensors in longitudinal cross–section for a fault–crossing tunnel; (d) strain sensors in the tunnel section. (unit: mm).
3.5. Model Fabrication
To better simulate the Xianglushan Tunnel, the tunnel lining, surrounding rock, and broken zone materials were prefabricated in sections and poured in layers. (1) For the lining production, the steel mold was prefabricated in sections and cured for 7 days at room temperature. The sensor was installed at the marked position, and then the section lining was bonded and formed with solid glue. (2) The surrounding rock material was mixed on site, and the elevation position of the layered pouring was marked in the model box in advance; the layered layer was used for compaction. The thickness of each compaction was 100 mm to ensure compact compaction [29]. (3) The crushing belt material was also mixed on site, and two partitions were made, which were placed in parallel according to the calculated position. This could prevent the surrounding rock material from slipping to the broken zone area; the broken zone material was poured by layered pouring and layered compaction. (4) According to the geological conditions of the site, the upper covering layer of the prototype tunnel was simulated with a grade V surrounding rock material with a thickness of 20 cm. After all of the pouring was completed, it was cured at room temperature for two days, and then the vibration test was carried out. The concrete construction drawing of the model is shown in Figure 3.
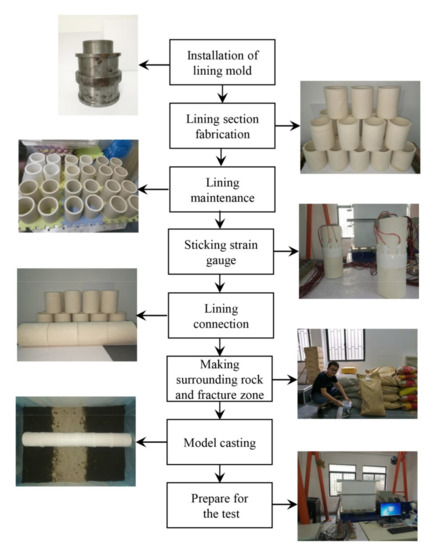
Figure 3.
Model building steps.
3.6. Test Schemes
Sine waves of different frequencies were used as the input seismic motion, and the time history and Fourier spectrum of the input motion are shown in Figure 4. There were a total of 18 test cases in which the same sine wave was multiplied by an increasing factor, and the peak ground acceleration (PGA) was 0.1 g, 0.2 g, 0.4 g, 0.6 g, 0.8 g and 1.0 g (g = 9.81 m/s2). The input frequencies of the model were 5 Hz, 7.5 Hz and 10 Hz. Transverse vibration under uniform seismic excitation was used in the test. This model test was a destruction test. Before the lining structure was destroyed, the above working conditions were loaded as much as possible. The sine wave peak intensity incremental loading method was used in the test; at each PGA, there were three loading frequencies, and the frequencies were also loaded sequentially from low to high. The test plan is shown in Table 5.
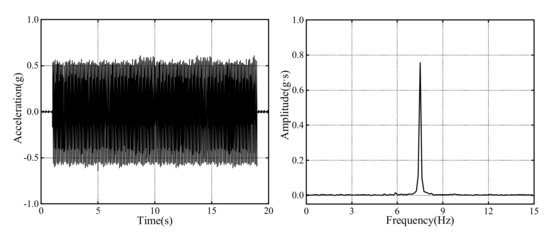
Figure 4.
Acceleration–time history and its corresponding Fourier spectrum (0.6 g).

Table 5.
Test cases.
4. Test Results
4.1. Boundary Effect
The surrounding rock near the prototype tunnel is in a semi-infinite state, whereas the model tunnel is in a constrained state. In the model box, the restraint of the model tunnel can be effectively alleviated by the surrounding flexible boundary materials. Therefore, a deviation index based on 2–norm is introduced to quantitatively describe the research boundary effect [30,31]. It can be calculated by the following formula:
where is the 2–norm deviation index, and and are the acceleration peaks of the acceleration sensor on the lining and the acceleration sensor on the vibrating table, respectively, as the target signal and the reference signal. In this model experiment, corresponds to A1, A3, and A5, and corresponds to A0.
Figure 5 shows the 2-norm curve diagram under different input PGAs under various working conditions. Figure 5a–c are the 2–norm deviation diagrams of section B–B, section C–C, and section D–D, respectively. The deviation index of 2–norm reflects the difference between the two signals. If the value of μ is zero, the two signals are exactly the same. Under different sections, the value was the largest when the fault dip was 30°, followed by 45°. The ordinary tunnel was the smallest, which meant that a smaller fault dip corresponded to a greater deviation in the acceleration response signal from the reference signal. The value of each section was less than 0.315, indicating that the test results would not be affected by boundary effects.
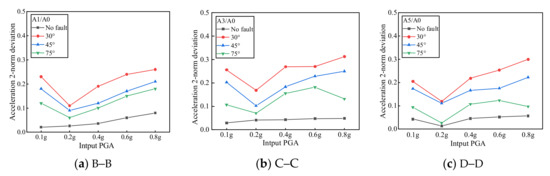
Figure 5.
Norm-2 index in the tunnel. (a) Section B–B; (b) Section C–C; (c) Section D–D.
4.2. Acceleration Response
4.2.1. Acceleration Time History
Because of the large amount of test data, the A3 (crown) and A4 (invert) test points on section C–C were used for analysis in the four sets of test conditions. Figure 6 shows the acceleration time history curves and their corresponding Fourier spectra of different working conditions at an input acceleration of 0.6 g and a frequency of 7.5 Hz. The acceleration time history curves were all sinusoidal fluctuations; the fluctuation range of the crown was larger than that of the invert. The main frequency of vibration was 7.5 Hz, which was the same as the input frequency, indicating that the fault did not affect the fluctuation variation law and the main frequency of vibration. However, there were obvious differences in the acceleration fluctuation range and Fourier amplitude under different working conditions. In Figure 6a, the acceleration peaks at the crown and invert were 0.68 g and 0.66 g, and the Fourier amplitudes were 0.68 gs and 0.65 gs, respectively. Figure 6b shows that the peak accelerations at the crown and invert were 0.94 g and 0.91 g, and the Fourier amplitudes were 0.83 gs and 0.78 gs, respectively. In Figure 6c, the acceleration peaks at the crown and invert were 0.84 g and 0.80 g, and the Fourier amplitudes were 0.77 gs and 0.73 gs, respectively. Figure 6d shows that the acceleration peaks at the dome and invert were 0.75 g and 0.74 g, and the Fourier amplitudes were 0.75 gs and 0.74 gs, respectively. The acceleration peak value and Fourier amplitude of the fault-crossing tunnels were obviously larger than those of the ordinary tunnel, indicating that the fault had an amplifying effect on the acceleration response.
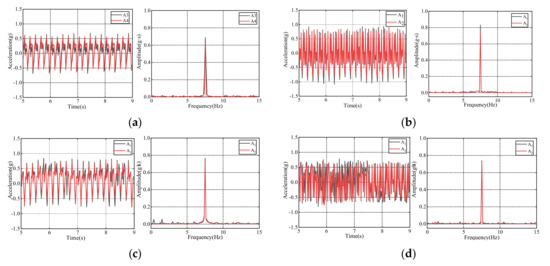
Figure 6.
Acceleration–time histories and their corresponding Fourier spectra of A3 (Crown) and A4 (Invert). (a) No fault; (b) dip angle of 30°; (c) dip angle of 45°; (d) dip angle of 70°.
4.2.2. Peak Acceleration
Figure 7 shows a histogram of acceleration peaks on three sections under four test conditions. Under the same peak acceleration (0.6 g), the peak acceleration of the crown on each section decreased as the fault dip decreased, and the peak acceleration of the ordinary tunnel was the smallest. Taking the peak acceleration of ordinary tunnel as the control group, the increase amplitude of peak acceleration under different inclination angles was calculated. Table 6 shows the peak increase range of the dome under different working conditions. At the crown, the peak increase of section C–C increased the most as the dip angle decreased, and the peak increase of section B–B was slightly larger than that of section D–D. Section C–C was at the fault location, and B–B was at the fault’s hanging wall, which meant that the fault would aggravate the acceleration dynamic response and make the acceleration changes on both sides of the fault appear asymmetrical. Figure 7b shows the acceleration peak diagrams of each section at the invert measurement points under different working conditions, which have the same law as the crown. Table 7 shows the increase amplitude of the peak acceleration at the invert under different working conditions. When the dip angle was 75°, the increase amplitude was between 108% and 117%. When the dip angle was 45°, the increase range was 115–127%. When the dip angle was 30°, the increase range was 126–144%. As the dip angle decreases, the increase was greater, indicating that the increasing effect of the fault dip on the acceleration response could not be ignored.
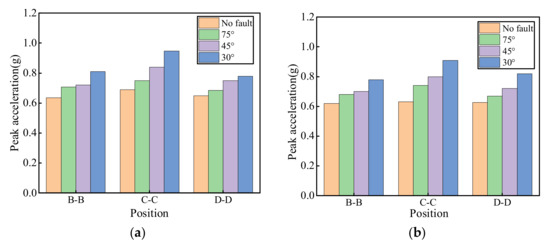
Figure 7.
Acceleration peaks on each section under different fault dips. (a) Crown; (b) invert.

Table 6.
Peak increase amplitude value at the crown.

Table 7.
Peak increase amplitude value at the invert.
The acceleration peak amplification factor was defined as the ratio of the peak acceleration collected by the measuring point to the input peak acceleration [26,32,33]. The distribution diagram of the amplification factor of each cross-section measuring point under the four test conditions is shown in Figure 8. When PGA was 0.1–0.4 g, the amplification factor decreases uniformly. When PGA was 0.4–0.8 g, the amplification coefficient decreased sharply. This was because in the early stage of vibration, the surrounding rock underwent a large movement, and the input PGA value was high, leading to the nonlinear development of surrounding rock and an increase in the damping and energy dissipation of surrounding rock. On different sections, the magnification factor of each test condition in Figure 8b was greater than that in Figure 8a,c, which was related to the location of fault C–C. The fault worsened the constraint effect of the surrounding rock and strengthened the tunnel response. Smaller fault dips resulted in larger magnification factors. Because the contact area between the fault and the tunnel increases as the dip angle decreases, a smaller distance between the fault tunnel led to a greater acceleration response.
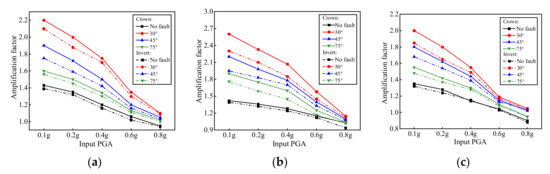
Figure 8.
Variation of amplification factor with input PGA at crown. (a) Section B–B; (b) Section C–C; (c) Section D–D.
The acceleration peak ratio α was defined as the ratio of the output acceleration peak value of the fault–crossing tunnels and the ordinary tunnel at the same measuring point. Figure 9 shows a graph of acceleration peak ratios under different test conditions and under different input PGAs. Figure 9a is a graph of the peak acceleration ratio of different test conditions on each section when the input PGA was 0.1 g. The figure shows that the three curves all have a triangular distribution; thus, a large value of α on the section C–C means that the vibration response at the fault was relatively strong. The dip angle was the largest at 30°, followed by 45°, and the smallest at 75°; the maximum was 1.83. Figure 9b–d show the acceleration peak ratio graphs when the PGA was 0.2 g, 0.4 g, and 0.6 g, respectively. As the PGA increased, the distribution law of the α value remained unchanged, but the α value continued to decrease. Therefore, the response at the fault is strong, and as the dip of the fault decreased, this effect became more pronounced. Cracks could be easily produced and cause structural damage, and the seismic design of the tunnel was unfavorable.
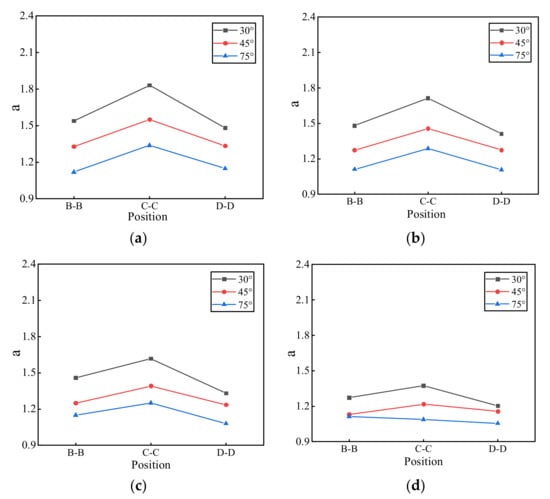
Figure 9.
Acceleration peak ratio of different input PGAs. (a) 0.1 g; (b) 0.2 g; (c) 0.4 g; (d) 0.6 g.
4.3. Strain Response
4.3.1. Dynamic Strain
Much research has shown that the crown, invert, arch shoulder, and arch springing of tunnel lining are easily damaged under strong earthquakes [23,34,35,36,37]. Therefore, this paper focused on the monitoring points on the inner and outer sides of the crown and invert and analyzed the dynamic strain response characteristics of the tunnel lining under different fault dip angles. Figure 10 shows the strain time history curves of the inner and outer sides of the upper dome and invert of section C–C under different test conditions. When the input PGA was 0.6 g, the strain time history curve fluctuations of the monitoring points of each working condition were similar to the input wave waveform, and they were all sinusoidal fluctuation curves. The strain value of the internal monitoring point was greater than that of the external monitoring point. The strain value of the monitoring points inside and outside the crown fluctuates in the range of negative values, and the strain value fluctuates within the range of positive values inside and outside the invert, indicating that the vault was in compression and the invert was in tension. However, the strain value of the lining at each monitoring point cannot be restored to zero, resulting in residual strain. The main reason for this pattern is that the surrounding rocks of the tunnel underwent permanent deformation under the action of the input wave, which caused additional seismic strain after the lining was vibrated. However, the strain value of the measuring point on each test condition was quite different. When the dip angle was 30°, the strain value and fluctuation range were the largest, followed by the dip angle of 45°, and the dip angle of 75° was the smallest. These three experimental conditions were much larger than the normal tunnel in the control group. Therefore, a smaller fault dip results in a greater seismic load applied to the tunnel lining across the fault.
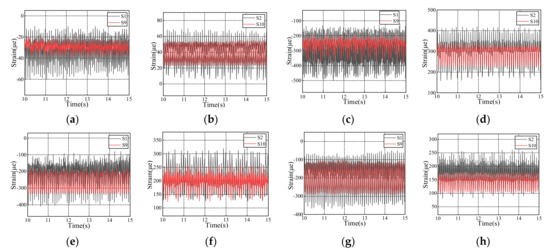
Figure 10.
Strain–time history curve under different test conditions. (a) Crown of ordinary tunnel; (b) invert of ordinary tunnel; (c) crown of the tunnel with a fault angle of 30°; (d) invert of the tunnel with a fault angle of 30°; (e) crown of the tunnel with a fault angle of 45°; (f) invert of the tunnel with a fault angle of 45°; (g) crown of the tunnel with a fault angle of 75°; and (h) invert of the tunnel with a fault angle of 75°.
4.3.2. Peak Strain
Figure 11 shows the peak strain when the input PGA is 0.6 g. Histograms of the strain peaks of the three monitoring sections are shown under four test conditions. In Figure 11a, the peak strain of the crown on each section increases as the dip angle decreases. The maximum strain peaks of the monitored sections B–B, C–C, and D–D were −410 με, −500 με, and −350 με, respectively. The strain peak at the fault was the largest, and the tunnel far away from the fault had a smaller strain value during vibration. Figure 11b was a graph of the peak strain of the invert measuring points on each section. The maximum strain peaks of the monitored sections B–B, C–C, and D–D were 320 με, 420 με, and 280 με, respectively. In sum, the fault clearly increases the strain response amplitude at section C–C, the axial strain response law was changed, and the strain peak values at different fault dip angles were different.
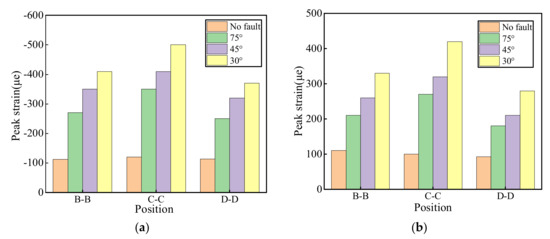
Figure 11.
Peak strain of each section. (a) Crown; (b) invert.
Therefore, according to Figure 11a,b, taking the peak strain of the ordinary tunnel as the control group, the increase amplitude of the peak strain at different inclination angles was calculated (Table 8 and Table 9). When the dip angle was 75° at the crown, the increase range in the peak strain was 212–292% (Table 8). When the dip angle was 45°, the increase range was 283–342%. When the dip angle was 30°, the increase range was 327–417%. When the dip angle was 75°, the peak strain increase range was 191–270% (Table 9). When the dip angle was 45°, the increase range was 228–320%. When the dip angle was 30°, the increase range was 300–420%. The above data reveal that there was little difference in the increase range of the dip angles of 75° and 45°, but the increase range was greatly increased from 45° to 30°. This shows that the strain response of the tunnel was more sensitive to the dip angle of the fault. A smaller dip angle led to a greater increase in the peak strain.

Table 8.
Magnification ratio of the peak strain of crown.

Table 9.
Magnification ratio of the peak strain of invert.
The above analysis reveals that the strain peak value of section C–C was the largest. Therefore, section C–C was used to study the response law under different PGAs. Figure 12 shows the strain peaks at different monitoring points on section C–C under different PGAs. Figure 12a is a graph of the peak strain changes at the monitoring points inside and outside the crown under different test conditions. The monitoring point at the crown was compressive strain, and the peak value of negative strain under various working conditions was increasing. However, with the increase of PGA, the increasing rate of peak value of strain was decreasing. The peak strains of the internal monitoring points were larger than those of the external monitoring points. As the dip angle of the fault decreases, the difference between the internal and external strain peaks increased. In Figure 12b, the monitoring point at the invert was tensile strain; as the PGA increased, the peak value of normal strain increased. In general, the peak strain and increase in the fault–crossing tunnels were far greater than those of ordinary tunnels. The dip angle of 30° was the largest, followed by the dip angle of 45°, and the dip angle of 75° was the smallest.
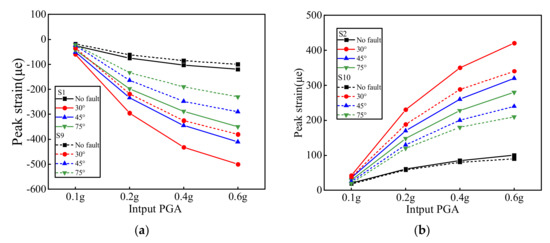
Figure 12.
Peak strain for different PGAs (Section C–C). (a) Crown; (b) invert.
The peak strain ratio (β) was defined as the ratio of the dynamic strain peak value of cross-fault tunnel and ordinary tunnel at the same section C–C monitoring point [27]. Figure 13 shows the strain peak ratio under different test conditions on section C–C. Figure 13a shows the β diagram of the monitoring points inside and outside the crown under different PGAs. The β values were all greater than 1 and increased as input PGA increased. When the PGA was 0.2 g, the increase in the β values was larger and then tended to plateau. The β values of different inclination angles differed; the dip angle of 30° was the largest, and 75° was the smallest. Figure 13b shows the β diagram of the monitoring points inside and outside the inverted arch under different PGAs, and the distribution law was the same as that of Figure 13a. According to the above analysis, the seismic strain of the tunnel lining was increased by about 1.2–4.2 times by the fault, which significantly increased the lining strain. As a result, the tunnel would be destroyed under a small PGA input, and the seismic resistance of the tunnel lining structure would be weakened.
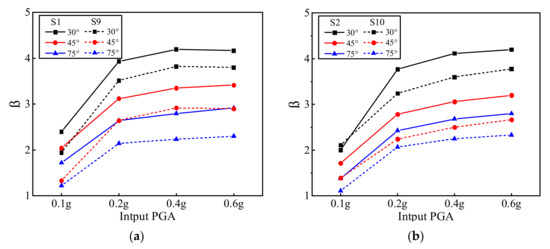
Figure 13.
Peak strain ratio (β) for different PGAs (Section C–C). (a) Crown; (b) invert.
5. Conclusions
Based on the prototype of the Xianglushan Tunnel Project in Central Yunnan, shaking table model tests were used to study the dynamic response characteristics of tunnel structures under different fault inclination angles (30°, 45° and 75°). The results of the four groups of experiments were compared, which were three groups of cross–fault tunnels and one group of ordinary tunnels. The acceleration and dynamic strain response characteristics of tunnel lining across different fault dip angles were discussed, and some insightful suggestions for specific engineering design were proposed. The main conclusions are as follows:
- (1)
- Compared with the ordinary tunnel, the acceleration fluctuation law of the tunnel under different fault inclination angles was similar, and the main frequency of vibration was the same as the input frequency. However, the fault–crossing tunnels had a significant amplification effect on acceleration, and the dip angle of different faults differed. When the dip angle was 30°, the acceleration amplification factor was the largest, 45° was in the middle, and 75° was the smallest, indicating that the fault intensifies the acceleration amplification: the smaller the fault dip, the more significant the amplification effect.
- (2)
- Compared with the acceleration peaks of different sections in ordinary tunnels, the acceleration response law in the axial direction was changed by the fault. The acceleration peaks of the sections at the fault were significantly larger than the sections on both sides. In addition, when the inclination angle was 75°, the acceleration range was 108%–117%; when the inclination angle was 45°, the increase range was 115%–127%; and when the inclination angle was 30°, the increase range was 126%–144%. As the inclination of the fault decreases, the tunnel acceleration response becomes stronger, indicating that the smaller the fault dip, the stronger the dynamic response of the tunnel lining structure.
- (3)
- Under the four test conditions, the difference in the peak strain of the inner and outer cross-sections was small, even at some monitoring points. Along the tunnel axis, the strain peaks of each test condition were quite different, and the strain peaks at the faults were larger than those of the other sections. Smaller dip angles corresponded to larger strain peaks. From the perspective of tunnel seismic resistance, smaller fault dip angles led to a stronger dynamic response, which was not conducive to tunnel seismic resistance.
- (4)
- Compared with the ordinary tunnel strain response, when the input acceleration was 0.6 g, the strain values of the cross–section at the fault were magnified. When the dip angle was 75°, the peak strain of the crown was magnified by 2.7 times, at 45° by 3.2 times, and at 30° by 4.2 times. This shows that as the dip angle of the fault decreases, the magnification continues to increase. Smaller dip angles led to sharper increases. Because of the limitations of the experimental conditions, only three sets of fault dip angles and one group of ordinary tunnels were examined in this experiment to analyze the dynamic response law of tunnel lining across different fault dip angles. Additional research is needed to identify the change rule under other dip angles. However, the selection of the inclination angle of this experiment and many conclusions of this study are generalizable to other similar tunnel projects.
Author Contributions
The paper was written by D.Z. under the guidance of Z.Z. and C.Z. The project administration was carried out by Z.Z. The data curation and methodology were proposed and by D.Z. and X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (No.2015CB057903), the National Natural Science Foundation of China (NO. 41831278) and supported by the Fundamental Research Funds for the Central Universities and Postgraduate Research and Practice Innovation Program of Jiangsu Province number (2019B74214, SJKY19_04533).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study. Written informed consent has been obtained from the patient(s) to publish this paper.
Data Availability Statement
The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kontoe, S.; Zdravkovic, L.; Potts, D.M.; Menkiti, C.O. Case study on seismic tunnel response. Can. Geotech. J. 2008, 45, 1743–1764. [Google Scholar] [CrossRef] [Green Version]
- Bao, Z.; Yuan, Y.; Yu, H. Multi-scale physical model of shield tunnels applied in shaking table test. Soil Dyn. Earthq. Eng. 2017, 100, 465–479. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Bobet, A.; Yuan, Y. Damage observation and assessment of the Longxi tunnel during the Wenchuan earthquake. Tunn. Undergr. Space Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, Z. Seismic damage classification and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Shen, Y.; Gao, B.; Yang, X.; Tao, S. Seismic damage mechanism and dynamic deformation characteristic analysis of mountain tunnel after Wenchuan earthquake. Eng. Geol. 2014, 180, 85–98. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gerolymos, N.; Drosos, V.; Georgarakos, T.; Kourkoulis, R.; Gazetas, G. Behaviour of deep immersed tunnel under combined normal fault rupture deformation and subsequent seismic shaking. Bull. Earthquake Eng. 2008, 6, 213–239. [Google Scholar] [CrossRef]
- Zhen, D.Z.; Cong, Z.; Jun, W.; Peng, Z.; Duan, Z. Cyclic Loading Test for the Small-Strain Shear Modulus of Saturated Soft Clay and Its Failure Mechanis. Geofluids. 2021, 6, 1–13. [Google Scholar]
- Fan, L.; Chen, J.L.; Peng, S.Q.; Qi, B.X.; Zhou, Q.W.; Wang, F. Seismic response of tunnel under normal fault slips by shaking table test technique. J. Cent. South Univ. 2020, 27, 1306–1319. [Google Scholar] [CrossRef]
- Tsinidis, G.; de Silva, F.; Anastasopoulos, I.; Bilotta, E.; Bobet, A.; Hashash, Y.M.A.; He, C.; Kampas, G.; Knappett, J.; Madabhushi, G.; et al. Seismic behaviour of tunnels: From experiments to analysis. Tunn. Undergr. Space Technol. 2020, 99, 10334. [Google Scholar] [CrossRef]
- Kun, M.; Onargan, T. Influence of the fault zone in shallow tunneling: A case study of Izmir Metro Tunnel. Tunn. Undergr. Space Technol. 2013, 33, 34–45. [Google Scholar] [CrossRef]
- Corigliano, M.; Scandella, L.; Lai, C.G.; Paolucci, R. Seismic analysis of deep tunnels in near fault conditions: A case study in Southern Italy. Bull Earthquake Eng. 2011, 9, 975–995. [Google Scholar] [CrossRef]
- Yang, Z.; Lan, H.; Zhang, Y.; Gao, X.; Li, L. Nonlinear dynamic failure process of tunnel-fault system in response to strong seismic event. J. Asian Earth Sci. 2013, 64, 125–135. [Google Scholar] [CrossRef]
- Huang, J.; Zhao, M.; Du, X. Non-linear seismic responses of tunnels within normal fault ground under obliquely incident P waves. Tunn. Undergr. Space Technol. 2017, 61, 26–39. [Google Scholar] [CrossRef]
- Guan, Z.; Zhou, Y.; Gou, X.; Huang, H.; Wu, X. The seismic responses and seismic properties of large section mountain tunnel based on shaking table tests. Tunn. Undergr. Space Technol. 2019, 90, 383–393. [Google Scholar] [CrossRef]
- Baziar, M.H.; Nabizadeh, A.; Lee, C.J.; Hung, W.Y. Centrifuge modeling of interaction between reverse faulting and tunnel. Soil Dyn. Earthq. Eng. 2014, 65, 151–164. [Google Scholar] [CrossRef]
- Shen, Y.S.; Wang, Z.Z.; Yu, J.; Zhang, X.; Gao, B. Shaking table test on flexible joints of mountain tunnels passing through normal fault. Tunn. Undergr. Space Technol. 2019, 98, 103299. [Google Scholar] [CrossRef]
- Yan, G.; Gao, B.; Shen, Y.; Zheng, Q.; Fan, K.; Huang, H. Shaking table test on seismic performances of newly designed joints for mountain tunnels crossing faults. Adv. Struct. Eng. 2020, 23, 248–262. [Google Scholar] [CrossRef]
- Jung-Woo, C.; Seokwon, J.; Sang-Hwa, Y. Optimum spacing of TBM disc cutters: A numerical simulation using the three-dimensional dynamic fracturing method. Tunn. Undergr. Space Technol. 2010, 25, 230–244. [Google Scholar]
- Dohyun, P.; Byungkyu, J.; Seokwon, J. A Numerical Study on the Screening of Blast-Induced Waves for Reducing Ground Vibration. Rock Mech. Rock Eng. 2009, 42, 449–473. [Google Scholar]
- Jeon, S.; Kim, J.; Seo, Y.; Hong, C. Effect of a fault and weak plane on the stability of a tunnel in rock—A scaled model test and numerical analysis. Int. J. Rock Mech. Min. Sci. 2004, 41, 658–663. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, F.; Li, N.; Swoboda, G.; Liu, N. Influence of fault on the surrounding rock stability of a tunnel: Location and thickness. Tunn. Undergr. Space Technol. 2017, 61, 1–11. [Google Scholar] [CrossRef]
- Ardeshirilajimi, S.; Yazdani, M.; Langroudi, A.A. Control of fault lay-out on seismic design of large underground caverns. Tunn. Undergr. Space Technol. 2015, 50, 305–316. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Sang, Y.; Lin, L. Experimental study on normal fault rupture propagation in loose strata and its impact on mountain tunnels. Tunn. Undergr. Space Technol. 2015, 49, 417–425. [Google Scholar] [CrossRef]
- Gaskin, Z.A. Shaking table testing of geofoam seismic buffers. Soil Dyn. Earthq. Eng. 2007, 27, 324–332. [Google Scholar]
- Wang, Z.Z.; Jiang, Y.J.; Zhu, C.A.; Sun, T.C. Shaking table tests of tunnel linings in progressive states of damage. Tunn. Undergr. Space Technol. 2015, 50, 109–117. [Google Scholar] [CrossRef]
- Ciulla, G.; D’Amico, A.; Brano, V.L. Evaluation of building heating loads with dimensional analysis: Application of the Buckingham π theorem. Energy Build. 2017, 154, 479–490. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Jiang, L.; Gao, Y. Shaking table test of seismic response of immersed tunnels under effect of water. Soil Dyn. Earthq. Eng. 2019, 116, 436–445. [Google Scholar] [CrossRef]
- Xin, C.L.; Wang, Z.Z.; Gao, B. Shaking table tests on seismic response and damage mode of tunnel linings in diverse tunnel-void interaction states. Tunn. Undergr. Space Technol. 2018, 77, 295–304. [Google Scholar] [CrossRef]
- Chen, J.; Shi, X.; Li, J. Shaking table test of utility tunnel under non-uniform earthquake wave excitation. Soil Dyn. Earthq. Eng. 2010, 30, 1400–1416. [Google Scholar] [CrossRef]
- Ding, X.; Feng, L.; Wang, C.; Han, L. Shaking table tests of the seismic response of a utility tunnel with a joint connection. Soil Dyn. Earthq. Eng. 2020, 133, 106–133. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A. Nonlinear Soil-Site Effects in Probabilistic Seismic-Hazard Analysis. B. Seismol. Soc. Am. 2004, 94, 2110–2123. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Z.D.; Zhu, S.; He, Z.; Zhu, D.; Liu, J.; Meng, S. Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory. Materials 2019, 12, 1505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, J.; He, S.; Qiu, J.; Chen, J.; Wang, L.; Wang, K.; Wang, J. Characteristics of seismic disasters and aseismic measures of tunnels in Wenchuan earthquake. Environ. Earth Sci. 2017, 76, 94. [Google Scholar] [CrossRef]
- Bahrampouri, M.; Rodriguez-Marek, A.; Bommer, J.J. Mapping the uncertainty in modulus reduction and damping curves onto the uncertainty of site amplification functions. Soil Dyn. Earthq. Eng. 2018, 02, 022. [Google Scholar] [CrossRef]
- Dhulipala, S.L.; Rodriguez-Marek, A.; Bahrampouri, M. Intensity Measure Adequacy Assessment for Nonlinear Site Response using Information Theory. Soil Dyn. Earthq. Eng. 2020, 134, 106144. [Google Scholar] [CrossRef]
- Zhu, Z.D.; Zhang, C.; Meng, S.S.; Zheng, Y.S.; Shan, Z.T.; Duan, Z. A Statistical Damage Constitutive Model Based on the Weibull Distribution for Alkali-Resistant Glass Fiber Reinforced Concrete. Materials 2019, 12, 1908. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).