3.1. Diurnal Temperature Fluctuation
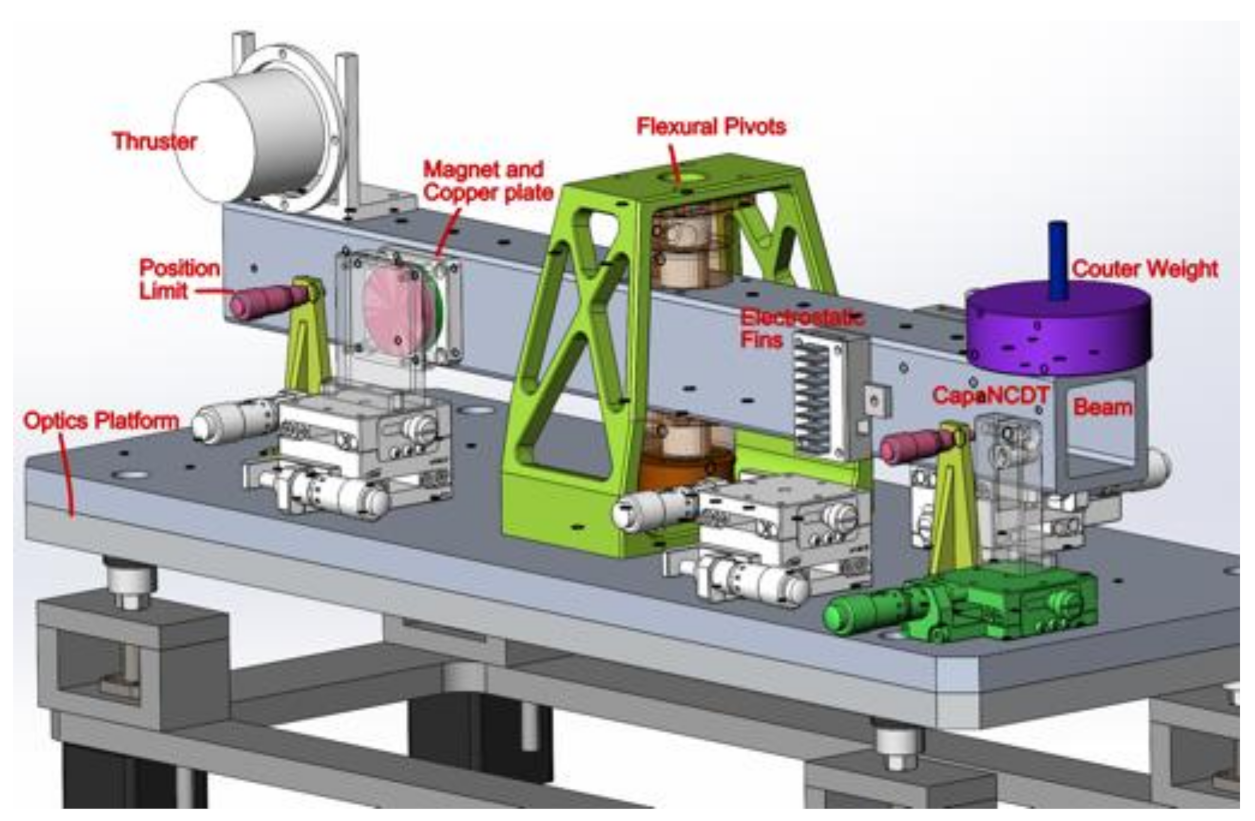
In order to provide a stable environment, the setup is placed on a passive vibration isolation optical platform and a windshield is used to prevent turbulence. The torsional stiffness coefficient of the flexural point is 0.245
, and the measuring moment arm was 0.18 m, so as to record the displacement by a capacitive sensor with a resolution lower than 1 nm at a sampling frequency of 5.21 Hz. As shown in
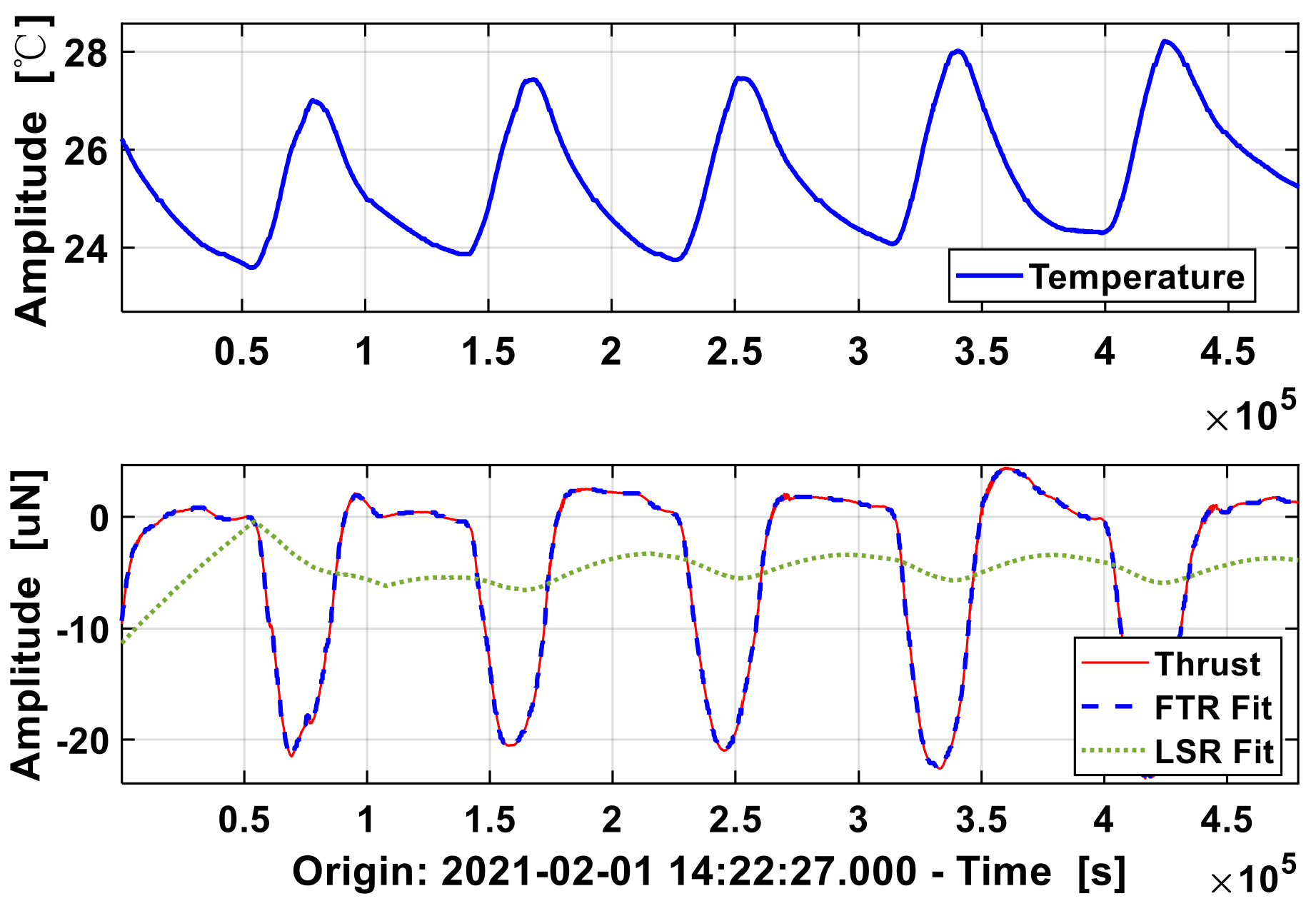
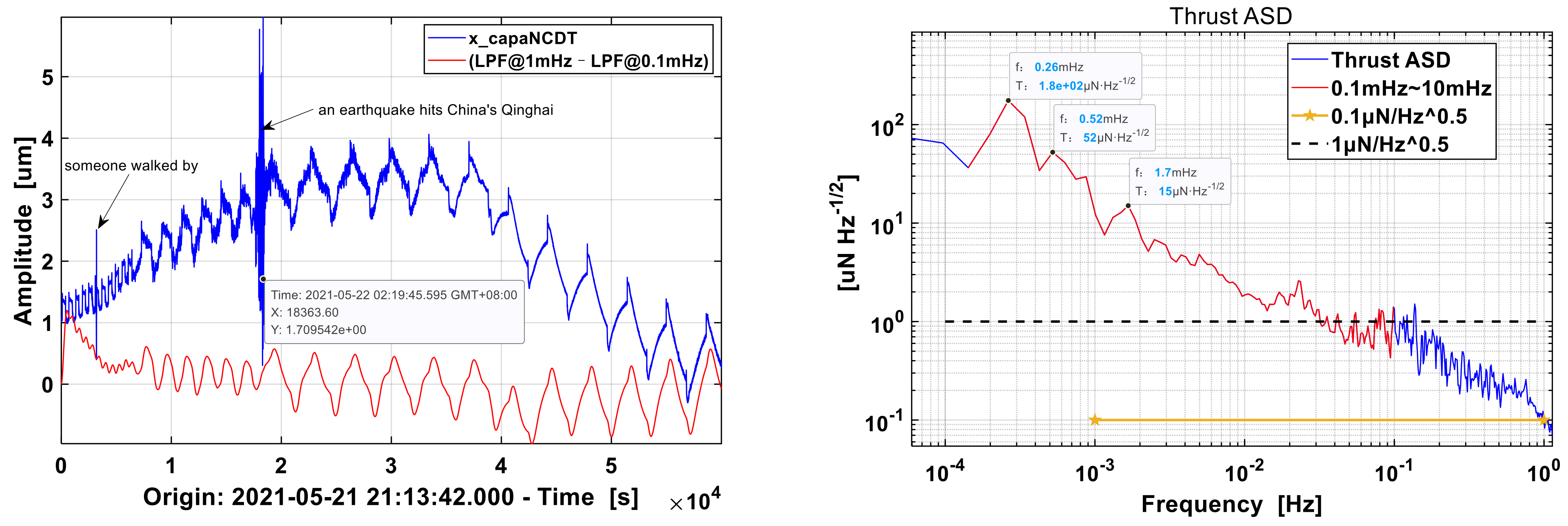
Figure 2, the temperature fluctuated between 24–28 °C, and the thrust of the torsion balance fluctuated between 0–20 μN after debias, showing a strong correlation with the diurnal alternation. As shown in
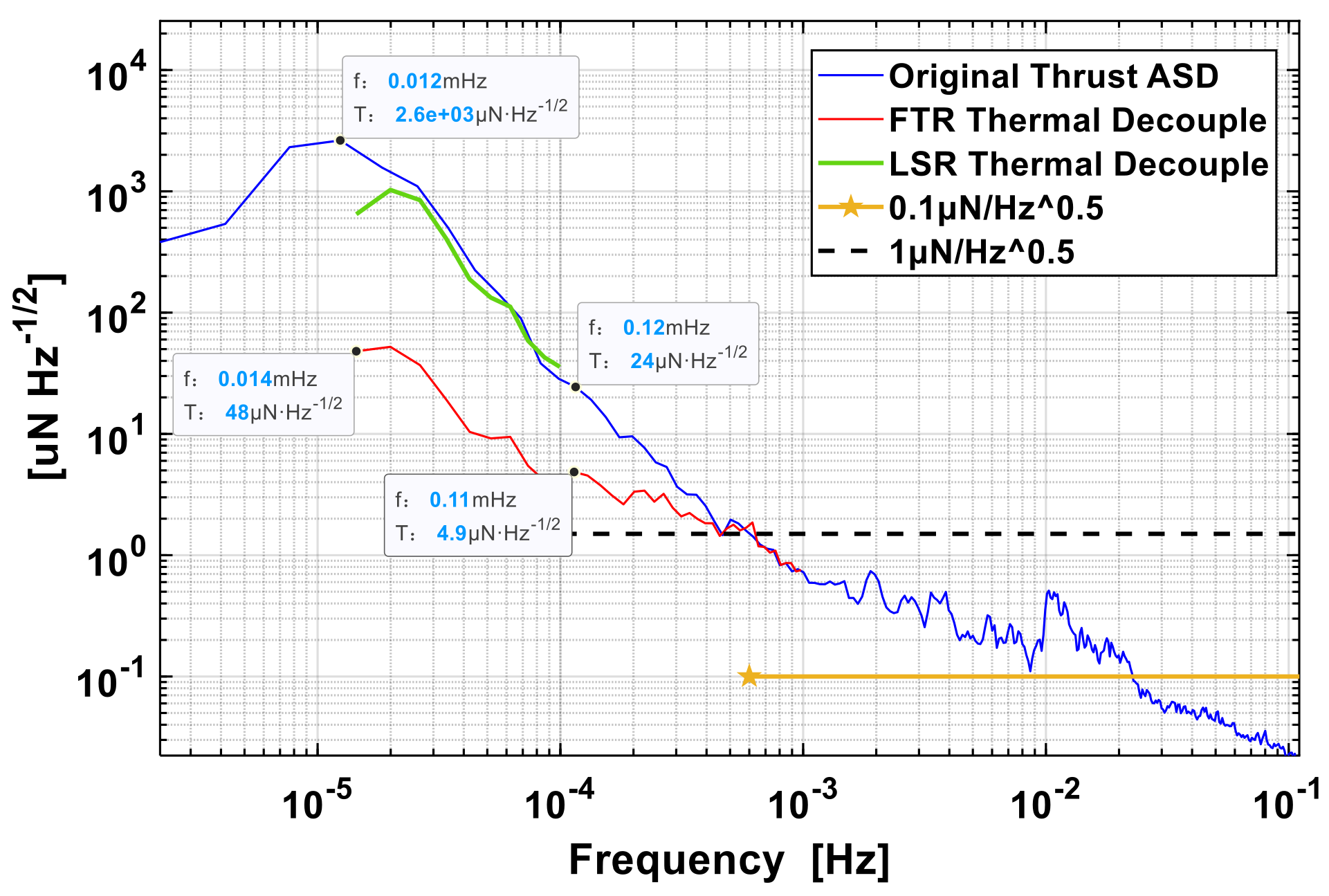
Figure 3, the thrust noise amplitude spectral density is less than 1 μN/Hz
1/2 at 1 mHz, but up to 24 μN/Hz at 0.12 mHz
1/2. The temperature change caused by thermal radiation of the sun amplifies the low frequency noise of the torsion balance below 1 mHz.
As the steps described earlier for thermal decoupling, displacement and temperature data are down-sampled to 0.1 Hz before regression learning. As shown in
Figure 2 below, the FTR fitted thrust (red dash line) is more accurate than that of LSR (green dot line), to predict the original the thrust and estimate transfer function. As shown in
Figure 3, thrust ASD (T-ASD) decreased from 0.11 mHz to 4.9 μN/Hz
1/2 after temperature drift correction, reduced to 48 μN/Hz
1/2 at 0.012 mHz (24-h), only 1/5th of the original. In addition, FTR has not only a larger amplitude decoupled than LSR does in fitting thermal thrust noise, but also a wider decoupled noise band of 1 mHz larger than 0.1 mHz of LSR. However, for the limitation of the temperature sampling frequency and the modulation transfer amplitude of the position PT1000 located, the noise reduction effect in this experiment is not obvious above 1 mHz, so shorter period temperature fluctuation is needed to testify.
3.2. Space-Time Variation of Temperature
The thermal decoupling of thrust is to subtract thermal effect from the displacement, and the perturbation is propagated from heat source (PTC) to PT1000 and torsion balance. Neither a strong temperature correlation between a PTC heater and a PT1000 sensor, nor a strong position correlation between the PT1000 and thrust response of torsion balance, means the correlation between thermal variation and thrust response of torsion balance. As shown in
Figure 4, one must first determine which point affects the deformation of torsion balance most, which means a location optimization of PTC heater or PT1000 sensor based on the covariance between their positions and thermal vibration of torsion balance. Meanwhile, thermal conduction is taken into consideration to magnify the temperature correlation between PTC heater and PT1000. Thus, an ideal temperature measuring point not only depends on the structure change of the torsion balance of PT1000 position, but also is closely related to the temperature changed by the heat source, for a good correlation with both sides is helpful to find the covariance and reduce thermal thrust noise.
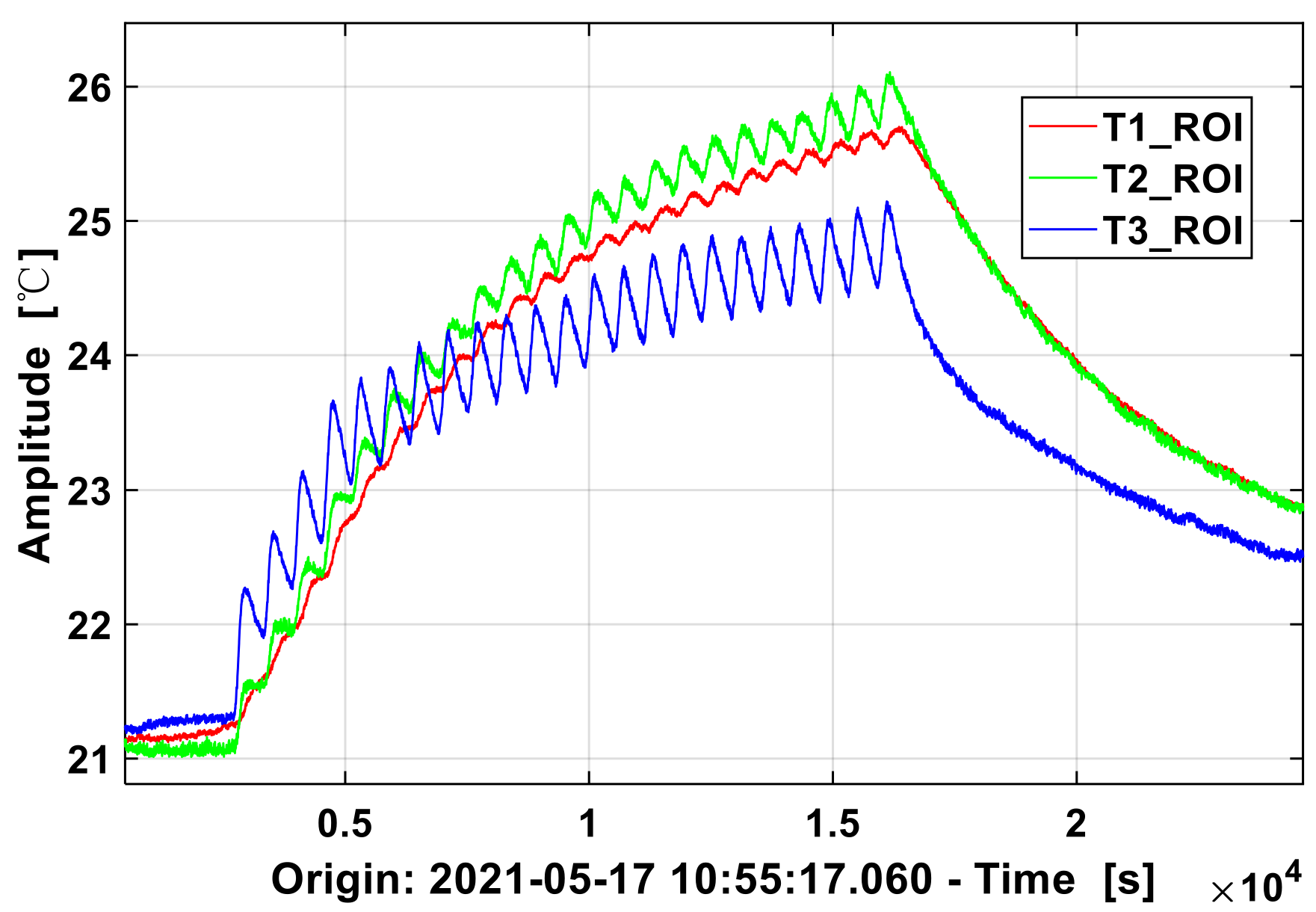
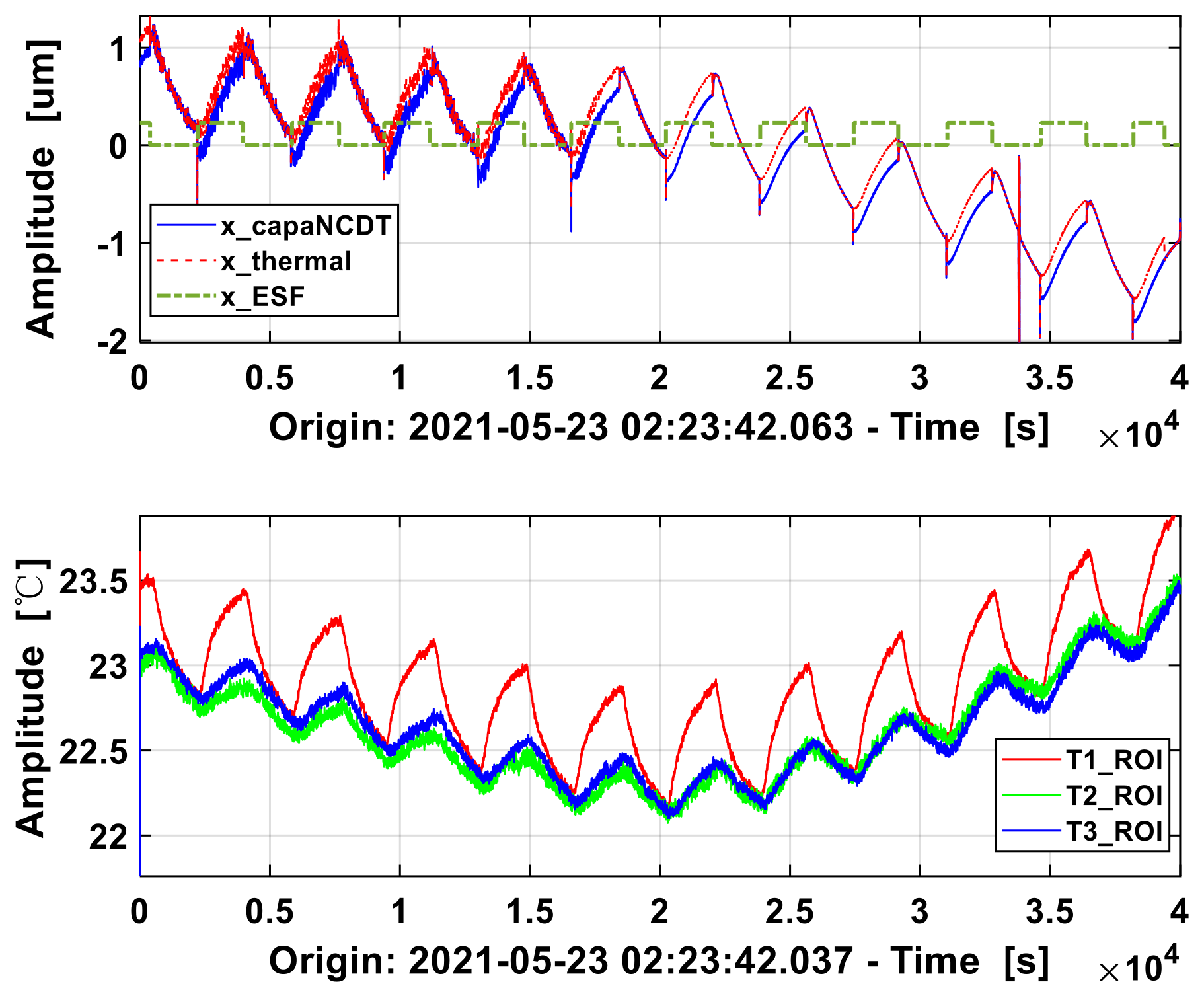
The relationship between the heat source and the temperature of the PT1000 sensor is discussed first. In order to shorten the experiment time compared with diurnal exposure, a heating pad was laid on the bottom of the base of torsion balance, and the relay switch was triggered regularly. The temperature at the flexible pivot (T1), the base of the torsion balance (T2) and the glass plate of the torsion balance (T3) were recorded at the sampling frequency of 0.1 Hz by heating for 2 min and turning off for 8 min. As shown in
Figure 5, under the action of heat source, T3 is the first place to receive the heat and starts to rise periodically from 2 °C and gradually converges to around 25 °C. The rise at T2 is delayed for the heat conduction is slower. However, after being heated up, the temperature converges to 26 °C, which is higher than T3 and close to the heat source. T1 is furthest away from the heat source and has the smallest heat exchange area, thus the fluctuation during heating is the least. Due to the delay of heat, when one point is in a heating period, the other point may be in a cooling period. The heat dissipation rates at different locations of the system reflects the eigen frequency. Rising fast and falling slow, the temperature showed hysteresis characteristics when the structure is repeatedly heated, which also aggravates the deformation, stiffness degradation and energy consumption of the torsional balance structure in the process of thermodynamic equilibrium.
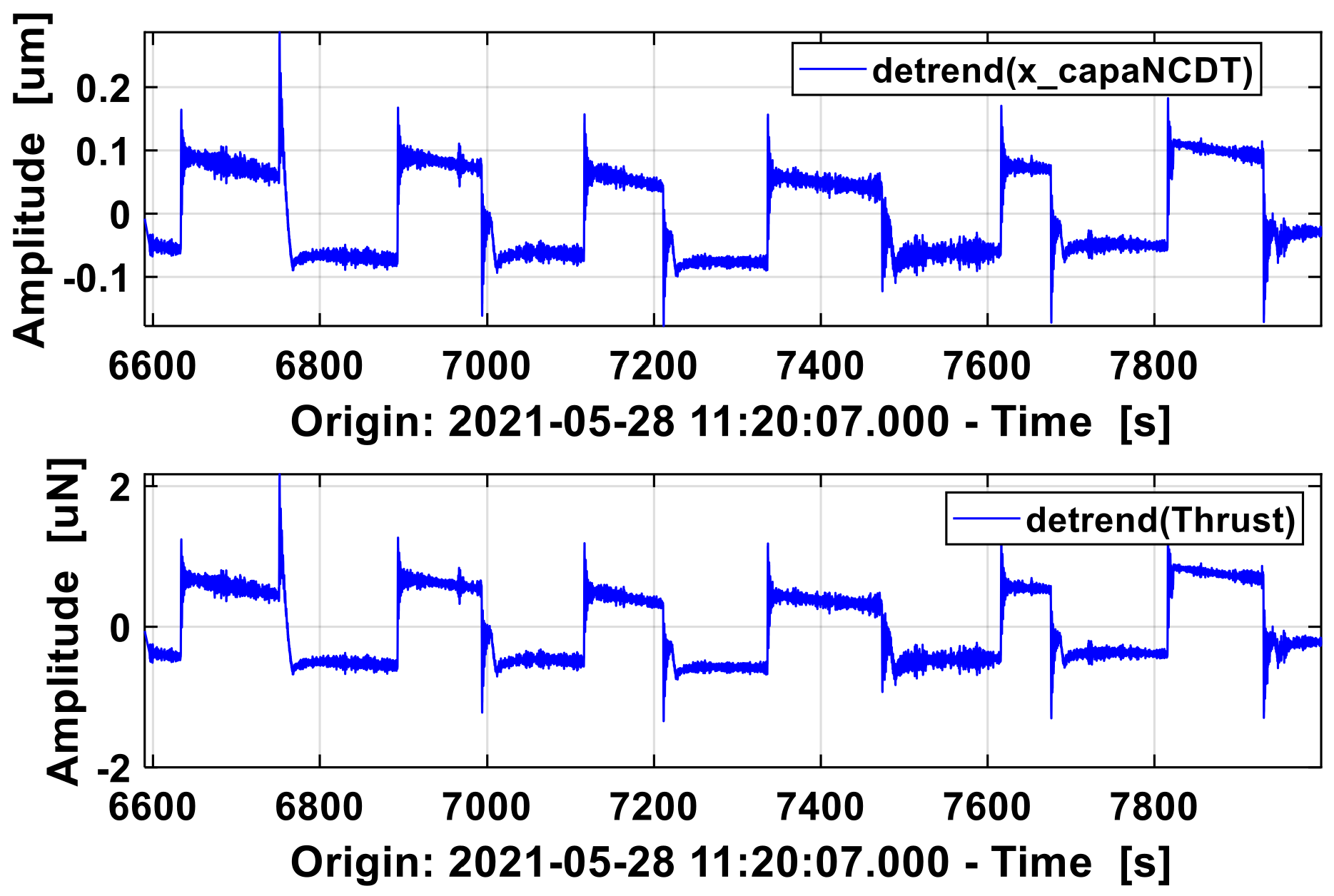
In the experiment above, a heating pad was used to heat the base of torsion balance, and the fluctuation of thrust balance was not obvious. In the next experiment, PTC heating was installed in the corner of the base below to lock the position that caused instability of the torsion balance. Regardless of the temperature of PT1000, to change the frequency of temperature fluctuations, PTC starts from turning on/off every 5 min at the beginning to turning on/off every 15 min and then to turning on/off every 30 min. The heat source square wave cycles range from 600 s, 1800 s and 3600 s, corresponding to frequencies of 1.7 mHz, 0.56 mHz and 0.27 mHz, respectively. As shown in
Figure 6, the displacement data x_capaNCDT at 0.1 mHz and 1 mHz were subtracted to get a relative periodic result (red line): as the PTC work, the displacement modulation amplitude of the torsion balance increases gradually. There were two transient, high-frequency impulses during the experiment, one caused by passing people, the second by accidentally caught earthquake shock. In addition, it is found that the vibration mode of the optical platform switched in a period of 24 h. During the rise from the evening to the next morning, the vibration of displacement at 0.02 Hz is larger, which becomes weaker during the fall from the morning of the next day to the evening. The change is not related to PTC heating, but to the background noise of larger system and longer period.
In the frequency domain, the thrust ASD resolves peak signals at 0.26 mHz, 0.52 mHz and 1.7 mHz, close to the PTC’s modulated frequencies at 0.27 mHz, 0.56 mHz and 1.7 mHz. The thermal noise at 0.26 mHz is the largest, and noise at 1.7 mHz is the smallest, and the frequency deviation of 0.52 mHz is large due to the fewer sampling cycles. The modulation transfer function of temperature to displacement resembles a low-pass filter, and the ASD above 50 mHz is less than 1 μN/Hz1/2, which provides a reference for the PT1000 sampling frequency. In addition, the heating position during the whole experiment is also a variable. The deformation of torsion balance is the direct cause of the fluctuation of thrust position, and the influence of the heat source is the indirect factor of thrust drift.
3.3. Square Wave Modulations of ESF and PTC
3.3.1. Temperature and Displacement
The test of the micro thruster on the torsion balance is accompanied by the load heating, which makes the zero level of the force measured by the torsion balance drift as the time changes. In order to test this situation, the ESF (almost zero heat consumption) and PTC heating plate were used to synchronize the switch every half an hour to realize the temperature rise and fall, and thrust square wave with a period of one hour. At the same time, three sets of PT1000 were arranged to record temperature changes, and capacitive sensor was used to record the displacement of torsion balance.
As shown in
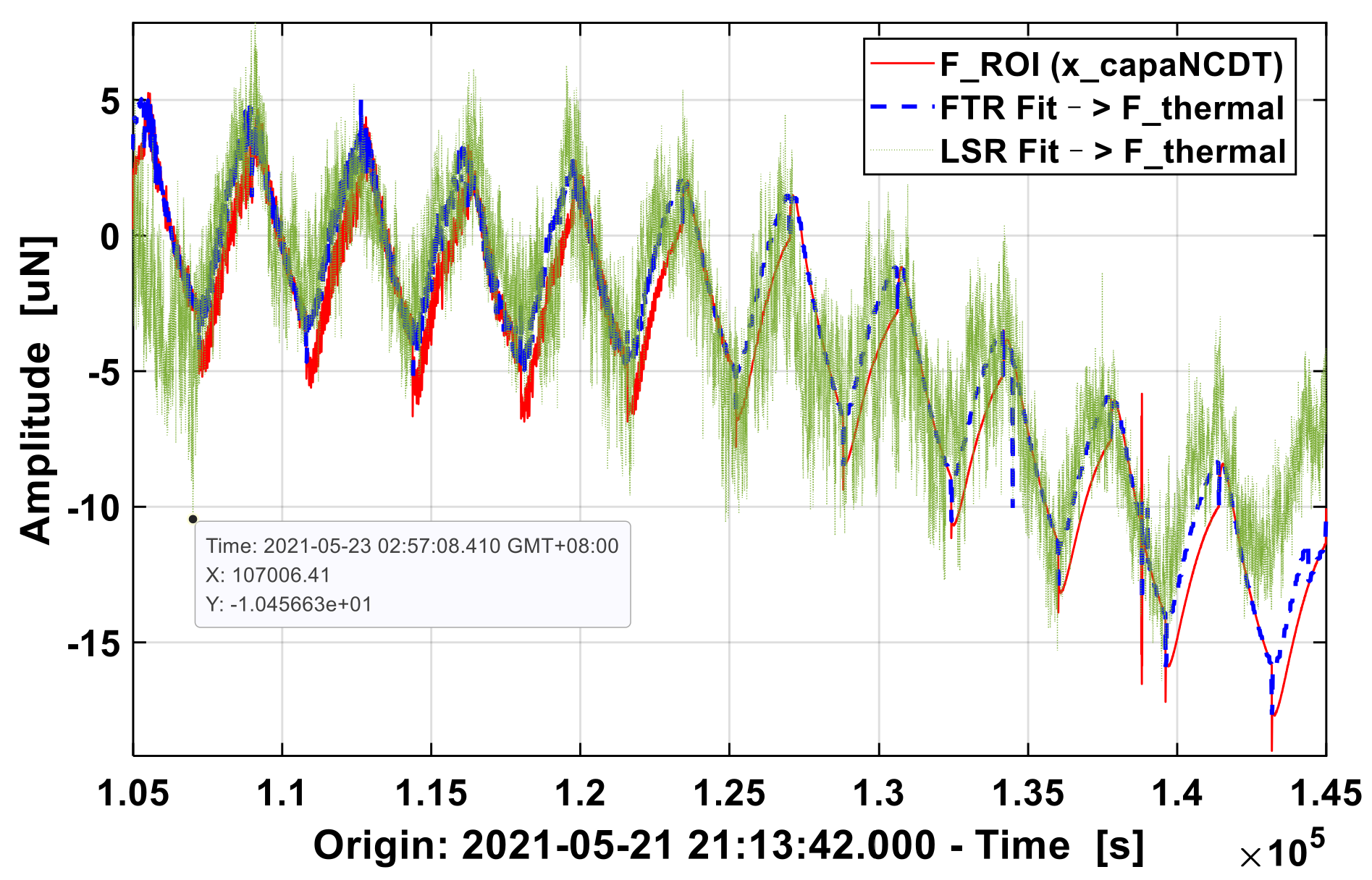
Figure 7, there seems a covariation between displacement (thrust) and temperature, but it is not a simple correlation. Before 3 × 10
4 s: thrust and temperature move in accordance with each other in the modulated frequency, but also in the larger low-frequency trend; however, after 3 × 10
4 s, although the temperature thrust is still correlated at the modulated frequency, the trend at lower frequencies is reversed. This is attributed to the fact that the heat balance of the system is determined not only by the modulated frequency of PTC heating, but also by the larger system environment (including the platform) and the external temperature exchange. For example, PTC heating can cause the torsion balance to fluctuate briefly with the modulation period, but a longer-term trend is determined by the heating and deformation of basement platform. The height of the four corners of the base varies relative to each other because of thermal expansion and cold contraction. Usually, the gravitational weight of torsion pendulum will not produce a displacement, but when the platform tilts 1 μrad, even a torsion bar of 0.1 kg will produce 1 μN as thrust increment, which needs to seek a new balance with flexible axis deformation. Additionally, 0.1 μm difference between the ends of length 0.1 m is enough to cause a horizontal change of 1 μrad. The thermal deformation of the material is extremely difficult to control, and the problem is worse when the heat power of the thruster and other loads is added.
In addition, the square wave electrostatic thrust of ESF drift due to the temperature effect. According to the differential signal, the original displacement data (solid blue line in
Figure 7 above) at the input square wave switch has a jump of about 0.23 μm, which corresponds to a thrust step of 1.7 μN. As the PT1000 at different locations are turned up or down due to the heat source, the temperatures all rise or fall in varying ranges (below
Figure 7). When the electrostatic thrust is constant, the displacement has a trend to change synchronously with the temperature. By completing the displacement data at the step, a relatively continuous thermal drift (red dashed line in
Figure 7) can be approximated. To extract on the square wave signal in the huge background of thermal drift, assuming the electrostatic force be constant during the square wave, the temperature (T1_ROI, T2_ROI, T3_ROI) are first used to fit the displacement data x_thermal without electrostatic force. Then, based on the thrust predicted by regression learning, the transfer function from the fitted thrust to the thrust calculted by the displacement data x_capaNCDT is estimated via ZDVF, and the thermal drift in the electrostatic force measured by torsion balance is filtered out to restore the static force. The difference between the thermal thrust predicted by PID-FTR and SVD-LSR were compared. As shown in
Figure 8, when fitting the thrust without ESF’s electrostatic force, the PID-FTR algorithm learned the drift perfectly, while the SVD-LSR algorithm had high-frequency residuals and ultra-low frequency deviations. Compared to the thrust F_ROI calculated from the original displacement data, the fitted drift thrust based on FTR regression was clearly separated in time, while the thermal drift thrust based on LSR regression is now and then too close or too far.
3.3.2. Thermal Noise Decoupling
After fitting the thermal thrust caused by temperature, the following work returns to the normal procedure: transfer function, z-domain fit, and signal subtraction. It should be noted that meaningful frequencies should be selected when fitting the transfer function of the system in z-domain. For the frequency of thermal thrust is low, the period interval of 20–2000 s can be selected.
As shown in
Figure 9, the solid blue line (F_ROI) represents the original thrust ASD, and the solid red line (F_ROI–F_SQUARE) represents the ASD after the electrostatic force deducted. It can be seen that they are basically close to each other, but the difference lies in the square wave, where the potential signal is embedded in the area between the envelope of 1 mHz–10 mHz. The blue and red dashed dotted line represent the thrust ASD results after FTR thermal thrust filtering, compared to the blue and red solid line, respectively. When the electrostatic force is absent, the thrust ASD is decoupled and reduced below 1.5 μN/Hz
1/2 in the full frequency band; even if the square wave is restored, it can be still locally reduced to 1.5 μN/Hz
1/2 at 0.5 mHz. What is different from the diurnal temperature variation, the thermal noise removal effect is more obvious near 10 mHz except at the modulation frequency of 0.29 mHz, while higher frequencies at 50 mHz still have no thermal noise removed. It indicates that the temperature acquisition frequency about 0.1 Hz is appropriate, and that the selection of temperature measurement points plays an important role in establishing the correlation between temperature and thrust drift of the torsion balance. Still, the results need to be verified by the restoration of electrostatic force in time domain again.
3.3.3. Restoration of Electrostatic Force
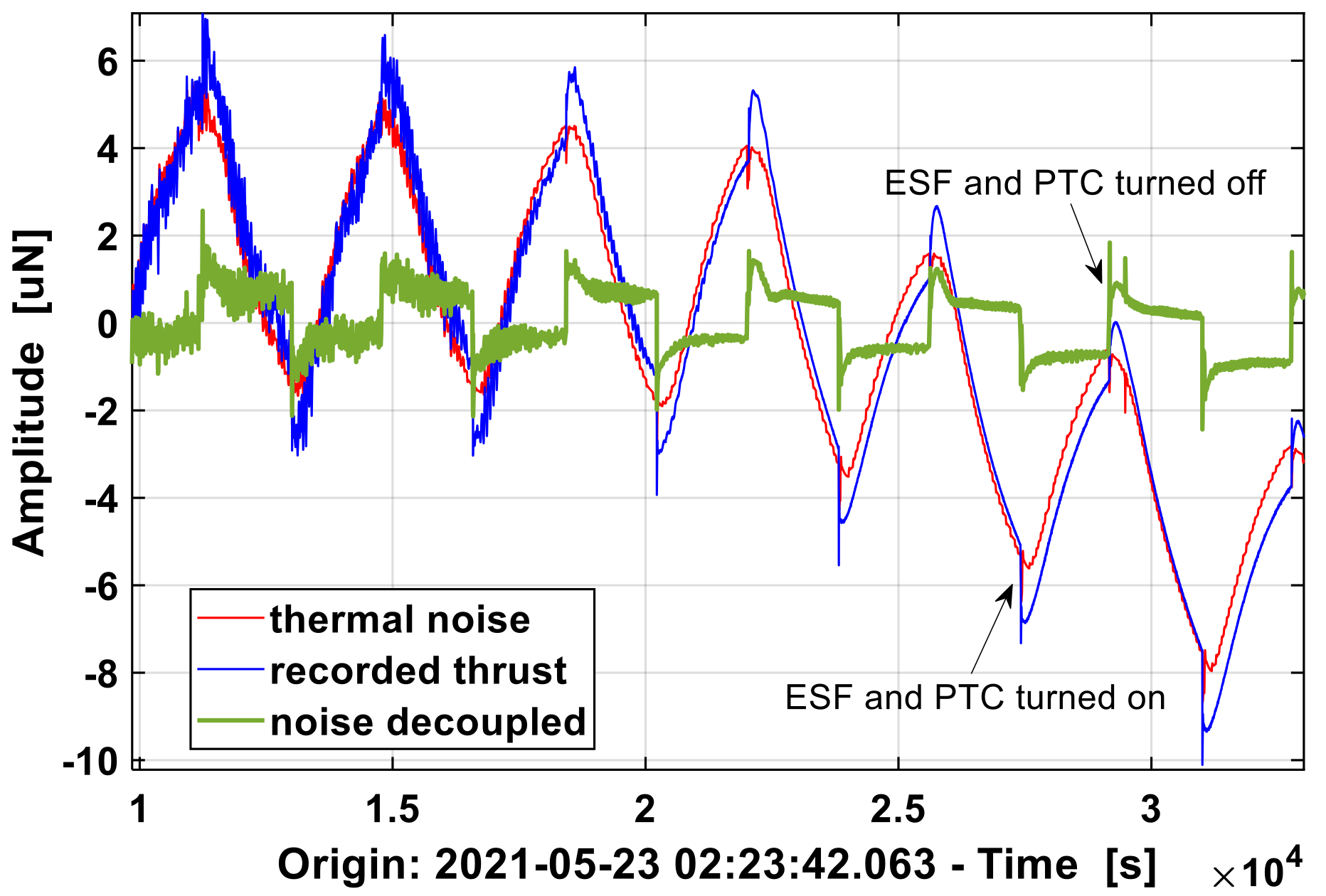
As mentioned above, PTC and ESF (10 V voltage loaded) will be turned on and off at the same time every half an hour during the experiment. The ESF step output electrostatic force is 0.23 μm × 7.56 μN/μm ≈ 1.7 μN. PTC heating makes the thrust characterized by the displacement of torsion balance drift gradually. As shown in
Figure 10, after dealing with the PID-FTR and ZDVF series of algorithm, the thrust measurement result with thermal noise removed from the time domain can be seen clearly: ESF’s real electrostatic force of 1.7 μN square wave is extracted from the oscillations of 7 μN affected by the temperature, along with the rising and falling template trigger position exactly. In addition to the electrostatic force, the recovered square wave retains vibrations other than thermal noise, such as the obvious 0.02 Hz vibration associated with the optical platform before 2 × 10
4 s, which disappear again as expected after 2 × 10
4 s. Therefore, the proposed process of thermal noise decoupling does not shave all the noise, but only removes the interference in the 0.5 mHz–50 mHz related to temperature fluctuation, which is more real and more effective than the direct low-pass or band-pass filtering of displacement data.
It is a little confusing that the electrostatic force restoration result after thermal noise removal is accompanied by overshoot in each step response. To determine whether it is the residual error processed by the algorithm, the PTC was turned off in contrast for pure electrostatic square wave of 1 μN turned on by ESF alone, and the existence of “burr” can still be observed as shown in
Figure 11. Burrs of micro size and unpredictable location are found to be a sign of parasitic capacitance in electrical circuits, which is the extra effect of ESF and other conductors that serve as plates between a dielectric when capacitive charge and discharge aroused by crosstalk when circuit switched. Since the burrs occur simultaneously with a square wave, their spectrum contains the character of the square wave, such as a series of odd number of harmonics ranging from low to high frequencies. The FTR thermal noise decoupling algorithm not only distinguishes the burrs’ variation below 50 mHz from the thermal variations finely, but also reserves partial high frequency (below 1 Hz) original information, which further demonstrates the effectiveness and pertinence of the algorithm.
In addition, both the time scale of FTR and the frequency range of ZDVF have the risk of underfitting or overfitting. As for the tuning of relevant parameters, on the one hand, the range of frequency coverage should be considered, and the adjustment should be made according to mean square error to obtain better fitting results. On the other hand, the spectral response of the actual physical quantity should also be used to iterate according to the thermal noise subtraction effect, and cross validated through a priori template (such as square wave). In general, datasets of different variation modes can be added to train the temperature’s prediction ability of the FTR model. The noise decoupling precision of ZDVF can be refined and enhanced by using different frequency modulation of temperature and different location acquisition temperature.