Bilateral Symmetry of Jumping and Agility in Professional Basketball Players: Differentiating Performance Levels and Playing Positions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Approach to the Problem
2.2. Participants
2.3. Variables
2.4. Statistical Analyses
3. Results
4. Discussion
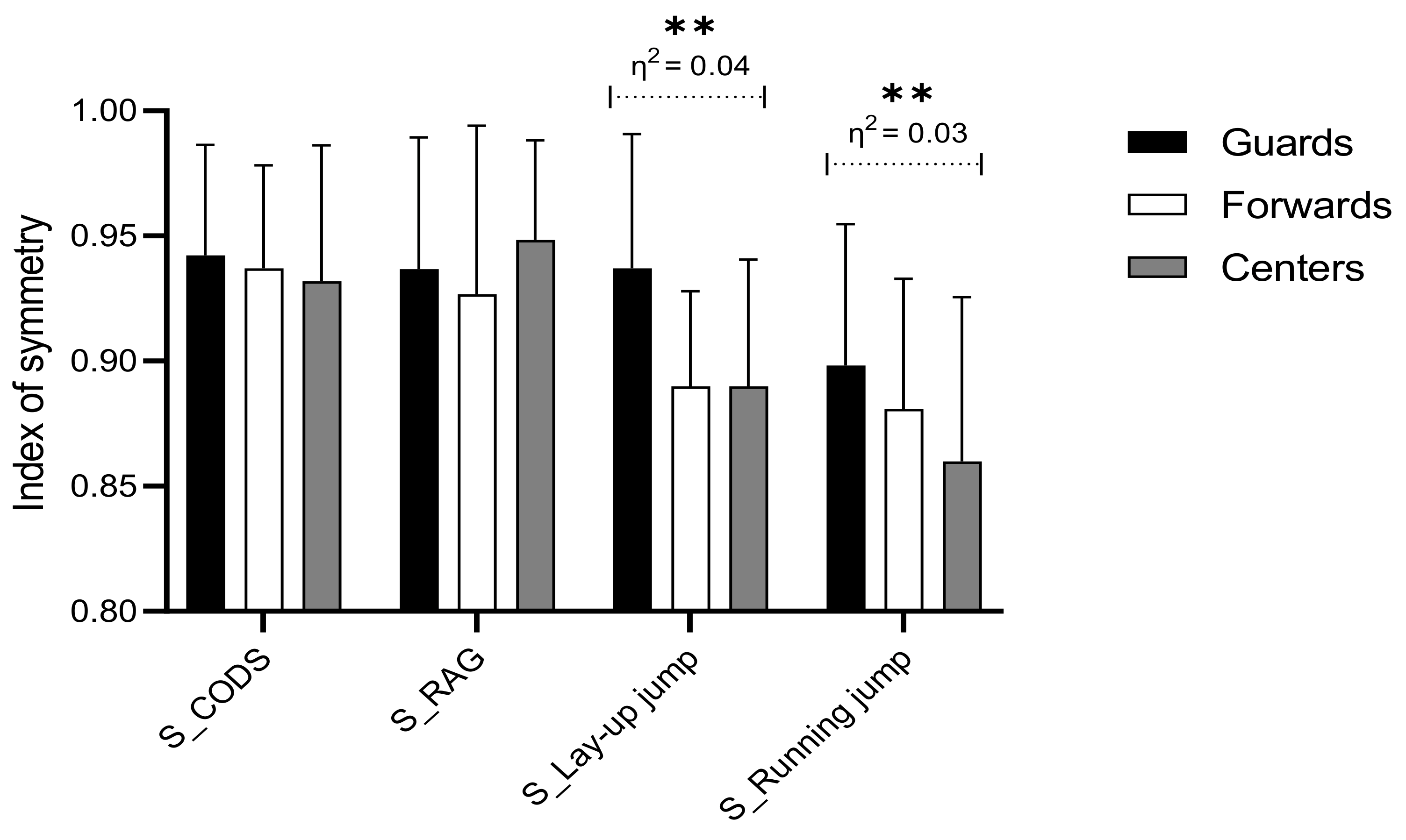
4.1. Symmetry of Agility Performances and Playing Positions
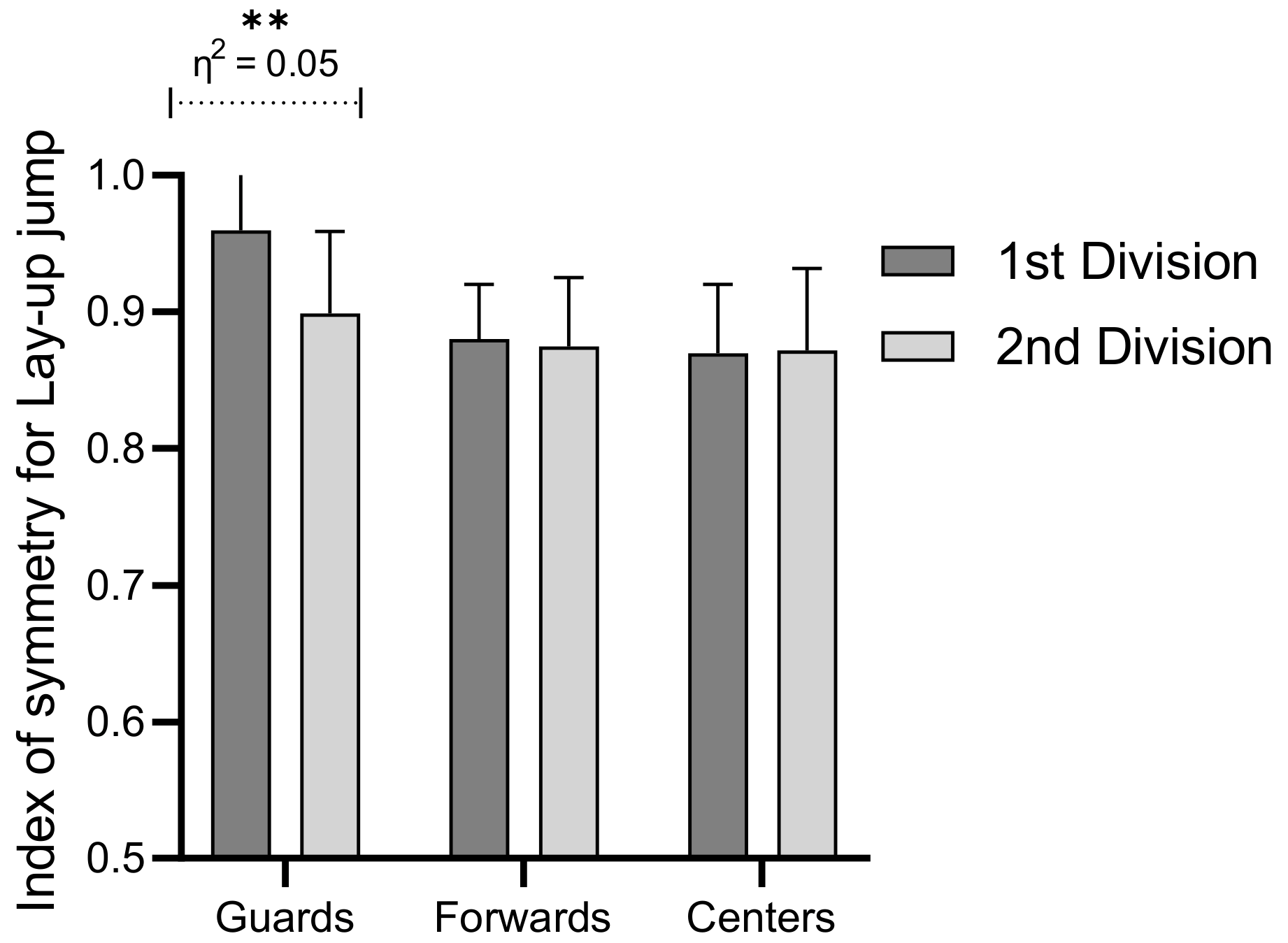
4.2. Symmetry of Jumping and Playing Positions
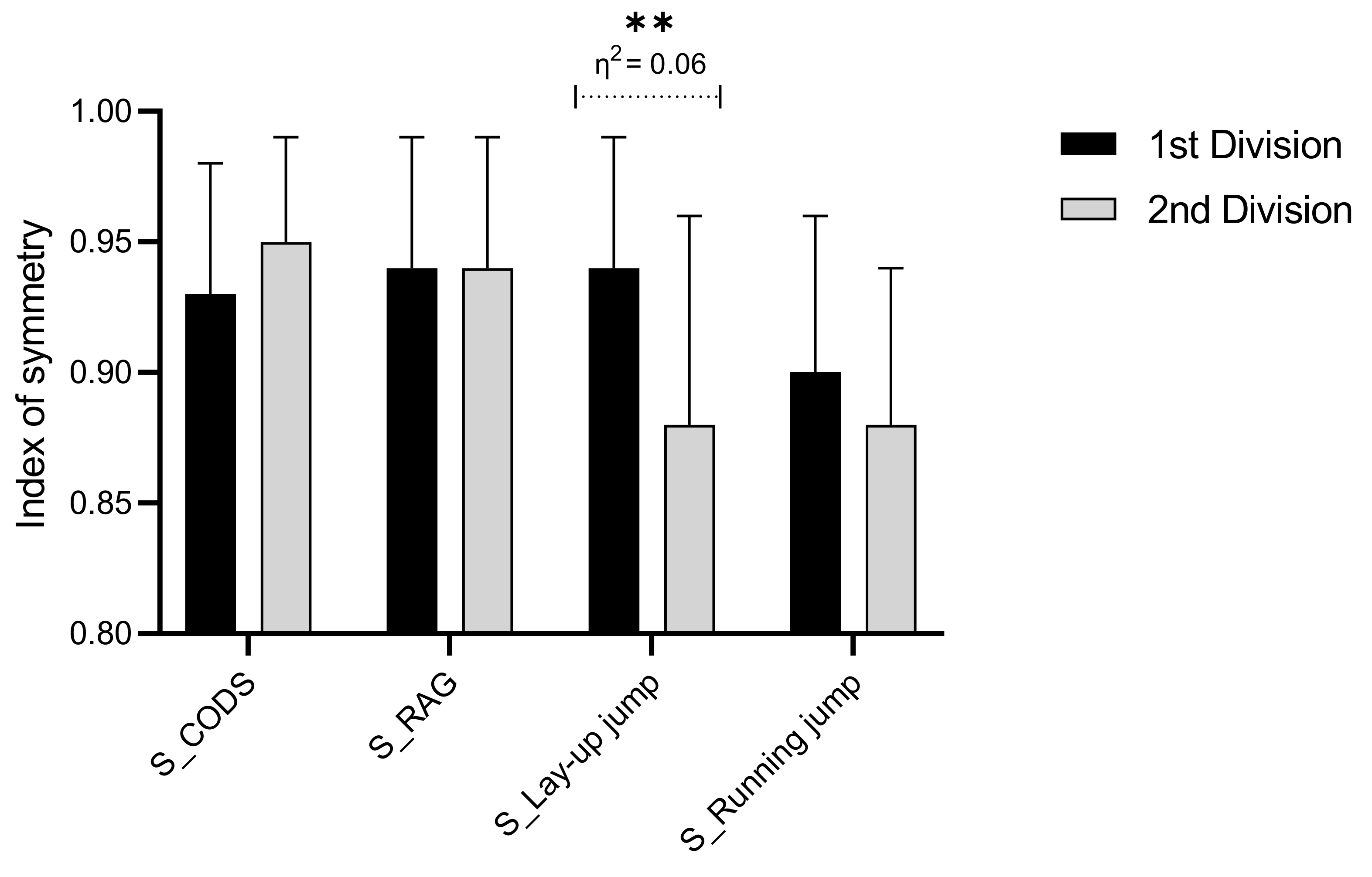
4.3. Symmetry of Jumping and Performance Levels
4.4. Symmetry of Agility and Performance Levels
4.5. Limitations and Strength of the Study
4.6. Practical Implications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdelkrim, N.B.; Chaouachi, A.; Chamari, K.; Chtara, M.; Castagna, C. Positional role and competitive-level differences in elite-level men’s basketball players. J. Strength Cond. Res. 2010, 24, 1346–1355. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, F.; Bao, D.; Liu, H.; Zhang, S.; Gómez, M.-Á. Key anthropometric and physical determinants for different playing positions during National Basketball Association draft combine test. Front. Psychol. 2019, 10, 2359. [Google Scholar] [CrossRef] [PubMed]
- Fort-Vanmeerhaeghe, A.; Montalvo, A.; Latinjak, A.; Unnithan, V. Physical characteristics of elite adolescent female basketball players and their relationship to match performance. J. Hum. Kinet. 2016, 53, 167–178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoare, D.G. Predicting success in junior elite basketball players—The contribution of anthropometic and physiological attributes. J. Sci. Med. Sport 2000, 3, 391–405. [Google Scholar] [CrossRef]
- Hoffman, J.R.; Tenenbaum, G.; Maresh, C.M.; Kraemer, W.J. Relationship between athletic performance tests and playing time in elite college basketball players. J. Strength Cond. Res. 1996, 10, 67–71. [Google Scholar]
- Chaouachi, A.; Brughelli, M.; Chamari, K.; Levin, G.T.; Abdelkrim, N.B.; Laurencelle, L.; Castagna, C. Lower limb maximal dynamic strength and agility determinants in elite basketball players. J. Strength Cond. Res. 2009, 23, 1570–1577. [Google Scholar] [CrossRef]
- Garcia-Gil, M.; Torres-Unda, J.; Esain, I.; Duñabeitia, I.; Gil, S.M.; Gil, J.; Irazusta, J. Anthropometric parameters, age, and agility as performance predictors in elite female basketball players. J. Strength Cond. Res. 2018, 32, 1723–1730. [Google Scholar] [CrossRef]
- Apostolidis, N.; Emmanouil, Z. The influence of the anthropometric characteristics and handgrip strength on the technical skills of young basketball players. J. Phys. Educ. Sport 2015, 15, 330–337. [Google Scholar]
- Struzik, A.; Pietraszewski, B.; Zawadzki, J. Biomechanical analysis of the jump shot in basketball. J. Hum. Kinet. 2014, 42, 73–79. [Google Scholar] [CrossRef] [Green Version]
- Miura, K.; Yamamoto, M.; Tamaki, H.; Zushi, K. Determinants of the abilities to jump higher and shorten the contact time in a running 1-legged vertical jump in basketball. J. Strength Cond. Res. 2010, 24, 201–206. [Google Scholar] [CrossRef]
- Ziv, G.; Lidor, R. Vertical jump in female and male basketball players--a review of observational and experimental studies. J. Sci. Med. Sport 2010, 13, 332–339. [Google Scholar] [CrossRef]
- Köklü, Y.; Alemdaroğlu, U.; Koçak, F.; Erol, A.E.; Fındıkoğlu, G. Comparison of chosen physical fitness characteristics of Turkish professional basketball players by division and playing position. J. Hum. Kinet 2011, 30, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Pehar, M.; Sekulic, D.; Sisic, N.; Spasic, M.; Uljevic, O.; Krolo, A.; Milanovic, Z.; Sattler, T. Evaluation of different jumping tests in defining position-specific and performance-level differences in high level basketball players. Biol. Sport 2017, 34, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Vukasevic, V.; Mitrovic, M.; Masanovic, B. A comparative study of motor ability between elite basketball players from different regions. Sport Mont 2020, 18, 3–7. [Google Scholar] [CrossRef]
- Scanlan, A.T.; Tucker, P.S.; Dalbo, V.J. The importance of open- and closed-skill agility for team selection of adult male basketball players. J. Sports Med. Phys. Fit. 2015, 55, 390–396. [Google Scholar]
- Sekulic, D.; Pehar, M.; Krolo, A.; Spasic, M.; Uljevic, O.; Calleja-González, J.; Sattler, T. Evaluation of Basketball-Specific Agility: Applicability of Preplanned and Nonplanned Agility Performances for Differentiating Playing Positions and Playing Levels. J. Strength Cond. Res. 2017, 31, 2278–2288. [Google Scholar] [CrossRef] [PubMed]
- Pehar, M.; Sisic, N.; Sekulic, D.; Coh, M.; Uljevic, O.; Spasic, M.; Krolo, A.; Idrizovic, K. Analyzing the relationship between anthropometric and motor indices with basketball specific pre-planned and non-planned agility performances. J. Sports Med. Phys. Fit. 2018, 58, 1037–1044. [Google Scholar] [CrossRef]
- Sarabon, N.; Smajla, D.; Maffiuletti, N.A.; Bishop, C. Strength, Jumping and Change of Direction Speed Asymmetries in Soccer, Basketball and Tennis Players. Symmetry 2020, 12, 1164. [Google Scholar] [CrossRef]
- Arboix-Alio, J.; Busca, B.; Busquets, A.; Aguilera-Castells, J.; de Pablo, B.; Montalvo, A.M.; Fort-Vanmeerhaeghe, A. Relationship between Inter-Limb Asymmetries and Physical Performance in Rink Hockey Players. Symmetry 2020, 12, 35. [Google Scholar] [CrossRef]
- Caraballo, I.; Casado-Rodriguez, F.; Gutierrez-Manzanedo, J.V.; Gonzalez-Montesinos, J.L. Strength Asymmetries in Young Elite Sailors: Windsurfing, Optimist, Laser and 420 Classes. Symmetry 2021, 13, 427. [Google Scholar] [CrossRef]
- Jeličić, M.; Sekulić, D.; Marinović, M. Anthropometric characteristics of high level European junior basketball players. Coll. Antropol. 2002, 26, 69–76. [Google Scholar]
- Weiner, J.S.; Lourie, J.A. Human biology, a guide to field methods. Science 1969, 167, 43. [Google Scholar]
- Bishop, C.; Read, P.; Lake, J.; Chavda, S.; Turner, A. Interlimb asymmetries: Understanding how to calculate differences from bilateral and unilateral tests. Strength Cond. J. 2018, 40, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Ceroni, D.; Martin, X.E.; Delhumeau, C.; Farpour-Lambert, N.J. Bilateral and gender differences during single-legged vertical jump performance in healthy teenagers. J. Strength Cond. Res. 2012, 26, 452–457. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.; Read, P.; Chavda, S.; Turner, A. Asymmetries of the lower limb: The calculation conundrum in strength training and conditioning. Strength Cond. J. 2016, 38, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Boone, J.; Bourgois, J. Morphological and physiological profile of elite basketball players in Belgium. Int. J. Sports Physiol. Perform. 2013, 8, 630–638. [Google Scholar] [CrossRef] [Green Version]
- Scanlan, A.T.; Tucker, P.S.; Dalbo, V.J. A comparison of linear speed, closed-skill agility, and open-skill agility qualities between backcourt and frontcourt adult semiprofessional male basketball players. J. Strength Cond. Res. 2014, 28, 1319–1327. [Google Scholar] [CrossRef]
- Sisic, N.; Jelicic, M.; Pehar, M.; Spasic, M.; Sekulic, D. Agility performance in high-level junior basketball players: The predictive value of anthropometrics and power qualities. J. Sports Med. Phys. Fit. 2015, 56, 884–893. [Google Scholar]
- Dežman, B.; Trninić, S.; Dizdar, D. Expert model of decision-making system for efficient orientation of basketball players to positions and roles in the game–Empirical verification. Coll. Antropol. 2001, 25, 141–152. [Google Scholar] [PubMed]
- Sugiyama, T.; Kameda, M.; Kageyama, M.; Kiba, K.; Kanehisa, H.; Maeda, A. Asymmetry between the dominant and non-dominant legs in the kinematics of the lower extremities during a running single leg jump in collegiate basketball players. J. Sports Sci. Med. 2014, 13, 951. [Google Scholar]
- Miletić, Đ.; Božanić, A.; Musa, I. Ambidexterity influencing performance in rhythmic composition–Gender differences. Acta Kinesiol. 2009, 3, 38–43. [Google Scholar]
- Grouios, G.; Tsormpatzoudis, C.; Alexandris, K.; Koidou, E. Handedness in sport. J. Hum. Mov. Stud. 2002, 43, 347–361. [Google Scholar]
- Cavill, S.; Bryden, P. Development of handedness: Comparison of questionnaire and performance-based measures of preference. Brain Cogn. 2003, 53, 149–151. [Google Scholar] [CrossRef]
- Grigore, M. Influence of dance sport on the development of the capacity for ambidexterity and laterality of juniors I (12–13 years old). J. Phys. Educ. Sport 2017, 17, 2250–2254. [Google Scholar]
- Epuran, M.; Horghidan, V. Psychology of physical education. Buchar. ANEFS 1994, 1, 88–90. [Google Scholar]
- Sabaté, M.; González, B.; Rodríguez, M. Brain lateralization of motor imagery: Motor planning asymmetry as a cause of movement lateralization. Neuropsychologia 2004, 42, 1041–1049. [Google Scholar] [CrossRef]
- Van Mier, H. Developmental differences in drawing performance of the dominant and non-dominant hand in right-handed boys and girls. Hum. Mov. Sci. 2006, 25, 657–677. [Google Scholar] [CrossRef] [PubMed]
- Provins, K.; Magliaro, J. The measurement of handedness by preference and performance tests. Brain Cogn. 1993, 22, 171–181. [Google Scholar] [CrossRef] [Green Version]
- Stöckel, T.; Weigelt, M. Brain lateralisation and motor learning: Selective effects of dominant and non-dominant hand practice on the early acquisition of throwing skills. Laterality Asymmetries Body Brain Cogn. 2012, 17, 18–37. [Google Scholar] [CrossRef] [PubMed]
- Haaland, E.; Hoff, J. Non-dominant leg training improves the bilateral motor performance of soccer players. Scand. J. Med. Sci. Sports 2003, 13, 179–184. [Google Scholar] [CrossRef]
- Alemdaroğlu, U. The relationship between muscle strength, anaerobic performance, agility, sprint ability and vertical jump performance in professional basketball players. J. Hum. Kinet. 2012, 31, 149. [Google Scholar] [CrossRef] [Green Version]
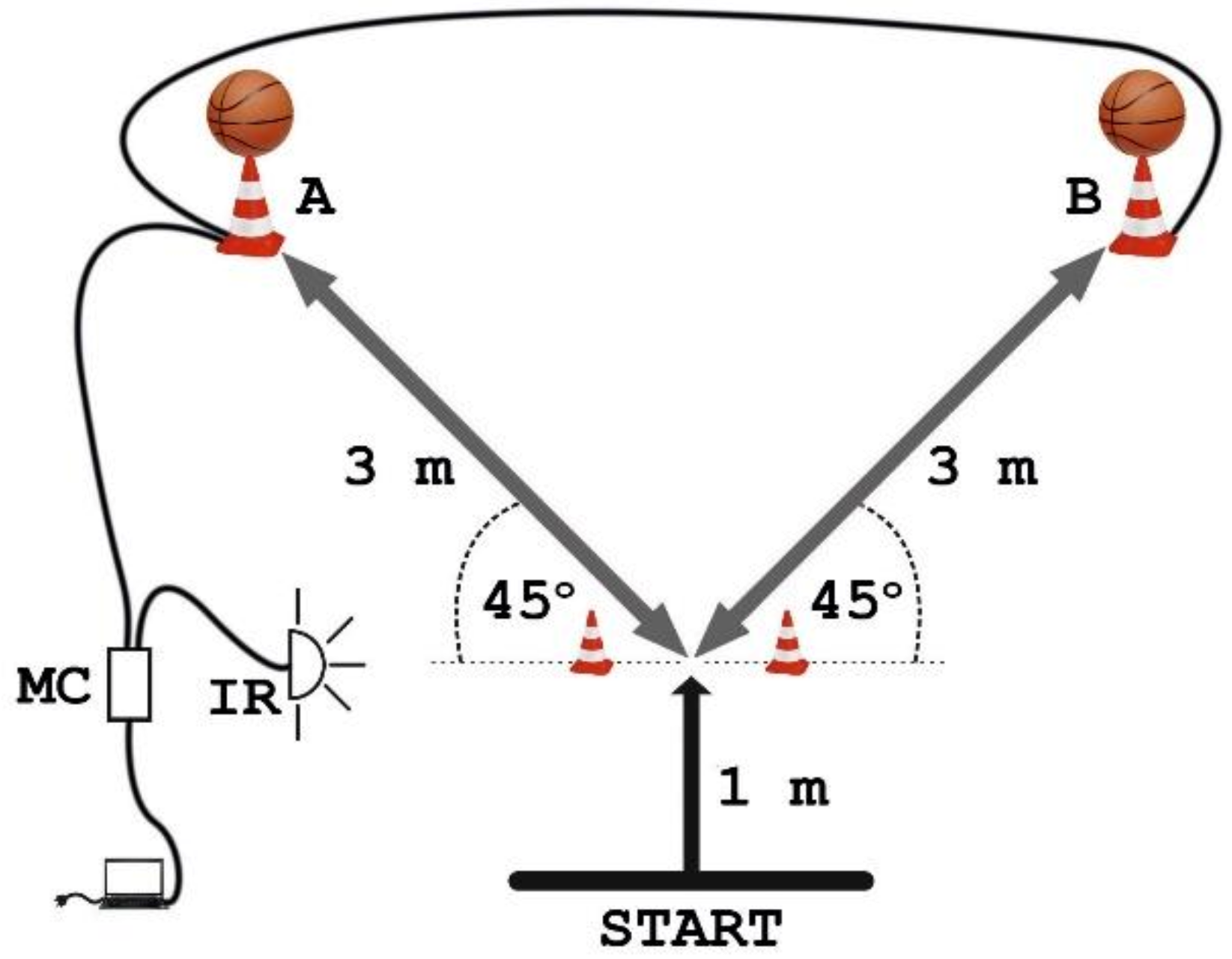
| Mean | Std. Dev. | KS (D) | ICC | CV | |
|---|---|---|---|---|---|
| Age (years) | 21.61 | 3.94 | 0.163 ** | ||
| Body height (cm) | 194.82 | 8.10 | 0.051 | ||
| Body mass (kg) | 89.33 | 10.91 | 0.072 | ||
| Body fat (%) | 8.98 | 3.41 | 0.131 | ||
| CODSdominant (s) | 1.72 | 0.15 | 0.113 | 0.87 | 0.08 |
| CODSnon-dominant (s) | 1.83 | 0.18 | 0.101 | 0.86 | 0.07 |
| RAGdominant (s) | 1.99 | 0.19 | 0.110 | 0.81 | 0.08 |
| RAGnon-dominant (s) | 2.14 | 0.18 | 0.124 | 0.80 | 0.09 |
| Lay-up jumpdominant (cm) | 72.21 | 10.57 | 0.118 | 0.90 | 0.05 |
| Lay-up jumpnon-dominant (cm) | 65.78 | 10.03 | 0.121 | 0.91 | 0.05 |
| Running jumpdominant (cm) | 75.74 | 12.00 | 0.132 | 0.88 | 0.06 |
| Running jumpnon-dominant (cm) | 68.19 | 10.73 | 0.131 | 0.90 | 0.05 |
| Playing Position | Performance Level | Interaction | |||||||
|---|---|---|---|---|---|---|---|---|---|
| F-Test | p | η2 | F-Test | p | η2 | F-Test | p | η2 | |
| S_CODS | 0.29 | 0.75 | 0.01 | 3.37 | 0.07 | 0.03 | 0.14 | 0.87 | 0.01 |
| S_RAG | 1.44 | 0.24 | 0.02 | 0.03 | 0.85 | 0.01 | 0.89 | 0.41 | 0.01 |
| S_Lay-up jump | 6.11 | 0.03 | 0.14 | 10.11 | 0.01 | 0.19 | 5.9 | 0.04 | 0.06 |
| S_Running jump | 5.81 | 0.04 | 0.06 | 0.45 | 0.5 | 0.01 | 0.39 | 0.67 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Versic, S.; Pehar, M.; Modric, T.; Pavlinovic, V.; Spasic, M.; Uljevic, O.; Corluka, M.; Sattler, T.; Sekulic, D. Bilateral Symmetry of Jumping and Agility in Professional Basketball Players: Differentiating Performance Levels and Playing Positions. Symmetry 2021, 13, 1316. https://doi.org/10.3390/sym13081316
Versic S, Pehar M, Modric T, Pavlinovic V, Spasic M, Uljevic O, Corluka M, Sattler T, Sekulic D. Bilateral Symmetry of Jumping and Agility in Professional Basketball Players: Differentiating Performance Levels and Playing Positions. Symmetry. 2021; 13(8):1316. https://doi.org/10.3390/sym13081316
Chicago/Turabian StyleVersic, Sime, Miran Pehar, Toni Modric, Vladimir Pavlinovic, Miodrag Spasic, Ognjen Uljevic, Marin Corluka, Tine Sattler, and Damir Sekulic. 2021. "Bilateral Symmetry of Jumping and Agility in Professional Basketball Players: Differentiating Performance Levels and Playing Positions" Symmetry 13, no. 8: 1316. https://doi.org/10.3390/sym13081316
APA StyleVersic, S., Pehar, M., Modric, T., Pavlinovic, V., Spasic, M., Uljevic, O., Corluka, M., Sattler, T., & Sekulic, D. (2021). Bilateral Symmetry of Jumping and Agility in Professional Basketball Players: Differentiating Performance Levels and Playing Positions. Symmetry, 13(8), 1316. https://doi.org/10.3390/sym13081316










