Spectral Curves for the Derivative Nonlinear Schrödinger Equations

Abstract

Currently, in nonlinear optics, models associated with various types of the nonlinear Schrödinger equation (scalar (NLS), vector (VNLS), derivative (DNLS)), as well as with higher and mixed equations from the corresponding hierarchies are usually studied. Typical tools for solving the problem of propagation of optical nonlinear waves are the forward and inverse nonlinear Fourier transforms. One of the methods for reconstructing a periodic nonlinear signal is based on the use of spectral data in the form of spectral curves. In this paper, we study the properties of the spectral curves for all the derivatives NLS equations simultaneously. For all the main DNLS equations (DNLSI, DNLSII, DNLSIII), we have obtained unified Lax pairs, unified hierarchies of evolutionary and stationary equations, as well as unified equations of spectral curves of multiphase solutions. It is shown that stationary and evolutionary equations have symmetries, the presence of which leads to the existence of holomorphic involutions on spectral curves. Because of this symmetry, spectral curves of genus g are covers over other curves of genus M and $N=g-M$, where M is a number of phase of solutions. We also showed that the number of the genus g of the spectral curve is related to the number of phases M of the solution of one of the two formulas: $g=2M$ or $g=2M+1$. The third section provides examples of the simplest solutions.

1. Introduction

The main tools for the study of nonlinear optical signals are the forward and inverse nonlinear Fourier transforms [1,2,3,4,5], and the main models of nonlinear optics are the scalar, vector, and derived nonlinear Schrödinger equations, as well as their higher forms from the corresponding hierarchies. A key feature of these equations is the fact that they are integrable nonlinear evolutionary differential equations. Integrable nonlinear equations can usually be obtained as conditions for the compatibility of two linear differential equations, called a Lax pair.

The first equation of the Lax pair for the scalar and vector Schrödinger equations has the form

$$i{\mathsf{\Psi }}_x+U\mathsf{\Psi }=0,$$

(1)

where

$$U=Q\left(x\right)-\lambda J,$$

(2)

J is some constant diagonal matrix with zero trace, $\lambda$ is a spectral parameter. In particular, these matrices are equal to:

$$J=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),Q\left(x\right)=\left(\begin{array}{cc}0& p\left(x\right)\\ -q\left(x\right)& 0\end{array}\right)$$

in the case of the scalar nonlinear Schrödinger equation and the equations from the Ablowitz-Kaup-Newell-Sigur hierarchy (AKNS) [6], and

$$\begin{array}{c}J={\displaystyle \frac{1}{3}}\left(\begin{array}{ccc}2& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right),Q\left(x\right)=\left(\begin{array}{ccc}0& p_1\left(x\right)& p_2\left(x\right)\\ -q_1\left(x\right)& 0& 0\\ -q_2\left(x\right)& 0& 0\end{array}\right).\end{array}$$

in the case of a two-dimensional vector nonlinear Schrödinger equation (Manakov system) [7].

Since spectral curves are used to reconstruct a periodic nonlinear signal (see, for example, [8,9]), it is important to know the properties of these curves for each integrable model. More than 30 years ago, Dubrovin B.A. showed [10] that the matrix $Q\left(x\right)$ is a matrix potential associated with a spectral curve of finite genus if there exists a monodromy matrix

$$M(x,\lambda )=\sum _{j=0}^n{m}_j\left(x\right){\lambda }^j$$

(3)

such that the functions $\mathsf{\Psi }$ and

$$\widehat{\mathsf{\Psi }}=M(x,\lambda )\mathsf{\Psi }$$

(4)

is simultaneously the solution of the Equation (1) (see also [8]). In this case, the equation of the spectral curve associated with this matrix $Q\left(x\right)$ has the form

$$det(\nu I-M)=\mathcal{R}(\nu ,\lambda )=0,$$

(5)

where I is the unit matrix. Thus, to find the equation of the spectral curve associated with the matrix Q, one must find the monodromy matrix M. Note that all the coefficients of the Equation (5) are integrals.

Substituting the function $\widehat{\mathsf{\Psi }}$ (4) in Equation (1) we obtain

$$\begin{array}{c}i{\widehat{\mathsf{\Psi }}}_x+U\widehat{\mathsf{\Psi }}=0\Rightarrow i{\left(M\mathsf{\Psi }\right)}_x+UM\mathsf{\Psi }=0\Rightarrow \\ i{M}_x\mathsf{\Psi }+iM{\mathsf{\Psi }}_x+UM\mathsf{\Psi }=0.\end{array}$$

Since the matrix-function $\mathsf{\Psi }$ is solution of the Equation (1), we have

$$i{M}_x\mathsf{\Psi }-MU\mathsf{\Psi }+UM\mathsf{\Psi }=0\mathrm{or}(i{M}_x+UM-MU)\mathsf{\Psi }=0.$$

Therefore the matrix M satisfies the equation

$$i{M}_x+UM-MU=0.$$

(6)

Substituting the sum (3) into the Equation (6) and equating the matrices for all powers of the spectral parameter $\lambda$, we obtain the following matrix structure M

$$M=V_n+\sum _{k=1}^{n-1}{c}_k{V}_{n-k}+c_{n}U+J_n,$$

where $J_n$ is a constant matrix, $\mathrm{Tr}\left(J_n\right)=0$,

$$V_1=\lambda U+V_1^0,V_{k+1}=\lambda V_k+V_{k+1}^0,k\ge 1.$$

Also, the Equation (6) implies recurrent relations between the elements of the matrices $V_k^0$. In addition, assuming $\lambda =0$ in the Equation (6), we can obtain a hierarchy of corresponding stationary equations that are satisfied by multiphase finite-gap solutions and their degeneracies.

Choosing the second equation of the Lax pair in the form

$$i{\mathsf{\Psi }}_{t_k}+V_k\mathsf{\Psi }=0,$$

(7)

from the condition of compatibility of the Equations (1) and (7) we obtain an integrable evolutionary nonlinear equation from the corresponding hierarchy. That is, using the structure of the monodromy matrix, we can construct the corresponding hierarchy of integrable nonlinear equations. For the Manakov system and the Kulish-Sklyanin model, this program was implemented in [11,12].

The first Lax pair equation for DNLS equations differs from the above equations in that the matrix U has a quadratic dependence on the spectral parameter. Therefore, the monodromy matrix $M(x,\lambda )$ has a different structure and a different relationship to the $V_k$ matrices (see, for example, [13]).

Let us note that three forms of the DNLS equations are most often considered:

• DNLSI or Kaup-Newell equation [13,14,15,16,17,18,19,20,21]

  $$i{p}_t+p_{xx}+{i\left(\right|p|}^2{p)}_x=0,$$

  (8)
• DNLSII or Chen-Lee-Liu equation [16,17,18,19,21,22]

  $$i{p}_t+p_{xx}+i{\left|p\right|}^2{p}_x=0,$$

  (9)
• DNLSIII or Gerdjikov-Ivanov equation [16,17,18,19,21,23,24]

  $$i{p}_t+p_{xx}-i{p}^2{p}_x^{*}+{\displaystyle \frac{1}{2}}{\left|p\right|}^{4}p=0,$$

  (10)

which are special cases of the generalized DNLS equation [25,26,27,28]. Let us note that there are also gauge transformations that transform these equations into each other and preserve the magnitude of the solution (see, for example, [16,21,29,30,31]).

Each of these nonlinear equations corresponds to its own matrix U. In particular, this matrix is equal to

$$U={\lambda }^2\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)+i\lambda \left(\begin{array}{cc}0& p\\ q& 0\end{array}\right)$$

for DNLSI equation,

$$U=({\lambda }^2+pq/4)\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)+i\lambda \left(\begin{array}{cc}0& p\\ q& 0\end{array}\right)$$

for DNLSII equation, and

$$U=({\lambda }^2+pq/2)\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)+i\lambda \left(\begin{array}{cc}0& p\\ q& 0\end{array}\right)$$

for DNLSIII eqaution.

It is easy to see that the U matrices discussed above can be written using a single formula

$$U=({\lambda }^2+spq)\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)+i\lambda \left(\begin{array}{cc}0& p\\ q& 0\end{array}\right).$$

(11)

where $s=0$ for DNLSI, $s=1/4$ for DNLSII, and $s=1/2$ for DNLSIII.

In present paper, using the matrix (11), we apply the Dubrovin’s method to construct a hierarchy of the DNLS equations and analyze the properties of multiphase solutions of this hierarchy. The Section 1 of the paper is devoted to finding the structure of the monodromy matrix and the recurrent relations between its elements. Also in the Section 1, the second Lax pair operators are proposed for constructing a hierarchy of generalized DNLS equations. In Section 2, the equations of spectral curves are considered and stationary equations are derived. A significant difference from the case of the scalar NLS equation is the difference between the genus of the spectral curve and the number of phases of the solution. Also in the Section 2, we show that the equations of spectral curves are invariant under the involution $\lambda \to -\lambda$. The Section 3 provides examples of null-phase and one-phase solutions of the coupled DNLS equations.

2. Generalized DNLS Equation

Let us consider the equation

$${\mathsf{\Psi }}_x=U\mathsf{\Psi },$$

(12)

where

$$U=(-i{\lambda }^2-ispq)J+\lambda Q,J=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),Q=\left(\begin{array}{cc}0& p\\ q& 0\end{array}\right),$$

p and q are functions, s is a constant.

Following [13], we take the monodromy matrix as a sum

$$M(\lambda ,x)=\sum _{j=0}^{2n}{M}_j\left(x\right){\lambda }^j,M_j\left(x\right)=\left(\begin{array}{cc}{a}_j\left(x\right)& b_j\left(x\right)\\ c_j\left(x\right)& -a_j\left(x\right)\end{array}\right).$$

(13)

It follows from the Equation (12) that the monodromy matrix M satisfies the equation (see, for example, Equations (4) and (6))

$${\partial }_{x}M-UM+MU=0.$$

(14)

Substituting the sum (13) in Equation (14) we have that the matrix $M(\lambda ,x)$ has a form

$$M(\lambda ,x)=a_{0}J+\sum _{j=1}^{2n}{a}_j{W}_j(\lambda ,x),$$

(15)

where $a_k$ are some constants,

$$\begin{array}{c}{W}_1=\lambda J+iQ,W_{2k}=\lambda W_{2k-1},W_{2k+1}=\lambda W_{2k}+\lambda W_{2k-1}^0+W_{2k}^0,\end{array}$$

(16)

$$\begin{array}{c}{W}_{2k-1}^0=\left(\begin{array}{cc}{F}_k(p,q)& 0\\ 0& -F_k(p,q)\end{array}\right),W_{2k}^0=\left(\begin{array}{cc}0& H_k(p,q)\\ G_k(p,q)& 0\end{array}\right).\end{array}$$

(17)

From the Equation (14) also follows the following relations on the elements of the matrices $W_m^0$

$$\begin{array}{cc}\hfill & H_1=ip{F}_1-is{p}^{2}q-{\displaystyle \frac{1}{2}}{p}_x,\hfill \\ \hfill & G_1=iq{F}_1-isp{q}^2+{\displaystyle \frac{1}{2}}{q}_x,\hfill \\ \hfill & {\left(F_k\right)}_x=p{G}_k-q{H}_k,\hfill \\ \hfill & H_{k+1}=ip{F}_{k+1}-spq{H}_k+{\displaystyle \frac{i}{2}}{\left(H_k\right)}_x,\hfill \\ \hfill & G_{k+1}=iq{F}_{k+1}-spq{G}_k-{\displaystyle \frac{i}{2}}{\left(G_k\right)}_x.\hfill \end{array}$$

(18)

In particular,

$$\begin{array}{cc}\hfill F_1(p,q)=& {\displaystyle \frac{1}{2}}pq,\hfill \\ \hfill H_1(p,q)=& -{\displaystyle \frac{1}{2}}{p}_x+{\displaystyle \frac{i}{2}}(1-2s)p^{2}q,\hfill \\ \hfill G_1(p,q)=& {\displaystyle \frac{1}{2}}{q}_x+{\displaystyle \frac{i}{2}}(1-2s)p{q}^2,\hfill \\ \hfill F_2(p,q)=& {\displaystyle \frac{1}{8}}(3-8s)p^2{q}^2-{\displaystyle \frac{i}{4}}(p{q}_x-q{p}_x),\hfill \\ \hfill H_2(p,q)=& {\displaystyle \frac{i}{8}}(3-12s+8s^2)p^3{q}^2+{\displaystyle \frac{3}{4}}(2s-1)pq{p}_x+{\displaystyle \frac{s}{2}}{p}^2{q}_x-{\displaystyle \frac{i}{4}}{p}_{xx},\hfill \\ \hfill G_2(p,q)=& {\displaystyle \frac{i}{8}}(3-12s+8s^2)p^2{q}^3-{\displaystyle \frac{3}{4}}(2s-1)pq{q}_x-{\displaystyle \frac{s}{2}}{q}^2{p}_x-{\displaystyle \frac{i}{4}}{q}_{xx},\hfill \\ \hfill F_3(p,q)=& {\displaystyle \frac{1}{16}}(5-24s+24s^2)p^3{q}^3+{\displaystyle \frac{1}{8}}{p}_x{q}_x+{\displaystyle \frac{3i}{8}}(2s-1)pq(p{q}_x-q{p}_x)\hfill \\ \hfill & -{\displaystyle \frac{1}{8}}(p{q}_{xx}+q{p}_{xx}),\hfill \\ \hfill H_3(p,q)=& {\displaystyle \frac{i}{16}}(5-30s+48s^2-16s^3)p^4{q}^3-{\displaystyle \frac{3}{16}}(5-20s+16s^2)p^2{q}^2{p}_x\hfill \\ \hfill & +{\displaystyle \frac{3}{4}}(1-2s)s{p}^{3}q{q}_x+{\displaystyle \frac{3i}{8}}(2s-1)q{p}_x^2+{\displaystyle \frac{i}{4}}(5s-1)p{p}_x{q}_x\hfill \\ \hfill & +{\displaystyle \frac{i}{8}}(2s-1)p^2{q}_{xx}+{\displaystyle \frac{i}{2}}(2s-1)pq{p}_{xx}+{\displaystyle \frac{1}{8}}{p}_{xxx},\hfill \\ \hfill G_3(p,q)=& {\displaystyle \frac{i}{16}}(5-30s+48s^2-16s^3)p^3{q}^4+{\displaystyle \frac{3}{16}}(5-20s+16s^2)p^2{q}^2{q}_x\hfill \\ \hfill & +{\displaystyle \frac{3}{4}}(2s-1)sp{q}^3{p}_x+{\displaystyle \frac{3i}{8}}(2s-1)p{q}_x^2+{\displaystyle \frac{i}{4}}(5s-1)q{p}_x{q}_x\hfill \\ \hfill & +{\displaystyle \frac{i}{8}}(2s-1)q^2{p}_{xx}+{\displaystyle \frac{i}{2}}(2s-1)pq{q}_{xx}-{\displaystyle \frac{1}{8}}{q}_{xxx}.\hfill \end{array}$$

From the Equations (16) and (17) the following equalities follow

$$W_{2k+2}={\lambda }^{2k}{W}_2+\sum _{j=1}^k\left(\begin{array}{cc}{\lambda }^2{F}_k& \lambda H_k\\ \lambda G_k& -{\lambda }^2{F}_k\end{array}\right){\lambda }^{2k-2j},$$

and

$$U=-i\left(W_2+2s{W}_1^0\right).$$

(19)

Taking the matrix $V_k$ in the form

$$V_k=-2^{k}i\left(W_{2k+2}+2s{W}_{2k+1}^0\right),$$

(20)

let us define the second equation of the Lax pair

$${\mathsf{\Psi }}_{t_k}=V_k\mathsf{\Psi }.$$

(21)

From the conditions of compatibility

$${\partial }_{t_k}U-{\partial }_x{V}_k+U{V}_k-V_{k}U=0$$

of the Equations (12) and (21) the following evolutionary nonlinear equations follow

$$\begin{array}{cc}\hfill {\partial }_{t_k}p& =-2^{k}i{\left(H_k\right)}_x+2^{k+1}spq{H}_k-2^{k+2}isp{F}_{k+1}\hfill \\ \hfill & =-2^{k+1}(H_{k+1}+i(2s-1)p{F}_{k+1}),\hfill \\ \hfill {\partial }_{t_k}q& =-2^{k}i{\left(G_k\right)}_x-2^{k+1}spq{G}_k+2^{k+2}isq{F}_{k+1}\hfill \\ \hfill & =2^{k+1}(G_{k+1}+i(2s-1)q{F}_{k+1}).\hfill \end{array}$$

(22)

The first coupled equation from this hierarchy has the form

$$\begin{array}{c}i{p}_{t_1}+p_{xx}+2i(2s-1)pq{p}_x+i(4s-1)p^2{q}_x+(4s-1)s{p}^3{q}^2=0,\\ -i{q}_{t_1}+q_{xx}-2i(2s-1)pq{q}_x-i(4s-1)q^2{p}_x+(4s-1)s{p}^2{q}^3=0.\end{array}$$

(23)

We believe that the Equation (23) is the most natural form of the generalized DNLS equation, since substituting $q=-p^{*}$ and the appropriate s into it, one can get one of the Equations (8)–(10). It is not difficult to see that the Equation (23) implies three main coupled DNLS equations.

• The coupled DNLSI for $s=0$

  $$\begin{array}{c}i{p}_{t_1}+p_{xx}-i{\left(p^{2}q\right)}_x=0,\\ -i{q}_{t_1}+q_{xx}+i{\left(q^{2}p\right)}_x=0.\end{array}$$
• The coupled DNLSII for $s=1/4$

  $$\begin{array}{c}i{p}_{t_1}+p_{xx}-ipq{p}_x=0,\\ -i{q}_{t_1}+q_{xx}+ipq{q}_x=0.\end{array}$$
• The coupled DNLSIII for $s=1/2$

  $$\begin{array}{c}i{p}_{t_1}+p_{xx}+i{p}^2{q}_x+{\displaystyle \frac{1}{2}}{p}^3{q}^2=0,\\ -i{q}_{t_1}+q_{xx}-i{q}^2{p}_x+{\displaystyle \frac{1}{2}}{p}^2{q}^3=0.\end{array}$$

Note that from the Equations (18) and (22), it follows that for any value of s, the equality

$${\partial }_{t_k}{F}_1=2^k{\partial }_x{F}_{k+1}$$

holds and, therefore, there exists a function $\phi$ such that $F_{k+1}=2^{-k}{\partial }_{t_k}\phi$ ($x\equiv t_0$). Let us note that similar equalities hold in the case of other integrable equations (see, for example, [11]).

3. Spectral Curves of the Multiphase Solutions

Substituting (13) into (14) and simplifying, we get

$$\begin{array}{cc}\hfill & {\left(M_0\right)}_x=ispq[M_0,J],\hfill \\ \hfill & {\left(M_1\right)}_x=ispq[M_1,J]-[M_0,Q],\hfill \\ \hfill & {\left(M_j\right)}_x=ispq[M_j,J]-[M_{j-1},Q]+[M_{j-2},J],j=2,\cdots ,2n,\hfill \end{array}$$

(24)

where $[A,B]=AB-BA$,

$$\begin{array}{cc}\hfill & M_0=a_{0}J+i{a}_{1}Q+\sum _{k=1}^{n-1}{a}_{2k+1}{W}_{2k}^0,\hfill \\ \hfill & M_j=a_{j}J+i{a}_{j+1}Q+\sum _{k=1}^{2n-j-1}{a}_{k+j+1}{W}_k^0,j=1,\cdots ,2n-2,\hfill \\ \hfill & M_{2n-1}=a_{2n-1}J+i{a}_{2n}Q,M_{2n}=a_{2n}J.\hfill \end{array}$$

(25)

For $j=0$ from (24) and (25) the following stationary equations follow

$$\begin{array}{cc}\hfill & a_1(i{p}_x-2s{p}^{2}q)+\sum _{k=1}^{n-1}{a}_{2k+1}\left({\left(H_k\right)}_x+2ispq{H}_k\right)=0,\hfill \\ \hfill & a_1(i{q}_x+2sp{q}^2)+\sum _{k=1}^{n-1}{a}_{2k+1}\left({\left(G_k\right)}_x-2ispq{G}_k\right)=0.\hfill \end{array}$$

(26)

These equations are satisfied by multiphase solutions of the evolutionary nonlinear Equation (22). As in the case of the Kaup-Newell hierarchy [13], the multiphase solutions must also satisfy the second set of stationary equations (obtained from (24) and (25) for $j=1$)

$$\begin{array}{cc}\hfill & 2a_{0}p+a_2(i{p}_x-2s{p}^{2}q)+\sum _{k=1}^{n-1}{a}_{2k+2}\left({\left(H_k\right)}_x+2ispq{H}_k\right)=0,\hfill \\ \hfill & 2a_0-a_2(i{q}_x+2sp{q}^2)-\sum _{k=1}^{n-1}{a}_{2k+2}\left({\left(G_k\right)}_x-2ispq{G}_k\right)=0.\hfill \end{array}$$

(27)

Since the equation of the spectral curve of the multiphase solution has the form

$$\mathcal{R}(\nu ,\lambda )=det(\nu I-M)=0,$$

where I is the unit matrix, and since $\mathrm{Tr}M=0$, in this case the spectral curve is given by the equation

$${\nu }^2=-detM=a_{2n}^2{\lambda }^{4n}+\sum _{k=1}^{4n}{f}_k(p,q){\lambda }^{4n-k}\mathrm{for}{a}_{2n}\ne 0,$$

(28)

and

$${\nu }^2=-detM=a_{2n-1}^2{\lambda }^{4n-2}+\sum _{k=1}^{4n-2}{f}_k(p,q){\lambda }^{4n-2-k}\mathrm{for}{a}_{2n}=0,$$

(29)

where $f_k(p,q)$ are integrals of the evolutionary nonlinear Equation (22). Since the curves (28) and (29) are hyperelliptic, their genus is $g=2n-1$ and $g=2n-2$, respectively.

It follows from Equation (18) that the functions $F_k$, $G_k$ and $H_k$ have the following symmetries

$$\begin{array}{cc}\hfill & F_k(-p,-q)\equiv F_k(p,q),\hfill \\ \hfill & G_k(-p,-q)\equiv -G_k(p,q),\hfill \\ \hfill & H_k(-p,-q)\equiv -H_k(p,q).\hfill \end{array}$$

Therefore, the stationary and evolutionary equations are invariant with respect to the involution ${\tau }_1:(p,q)\to (-p,-q)$.

Since the matrices $W_k$ (17) have the symmetry ${\tau }_2:(\lambda ,p,q)\to (-\lambda ,-p,-q)$, the monodromy matrix M also has this symmetry. Due to the fact that the equation of the spectral curve of multiphase solutions is invariant with respect to two involutions ${\tau }_1$ and ${\tau }_2$ simultaneously, it has the following symmetry

$$\mathcal{R}(\nu ,-\lambda )\equiv \mathcal{R}(\nu ,\lambda ).$$

Therefore all coefficients $f_{2k-1}$ ($k\in \mathbb{N}$) are equal to zero.

4. Examples

4.1. Case $g=0$

If $g=0$, then $n=1$, $a_2=0$ and $a_1=1$. Therefore, a matrix M has a form

$$M(\lambda ,x)=a_{0}J+W_1=\left(\begin{array}{cc}\lambda +a_0& ip\\ iq& -\lambda -a_0\end{array}\right).$$

(30)

It follows from the Equation (30) that the spectral curve is given by the equation

$${\nu }^2={(\lambda +a_0)}^2-pq.$$

Therefore, the product $pq$ is a constant, $pq=p_0{q}_0$.

From the Equation (14) for $N=0$, the following stationary equations follow

$$\begin{array}{c}{a}_{0}p=0,a_{0}q=0,\\ i{p}_x-2s{p}^{2}q=0,i{q}_x+2sp{q}^2=0.\end{array}$$

Solving these equations for $pq=p_0{q}_0$, we have: $a_0=0$,

$$p=p_0{e}^{iKx},q=q_0{e}^{-iKx},K=-2s{p}_0{q}_0.$$

Substituting these expressions in Equation (23), we obtain the solution of Equation (23) in the form of a plane wave

$$p=p_0{e}^{iKx+i\kappa t_1},q=q_0{e}^{-iKx-i\kappa t_1},K=-2s{p}_0{q}_0,\kappa =-3s{\left(p_0{q}_0\right)}^2.$$

(31)

Since $a_0=0$ and $pq=p_0{q}_0$, the equation of the spectral curve of this solution has the form

$${\nu }^2={\lambda }^2-p_0{q}_0.$$

4.2. Case $g=1$

If $g=1$, then $n=1$ and $a_2=1$. Therefore, a matrix M has a form

$$M(\lambda ,x)=a_{0}J+a_1{W}_1+W_2.$$

(32)

From the Equation (14) for $g=1$, the following stationary equations follow

$$\begin{array}{c}{a}_1(i{p}_x-2s{p}^{2}q)=0,a_1(i{q}_x+2sp{q}^2)=0,\\ 2a_{0}p+(i{p}_x-2s{p}^{2}q)=0,2a_{0}q-(i{q}_x+2sp{q}^2)=0.\end{array}$$

(33)

From the Equation (33) it follows that if $a_1\ne 0$, then $a_0=0$ and the solution of the Equation (23) has the form of a plane wave (31). Therefore, we assume that $a_1=0$ and $a_0\ne 0$.

Calculating the equation of the spectral curve, we get

$${\nu }^2={({\lambda }^2+a_0)}^2-{\lambda }^{2}pq.$$

Since the coefficients of this equation are constant values, the equation $pq=p_0{q}_0$ also holds in this case. Solving the Equation (33) for $a_1=0$, $pq=p_0{q}_0$, we have

$$p=p_0{e}^{iKx},q=q_0{e}^{-iKx},K=2(a_0-s{p}_0{q}_0).$$

Substituting these expressions in the Equation (23), we get the solution of the Equation (23) in the form of a plane wave

$$\begin{array}{c}p=p_0{e}^{iKx+i\kappa t_1},q=q_0{e}^{-iKx-i\kappa t_1},K=2(a_0-s{p}_0{q}_0),\\ \kappa =-4a_0^2+2(4s+1)a_0{p}_0{q}_0-3s{\left(p_0{q}_0\right)}^2.\end{array}$$

(34)

It is easy to see that the solution (31) is a special case of the solution (34) for $a_0=0$.

This example illustrates the fact that the genus $g=1$ of the spectral curve in the case of DNLS equations does not coincide with the number of phases ($m=0$).

4.3. Case $g=2$

4.3.1. General Formulas

Let us assume $g=2$, $n=2$, $a_4=0$, $a_3=1$. Then the matrix M has the form

$$M(\lambda ,x)=a_{0}J+a_1{W}_1+a_2{W}_2+W_3.$$

(35)

From the Equation (14) for $g=2$, the following stationary equations follow

$$\begin{array}{cc}\hfill & 2a_{0}p+a_2\left(i{p}_x-2s{p}^{2}q\right)=0,\hfill \\ \hfill & 2a_{0}q-a_2\left(i{q}_x+2sp{q}^2\right)=0,\hfill \\ \hfill & a_1\left(i{p}_x-2s{p}^{2}q\right)\hfill \\ \hfill & +(2s-1)s{p}^3{q}^2+i(1-3s)pq{p}_x+{\displaystyle \frac{i}{2}}(1-2s)p^2{q}_x-{\displaystyle \frac{1}{2}}{p}_{xx}=0,\hfill \\ \hfill & a_1\left(i{q}_x+2sp{q}^2\right)\hfill \\ \hfill & -(2s-1)s{p}^2{q}^3+i(1-3s)pq{q}_x+{\displaystyle \frac{i}{2}}(1-2s)q^2{p}_x+{\displaystyle \frac{1}{2}}{q}_{xx}=0.\hfill \end{array}$$

(36)

For $a_2\ne 0$, the condition of compatibility of the Equation (36) implies the constancy of the product $pq$. Therefore, we will assume that $a_2=a_0=0$.

Calculating the equation of the spectral curve, we get

$${\nu }^2={\lambda }^6+2a_1{\lambda }^4+f_4{\lambda }^2+f_6,$$

where the integrals $f_k$ equal to

$$\begin{array}{cc}\hfill & f_4=a_1^2-a_{1}pq+{\displaystyle \frac{1}{4}}(8s-3)p^2{q}^2+{\displaystyle \frac{i}{2}}(p{q}_x-q{p}_x),\hfill \\ \hfill & f_6=-{\displaystyle \frac{1}{4}}pq{(2a_1+(1-2s)pq)}^2+{\displaystyle \frac{i}{4}}(2a_1+(1-2s)pq)(p{q}_x-q{p}_x)-{\displaystyle \frac{1}{4}}{p}_x{q}_x.\hfill \end{array}$$

(37)

From the Equations (36) and (37) it follows that the function $u\left(x\right)=pq$ satisfies the equation

$$u_{xx}=-{\displaystyle \frac{1}{2}}{u}^3-3a_1{u}^2+(2f_4-6a_1^2)u-4(a_1^3-a_1{f}_4+2f_6)$$

(38)

or

$${\left(u_x\right)}^2=-{\displaystyle \frac{1}{4}}{u}^4-2a_1{u}^3+(2f_4-6a_1^2)u^2-8(a_1^3-a_1{f}_4+2f_6)u+c_1,$$

(39)

where $c_1$ is the integration constant. It follows from the Equation (39) that $u\left(x\right)$ is an elliptic function or its degeneracy.

From (37) it is not difficult to find the Wronskian of the functions p and q

$$W[p,q]={\displaystyle \frac{i}{2}}(8s-3)u^2-2i{a}_{1}u+2i(a_1^2-f_4).$$

Knowing the Wronskian of functions and their product, it is not difficult to find the functions themselves

$$\begin{array}{cc}\hfill p\left(x\right)& =\sqrt{u}exp\left\{-{\displaystyle \frac{1}{2}}\int {\displaystyle \frac{Wdx}{u}}\right\}\hfill \\ \hfill & =\sqrt{u}exp\left\{-i\int \left({\displaystyle \frac{8s-3}{4}}u-a_1-{\displaystyle \frac{f_4-a_1^2}{u}}\right)dx\right\},\hfill \\ \hfill q\left(x\right)& =\sqrt{u}exp\left\{{\displaystyle \frac{1}{2}}\int {\displaystyle \frac{Wdx}{u}}\right\}\hfill \\ \hfill & =\sqrt{u}exp\left\{i\int \left({\displaystyle \frac{8s-3}{4}}u-a_1-{\displaystyle \frac{f_4-a_1^2}{u}}\right)dx\right\}.\hfill \end{array}$$

(40)

Substituting (40) in (36), (37) and simplifying with the relations (38), (39), we get the value of $c_1$:

$$c_1=-4{(a_1^2-f_4)}^2.$$

It is not difficult to check that the corresponding onee-phase solution of the Equation (23) has the form

$$\begin{array}{cc}\hfill & p(x,t_1)=\sqrt{u\left(X\right)}exp\left\{-i\int \left({\displaystyle \frac{8s-3}{4}}u\left(X\right)-a_1-{\displaystyle \frac{f_4-a_1^2}{u\left(X\right)}}\right)dx+iK{t}_1\right\},\hfill \\ \hfill & q(x,t_1)=\sqrt{u\left(X\right)}exp\left\{i\int \left({\displaystyle \frac{8s-3}{4}}u\left(X\right)-a_1-{\displaystyle \frac{f_4-a_1^2}{u\left(X\right)}}\right)dx-iK{t}_1\right\},\hfill \end{array}$$

(41)

where $X=x-2a_1{t}_1$, $K=4s{f}_4-2(2s+1)a_1^2$.

In this case, a spectral curve of the genus $g=2$ corresponds to the one-phase solution with the phase X.

4.3.2. Quasi-Rational Travelling Wave

Let us consider a degenerate spectral curve, which is given by the equation

$${\nu }^2={\left({\lambda }^2+a^2\right)}^3,a\in \mathbb{R}.$$

(42)

In this case

$$a_1={\displaystyle \frac{3}{2}}{a}^2,f_4=3a^4,f_6=a^6,c_1=-{\displaystyle \frac{9}{4}}{a}^8.$$

For these parameter values, the function $u\left(x\right)$ satisfies the equation

$${\left(u_x\right)}^2=-{\displaystyle \frac{1}{4}}{(u+a^2)}^3(u+9a^2).$$

Solving this equation, we get

$$u=-{\displaystyle \frac{a^2(4a^4{x}^2+9)}{4a^4{x}^2+1}}.$$

It follows from Equation (41) that the corresponding solution has the form

$$\begin{array}{cc}\hfill & p(x,t_1)=ia\sqrt{{\displaystyle \frac{4a^4{(x-3a^2{t}_1)}^2+9}{4a^4{(x-3a^2{t}_1)}^2+1}}}{e}^{i{\varphi }_1(x,t_1)+i(8s-3){\varphi }_2(x,t_1)+2is{a}^{2}x-3is{a}^4{t}_1},\hfill \\ \hfill & q(x,t_1)=ia\sqrt{{\displaystyle \frac{4a^4{(x-3a^2{t}_1)}^2+9}{4a^4{(x-3a^2{t}_1)}^2+1}}}{e}^{-i{\varphi }_1(x,t_1)+-i(8s-3){\varphi }_2(x,t_1)-2is{a}^{2}x-3is{a}^4{t}_1},\hfill \end{array}$$

(43)

where

$$\begin{array}{cc}\hfill & {\varphi }_1(x,t_1)=arctan\left(2a^2(x-3a^2{t}_1)/3\right),\hfill \\ \hfill & {\varphi }_2(x,t_1)=arctan\left(2a^2(x-3a^2{t}_1)\right).\hfill \end{array}$$

It follows from the identity

$$e^{iarctan\left(A\right)}=cos(arctan\left(A\right))+isin(arctan\left(A\right))={\displaystyle \frac{1+iA}{\sqrt{A^2+1}}}$$

(44)

that the solution (43) of the Equation (23) can be written by the following equalities

$$\begin{array}{cc}\hfill & p(x,t_1)={\displaystyle \frac{ia(3+2i{a}^2(x-3a^2{t}_1)){(1+2i{a}^2(x-3a^2{t}_1))}^{8s-3}}{{(4a^4{(x-3a^2{t}_1)}^2+1)}^{4s-1}}}{e}^{2is{a}^{2}x-3is{a}^4{t}_1},\hfill \\ \hfill & q(x,t_1)={\displaystyle \frac{ia(3-2i{a}^2(x-3a^2{t}_1)){(1-2i{a}^2(x-3a^2{t}_1))}^{8s-3}}{{(4a^4{(x-3a^2{t}_1)}^2+1)}^{4s-1}}}{e}^{-2is{a}^{2}x+3is{a}^4{t}_1}.\hfill \end{array}$$

(45)

For $4s\in \mathbb{Z}$ the solution (45) is a quasi-rational travelling wave. It is easy to see that the solution (45) satisfies the condition $q=-p^{*}$. Figure 1 shows the magnitude of the solution (45) for $a=1$.

4.4. Case $g=3$

4.4.1. General Formulas

Let us assume $g=3$, $n=2$, $a_4=1$. Then the matrix M has the form

$$M(\lambda ,x)=a_{0}J+a_1{W}_1+a_2{W}_2+a_3{W}_3+W_4.$$

(46)

From the Equations (26) and (27) it follows that to construct new solutions, ones should put $a_1=a_3=0$. The stationary equations in this case have the form

$$\begin{array}{cc}\hfill & 2a_{0}p+a_2\left(i{p}_x-2s{p}^{2}q\right)\hfill \\ \hfill & +(2s-1)s{p}^3{q}^2+i(1-3s)pq{p}_x+{\displaystyle \frac{i}{2}}(1-2s)p^2{q}_x-{\displaystyle \frac{1}{2}}{p}_{xx}=0,\hfill \\ \hfill & -2a_{0}q+a_2\left(i{q}_x+2sp{q}^2\right)\hfill \\ \hfill & -(2s-1)s{p}^2{q}^3+i(1-3s)pq{q}_x+{\displaystyle \frac{i}{2}}(1-2s)q^2{p}_x+{\displaystyle \frac{1}{2}}{q}_{xx}=0.\hfill \end{array}$$

(47)

Calculating the equation of the spectral curve, we get

$${\nu }^2={\lambda }^8+2a_2{\lambda }^6+f_4{\lambda }^4+f_6{\lambda }^2+a_0^2,$$

where the integrals $f_k$ equal to

$$\begin{array}{cc}\hfill f_4=& 2a_0+a_2^2-a_{2}pq+{\displaystyle \frac{1}{4}}(8s-3)p^2{q}^2+{\displaystyle \frac{i}{2}}(p{q}_x-q{p}_x),\hfill \\ \hfill f_6=& a_0(2a_2+pq)-{\displaystyle \frac{1}{4}}pq{(2a_2+(1-2s)pq)}^2\hfill \\ \hfill & +{\displaystyle \frac{i}{4}}(2a_2+(1-2s)pq)(p{q}_x-q{p}_x)-{\displaystyle \frac{1}{4}}{p}_x{q}_x.\hfill \end{array}$$

(48)

From the Equations (47) and (48) it follows that the function $u\left(x\right)=pq$ satisfies the equation

$$\begin{array}{cc}\hfill u_{xx}=& -{\displaystyle \frac{1}{2}}{u}^3-3a_2{u}^2+2(f_4-3a_2^2+6a_0)u\hfill \\ \hfill & -4(a_2^3-2a_0{a}_2-a_2{f}_4+2f_6)\hfill \end{array}$$

(49)

or

$$\begin{array}{cc}\hfill {\left(u_x\right)}^2=& -{\displaystyle \frac{1}{4}}{u}^4-2a_2{u}^3+2(f_4-3a_2^2+6a_0)u^2\hfill \\ \hfill & -8(a_2^3-2a_0{a}_2-a_2{f}_4+2f_6)u+c_1,\hfill \end{array}$$

(50)

where $c_1$ is the integration constant. It follows from the Equation (50) that $u\left(x\right)$ is an elliptic function or its degeneracy.

From (48) we find the Wronskian of the functions p and q

$$W[p,q]={\displaystyle \frac{i}{2}}(8s-3)u^2-2i{a}_{2}u+2i(2a_0+a_2^2-f_4).$$

Knowing the Wronskian of functions and their product, it is not difficult to find the functions themselves

$$\begin{array}{cc}\hfill & p\left(x\right)=\sqrt{u}exp\left\{-i\int \left({\displaystyle \frac{8s-3}{4}}u-a_2-{\displaystyle \frac{f_4-a_2^2-2a_0}{u}}\right)dx\right\},\hfill \\ \hfill & q\left(x\right)=\sqrt{u}exp\left\{i\int \left({\displaystyle \frac{8s-3}{4}}u-a_2-{\displaystyle \frac{f_4-a_2^2-2a_0}{u}}\right)dx\right\}.\hfill \end{array}$$

(51)

Substituting (51) in (47), (48) and simplifying with the relations (49), (50), we get the value of $c_1$:

$$c_1=-4{(2a_0+a_2^2-f_4)}^2.$$

It is not difficult to check that the corresponding one-phase solution of the Equation (23) has the form

$$\begin{array}{cc}\hfill & p(x,t_1)=\sqrt{u\left(X\right)}exp\left\{-i\int \left({\displaystyle \frac{8s-3}{4}}u\left(X\right)-a_2-{\displaystyle \frac{f_4-a_2^2-2a_0}{u\left(X\right)}}\right)dx+iK{t}_1\right\},\hfill \\ \hfill & q(x,t_1)=\sqrt{u\left(X\right)}exp\left\{i\int \left({\displaystyle \frac{8s-3}{4}}u\left(X\right)-a_2-{\displaystyle \frac{f_4-a_2^2-2a_0}{u\left(X\right)}}\right)dx-iK{t}_1\right\},\hfill \end{array}$$

(52)

where $X=x-2a_2{t}_1$, $K=4s{f}_4-2(2s+1)a_2^2-4(2s-1)a_0$.

In this case, a spectral curve of the genus $g=3$ corresponds to the one-phase solution with phase X.

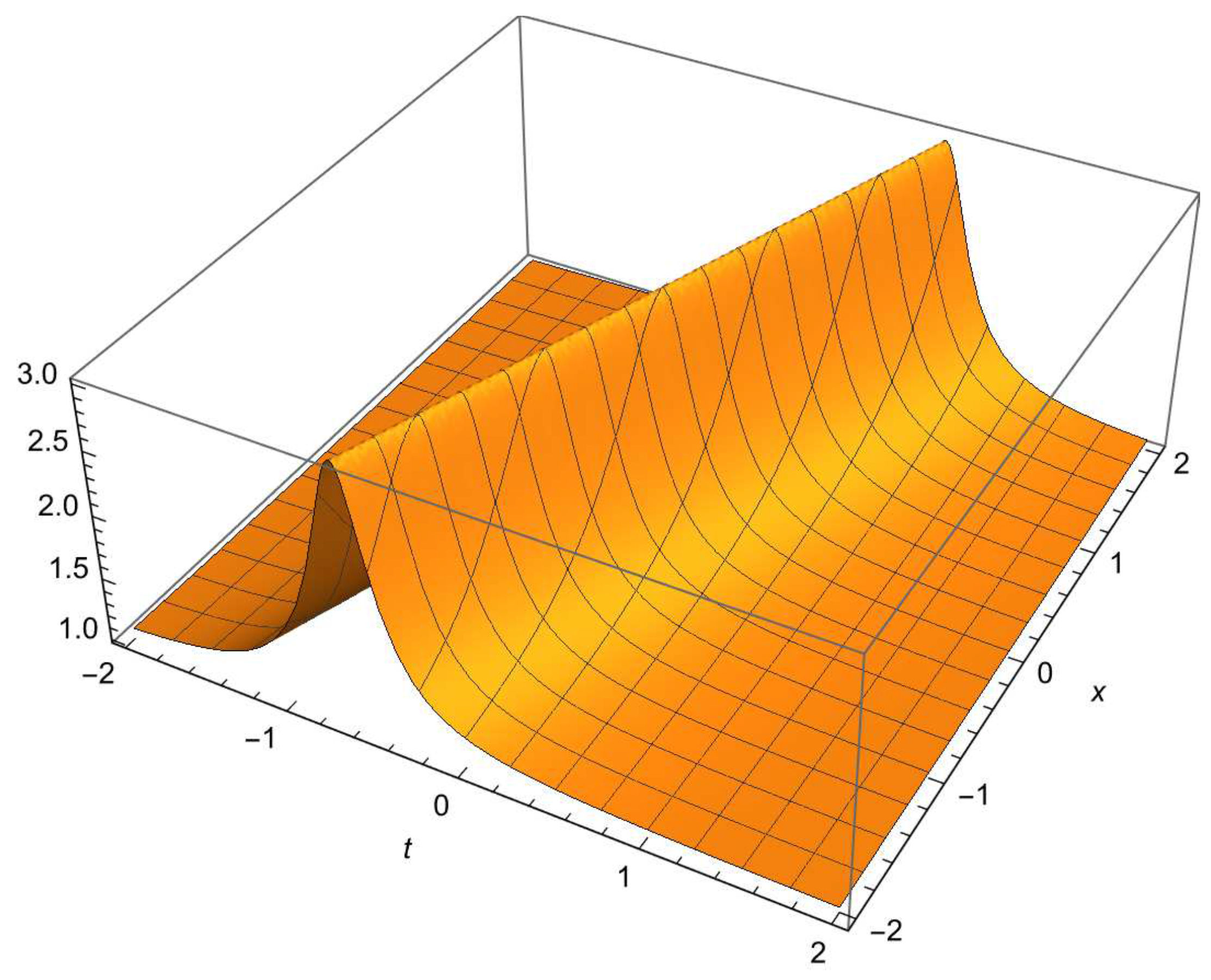
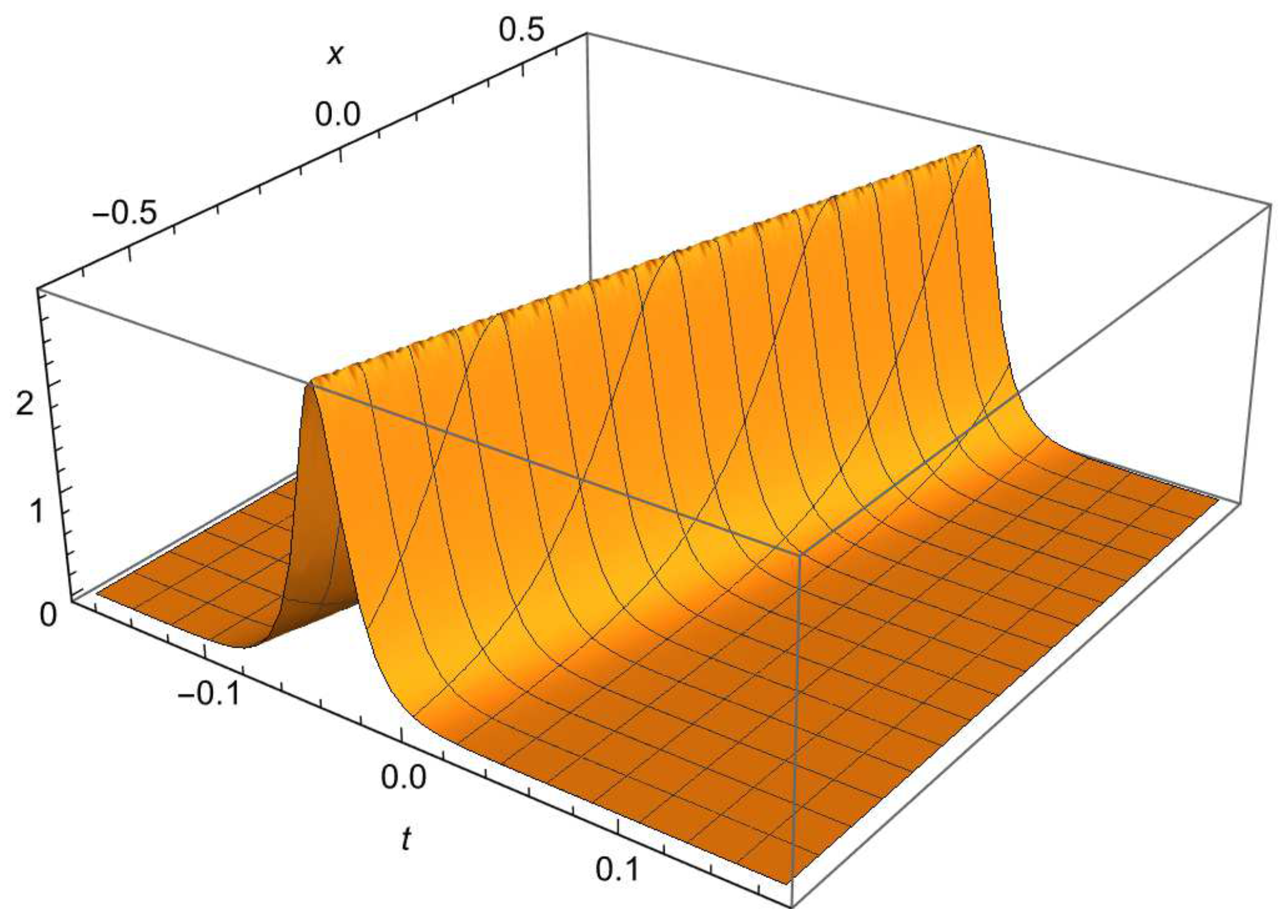
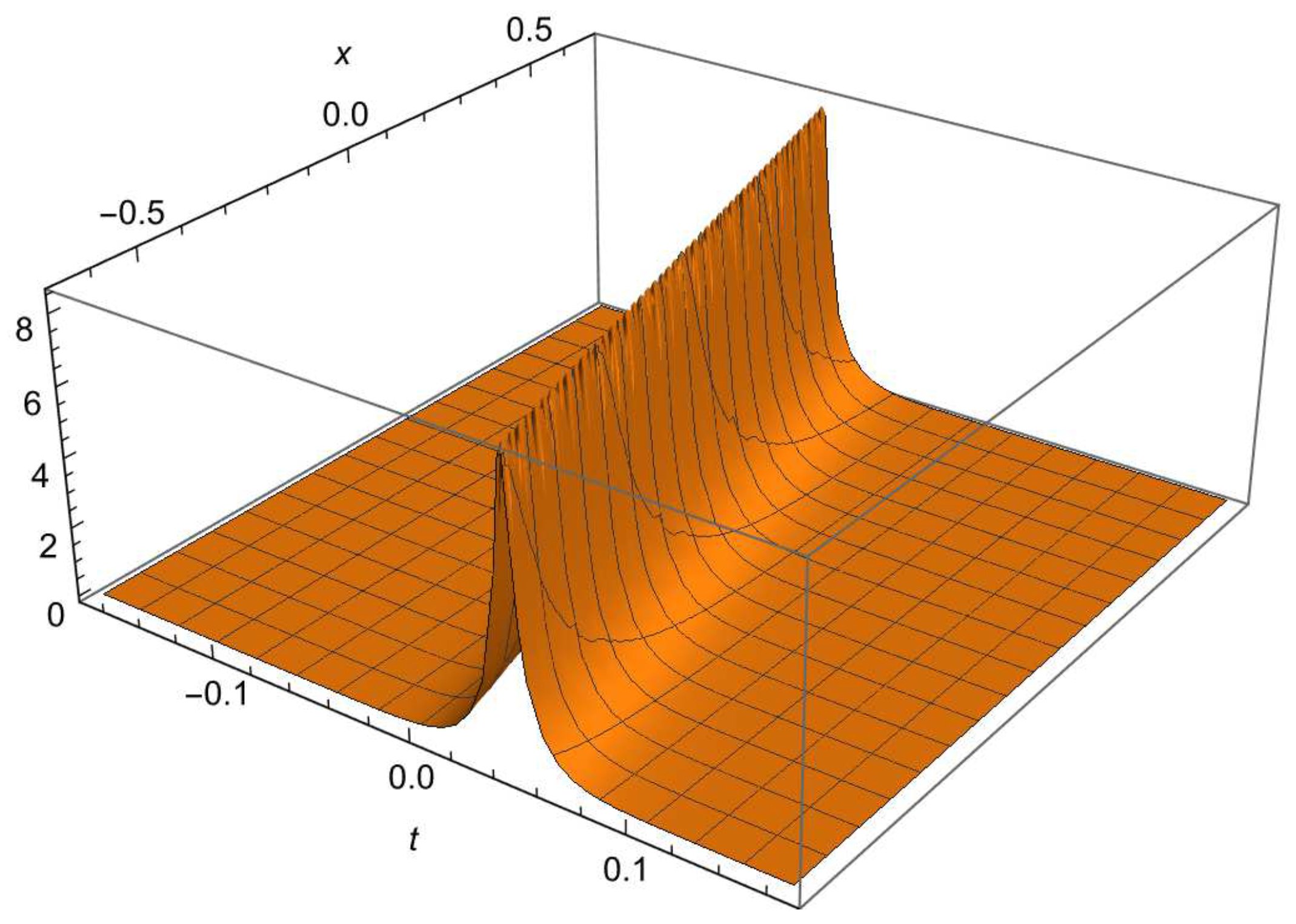
4.4.2. Soliton Solution

Let us consider a degenerate spectral curve, which is given by the equation

$${\nu }^2={\left({({\lambda }^2+a)}^2+b^2\right)}^2,a,b\in \mathbb{R}.$$

(53)

In this case

$$a_0=a^2+b^2,a_2=2a,f_4=2(3a^2+b^2),f_6=4a(a^2+b^2),c_1=0.$$

For these parameter values, the function $u\left(x\right)$ satisfies the equation

$${\left(u_x\right)}^2={\displaystyle \frac{1}{4}}(64b^2-16au-u^2)u^2.$$

Therefore,

$$x=\int {\displaystyle \frac{2du}{u\sqrt{64b^2-16au-u^2}}}.$$

Calculating the integral and expressing the function $u\left(x\right)$ from it, we get

$$u\left(x\right)={\displaystyle \frac{8b^2}{\sqrt{a^2+b^2}cosh\left(4bx\right)+a}}.$$

(54)

Thus, the one-phase solution of the Equation (23) constructed from the spectral curve (53) has the form

$$\begin{array}{cc}\hfill & p(x,t_1)={\displaystyle \frac{2\sqrt{2}b\epsilon e^{-i(8s-3)\varphi (x,t_1)+2iax+4i(b^2-a^2)t_1}}{\sqrt{\sqrt{a^2+b^2}cosh(4bx-16ab{t}_1)+a}}},\hfill \\ \hfill & q(x,t_1)={\displaystyle \frac{2\sqrt{2}b{e}^{i(8s-3)\varphi (x,t_1)-2iax-4i(b^2-a^2)t_1}}{\epsilon \sqrt{\sqrt{a^2+b^2}cosh(4bx-16ab{t}_1)+a}}},\hfill \end{array}$$

where

$$\varphi (x,t_1)=arctan\left({\displaystyle \frac{\sqrt{a^2+b^2}-a}{b}}tanh(2bx-8ab{t}_1)\right).$$

It follows from the identity (44) that this solution of the Equation (23) is defined by the following equalities

$$\begin{array}{cc}\hfill & p(x,t_1)={\displaystyle \frac{2\sqrt{2}b\epsilon {\left(bcoshX-icsinhX\right)}^{3-8s}{e}^{2iax+4i(b^2-a^2)t_1}}{c^{(3-8s)/2}{\left(\sqrt{a^2+b^2}cosh2X+a\right)}^{2-4s}}},\hfill \\ \hfill & q(x,t_1)={\displaystyle \frac{2\sqrt{2}b{\left(bcoshX+icsinhX\right)}^{3-8s}{e}^{-2iax-4i(b^2-a^2)t_1}}{\epsilon c^{(3-8s)/2}{\left(\sqrt{a^2+b^2}cosh2X+a\right)}^{2-4s}}},\hfill \end{array}$$

(55)

where $X=2bx-8ab{t}_1$, $c=\sqrt{a^2+b^2}-a$. For $\left|\epsilon \right|=1$, the solution (55) satisfies the condition $q(x,t_1)=p^{*}(x,t_1)$. Figure 2 shows the magnitude of the soliton (55) for $a=4$, $b=3$, $\epsilon =1$.

Changing the sign before the square root in the expression (54), we get

$$u\left(x\right)={\displaystyle \frac{-8b^2}{\sqrt{a^2+b^2}cosh\left(4bx\right)-a}}$$

and

$$\begin{array}{cc}\hfill & p(x,t_1)={\displaystyle \frac{2\sqrt{2}ib\epsilon {\left(bcoshX+i{c}_{1}sinhX\right)}^{3-8s}{e}^{2iax+4i(b^2-a^2)t_1}}{c_1^{(3-8s)/2}{\left(\sqrt{a^2+b^2}cosh2X-a\right)}^{2-4s}}},\hfill \\ \hfill & q(x,t_1)={\displaystyle \frac{2\sqrt{2}ib{\left(bcoshX-i{c}_{1}sinhX\right)}^{3-8s}{e}^{-2iax-4i(b^2-a^2)t_1}}{\epsilon c_1^{(3-8s)/2}{\left(\sqrt{a^2+b^2}cosh2X-a\right)}^{2-4s}}},\hfill \end{array}$$

(56)

where $X=2bx-8ab{t}_1$, $c_1=\sqrt{a^2+b^2}+a$. For $\left|\epsilon \right|=1$ the solution (56) satisfies the condition $q(x,t_1)=-p^{*}(x,t_1)$. Figure 3 shows the magnitude of the soliton (56) for $a=4$, $b=3$, $\epsilon =1$.

Let us note that solutions (55) and (56) correspond to the same spectral curve (53).

4.4.3. One-Phase Periodic Solution

Let a degenerate spectral curve be given by the equation

$${\nu }^2={\left({({\lambda }^2+a)}^2-b^2\right)}^2,a>b>0.$$

(57)

This equation can be obtained from (53) by replacing $b\to ib$. It is not difficult to check that the corresponding solutions of the DNLS equations can also be obtained using this substitution:

$$u\left(x\right)={\displaystyle \frac{-8b^2}{\sqrt{a^2-b^2}cos\left(4bx\right)+a}},$$

(58)

and

$$\begin{array}{cc}\hfill & p(x,t_1)={\displaystyle \frac{2\sqrt{2}ib\epsilon {\left(bcosX+i{c}_{2}sinX\right)}^{3-8s}{e}^{2iax-4i(b^2+a^2)t_1}}{c_2^{(3-8s)/2}{\left(\sqrt{a^2-b^2}cos2X+a\right)}^{2-4s}}},\hfill \\ \hfill & q(x,t_1)={\displaystyle \frac{2\sqrt{2}ib{\left(bcosX-i{c}_{2}sinX\right)}^{3-8s}{e}^{-2iax+4i(b^2+a^2)t_1}}{\epsilon c_2^{(3-8s)/2}{\left(\sqrt{a^2-b^2}cos2X+a\right)}^{2-4s}}},\hfill \end{array}$$

(59)

where $X=2bx-8ab{t}_1$, $c_2=a-\sqrt{a^2-b^2}$. For $\left|\epsilon \right|=1$ the solution (59) satisfies the equation $q(x,t_1)=-p^{*}(x,t_1)$. Figure 4 shows the magnitude of the one-phase periodic solution (59) for $a=4$, $b=3$, $\epsilon =1$.

By changing the parameter $a\to -a$ in the curve Equation (57):

$${\nu }^2={\left({({\lambda }^2-a)}^2-b^2\right)}^2,a>b>0,$$

(60)

we get the following equalities

$$u\left(x\right)={\displaystyle \frac{8b^2}{\sqrt{a^2-b^2}cos\left(4bx\right)+a}},$$

(61)

and

$$\begin{array}{cc}\hfill & p(x,t_1)={\displaystyle \frac{2\sqrt{2}b\epsilon {\left(bcosX-i{c}_{2}sinX\right)}^{3-8s}{e}^{2iax-4i(b^2+a^2)t_1}}{c_2^{(3-8s)/2}{\left(\sqrt{a^2-b^2}cos2X+a\right)}^{2-4s}}},\hfill \\ \hfill & q(x,t_1)={\displaystyle \frac{2\sqrt{2}b{\left(bcosX+i{c}_{2}sinX\right)}^{3-8s}{e}^{-2iax+4i(b^2+a^2)t_1}}{\epsilon c_2^{(3-8s)/2}{\left(\sqrt{a^2-b^2}cos2X+a\right)}^{2-4s}}},\hfill \end{array}$$

(62)

where $X=2bx-8ab{t}_1$, $c_2=a-\sqrt{a^2-b^2}$. For $\left|\epsilon \right|=1$ the solution (59) satisfies the condition $q(x,t_1)=p^{*}(x,t_1)$.It is not difficult to see that the solutions (59) and (62) have the same magnitude.

5. Concluding Remark

As a result of the analysis of the examples, we can make the conjecture.

Let us write the equation of the spectral curve of a M-phase solution in the following form

$${\mathsf{\Gamma }}_g:{\nu }^2=P_{g+1}\left({\lambda }^2\right),$$

(63)

where $P_k\left(\mu \right)$ is a polynomial of $\mu$ of degree k. Then the genus g of the spectral curve (63) is equal: $g=2M$ for even g and $g=2M+1$ for odd g. Therefore the spectral curve of a M-phase solution of the derived NLS equation is a covering of the algebraic cuve of the genus M:

$${\mathsf{\Gamma }}_M:{\nu }^2=P_{g+1}\left(\mu \right).$$

(64)

Hence, it seems that finite-gap solutions should be constructed not according to curve ${\mathsf{\Gamma }}_g$ (63), but according to curve ${\mathsf{\Gamma }}_M$ (64).

It is well known that the presence of symmetry $\lambda \to -\lambda$ of the hyperelliptic curve ${\mathsf{\Gamma }}_g$ (63) leads to the fact that it is a cover over two other curves: ${\mathsf{\Gamma }}_M$ (64) and

$${\mathsf{\Gamma }}_N:{\nu }^2=\mu P_{g+1}\left(\mu \right),$$

(65)

where $N=g-M$ is a genus of the curve (65). In the future, we plan to investigate the roles of curves ${\mathsf{\Gamma }}_M$ and ${\mathsf{\Gamma }}_N$ in the process of constructing finite-gap multiphase solutions.