Relation between Quantum Walks with Tails and Quantum Walks with Sinks on Finite Graphs
Abstract
:1. Introduction
2. Preliminary
2.1. Graph Notation
2.2. Definition of the Grover Walk
2.3. Boundary Operators
3. Definition of the Grover Walk on Graphs with Sinks
4. Main Theorem
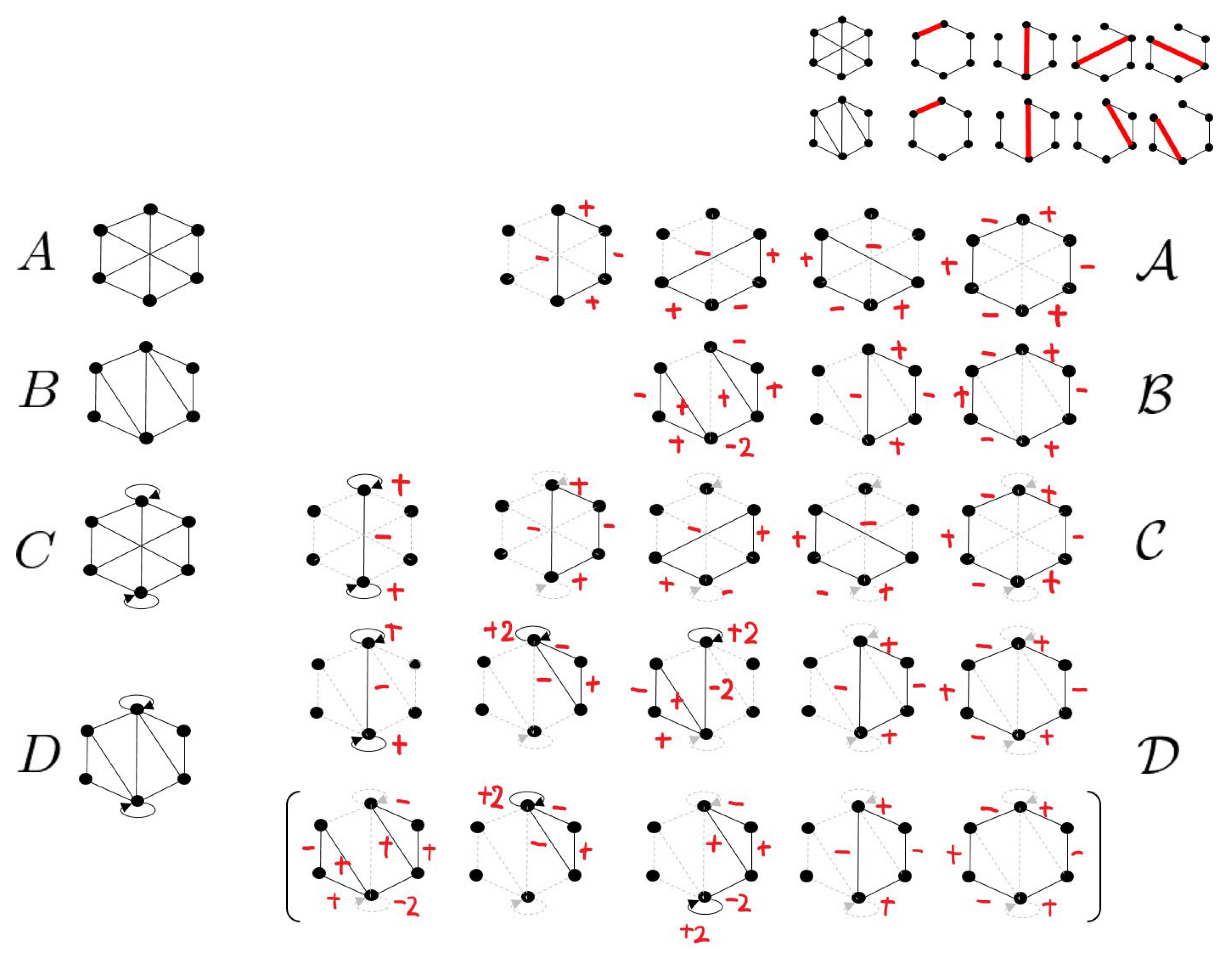
- Case A:
- and is a bipartite graph;
- Case B:
- and is a non-bipartite graph;
- Case C:
- and is a bipartite graph;
- Case D:
- and is a non-bipartite graph.
- 1.
- exists.
- 2.
- The survival probability γ is expressed by
5. Example
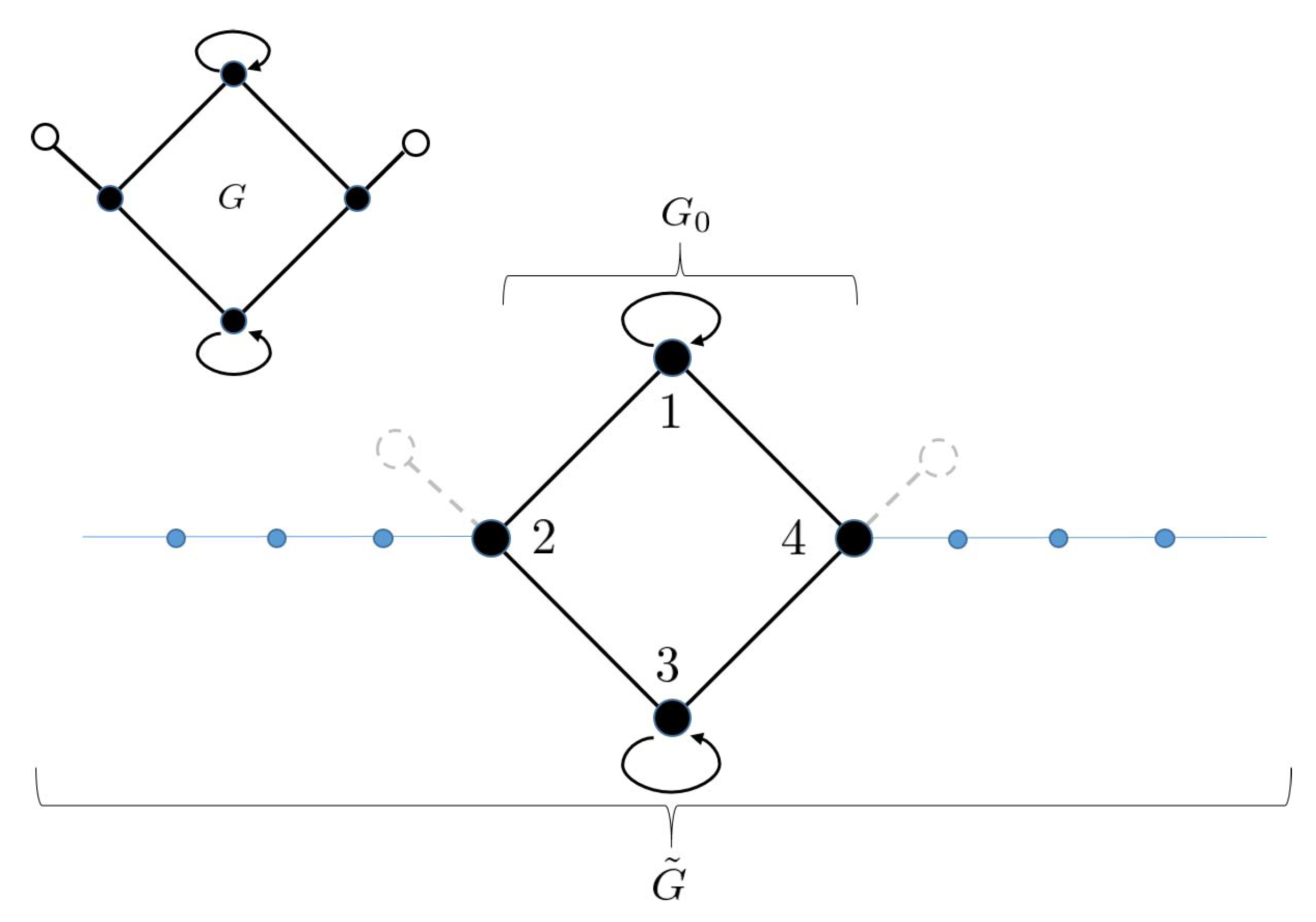
6. Relation between Grover Walk with Sinks and Grover Walk with Tails
6.1. Grover Walk on Graphs with Tails
6.2. Relation between Grover Walk with Sinks and Grover Walk with Tails
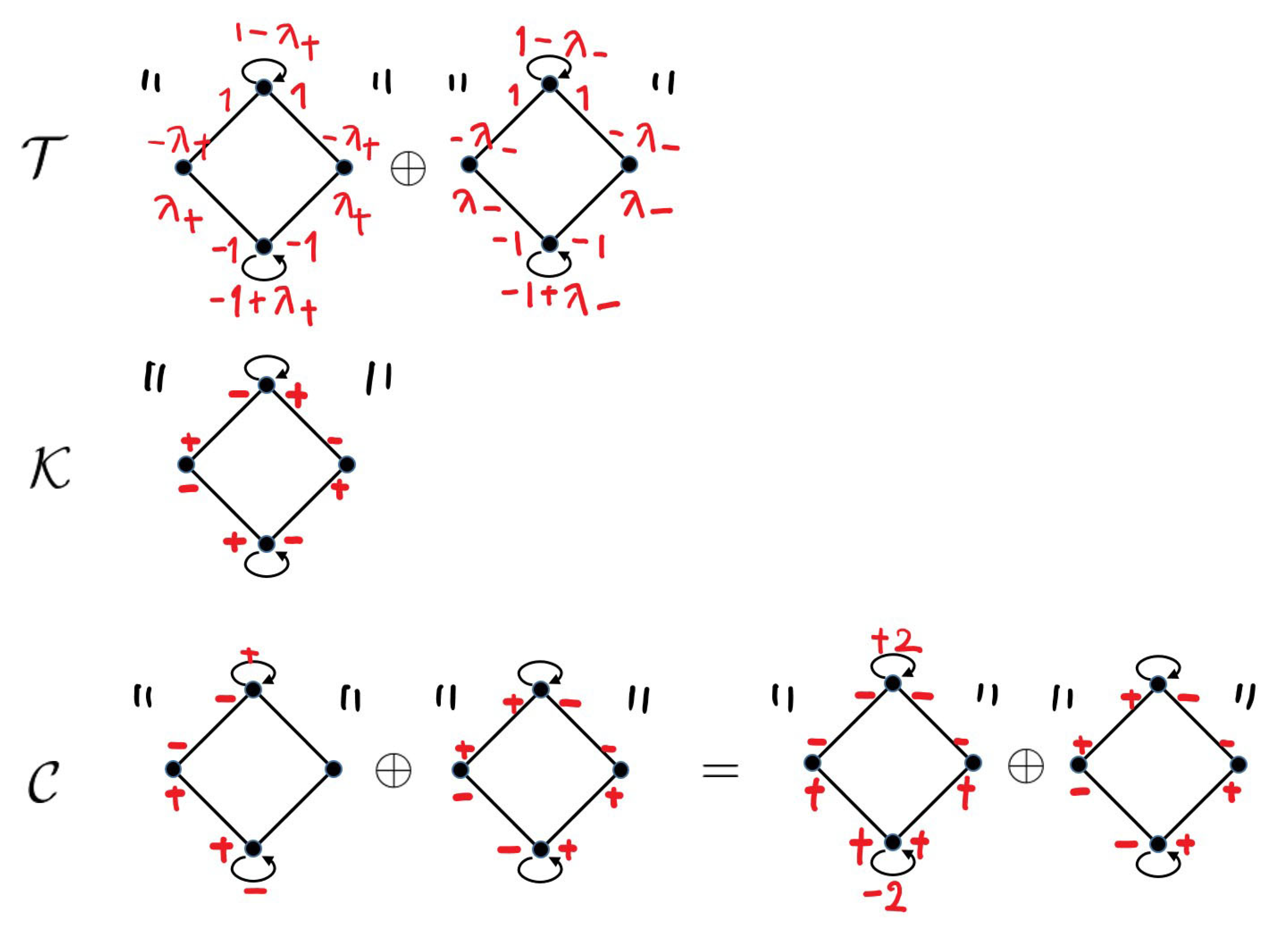
7. Centered Generalized Eigenspace of E for the Grover Walk Case
7.1. The Stationary States from the Viewpoint of the Centered Generalized Eigenspace
- 1.
- For any , it holds that , i.e.,
- 2.
- Let be the projection operator on along with ; that is, and . Then, is the orthogonal projection onto , i.e., .
- 3.
- The operator E acts as a unitary operator on , that is, and for any with .
- 1.
- The state in Theorem 2 belongs to for any time step .
- 2.
- The state of QW with sinks, , asymptotically belongs to in the long time limit n.
7.2. Characterization of Centered Generalized Eigenspace by Graph Notations
- 1.
- if and only if .
- 2.
- if and only if supp for any .
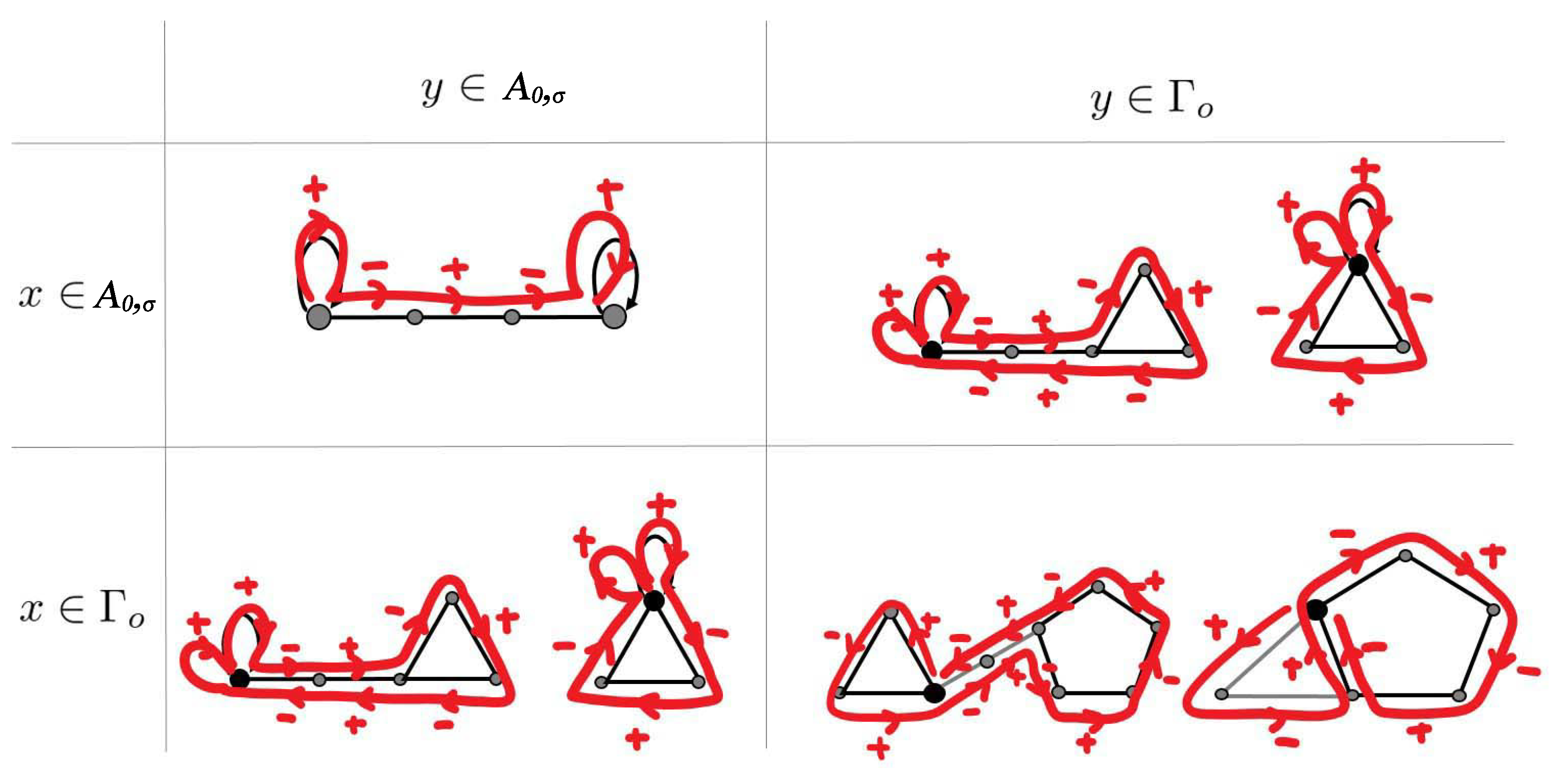
- 1.
- , case:If is a bipartite graph, let us fix an odd length fundamental cycle and pick up another . We set the following walk q and define the function on ; , induced by :
- (a)
- case: We set q as the shortest closed walk starting from a vertex and visiting all the vertices of and ; that is, . Here, and the suffices are modulus of r and s.
- (b)
- case: Let us fix the shortest path between and c by . Denoting the vertex in connecting to p by , we set q by the shortest closed walk q starting from and visiting all the vertices; that is, , where , .
Note that, by the definition of the fundamental cycle, the intersection is a path in Case (1). Since is connected, there is a path connecting to c and we fix such a path for every pair of in Case (2). - 2.
- and case:If the number of self-loops , let us fix a self-loop from and a path between to each . Let us denote the path between and a by . Then, we set the walk from to a by and .
- 3.
- and case:If and is a non-bipartite graph, let us fix a self-loop and pick up an odd cycle ; if the self-loop , we set the walk starting from visiting all the vertices and returning back to by ; and, for , let us fix a path between and and set the walk starting from visiting all the vertices and returning back to ; . Then, we set .
- 4.
- and case:Let us fix an odd length fundamental cycle and pick up a self-loop . Let us set a short length path p between and . Then, we consider the same walk q as in Case (3) and set
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ambainis, A. Quantum walks and their algorithmic applications. Int. J. Quantum Inf. 2003, 1, 507–518. [Google Scholar] [CrossRef] [Green Version]
- Ambainis, A.; Bach, E.; Nayak, A.; Vishwanath, A.; Watrous, J. One-Dimensional Quantum Walks. In Proceedings of the 33rd Annual ACM Symposium on Theory of Computing 2001, Heraklion, Greece, 6–8 July 2001; p. 37. [Google Scholar]
- Konno, N.; Namiki, T.; Soshi, T.; Sudbury, A. Absorption problems for quantum walks in one dimension. J. Phys. A Math. Gen. 2003, 36, 241. [Google Scholar] [CrossRef] [Green Version]
- Bach, E.; Coppersmith, S.; Goldschen, M.P.; Joynt, R.; Watrous, J. One-dimensional quantum walks with absorbing boundaries. J. Comput. Syst. Sci. 2004, 69, 562. [Google Scholar] [CrossRef] [Green Version]
- Yamasaki, T.; Kobayashi, H.; Imai, H. Analysis of absorbing times of quantum walks. Phys. Rev. A 2003, 68, 012302. [Google Scholar] [CrossRef] [Green Version]
- Inui, N.; Konno, N.; Segawa, E. One-dimensional three-state quantum walk. Phys. Rev. E 2005, 72, 056112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Štefaňák, M.; Novotný, J.; Jex, I. Percolation assisted excitation transport in discrete-time quantum walks. New J. Phys. 2016, 18, 023040. [Google Scholar] [CrossRef]
- Mareš, J.; Novotný, J.; Jex, I. Percolated quantum walks with a general shift operator: From trapping to transport. Phys. Rev. A 2019, 99, 042129. [Google Scholar] [CrossRef] [Green Version]
- Mareš, J.; Novotný, J.; Štefaňák, M.; Jex, I. A counterintuitive role of geometry in transport by quantum walks. Phys. Rev. A 2020, 101, 032113. [Google Scholar] [CrossRef] [Green Version]
- Mareš, J.; Novotný, J.; Jex, I. Quantum walk transport on carbon nanotube structures. Phys. Lett. A 2020, 384, 126302. [Google Scholar] [CrossRef] [Green Version]
- Ohtsu, M.; Kobayashi, K.; Kawazoe, T.; Yatsui, T.; Naruse, M. Principles of Nanophotonics; Taylor and Francis: Boca Raton, FL, USA, 2008. [Google Scholar]
- Nomura, W.; Yatsui, T.; Kawazoe, T.; Naruse, M.; Ohtsu, M. Structural dependency of optical excitation transfer via optical near-field interactions between semiconductor quantum dots. Appl. Phys. B 2010, 100, 181–187. [Google Scholar] [CrossRef]
- Krovi, H.; Brun, T.A. Hitting time for quantum walks on the hypercube. Phys. Rev. A 2006, 73, 032341. [Google Scholar] [CrossRef] [Green Version]
- Krovi, H.; Brun, T.A. Quantum walks with infinite hitting times. Phys. Rev. A 2006, 74, 042334. [Google Scholar] [CrossRef] [Green Version]
- Higuchi, Y.; Konno, N.; Sato, I.; Segawa, E. Spectral and asymptotic properties of Grover walks on crystal lattices. J. Funct. Anal. 2014, 267, 4197–4235. [Google Scholar] [CrossRef]
- Feldman, E.; Hillery, M. Quantum walks on graphs and quantum scattering theory. In Coding Theory and Quantum Computing (Contemporary Mathematics); Evans, D., Holt, J., Jones, C., Klintworth, K., Parshall, B., Pfister, O., Ward, H., Eds.; American Mathematical Society: Providence, RI, USA, 2005; Volume 381, pp. 71–96. [Google Scholar]
- Feldman, E.; Hillery, M. Modifying quantum walks: A scattering theory approach. J. Phys. A Math. Theor. 2007, 40, 11343–11359. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M. Dynamical Systems: Stability, Symbolic Dynamics, and Chaos; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Higuchi, Y.; Segawa, E. Dynamical system induced by quantum walks. J. Phys. A Math. Theor. 2019, 52, 39. [Google Scholar] [CrossRef] [Green Version]
| State in | |||
|---|---|---|---|
| QW with tails in the setting of Theorem 2 [19] | (for any n) | ||
| QW with sinks | (asymptotically) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konno, N.; Segawa, E.; Štefaňák, M. Relation between Quantum Walks with Tails and Quantum Walks with Sinks on Finite Graphs. Symmetry 2021, 13, 1169. https://doi.org/10.3390/sym13071169
Konno N, Segawa E, Štefaňák M. Relation between Quantum Walks with Tails and Quantum Walks with Sinks on Finite Graphs. Symmetry. 2021; 13(7):1169. https://doi.org/10.3390/sym13071169
Chicago/Turabian StyleKonno, Norio, Etsuo Segawa, and Martin Štefaňák. 2021. "Relation between Quantum Walks with Tails and Quantum Walks with Sinks on Finite Graphs" Symmetry 13, no. 7: 1169. https://doi.org/10.3390/sym13071169
APA StyleKonno, N., Segawa, E., & Štefaňák, M. (2021). Relation between Quantum Walks with Tails and Quantum Walks with Sinks on Finite Graphs. Symmetry, 13(7), 1169. https://doi.org/10.3390/sym13071169






