A Fractional Approach to a Computational Eco-Epidemiological Model with Holling Type-II Functional Response
Abstract
:1. Introduction
2. An Overview of Fractional Calculus
3. The Model Formulation
4. Mathematical Analysis for Model
4.1. The Equilibrium Points
- that explains the trivial equilibrium point.
- which is meaningless from a biological point of view.
- that explains the existence of susceptible prey-only situation.
- that explains the coexistence of suspected prey and predator populations situation. A sufficient condition for the existence of these points is that we have
- that implies the coexistence of suspected and infected prey populations in the model. A sufficient condition for the existence of these points is that we have
4.2. The Existence of the Solution
4.3. The Uniqueness of the Solution
5. An Approximate Approach to the Solution
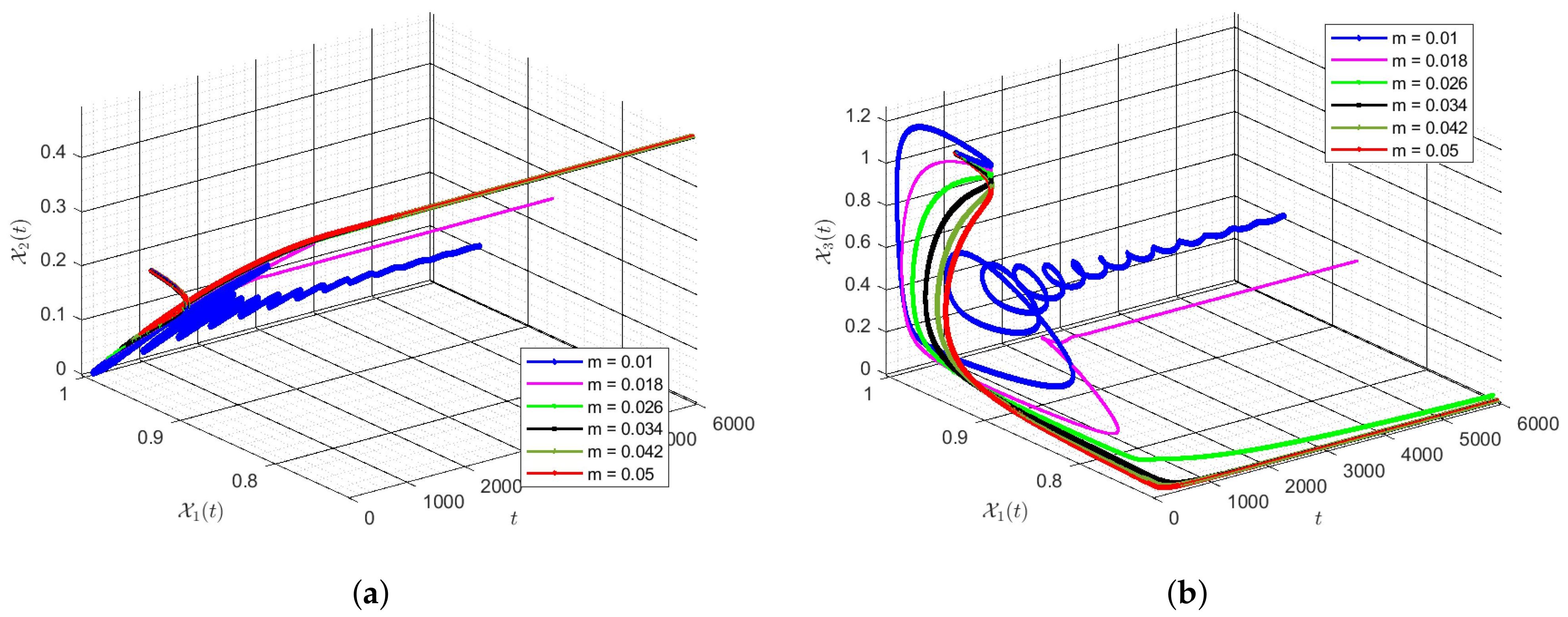
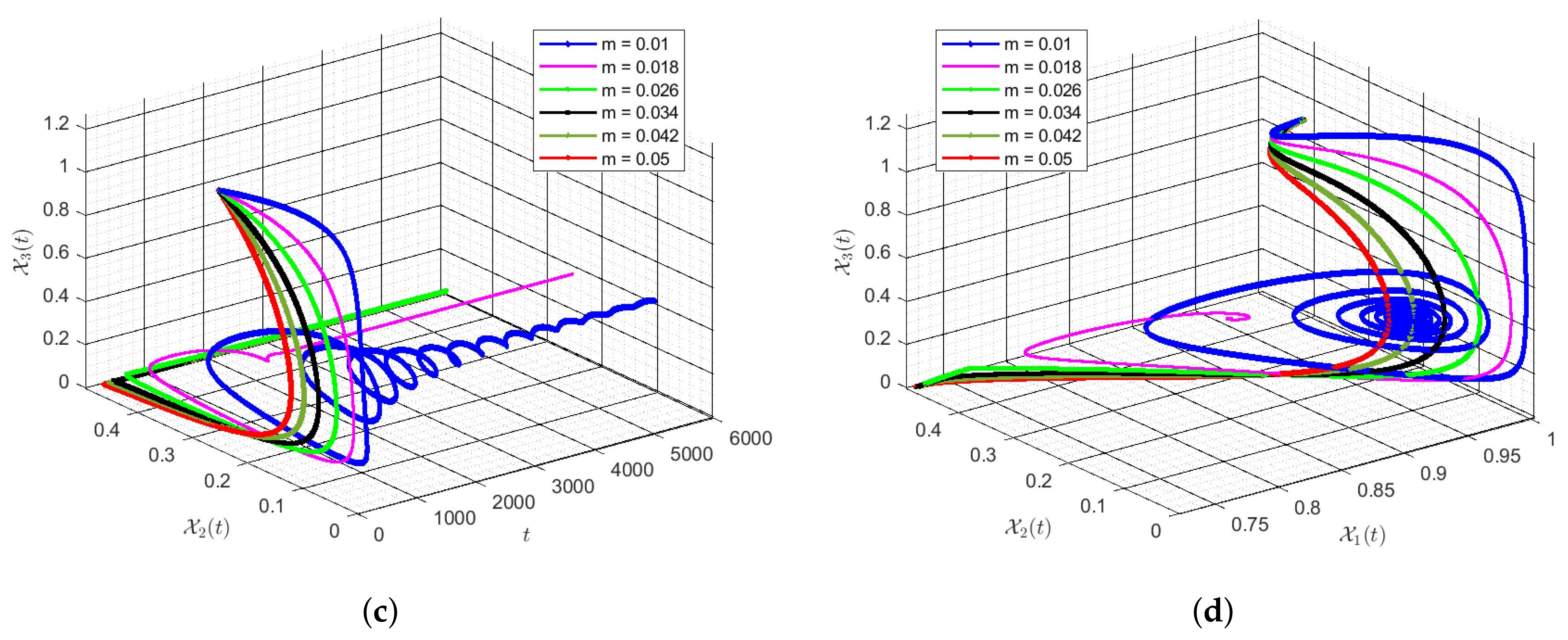
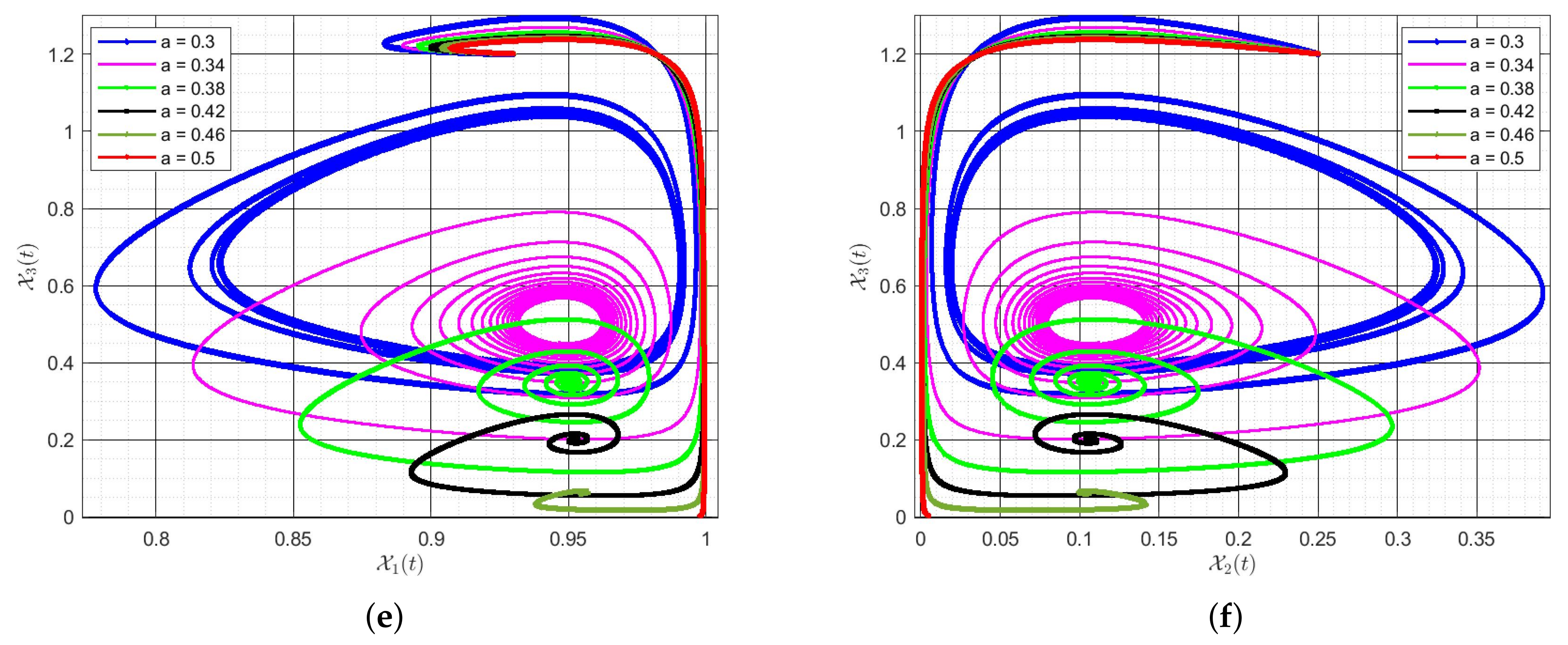
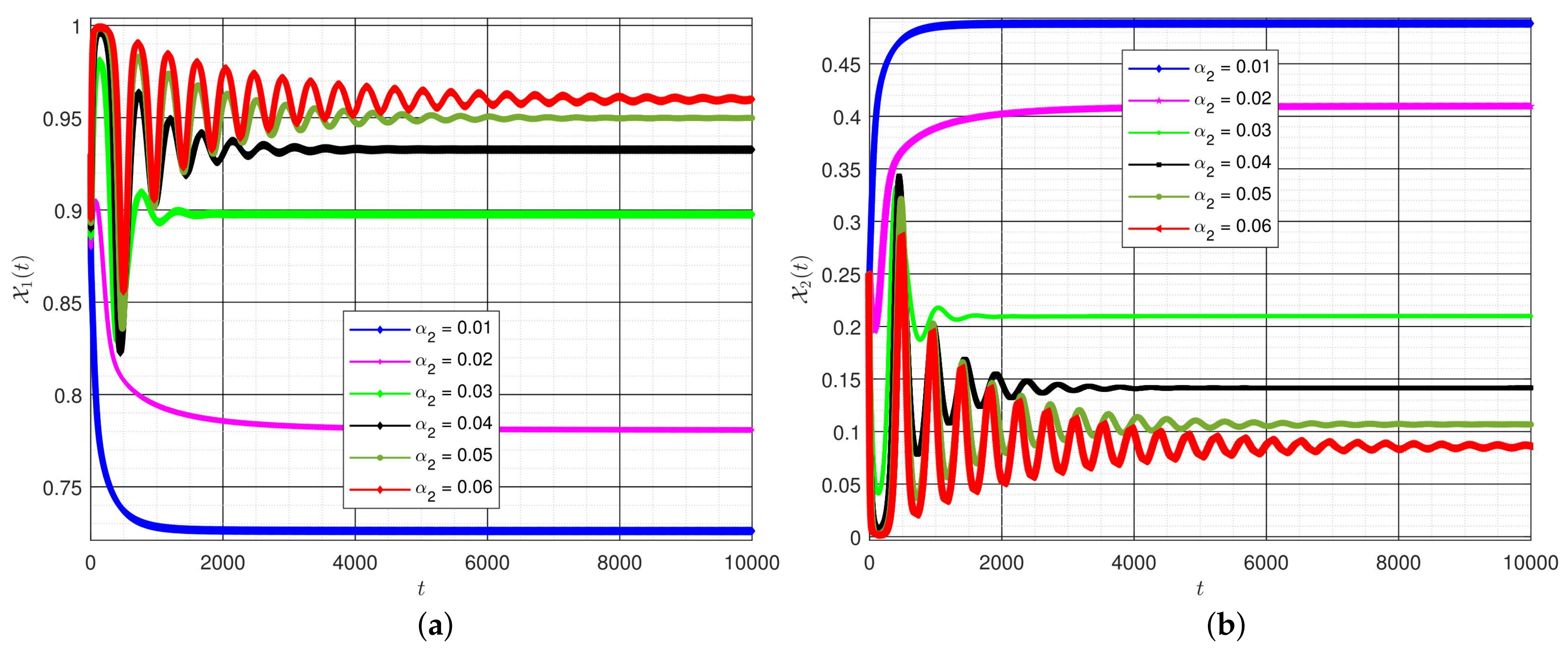
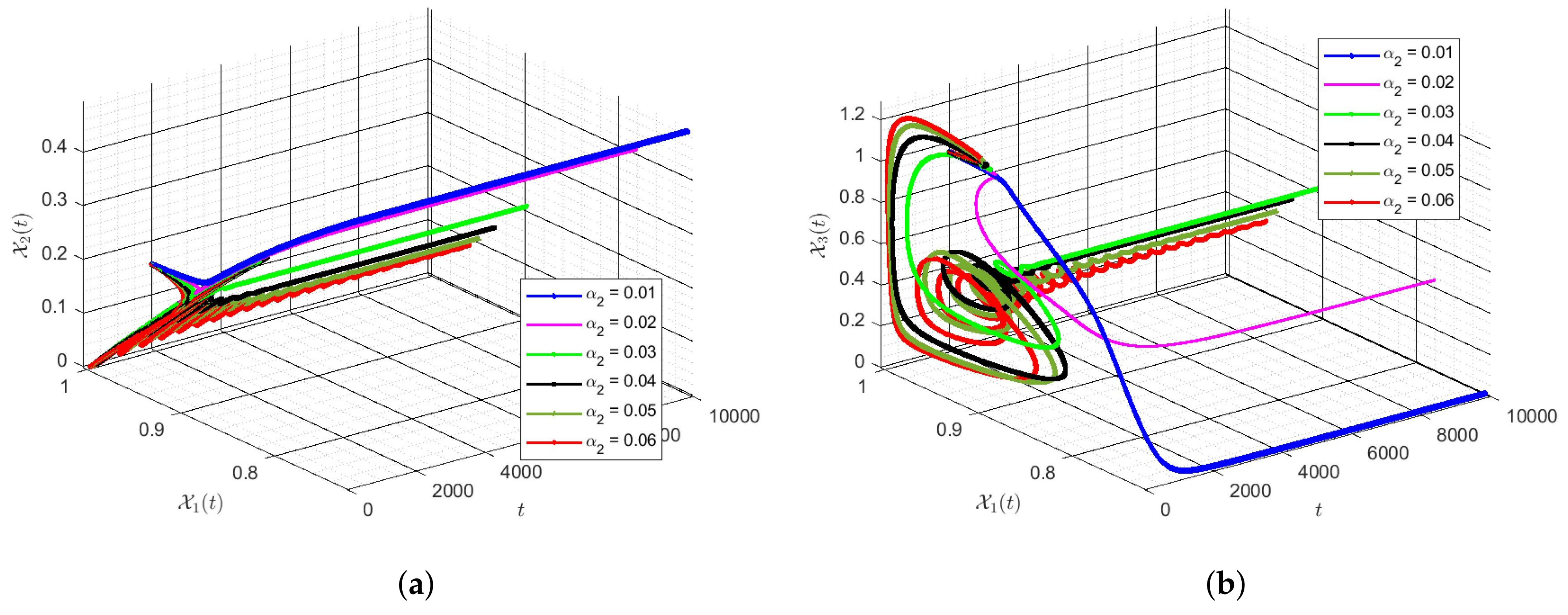
6. Discussion of Simulation Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Murray, J.D. Mathematical Biology: I. An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 17. [Google Scholar]
- De Vries, G.; Hillen, T.; Lewis, M.; Müller, J.; Schönfisch, B. A Course in Mathematical Biology: Quantitative Modeling with Mathematical and Computational Methods; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Nabti, A.; Ghanbari, B. Global stability analysis of a fractional SVEIR epidemic model. Math. Methods Appl. Sci. 2021, 44, 8577–8597. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. The population dynamics of microparasites and their invertebrate hosts. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1981, 291, 451–524. [Google Scholar]
- Berezovskaya, F.S.; Song, B.; Castillo-Chavez, C. Role of prey dispersal and refuges on predator-prey dynamics. SIAM J. Appl. Math. 2010, 70, 1821–1839. [Google Scholar] [CrossRef]
- Djilali, S.; Ghanbari, B. Dynamical behavior of two predators–one prey model with generalized functional response and time-fractional derivative. Adv. Differ. Equ. 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Vineis, P. Exposomics: Mathematics meets biology. Mutagenesis 2015, 30, 719–722. [Google Scholar] [CrossRef] [Green Version]
- Bellomo, N.; Elaiw, A.; Althiabi, A.M.; Alghamdi, M.A. On the interplay between mathematics and biology: Hallmarks toward a new systems biology. Phys. Life Rev. 2015, 12, 44–64. [Google Scholar] [CrossRef]
- Djilali, S.; Bentout, S.; Ghanbari, B.; Kumar, S. Spatial patterns in a vegetation model with internal competition and feedback regulation. Eur. Phys. J. Plus 2021, 136, 1–24. [Google Scholar] [CrossRef]
- Levin, S.A. Frontiers in Mathematical Biology; Springer: Berlin, Germany, 1994. [Google Scholar]
- Britton, N. Essential Mathematical Biology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Ghanbari, B.; Gómez-Aguilar, J. Analysis of two avian influenza epidemic models involving fractal-fractional derivatives with power and Mittag-Leffler memories. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 123113. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, B.; Günerhan, H.; Srivastava, H. An application of the Atangana-Baleanu fractional derivative in mathematical biology: A three-species predator-prey model. Chaos Solitons Fractals 2020, 138, 109910. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Rezazadeh, H.; Domiri Ganji, D. On the solution of time-fractional dynamical model of Brusselator reaction-diffusion system arising in chemical reactions. Math. Methods Appl. Sci. 2020, 43, 3903–3913. [Google Scholar] [CrossRef]
- Ghanbari, B. On novel nondifferentiable exact solutions to local fractional Gardner’s equation using an effective technique. Math. Methods Appl. Sci. 2021, 44, 4673–4685. [Google Scholar] [CrossRef]
- Aminikhah, H.; Sheikhani, A.H.R.; Houlari, T.; Rezazadeh, H. Numerical solution of the distributed-order fractional Bagley-Torvik equation. IEEE/CAA J. Autom. Sin. 2017, 6, 760–765. [Google Scholar] [CrossRef]
- Ghanbari, B.; Yusuf, A.; Baleanu, D. The new exact solitary wave solutions and stability analysis for the (2 + 1) (2+1)-dimensional Zakharov–Kuznetsov equation. Adv. Differ. Equ. 2019, 2019, 49. [Google Scholar] [CrossRef] [Green Version]
- Rahman, G.; Nisar, K.S.; Ghanbari, B.; Abdeljawad, T. On generalized fractional integral inequalities for the monotone weighted Chebyshev functionals. Adv. Differ. Equ. 2020, 2020, 368. [Google Scholar] [CrossRef]
- Srinivasa, K.; Rezazadeh, H. Numerical solution for the fractional-order one-dimensional telegraph equation via wavelet technique. Int. J. Nonlinear Sci. Numer. Simul. 2020, 1. [Google Scholar] [CrossRef]
- Ghanbari, B.; Nisar, K.S.; Aldhaifallah, M. Abundant solitary wave solutions to an extended nonlinear Schrödinger’s equation with conformable derivative using an efficient integration method. Adv. Differ. Equ. 2020, 2020, 328. [Google Scholar] [CrossRef]
- Ahmed, N.; Rafiq, M.; Adel, W.; Rezazadeh, H.; Khan, I.; Nisar, K.S. Structure Preserving Numerical Analysis of HIV and CD4+ T-Cells Reaction Diffusion Model in Two Space Dimensions. Chaos Solitons Fractals 2020, 139, 110307. [Google Scholar] [CrossRef]
- Jones, D.S.; Plank, M.; Sleeman, B.D. Differential Equations and Mathematical Biology; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Ghanbari, B.; Kumar, S. A study on fractional predator–prey–pathogen model with Mittag–Leffler kernel-based operators. Numer. Methods Partial. Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Inan, B.; Osman, M.S.; Ak, T.; Baleanu, D. Analytical and numerical solutions of mathematical biology models: The Newell-Whitehead-Segel and Allen-Cahn equations. Math. Methods Appl. Sci. 2020, 43, 2588–2600. [Google Scholar] [CrossRef]
- Ghanbari, B. Abundant exact solutions to a generalized nonlinear Schrödinger equation with local fractional derivative. Math. Methods Appl. Sci. 2021, 44, 8759–8774. [Google Scholar] [CrossRef]
- Ghanbari, B.; Rada, L. Solitary wave solutions to the Tzitzeica type equations obtained by a new efficient approach. J. Appl. Anal. Comput. 2019, 9, 568–589. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Günerhan, H.; Ghanbari, B. Exact traveling wave solutions for resonance nonlinear Schrödinger equation with intermodal dispersions and the Kerr law nonlinearity. Math. Methods Appl. Sci. 2019, 42, 7210–7221. [Google Scholar] [CrossRef]
- Ghanbari, B.; Djilali, S. Mathematical analysis of a fractional-order predator-prey model with prey social behavior and infection developed in predator population. Chaos Solitons Fractals 2020, 138, 109960. [Google Scholar] [CrossRef]
- Munusamy, K.; Ravichandran, C.; Nisar, K.S.; Ghanbari, B. Existence of solutions for some functional integrodifferential equations with nonlocal conditions. Math. Methods Appl. Sci. 2020, 43, 10319–10331. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, H.; Thounthong, P.; Chu, Y.M.; Cesarano, C. Solution of multi-term time-fractional PDE models arising in mathematical biology and physics by local meshless method. Symmetry 2020, 12, 1195. [Google Scholar] [CrossRef]
- Khan, Y.; Vazquez-Leal, H.; Wu, Q. An efficient iterated method for mathematical biology model. Neural Comput. Appl. 2013, 23, 677–682. [Google Scholar] [CrossRef]
- Kaur, D.; Agarwal, P.; Rakshit, M.; Chand, M. Fractional Calculus involving (p, q)-Mathieu Type Series. Appl. Math. Nonlinear Sci. 2020, 5, 15–34. [Google Scholar] [CrossRef]
- Gençoglu, M.T.; Agarwal, P. Use of Quantum Differential Equations in Sonic Processes. Appl. Math. Nonlinear Sci. 2020, 6, 21–28. [Google Scholar] [CrossRef]
- Aidara, S.; Sagna, Y. BSDEs driven by two mutually independent fractional Brownian motions with stochastic Lipschitz coefficients. Appl. Math. Nonlinear Sci. 2019, 4, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Yuan, J.; Gao, W. Analysis of fractional factor system for data transmission in SDN. Appl. Math. Nonlinear Sci. 2019, 4, 191–196. [Google Scholar] [CrossRef] [Green Version]
- Al-Ghafri, K.S.; Rezazadeh, H. Solitons and other solutions of (3 + 1)-dimensional space–time fractional modified KdV–Zakharov–Kuznetsov equation. Appl. Math. Nonlinear Sci. 2019, 4, 289–304. [Google Scholar] [CrossRef] [Green Version]
- Ziane, D.; Cherif, M.H.; Cattani, C.; Belghaba, K. Yang-Laplace Decomposition Method for Nonlinear System of Local Fractional Partial Differential Equations. Appl. Math. Nonlinear Sci. 2019, 4, 489–502. [Google Scholar] [CrossRef] [Green Version]
- Sulaiman, T.A.; Bulut, H.; Atas, S.S. Optical solitons to the fractional Schrdinger-Hirota equation. Appl. Math. Nonlinear Sci. 2019, 4, 535–542. [Google Scholar] [CrossRef] [Green Version]
- İlhan, E.; Kıymaz, İ.O. A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 171–188. [Google Scholar]
- Biswas, S.; Sasmal, S.K.; Samanta, S.; Saifuddin, M.; Pal, N.; Chattopadhyay, J. Optimal harvesting and complex dynamics in a delayed eco-epidemiological model with weak Allee effects. Nonlinear Dyn. 2017, 87, 1553–1573. [Google Scholar] [CrossRef]
- Saifuddin, M.; Samanta, S.; Biswas, S.; Chattopadhyay, J. An eco-epidemiological model with different competition coefficients and strong-Allee in the prey. Int. J. Bifurc. Chaos 2017, 27, 1730027. [Google Scholar] [CrossRef]
- Saifuddin, M.; Biswas, S.; Samanta, S.; Sarkar, S.; Chattopadhyay, J. Complex dynamics of an eco-epidemiological model with different competition coefficients and weak Allee in the predator. Chaos Solitons Fractals 2016, 91, 270–285. [Google Scholar] [CrossRef]
- Naik, P.A.; Zu, J.; Ghoreishi, M. Stability analysis and approximate solution of SIR epidemic model with crowley-martin type functional response and Holling type-II treatment rate by using homotopy analysis method. J. Appl. Anal. Comput. 2020, 10, 1482–1515. [Google Scholar]
- Yavuz, M.; Özdemir, N. Comparing the new fractional derivative operators involving exponential and Mittag-Leffler kernel. Discret. Contin. Dyn. Syst. S 2020, 13, 995. [Google Scholar] [CrossRef] [Green Version]
- Naik, P.A.; Zu, J.; Owolabi, K.M. Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order. Phys. A Stat. Mech. Its Appl. 2020, 545, 123816. [Google Scholar] [CrossRef]
- Yavuz, M.; Yokus, A. Analytical and numerical approaches to nerve impulse model of fractional-order. Numer. Methods Partial. Differ. Equ. 2020, 36, 1348–1368. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Gómez-Aguilar, J.; Karaagac, B. Modelling, analysis and simulations of some chaotic systems using derivative with Mittag–Leffler kernel. Chaos Solitons Fractals 2019, 125, 54–63. [Google Scholar] [CrossRef]
- Qureshi, S.; Atangana, A. Fractal-fractional differentiation for the modeling and mathematical analysis of nonlinear diarrhea transmission dynamics under the use of real data. Chaos Solitons Fractals 2020, 136, 109812. [Google Scholar] [CrossRef]
- Ul Rehman, A.; Singh, R.; Agarwal, P. Modeling, analysis and prediction of new variants of covid-19 and dengue co-infection on complex network. Chaos Solitons Fractals 2021, 150, 111008. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, P.; Singh, R. Modelling of transmission dynamics of Nipah virus (Niv): A fractional order approach. Phys. A Stat. Mech. Its Appl. 2020, 547, 124243. [Google Scholar] [CrossRef]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana–Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. A Stat. Mech. Its Appl. 2020, 542, 123516. [Google Scholar] [CrossRef]
- Lizzy, R.M.; Balachandran, K.; Trujillo, J.J. Controllability of nonlinear stochastic fractional neutral systems with multiple time varying delays in control. Chaos Solitons Fractals 2017, 102, 162–167. [Google Scholar] [CrossRef]
- Jajarmi, A.; Yusuf, A.; Baleanu, D.; Inc, M. A new fractional HRSV model and its optimal control: A non-singular operator approach. Phys. A Stat. Mech. Its Appl. 2020, 547, 123860. [Google Scholar] [CrossRef]
- Ghanbari, B.; Atangana, A. Some new edge detecting techniques based on fractional derivatives with non-local and non-singular kernels. Adv. Differ. Equ. 2020, 2020, 435. [Google Scholar] [CrossRef]
- Mazzoleni, S.; Russo, L.; Giannino, F.; Toraldo, G.; Siettos, C. Mathematical modelling and numerical bifurcation analysis of inbreeding and interdisciplinarity dynamics in academia. J. Comput. Appl. Math. 2021, 385, 113194. [Google Scholar] [CrossRef]
- Djilali, S.; Ghanbari, B.; Bentout, S.; Mezouaghi, A. Turing-Hopf bifurcation in a diffusive mussel-algae model with time-fractional-order derivative. Chaos Solitons Fractals 2020, 138, 109954. [Google Scholar] [CrossRef]
- Babaei, A.; Ahmadi, M.; Jafari, H.; Liya, A. A mathematical model to examine the effect of quarantine on the spread of coronavirus. Chaos Solitons Fractals 2021, 142, 110418. [Google Scholar] [CrossRef] [PubMed]
- Cressman, R.; Garay, J. A predator–prey refuge system: Evolutionary stability in ecological systems. Theor. Popul. Biol. 2009, 76, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Wei, J.; Yu, J. Stationary patterns of a diffusive predator–prey model with Crowley–Martin functional response. Nonlinear Anal. Real World Appl. 2018, 39, 33–57. [Google Scholar] [CrossRef] [Green Version]
- Ghanbari, B.; Djilali, S. Mathematical and numerical analysis of a three-species predator-prey model with herd behavior and time fractional-order derivative. Math. Methods Appl. Sci. 2020, 43, 1736–1752. [Google Scholar] [CrossRef]
- Agarwal, P.; Singh, R.; ul Rehman, A. Numerical solution of hybrid mathematical model of dengue transmission with relapse and memory via Ada–Bashforth–Moulton predictor-corrector scheme. Chaos Solitons Fractals 2021, 143, 110564. [Google Scholar] [CrossRef]
- Owolabi, K.M. High-dimensional spatial patterns in fractional reaction-diffusion system arising in biology. Chaos Solitons Fractals 2020, 134, 109723. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A. Mathematical Modelling and Analysis of Fractional Epidemic Models Using Derivative with Exponential Kernel. In Fractional Calculus in Medical and Health Science; CRC Press: Boca Raton, FL, USA, 2020; pp. 109–128. [Google Scholar]
- Ghanbari, B. A new model for investigating the transmission of infectious diseases in a prey-predator system using a non-singular fractional derivative. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Ghanbari, B. On the fuzzy fractional differential equation with interval Atangana–Baleanu fractional derivative approach. Chaos Solitons Fractals 2020, 130, 109397. [Google Scholar] [CrossRef]
- Wang, J.L.; Li, H.F. Memory-dependent derivative versus fractional derivative (I): Difference in temporal modeling. J. Comput. Appl. Math. 2021, 384, 112923. [Google Scholar] [CrossRef]
- Jajarmi, A.; Ghanbari, B.; Baleanu, D. A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 093111. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Moustapha, M.V.; Nofal, T.A.; Rashid, S.; Ahmad, H. Generalized thermoelasticity based on higher-order memory-dependent derivative with time delay. Res. Phys. 2021, 20, 103705. [Google Scholar]
- Ghanbari, B.; Gómez-Aguilar, J. Modeling the dynamics of nutrient–phytoplankton–zooplankton system with variable-order fractional derivatives. Chaos Solitons Fractals 2018, 116, 114–120. [Google Scholar] [CrossRef]
- Inc, M.; Acay, B.; Berhe, H.W.; Yusuf, A.; Khan, A.; Yao, S.W. Analysis of novel fractional COVID-19 model with real-life data application. Res. Phys. 2021, 23, 103968. [Google Scholar]
- Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Alotaibi, N.D. A fractional-order SIRD model with time-dependent memory indexes for encompassing the multi-fractional characteristics of the COVID-19. Chaos Solitons Fractals 2021, 143, 110632. [Google Scholar] [CrossRef]
- Ghanbari, B. On forecasting the spread of the COVID-19 in Iran: The second wave. Chaos Solitons Fractals 2020, 140, 110176. [Google Scholar] [CrossRef]
- Oud, M.A.A.; Ali, A.; Alrabaiah, H.; Ullah, S.; Khan, M.A.; Islam, S. A fractional order mathematical model for COVID-19 dynamics with quarantine, isolation, and environmental viral load. Adv. Differ. Equ. 2021, 2021, 106. [Google Scholar] [CrossRef] [PubMed]
- Furati, K.; Sarumi, I.; Khaliq, A. Fractional model for the spread of COVID-19 subject to government intervention and public perception. Appl. Math. Model. 2021, 95, 89–105. [Google Scholar] [CrossRef]
- Djilali, S.; Ghanbari, B. Coronavirus pandemic: A predictive analysis of the peak outbreak epidemic in South Africa, Turkey, and Brazil. Chaos Solitons Fractals 2020, 138, 109971. [Google Scholar] [CrossRef]
- Higazy, M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals 2020, 138, 110007. [Google Scholar] [CrossRef]
- Gao, W.; Ghanbari, B.; Baskonus, H.M. New numerical simulations for some real world problems with Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2019, 128, 34–43. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Ghanbari, B.; Kumar, S.; Kumar, R. A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative. Chaos Solitons Fractals 2020, 133, 109619. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos Solitons Fractals 2020, 135, 109811. [Google Scholar] [CrossRef]
- Owolabi, K.M. Numerical approach to chaotic pattern formation in diffusive predator–prey system with Caputo fractional operator. Numer. Methods Partial. Differ. Equ. 2021, 37, 131–151. [Google Scholar] [CrossRef]
- Ghanbari, B. Chaotic behaviors of the prevalence of an infectious disease in a prey and predator system using fractional derivatives. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Lu, J.; Meng, B. Stability, bifurcation and chaos of a discrete-time pair approximation epidemic model on adaptive networks. Math. Comput. Simul. 2021, 182, 182–194. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Chakraborty, S.; Chakraborty, S. Chaos and coexisting attractors in replicator-mutator maps. J. Phys. Complex. 2021, 2, 035005. [Google Scholar] [CrossRef]
- Ghanbari, B. On the modeling of the interaction between tumor growth and the immune system using some new fractional and fractional-fractal operators. Adv. Differ. Equ. 2020, 2020, 585. [Google Scholar] [CrossRef]
- Al-Hussein, A.B.A.; Tahir, F.R.; Pham, V.T. Fixed-time synergetic control for chaos suppression in endocrine glucose–insulin regulatory system. Control Eng. Pract. 2021, 108, 104723. [Google Scholar] [CrossRef]
- Borovik, A. A mathematician’s view of the unreasonable ineffectiveness of mathematics in biology. Biosystems 2021, 205, 104410. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, B. A fractional system of delay differential equation with nonsingular kernels in modeling hand-foot-mouth disease. Adv. Differ. Equ. 2020, 2020, 536. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Sun, K.; Peng, Y. Detecting chaos in fractional-order nonlinear systems using the smaller alignment index. Phys. Lett. A 2019, 383, 2267–2271. [Google Scholar] [CrossRef]
- Ghanbari, B.; Gómez-Aguilar, J. Two efficient numerical schemes for simulating dynamical systems and capturing chaotic behaviors with Mittag–Leffler memory. Eng. Comput. 2020, 1–29. [Google Scholar] [CrossRef]
- Skokos, C.; Antonopoulos, C.; Bountis, T.; Vrahatis, M. Detecting order and chaos in Hamiltonian systems by the SALI method. J. Phys. Math. Gen. 2004, 37, 6269. [Google Scholar] [CrossRef]
- Djilali, S.; Ghanbari, B. The influence of an infectious disease on a prey-predator model equipped with a fractional-order derivative. Adv. Differ. Equ. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Skokos, C.; Antonopoulos, C.; Bountis, T.C.; Vrahatis, M.N. How does the Smaller Alignment Index (SALI) distinguish order from chaos? Prog. Theor. Phys. Suppl. 2003, 150, 439–443. [Google Scholar] [CrossRef] [Green Version]
- Ghanbari, B. On the modeling of an eco-epidemiological model using a new fractional operator. Res. Phys. 2021, 21, 103799. [Google Scholar]
- Skokos, C. Alignment indices: A new, simple method for determining the ordered or chaotic nature of orbits. J. Phys. Math. Gen. 2001, 34, 10029. [Google Scholar] [CrossRef]
- Atangana, A. Blind in a commutative world: Simple illustrations with functions and chaotic attractors. Chaos Solitons Fractals 2018, 114, 347–363. [Google Scholar] [CrossRef]
- Ghanbari, B. On approximate solutions for a fractional prey–predator model involving the Atangana–Baleanu derivative. Adv. Differ. Equ. 2020, 2020, 679. [Google Scholar] [CrossRef]
- Toufik, M.; Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 2017, 132, 444. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Yasar, B.Y. Generalized Mittag-Leffler function and its properties. New Trends Math. Sci. 2015, 3, 12. [Google Scholar]
- Alzahrani, A.K.; Alshomrani, A.S.; Pal, N.; Samanta, S. Study of an eco-epidemiological model with Z-type control. Chaos Solitons Fractals 2018, 113, 197–208. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef] [Green Version]
- Ghanbari, B.; Kumar, D. Numerical solution of predator-prey model with Beddington-DeAngelis functional response and fractional derivatives with Mittag-Leffler kernel. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 063103. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, B.; Cattani, C. On fractional predator and prey models with mutualistic predation including non-local and nonsingular kernels. Chaos Solitons Fractals 2020, 136, 109823. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Günay, B.; Agarwal, P.; Guirao, J.L.G.; Momani, S. A Fractional Approach to a Computational Eco-Epidemiological Model with Holling Type-II Functional Response. Symmetry 2021, 13, 1159. https://doi.org/10.3390/sym13071159
Günay B, Agarwal P, Guirao JLG, Momani S. A Fractional Approach to a Computational Eco-Epidemiological Model with Holling Type-II Functional Response. Symmetry. 2021; 13(7):1159. https://doi.org/10.3390/sym13071159
Chicago/Turabian StyleGünay, B., Praveen Agarwal, Juan L. G. Guirao, and Shaher Momani. 2021. "A Fractional Approach to a Computational Eco-Epidemiological Model with Holling Type-II Functional Response" Symmetry 13, no. 7: 1159. https://doi.org/10.3390/sym13071159
APA StyleGünay, B., Agarwal, P., Guirao, J. L. G., & Momani, S. (2021). A Fractional Approach to a Computational Eco-Epidemiological Model with Holling Type-II Functional Response. Symmetry, 13(7), 1159. https://doi.org/10.3390/sym13071159







