Abstract
Using a small number of mathematical transformations, this article examines the nature of fractional models described by fractional differential equations or pseudo state space descriptions. Computation of the impulse response of a fractional model using the Cauchy method shows that they exhibit infinitely small and high time constants. This impulse response can be rewritten as a diffusive representation whose Fourier transform permits a representation of a fractional model by a diffusion equation in an infinite space domain. Fractional models can thus be viewed as doubly infinite dimensional models: infinite as distributed with a distribution in an infinite domain. This infinite domain or the infinitely large time constants of the impulse response reveal a property intrinsic to fractional models: their infinite memory. Solutions to generate fractional behaviors without infinite memory are finally proposed.
1. Introduction
A confusion or rather an implicit link exists between fractional behaviors (of physical, biological, thermal, etc., origin) and fractional models (a tool to model fractional behaviors) [1]. To deliberately limit this confusion, the name “fractional behavior” is replaced by “power-law behaviors”, which well expresses the idea that studied behaviors exhibit, in a limited frequency or time domain, a power-law-type response.
It is now evident that power-law behaviors are ubiquitous in numerous domains and that appropriate modelling tools are needed. Due to the dynamic behavior similarity between power-law behaviors and fractional models, the latter have therefore naturally been used as modelling tools.
The field of fractional calculus research has thus undergone numerous (although perhaps not fundamental) developments [2] and many applications of fractional order derivatives now exist [3]. Fractional calculus has become a common modeling tool in many fields [4,5,6,7].
However, this link between power-law behaviors and fractional models often found in the literature does not result from physical justification, as noted in the present paper. Many researchers have nevertheless contributed to the study of fractional calculus and fractional models, sometimes yielding to the ease of generalizing the results dedicated to classical integer systems (which are sometimes referred to as “fractionalizations”).
However, it is also well known that fractional models have several drawbacks [8,9,10]. The most important of these, from which some others derive, is they were not deduced from physical considerations but are only generalizations of existing (integer) tools. Consequently, fractional models are imbued with an intrinsic and unrealistic property: they are doubly infinite dimensional models:
- -
- infinite as they are distributed
- -
- and infinite as they are defined (the parameter distribution) in an infinite spatial domain.
It is only by trying to analyze the physical meaning of fractional models that this property is revealed.
Giving meaning to fractional models (a posteriori) has nevertheless been a concern of many researchers. Mathematical [11,12], physical [13,14], geometrical [15,16], and statistical [17] meanings were therefore sought but these approaches do not help to understand their nature and, in particular, their advantages and disadvantages. It was even attempted to deduce a model from a physical phenomenon [18,19] but infinite spatial dimensions were considered in order to do so, which tends on the contrary to demonstrate the physical inconsistency of a fractional model.
The infinite spatial dimension is the conclusion also reached in this work after some mathematical transformations that lead to a representation of a fractional model by a diffusion equation. This representation is obtained through the Fourier transform of the diffusive representation of a fractional model. It is also shown that the diffusive representation can be deduced from the impulse response of a fractional model computed using the Cauchy method. The diffusive representation obtained exhibits infinitely large time constants that are a consequence of the definition of fractional models in an infinite spatial domain. This infinite dimension or these infinitely large time constants are responsible for the infinite memory of fractional models. All these concepts are detailed and demonstrated in this paper. Finally, a list of alternative solutions to fractional models to produce power-law behaviors is given.
2. A physical and Systemic Analysis of Fractional Models
2.1. Model Definition
Although the terms used to designate them are very similar, power-law behavior and fractional models are two different concepts. Power-law (dynamical) behavior qualifies the nature of some real systems that exhibit a power law behavior in a limited time or frequency band (the system impulse response behaves as in a given time band or the system frequency response behaves as in a given frequency band). Fractional models are a class of models that was introduced to capture power-law behaviors. Without considering physical justifications, fractional models were introduced by simply generalizing existing modelling tools, by simply replacing the classical differentiation operators by fractional differentiation operators. These fractional derivation operators had long been mathematically defined and were in fact known to exhibit power-law behaviors (but not only over a limited time or frequency band). For this reason, fractional differential equations appeared as possible models to capture some power-law behaviors.
With and respectively as input and output, a fractional differential equation is found in the literature with the form:
In Relation (1) and . and denote, respectively, fractional differentiation operators of orders and [20]. Various definitions can be used to describe these operators [21], which raises the question of choice. These definitions are in certain respects equivalent, but differences exist, notably regarding how initial conditions are taken into account.
The “fractionalization” of another well-known modelling tool was also proposed in the literature if the differentiation orders and met the following conditions:
These conditions, known as commensurability conditions, enable Relation (1) to be rewritten as (under null initial conditions):
This representation is known in the literature as a pseudo state space description. “Pseudo” because the vector cannot be viewed as the model state since this is not the minimal amount of information required to predict the future of the model. In Relation (3), is the fractional order of the model and , , , and are constant matrices.
Application of the Laplace transform to Relations (1) or (3) (with null initial conditions) permits a transfer function representation of the form:
Models (1) and (3) are very widely used in the literature when talking about fractional models.
Example 1.
The following fractional model, which will be used repeatedly throughout the article, is now considered:
As all the fractional orders are multiples of 0.6, such a model admits the following pseudo state space description:
with
This model transfer function is thus given by:
As previously mentioned, the definition of these models did not result from physical analyses; they are “fractionalizations” of classical models. The objective of the following sections is therefore to propose an analysis of the physical meaning of these models.
2.2. Poles and Time Constants Distribution and Infinite Memory
The first physical analysis proposed is based on the impulse response of the Models (1) and (3). This impulse response is given by the inverse Laplace transformation relation:
In Relation (9), the value of is chosen to be greater than the singular point abscissa and the integral computation is performed on the Bromwich–Wagner path of Figure 1 that bypasses the negative axis around the branching point for . It thus avoids the complex plane domain for which the transfer function is not defined, i.e., the segment [−∞, 0]. As shown by Figure 1, the path is the union of six sub-paths: .

Figure 1.
The path considered for impulse response computation of .
Using the residue theorem, Relation (9) can be rewritten as:
with, in the case of a simple pole for :
Relation (10) thus imposes the computation of the poles of and shows that the impulse responses of Models (1) and (3) can be split into two parts:
The function is computed from the poles of Models (1) and (3) (residues of the Cauchy method). The function is linked to the diffusive part of the model. The name “diffusive” is explained in the sequel (see Section 2.3). The function is defined by [22]:
in which the function is given [23] by:
The Laplace transform of function is given by:
Example 2.
The model defined by Relation (5) is again considered. The corresponding transfer function (Relation (8)) can be rewritten as:
The poles of the model, denoted
, are the values of s such that
and:
or:
and thus:
if there exist values of k such that:
Two poles are produced by Relation (20):
that generate the function:
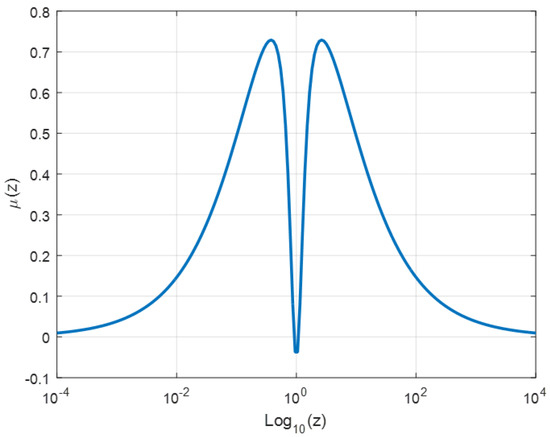
According to Relations (13) and (14), the function is given by:
which corresponds to Relation (13) with:
which is represented by Figure 2.

Figure 2.
Function .
If an input is applied to the diffusive part with an impulse response , the output is the convolution product:
Introducing the function such that:
Relation (25) can be rewritten as:
This representation is known in the literature as the diffusive representation [22,23].
Representations (15) and (27) of fractional models are particularly interesting because they make it possible to reveal properties that are poorly known and yet fundamental, because they provide information on the internal nature of fractional models and about how to initialize them. Relation (15) highlights that Models (1) and (3) have poles (values of ) distributed from 0 to . Models (1) and (3) are thus fitted with infinitely fast and infinitely slow time constants (they are attenuated by the function , but they exist). Relation (27) reveals the impact of these poles (or time constants) on the initialization of fractional models. All the poles must be initialized as the function must be initialized with . This provides fractional models with an infinite memory.
Note that a link between fractional operators and poles distribution from 0 to was also highlighted in [24].
2.3. Spatial Definition and Infinite Memory
In this section, we try to obtain a spatial representation of fractional models. To this end, Model (27) is rewritten as:
The changes of variable and are respectively used in the first and second integral of Relation (28). The resulting model is thus:
with . After simplifications, Relation (29) becomes:
If the inverse Fourier transform is applied to the first equation of Relation (30) (on variable ), it can be rewritten as:
where:
As is a real and even function, according to the Fourier transform properties, the function is also a real and even function. Model (30) can be rewritten as:
As:
Relation (33) becomes:
with .
As is a real and even function, the function is also a real and even function. The integral defining in Relation (35) can thus be rewritten as follows:
and Model (35) can be rewritten as:
Relation (37) provides information on the nature of fractional models. As illustrated by Figure 3, they can be described by a diffusion equation in an infinite dimensional domain (). They can thus be seen as doubly infinite models (infinite because distributed and infinite as defined on an infinite spatial domain). This infinite spatial domain imposes an initialization with an infinite amount of information: .

Figure 3.
Spatial representation of the diffusive part of a fractional model.
Example 3.
The model defined by Relation (5) is once again considered. The response of the diffusive part of the impulse responsegiven by Relation (23) to an inputis provided by the diffusion Equation (37) defined on an infinite spatial domain, where the functionis defined by:
which is also equal to:
As an intermediate conclusion, it can be claimed that any power-law behavior modelling using Models (1) or (2) [25,26] embeds a physical system into a model with infinite spatial dimensions.
3. Other Modelling Solutions
There is a need for modelling tools that can capture power-law behaviors. Fractional models are only one class of model possible, but they have several disadvantages, mainly resulting from their intrinsic property revealed in the previous sections: their infinite memory. As briefly described in the next sections and also discussed in [9], other solutions are possible that address the drawbacks associated with fractional models.
3.1. Kernels with Limited Memory
The Riemann–Liouville or Caputo definitions are most widely used in the literature for fractional differentiation operators in Relations (1) and (3). These operators are based on the fractional integrator operator in their definitions. The fractional integral of a function is given by [20]:
This operator is in fact the convolution product of the function to integrate with the singular kernel:
The infinite memory problem can be solved by modifying this kernel. This solution is often used in the literature to introduce the concept of tempered fractional integration [27]:
The Laplace transform of this kernel is given by:
In the frequency domain, this kernel no longer exhibits a power-law behavior at low frequency. Computation of its impulse response using the method described in Section 2.1 leads to:
This relation shows that the kernel no longer exhibits infinitely large time constants, but still has infinitely small time constants, which is questionable from a physical perspective.
We must therefore go further, and introduce kernels without any power-law behavior at low and high frequencies. The following kernel [28], whose impulse response is:
where is a two-variable hypergeometric function defined by [29]:
is a possible candidate. The Laplace transform of this kernel is defined by [29] (p. 238):
Computation of its impulse response using the method described in Section 2.1 leads to:
where is the Heaviside function. Relation (48) shows that this kernel has time constants distributed in a limited domain.
3.2. Volterra Integro-Differential Equations
It can be easily demonstrated [30] that Representation (3) is a special case of a Volterra equation of the form:
with:
If Constraint (50) is not imposed, it is possible to generate more varied behaviors with the Relation (49) while leaving free the choice of the kernel , in particular those mentioned in the previous section. Thus, many kinds of power-law behaviors can be generated by Relation (50) and integro-differential equations in general, while overcoming the drawbacks associated with the Models (1) and (3) with an adequate choice of the kernels.
3.3. Time Delay Models
It is shown in [31,32] that power-law behaviors can be generated using distributed time delay models of the form:
The conditions on parameters , , , and on the kernel to reach a power-law behavior are also defined in [30,31]. The latter paper shows that the dynamic behavior of a lithium-ion battery can be modelled with this class of equation.
3.4. Nonlinear Models
Random Sequential Adsorption (RSA) was studied in [33,34]. RSA exhibits a power-law behavior that a fractional model cannot correctly capture. In the above cited paper, this behavior is captured using a drift free control affine nonlinear model of the form:
where the function is a polynomial to be identified in order to fit the analyzed behavior. Relation (52) is thus a potential model class for power-law behavior modelling, and was used in [34] to model hydrogen adsorption.
3.5. Time-Varying Models
Without referring to fractional models, the Avrami model is often used to model the kinetics of crystallization, in addition to other phase changes or chemical reactions [35,36]. This model is described by the relation:
The Laplace transform of Relation (52) is given by:
Figure 4 shows the frequency response of and demonstrates a power-law behavior because the phase is constant and equal to −ν90° for frequencies greater than .
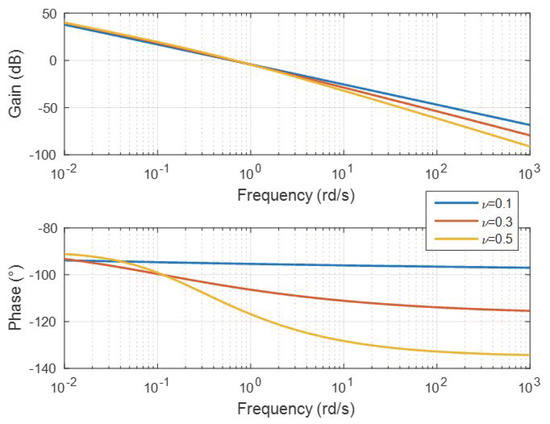
Figure 4.
Frequency response of for , , , .
Function in Relation (53) is also a solution of the differential equation:
This equation involves singular coefficients. Such a matter can be solved by a differential equation of the form:
where is a constant that also exhibits a power-law behavior and thus shows that time-varying models can capture power-law behaviors.
3.6. Diffusion Equation with Spatially Variable Coefficients
With a judicious choice of the spatial functions and , it is shown in [37] that the following heat equation:
generates power-law behaviors. An infinite number of combinations are possible for the functions and . This leaves considerable room for theoretical investigations in the search for these functions, prior to the analysis of the properties of Equation (57), and also for the development of methods to identify the functions and based on real data.
4. Concluding Remarks
Fractional operators and the resulting fractional models are known for their memory property. This is an interesting property that makes it possible to capture power-law behaviors that are often encountered in modelling problems. For this class of behaviors, the need exists for models with a memory, but not with an infinite memory; this is unfortunately the case with fractional models. Their infinite memory is demonstrated in this paper by applying mathematical transformations that are described by Figure 5. These transformations highlight that fractional models (described by a fractional differential equation or a pseudo state space description) are fitted with infinitely small and infinitely large time constants. They also describe a fractional model with a diffusion equation defined in an infinite spatial domain. These infinitely large time constants or the infinite spatial domain are precisely the reasons why the models have an infinite memory.

Figure 5.
Various representations of fractional models exhibiting the same problem: infinite memory.
Regrettably, many studies dedicated to fractional models appear to ignore this means of considering fractional models, which leads to errors in how these models are initialized. Due to its infinite memory, it is necessary to consider all of a model’s past, rather than only an initial condition as with the Caputo definition. This is also described in Figure 5.
Fractional models are, however, just one class of models among many that are able to capture power-law behaviors without the drawbacks of fractional models. Other solutions are presented in the paper: operators with limited memory kernels, Volterra equations, distributed time delay models, time-varying models, nonlinear models, and diffusion equations with spatially variable coefficients. Consideration of power-law behaviors without being limited to fractional models provides countless opportunities for research in the field of model analysis and identification.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Tarasov, V. Review of some promising fractional physical models. Int. J. Mod. Phys. B 2013, 27, 1330005. [Google Scholar] [CrossRef] [Green Version]
- Tenreiro Machado, J.A.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Agarwal, R.P. Fractional calculus in the sky. Adv. Differ. Equ. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Lopes, A.; Copot, D.; Machado, J.; Bates, J. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Stowell, H.H.; Zayernouri, M.; Hansen, S.E. A review of applications of fractional calculus in Earth system dynamics. Chaos Solitons Fractals 2017, 102, 29–46. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef] [Green Version]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef] [PubMed]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. A commentary on fractionalization of multi-compartmental models. J. Pharm. Pharm. 2010, 37, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Sabatier, J.; Farges, C.; Tartaglione, V. Some Alternative Solutions to Fractional Models for Modelling Power Law Type Long Memory Behaviours. Mathematics 2020, 8, 196. [Google Scholar] [CrossRef] [Green Version]
- Balint, A.M.; Balint, S. Mathematical Description of the Groundwater Flow and that of the Impurity Spread, which Use Temporal Caputo or Riemann–Liouville Fractional Partial Derivatives, is Non-Objective. Fractal Fract. 2020, 4, 36. [Google Scholar] [CrossRef]
- Gorenflo, R. Afterthoughts on interpretation of fractional derivatives and integrals. In Transform Methods and Special Functions; Rusev, P., Dimovski, I., Kiryakova, V., Eds.; Varna’96, Institute of Mathematics and Informatics, Bulgarian Academy of Sciences: Sofia, Bulgaria, 1998. [Google Scholar]
- Mainardi, F. Considerations on fractional calculus: Interpretations and applications. In Transform Methods and Special Functions; Rusev, P., Dimovski, I., Kiryakova, V., Eds.; Varna’96, Institute of Mathematics and Informatics, Bulgarian Academy of Sciences: Sofia, Bulgaria, 1998. [Google Scholar]
- Nigmatullin, R.R. Fractional integral and its physical interpretation. Theor. Math. Phys. 1992, 90, 242–251. [Google Scholar] [CrossRef]
- Rutman, R.S. On physical interpretations of fractional integration and differentiation. Theor. Math. Phys. 1995, 105, 393–404. [Google Scholar] [CrossRef]
- Ben Adda, F. Geometric interpretation of the fractional derivative. J. Fract. Calc. 1997, 11, 21–52. [Google Scholar]
- Podlubny, I. Geometric and physical interpretation of fractional integration and fractional differentiation. J. Fract. Calc. Appl. Anal. 2002, 5, 357–366. [Google Scholar]
- Tenreiro Machado, J.A. A probabilistic Interpretation of the Fractional-Order differentiation. J. Fract. Calc. Appl. Anal. 2003, 6, 73–80. [Google Scholar]
- Metzler, R.; Joseph, K.J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 2000, 61, 132–138. [Google Scholar] [CrossRef] [PubMed]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1993. [Google Scholar]
- Capelas de Oliveira, E.; Tenreiro, M.J.A. A review of definitions for fractional derivatives and integral. Math. Phys. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef] [Green Version]
- Montseny, G. Diffusive representation of pseudo-differential time-operators. ESAIM Proc. 1998, 5, 159–175. [Google Scholar] [CrossRef]
- Matignon, D. Stability properties for generalized fractional differential systems. ESAIM Proc. 1998, 5, 145–158. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Mainardi, F. Linear models of dissipation in anelastic solids. La Riv. del Nuovo Cimento 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Ionescu, C.; De Keyser, R.; Sabatier, J.; Oustaloup, A.; Levron, F. Low frequency constant-phase behavior in the respiratory impedance. Biomed. Signal Process. Control 2011, 6, 197–208. [Google Scholar] [CrossRef]
- Malti, R.; Sabatier, J.; Akçay, H. Thermal modeling and identification of an aluminum rod using fractional calculus. IFAC Proc. 2009, 42, 958–963. [Google Scholar] [CrossRef] [Green Version]
- Meerschaert, M.M.; Sabzikar, F.; Chen, J. Tempered fractional calculus. J. Comput. Phys. 2015, 293, 14–28. [Google Scholar] [PubMed] [Green Version]
- Sabatier, J. Non-Singular Kernels for Modelling Power Law Type Long Memory Behaviours and Beyond. Cybern. Syst. 2020, 51, 383–401. [Google Scholar] [CrossRef]
- Erdelyi, A. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Sabatier, J. Fractional State Space Description: A Particular Case of the Volterra Equations. Fractal Fract. 2020, 4, 23. [Google Scholar] [CrossRef]
- Sabatier, J. Distributed time delay systems for power law type long memory behaviors modelling. In Proceedings of the 58th IEEE Conference on Decision and Control (CDC 2019), Nice, France, 11–13 December 2019. [Google Scholar]
- Sabatier, J. Power Law Type Long Memory Behaviors Modeled with Distributed Time Delay Systems. Fractal Fract. 2020, 4, 1. [Google Scholar] [CrossRef] [Green Version]
- Tartaglione, V.; Farges, C.; Sabatier, J. Dynamical modelling of random sequential adsorption. In Proceedings of the European Control Conference (ECC 2020), Saint Petersburg, Russia, 12–15 May 2020. [Google Scholar]
- Tartaglione, V.; Farges, C.; Sabatier, J. Nonlinear dynamical modeling of adsorption and desorption processes with power-law kinetics: Application to CO2 capture. Phys. Rev. E 2020, 102, 052102. [Google Scholar] [CrossRef] [PubMed]
- Avrami, M. Kinetics of Phase Change. I. General Theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Fanfoni, M.; Tomellini, M. The Johnson-Mehl- Avrami-Kohnogorov model: A brief review. Nuovo Cimento D 1998, 20, 1171–1182. [Google Scholar] [CrossRef]
- Sabatier, J. Beyond the particular case of circuits with geometrically distributed components for approximation of fractional order models: Application to a new class of model for power law type long memory behaviour modelling. J. Adv. Res. 2020, 25, 243–255. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).