Abstract
The effect of external and internal elastic strain fields on the anisotropic diffusion of radiation defects (RDs) can be taken into account if one knows the dipole tensor of saddle-point configurations of the diffusing RDs. It is usually calculated by molecular statics, since the insufficient accuracy of the available experimental techniques makes determining it experimentally difficult. However, for an RD with multiple crystallographically non-equivalent metastable and saddle-point configurations (as in the case of di-interstitials), the problem becomes practically unsolvable due to its complexity. In this paper, we used a different approach to solving this problem. The molecular dynamics (MD) method was used to calculate the strain dependences of the RD diffusion tensor for various types of strain states. These dependences were used to determine the dipole tensor of the effective RD saddle-point configuration, which takes into account the contributions of all real saddle-point configurations. The proposed approach was used for studying the diffusion characteristics of RDs, such as di-interstitials in FCC copper (used in plasma-facing components of fusion reactors under development). The effect of the external elastic field on the MD-calculated normalized diffusion tensor (ratio of the diffusion tensor to a third of its trace) of di-interstitials was fully consistent with analytical predictions based on the kinetic theory, the parameters of which were the components of the dipole tensors, including the range of non-linear dependence of the diffusion tensor on strains. The results obtained allowed for one to simulate the anisotropic diffusion of di-interstitials in external and internal elastic fields, and to take into account the contribution of di-interstitials to the radiation deformation of crystals. This contribution can be significant, as MD data on the primary radiation damage in copper shows that ~20% of self-interstitial atoms produced by cascades of atomic collisions are combined into di-interstitials.
1. Introduction
The efficiency of the development of structural and functional materials depends on the level of available knowledge of the laws and mechanisms for the formation of radiation microstructures, defects, and properties of the materials. High-dose reactor tests of materials for determination of the degree of radiation change (degradation) of their structure, and properties are very expensive and time-consuming. Moreover, it is difficult to obtain a neutron spectrum in a fission reactor relevant to a fusion reactor environment. To support the development of advanced materials for nuclear fusion technology, theoretical, modelling, and simulation research is necessary to determine parameters of materials and to build physically based models of material property changes under irradiation in conditions specific to fusion reactors.
To build physical models of crystal deformation under damaging radiation (e.g., radiation creep, radiation void swelling), it is necessary to determine the effect of external and internal elastic strain fields on the anisotropic diffusion of radiation defects [,,,]. This effect can be taken into account if one knows the dipole tensor of saddle-point configurations of the diffusing RDs [,,]. The dipole tensor Pij (i, j = 1, 2, 3) is usually calculated by molecular statics [,,,,,,], since the insufficient accuracy of the available experimental techniques makes determining it experimentally difficult. Different techniques within molecular statics have been developed for calculation of the dipole tensor. The first one is to calculate this quantity by summing the first moments of the forces acting on the atoms, fixed at their perfect lattice positions, in the region surrounding the region of free atoms in which the defect is located [,,,]. The second technique uses a direct relation between the dipole tensor and the strain derivative of the defect formation energy, calculated at constant strain []. The third technique uses the proportionality of the dipole tensor to the volume-averaged stress caused by a defect in the simulation box with periodic boundary conditions [,]. All of these techniques give the same result. However, for an RD with multiple crystallographically non-equivalent metastable and saddle-point configurations, the problem of anisotropic diffusion modelling becomes practically unsolvable, due to the need to use physically unreasonable simplifications or assumptions.
In this paper, we used a different method for solving this problem. It was demonstrated in [] that the molecular dynamics (MD) method can be successfully used to study anisotropic diffusion of point defects in metals under external stress fields. We used the MD method to calculate the strain dependences of the RD diffusion tensor Dij for various types of strain states given by the strain tensor εkl (k, l = 1, 2, 3). These dependences were used to determine the RD elastodiffusion tensor dijkl, the components of which are the coefficients for linear terms of the expansions in the degrees of strain of the calculated strain dependences. The crystal symmetry and the defect diffusion mechanism determine the symmetry of the tensor, which corresponds to the dipole tensor of the effective saddle-point configuration of the defect, which takes into account the contributions of all real saddle-point configurations. Figure 1 schematically illustrates the idea of the proposed method for calculation of Pij.
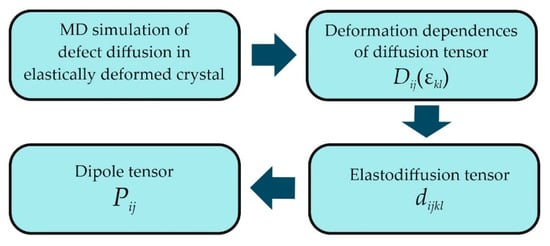
Figure 1.
A schematic illustrating the idea of the proposed method for calculation of the dipole tensor of the radiation defect saddle-point configuration.
For crystals of a cubic crystal system, the diffusion tensor for small strains can be written as []:
where D(0) = 1/3 Tr Dij(0) is a third of the trace of the tensor Dij, in the absence of external strains, and δij is the Kronecker symbol (here and hereafter, the Einstein summation convention for a set of indexed terms is used). The tensor dijkl has the same symmetry as the tensor of elastic constants of the crystal cijkl, which means that it has three independent components, d11, d12, d44 (in the Voigt notation), for cubic crystal system crystals. As the three independent values defining the tensor dijkl, it is more convenient to choose its three eigenvalues: d(1) = d11 + 2d12, d(2) = d11 − d12, d(4) = 2d44.
The strain tensor can be represented in the form [] (here and hereafter, a crystallographic coordinate system (CCS) with axes along ⟨100⟩ is used, unless otherwise specified):
where
Rewriting Equation (1), taking into account (2, 3), gives:
Thus, for a full determination of dijkl in the cubic crystal system crystals, it is sufficient to consider only three specific strain states, for example, V1, V2, V4. Knowing dijkl, we could determine the dipole tensor of the effective RD saddle-point configuration [], allowing us to simulate the diffusion of defects in elastic fields of any arbitrary type, including inhomogeneous ones (e.g., dislocation fields).
In this paper, the proposed method was used to determine the dipole tensor of the effective saddle-point configuration of di-interstitials in an FCC copper crystal. Copper and copper-based alloys (e.g., CuCrZr alloy) are planned to be used as functional materials of fusion reactors [,,], since these materials possess excellent thermal and electrical conductivity. Di-interstitials are one of the most frequently formed types of self-interstitial atomic clusters under damaging irradiation (cluster analysis of MD data, spatial distributions of self-interstitial atoms (SIAs) produced by atomic collision cascades with damaging energies from 1 to 50 keV in Cu, suggested that ~20% of SIAs are combined into di-interstitials [,,]). They have multiple different metastable and saddle-point configurations, which makes them convenient to demonstrate the physical advantages of the method used on this type of RDs. The components Pij for di-interstitials are approximately twice as large as for single SIAs []. This leads to a stronger elastic interaction of the di-interstitials with external elastic fields compared to single SIAs, since in the linear approximation, the interaction energy is equal to [,].
Therefore, the contribution of di-interstitials to crystal radiation deformation under cascade-forming irradiation becomes significant, despite the fact that less of them are generated as compared to single SIAs.
2. Simulation Technique
2.1. Molecular Dynamic Model
The MD techniques used in this work closely follow the ones described in [], which contains their detailed explanations. Di-interstitial diffusion was simulated using interatomic interaction potential [], since it describes the set of experimental data on the bulk properties of copper crystals and their self-point defects well [,]. The model crystallite was a microcanonical ensemble with periodic boundary conditions. The crystal lattice constant a, before the onset of strains, was chosen in such a way that at a given temperature T, the pressure P in the crystallite was equal to zero, with an accuracy of 0.1 eV/nm3. The time step value was chosen in such a way that the mean atom displacement per iteration was ~0.005a. Verlet integration was used to integrate the equations of motion []. The locations of the two SIAs making up the di-interstitial were determined by analyzing the number of atoms in the Wigner–Seitz cells (WSC). The position of the di-interstitial was taken to be that of one of the two SIAs.
The model crystallites were rectangular parallelepipeds. Their characteristics (edge directions, lengths, number of atoms in the crystallite) are summarized in Table 1. The model crystallites were strained by giving the model crystallite atoms displacements ui = εij xj, where xj are the atomic coordinates before straining.

Table 1.
Characteristics of model crystallites used in simulating strain states Vα (α = 1, 2, 4). The values of ε1, ε2, ε4 were set to 0, ±0.001, ±0.005.
2.2. Calculated Diffusion Characteristics
To calculate the RD diffusion tensor Dij, each simulated diffusion trajectory of the defect was divided into several isochronous intervals of duration τ. The value of τ for each temperature and strain was set from a compromise between the need for a large number of isochronous intervals to increase the calculation accuracy and the need for a sufficient number of jumps to be contained within the isochronous intervals to reproduce the main correlations and physical features of the RD diffusion []. For each isochronous interval, the di-interstitial displacement vector Rnm was calculated; here, n is the trajectory number, and m is the isochronous interval number. Next, the quantity D = ⟨Rnm⊗Rnm⟩/2τ was calculated; here, D is the matrix defining the tensor Dij in the CCS, and the operation ⟨…⟩ denotes averaging over all n and m. The diffusivity D was defined as Tr Dij/3. The errors of D and the tensor components Dij were estimated as standard errors for the specified set of n and m. A total of 100 diffusion trajectories were simulated for each given set of strain state and temperature. The total physical simulation time of 100 trajectories ranged from 8.49 µs to 6.61 ns, with a change in T from 300 K to 1100 K (2.06 μs at 500 K). The data set obtained allowed for calculating the diffusion characteristics with such high accuracy that the effect of crystal strains on them was made significant, even at the 0.1% strain.
The tracer diffusivity Dtr (self-diffusivity per one SIA) was calculated by the Einstein–Smoluchowski relation [], using the initial and end positions of the model crystallite atoms for each of the 100 program runs simulating the di-interstitial diffusion. For each dataset, the self-diffusivity intermediate values were calculated. The final Dtr value was obtained by their averaging. The Dtr error was estimated as the standard error for the specified set of 100 intermediate values.
The correlation factor f tr was calculated as the ratio of Dtr to D. Since the value of f tr is sensitive to the defect diffusion mechanism, it can be used to indicate changes in the di-interstitial diffusion mechanism with changes in temperature or cluster size. For example, in the case of a one-dimensional diffusion of crowdions, f tr = 0 [], whereas in the case of a three-dimensional diffusion of ⟨100⟩ dumbbells under Johnson’s mechanism, f tr = 0.44 []. The di-interstitial diffusion mechanism can be mixed when the di-interstitial makes a specific number of jumps along one of the directions ⟨110⟩, subsequently changing this migration direction.
2.3. Specific Features of the Diffusion Tensor in FCC Crystals
During the diffusion of a di-interstitial in an FCC Cu crystal, its constituent SIAs usually make jumps to the first nearest neighbors (NN). Since the share of jumps to the second NN is a hundredths of a percent of the total number at the considered temperatures and strains, it was further assumed that the di-interstitial makes jumps only to the first NN. If the di-interstitial makes a random walk with probability nk of making a jump in the direction k (k = 1, 2…6 for jump directions parallel to the directions [110], , [101], , [011], , respectively, n1 + n2 +…+ n6 = 1), the normalized diffusion tensor in the CCS takes the form:
One can see from (6) that , while the absolute values of the components cannot exceed 3/2.
3. Results
3.1. Diffusivity
Figure 2 shows the MD-calculated dependences D(T) and f tr(T) for di-interstitials in Cu in the absence of external elastic fields (here and hereafter, the data inaccuracy in the figures is not indicated, since it was smaller than the size of the symbols presented on the graphs). The dependence D(T) was non-linear in Arrhenius coordinates (Figure 2a): the parameters of Arrhenius approximations at low and high temperatures differed (Table 2). Despite the low activation energy, which is usually inherent in one-dimensional diffusion of self-point defects in metals, di-interstitial diffusion is essentially three-dimensional: ftr values are markedly different from zero and increase with temperature (Figure 2b) from 0.17 at 300 K to 0.36 at 700 K.
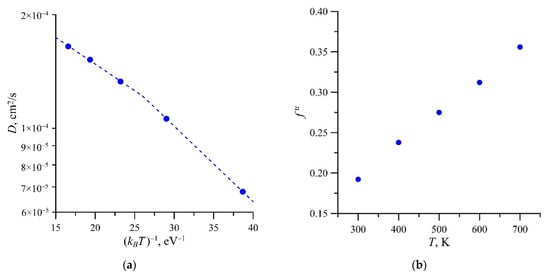
Figure 2.
MD-calculated temperature dependences of the di-interstitial (a) diffusivity and (b) tracer correlation factor in Cu. The dashed lines denote Arrhenius approximations (parameters are given in Table 2).

Table 2.
Parameters of Arrhenius approximations (preexponential factor D0, activation energy EA) of calculated dependences D(T) for di-interstitials in Cu.
Figure 3 shows the MD-calculated dependences D(εα), where α = 1, 2, 4, for the di-interstitials in Cu at 500 K. These dependences were approximated well by the expressions:
where D(0) = 1.33·10–4 cm2/s. The dependences D(ε2) and D(ε4) are even, since due to the crystal’s symmetry, its rotation by 90° around the axis [001] is equivalent to a change in the sign of the strain state to the opposite, while the crystal rotation cannot change the properties of its defects.
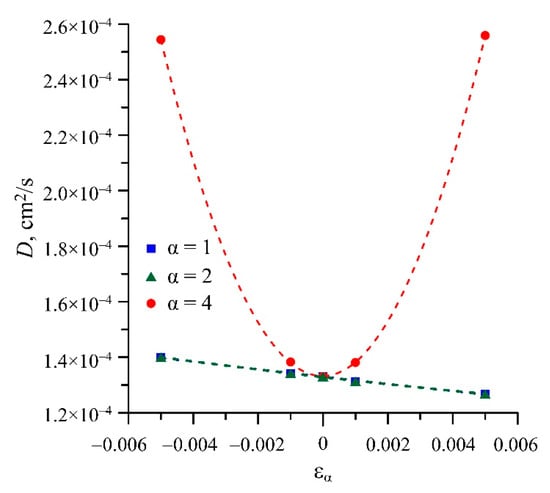
Figure 3.
Dependences D(εα) for α = 1, 2, 4, in Cu at 500 K. Symbols are MD data. The dashed curves are the approximations (7), (8), and (9).
3.2. Normalized Diffusion Tensor
For εij = 0, within the calculation inaccuracy for the considered T. Strain state V1 does not change the symmetry of the crystal, so must also be true. Strain states V2 and V4 lower the symmetry of the crystal, which should lead to a change in , imposing certain relations for its components (Table 3). For the MD-calculated dependences , these relations are actually fulfilled within the framework of the calculation inaccuracy (Figure 4 and Figure 5).

Table 3.
Relations for the components of the normalized diffusion tensor, (i, j = 1, 2, 3), under strain states Vα (α = 1, 2, 4) following from the crystal symmetry.
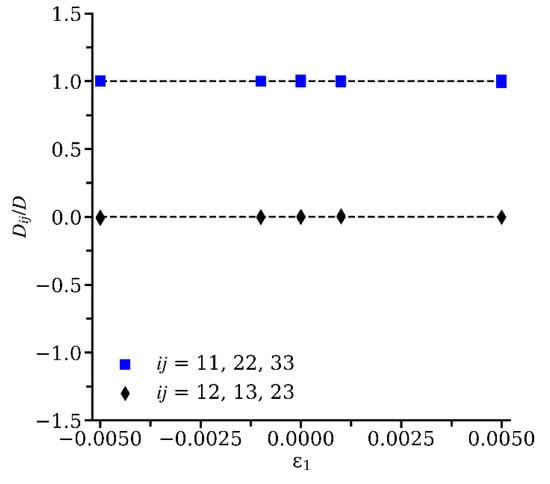
Figure 4.
Dependences in Cu at 500 K. Symbols are MD data.
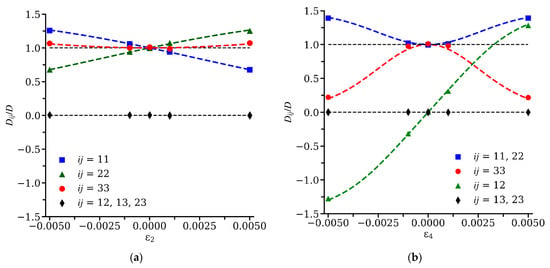
Figure 5.
Dependences in Cu at 500 K: (a) α = 2; (b) α = 4. Symbols are MD data. The dashed curves are the Equations (15) and (16).
3.3. Elastodiffusion and Dipole Tensors
The eigenvalues of the elastodiffusion tensor d(α) can be obtained by adjusting their values in such a way that expression (4) would describe the calculated dependences in the region of the small εα, in which the linear nature of such dependences is observed. For the specified region, the expressions following from (4) are valid:
Using Equations (10)–(12) to adjust the MD data presented in Figure 3 and Figure 5 in the region |εα| ≤ 0.1% gave, for d(α)/(D(0)β), the values 4.945 eV, –2.693 eV, 14.085 eV for α = 1, 2, 4, respectively.
In [], it was analytically shown that the eigenvalues of the elastodiffusion tensor in cubic crystal system crystals could be determined if the dipole tensors of the defect in the stable and saddle-point configurations are known. Table 4 shows the relations obtained in [] connecting d(α) with and for different symmetries of the defect saddle-point configurations.

Table 4.
Eigenvalues of the elastodiffusion tensor for various symmetries of the defect saddle-point configurations.
Di-interstitial diffusion is characterized by a combination of different diffusion mechanisms; hence, a di-interstitial has multiple different saddle-point configurations. However, using the relations in Table 4, it is possible to obtain the dipole tensor of the effective saddle-point configuration to which all real saddle-point configurations contribute (each with its own weight).
All three calculated eigenvalues d(α) were nonzero for Cu, which corresponded, according to Table 4, to the orthorhombic symmetry of the effective saddle-point configuration of the di-interstitial. Therefore, for the components , the following expressions are true:
The molecular statics calculation gave for a stable di-interstitial configuration. Substituting the calculated values of d(α) and to (13), we get
4. Discussion
Knowledge of the dipole tensor of the defect saddle-point configuration allows calculation of its diffusion tensor for any strain state and simulation of the RD anisotropic diffusion in mechanical fields, generated by external crystal loads and/or internal sources (dislocations, sub-boundaries, etc.), by the object kinetic Monte Carlo (OKMC) method, taking into account both the effects of elastic crystal anisotropy and crystal symmetry []. The probabilities nk used in the OKMC method can be represented as []:
where is the interaction energy of the defect saddle-point configuration for the migration direction k, with the strain field εij calculated by Equation (5). Applying Equation (14) to (6), and introducing the designation , , we obtain for non-zero components under strain states V2 and V4:
Figure 5 shows the dependences (15) and (16) and the corresponding MD dependences. Equations (15) and (16) that use the dipole tensor as a parameter described the MD data with high accuracy for all the considered strain values, including in the region of nonlinear dependence on strains, which favorably distinguishes them from expression (4) that uses the elastodiffusion tensor as a parameter, which accurately described the MD data for |ε4| ≤ 0.001 only. Therefore, the dipole tensor of the effective saddle-point configuration of the di-interstitial for FCC Cu obtained in this study allowed for simulating of di-interstitial anisotropic diffusion in different elastic fields with high accuracy.
As a specific result, we note how it followed from Equations (15) and (16) that, with an increase in |ε2| and |ε4|, the tensor tended to a form corresponding to two-dimensional (in the planes (100) for ε2 > 0 and (010) for ε2 < 0) and one-dimensional (in the directions [110] for ε4 > 0 and for ε4 < 0) diffusion of di-interstitials, respectively:
5. Conclusions
A new method for calculation of the dipole tensor of the saddle-point configuration of radiation defects was proposed. In this method, the molecular dynamics method was used to calculate the strain dependences of the RD diffusion tensor for homogeneous elastic fields of different types. These dependences were used to determine the RD elastodiffusion tensor. The crystal symmetry and the RD diffusion mechanism determined the tensor symmetry. This corresponded to the dipole tensor of the effective RD saddle-point configuration, which takes into account the contributions of all real saddle-point configurations.
The proposed approach was used for studying di-interstitial diffusion characteristics in copper. The symmetry of the calculated dipole tensor of the effective saddle-point configuration was orthorhombic. For all the strain states considered, the effect of the external elastic strain field on the MD-calculated normalized di-interstitial diffusion tensor (ratio of diffusion tensor to a third of its trace) was fully consistent with theoretical expressions, the parameters of which were the components of the dipole tensor, including those outside the range of linear dependence of the diffusion tensor on strains.
The results obtained allowed for simulation of di-interstitial anisotropic diffusion in external and internal elastic fields and for taking into account the di-interstitial contribution to crystal radiation deformation. This contribution is significant, since, as MD data on the primary radiation damage in copper showed, ~20% of self-interstitial atoms produced by cascades of atomic collisions are combined into di-interstitials.
The equations given in the present work are ready to use to study the defect diffusion characteristics in FCC and BCC crystals. However, one can apply the proposed approach to crystals of systems other than the cubic one.
Author Contributions
Conceptualization, A.B.S.; methodology, A.B.S. and D.N.D.; software, A.B.S., D.N.D. and P.A.S.; validation, D.N.D. and A.B.S.; formal analysis, A.B.S. and D.N.D.; investigation, D.N.D. and A.B.S.; resources, A.B.S.; data curation, D.N.D.; writing—original draft preparation, D.N.D.; writing—review and editing, A.B.S.; visualization, D.N.D. and A.B.S.; supervision, A.B.S.; project administration, A.B.S.; funding acquisition, A.B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Research Center “Kurchatov Institute”, grant number 1934a from 28 September 2020.
Data Availability Statement
Not applicable.
Acknowledgments
The study was carried out using computing resources of the federal collective usage center, Complex for Simulation and Data Processing for Mega-science Facilities at NRC “Kurchatov Institute”, http://ckp.nrcki.ru/, accessed on 27 June 2021.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Dederichs, P.H.; Schroeder, K. Anisotropic diffusion in stress fields. Phys. Rev. B 1978, 17, 2524–2536. [Google Scholar] [CrossRef]
- Saralidze, Z.K. Radiational growth due to diffusional anisotropy. At. Energy 1978, 45, 697–700. [Google Scholar] [CrossRef]
- Saralidze, Z.K.; Indenbom, V.L. Chapter 12—Dislocations in irradiated crystals. In Modern Problems in Condensed Matter Sciences; Indenbom, V.L., Lothe, J., Eds.; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1992; Volume 31, pp. 699–744. [Google Scholar] [CrossRef]
- Sivak, A.B.; Sivak, P.A.; Romanov, V.A.; Chernov, V.M. Effect of external stresses on efficiency of dislocation sinks in BCC (Fe, V) and FCC (Cu) crystals. Inorg. Mater. Appl. Res. 2015, 6, 466–472. [Google Scholar] [CrossRef]
- Kröner, E. Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Arch. Ration. Mech. Anal. 1959, 4, 273–334. [Google Scholar] [CrossRef]
- Leibfried, G.; Breuer, N. Point Defects in Metals I. In Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 1978; Volume 81. [Google Scholar] [CrossRef]
- Dederichs, P.H.; Lehmann, C.; Schober, H.R.; Scholz, A.; Zeller, R. Lattice theory of point defects. J. Nucl. Mater. 1978, 69–70, 176–199. [Google Scholar] [CrossRef]
- Schober, H.R.; Ingle, K.W. Calculation of relaxation volumes, dipole tensors and Kanzaki forces for point defects. J. Phys. F Met. Phys. 1980, 10, 575–581. [Google Scholar] [CrossRef]
- Simonelli, G.; Pasianot, R.; Savino, E.J. Point-defect computer simulation including angular forces in bcc iron. Phys. Rev. B 1994, 50, 727–738. [Google Scholar] [CrossRef]
- Sivak, A.B.; Romanov, V.A.; Chernov, V.M. Influence of stress fields of dislocations on formation and spatial stability of point defects (elastic dipoles) in V and Fe crystals. J. Nucl. Mater. 2003, 323, 380–387. [Google Scholar] [CrossRef]
- Puls, M.P.; Woo, C.H. Diaelastic polarizabilities due to vacancies and interstitials in metals. J. Nucl. Mater. 1986, 139, 48–59. [Google Scholar] [CrossRef]
- Clouet, E.; Garruchet, S.; Nguyen, H.; Perez, M.; Becquart, C.S. Dislocation interaction with C in a-Fe: A comparison between atomic simulations and elasticity theory. Acta Mater. 2008, 56, 3450–3460. [Google Scholar] [CrossRef]
- Ma, P.-W.; Dudarev, S.L. Nonuniversal structure of point defects in face-centered cubic metals. Phys. Rev. Mater. 2021, 5, 013601. [Google Scholar] [CrossRef]
- Chan, W.-L.; Averback, R.S.; Ashkenazy, Y. Anisotropic diffusion of point defects in metals under a biaxial stress field simulation and theory. J. Appl. Phys. 2008, 104, 023502. [Google Scholar] [CrossRef]
- Merola, M.; Loesser, D.; Martin, A.; Chappuis, P.; Mitteau, R.; Komarov, V.; Pitts, R.A.; Gicquel, S.; Barabash, V.; Giancarli, L.; et al. ITER plasma-facing components. Fusion Eng. Des. 2010, 85, 2312–2322. [Google Scholar] [CrossRef]
- Norajitra, P.; Giniyatulin, R.; Ihli, T.; Janeschitz, G.; Krauss, W.; Kruessmann, R.; Kuznetsov, V.; Mazul, I.; Widak, V.; Ovchinnikov, I.; et al. He-cooled divertor development for DEMO. Fusion Eng. Des. 2007, 82, 2740–2744. [Google Scholar] [CrossRef]
- Shpanskiy, Y.S.; The DEMO-FNS Project Team. Progress in the design of the DEMO-FNS hybrid facility. Nucl. Fusion 2019, 59, 076014. [Google Scholar] [CrossRef]
- Bacon, D.J.; Osetsky, Y.N.; Stoller, R.; Voskoboinikov, R.E. MD description of damage production in displacement cascades in copper and α-iron. J. Nucl. Mater. 2003, 323, 152–162. [Google Scholar] [CrossRef]
- Miyashiro, S.; Fujita, S.; Okita, T. MD simulations to evaluate the influence of applied normal stress or deformation on defect production rate and size distribution of clusters in cascade process for pure Cu. J. Nucl. Mater. 2011, 415, 1–4. [Google Scholar] [CrossRef]
- Yang, Y.; Okita, T.; Itakura, M.; Kawabata, T.; Suzuki, K. Influence of stacking fault energies on the size distribution and character of defect clusters formed by collision cascades in face-centered cubic metals. Nucl. Mater. Energy 2016, 9, 587–591. [Google Scholar] [CrossRef][Green Version]
- Osetsky, Y.N. Atomistic study of diffusional mass transport in metals. Defect Diffus. Forum 2001, 188–190, 71–92. [Google Scholar] [CrossRef]
- Mishin, Y.; Mehl, M.J.; Papaconstantopoulos, D.A.; Voter, A.F.; Kress, J.D. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys. Rev. B 2001, 63, 224106. [Google Scholar] [CrossRef]
- Sivak, A.B.; Demidov, D.N.; Sivak, P.A. Diffusion characteristics of self-point defects in copper: Molecular dynamics study. PAS&T. Ser. Thermonucl. Fusion 2021, 44, 106–118. [Google Scholar] [CrossRef]
- Verlet, L. Computer «experiments» on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Allnatt, A.R.; Lidiard, A.B. Atomic Transport in Solids; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Manning, J.R. Diffusion Kinetics for Atoms in Crystals, 1st ed.; D. Van Nostrand Company: Toronto, ON, Canada, 1968. [Google Scholar]
- Benoist, P.; Bocquet, J.-L.; Lafore, P. La correlation entre sauts atomiques: Une nouvelle methode de calcul. Acta Metall. 1977, 25, 265–275. [Google Scholar] [CrossRef]
- Sivak, A.B.; Romanov, V.A.; Chernov, V.M. Diffusion of self-point defects in body-centered cubic iron crystal containing dislocations. Crystallogr. Rep. 2010, 55, 97–108. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).