Abstract
A general formula for inversion in a relativistic Clifford–Dirac algebra has been derived. Identifying the base elements of the algebra as those of space and time, the first order differential equations over all quantities proves to encompass the Maxwell equations, leads to a natural extension incorporating rest mass and spin, and allows an integration with relativistic quantum mechanics. Although the algebra is not a division algebra, it parallels reality well: where division is undefined turns out to correspond to physical limits, such as that of the light cone. The divisor corresponds to invariants of dynamical significance, such as the invariant interval, the general invariant quantities in electromagnetism, and the basis set of quantities in the Dirac equation. It is speculated that the apparent 3-dimensionality of nature arises from a beautiful symmetry between the three-vector algebra and each of four sets of three derived spaces in the full 4-dimensional algebra. It is conjectured that elements of inversion may play a role in the interaction of fields and matter.
1. Introduction
This paper investigates the interplay between the mathematics of inversion, division and differentiation in a particular relativistic non-division algebra and the physics well-described by that mathematics. The main result is purely mathematical: a general formula for the inversion of a general multi-vector within the algebra. The main interest, however, lies in the how and the why of the relation of the mathematics to physical reality. Springing between mathematics and physics can be confusing. To help in this, lower case letters will be used to describe pure mathematics. Where physical associations are brought in, upper case letters will be used. The physics presented will be either illustrative or speculative.
For the identification with physics, the inversion symmetries of relativistic space, time and products and quotients of space and time, will prove central. It will be shown that the physical relevance of inversion in particular and division and differentiation in general is remarkably broad, encompassing classical electromagnetism, a new relativistic quantum mechanics, and the physical structure, mutual interaction and apparent dimensionality of reality. A, perhaps unexpected, result is that the study of relativistic inversion leads to many of the major invariants of classical physics, some more usually thought to be in the quantum domain, and some new ones which may prove to be of service in the future.
Relativistic algebras, such as any Dirac algebra, are not division algebras in that there are areas other than zero where division is not defined. Physically, such a property is required to properly parallel aspects of relativistic space-time. It is immediately obvious, for example, that inversion is necessarily undefined for a 4-vector v anywhere on the light cone: the inverse of any vector is another 4-vector which may be written as . The denominator is zero on the light cone, and hence the inverse becomes undefined. The Clifford algebra , often denoted the space-time algebra or just the STA for short, has been designed to parallel as closely as possible the nature of relativistic space-time [1,2,3,4,5,6,7,8]. It is that Clifford algebra with the Lorentz metric . Other authors have noted that, because is isomorphic to the base elements of a particular Dirac algebra [2,9,10], another appropriate name for it is a Clifford–Dirac algebra, and this name is also in current popular usage [11]. In this algebra, there are many multivector combinations where division is undefined, and the denominators which may have zero values prove to be related to important invariants that govern the relativistic scaling of 4-vectors and fields, among other things.
In any event, even though the algebra is not a division algebra, it appears to be of utility, not only in describing spin- [5,12] but also, for example, in describing aspects of physics such as the Maxwell equations [3,13,14]. In this context, the development leads not only to a description of the physics, which is comparable to that of other methods, but also to one that is in some respects more elegant. In particular, the formulation leads to all four Maxwell equations at once [2,4,8,13,14,15,16,17], rather than to the pair of inhomogenous equations for the field and the homogeneous equations for the dual field separately as is the case in the more usual textbook approach [18]. How can this be? How is it that an ill-behaved [11] non-division algebra can successfully describe wide areas of physics?
In short, the physical reason is that the world observed in experiment does scale relativistically. The mass-energy of a particle as it approaches the limit of light-speed for example, tends to infinity. The quantities describing dynamics in Maxwell and Dirac theory are 4-vector differentials and contain an implicit inverse. For the description of dynamics within the algebra, however, the scaling of each component taken separately is precisely unity. It is not in the case of individual elements of the algebra, but in combinations of non-zero elements where division may scale or become undefined. In fact, one may turn the perspective around, and say that, for properly relativistic algebras only quantities with this unit property may be important for a local description of dynamics—as they lead to possible unitary operators which conserve important quantities such as energy and momentum.
Now, one comes to the physical utility of inverses (and hence division) in this context. Division may seem familiar, and is so for simple numbers: the inverse of three is a third. What, physically, does inversion mean in the context of the inverse of space? Time? Space-time? Space divided by time? Space-time on the light-cone? If one can find an inverse at all, the product of this with its starting quantity leads, by definition, to a unit Lorentz scalar. It may be suspected, as indeed turns out to be the case, that finding such combinations may lead, in turn, to unitary processes which leads in turn to "allowed” and interesting dynamics. The extension of the unit relativistic vectors of space and time leads to a rich set of combinations of derived elements, corresponding to combinations of physical areas, volumes and a unit “point”, as well as base lines, where division is undefined.
The structure of this paper is as follows. For those unfamiliar with Dirac–Clifford algebras and their sub-algebras, the essential properties are described [1,2,3,4,5,6,7,8,14]. Applying this to the physics of electromagnetism, the algebra is used to derive a general first order relativistic differential equation, encompassing field, mass, spin and potential [16]. The new equation has some similarities to the Dirac equation, but the mass, gauge and spin are treated as intrinsic elements on the same footing as the electromagnetic field. The field-only case of the new equations is exactly the Maxwell equations. Returning to the mere mathematics, inverses are found for various quantities of importance, including the general case for the algebra. It is shown that the areas where division is undefined correspond to null-hyperplanes which cut through the extended structure of the algebra. Returning once again to possible physical consequences, it is shown that many of these null-hyperplanes correspond to limiting cases of interest, such as the zero-length interval (null-vector) of space-time in Einstein’s special relativity, the corresponding case in energy–momentum and invariant quantities important in electromagnetism. Some of these particular cases are discussed. The article concludes with the conjecture that the mathematics of relativistic inversion may be related to the physics of interaction.
2. The Clifford–Dirac Algebra
Dirac developed his algebra in the first instance to pass to a linearisation of the energy momentum Hamiltonian in relativistic quantum mechanics. Clifford algebras have been used, through their geometric product over the basis vectors of space and time, to represent the full range of boosts and non-commuting rotations between them. The sub-algebra of the Dirac -matrix algebra (excluding ) is isomorphic to the Clifford algebra . It is this real Clifford–Dirac algebra that we will use to investigate physical inverses here. The subscripts 1 and 3 just refer to one unit element (identified with time) of the 4-vector generator set squaring to the positive scalar and three elements (identified with three directions in space) squaring to the negative scalar element. Note that though the standard Dirac -matrices are a representation of this Clifford algebra, any specific matrix representation is irrelevant to any of the arguments which follow. In this algebra, a contravariant 4-vector a may be written
with the being real coefficients and the gammas time and three spatial unit vectors, respectively. The 0 index represents the temporal, and the 1, 2, 3 the right-handed triple of spatial unit vectors in any well behaved orthonormal co-ordinate system. Such systems may include spherical, cylindrical or toroidal co-ordinate systems, but for definiteness here, the generators of the algebra are mapped onto unit Cartesian basis of Minkowski space-time as
A 4-vector, containing the proper Clifford elements, is written in plain type. Bold type is used to denote a three component object, here the spatial part of a 4-vector. The column notation extracts the 3-vector part of the 4-vector, and allows one to keep track of the conventional 3-vector projections whilst maintaining a proper underlying 4-vector algebra. This will help to show why the physical universe may appear three-dimensional, while the underlying basis remains four-dimensional. Note that lower indices are used in the case of contravariant vectors, as this simplifies the notation for squared quantities. Greek indices run from 0 to 3. Latin indices run from 1 to 3.
The 16 terms of the full ordered geometric product between two 4-vectors a and b is defined as
the first part of which is the symmetric part and corresponds to the 4-vector scalar product in the simple vector case:
It is worth noting that in the present paper, the symmetric part of the geometric product is denoted by a small circle in order to avoid any confusion with the dot product: , the scalar or inner product between ordinary 3-vectors (denoted by boldface). It is crucial to understand that the symmetry or anti-symmetry of the product is not here related to the scalar. As will become clear, it is division—or, more specifically, a product involving a mutual inversion—that may generate Lorentz scalar objects from general multi-vector distributions.
The second part of the product, the antisymmetric part, behaves in some respects (at least between two vectors) like the usual Heaviside–Gibbs cross product of 3-space, ×, but is distinguished here by the wedge symbol [4]:
The anti-commutator of the basis vectors is
where the metric tensor has the Lorentz metric,
where is the unit scalar in the algebra. This should not be confused with the real number 1, which represents one unit of a quantity. Note that a convention is adopted, not only in an effort to keep the terms compact, but also to make explicit that these are new elements in a group of sixteen orthogonal elements [6].
The square of a vector a gives precisely the Lorentz-invariant scalar product:
For example, for the case where the magnitudes specify the location of a pair of events in any given space-time frame, the proper invariant interval between them is:
where is positive-definite and time-like () for subluminal world lines, but goes to zero on the light-cone, where division is undefined.
Starting with the unit basis elements , using the antisymmetric product, Equation (5), unit elements of higher grade can be formed. There are 6 independent terms of the form which we abbreviate with , the bivector unit basis elements. In the space-time association, just as the form a basis for translations in Minkowski 4-space, the higher grade elements form the basis elements of boosts (Lorentz transformations) and the the basis elements of rotations, with their proper non-commutative properties included [4,6,13]. Note that for ; any exchange of adjacent indices generates a factor of minus one. There are four independent trivectors (the pseudo 4-vector basis elements) of the form , and a single independent quadrivector , the pseudoscalar. Together with the generator basis vectors and the unit scalar one has 16 linearly independent unit elements which, together with their counterparts with negative sign, form an algebraic group of 32 elements. The real algebra with this group requires only the positive 16 unit basis elements, because the minus sign may be absorbed in the real coefficients. So-called multivectors can be formed using these elements. This allows us to use the standard vector calculus notation and the Dirac algebra simultaneously. To many readers, this will appear to be helpful in recognising known physics even if geometric algebra is new to them. Let small letters refer to the nature of the basis element: scalar s, vector v (polar vector), bivector (boost b (polar vector) and rotor r (axial vector)), trivector t (pseudo vector or axial vector) and quadrivector q (pseudoscalar), then the most general multivector , containing all 16 basis elements, may be written as
Bold letters are a triple of real number components. These real components may aquire physical dimension when used to describe physics, though this is irrelevant to the mathematical results. In this way, the gamma components may be kept dimensionless, by definition. It is the real factor that may be used to carry the units of space and time, field and spin in what follows. For example, the commuting real number triple of components is such that , where the are real number components ( or momentum or field strength components etc.), some or all of which may be zero. The linearly independent multivector elements are carried by the components, which are written in column form to emphasise that the full relativistic algebra has four linearly independent three-component bases, with different commutation, multiplication and division properties to each other. In elementary texts these four groups of three are often projected onto one another and/or onto 3-dimensional vectors. Such projections have caused much confusion in the past [3,4,6]. A discussion of the nature of these four 3-spaces will be resumed after making connections with the Maxwell equations and relativistic quantum mechanics below.
Proper elements with naturally just one component are distingushed with the suffix “0”. Explicitly, these are the scalar element , the temporal element , the spatial tri-vector element and the dual quadri-vector element . All elements have magnitudes given by real numbers—the proper Clifford–Dirac element being given explicitly in the column-vector or unit element in the definition of Equation (10). The advantage of the 3-component column vector notation is that it makes explicit the four 3-spaces, that of the basis vector set and the other three derived as products or quotients of these. Furthermore, it allows a connection to the other linearly independent sets of three component objects. This aids the connection between the 4-dimensional and the historical Heaviside–Gibbs 3-vector algebra notation, as will become apparent in the next section. By keeping the unit basis elements explicit, we not only allow for distinction of the grade of a multivector component, but also find these distinctions to be of value in the classification of inverses. As mentioned before, lower case letters will be used for mere mathematics, where physics is discussed upper case letters will be introduced.
A short calculation shows that , . The sixteen element set generated from the basis on the Lorentz metric forms a “geometric” Dirac algebra, the Clifford algebra of space-time . The inversion of these unit elements is always defined. Individual inverted elements have the same nature and the same magnitude but may change sign and hence reverse “direction”. A major advantage of the algebra is that one need not carry both co- and contra-variant basis vectors as multiplication and division keeps track of the proper signs in differential equations, products and quotients. Multi-vectors with more than one non-zero component may also scale in magnitude under inversion, as will be discussed in detail in what follows. Of the 10 elements which square to , not one commutes with all other elements, that is, none behave like the complex number . There is no unless one explicitly adds the unit imaginary. That is, the Dirac -matrices are representations of the group that forms the basis for the Clifford algebra of spacetime [1,5,6,9], but the Dirac matrix algebra M4( 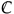 ) (the algebra of complex matrices) is the complexification of both the spacetime algebra:
) (the algebra of complex matrices) is the complexification of both the spacetime algebra: 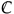 M4(
M4( 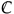 ) and the Majorana algebra
) and the Majorana algebra 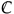 M4(
M4( 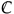 ) [6]. For the even subalgebra , the quadrivector takes the role of the unit imaginary number because it commutes with all the even elements. As mentioned above, the full algebra has important self-contained sub-algebras. Explicitly the subset is isomorphic to the complex algebra and the subset is isomorphic to the quaternion algebra. It is no accident that these subsets of the full relativistic algebra have been used successfully to describe non-relativistic physics for more than a century. In contrast to projections onto 3-dimensional spaces, physics described within these subsets does not compromise the underlying 4-dimensional form.
) [6]. For the even subalgebra , the quadrivector takes the role of the unit imaginary number because it commutes with all the even elements. As mentioned above, the full algebra has important self-contained sub-algebras. Explicitly the subset is isomorphic to the complex algebra and the subset is isomorphic to the quaternion algebra. It is no accident that these subsets of the full relativistic algebra have been used successfully to describe non-relativistic physics for more than a century. In contrast to projections onto 3-dimensional spaces, physics described within these subsets does not compromise the underlying 4-dimensional form.
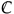 ) (the algebra of complex matrices) is the complexification of both the spacetime algebra:
) (the algebra of complex matrices) is the complexification of both the spacetime algebra: 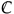 M4(
M4( 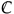 ) and the Majorana algebra
) and the Majorana algebra 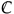 M4(
M4( 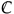 ) [6]. For the even subalgebra , the quadrivector takes the role of the unit imaginary number because it commutes with all the even elements. As mentioned above, the full algebra has important self-contained sub-algebras. Explicitly the subset is isomorphic to the complex algebra and the subset is isomorphic to the quaternion algebra. It is no accident that these subsets of the full relativistic algebra have been used successfully to describe non-relativistic physics for more than a century. In contrast to projections onto 3-dimensional spaces, physics described within these subsets does not compromise the underlying 4-dimensional form.
) [6]. For the even subalgebra , the quadrivector takes the role of the unit imaginary number because it commutes with all the even elements. As mentioned above, the full algebra has important self-contained sub-algebras. Explicitly the subset is isomorphic to the complex algebra and the subset is isomorphic to the quaternion algebra. It is no accident that these subsets of the full relativistic algebra have been used successfully to describe non-relativistic physics for more than a century. In contrast to projections onto 3-dimensional spaces, physics described within these subsets does not compromise the underlying 4-dimensional form.3. On the Inversion of Space and Time: Frequencies and Differentials
For the quotients , which correspond to the covariant basis vectors, we have
As a consequence of the quotient, the vector differential operator has opposite space sign to the vector:
Note that a proper differential contains implicitly an inversion of the basis elements. In any event, a differential is a special kind of division: in the vector differential, these are a sum of a divisions by an infinitesimal time or (each of three perpendicular directions) of space. Clearly, the operation of this differential operator d on some multivector Ψ, therefore, results in a change of grade. Note that though the metric has been inserted as an axiom, derived from careful experimentation on reality, it is perhaps better explained in terms of the inversion of the base unit elements, taken separately. The algebra is such that the inverse of the unit temporal element is the unit temporal element. The inverse of each of the three spatial unit vectors is the negative of that unit vector as in Equation (11) above. In describing dynamics, then, one can make do with a single direction of time (or frequency), but one needs to have two directions in all three spatial directions, as any inverse, or differential, generates such vectors.
Consider the inversion of time, measured in seconds. This is frequency, measured in Hertz. One may imagine that one lives “in” time, and that time is that which is measured by clocks. Think though: the ticking of a clock is really a frequency. The fundamental quantisation rules and conserved quantities are more in terms of frequency than time. Quantum energy is Planck’s constant times frequency . The stability of (e.g., atomic) clocks is down to the absolute nature of the conservation of energy, not to any underlying grid of time. It is energy, not time, that is absolutely conserved. Likewise, marked on a ruler are ticks denoting space, but those ticks may be seen as the peaks of a spatial wave delineating a spatial frequency. If one measures the width of a road, using a metre stick for example, one divides the width of the road by the stick to get the number of metres. One could call the metre stick, or any other ruler, in this sense a dividing stick. Now, there is, of course, a symmetry between an object and its inverse. If that symmetry were perfect, and one were trapped in one or the other, would it be possible to determine whether one lived in time or frequency space? Luckily, we do not need to make the choice, because inversion will prove an essential part of the dynamics in the arguments to follow. It is certainly an integral part of the mathematics we use to describe dynamics in differential equations. Existing in either space and time alone or inverse space and inverse time alone would be void of dynamics, at least those dynamics described by differential equations. Such a world would be rigid with no motion of any kind, let alone the ability to think about it. Necessarily, we live in both space and time and inverse space and inverse time. The latter pair are in the realm of quantisation, and the former in freedom to move forwards and backwards in space, if not in time.
4. A Physical Application: The Extended Maxwell Equations
Let us move from the mathematical and the philosophical to a concrete physical example. Consider some relativistic, coherent, harmonic, self-repeating multivector wave-function representing an elementary particle or exitation, that maps immediately to itself after a single spatial and temporal step involving a change of phase. It has been argued in earlier work that merely complex two component wave-functions are not complex enough to properly represent a fully relativistic wave function, but that one needs at least four components with a phase-harmony [16], and that the present algebra is perfect for this task. In any case, one may describe the dynamics as a fundamental process such that . Alternatively, one may consider constraints on allowed changes using a differential equation such that , expressing that the net result of the internal changes is balanced so that there is no net change of the initial wave-function in that first order process. Both describe the same physical process of an isolated state continuously re-forming itself in a coherent wave. The differential equation approach is the traditional way in which dynamics is described, and it is that route which will be followed in the first instance. The second will be returned to later in the discussion on interaction.
The simplest case of = 0 for the complete multivector set is an extended set of eight coupled first order differential equations the first four of which parallel exactly the Maxwell equations in the rest-massless case. This has been discussed extensively in earlier work [14,15,16], but sufficient detail will be given here to be able to understand what it means in the inversion of an extended field distribution in the sections below.
To make a connection between the mathematics and the physics, let the 4-vector be taken to describe the 4-vector potential in the first instance, as this corresponds most closely with the description in elementary textbooks [18].
Starting with a vector 4-potential defined over all space-time x, the vector differential yields elements of the electromagnetic field. How that plays out and is connected to the Maxwell equations is discussed briefly. In what follows, natural units are used, , ℏ and c are set equal to unity. Let the 4-potential be with the scalar potential and the vector potential. In accordance with the previous section:
The 4-derivative is . It turns out that the patterns of terms in the full 4-space algebra are similar to those in the 3-space algebra. This means that the end result may be written in terms of the familiar 3-space forms, such as A, the electric field E and magnetic field B, and the standard dot and cross product, whilst the full geometric algebra is maintained by means of the positional column notation introduced above for the proper components. With these conventions, the terms of the full product may be written as
which is the sum of a scalar part S and a bivector part F, so we can write , with
Note that the quantities associated with the gradient and curl here map to two distinct, linearly independent bi-vector spaces, electric field space and magnetic field space, denoted by the column vectors in the full 4-dimensional algebra. The scalar S is intimately related to the usual gauge, as will become clear, though here a second gauge, related to the dual scalar, may also be present. Setting (for all coordinates) corresponds to the Lorenz gauge condition.
In Equation (14), we can identify, in the usual way, the electric field and the magnetic field , where the sign convention is that of Jackson [18]. Together, these terms form a six-component object known as the Riemann–Silberstein vector which we denote by F. This corresponds to the antisymmetric Faraday or field-strength tensor [18], but here it takes the spinor form [19,20]:
In Equation (16), the electric and magnetic fields have a bivector form, a boost and a rotor , respectively, rather than appearing as a set of tensor components. Since the vector has been defined as proper 4-vector from the start, as has the 4-vector derivative, the fields here transform as do the fields in the simpler tensor formalism. This is as has been discussed in earlier work [13,16], and as should be expected for an intrinsically relativistic algebra. The proper relativistic transformations are also, of course, an essential part of the inversion of complex distributed multi-vectors. An extension to invariants and relativistic scaling to completely general multi-term multi-vectors involving the tri-vector (spin) and mass and dual mass terms will be derived in the sections to follow.
The physical assignation of the vector and bi-vector terms has been discussed, but what of the other three, the scalar, tri-vector and quadri-vector? In earlier work, in line with their relativistic transformation properties, we have related these to root-mass, intrinsic spin and dual root mass, respectively, [16]. Here, we will use the initial capitals of their physical multi-vector form, S for the scalar, Q for the quadrivector and T for the trivector components. Explicitly, we may define a physical field, root-mass, intrinsic spin and dual root-mass multivector as:
As in Equation (14), Equation (12) acting on Equation (10) one may form a general set of first order equations for a non-interacting multivector field in free space as . This may be expanded in terms of the full 4-space products, and terms may be gathered in the 3-space quantities to give
Here, the unit elements have been placed to left to keep them out of the way. This has no consequence as they commute with the expression to their right. The magnitudes may be unified by taking square root rest mass, energy or probability density. The first four equations are the extended Maxwell equations, including root mass (S) and possible dual root rest mass (Q) terms. If one considers the rest-massless and spinless case where all terms except the field are zero, i.e., , then only the first four equations apply and S and Q are zero then, by inspection, is exactly the full set of Maxwell equations, though with the proper multivector form of the equations within the formalism. The full set of equations has a similar form to the Dirac equation, but with the rest mass and the spin on the same footing as the physical fields [16].
It should be noted that, although the conventional approach has been followed here in associating the 4-vector with a 4-vector potential, it is equally possible to derive the physical electromagnetic fields from the 4-trivector potential T. This allows one to associate the field with the physical spin, rather than the field with a non-physical vector potential. This approach would also have the distinct advantage that the 4-vector would be left free to describe a physical 4-current. In previous work [21], it has been shown that the quantised charge could be derived in terms of the quantised angular momentum, or vice versa within a simple semi-classical model of the electron as a self-localised photon. The relativistic quantum theory discussed above has shown solutions with non-trivial toroidal topology which are necessarily charged [16] which fit seamlessly with the earlier semi-classical model, while providing a mechanism for the self-confinement of the electron charge.
5. On Invariants, Inversion and the Hyperplanes Where Division Is Not Defined
Let us now pass to the main purpose of this paper, a consideration of where and how division is, and is not, defined within the relativistic Clifford–Dirac algebra . The mutual inverse of an object within the algebra is defined as that thing required to multiply to the unit scalar element , such that . This allows the identification of those special multivectors where a “multiplicative division” or inverse does not exist, and hence where division is not defined [11]. It turns out that inversions hinge upon finding (Lorentz) scalar invariants in the divisor. Some of these invariants, such as the invariant interval and invariant mass-energy are very familiar. Others are new, but may also have direct bearing on the constraints of physical systems imposed by the nature of the underlying physics of space and time.
In many algebras, including the real, the complex and the quaternion algebras, zero is the only element which has no inverse. Here, there are many more combinations for which an inverse does not exist. These are referred to as null-hyperplanes, since they correspond to objects of zero length, a so-called null-vector (such as a Riemann–Silberstein vector for the electromagnetic field), as also proposed by Kramers [19] and Weyl [10]. We first discuss some specific familiar cases and then go on to present a general form for the inverse.
First, consider the 4-vector case:
An inverse vector maps to a vector in the same direction for a timelike interval and a vector in the opposite direction for a spacelike interval, such as the unit spatial elements themselves. Note, for the case of the space-time coordinates and , the divisor corresponds to the invariant interval squared and that all inverses are scaled precisely relativistically according to this interval, as they should be. The scaling is unitary for any multivectors with a single component, such as the unit vector elements themselves. In particular in the vector differential operator of Equation (12) there is unitary scaling since the implied divisions are taken with respect to each unit element separately. In this special case, division is not only always defined, but the resulting operator is unitary in each and every frame. There appears to be a connection between the proper nature of division, the scalar invariants engendered by this process and allowed dynamical process in nature, well-described by the unitary vector differential operators of the Dirac, Maxwell and the extended Maxwell equations above.
On the lightcone, the interval goes to zero, and there is no inverse if . That is the plane where division is undefined corresponds exactly to the physical limitations imposed by the speed of light: all intervals at lightspeed are zero. There are, of course, many interesting invariants with the vector form. For example, the corresponding invariant in the case of the 4-vector potential is a charge invariant [22].
Consider further the combination of a scalar and a Lorentz boost:
This is the form for the energy and momentum density in the field, in which case the divisor corresponds to an invariant mass . This has no inverse if and corresponds to the lightcone as well. The divisor is a true scalar in the algebra and, as such, is invariant under a Lorentz transformation, a property shared with the pseudoscalar, which will appear in some of the more general cases which follow. Note the distinctions between the proper multi-vector form and the component form, for example and . Note that the inverse vector is another vector in the same direction, whereas in the case of scalar plus boost, the inverse acquires a minus sign in the spatial component.
It is possible to extend the vector null-hyperplane to include the scalar and the pseudoscalar as well:
This has no inverse if . In the context of electromagnetism, it contains the gauge term (scalar) as well as the quadrivector (the dual of the gauge). We see that the addition of a gauge field shifts the null-multi-vectors off the lightcone. This has applications in the description of massive, rather than massless systems [16,17].
The combination with all the elements that square to also has a null-hyperplane:
There is no inverse, for example, if . Multivectors with all elements squaring to will prove essential in the derivation of a completely general inverse as will be shown by the end of this section.
Consider the following:
This has no inverse if , and connects all the single element “time like” parts of the algebra. Dynamics over this set would imply an interaction between time and the gauge fields, which, it may be speculated, could lead to extra quantisation conditions on any full set of interacting fields [21].
In view of the previous examples, it is now clear that the following formula helps in finding in many (simple) cases:
Here, we have defined the “diamond” conjugate of a multivector as
where is the scalar part of . This conjugate reverses the sign of all “directed” elements of a multivector, that is all elements except the scalar. Note that
The method of finding the inverse by using Equation (29) is guaranteed only if is a scalar, so that . It can, however, also be used iteratively on , etc. To make clear a possible connection with the physics, here we calculate the inverse in terms of the quantities used for the field quantities in the section on the extended Maxwell equations, , , with and . Note again the relationship between b and b see also Equations (15) and (16). For the complete even subgroup, and using the example of the physical square-root mass S, dual root mass Q and the electromagnetic field F leads to:
The invariant divisor in Equation (34) brings out an important invariant in electromagnetism [12], which will be returned to later.
If is a multivector, corresponds to its Hermitian conjugate , where is the reversed ordering of all multivector components of . The operation reverses the sign of all basis elements of the algebra which square to , so that in the product all “oscillating” terms (those squaring to , and hence able to describe oscillations in multi-vector wavefunctions [16]) are quenched.
Note that contains no more than just the six multivector components that square to , and this appears to be a good starting point for further reduction to a scalar (real number). Using the process and Equations (25) and (26) the general case of the inverse of follows as
where the expression in the denominator is always a true (Lorentz) scalar. The derivation of the general inverse to any multivector in this algebra is the main result of this paper. Here, and we have used Equation (30). Note that, in the general case, the denominator has a fourth power character. In many simpler cases, a second power suffices.
Note also that
and that and have the same null-hyperplanes. Note also that and the product is an invariant scalar. This invariant scalar can be expressed in terms of the components of :
Hence
where the positive scalar is defined as
The second important new result of this paper is that, for the general case, all null-hyperplanes are given by and that is the difference of two positive definite scalars which represents a general invariant in this formulation. The potential utility of this is to generate the proper set of Lagrangians appropriate to further development of the physics.
As an example of the connection between inversion and invariants take , then
and
If we substitute and and and hence , we find:
the first line representing the density and flow of electromagnetic energy and in the second line both terms are Lorentz invariants, where the first term is itself the square of the Lagrangian density of the free electromagnetic field. Hence, we should perhaps try:
In any case, when our Ψs are representing fields, then corresponds to an invariant energy or mass density squared.
6. The Relation between Inversion, Dynamics and Invariance
It is striking that the set of divisors which may go to zero are related to the appropriate invariants, the 4-vector position to the invariant interval and the 4-momentum to the invariant mass. It would seem that, while the dynamics is well described by elementary unitary inversions, the combinations where division—and hence inversion—becomes undefined are those with important invariants and important physical limits.
Earlier, it has been argued that the way in which the inverse vector scales as the lightcone is approached is just the way space and time scale in special relativity, with division being undefined on the lightcone itself. The scaling of inverses reflects, and in a real sense underlies, the scalings familiar from special relativity. In particular, note that the divisors, in the most general case, correspond to important physical invariants or their squares. For example, for the case of field alone corresponding to electromagnetism, these are the base invariants of electromagnetism and .
It has been shown above that the non-definition of division everywhere is no impediment to the development of a powerful vector differential algebra. Indeed, the subtlety and beauty of the interactions between the non-commuting basis elements and the 4-vector derivative encompasses the Maxwell equations and in some respects extends the study of relativistic quantum mechanics. We now try to shed some light on how and why the vector differential Equation (12) should prove so potent in the description of that subset of reality described by the Maxwell equations.
Consider the field product for
The scalar part represents the energy density of the electromagnetic field and the bivector part the Poynting vector, which represents an electromagnetic momentum density. As has been discussed in the previous section, this combination has a null-hyperplane which behaves similarly in many respects to that of the vector. To see this, consider the case of Equation (21) for which has divisor . The divisor here corresponds to the invariant mass density, and is undefined in the case of a zero mass density. Since (rest) massless particles and fields are lightspeed this again corresponds to the lightcone. The scalar plus bivector combination is not a 4-vector, but its divisor scales in the same way as that of a 4-vector under Lorentz transformations. Taking a time derivative of this form yields a true 4-vector if taken with respect to the local particle “clock”. It can also be transformed into a true 4-vector by multiplying by a unit vector in the time direction. It needs to be realised, however, that this is a frame dependent operation.
Using the general formula, it is possible to find the following simple cases which include the spin source and spatial bivector:
and the simple case
This would have no inverse if , which would imply and , so would be zero anyway. This means that there is no null-hyperplane in this case, and hence division is defined for all combinations of such elements except zero itself. This special combination, which forms a sub-group within the algebra, is isomorphic to the quaternions which themselves form a division ring. Physically, this means that processes of a rotational nature are unrestricted, unitary and have no limit. Physically, one may go round and round as much as one wishes, both in the mathematics and in reality, without having to scale or to transform through the scalar.
Furthermore, note the following cases
and
for which division is always defined.
As a further example of the physical utility of these null-hyperplanes within the Clifford–Dirac algebra, it is instructive to consider the “null vectors” of Kramers [19], in particular the Riemann–Silberstein vector. For these, we have , c.f. Equation (32):
This requires and , corresponding to the free electromagnetic wave and it corresponds to the case where there is no inverse for
Again, the null-vector of Equation (55) appears as a divisor. In each of the cases above, it would seem that the physics is constrained by the existence of each of these null-hyperplanes, and conversely, that the investigation of the corresponding invariant divisors may throw further light on the physics.
Another null-hyperplane of potential physical importance is that with respect to the scalar, the tri-vector and the pseudoscalar:
which is precisely analogous to the case of the vector, scalar and the pseudoscalar of Equation (23). The tri-vector quantities here represent a product of a momentum density, with a perpendicular vector. This is analogous to an intrinsic angular momentum density [14,16]. The invariants in the divisor here may, therefore, prove important in the physical description of the quantum mechanical spin.
Given the general result, the Lorentz invariant scalar quantity may be interpreted as being related to some effective square-root invariant (or rest) mass such that:
and where the scalar then takes the role of the square of the total mass or, equivalently, the square of the total energy of the system. In this picture, the rest mass is not static, but arises from any internal force balance and dynamics of . Note that the effective rest mass of light speed objects is zero and that it is real for sub-luminal objects (and would be imaginary for super-luminal objects).
We can get some idea of the meaning of Equation (59) by looking at the simple example so that and where . This implies that which, as expected, corresponds to with , and .
We may also write:
where in a simplified case may be interpreted to be equivalent to the square of some field :
This means that the rest mass of a particle may be related to an effective scalar potential which depends on a field and a (square-root) mass . A potential of quartic form may take the form of a Mexican hat. This is similar in form to that needed for spontaneous symmetry breaking in the Higgs mechanism, for example, such that the ground-state level of the energy, and hence its associated mass, are non-zero. Interestingly, the field does not need to be merely scalar itself, as long as is scalar, but that simply means that and that may only contain any single element or a selection of more elements such as but at maximum only five components, given by or or or .
In the preceding, we have started with a Dirac algebra and have looked for inverses whose product yielded a simple scalar. In a sense, this is the reverse process to that followed by Dirac. He started with a square root scalar operator and was forced to introduce what is now known as a Dirac algebra to linearise it. Introducing the scalar operator , the classical relativistic Hamiltonian and demanding it be linear in the components of the momentum , and we obtain:
Together with the energy , this leads to the relativistic quantum mechanical operator equation
Note that the resulting operator contains only the basis elements that square to . Hence, by demanding this equation to be roughly equivalent to the classical scalar equation, Dirac obtained his non-commutative algebra. Originally, the notation and was used. Squaring the original relativistic equation that contains the classical Hamiltonian appears to be equivalent to the multiplication of the linearized equation Equation (63) with the conjugate operator .
In the context of the previous section, this operator is recognized as the “diamond" conjugate of the linear operator in Equation (63). Denote the multivectors with elements squaring to plus one, , which have the property . These appear to play a central role within the algebra: the same pair of conjugate multivectors and are essential both in forming the Dirac linear operator as well as in properly defining division and finding inverses within the space-time algebra.
In the context of the Dirac equation, the Dirac algebra has proven successful in describing, amongst many other things, half integral spin and the existence of the positron. It has been developed to be consistent with special relativity: invariant for scalars , covariant for vectors and tri-vectors , and with the proper transformations of the fields , and, of course, it is all of these things. Any relativistic algebra must necessarily contain a proper description, at the very least, of connections on the light cone with invariant interval zero. Comparing Equation (63) with Equations (25) and (26), one observes that all the terms squaring to positive unity are represented, except one, which corresponds to the directed volume element . The Dirac equation properly describes the half-integral spin, but says nothing about the charge, though Dirac tried to remedy this in later work [22]. The present authors have also made progress in trying to make this link using variants of Equation (18), where the mass is introduced in a more sophisticated way [15,16,21]. The relationship of to the angular momentum density is the same as that of the charge to the current density. In his paper, on “A new classical theory of electrons”, Dirac concluded [22]: “To make this passage one will presumably have to replace the square root in the Hamiltonian with something involving spin variables. This may be a difficult problem, but one can hope that its solution will lead to the quantization of electric charge and will fix e in terms of h.” The present process seems to provide a non-arbitrary technique for deciding which terms should appear in an extended dynamical theory. In particular, the term in seems a prime candidate for an attempt to make further progress along the path followed by Dirac.
7. On the Perceived Dimensionality of Reality
The Maxwell equations were first derived in a world-view which was wholly 3-dimensional. In the twentieth century, it became clear that the universe is more complicated than that, and 4-dimensional space-time was introduced. Despite this, during the twentieth century, the Maxwell equations have remained of value in science and engineering and the electric field has remained a three-component object. The magnetic field likewise. It remains, however, that the electric (or magnetic) field is not a vector. They do not have the proper number of components for a 4-vector, and never did; neither 6 nor 3 equals 4. The field elements do not transform in the same way as those of a vector. Both are relativistically part of the same six-component electromagnetic field, described by a six-component anti-symmetric tensor in the standard formalism. In different inertial frames, one persons electric field is another’s magnetic, and vice versa, but those transformations are not those of the three spatial components of a 4-vector. It is those components “perpendicular” to the boost that transform for fields, not those “parallel” to it [18]. The electromagnetic field is, as has been derived in the last section, a bi-vector and not a vector. Projecting the electric field as a vector, just because the majority of undergraduate texts say so, is a big mistake which has consequences for proper thinking.
Despite the huge revolutions in the early twentieth century, the perceived universe continued to look remarkably three dimensional. Why? In the context of physical objects whose very integrity involves bonds intermediated through such things as the electric field, the answer becomes clear in the present context: the differential, a special kind of division involving inverse base elements, generates sets of three-component physical objects embedded in a 4-dimensional space extended through products and quotients as in Equation (17). There is a beautiful symmetry between 3-space and elements of extended 4-space. In any given frame, one has a 3-component electric field, a 3-component magnetic field and 3-components of intrinsic spin as well as the initial 3-vector spatial components. The physical universe observed is, then, not merely 3-dimensional. It is also not just 4-dimensional. It is effectively four 3-dimensional systems superimposed with each other and incorporating a further four single degrees of freedom, as illustrated in the definition of a general multivector Equation (10) and the extended Maxwell equations Equation (18). These four 3-component objects behave the same way as each other under rotations [13], justifying the coherence of any slowly-rotated physical object. As discussed above, however, they may behave differently under products, quotients and inversions. Consider the ordered product of the first element in any column with the second element in the same column. The result is always ± the third component of the rotor (those elements isomorphic to the quaternions) viz: . In the parlance of projected “handedness”, in 3-dimensional space, one would say that three of the four pairs yield a right-handed product and the fourth a left-handed product. The same argument for products applies equally in the implementation of ordered quotients–divisions. One might, seeming wise, argue that this is fine; we know that nature is handed. This is a poor form of wisdom though, as 4-dimensional hands do not have a well-defined property of “handedness”. What matters here is the implicit ordering of products and quotients, leading to the proper signs in a non-commuting algebra which has been designed to parallel the nature of space-time as closely as possible. Even then, the choice of order is not without consequence in such an algebra for the signs. Should one take time before space or space before time in space-time bivectors? A short calculation shows that, though this gives a conventional sign change of the components, the product or quotient for such bivectors remains intrinsically left-handed as . If both possibilities work equally well, it is perfectly possible that nature may choose both, and that this may be the underlying cause of such things as the two and only two component nature of the fermion intrinsic spin. A full discussion of how this plays out is beyond the scope of this paper, but the interested reader can explore this on the quantum bicycle society website, quicycle.com, where Innes Anderson-Morrison has implemented an algebraic tool up to the task of exploring the various metrics, combinations and permutations. The base conclusions and elements remain the same as discussed in the previous section, but the signs change here and there without affecting the main conclusions. In a work in progress, on the same website, Arnie Benn has explored how this feeds through to the dimensionality of atoms and molecules. The argument here is that the apparent dimensionality of matter is not so much constrained by the three vector dimensions of space, but more through the three components of the electric field, largely responsible for chemical binding, though the spin plays a vital role at short range. Note also that the dimensionality of the visually observed universe on the larger scale is intermediated by photon exchange. Light is constrained by the six components (two sets of three) of the electromagnetic field. In this view, the structure of the universe is much more complicated than merely 4-dimensional, though it “looks” very three dimensional in terms of the exchanges which paint the world observed.
8. Conjecture on the Relation between Inversions and Interactions
This section moves beyond mathematical results, past physical speculation, firmly into the realm of conjecture. It is proposed that the process of mutual exchange of a scalar energy from one self-contained self-perpetuating, coherent quantum system to another may require a mutual inverse between the emitter and absorber. It is suggested that it is something looking like a mutual inverse element (up to a scalar scaling factor) that allows the condensation of the whole extended hypercomplex state of the emitter, together with the equally hypercomplex state (but effectively inverse) of the absorber to that of a simple scalar overall. It is further speculated that the product of (extended) field and inverse (extended) field constitutes the scalar invariant mass-energy exchange between them. The conjecture is that “quantum collapse" is intermediated through a kind of inversion.
Consider the process of photon emission, transport in space-time, and subsequent absorption. From the point of view of the absorber, an incoming photon wave is collapsed on absorption to a scalar rest-mass energy incorporated into the structure of the absorber. Emission is the reverse process, the inverse process. For the electromagnetic field component of the photon , the absorber must, therefore, provide a field such that the product is a simple scalar. Such a field is an inverse up to an amplitude, where that amplitude squared is related to the energy absorbed. To collapse what may be a (hyper) complex incoming photon wavefunction one needs an inverse both in field and in form. Insofar as the algebra is a good basis for the description of the field of light, then the field inverse is given by Equation (63).
As well as inverting the field at each point, the absorber should invert the extended field configuration as well. Inversion in a unit spherical shell has been studied extensively in the past. The techniques have fallen somewhat out of fashion as a means for solving field patterns around complex objects, as numerical computer based methods have gained ground. The techniques and concepts, however, are well-described in many older textbooks. Here, chapter, section and page references are those of the 1961 book by Moon and Spencer [23]. The inversion of form envisaged is that of inversion in a unit sphere, as described in chapter 12. The diagram on page 337 is beautiful and apposite. It is worth noting that a (spherical) polar distribution inverts to a (bispherical) bipolar distribution and vice versa (see page 346). The appropriate “unit length” for the radius of the inversion sphere is related to the wavelength of the exchange photon. Briefly, the inverse of a sphere outside the unit inversion sphere, is a sphere inside the unit sphere, displaced to the near side, and not touching the inversion centre. The inverse of a plane outside the inversion sphere is a sphere inside the inversion sphere, touching the inversion centre. In either case, if the emitted wave is spherical, or effectively planar at the absorber, and large compared to typical emitters such as atoms and molecules (which is certainly the case for visible light) the inverse at the absorber is a very small sphere close to (or touching if planar) the inversion centre. One may distinguish three relevant spheres: the sphere of inversion already discussed, the sphere associated with the emission, which may be denoted the sphere of creation, and, finally, the sphere associated with the collapse of the photon wave to a scalar, the reciprocal sphere of collapse. The conjecture is consistent with quantum electrodynamics, as it merely proposes a physical process for emission and absorption of photons, not their probability. Interestingly, however, if the interaction process does prove to require a symmetric inverse, this will couple long and short length-scales at emitter and absorber, if one finds a short-scale limit for one, such as the intrinsic electron size-scale [16,21], this will impose a reciprocal long-scale limit on the other, helping to limit divergences.
There is little physical difference between photon emission and absorption over a distance corresponding to a thousand wavelengths, or a million, or a quadrillion. It seems unlikely that inversion is the only process in the exchange. It is considered that there are two kinds of process at work in photon exchange: the creation and subsequent annihilation proposed to be related to physical inversion here, and the intermediate transmission of the energy as light over many repetitions of wavelength governed by differential equations in the usual way. The latter process is well described by equations such as the extended Maxwell–Dirac equation or the generalised wave equation which constrain the evolution of a quantum wave in free space with no external influences. It is worth noting that in the transmission phase, which may literally extend across astronomical distances, one is talking about light. At lightspeed, the relativistic transformations are such that the appropriate interval goes to zero. For an exchange photon at lightspeed, the emitter and absorber are at the same point in space-time. Leaving aside the minor detail that all real photons are not quite on mass-shell, this means that, in this sense, the whole universe is “local” for light. All that happens for larger and larger distances is that the wave-front of the light becomes, effectively, more and more planar. This has little physical effect for the inversion part of the process, because all that happens is that the sphere of collapse moves a little closer to the centre of the sphere of inversion. Maxwell’s equations do not include spin, but the extended equations Equation (18) do. Real exchange photons may carry spin. It is apparent from Equation (57) that the inversion in spin-space takes a similar form. It is worth noting that this conjecture, even if it should prove to have a kernel of truth, requires much future work to deal with such things as the proper integration of such processes over all space and all time and the relationship between the products, quotients and differences of fields and spin. There remains, as always, much work to be done.
9. Conclusions
The results of this paper have centred on the mathematics of inversion, multiplication and division in a particular relativistic algebra. That division within the algebra represents some aspect of an allowed physical process in reality is supported by the fact that the dynamics of the first order 4-differential of field, is exactly the full set of Maxwell equations. The Maxwell equations balance spatial derivatives of nested spatio-temporal and temporo-spatial elements with both temporal and spatial derivatives. Apparently, whatever division or differentiation represents in the reality of fields, space and time, such objects may balance one another in allowed continuous transformations. Extending the Maxwell equation to include all the multivector terms leads to a further four coupled differential equations which mesh in with the extended Maxwell equations. The complete equation is similar to, but perhaps even more beautiful than the Dirac equation, as rest mass in is introduced as a pair of dynamical terms rather than as an inert lump, and the odd terms may be used to represent intrinsic spin and current directly [16]. This means that the relation between the physics and the maths in this new relativistic quantum mechanics is more direct. The fact that the new equation is even more beautiful is no guarantee, of course, that it is more correct.
That many derived invariants may take the value zero for non-zero components, means that the algebra is laced with a network of null-hyperplanes where division is not defined. In categorising these a new multi-vector conjugate has been defined. The main result of the paper has been an explicit formula for the inverse in the general multivector case. Here, the divisor has a fourth-power character. It has been shown that the inverses scale relativistically in a way which parallels that which is observed in nature. Those sets of quantities that admit zero divisors embody some of the important invariant quantities of relativity and electromagnetism. For example, division is not defined on the lightcone, and the scalar divisor corresponds here to the invariant interval.
Further, other combinations parallel those familiar invariants of energy and momentum and the important invariants of the electromagnetic field. One set parallels, with one exception, the set of quantities in the Dirac equation on which the 4-vector derivative, described above, acts. That missing quantity in the set, exposed by this analysis, may prove an element in the essential root-Hamilitonian that Dirac sought to describe the underlying nature of charge in the further development of his famous theory.
In addition to all of this, there is another simple hyperplane where division becomes undefined, involving the scalar (energy) and the angular momentum(spin) which has not yet been investigated widely. This is an area which clearly merits further work.
In any event, there seem to be three kinds of regime for relativistic inversion. The first are areas where division is unitary. Such areas allow the definition of allowed dynamical processes. These include the development of 4-vector differential equations such as the Maxwell equations, as well as the rotations described by that subset of the full algebra isomorphic to quaternions. The second area is that of scaling, where vector and multi-vector quantities transform relativistically as expected The third is the area where division may become undefined, which corresponding to limiting cases where neither the mathematics nor nature goes. The divisors in the inversion process correspond to scalar quantities which are invariant in all Lorentz frames.
On the basis of the structure of the relativistic algebra at hand, it has been speculated that the apparent 3-dimensional structure of observed reality is, in fact, more complicated at root. It would appear that the extended algebra has four, linearly independent 3-component spaces, which may appear superimposed to perception. These four may be denoted electric field space, magnetic field space, spin space and space space. Here, each has been distinguished by its own three-component column vector.
It has been conjectured that inversion may play a role in quantum creation and quantum collapse, such that photon energy exchange involves both unitary processes described by differential equations, and creation and destruction operations at emitter and absorber which parallel the mathematical process of inversion in some respects.
We conclude that the fact the Clifford–Dirac algebra is not a division algebra, does not disqualify it as a candidate algebra of reality. On the contrary, there is a case to be made for the reverse proposition: that the manner and areas where division is undefined, or scaled or unitary in the algebra are precisely those required to properly parallel both the process and structure of physical reality. The evidence appears to require the symmetry that reality encompasses relativistic space and time, inverse space and inverse time and all products and quotients between them.
Author Contributions
Conceptualization, M.B.v.d.M. and J.G.W.; methodology, M.B.v.d.M. and J.G.W.; writing—original draft preparation, M.B.v.d.M. and J.G.W.; writing—review and editing, J.G.W. All authors have agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We acknowledge Phil Butler who introduced us to the algebra. Thanks to Mischa Megens, Sjoerd Stallinga and Nina Sobieraj for a careful reading of the manuscript and valuable comments. Thanks to Stephen Leary, Mayank Drolia and Graeme W. Williamson for valuable discussions. Thanks to Innes Anderson-Morrison for many conversations and the development of algebraic tools. Special thanks to Inge Mulder for her invaluable support. John acknowledges three wonderful decades of mutual exploration of the nature of the universe with Martin. R.I.P. best friend.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Clifford, W.K. Applications of Grassmann’s extensive algebra. Am. J. Math. 1878, 1, 350–358. [Google Scholar] [CrossRef]
- Hestenes, D. Space-Time Algebra; Gordon and Breach: New York, NY, USA, 1966. [Google Scholar]
- Riesz, M. Clifford Numbers and Spinors; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Gull, S.; Lasenby, A.; Doran, C. Imaginary Numbers Are Not Real—The Geometric Algebra of Spacetime. Found. Phys. 1993, 23, 1175. [Google Scholar] [CrossRef]
- Rodrigues, W.A., Jr.; de Souza, Q.A.G.; Vaz, J., Jr.; Lounesto, P. Dirac-Hestenes Spinor Fields on Riemann-Cartan Manifolds. Int. J. Theor. Phys. 1996, 35, 1849–1900. [Google Scholar] [CrossRef] [Green Version]
- Lounesto, P. Clifford Algebras and Spinors; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Rowlands, P.; Cullerne, J.P. The Dirac Algebra and its Physical Interpretation. arXiv 2000, arXiv:quant-ph/0010094. [Google Scholar]
- De Sabbata, V.; Datta, B.K. Geometric Algebra and Applications to Physics; Taylor & Francis: New York, NY, USA, 2007. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics, 4th ed.; Oxford University Press: London, UK, 1958. [Google Scholar]
- Weyl, H. Space-Time-Matter; Dover Publications: New York, NY, USA, 1922. [Google Scholar]
- Penrose, R. The Road to Reality; Jonathan Cape: London, UK, 2004. [Google Scholar]
- Armour, R.S. Spin–1/2 Maxwell Fields. Found. Phys. 2004, 34, 815. [Google Scholar] [CrossRef] [Green Version]
- Leary, S.J. Investigation of Electromagnetism in a Real Dirac Algebra. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2007. [Google Scholar]
- Williamson, J.G.; Leary, S.J. Absolute relativity and the quantisation of light. In Proceedings of the SPIE Optics + Photonics, San Diego, CA, USA, 9–13 August 2015. [Google Scholar]
- Williamson, J.G. The nature of the photon and the electron. In Proceedings of the SPIE Optics + Photonics, San Diego, CA, USA, 9–13 August 2015. [Google Scholar]
- Williamson, J.G. A new linear theory of light and matter. J. Phys. Conf. Ser. 2019, 1251, 012050. [Google Scholar] [CrossRef]
- Williamson, J.G. A new theory of light and matter. In Proceedings of the Frontiers of Fundamental Physics 14 (FFP14), Marseille, France, 15–18 July 2014. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Kramers, H.A. Quantum Mechanics; North-Holland: Amsterdam, The Netherlands, 1957. [Google Scholar]
- Sakurai, J.J. Advanced Quantum Mechanics; Addison-Wesley: Reading, MA, USA, 1967. [Google Scholar]
- Williamson, J.G.; van der Mark, M.B. Is the electron a photon with toroidal topology? Ann. Fond. Louis Broglie 1997, 22, 133. [Google Scholar]
- Dirac, P.A.M. A new classical theory of electrons. Proc. R. Soc. A 1951, 209, 291. [Google Scholar]
- Moon, P.; Spencer, D.E. Field Theory for Engineers; van Nostrand: Princeton, NJ, USA, 1961. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).