Abstract
This paper aims at explaining that a key to understanding quantum mechanics (QM) is a perfect geometrical understanding of the spinor algebra that is used in its formulation. Spinors occur naturally in the representation theory of certain symmetry groups. The spinors that are relevant for QM are those of the homogeneous Lorentz group SO(3,1) in Minkowski space-time and its subgroup SO(3) of the rotations of three-dimensional Euclidean space . In the three-dimensional rotation group, the spinors occur within its representation SU(2). We will provide the reader with a perfect intuitive insight about what is going on behind the scenes of the spinor algebra. We will then use the understanding that is acquired to derive the free-space Dirac equation from scratch, proving that it is a description of a statistical ensemble of spinning electrons in uniform motion, completely in the spirit of Ballentine’s statistical interpretation of QM. This is a mathematically rigorous proof. Developing this further, we allow for the presence of an electromagnetic field. We can consider the result as a reconstruction of QM based on the geometrical understanding of the spinor algebra. By discussing a number of problems in the interpretation of the conventional approach, we illustrate how this new approach leads to a better understanding of QM.
1. Introduction
1.1. Three Famous Quotes
Richard Feynman [1] (recipient of the Nobel prize of physics in 1965), is notorious for his statement:
“I think that I can safely say that nobody understands quantum mechanics”.
On the other hand Michael Atiyah (winner of the Fields medal in 1966) is not less notorious for having stated:
“No one fully understands spinors. Their algebra is formally understood but their general significance is mysterious. In some sense they describe the “square root” of geometry and, just as understanding the square root of −1 took centuries, the same might be true of spinors” [2].
“ ...the geometrical significance of spinors is still very mysterious. Unlike differential forms, which are related to areas and volumes, spinors have no such simple explanation. They appear out of some slick algebra, but the geometrical meaning is obscure ...” [3].
There is an obvious analogy here. Both scientists express their dismay with something they consider not to be properly understood. At least a part of Feynman’s problems might be directly due to the fact that Atiyah’s problems are integrally copied into QM as a consequence of the use the latter makes of spinors. Therefore, understanding spinors is a prerequisite for understanding QM. After reading the quotes, it seems obvious that solving the problems mentioned could really be a tall order. However, there is a tiny hole through which we can make our way towards a new vantage point, offering a different angle of approach that allows for solving the problem of the meaning of spinors in SU(2). Pointing this out and developing the ideas further is the purpose of the present paper. Spinors are part of the group representation theory of the homogeneous Lorentz group in Minkowski space-time and of the rotation groups in the Euclidean vector spaces . The whole of QM is written in the language of such spinors, i.e., a language of symmetry.
1.2. Nobody Understands Spinors
Many people have difficulties in apprehending the concept of spinors. In search for enlightenment, the reader will discover that it is very hard to find a clear definition of what a spinor is in the literature. Cartan, e.g., states in his monograph [4]: “A spinor is a kind of isotropic vector”. Using a terminology “a kind of” can hardly be considered to be a valid part of a clear definition. Additionally, a literature search reveals that this is an ever recurring theme. In all of the various presentations I was able to consult, one just develops the algebra and states at the end of it that certain quantities that are introduced in the process are spinors. This is completely at variance with the usual practice, where the definition of a concept precedes the theorem about that concept. This way of introducing spinors leaves us without any clue as to what is going on behind the scenes, e.g., in the form of a conceptual mental image of what a spinor is supposed to be. What we are hitting here are actually manifestations of the state of affairs described by Michael Atiyah in the two quotes that are reproduced in Section 1.1.
What is going on here? In algebraic geometry, geometry and algebra go hand-in-hand. We have a geometry, an algebra and a dictionary in the form of a one-to-one correspondence that translates the algebra into the geometry and vice versa. As may transpire from what Atiyah says, the problem with the spinor concept is, thus, that, in the approaches that are presented in textbooks, the algebra and the geometry have not been developed in parallel. It is all “algebra first”. We have only developed the algebra and neglected the geometry and the dictionary. The approach has even been so asymmetrical that we are no longer able to guess the geometry from the algebra.
Here, it is perhaps worth formulating a provocative question. Spinors occur in the representation SU(2) of the three-dimensional rotation group in . As it uses spinors, which seem particularly difficult to understand, SU(2) appears to be a mystery representation of the three-dimensional rotation group. Now, here is the question: how on Earth can it be that there is something mysterious about the three-dimensional rotation group? Is it not mere Euclidean geometry? This seems to suggest that there might be something simple that we have overlooked and that has escaped our attention.
Indeed, we will see that this is true. In the first part of this article we will restore the balance between the algebra and the geometry by providing the reader also with the geometry and the dictionary. This way, he will be able to clearly understand the concept of spinors in SU(2). The reader will see that the strategy followed to solve the riddle what the square root of a vector might mean is somewhat analogous to the one that solves the puzzle of what the square root of means, as will be discussed in detail in Section 2.6. We will define the spinor concept in its own right and show afterwards that one can define an isomorphism that allows for interpreting a spinor as “squaring to a vector”.
Thus, we will try to build the theory of spinors starting from geometry. This way the underlying ideas will become clear in the form of “visual” geometrical clues. This will suffice for what the reader will need to know about spinors in the rotation and the Lorentz groups for applications in QM. When the reader will have understood the ideas that are underlying the geometrical approach to spinors, he should, in principle, be able to design or complete the proofs of this approach himself by applying these ideas. With our apologies to the mathematicians amongst the readership, we will, therefore, not strive for a formal perfection of our presentation. Our presentation may, in this respect, be considered as clumsy or deficient from the viewpoint of mathematical rigour, but, as explained above, mathematically rigorous presentations have their own inconvenience, viz. that they may render it very difficult to perceive the underlying ideas. Our aim is not to give a perfect formal account of the mathematical theory (see, e.g., [5,6]). Such accounts were already written more than hundred years ago (fine introductions for physicists are [7] and Chapter 41 of [8]. Some more general works about group theory are [9,10,11,12,13,14]).
The aim of the paper is to provide new geometrical insight in the theory, something even mathematicians might value, and confer to the reader all of the insight needed. Because the ultimate goal is to obtain a better understanding of QM, I just cannot afford getting the reader lost by an austere formal presentation.
We want to render the ideas so clear and utterly obvious that the reader will become fluent enough to derive all further developments himself without any substantial difficulty. The self-learning that will intervene in carrying out this exercise will certainly help him to become much better acquainted with the subject matter than reading and mechanically checking the algebra of an exhaustive and formally perfect account of it in a book.
Remark 1.
We can take advantage of the second quote of Aityah to point out that it will be shown that there are two completely distinct algebras at stake in the Clifford algebra on which spinor algebra is based: one for the group elements and one for vectors and multi-vectors. A same algebraic expression in the two algebras can thereby represent two completely distinct geometrical objects, e.g., a reflection with respect to a plane and a unit vector. These two algebras should therefore not be confused. The algebra for vectors and multi-vectors comprises what is called the exterior algebra. The differential forms mentioned by Atiyah are a language to deal with this exterior algebra. Clifford algebra is another such language. The differential forms are anti-symmetric multi-vectors. The spinors belong to the other algebra and represent group elements.
Remark 2.
It has become fashionable to express QM in the language of geometrical algebra, based on the work of Hestenes [15]. However, Hestenes adopts the Clifford algebra as God-given. It conveniently descends from heaven and some of its results seem to follow by magic from thin air, just by adopting some stunning rules, e.g., that we can sum objects of different dimensions. What we need and will develop is an approach that digs deeper into the mathematical foundations and also under-builds the Clifford algebra by constructing it from scratch, such that it can be seen where it comes from. Despite the lesser elegance this may entail for the presentation, this additional insight is absolutely necessary to fully understand QM. The complex number ı is not a generator for rotations as Hestenes claims. He also eludes answering the question of what it means to sum objects of different dimensions, despite the fact that this is a totally legitimate question (see Section 2.8).
The development of the spinor theory that will be given in this article is an improvement of our presentation of spinors given in Chapter 3 of reference [16]. There is, of course, some overlap with reference [16] but not everything is systematically reproduced here. There is a substantial overlap with the HAL archive deposit [17] which also gives the full details about the generalisation of the group theory of spinors to SO(n), which we are not reproducing here based on considerations regarding length and context.
1.3. Nobody Understands Quantum Mechanics
Feynman’s statement reflects an unprecedented, very unpleasant situation in physics. We find it enlightening to formulate the problem of the meaning of QM exactly in the same terms as the problem of the meaning of spinors. As a matter of fact, QM provides us with a complete set of algebraic rules to calculate and predict the outcome of the experiments with staggering precision. However, the reverse side of the medal is that nobody knows what this algebra means, i.e we do not know what the corresponding geometry and the dictionary are. This situation of a complete divorce between algebra and geometry has been summarized in a poignant way by Mermin by introducing the catchphrase that what one ought to do is to just “shut up and calculate” [18]. This is a source of frustration (for physicists) and distress (for students). Are we really condemned to spend a lifetime in physics calculating as a headless chicken?
Remark 3.
The example often cited to illustrate the degree of precision quantum theory can reach is the comparison (see e.g., [19], p. 162, [20,21]) between the experimentally measured value 0.001 159 652 180 73(2) and the theoretically calculated value 0.001 159 652 181 643(764) for , where g is the anomalous g-factor of the electron.
In view of this nagging lack of understanding, some people have recently proposed reconstructing QM from scratch [22]. The present paper proposes such a reconstruction in a way that is perhaps totally different from what a physicist might expect, because it starts the journey by digging into the mathematics of spinors, and then derives the Dirac equation from scratch with the rigour of a mathematical proof. This can then serve as a clear and mystery-free starting point for trying to make sense of the meaning of QM.
A first justification for this claim is the following argument. Establishing the geometrical meaning of spinors in mathematics comes logically prior to any possible application of spinors in QM. At the time that we start doing the physics, the geometrical meaning is already established as a mathematical fact beyond any further discussion. Mathematics can only be right or wrong and everybody can check whether the correspondence between the geometry and algebra laid down in the dictionary proposed is correct or otherwise. Therefore, using the geometrical meaning of spinors to interpret the formalism of QM, which is written in the language of spinors, is immune to any questioning because it is pure mathematics and situated outside the scope of a debate in physics. Furthermore, the geometrical meaning that we will propose does not alter or affect the algebra. It is just added as perfectly fitting new insight, such that the algebra used in our new approach to QM remains the same as in the traditional approach to QM. Therefore, the new approach will automatically reproduce the agreement of the theory with the experimental data that were obtained in the traditional approach and it will, therefore, be an unassailable reconstruction of QM.
A second justification for the claim is the analysis that we were able to make of a number of quantum paradoxes considered to elude any intuitive explanation, as we will discuss in Section 4.5. The most convincing case is, in my opinion, the solution of the paradox of the Stern–Gerlach experiment [23]. Its analysis does not only validate the reconstruction by showing that it permits really to come to grasps with the counter-intuitive results of this experiment. The more rigorous and general new approach also lays bare a number of limitations and intellectual cracks in the standard approach. Within the new framework, all of these disturbing little wrinkles can be spotted and ironed out.
We hope that, together with [23], this paper can provide a decent introduction to this new approach to QM based on the understanding of spinors. The two papers could constitute a solid starting basis for further study of my other results and of the foundations of QM in general.
1.4. Remarks about Style and Notation
The style of the present paper may look very informal, but there is a strong commitment behind this choice of presentation. In fact, due to a concern of absolute rigour, the presentations by mathematicians are, in general, so formal that it is for laymen completely impossible to make sense of them. The chilling effect of this formal abstraction has been described by Dieudonné [24]. Such austere presentations might be all right for mathematicians, but other people than mathematicians may need to use their theories. We hope that a pleasant, less highbrow, presentation can be a good trade-off between rigour and intuition that will be accessible to as broad a community as possible. The impenetrability of the original publications may tempt people who need to use the mathematics into trying to develop parallel ad hoc interpretations and, it is at this point, that over-interpretations and errors can creep in with dire consequences. This has happened many times in standard QM and we will have to point out a few of such mishaps in the present paper.
Let us now spell out a number of notations and conventions that we will use. We will note, by F(), the set of all mappings from the set A to the set B. We will note, by L(), the set of all linear mappings from the vector space V to the vector space W. Thus, they correspond to matrices if and . One often notes L() as M in the literature, while one notes L() as M. The notation SU(2) refers to the special unitary group of dimension 2. It is the group of complex matrices , which satisfy the conditions (special) and (unitary). We will see that it is a representation of the rotation group in .
The n-dimensional rotation group in , the matrix group SO(n) that represents it in and the corresponding matrix group we construct in this paper and [17] are strictly spoken three different mathematical objects that are linked by group isomorphisms. However, these isomorphisms justify the abus de language to treat these mathematical objects as identical. For convenience, we will note the n-dimensional rotation group in by its most intuitive representation SO(n). This way we will speak about the spinors of SO(n), although, in reality, they are not concepts that occur in the matrix representation SO(n), but in the representation that acts on a subset , constructed in this paper and [17]. Here, , where is the integer part. We will use this notation throughout the paper. The quantity naturally enters into the discussions, as will become clear when we go along with developing the presentation. The notation SL(2,) stands for the special linear group of complex matrices with . We will encounter it as a representation of the homogeneous Lorentz group in Section 3.
As will be explained, the rotation groups SO(n) can be obtained as a subgroup of a larger group that is generated by reflections. We will call the group elements that are obtained by an even number of reflections rotations, and call the group elements obtained from an odd number of reflections reversals. Reflections are special reversals. General reversals are products of a reflection and a rotation.
2. Spinors in the Rotation Groups SO(n)
2.1. Methodology
To develop the theory of spinors for the rotation groups SO(n), we will start from a simple specific case and then see how we can generalize it. We will this way discover and take the ideas and the difficulties one by one, while, in a general abstract approach, many of the underlying ideas may become hidden. The representation SU(2) for the rotations in is the simplest case in point. We understand the formalism for SO(3) very well. We rotate vectors, written as column matrices by multiplying them to the left by rotation matrices. It is natural to expect that the same philosophy will apply in SU(2) and to attempt to make sense of SU(2) by analogy with what happens in SO(3). However, as we will see, such heuristics are a deadlock. It is the blind spot of our unawareness about this deadlock that impedes us figuring out what spinors are about. The spinors, which are the matrices on which the SU(2) rotation matrices are operating do not correspond to images of vectors of or .
2.2. Preliminary Caveat: Spinors Do Not Build a Vector Space
2.2.1. Summing Spinors Is a Priori Not Defined
As we will see, spinors in SU(2) do not build a vector space but a curved manifold. This is almost never clearly spelled out. A consequence of this is that physicists believe that the linearity of the Dirac equation (and the Schrödinger equation) implies the superposition principle in QM, which is wrong because the spinors are not building a vector space. In this respect, Cartan stated that physicists are using spinors like vectors. This confusion plays a major rôle in one of the meanest paradoxes of QM, viz. the double-slit experiment [25].
It is important to point out that, within the context of pure group theory, it is even a transgression to make linear combinations of rotation matrices in SO(3). A linear combination of rotation matrices will, in general, no longer be a rotation matrix. Within L or L, we can nevertheless try to find a meaning for such linear combinations, because the matrices are operating on elements of a vector space or , yielding again elements of the same vector space or . The matrix group SO(3) is embedded within the matrix group L. The linear combinations of the matrices in L can then be interpreted by falling back on the meaning of linear combinations of vectors in the image space. However, in SU(2), this will not be possible, as the spinors are not building a vector space (see Remark 4 in Section 2.3 below).
The caveat that we are introducing here is actually much more general. In group representation theory, one introduces purely formal expressions , which build the so-called group ring [26]. This happens, e.g., when we construct so-called all-commuting operators, which are also called Casimir operators [27]. Here, are the representation matrices of the group elements of the group with operation ∘ and are elements of a number field , which can, e.g., be or . This is purely formal, as, in the definition of a representation , we define the operation , but we do not define the operation as corresponding to , for the very simple reason that is in general not defined. Only the operation ∘ has been defined. Thus, a good text book should insist on the fact that introducing is purely formal (see e.g., [27], p. 7) in the sense that it is pure algebra without geometrical counterpart. To illustrate this, we could ask the question what the meaning of the sum of two permutations p and q:
in the permutation group S is supposed to be. To illustrate this further, imagine the group of moves of a Rubik’s cube. It is obvious in this example that is defined, while is not. Giving geometrical meaning to requires introducing new definitions. This will be done in Section 2.5. As we will see, it can be done by introducing sets. E.g., we can define as the set . This way, we can give a meaning to expressions of the type , with . Giving meaning to , with will require further efforts. We will dwell further on this issue of making linear combinations of spinors in Section 2.5.
2.2.2. Ideals
A concept that is very instrumental in reminding us of the no-go zone of linear combinations of spinors is the concept of an ideal. The spinors of SO(n) build a set , such that, for all rotation matrices (which work on them by left multiplication), also belongs to the set: . One summarizes this by stating that is a left ideal. Here, G can stand for SU(2) or SO(n). The crucial point is that this does not imply that the set of spinors would be a vector space, such that: . For the group SO(3) we can easily point out two trivial ideals, which are topologically disconnected, viz. the proper rotations and the reversals (which include the reflections), because it is impossible to change a left-handed frame into a right-handed frame by a proper rotation.
2.3. Construction of SU(2): The Geometrical Meaning of Spinors
The idea behind the meaning of a spinor of SU(2) is that we will no longer rotate vectors, but that we will “rotate” rotations. To explain what we mean by this, we start from the following diagram for a group G:
This diagram tries to illustrate a table for group multiplication. Admittedly, we will not be able to write down such a table for an infinite group, but we will only use it to render more vivid the ideas. Such a table tells us everything about the group we need to know: one can check on such a table that the group axioms are satisfied, and one can do all the necessary calculations. For the rotation group, we do not need to know how the rotations work on vectors. We might need to know how they work on vectors to construct the table, but once this task has been completed, we can forget about the vectors. The infinite table in Equation (2) defines the whole group structure. When we look at one line of the table—the one flagged by the arrow—we see that we can conceive a group element in a hand-waving way as a “function” that works on the other group elements according to: . Thus, we can identify with a function. More rigorously, we can say that we represent the group element by a group automorphism F. A rotation operates in this representation not on a vector, but on other rotations. We “turn rotations” instead of vectors. This is a construction that always works: The automorphisms of a group G are themselves a group that is isomorphic to G, such that they can be used to represent G.
It can be easily seen that this idea regarding the meaning of a spinor is true. As we will show below in Equation (8), the general form of a rotation matrix in SU(2) is:
A spinor can then be seen to be just a stenographic notation for a SU(2) rotation matrix by taking its first column :
This is based on the fact that the first column of contains already the whole information about and that . Instead of , we can write then without any loss of information. Additionally, we can alternatively use the second column as a shorthand and as a (so-called) conjugated spinor. (In [23] it is explained that corresponds to a reversal. But in this paper we will hardly pay attention to the conjugated spinors. We will, almost all the time, focus our attention on the first column as the representation of a rotation). We have this way discovered the well-defined geometrical meaning of a spinor. As already stated, it is just a group element. This is all that spinors in SU(2) are about. Spinors code group elements. Within SU(2), rotation matrices operate on spinor matrices. These spinor matrices represent themselves the rotations that are “rotated”. Explaining that a spinor in SU(2) is a rotation is in our opinion far more illuminating than describing it as the square root of an isotropic vector according to the textbook doctrine. It is this insight that breaks the deadlock of our incomprehension. We will explain the textbook relationship between spinors and square roots of isotropic vectors in Section 2.7.
Stating that a spinor in SU(2) is a rotation is actually an abus de langage. A spinor is, just like a SO(3) rotation matrix, an unambiguous representation of a rotation within the group theory. But due to the isomorphism we can merge the concepts and call the matrix or the spinor a rotation, in complete analogy with what we proposed in Section 1.4. For didactical reasons, we can consider a spinor as conceptually equivalent to a system of “generalized coordinates” for a rotation.
We should not be surprised by the removal of the vectors from the formalism in favour of the group elements themselves, as described above. Group theory is all about this kind of abstraction. We try to obtain general results from just a few abstract axioms for the group elements, without bothering about their intuitive meaning in a more specific context of a practical realization. Additionally, as far as representations are concerned, we do not have to get back to a specific context. We always have a representation at hand in the form of group automorphisms. This is a well-known fact, but in its general abstract formulation this fact looks indeed very abstract. Here, we can see what this abstract representation in terms of automorphisms intuitively means in the context of the specific example of the rotation group. The idea is then no longer abstract: We can identify the matrices of SU(2) with the group automorphisms , and the rotation matrices with the group elements , such that is algebraically represented by: .
Remark 4.
From this, it must be already obvious that spinors in SU(2) do not build a vector space as we stressed in Section 2.2. The three-dimensional rotation group is not a vector space, but a curved manifold (because the group is non-abelian). We cannot try to find a meaning for a linear combination of SU(2) matrices , in analogy to what we can do with matrices in SO(3), where we can fall back on the fact that matrices of the image space correspond to elements of a vector space or . The reason for this is that the spinors do not build a vector space, such that we cannot define by falling back on some definition for in the image space. Additionally, the very reason why we cannot define , is that we cannot define . In trying to define linear combinations of SU(2) matrices or spinors, we thus hit a vicious circle from which we cannot escape. Furthermore, the relation between spinors and vectors of is not linear as may have already transpired from Atiyah’s statement cited above and as we will explain below (see Section 2.7). This frustrates all attempts to find a meaning for a linear combination of spinors in SU(2) based on the meaning of the linear combination with the same coefficients in SO(3). Therefore, trying to make sense of linear combinations of spinors is an impasse.
Remark 5.
We can extrapolate [17] the idea that the representation theory “rotates rotations rather than vectors” to SO(n), such that we will then obtain a good geometrical intuition for the group theory. If we could also extrapolate to SO(n) the idea that spinors are group elements, we would then obtain a very good intuition for spinors that is generally valid. We could then, e.g., also understand why spinors constitute an ideal . The ideal would then just be the group and the group is closed with respect to the composition of rotations.
Remark 6.
Unfortunately, things are not that simple and we will not be able to realize this dream. The idea that spinors are just rotations gives us a very nice intuition for them in SU(2). However, the interpretation in SU(2) of a single column matrix as a shorthand for the whole information needed to define a group element unambiguously is not correct in general. A first example of a case where the column matrices cannot be identified with group elements is the representation SL(2,) of the homogeneous Lorentz group. In fact, defining an element of the homogeneous Lorentz group requires specifying six independent real parameters. That information cannot possibly be present in a single column of the representation matrix. A second example is the representation that is given by the Clifford algebra of SO(n). Characterizing an element of the rotation group SO(n) of requires specifying independent real parameters (see the discussion about the Vielbein in Section 2.7.1). The complete information regarding these independent real parameters cannot always be crammed into the complex column matrices used in the representations, because there is a small set of values of n for which . The information about a group element contained in a column matrix is in these cases thus forcedly partial. These examples show that the identification between group elements and the column matrices that we call spinors anticipated here is not true in general. Thus, the general meaning of a spinor cannot be that it is a group element. What the general meaning could be becomes then less clear such that one has to consider like Cartan isotropic vectors, representing oriented planes, as discussed in [17].
However, due to the fact that we are forced to introduce a superposition of two states in order to derive the Dirac equation (see Section 4.1), the column matrices used in the Dirac theory will again contain all of the information regarding the group elements. For the applications in QM, we can therefore maintain the idea that a spinor is a group element! Furthermore, what we stated in the previous remark does not imply that we do not understand the algebra of the representation. In fact, the representation matrices of the group SO(n) do represent the group elements. For the application in QM, this means that we will really completely understand the formalism. In the approach to the general case SO(n) the main idea will, thus, be to consider the formalism just as a formalism of rotation matrices and the column matrices as auxiliary sub-quantities which encase only a subset of the complete information about group elements.
Remark 7.
We must point out that we do not know with certainty to which extend Atiyah wanted to be general when he talked about “the square root of geometry”. We think that what Atiyah had in mind was based on Equations (29) and (57), rather than making a general statement for SO(n). We can see from Equations (29) and (57) that the terminology “square root” used by Atiyah is only a loose metaphor, and in the generalization of the approach to groups of rotations in , with , the metaphor will become even more loose [17]. For SO(n), the ideas can be based on the developments in Section 2.6, where we point out a quadratic relationship between vectors and spinors, which is generally valid.
However, for the moment, we want to explore the idea of a single-column spinor that contains the complete information about a rotation in SU(2), where the intuitively attractive idea that a column spinor represents a group element is viable. It remains to explain under which form the information regarding the rotation is wrapped up inside this column matrix. This is done in several steps.
2.4. Generating the Group From Reflections
The first step is deciding that we will generate the whole group of rotations and reversals from reflections, based on the idea that a rotation of SO(3) is the product of two reflections, as explained in Figure 1. Therefore, we need to cast a reflection into the form of a -matrix. The coordinates of the unit vector , which is the normal to the reflection plane that defines the reflection A, should be present as parameters within the reflection matrix but we do not know how. Therefore, we heuristically decompose the matrix that codes the reflection A defined by linearly as , where are unknown matrices, as summarized in the following diagram:
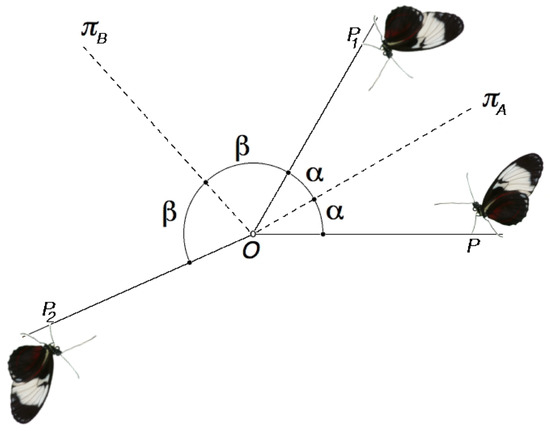
Figure 1.
A rotation R in as the product of two reflections A and B defined by their reflection planes and . The planes and in intersect along a straight line ℓ that is defined by . The plane of the figure is taken perpendicular to the line ℓ and intersects ℓ in the point O. We use the names and of the planes to label their intersections with the plane of the figure. The position vector of the point P to be reflected is at an angle with respect to . We call and . The position vector is at angle with respect to . The angle between and is then . As can be seen from their operations on the Heliconius butterfly, reflections have negative parity, but the product of two reflections conserves the parity. Therefore, the product of the two reflections is a rotation , with axis ℓ and rotation angle . Only the relative angle between and appears in the final result, not its decomposition into and . Hence, the final result will not be changed when we turn the two planes together as a whole around ℓ keeping fixed (After [16]).
If we know the matrix , this will tell us where and with which coefficients pops up in . The same applies mutatis mutandis for and . The matrices , we use to code this way reflection matrices within , can be found by expressing isomorphically through what defines a reflection, viz. that the reflection operator A is idempotent. We find out that this can be done, provided the three matrices simultaneously satisfy the six conditions , i.e., provided we take, e.g., the Pauli matrices for . Here, is the unit matrix.
Remark 8.
Physicists among the readers will recognize that this construction is algebraically completely analogous to the one that introduces the gamma matrices in the Dirac equation. However, geometrically, it is entirely different. Dirac’s approach aims at taking the “square root of the Klein-Gordon equation”. Thus, it searches a way to write vectors, e.g., the four-vector as a linear expression that permits to interpret it as the square root of a quadratic form, e.g., , as e.g., explained by Deheuvels [28]. Therefore, Dirac’s derivation is taking place within the context of the algebra of vectors and multi-vectors. Our approach consists in finding the expression for reflections. Our derivation takes thus place within the algebra of group elements. The two approaches do not define the same geometrical objects and not the same algebras.
Remark 9.
We may note that, to an extent, the fact that our heuristics work is a kind of a fluke, because the fact that the reflection matrix is linear in , , within SU(2) is special and not general. It is typical of the spinor-based representations that we present in this paper. A counter-example is the expression for a reflection matrix in SO(3), which is quadratic in the parameters , , and :
Writing this way permits to verify immediately algebraically that it corresponds to . Writing as in Equation (6) shows that the expression is purely quadratic. This is due to the fact that vectors in SO(3) are rank-2 tensor products of the spinors of SU(2), as we will discuss in this paper. We may also note that we have defined the reflection matrices without defining a “vector space” on which they would be working. They are defined en bloc, and it is this aspect that saddles us up with the problem of the meaning of the column matrices, called spinors, which occur in the formalism. We are used to qualify such column matrices as column vectors, but, as we pointed out, spinors are not vectors. Thus, it is no longer natural to break down the square matrices into columns. The complete information resides in the block of the square matrix. When we break up that block into columns, the information contained in a column may be partial, and perhaps the question what a column then means might be ill-conceived (see [17], pp. 22–23). This complies with the idea that is expressed in Remark 6 in Section 2.3.
We discuss, in Section 2.9 of [17], that the solution is not unique and that there are many other possible choices. However, we follow here the tradition to adopt the choice of the Pauli matrices. The reflection matrix is thus given by:
The symbol serves here to warn that the notation is a purely conventional shorthand for . It does not express a true scalar product involving , but just exploits the mimicry with the expression for a scalar product to introduce the shorthand.
By expressing a rotation as the product of two reflections, one can then derive the well-known Rodrigues formula:
for a rotation by an angle around an axis that is defined by the unit vector . To derive this result, it suffices to consider two reflections A (with matrix ) and B (with matrix ), whose planes contain , and that have an angle between them. Using the algebraic identity then yields the desired result. There is an infinite set of such pairs of planes, and which precise pair one chooses from this set does not matter.
Starting from Equation (8), it is easy to check that each rotation matrix has the form that is given by Equation (3) and, therefore, belongs to SU(2). Conversely, each element of SU(2) is a rotation matrix. We can now also appreciate why SU(2) is a double covering of SO(3). Consider the matrix product:
in the derivation of the Rodrigues equation in Equation (8). Imagine that we keep A fixed and increase the angle between the reflection planes and of A and B from onwards. Of course, is the angle of the rotation . This means that the reflection plane with normal vector that defines B is rotating. In the matrix product that occurs in Equation (9), the numbers in the matrix would remain fixed, while the numbers in the matrix would be continuously changing, like the digits that display hundredths of seconds on a wrist watch. When the starting value of the angle between the reflection planes and is zero, the reflection planes are parallel, , and the starting value of is . When reaches the value , the rotating reflection plane will have come back to its original position parallel to the fixed reflection plane , and the resulting rotation will correspond to a rotation over an angle .
As far as group elements are concerned, we have, thus, made a full turn both of the reflection B and the rotation when will have made a turn of in . This is because we only need to rotate a plane in over to bring it back to its original position. The consequence of this is that we can define any plane (or reflection U) always equivalently by two normal unit vectors and . These full turns of B and within the group must be parameterized with a “group angle” if we want to express the periodicity within the rotation group in terms of trigonometric functions. However, for the normal vector , which we have used to define B and that belongs to , this is different. For , its starting value is . For , its value has become , such that we obtain in Equation (9). There is nothing wrong with that because both the normal vectors and define the same plane . Thus, each group element g is represented by two matrices and . As the group elements B and have recovered their initial values, we have . In general, we have . Only after a rotation over a “group angle” , which corresponds to a rotation of over an angle will we obtain the values and .
Remark 10.
It is often presented as a mystery of QM that one must turn the wave function over before we obtain the starting configuration () again. There is even a beautiful neutron experiment that has been performed to provide physical proof for the truth of this fact to physicists [29]. We can see, from a proper understanding of the group theory, that this is quite trivial and it is a mathematical rather than physical truth. Most textbooks mystify this subject matter by invoking topological arguments. We explain this link with topology in [16], Subsection 3.11.2, and Figure 3.5, where we compare a full turn on the group with a full turn on a Moebius ring. This link is thus conceptually very clear and simple. However, in the illustration of this topological argument by Feynman [30], Dirac [31], or Misner et al. [8], the connection between the topological argument and the physical model is hard to see. It is, e.g., very difficult to follow how disentangling the threads in the work of Misner et al. would make the point.
Remark 11.
Representing a rotation as the product of two reflections is convenient for calculating the product of two rotations. Consider two rotations and . Call π the plane that is defined by and . Call the plane of the reflection that defines as and the plane of the reflection that defines as . It then follows that .
2.5. Fleshing out the Caveat: A Superposition Principle for Spinors?
2.5.1. An SU(2)-Specific Approach
In Section 2.2, we issued the warning that spinors can a priori not be summed. We can now illustrate how the procedure of summing spinors is geometrically obscure. Consider a rotation over an angle around the axis that is defined by the unit vector , and a rotation over an angle around the axis defined by the unit vector . Using Equation (8), we have then:
Summing and as though they were vectors is algebraically perfectly feasible. We obtain:
However, what does the result mean geometrically? The quantity cannot represent a rotation because . It is therefore not a true spinor. It corresponds obviously to , and as explained in Remark 4 in Section 2.3 we cannot interpret the way we can interpret a sum of rotation matrices in SO(3), because the spinors do not build a vector space. To interpret , we would need an interpretation of sums of spinors, and to interpret sums of spinors we would need an interpretation of sums of rotation matrices. Therefore, when we try to transpose the ideas from SO(3) to SU(2), we end up running in circles.
However, suppose now that we try to normalize the result in Equation (11) to 1, as physicists do routinely. The result will then remain a linear combination of spinors, but it is now a special one, whereby the coefficients used in the linear combination preserve the normalization. One must then find a rationale to explain what the geometrical idea behind such a procedure could be. Mind, in this respect, that we have no idea about the geometrical meaning of in the first place. How do we justify defining a procedure on a quantity that is undefined? Thus, the procedure remains geometrically impenetrable, and we have rendered the situation worse. We have now concealed the fact that there are conceptual problems with making linear combinations of spinors, because the final quantity obtained is now (almost always) algebraically identical to a true spinor. Let us prove this. To normalize according to the Hermitian norm, we calculate:
Here:
allows for a geometrical interpretation: is the rotation angle of the product rotation as shown e.g., in Appendix C of the monograph of Jones [12]. We are already running into trouble here, because it is certainly conceivable that . The result is then zero, such that it cannot be normalized to 1. This happens e.g., when we define by: and . This is actually the only way that this can happen, because implies , such that and . This example is the absolute proof for the fact that the sum of two spinors is not a spinor. Let us now continue carrying out the algebra keeping this in mind and check whether there could be other problems. Writing the sum in the form of the Rodrigues equation Equation (8) makes it clear that the vector:
plays a prominent rôle in the algebra. Let us now assume that and calculate the result of normalizing the purely formal algebraic sum to 1. This yields:
Let us now try to identify the right-hand side with a spinor representing a rotation over an angle around an axis that is defined by the unit vector :
Very obviously, the rotation angle must then be given by:
However, we must check whether this is a meaningful expression. The rotation angle will only be defined if . To check this, we square both sides and rewrite 2 as . We obtain then the inequality:
where we have used the definition of . Simplification leads to:
such that the inequality is indeed satisfied. It must be noted now that can be larger than 1 (but not larger than 2). Therefore, it is a priori not obvious that we can identify:
where is a unit vector. However, the calculations that occur in the simplification from Equation (18) to Equation (19) show that , such that we have indeed . Thus, we can calculate the unit vector from:
While the normalized sum of two spinors can this way be interpreted in terms of a well-defined rotation , it is not obvious what this is kind of operation is then supposed to mean geometrically. The meaning of the unit vector is at least algebraically clear as the sum of two wedge products. However, the definition of the rotation angle looks impenetrable.
A superposition principle for spinors, i.e., summing and making linear combinations of them with a wave picture in mind, as physicists routinely do, is thus an all but self-evident procedure. Within the initial set of underlying ideas this procedure is a priori geometrically meaningless, despite its misleading apparent algebraic simplicity. Interpreting a sum of spinors, as presented in this paragraph, is actually a conceptual impasse, because the sum can be zero. The use of the superposition principle in physics therefore requires a supplementary geometrical justification. That this caveat is not futile at all can be appreciated from the fact that it is the very introduction of the superposition principle that transforms the spinor formalism, which is, in essence, purely geometrical and classical, into a much less obvious Hilbert space formalism of QM. One of the mysterious creatures that we introduce this way is Schrödinger’s cat. This need for a justification of the superposition principle is further directly related to the conceptual difficulties encountered under the form of the so-called particle-wave duality in QM. Additionally, in interference, we become directly confronted with the fact that the sum of two spinors can be zero when , as outlined above. This leads to severe conceptual difficulties.
2.5.2. General Group-Theoretical Approach
We may note that the ad hoc attempt to interpret the meaning of an element of the group ring presented in Section 2.5.1 is specific to SU(2). It does not solve the problem of the meaning of an element of the group ring for the permutations in Equation (1) or for moves of the Rubik’s cube. Additionally, even within SU(2) it fails, as it is meaningless. We will refrain from interpreting the group theory in terms of a vector space and proceed as always on the basis of purely group-theoretical considerations. Formal sums of group elements and group rings occur all the time in the group theory (see e.g., [27]). In this context, one encounters e.g., formal identities:
Here are all group elements. In fact, all this expresses is an identity for sets:
From a purely group-theoretical viewpoint, we can thus interpret sums of group elements in terms of sets. The interpretation is naturally provided by the group theory. Here, the coefficients in the linear combinations are all equal to one. We can extend this idea further and allow for integer values. We could, e.g., imagine that we have a collection of 3000 Rubik’s cubes, whereby 2000 of the cubes have the configuration of group element and 1000 the configuration of group element . We could then note the collection as , or in terms of frequencies as . In QM, we will note this collection as . It based on the fact that spinors in SU(2) satisfy the identity , such that, if we want to count objects, e.g., electrons, which all carry just one spinor with them in order to describe their state, then we must do it by counting . We must postpone the in-depth discussion of this to Section 4.5.1 when we will have derived the Dirac equation.
2.6. A Parallel Formalism For Vectors
By construction, the representation SU(2) contains for the moment, (as we explained) deliberately, only group elements. Of course, it would be convenient if we were also able to calculate the action of the group elements on vectors. This is our next step. We can figure out how to do this based on the fact that we have already used a unit vector to define a reflection A and its corresponding reflection matrix . Inversely, the reflection A also defines up to a sign, such that there exists a one-to-one correspondence between reflections A and the two-member sets of unit vectors (and the corresponding two-member sets of reflection matrices ). This one-to-one correspondence between two-member sets of vectors and reflections will actually impose the formalism for vectors upon us. We can consider that a reflection A and its parameter set are conceptually the same thing.
When a reflection travels around the group, the two-member set of vectors will travel together with it. Let us explain what we mean by the informal term “traveling” here. In SO(3), a vector has a representation matrix . It is transformed by a group element g with representation matrix into another vector : we just calculate the representation matrix of as . The vector travels this way under a group action to another vector . The point we want to make is that in SU(2), things are not as simple. Under the action of a group element g with matrix representation , a reflection A will not travel to another reflection .
Let G be the group that is generated by the reflections. The subgroup of pure rotations is the subset that is obtained from an even number of reflections. The subset obtained from an odd number of reflections is not a subgroup. It contains the reflections and the reversals. Reflections are of course geometrical objects of a different type than reversals and pure rotations. This also transpires from the fact that a reflection is defined by a unit vector , where is the unit sphere in . Thus, it is defined by two independent real parameters while rotations and reversals are defined by three independent real parameters. Group elements and are of the same geometrical type if they are related by a similarity transformation: . They have then the same group character.
In general, a new group element obtained by operating with an arbitrary group element on the reflection A will no longer be a reflection that can be associated with a unit vector, like it was the case for A, because, in general, can be of a different geometrical type than A. Group elements that transform a reflection A into an other reflection, B, are the identity element and rotations R that can be written as . For this to be possible, the rotation axis of R must belong to the reflection plane of A. In other words, the reflections do not travel according to the general rule .
In order to transform a reflection A always into another reflection, we must use a similarity transformation: . Hence, if B and A are reflections, defined by the unit vectors and , then there exists a group element , such that and . Hence, if A is a reflection operating on , then the similar reflection B that operates on will be represented by . The reflection plane and normal of this reflection B will have the same angles with respect to as and with respect to . Thus, we can move this way the reflection A in around to group elements B in , and, of course, the parameter set will travel with it from to to a parameter set . The ambiguity between and is also carried along. For the representation matrices of reflections we have thus:
whereby we allow for the ambiguity in the sign of , because Equation (24) is not a transformation law for vectors, but for reflections and their associated two-member sets of vectors.
Of course, the idea would be that and , but the combined presence of and does not permit reproducing the change of sign in the formalism, because it has been designed for group elements, not for vectors. This is very clear for , while in the formalism , which is the correct calculation for . On the other hand, a vector that is perpendicular to is characterized by .
To see this, consider the rotation R that transforms into and into . For the reflections and , we have . The similarity transformation based on will transform into the reflection A with matrix representation and into the reflection B with matrix representation . Applying the similarity transformation to proves then the identity. Therefore, , while the vector belongs to the reflection plane and it should not change sign under the reflection A.
Thus, we see that, in all cases, we get the sign of the reflected vector wrong. Thus, we can lift the ambiguity and treat the vectors correctly by introducing the sign by brute force:
In doing so, we quit the formalism for group elements and enter a new formalism for vectors. The transition is enacted by conceiving and elaborating the idea that we can use the matrix also as the representation of the unit vector , since the matrix contains the components of the vector and the reflection A defines . To get rid of the ambiguity about the signs of the vectors that exist within the definition of the reflection matrices, it suffices to use as a representation for a unit vector , and to introduce the rule that is transformed according to:
This will be further justified below. The transformation under other elements is then obtained by using the decomposition of g into reflections. This way, we have developed a parallel formalism for the matrices , wherein takes now a different meaning, viz. that of a representation of a unit vector and obeys a different kind of transformation algebra, that is no longer linear, but quadratic in the transformation matrices. This idea can be generalized to a vector of arbitrary length v, which is then represented by . In fact, the scalar v is a group invariant, because the rotation group is defined as the group that leaves v invariant. We have then .
This idea that, within SU(2), a vector is represented by a matrix according to the isomorphism:
was introduced by Cartan [4]. It is a definition that makes it possible to do calculations on vectors. In reading Cartan, one could get the impression that we have the leisure to introduce this definition at will. In reality, it is not a matter of mere definition. While introducing the idea as a definition would not lead to errors in the formalism, it would nevertheless be a false presentation of the state of affairs, because it is no longer at our discretion to define things at will. As we can see from the reasoning above, the definition is entirely forced upon us by the one-to-one correspondence between sets of unit vectors , and reflections A.
We cannot stress enough that, even if reflections L and unit vectors are both represented by the same matrix , they are obviously completely different quantities, belonging to completely different spaces L and and completely different algebras.
Using , one can derive, from the rule , that , which can be seen as an alternative definition of the parallel formalism for vectors. As anticipated above, we can use this result to check the correctness of the rule of Equation (26) geometrically. It suffices in this respect to observe that the reflection A, defined by the unit vector , transforms into . Expressed in the matrices this yields: .
We see that the transformation law for vectors is quadratic in in contrast with the transformation law for group elements g, which is linear: . Vectors transform thus quadratically as rank-2 tensor products of spinors, whereas spinors transform linearly. This gives us a full understanding of the relationship between vectors and spinors. It is much easier to understand this relationship in the terms that are used here, vectors are quadratic expressions in terms of spinors, than in the equivalent terms used by Atiyah, spinors are square roots of vectors.
Remark 12.
This solution is analogous to the solution proposed by Gauss, Wessel, and Argand to solve the problem of the meaning of . As described on p. 118 of reference [24], one first defines as , with two operations + and × defined by and . One then shows that is isomorphic to , where . This permits identifying and justifies introducing the notations , and . One can prove then that .
The fact that this solution for the riddle what the meaning of a spinor is has escaped attention is due to the fact that spinors are in general introduced based on the construction proposed in Equation (29) below. This construction emphasizes the fact that a spinor is a kind of square root of a vector at the detriment of the notion developed here and that a vector is a rank-2 expression in terms of spinors. However, these relations between spinors and vectors are a property that only constitute a secondary notion, which is not really instrumental in clarifying the concept of a spinor. The essential and clarifying notion in SU(2) is that a spinor corresponds to a rotation.
The reader will notice that the definition with is analogous to Dirac’s way of introducing the gamma matrices to write the energy-momentum four-vector as and postulating . In other words, it is the metric that defines the whole formalism, because we are considering groups of metric-conserving transformations (as the definition of a geometry in the philosophy of Felix Klein’s Erlangen program).
For more information regarding the calculus on the rotation and reversal matrices, we refer the reader to reference [16]. Let us just mention that as a reflection A works on a vector according to , a rotation will work on it according to . The identity explains, in an alternative way, why the representation that we end up with is SU(2).
In summary, there are two parallel formalisms in SU(2), one for the vectors and one for the group elements. In both formalisms, a matrix can occur, but with different meanings. In a formalism for group elements, fulfils the rôle of the unit vector that defines the reflection A, such that we must have , and then the reflection matrix transforms according to: under a group element g with matrix representation . The new group element that is represented by will then, in general, no longer be a reflection that can be associated with a unit vector like it was the case for . In a formalism of vectors, can be different from 1 and the matrix (that represents now a vector) transforms according to: . Here can be associated again with a vector.
We cannot emphasize enough that the vector formalism is a parallel formalism that is different from the one for reflections, because the reflections that are defined by and are equivalent, while the vectors and are not. Here, we have two concepts that are algebraically identical but not geometrically and this is the source of a lot of confusion. The folklore that one must rotate a wave function by to obtain the same wave function again is part of that confusion. The reflection operator is a thing that is entirely different from the unit vector , even if their expressions are algebraically identical. By rotating a reflection plane over an angle , we obtain the same reflection, while it takes rotating over an angle to obtain the same vector .
Remark 13.
Both in the representation matrices for reflections A and for vectors , the quantities , , are the three Pauli matrices. In the representation () defined by Equation (27), the Pauli matrices are just the images, i.e., the coding of the three basis vectors . As clearly indicated in the diagram of Equation (5), σ is a shorthand for the triple . The use of the symbol serves to draw the attention to the fact that the notation is a purely conventional shorthand for , which codes the vector within the formalism. Thus, it is analogous to writing pedantically as: . The danger of using the convenient shorthand is that it conjures up the image of a scalar product, while there is no scalar product whatsoever.
The fact that represents the vector , and that the Pauli matrices just represent the basis vectors , was clearly stated by Cartan, but physicists nevertheless have hineininterpretiert the vector as a scalar product in the theory of the anomalous g-factor for the electron. Here, μ would be the magnetic dipole of the electron and its potential energy with the magnetic field . In reality, just expresses the magnetic-field pseudo-vector . The quantity can never represent the spin, because it is already defined in Euclidean geometry before we apply this geometry to the physics where we want to consider spin. This reveals that physicists do not only use spinors like vectors: They also use vectors like scalars. We have fully discussed and tidied up this problem in [23], where we have proposed a better interpretation of the Stern–Gerlach experiment.
Remark 14.
A similar confusion arises in the definition of the helicity of the neutrino [19], pp.105–106, Equation (5.30), [32]. It is defined as , and claimed to be “the projection” of the “spin” on the unit vector . This is again a confusion between the shorthand notation for the representation of the vector and a true scalar product. As just mentioned, in reality, just represents the unit vector . The factor has been added only due to the confusion and the belief that would then be the spin operator, while the true spin operator is . There is absolutely no reference to spin whatsoever in the operator . The definition leads to a confusing discussion about the difference between helicity and chirality in textbooks. This example shows that physicists cannot deny that they have considered and as a true scalar products.
2.7. The Quadratic Relation between Vectors and Spinors
2.7.1. Isotropic Vectors
We will illustrate the quadratic relationship between spinors and vectors further in what we can consider as the final step in the construction of the formalism. We can picture a rotation R by a rotated triad of three basis vectors and . This is a 1-1-correspondence. The triads visualize rotations and vice versa. This is a second important idea, which can be carried over to the general case of SO(n): we can code group elements by identifying them with a rotated basis of , a so-called Vielbein. This is a German word meaning “many legs”, and the idea is that each basis vector is a leg. The first unit vector of the Vielbein of corresponds to independent real parameters due to the normalization condition. The second unit vector corresponds to independent real parameters due to the normalization and the orthogonality conditions. The third unit vector corresponds to independent real parameters, etc. This shows that the Vielbein or a rotation in corresponds to independent real parameters, as we claimed previously in Remark 6 in Section 2.3.
In SU(2), we can code the basis triad within an isotropic vector . This is also a 1-1-correspondence. From , we can get and back by taking real and imaginary parts, while . Thus, we can represent a rotation by an isotropic vector, a vector, whose square is 0.
Remark 15.
It is often stated in this respect that an isotropic vector has zero length and that it is orthogonal to itself. This is however based on the wrong notion that the extrapolation to of the Euclidean norm, defined by: , , would still be a correct norm function for . The correct norm to be used for is the Hermitian norm defined by: .
Remark 16.
Presented this way, this idea may look like a stroke of genius. However, in reality, it is just the consequence of embedding within . Thus, we can embed within . Instead of the basis of the mutually orthogonal unit vectors , , , of as a basis for , one can use a coordinate transformation and use the alternative orthogonal basis , and , for (see paragraph 4.6.1 of [17]). This basis can also be normalized while using the Hermitian norm. The subspace spanned by and suffices to define the complete Vielbein of and it is isomorphic to . The space is a subspace of , and, once we have defined it, this way it becomes possible to also treat in terms of . This is the reason why we will end up with a formalism SU(2). Thus, the use of isotropic vectors is just a consequence of introducing , but the idea becomes somewhat concealed by the fact that we work with instead of , such that we do not have to tip us off.
The reference triad is coded by the isotropic vector , with representation matrix:
Now consider the rotation matrix from Equation (3). Under the rotation , the isotropic vector with matrix will be transformed to the isotropic vector with representation matrix . This rotated isotropic vector codes the rotated triad and, thus, also the rotation . The representation matrix is given by:
As for an isotropic vector we have , it follows that . This implies that the columns of the matrix are proportional. Additionally, the lines of are proportional. This is the reason why we can write as a tensor product as done in Equation (29), introducing the column “spinor” and the conjugated row “spinor” . We are putting here the words spinor between quotes, because, for the moment, it is not yet obvious that they correspond to the same concept as the one we introduced above. We will address this issue very soon. The notation just serves to distinguish row spinors from column spinors . Below we will explain the reason for this rather complicated looking notation . The square roots are introduced for normalization purposes. There is some possibility of confusion with the terminology here. From the purely algebraic point of view of matrix algebra, we could call these spinor quantities column “vectors” and row ’vectors”, but from the geometrical point of view, spinors are not vectors, because they code rotations, and rotations do not build a vector space.
Remark 17.
When we will try to generalize the formalism to SO(n), we will no longer be able to factorize the matrix of an isotropic vector, as done here. For a matrix of rank , we can no longer conclude, from , that there exist matrices χ and matrices , such that , because this would imply that all of the columns of are proportional and all rows of are proportional, while it suffices that only two columns and two rows of are proportional.
For the moment, we can see how for the specific case of SU(2), the gimmick permits us to “halve” the formalism. In fact, the isotropic vector that codes the rotation transforms under rotations quadratically according to , with multiplications on both sides. We could obtain the same result by stipulating that we must transform and . Now, a spinor that contains the same information as a rotation matrix transforms linearly according to , with only left multiplications. On the other hand, an isotropic vector contains the same information as a rotation matrix, because it codes the triad.
Let us now show that the “spinor” formalism for the isotropic vector is algebraically identical to the spinor formalism for the rotations, such that is indeed algebraically a spinor. The reference triad is coded by the isotropic vector , leading to:
This reference triad corresponds to the identity matrix. The corresponding spinor , is indeed equal to , such that we have checked that the formalism based on multiplying to the left according to is just identical to the formalism that is based on multiplying according to , such that , while corresponds to the conjugated spinor.
To summarize, it is not possible in SU(2) to build a linear representation that is based on vectors because vectors are of rank two in terms of spinor quantities, but is possible to build a linear representation based on spinors by “halving” the formalism. We could also proceed by only right multiplications on according to , but that would be completely equivalent. The conjugated spinor transforms like , by left multiplication by , and it gives rise to the second column of the matrix in Equation (3). It contains the same information as . Using instead of allows for us to then also limit ourselves to calculations that contain only left multiplications. In other words, in the notation , the symbol † is supposed to flag that it is transformed by right multiplication by , while the dot is used to distinguish quantities from quantities , showing that the quantities have originally entered the formalism under the form of row spinors . Whereas, the formalism was not linear in the parameters of the rotation matrix , halving the formalism to has rendered it linear.
Because a rotation only depends on three independent real parameters, we can normalize these spinors to 1, such that . In fact, the normalization is a consequence of the fact that the matrix in Equation (3) belongs to SU(2). The spinor contains thus exactly three independent parameters that characterize a rotation (e.g., the three Euler angles, or a rotation axis that is defined by a unit vector and a rotation angle ). From these spinors and using the identity , we can calculate backwards to . The result is:
From this, we can recover the basis vectors , :
and, from this, finally :
We can also calculate and from x, y, and z, and this leads to the expressions that are introduced by Cartan:
This shows how the reference triad of basis vectors is expressed within a spinor. Similar expressions can be derived to show e.g., how the three Euler angles are expressed within a spinor. The Rodrigues formula shows how the rotation axis and the rotation angle are expressed within the spinor.
Remark 18.
In many textbooks, spinors are introduced on the basis of this algebra for the isotropic vector, putting the emphasis on halving the formalism. It is this approach that leads to the idea that a spinor is the square root of a vector, based on the fact that the isotropic vector appears as a tensor product of two spinors in Equation (29). This tensor product is not a pure square, because the spinors χ (a rotation) and (a reversal) are not identical, such that calling the spinor the square root of the vector is only a loose informal description. Here, the presence of the square roots in Equation (34) can also inspire the idea that a spinor is the “square root” of a vector. Finally, the Rodrigues equation Equation (8) can also be expressed as . Within this algebraic form, the presence of in the exponentials also leads to the idea of a “square root”. But we can appreciate from our approach that in SU(2) the true meaning of a spinor is not that it is “a kind of isotropic vector” as stated by Cartan, but just a rotation. In generalizing this idea, we can change the definition of a spinor to make it just a group element rather than a column matrix. The isotropic vector is merely a secondary tool to express this idea through quite ingenious “slick algebra”. The basic idea that a spinor is a rotation is much simpler and developing it requires much less ingenuity.
Remark 19.
In reference [16], pp. 63–66, we also discuss the way SU(2) is introduced in textbooks based on a stereographic projection. We show that this method is, in reality, conceptually flawed, because it only considers the basis vector , which cannot represent the complete information about a rotation. A rotation of to does not define a unique rotation, as one can afterwards still rotate the basis triad freely around over a rotation angle φ.
Remark 20.
Many a physicist will be used to the concept of infinitesimal generators used to define the Lie algebra. In this context, the infinitesimal generators pick up algebraic expressions that are algebraically identical to those for the reflection matrices. We must point out that this algebraic identity is a mere coincidence. The definitions of the Pauli matrices in terms of reflection matrices and in terms of infinitesimal generators are conceptually completely different. Indeed, one should already feel rather puzzled by the fact that due to the algebraic identity a reflection operator appears to be related to an infinitesimal rotation. The solution of this riddle becomes obvious by considering rotations or Lorentz transformations in . We then have four reflection operators, while there are six infinitesimal generators, such that the two concepts are now clearly seen not to be equivalent. The four reflection operators have four-dimensional vector symmetry and are true generators for the rotation group. The infinitesimal generators have six-dimensional tensor symmetry. They are a vector basis for the six-dimensional tangent space to the Lie group. This also explains why the infinitesimal generators for SU(3) cannot be found by following the strategy that is outlined in Section 2.4.
Remark 21.
The set of all isotropic vectors of is the isotropic cone . Biedenharn and Louck [33] evoke the relation between a spinor and an isotropic vector . There is only one element that belongs to real space . Biedenharn and Louck conclude, from this observation, that spinors certainly cannot be objects that rotate in physical space. This is very obviously not true and the confusion is due to the notation , which suggests that the isotropic vector could be a set of position coordinates, while it is obvious from the development that the isotropic vector is meant to be a set of rotation coordinates.
2.7.2. Real Unit Vectors
Equation (29) is the reason why one says that a spinor is a square root of a vector. We can see that this is only very approximately true, as the two spinors and are different. There is a relation between spinors and vectors that illustrates, in a much more direct and less artificial way, how vectors are “squares” of spinors. Consider a rotation R with matrix that turns the reference triad. The vector of the rotated reference triad in Equation (33) can be expressed as:
In fact,
Under the rotation , this transforms to:
where we have used and to obtain the desired result. With respect to this identity, introducing the isotropic vectors to argue that vectors are rank-2 quantities in terms of spinors is, thus, rather a step away from a truly illuminating conceptual understanding of the quadratic relationship. It makes everything more difficult and less clear. We can illustrate this relation between a vector and its spinor in SU(2). We represent the vector by its spherical coordinates as follows:
Note that we use and as different symbols in this article. The same applies for and . The rotation that is required to rotate to along a great circle has axis and angle . The angle of rotation is counterclockwise when we look at it from the point . The rotation is thus expressed by:
One can then check that , and that:
Thus, the spinor that we can associate with is the rotation required to turn to . We can also write as:
This is based on:
The various column spinors we obtain are the columns of the rotation matrix. The line spinors are their Hermitian conjugates. The conjugated spinors can be obtained by considering:
Under the rotation this transforms to:
such that:
Thus, the conjugated spinor is the alternative spinor obtained by taking the second column of the rotation matrix. We may note that representation matrices of all the basis vectors are linked by a similarity transformation to , such that they all have eigenvalues 1 and .
2.8. Justifying the Introduction of a Clifford Algebra
The author has figured out the whole contents of the present paper from scratch, because he found the textbook presentations impenetrable. The author has also not studied books on Clifford algebra [34] in depth, such that some works may well provide the motivation we will try to give here, and that we were not able to spot in textbooks. Our criticism is based on the observation that, very often, mathematical objects that algebraically look identical are, in reality, entirely different geometrical objects. We have seen that we can introduce representations for vectors into the formalism by extrapolating the meaning of the algebra of the representations of reflection operators L. We have seen how confusing L and through the algebraic identity of their representation matrices can trap us into a conceptual impasse of trying to give geometrical meaning to mindless algebra. This is not the end of the story. Whereas, it is meaningful in the group theory to consider the product of two reflections B and A and the corresponding representation matrix , it is a priori not defined what the purely formal product of two vectors and defined by is supposed to mean. Here, again, entirely different geometrical objects are represented by identical algebraic expressions. We have learned definitions for and for , but not for . However, inspection of the algebra reveals that:
an algebraic identity that we used in deriving Equation (8). Here, we recognize the familiar quantities and . Whereas, this kind of algebra is meaningful for reflection matrices, it is a priori not meaningful for vectors. It can be given a meaning a posteriori in terms of vectors, at the risk of introducing confusion by ignoring the fact that the vector formalism is a parallel formalism, as we clearly outlined from the outset. Based on this confusion, one can obtain then a formalism, whereby one sums quantities that are not of the same type, by writing expressions of the type:
as a shorthand for Equation (46). What Clifford algebra does is defining mano militare that such expressions are meaningful as an algebra on multi-vectors. In general, such a definition is introduced out of the blue. By focusing on the purely algebraic part of the formalism, it is possible to confuse the vectors and the reflection matrices . This has several inconveniences. First of all, it is puzzling for the reader to understand where this idea comes from, because the algebra adds quantities of different symmetries and dimensions. All at once, one teaches him that, from now on, one can add kiwis and bananas, while one has told him before during his whole life that this is not feasible. Moreover, this is done tacitly, as though this would not be a problem at all. Nothing is done to ease away the bewilderment of a critical reader. One only laconically teaches him how to get used to it without asking further questions. One just rolls out the algebra, such that the reader can learn to imitate it mindlessly. As this is rather easy, the reader will quickly become acquainted with it, such that the justified initial questions will be silenced. However, it takes an algebraic shortcut to the full geometrical explanation by exploiting algebraic coincidences.
The second problem is that after the introduction of the definition of the Clifford algebra with its cuisine of adding kiwis and bananas, all the geometry of the rotations seems to follow effortlessly from this definition in an extremely elegant way. This gives the impression that everything is derived by magic from thin air, which really leaves one left wondering. In fact, the only vital ingredient that is needed to obtain this powerful and elegant formalism seems to be the impenetrable slight of hand of adding kiwis and bananas.
For sure, our presentation looks somewhat more cumbersome and less elegant than the approach where one takes off from the definition of the Clifford algebra in grand style. However, that elegant grand style is only a short-cut to the detailed explanation, and it is obtained by sweeping some more tedious parts under the carpet. The strong point of our approach is that it provides the detailed geometrical motivation for the complete Clifford algebra. An interesting feature that also exists in our approach is that we can consider all kinds of products:
The worked-out algebra contains expressions that correspond to hyper-parallelepipeds and other quantities of various dimensions (that can be symmetrical or anti-symmetrical). The symmetry is signalled by the presence or absence of a factor ı. These quantities transform under a rotation to:
Thus, that we can rotate all of these quantities within a unique formalism is not an asset of Clifford algebra that would not exist in our exploratory approach. We see that, by formalizing the algebra for the sake of elegance, we can obtain a very abstract formulation whereby we loose completely sight of the clear geometrical ideas. Mathematicians would argue that this does not matter. However, the problem is that now confusion reigns. Additionally when the cat is away, the mice will play. The abstraction eases extrapolating the algebra in a meaningless way beyond the limits defined by its geometrical meaning, e.g., by introducing linear combinations of spinors. From that point on the framework may now contain some well-hidden logical nonsense, as taking linear combinations of spinors is not a granted procedure. The structure that results from this transgression is the very elegant Hilbert space formalism of QM. This is now highly abstract, and any obvious link with the original geometrical meaning has been completely flushed. This favours an attitude where calculating becomes much more important than thinking. As matter of fact, in QM, the leitmotiv has become to “shut up and calculate”. Additionally, after hiding away this way, the whole geometrical meaning of the formalism, a physicist may enter the room and ask: I have a beautiful formalism that grinds out theoretical predictions which agree with the experimental data to unprecedented precision, but I just cannot figure out what it means.
2.9. Construction of a Basis of Reflection Matrices for
We now want to indicate how one can generalize the methods that are described in this Section to SO(n), with , briefly outlining how the reflection matrices of are defined by generalizing the approach that is explained in Section 2. The full details are given in [17]. It has to be pointed out that defining a rotation in will require, in general, more than two reflections for [35].
We start from the rotation group SO(3) of and the Pauli matrices. They satisfy . We will be able to proceed in steps whereby, at each step, we can add two basis vectors while we double the size of the representation matrices. In other words, SO(4) and SO(5) will be represented by matrices, SO(6) and SO(7) by matrices, and so on. In general, SO(n) will thus be represented be matrices. The whole procedure can be proved by Peano induction. The procedure echoes the procedure for Pauli matrices at the block level. The reason for increasing the size of the representation matrices from to is that there are no further representation matrices available for introducing new basis vectors with the set of matrices. If we note the matrices that present the basis vectors of as , and the matrices that present the basis vectors of as the algorithm based on Peano induction is given by:
Proving all of this by Peano induction is straightforward. This is all typical of what we stated in Section 1.2, viz. that what we have explained should put the reader into a position, wherein he can now effortlessly carry out this generalization himself.
3. Spinors in the Homogeneous Lorentz Group
As students, we learn the theory of special relativity by studying boosts along the x-axis. Such collinear boosts form a group noted as SO(1,1), which is abelian. This approach does not prepare us for the additional difficulties that occur in the homogeneous Lorentz group SO(3,1), which is non-abelian and allows for boosts allowed in all directions of . The difficulty stems from the fact that the composition of two non-collinear boosts is no longer a simple boost, but the product of a boost and a rotation. Consequently, SO(3) is a subgroup of the homogeneous Lorentz group. It is then obvious that the group is non-abelian. A general element of the group depends on six independent real parameters, three for the boosts and three for the rotations. This number of six also follows from the rule that is derived from the number of independent real parameters needed to specify the tetrad of the four basis vectors or the so-called Vierbein.
Because space-time is four-dimensional, we have , and we need reflection matrices. The conditions to expresses that these reflection matrices must be idempotent are now different due to the fact that the metric is now given by , such that we must now find matrices that satisfy . Here are the elements of the metric tensor and is the unit matrix. Hence, , , and all other elements are zero. We may note that the reflection matrix squares to , while the reflection matrix squares to , but this is not a real problem, because the representation is a double covering, whereby both and represent the identity element. Rather than following the algorithm that is given in Section 2.9 to determine the gamma matrices, here we will adopt the so-called Cartan–Weyl representation:
Here stands again for the matrix. Thus, we will use the same symbol for different objects, but within a given context there will be no confusion. We have added , because it is also often used. We will use sans-serif characters to note matrices. A unit four-vector , and a reflection A defined by the unit vector are thus represented by the matrix:
The proper homogeneous Lorentz transformations are obtained from an even number of reflections. The transformations obtained from an odd number of reflections will be called reversals or improper Lorentz transformations. In the Cartan–Weyl representation, proper Lorentz transformations are therefore block diagonal, while the reversals have a block structure along the secondary diagonal. Therefore, a column vector of a representation matrix of a homogeneous Lorentz transformation will only contain two complex entries, which is not sufficient for completely characterizing the six real independent parameters that are needed to define the transformation completely. Thus, we see that, if we consider a spinor as a column matrix, then it does not specify a group element. However, as we shall show below, to be able to derive the Dirac equation, one must introduce a superposition state of a proper Lorentz transformation and a reversal, and the consequence of this will be that a column matrix again contains all of the information regarding a group element.
The matrices and , where is a four-vector that is no longer of unit length are used in the so-called SL(2,) representations of the Lorentz group (Note that the symbol ★ used here is not the symbol for complex conjugation *). They are obtained one from another by the parity transformation . They are related by , and . Thus, they are each others inverses when . The entries of are the minors of those of and vice versa. Furthermore, . The scalar product of two four-vectors and is given by . For a product of two reflection matrices, we have:
Subsequently, we have . Let us now choose , and call . We have then such that SL(2,). Concomitantly . Furthermore: such that and finally, , such that:
Let us now introduce the notation for SL(2,):
We have then:
This way, we can make all of the calculations for the Lorentz group by restricting the use of the matrices to SL(2,).
Remark 22.
As explained below, all rotations and all boosts can be represented by SL(2,) matrices and, thus, also all of their products. Thus, the representation SL(2,) contains all of the orthochronous Lorentz transformations. The matrices , with are topologically disconnected from the matrices of SL(2,), which indicates that they constitute the antichronous Lorentz transformations. A negative determinant can only be obtained by combining reflections with unit vectors and . The simplest example is the product of and . The first reflection is the time reversal T, while the second reflection does not compensate for it, such that the product is indeed antichronous. Boosts are obtained from two reflections with unit vectors of the type , rotations are obtained from two reflections with unit vectors of the type . A composition of two non-collinear boosts cannot be obtained from two reflections, in conformity with the remark that we made regarding SO(n) at the beginning of Section 2.9.
Remark 23.
The SL(2,) representations have one drawback, viz. that the identity element, , and the time reversal operation T are all represented by . This ambiguity can be a source of errors. In the Cartan–Weyl representation, the ambiguity is lifted because . The matrix then represents T in the group algebra and in the multi-vector algebra.
Remark 24.
In SU(2), Equation (29) shows how we can represent an isotropic vector (which has “zero length”) as a “square” of a spinor. We can do exactly the same in SL(2,) for four vectors of “zero length” with representation matrices . In SU(2), the spinor contained all of the information regarding the rotated reference frame and, thus, also all of the information about the rotation. It was the first column of the rotation matrix. In SL(2,), the images of these four vectors of zero length now represent the full information about the transformed reference frame and, thus, about the Lorentz transformation (in Equation (55)). The four vectors of zero length are [36]: , , , and , with respective representation matrices:
Note that the spinors that occur in or in are only determined by the values of or up to a phase factor, such that and do not yield the full information regarding the reference tetrad, while the two spinors that occur in the theoretical expressions do contain the full information. These two spinors correspond to the columns of . These spinors can be considered to be square roots of vectors in the sense given by Atiyah.
Because vectors must be transformed by similarity transformations , the vectors in the two SL(2,) representations will transform according to (which is well known, see e.g., [12], p. 174, Equation (9.39)) and . Because the SL(2,) matrices are subject to the condition that their determinant is equal to 1, they can contain exactly the six independent real parameters needed to specify a Lorentz transformation. We can use the transformation property to calculate, backwards, the SL(2,) transformation matrix of a boost with velocity :
The rotation matrices are taken over from SU(2), which is embedded in SL(2,). For a boost , we, thus, have , while, for a rotation , we have . The calculations are really lengthy and tedious, but with the aid of the formalism of SL(2,) we can prove that the composition of two non-collinear boosts is the product of a rotation and a boost, as we stated at the beginning of this section:
Here, , , . We note the unit vector perpendicular to the plane that is defined by and , and that defines the rotation axis as . The rotation angle is . The angle between and is called , such that: and . The rotation and the boost are then defined by:
There also exists an equation with a reverse order of boost and rotation. The ordeal of going through similar tedious calculations, as for the first identity, can now be avoided by taking the Hermitian conjugate of this first identity which is: and then carrying out the substitution . There is a whole monograph by Ungar dedicated to the calculation of compositions of Lorentz transformations within the homogeneous Lorentz group [37], i.e., the hyperbolic geometry of the Lorentz group. Ungar also introduces the concept of gyro-vectors. The fact that non-collinear boosts lead to Lorentz transformations that are no longer pure boosts leads to a Thomas precession when a spinning particle follows an orbit [38,39].
Using the same reasoning within the Dirac representation, as used in SU(2), it is easy to see that the rotation that corresponds to the SU(2) matrices is now represented by the two matrices with the block structure:
This also follows from Equation (54) and . The ± sign stil occurs here, because . The matrices that we use are still constituting a double-covering of the proper Lorentz group.
4. Spinor-Based Approach to Quantum Mechanics
4.1. The Dirac Equation from Scratch
The following derivation of the free-space Dirac equation from scratch has been discussed in the monograph [16], especially in pp. 153–168, with additions scattered over various papers (the Appendix of [40], pp. 1–2 of [41]). For this reason, here we provide the complete derivation in a presentation that, in our opinion, is also more clear.
We start from the assumption that an electron at rest spins with an angular frequency around a fixed spin-axis that is defined by a unit vector (see Figure 2). We have no theoretical justification for this assumption. We were just led by curiosity and introduced it ex nihilo. We have no other justification for it than that we are able to derive the Dirac equation from it (and some other assumptions, like , we will introduce below) by a rigorous mathematical proof.
Figure 2.
In the Dirac equation, the spinning electron is described in its rest frame in exactly the same way as a spinning top. The symmetry axis of the top corresponds to the axis of rotation, as represented by the unit vector . The spinning motion with angular frequency can be characterized by an orthogonal basis of unit vectors attached to the top and turning with it. This rotating basis completely defines the rotation, its SU(2) representation matrix , and its spinor used to describe the spinning motion. In the wave function, defined with the aim of describing the dynamical state of an electron in all of its possible positions of , a virtual electron is placed in each point of of the rest frame. Putting this rest frame in motion at a constant boost velocity then yields the wave function in the main text. The phase velocity of this wave is . The free-space Dirac equation describes the wave function that is constructed from , as described in the main text. No specific shape for the electron is assumed in the calculations, because it is unknown. In lack of any specific information, Occam’s razor tells us to take a spinning sphere.
Remark 25.
Lorentz objected that the electron cannot spin, because this assumption cannot explain the magnetic moment of the electron. In fact, if all the charge of the electron were put on its equator and made to travel at the speed of light by the spinning motion, then this would still not be sufficient to produce the magnetic moment. Moreover, the present experimentally established upper bound for the radius of the electron is much smaller than the value for the electron radius Lorentz adopted. However, this argument by Lorentz does not hold sway, since, as we explained in [23], the magnetic moment is not due to a current loop. The algebraic expressions for the normal and for the anomalous Zeeman effect have completely different symmetries in the Clifford algebra, because the dot product in the normal Zeeman effect is a true scalar product, while the dot product in the anomalous Zeeman effect is a shorthand, which expresses a vector. Here, represents the three angular-momentum operators. The interaction responsible for the anomalous Zeeman effect appears in the algebra as a direct coupling between a point charge and the magnetic field, not as the interaction of a current loop with the magnetic field. For the electron, the value is almost exact, which further supports the thesis that its magnetic moment is not produced by current loops. The exchange mechanism of Heisenberg and Majorana based on the Coulomb interaction and the exclusion principle shows that the magnetic moment of the electron can be explained without current loops.
Remark 26.
The neutron has a g-factor of -3.826 085 45(90) despite the fact that it “has no charge”. The reason for this is that it is made up of positive and negative quarks. The charges of these quarks cancel, but the magnetic moments that are induced by the current loops of the quarks add up, because the opposite charges are circulating in opposite senses. This observation alone would already have been sufficient to point out that, even within a paradigm of current loops, Lorentz’s objection was not completely waterproof.
We can express the assumed spinning motion with the aid of the Rodrigues equation Equation (8) by replacing . Here, is the proper time. The rest mass of the electron will be noted as . This now describes the spinning motion of an object, e.g., a particle or a top. This is analogous to the way we use in Newtonian mechanics to describe the motion of an object along its orbit.
Remark 27.
There is a tedious technicality that is involved with the definition of the spin axis and the unit vector parallel to it. SU(2) treats rotations, while we are dealing here with a spinning motion. The axis of a spinning object is not exactly the same concept as the axis of a rotation. This is discussed in ([16] pp. 129–148). The unit vector that defines the spinning motion will coincide, e.g., with the physical symmetry axis of a spinning top. We can, e.g., imagine that we rotate ourselves with respect to the spinning top. The spin axis will then still be the symmetry axis. Thus, the spin axis transforms as a vector, because all we can do as human beings by moving corresponds to vector transformations. Thus, the spin vector is a vector, and it will be transformed according to in SU(2) or more generally in SL(2,). On the other hand, one speaks about the axis of a rotation , which implies that it is associated with the group element and will, therefore, transform according to . Therefore, the unit vector that we can draw parallel to the axis of a rotation does not transform as a vector. As human beings, we cannot bring about a transformation by physical motion (see Section 2.6).
The time derivative of yields:
where the spinor is the first column of . In order to derive Equation (65) from Equation (8), it has been assumed that . The choice to consider that can also vary leads to much more complicated equations with extra terms. Hence, we have introduced the underlying assumption that the orientation of the spin axis remains fixed. Thus, we must remember in the further derivation of the Dirac equation below that it is only valid for an electron with a fixed orientation of its spin axis. The case of a precessing spin axis is a priori not covered by this derivation. Therefore, the Dirac equation cannot be used to study precession, a limitation beyond guessing in Dirac’s derivation of the equation.
Equation (65) is defined for a single spinning top or electron at some unspecified position . Thus, the function is a function of the variable , but not of the variable for the position. Hence, it cannot be differentiated with respect to x, y, or z. Therefore, the spinor corresponding to is not a spinor wave function F, but a function F. It is here that we must adopt Ballentine’s statistical interpretation [42,43] in order to introduce a wave function F. The wave function will describe a statistical ensemble of imaginary non-interacting electrons who are all in the identical state at time with the same phase angle. Because we want the probability that an electron is in a certain position to be the same for all , we must put one imaginary electron at each position . This leads to the replacement of FSU(2)): in Equation (65) by a function FSU(2)): . This has been discussed in full detail in Appendix B of [23]. The equation remains the same, but the meaning of has changed, because its spatial domain has been changed from one point in to the whole of . It now allows an electron to be anywhere with equal probability.
The simultaneity of electron positions within the wave function does not imply simultaneity in the real world. It only reflects a simultaneity of description of the possible events (see also Section 4.3). The wave function is a mathematical tool that will be used to calculate probabilities in experiments at any moment we want in time. The velocity of the imaginary electrons is zero. Thus, the function obeys the Heisenberg uncertainty relation, because the velocity is exactly known, while the position is completely unknown. However, this has nothing to do with physics, it is a merely mathematical construction. It is based on the idea that it is rather convenient to describe the electron over whole Euclidean space or whole Minkowski space-time . The function now describes a statistical ensemble of spinning electrons in uniform motion (which is here rest). The modified Equation (65) can now be lifted to the Cartan–Weyl representation using Equation (64). We can then write the following differential equation
This expresses that the spin vector (defined in Equation (8)) is an axial vector, which does not change sign under a parity transformation P, because P flips the signs of and simultaneously. If we had used a block-diagonal expression for , the identity could never have turned out correctly, because the four-potential is a four-vector and the global block structures must match. This lifts the differential equation in the SU(2) representation to the Dirac representation. The electrons are, for the moment, at rest. We will now use covariance to put them all into the same uniform motion with non-zero velocity . Under a general Lorentz transformation , we have:
The signs that go with follow from the fact that, for an electron at rest, we must obtain twice Equation (65). This evidences that is an axial vector. We define:
Here, we have used the general structure derived in Equation (54). The result of carrying out the Lorentz transformations in Equation (67) is:
This corresponds to the fact that the true general form of the four-gradient is and the true general form of the spin vector . We can, in the rest frame, replace by the four-gradient because yields in the rest frame the same result on the wave function as . Note that the operations on are defined, while they are not defined for the function in Equation (65). Equation (69) can also be written as:
where we have dropped the accent on , in order to write the covariant equation in its standard form. We introduce the notation:
and define:
such that:
The reason why we introduce this mixed state is that the operator corresponding to the spin axis in Equation (69) is a reflection, while is a Lorentz transformation. Thus, we have a reversal on the right-hand side. We can never simplify this to to obtain the Dirac equation, because a reversal can never become equal to a proper Lorentz transformation (actually multiplied by a constant ). In the Cartan–Weyl representation, the algebra makes this very obvious, because the block structures of a proper Lorentz transformation and a reversal do not even match. Therefore, we must replace the pure state by a mixed state . This mixed state corresponds conceptually to a set, as explained in Section 2.5.2.
Remark 28.
This can be further illustrated by the analogous problem in SU(2), which is that we can never simplify to , because is a reversal and is a rotation. In general, we will also not be able to simplify to χ. In the analogy is the counterpart of and χ is the counterpart of Φ. To obtain a simplifying identity , leading to a Dirac-like equation, we can consider the set , which corresponds to the mixed state . For the set , we have then and for the corresponding mixed state . In the analogy, the mixed state ψ is the counterpart of the mixed state Ψ.
This fact that the wave function is now a mixed state once more stresses that the wave function describes a statistical ensemble. The covariance of Equation (73) follows from:
As we have assumed that does not vary with time:
By covariance, we then have:
such that:
Hence:
With the aid of Equation (73), this implies:
In summary:
which, after substituting , yields the celebrated Dirac equation:
We have already discussed this substitution in [23]. It implies that the whole rest energy of the electron corresponds to the kinetic energy of its spinning motion. We introduce this assumption for the sole reason that it permits recovering the Dirac equation. It is an equation that marries QM () with special relativity () in a very simple identity. Thus, this is really a completely rigorous derivation of the Dirac equation from scratch. Because of the definition of in Equation (68), is here defined as:
The matrix corresponding to the first block column of corresponds to Equation (5.52) on p. 163 of [16]. In order to highlight the transformation properties of this matrix under Lorentz transformations, it can be further elaborated to yield Equation (5.58) on p.166 of [16]. The columns of are called bi-spinors, because they combine two columns from SL(2,) matrices.
4.2. Consequences
From the Dirac equation, we can derive the Schrödinger and the Pauli equation, such that the new approach offers a broad platform for dealing with QM. The Dirac equation here has been derived with the rigour of a mathematical proof, while the traditional equations were obtained by educated guessing from the de Broglie ansatz, which has also been conjectured. The advantage of our approach resides in the fact that we now know exactly on what kind of assumptions the derivation of the Dirac equation has been based. This is not the case in the traditional approach and, as the wave mechanics are able to describe many stunning experimental results that seem to defy any attempt of common-sense explanation, one can become convinced that the Dirac equation must be based on some very magical unknown quantum axioms. The problem is that this opens the door to an infinite set of fazing assumptions. There have been many attempts at interpreting QM, e.g., the many-worlds interpretation [44], Cramer’s transactional interpretation [45], and Bohm’s approach [46,47], just to mention some of them (see also [48,49,50]). And indeed, many of the interpretations carry some exotic perfume of quantum magic floating around them, with assumptions that run contrary to daily-life experience, like the existence of many parallel worlds or signalling backwards in time. This is something we wanted to avoid at any price in our approach, because such assumptions cannot be proved or contradicted by direct telltale experiments. The result is that we are left wondering what we should think about them and it remains anybody’s guess as to which of these assumptions could be physically the more acceptable.
Therefore, it is quite sobering to learn that the derivation of the Dirac equation presented here is entirely classical. This raises the question where the quantum magic then comes from. This, of course, requires a very detailed discussion (see below). It could be that the secret is somewhere hidden in the way that we use this equation. For this reason, it is important to be sure that we absolutely understand all of the mathematics, which is why it is convenient that we have built up everything from scratch. It should permit to know whether there are problems in the way that we use the equation by a very thorough investigation on a case-by-case basis. Therefore, we have tried to analyze a number of quantum paradoxes in order to figure out if their explanation might require some magic after all (see [23] and below in Section 4.5.2). In any case, the entirely classical derivation prompts for caution. We might be over-interpreting some things and we should try to avoid introducing axioms that are too remote from the possibility of experimental testing.
Dirac’s historical derivation has been carried out within the algebra of the vectors and multi-vectors (i.e., the exterior algebra), such that its real meaning remained hidden, as we have pointed out. We have derived it here within the algebra of the group elements, which permits us to see that the Dirac equation describes a statistical ensemble of spinning electrons in uniform motion. In the traditional derivation based on the multi-vector algebra, we cannot even imagine that it is missing this crucial point, and that the real stage for the scene is the algebra of group elements. Consequently, the possibility that the electron could spin is firmly denied by the standard dogma. Lorentz’s objection might have been one of the reasons for this. Another reason could be Biedenharn and Louck’s argument that we mentioned in Remark 21 in Section 2.7.1. Thus, our approach is at variance with the standard dogma, but it cannot be attacked on the basis of this fact, because it is an alternative approach to QM that leads to the same algebraic results as the traditional approach and, therefore, is in a completely equivalent agreement with experimental results. The surplus values of our approach are the mathematical rigour and its conceptual clarity.
The operator identies and play a crucial rôle in the traditional derivations of the Schrödinger and Dirac equations. They have been obtained by guessing, as mentioned above. The identities and do not play any rôle at all in our derivation of the Dirac equation. They are just a corollary of the proof. The lack of rigour and clarity in the procedure to define quantum operators, even within the context of the scalar Schrödinger equation, has been pointed out by Messiah [51], who evoked that the correct forms are obtained in a process of trial and error. The extrapolation of the definition of these identities from the context of a scalar wave function for the Schrödinger equation to the context of spinor wave functions in the Pauli and Dirac equations is also far from self-evident, as, e.g., a spinor of SU(2) can contain two different angular frequencies . When we apply the operator to such a spinor , we do no longer obtain the neat result , but . In order to overcome this problem, we have been forced to introduce mixed states . This has been further discussed in Remark 28 in Section 4.1 and in [23]. In the treatment of precession in a magnetic field, this problem becomes worse because the angular frequencies can now take two different absolute values, as discussed in the treatment of the Stern–Gerlach experiment in [23].
In our approach, negative frequencies are just related to inverting the sense of the spinning motion, because we have not introduced anti-particles at any stage in the derivation. There are no anti-particles in the geometry that we have used. We have further discussed the interpretation of negative frequencies in the traditional approach on p. 7 of [23]. The negative frequencies correspond to positive energies .
As already mentioned, we are unwittingly responsible ourselves for the Heisenberg uncertainty relation between position and momentum, because it is introduced by the mathematical construction of the wave function.
Within the scope of the present derivation of the Dirac equation, it is not possible to consider fermions with zero rest mass propagating at the speed of light c, due to the fact that the derivation starts from considering a spinning particle in its rest frame, while a particle propagating at the speed of light does not have a rest frame. Because Dirac guessed his equation, he could not suspect this limitation of the domain of validity of his equation. This led him to the assumption that neutrinos were fermions, which could be described by the Dirac equation, whereby the rest mass is put to zero. This conception of the neutrino as a fermion with zero rest mass and travelling at the speed of light c has prevailed for a long time. It is finally the results about the neutrino oscillations from Super Kamiokande [52] that have invalidated Dirac’s neutrino theory, while they are in agreement with our derivation of the Dirac equation.
Our derivation of the Dirac equation has been made entirely within the framework of special relativity, such that it does not contain any incompatibility between special relativity and QM. However, we constructed the wave function, starting from a Lorentz frame at rest in flat Minkowski space-time and then used covariance to introduce Lorentz frames in uniform motion with respect to this original frame. This is how the wave function corresponds to the description of a statistical ensemble of spinning electrons in uniform motion. This is a global approach and it is not at all obvious how one can generalize this procedure to curved space-time manifolds with local frames of different velocities.
It must be stressed that all of the electrons within the statistical ensemble described by the wave function are moving at a well-defined uniform speed . The phase of the wave function is a scalar invariant whose value in the rest frame is . The two expressions are just related by a boost. The value is obtained from by applying the identity . The boost with velocity v transforms into (if we take parallel to the x-axis ). If we wanted to interpret this expression for the proper time in terms of a wave moving in space, we could rewrite it as and conclude that the phase velocity of the wave is . Indeed, this is actually correct (see Figure 3). The phase velocity in a frame at rest is infinite and it just corresponds to the velocity of the signal that would be needed to synchronize all the clocks in the reference frame up to infinite distance. All of the clocks will then have the same phase. In a frame moving with the velocity v, this infinite velocity becomes . In other words, is nothing more than the slope of the time axis in a Minkowski space-time diagram. The super-luminal phase velocities are just due to the introduction of a Lorentz frame, wherein all of the clocks have been synchronized up to infinite distance. The clocks that we use in the wave function are the spinning motions of the electrons, and we have synchronized all of their phases by the construction of the wave function. Because the electrons are all traveling at the speed , there is no need for introducing wave packets to build an electron with a speed that is given by the group velocity , because all of the electrons are already traveling at the speed . In other words, no wave packets are needed, and the electron can remain a point particle.
Figure 3.
Minkowski space-time diagram, showing the axes of a frame at rest and of a frame traveling at a boost velocity v with respect to it. The slopes of the various axes are shown. The slope ∞ is the phase velocity of the Dirac wave in the rest frame. It is the velocity of the signal that would be needed to synchronize all of the clocks up to infinite distance in the rest frame. In the frame traveling at the boost velocity v, this phase velocity becomes . Despite this super-luminal phase velocity for the wave, the electrons are traveling at the sub-luminal velocity v. Thus, there is no need for introducing wave packets with a group velocity , as we have already .
The wave function is not a matter wave in the way it has been originally conjectured. The introduction of the wave packets leads to other problems, because the speeds of the waves that contribute to the wave packet are different, such that the wave packet spreads out with time and the “particle aspect” of the wave packet is lost. This prompts speculations regarding a collapse of the wave function as the result of a measurement. It further prompts theoretical considerations regarding solitons. It is a whole concatenation of problems resulting from the over-interpretation in terms of matter waves of a purely mathematical wave function. Of course, we have been duped by the fact that, historically, it went in reverse order. The matter waves were conjectured first, and it is only later that the wave functions became the spinors and probability amplitudes of QM. Finally, we must note that the wave function we have constructed is completely coherent. We propose some thoughts about this choice in Section 4.3.
There is no collapse of the wave function. The wave function is not a matter wave, a real physical entity that could physically collapse, but a purely mathematical tool and the electron is not a wave packet. The purpose of the wave function is not to describe single events, but probabilities of events for a large statistical ensemble. We can state this with confidence in the new approach, because it has just been constructed that way. For a dice, you could define a probability function F, where and , or somewhat artificially a wave function F, such that , . That function f and the wave function do not collapse when somebody throws a dice and obtains 5. The only thing that has collapsed is that person’s prior lack of knowledge about the outcome for the dice.
4.3. Why We Can Use Coherent-Source Boundary Conditions for an Incoherent Source
What one does in solving a wave equation and imposing the boundary conditions is assuming that the source is coherent. We could, e.g., consider plane waves impinging on a set-up, and then everywhere on the plane of the source, we would attribute the same phase to the particle by the boundary conditions. This is not self-evident, because the source may be incoherent. This shows that, in this kind of problem, the phase itself is not important, and that it is the phase difference built up starting from the source that counts. That is then the reason why we can act as though the sources were coherent. It is this phase relation imposed at the source that then applies to all particles. In fact, we can put all initial phases equal to zero and keep in mind the error that this induces. Then we can correct for this error again at the end. (If this were to be incorrect, because, e.g., an electron has undergone a spin flip during its trajectory, then the coherence of the wave solution would have been lost anyway). Because what we finally measure is or for each particle, this will not change the experimental results. What counts in the end is the amplitude rather than the phase of the wave, and that the interactions that occur after leaving the source are not incoherent, such that they do not provoke decoherence [40].
Remark 29.
This may sound absurd, because, when you have two particles with dynamics described by and (e.g., within the context of a Schrödinger equation), then correcting their phases by and , might destroy the interference in : . However, the idea that you should add up two electron spinors and then square the result, is wrong and never applies.
Each particle must be counted in its own right, because, in the build-up of an interference pattern, the particles appear as dots on a detector screen one-by-one [53,54]. Hence, we must always determine the quantities of single particles according to , never according to . When there is an interference pattern, the weights of the functions and of two individual particles obey and comply already with the number of particles implied by the intensity of the interference term that one would write down according to the textbook rule, where R and L could, e.g., refer to the left and right slit in the double-slit experiment, see Equation (4) of Ref. [25]. E.g., if there were destructive interference there would be just no particles j with spinor present in , such that the weight coefficients and in the set described by must satisfy , rather than . Here and are defined within the double-slit experiment and different from the single-slit wave functions and . This requires a very detailed discussion (see [25] and Section 4.5.1).
If the particles are electrons and the wave functions are spinors of SU(2), the idea remains the same, but the argument must be written differently, because the phases are rather changed by some rotations and . The rest of the argument remains mutatis mutandis the same, because, for the SU(2) matrices , we have . We can even consider the case that the spins of the electrons that are emitted by the source are not aligned, but this is more elaborate. In fact, we must then reconstruct the SU(2) matrices from their corresponding spinors , develop the proof on the SU(2) matrices, and then switch back to the corresponding spinors in order to be able to derive the final result. The reason for this is that we can write a similarity transformation for the SU(2) matrices, but not for the spinors, because we cannot multiply a spinor to the right with a SU(2) matrix. The procedure for performing a similarity transformation on a spinor is visualized in the following equation and commuting diagram:
Within the context of the Dirac equation, the analogous correspondence between the spinors and representation matrices of SL(2,) is given by Equations (4.9) and (5.58) in [16]. The relation between the representation matrices of SL(2,) and the representation matrices in the Cartan representation of the Dirac formalism is also given in [16]. A change of axis , as embodied by a corresponding change of group elements , is obtained by a similarity transformation , based on a rotation . This will then evolve with time to (as proved in [16], pp. 310–313), whose spinor will now comply with the boundary conditions for a coherent source. The correction in the end to recover the correct incoherent-source value is then just the reverse similarity transformation. Additionally, then, we will see that the spinors and will yield the same result . The main idea that makes this all work is that, in a coherent process, the spin axis does not change due to the interaction with the measuring device, or else the process would be incoherent. A change of would be accompanied with a corresponding change in the measuring device due to conservation laws. In the double-slit experiment, this would, e.g., permit knowing through which slit the particle has gone. We may note that, to our knowledge, the issue that, in general, the source will be incoherent, has never been addressed in examples of solving Schrödinger, Pauli, or Dirac equations in textbook examples. The source has always been tacitly implied to be coherent by the choice of the boundary conditions. This has been then a kind of blind spot. The problem cannot be solved without a proper understanding of spinors and of the relationship between the particles and waves.
4.4. The Minimal Substitution
The minimal substitution was introduced in classical mechanics to calculate orbits. It was validated by comparing the results of the calculations that were performed with it in the Lagrange–Hamilton formalisms with those of traditional Newtonian mechanics. It was then proved to also work for relativistic orbits. It is kind of startling that traditional QM explains to you first that it is entirely different from classical mechanics, and that we must stop thinking about orbits, and then introduces the minimal substitution without any comment as though it would be self-evident.
We can propose the following justification for it. Just as the equation and the four-vector can serve to define a global Lorentz transformation for the wave function in the free-space Dirac equation, and the four-vector can be used to define a field of local Lorentz transformations for the wave function of the Dirac equation in the presence of an electromagnetic potential. This substitution is also covariant.
4.5. Discussion
4.5.1. The Born Rule, Schrödinger’s Cat, the Particle-Wave Duality and the Double-Slit Experiment
In solving the Schrödinger and Dirac equations, we impose boundary conditions. This shows that the probabilities we use are conditional. The condition is the experimental set-up. Indeed, the probabilities do depend on the experimental set-up, as Bohr has claimed. The boundaries that we use are idealized, e.g., the walls of the slits are considered to be perfectly planar, while, on a microscopic scale, they must present some roughness, and they are made of molecules or atoms. Following Einstein, here we could imagine lots of hidden variables that do not reside within the particles but are located within the set-up itself (see Section 4.5.2). Therefore, the viewpoints of Einstein and Bohr are not entirely mutually exclusive.
It is now time to complete the work that we started in Section 2.5.2. We have, for the moment, considered one electron in each point . We could consider that there is a larger number of electrons in each point. Following the ideas that are expressed in Section 2.5.2, we would thus have to consider to start with, as each electron would have its copy of the matrix or spinor attached to it. However, as the spinors of SU(2) satisfy the condition we must calculate the number of electrons by using the quantity . This leads then to the rule that we must use . We can extrapolate this idea to the case that we use probability densities and then also normalize the wave function. It may represent a lot of effort to write all this down in a mathematically tidy way, but the rationale presented here gives us a justification for the Born rule.
The construction of mixed states as corresponding to sets gives us a simple interpretation for the wave function of Schrödingers cat. The wave function does not describe a cat that is half dead and half alive, but an ensemble of cats, whereby half of the cats are dead and half of them alive. In this approach, the algebra cannot be taken literally. We must refrain from insisting on carrying out the algebra to the very end, by treating spinors like vectors, as in the example shown in Section 2.5.2, where we obtained . The mixed state must be considered as a juxtaposition, rather than as a real algebraic sum. It would be preferable to write rather than , because carrying out the algebra by brute force anyway is incorrect mathematics and the notation just sticks to the real meaning.
However, this solution of refraining from brute-force algebra raises a severe issue in the case of interference, e.g., in the double-slit experiment, where indeed leads to a zero physical intensity, which suggests that the procedure should be taken seriously anyway. Interpreting in terms of sets is here certainly not meaningful. It would imply that the union of two non-empty sets would be empty. Therefore, in Section 4.3 we have proposed that the individual particles must already comply with the intensity pattern.
In fact, based on the way that we constructed the wave function we can also propose a solution for the conundrum of the particle-wave duality. What behaves as a wave is the wave function, i.e., the statistical ensemble of the electrons that have been used in the experiment. It is this wave as a whole that can flow as a dense fluid of non-interacting electrons through both slits in a double-slit experiment. The fluid is virtual and it has been created by the simultaneity of description we have used in defining the wave function in Section 4.1. The single electrons behave as particles, and each of them goes through a single slit. The idea that an electron can go through both slits simultaneously and interfere with itself is, of course, related to the concept of wave packets. We have explained that the superluminal phase velocities do not justify introducing wave packets. The electrons are detected as points on a detector screen and are, therefore, always particles.
Still, there seems to be a contradiction that puts us on a tight rope, because we need to explain the interference pattern. This apparent contradiction can be solved, as follows. The boundary conditions that we impose on the wave equations are non-local, because the macroscopic set-up of the experiment is non-local. The wave function itself is also non-local, because, in its construction, we have synchronized clocks in a Lorentz frame up to infinite distance. Thus, we are trying to solve a differential equation with non-local boundary conditions that will lead to a non-local solution. We could first try to find all solutions by making the calculations as though we took the sums in the superposition state seriously, although we know that we should not for the reasons that are described above and that all trace back to the undeniable fact that we cannot add spinors like vectors. In other words, we cheat and ignore the taboo. This way, we could set up a pool of all possible solutions for the differential equation ignoring the existence of any taboo. The correct solutions that do respect the taboo will then also be present within this pool of all possible solutions.
Afterwards, one can check which solutions in the pool allow for an alternative interpretation in terms of spinors or sets of spinors. This way, we can get away with the unethical behaviour of cheating by basing ourselves on the accomplished fact that we have found a solution that has stood the test. An example of this procedure for finding an alternative interpretation is given in reference [25], where the calculation , which would be valid for vectors, is not valid for spinors, as shown above in Section 2.5.1. One can then argue that the algebra used to obtain the solution is logically flawed for spinors, but valid for finding the pool of solutions of the differential equation for vectors. The vector solutions are found by using a Huygens’ principle for the solution of differential equations of a certain type [55,56]. This Huygens’ principle is completely devoid of any physical meaning. It is just a mathematical method that has been proved to work for certain types of differential equations. This transpires already in Kirchhoff’s elaboration [57] of the Huygens’ principle for electromagnetic waves, whereby one is forced to accept that they can sometimes travel backwards in space again. Feynman’s description is even more eloquent [58] with “photons going faster or slower than the conventional speed of light, electrons going backwards in time”. However, we should not be amazed that we need such unphysical and non-local aspects as going backwards in space and in time, or traveling faster than light, because we must find an overall solution that satisfies all of the non-local boundary conditions. All that we must keep in mind is that it is not real. When one has solved the problem at one boundary, one must still solve it at other boundaries and this really might require accepting unphysical propagation for the waves in the Huygens’ principle. However, the result of the correct mathematical procedure is with high precision , as, e.g., shown by Feynman’s all-histories elaboration of the Huygens’ principle.
We have worked out these ideas for the double-slit experiment [25], which contains much more than the incomplete discussion that we can present here. Let us remind that we have derived the Dirac equation by rigorous mathematics. It leads to a differential equation that we can solve rigorously. That is a first mathematically rigorous track. This track reproduces the experimental results. Next, we follow a second mathematical track. We use probability calculus and come to the conclusion that the solution of the differential equation does not comply with our intuition, which tells us that we should just measure the sum of the probabilities observed in two single-slit experiments. It is very important to realize, at this point, that the paradox here is no longer between the physics and the mathematics, but between two different mathematical tracks. The solution of the paradox must thus reside entirely within the mathematics such that no quantum magic can be involved.
Solving the mathematical paradox takes more than we have developed up to now. An essential rôle is played by the fact that it is impossible to know through which slit the particle has gone [25]. This is because coherent interactions do not leave any information behind on the crime scene of their passage through the set-up, such that we cannot possibly know the exact trajectory the electron has taken, because no information has been created. The answer to the question through which slit the particle has traveled is undecided, just like the question of whether the fifth postulate of Euclidean geometry is true cannot be answered on the basis of the first four postulates because they do not contain the required information. It is as giving a list of commercial items loaded into a ship and then asking what the age of the captain is.
The information that would allow for answering the question “which way” does not exist. That is what defines the conditional probabilities and the boundary conditions that are imposed by the double-slit set-up. We should not mix up conditional probabilities from different set-ups, because they can define incompatible conditional probabilities. Undecided events and their conditional probabilities cannot be treated in terms of the conditional probabilities from other set-ups, which contain and create entirely different information to the extent that the question of “which way” can now be decided. Such other set-ups just define different conditional probabilities, because each set-up has its own conditional probabilities. The conditional probability that we do not know through which slit the electron has gone cannot be constructed from the conditional probabilities, where we know that the electron has gone through a given slit. Certainly, the electron has gone through one of the two slits, but the information is not available. Respecting this caveat is exactly what the mathematics do when you solve the differential equation with the boundary conditions of the double-slit experiment. When we use intuitive probability calculus, we are trampling this caveat, by only considering the locality of the interactions. Perhaps because our macroscopic intuition is entirely based on incoherent processes where the answers to questions are always decided.
The explanation offered must be considered to be cogent to the extent that there is no other way to avoid completely illogical conclusions, e.g., that, at the quantum level, other rules of probability calculus would prevail. This is wrong because we have already pointed out that the solution of the paradox does not reside within the physics. We must also reject it because we should not accept the defeatist philosophy that we cannot think rationally. We should not loose our head and resort to quantum magic in moments of adversity, but stay cool and remain convinced that another, purely logical explanation must exist.
The Schrödinger equation has been used with full generality for all kinds of different particles, like He atoms, electrons, and C molecules. The tacit assumption that all of these different types of particles obey the same equation has been adopted as self-evident. In reality, it would have to be proved for each type of particle and that it works with such generality must be considered to be a fluke. Nature could have just been different.
4.5.2. Conclusions
Where do we stand now? What we have learned is that the Dirac equation can be derived without introducing extraordinary assumptions, such as many worlds or signalling back in time. One might now reason, as follows. We have a spinor formalism that we understand. With this spinor formalism, a huge corpus of calculations has been constituted that correctly reproduce the experimental results. Hence, all that remains to be done is to use the geometrical interpretation to know what the calculations mean.
However, this could be too optimistic. The problem is that, during all these years it has not been known what the formalism means. Not knowing what the formalism means can be full of boobytraps. It can lead to over-interpretations or transgressions of the domain of validity of the calculations. There may remain problems in the way that we have used the Dirac equation. The reader can consult [23] to check that there are a lot of occasions where things can just go wrong. This lays bare the intellectual limits of the punch line “shut up and calculate”, with its force-feeding of black-box algebra. It presents a state of affairs that is not satisfactory as acceptable. Therefore, we can only try to apply the spinor formalism with the new understanding in order to check whether we can figure out an explanation for a given experiment. This boils down to case-by-case investigations. (Some introductions to QM that describe such cases are [59,60,61,62,63,64]. Some reprint collections are [65,66,67]). For each experiment, this can remain very difficult in its own right.
We have undertaken a survey to check whether the solution of some quantum paradoxes may not require quantum magic after all. We have already mentioned this to a certain extent in Subsection 1.3 on pp. 7–9 of [23]. We have treated a number of problems and come to the conclusion that they do not require quantum magic. We have been able to derive the Dirac equation, starting from some very clear and simple assumptions. We have solved the paradox of the particle-wave duality (see Section 4.5.1 and [25,41]). We have solved the problem of the paradox of Schrödinger’s cat (see Section 4.5.1, Subsection 2.3.2 of [17,40]). We have offered an explanation for the double-slit experiment in [25,41] (which can be further enriched by Section 4.3 or the Appendix of [40] to deal with incoherent sources). We have explained why the phase velocity of the wave function is . We have explained the Stern–Gerlach experiment in [23]. The work of Hansen and Ravndal [68] already explains tunnelling, such that it no longer has to be addressed anymore. The problem of entanglement and hidden variables [69,70,71] has been settled by many authors, starting with Kupczynski back in 1987 [72], who have pointed out an error in the derivation of the Bell inequalities. The error is that a common probability distribution has been assumed for the four individual experiments (corresponding to four combinations of polarizer settings), while the experimental probabilities are defined on the more restricted probability distributions of the individual experiments. This leads to a normalization problem. This error is closely related to the one that we encountered in the discussion of the double-slit experiment, viz. that we should not combine conditional probabilities defined by different experimental set-ups. In both cases QM teaches us is that, in following, our common-sense intuition about probability calculus we expose ourselves to committing subtle, subliminal logical errors, which can be really hard to spot, such that it looks almost as though we cannot think straight.
4.5.3. Epilogue
We are now reaching the end of a very long journey. I started with three quotes and I think I could end with a fourth one by Murray Gell-Mann [73] recipient of the 1969 Nobel prize in physics:
“Niels Bohr brainwashed a whole generation of theorists into thinking that the job [interpreting quantum theory] was done 50 years ago”.
Bohr has brainwashed more than one generation. For students in the past, QM may have looked frustrating and even ugly. The main message from this paper is that we should never again accept something like the Copenhagen interpretation, with all its internal contradictions. We must break away from it, in the words of Dieudonné [24]: “Pour l’honneur de l’esprit humain” (For the sake of the honour of the human spirit). I hope that for future students QM may from now on look more like an enthralling poem of very beautiful mathematics.
Funding
This research received no external funding
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author thanks P. Rowlands and Symmetry for the invitation to submit this paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Feynman, R.P. The Character of Physical Law; Messenger Lectures; Modern Library: New York, NY, USA, 1965. [Google Scholar]
- Farmelo, G. The Strangest Man. In The Hidden Life of Paul Dirac: Quantum Genius; Faber and Faber: London, UK, 2009; p. 430. [Google Scholar]
- Pais, A.; Jacob, M.; Olive, D.I.; Atiyah, M. Paul Dirac—The Man and His Work; Cambridge University Press: Cambridge, UK, 1998; pp. 113–114. [Google Scholar]
- Cartan, E. The Theory of Spinors; Dover: New York, NY, USA, 1981. [Google Scholar]
- Penrose, R.; Rindler, W. Spinors and Space-Time, Volume I, Two-spinor Calculus and Relativistic Fields; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Naimark, M.A. Linear Representations of the Lorentz Group; Pergamon Press: Oxford, UK, 1964. [Google Scholar]
- Hladik, J.; Cole, J.M. Spinors in Physics; Springer: New York, NY, USA, 2012. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman: San Francisco, CA, USA, 1970. [Google Scholar]
- Chaichian, M.; Hagedorn, R. Symmetries in Quantum Mechanics, from Angular Momentum to Supersymmetry; IOP: Bristol, UK, 1998. [Google Scholar]
- Cornwell, J.F. Group Theory in Physics; Academic Press: London, UK, 1984. [Google Scholar]
- Inui, T.; Tanabe, Y.; Onodera, Y. Group Theory and Its Applications in Physics; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Jones, H.F. Groups, Representations and Physics; Adam Hilger: Bristol, UK, 1990. [Google Scholar]
- Sternberg, S. Group Theory and Physics; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Harter, W.G. Principles of Symmetry, Dynamics and Spectroscopy; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Hestenes, D. Zitterbewegung in Radiative Processes. In The Electron, New Theory and Experiment; Hestenes, D., Weingartshofer, A., Eds.; Fundamental Theories of Physics; Springer: Berlin/Heidelberg, Germany, 1991; pp. 21–36. [Google Scholar]
- Coddens, G. From Spinors to Quantum Mechanics; Imperial College Press: London, UK, 2015. [Google Scholar]
- Coddens, G. Spinors for Everyone. Available online: https://hal.archives-ouvertes.fr/cea-01572342v1 (accessed on 11 April 2021).
- Mermin, N.D. What’s Wrong with this Pillow. Physics Today, April 1989; 9. [Google Scholar]
- Halzen, F.; Martin, A.D. Quarks and Leptons, An Introductory Course in Modern Particle Physics; John Wiley and Son: Hoboken, NJ, USA, 1984. [Google Scholar]
- Hanneke, D.; Hoogerheide, S.F.; Gabrielse, G. Cavity Control of a Single-Electron Quantum Cyclotron: Measuring the Electron Magnetic Moment. Phys. Rev. 2011, 83, 052122. [Google Scholar] [CrossRef]
- Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. Tenth-Order QED Contribution to the Electron g-2 and an Improved Value of the Fine Structure Constant. Phys. Rev. Lett. 2012, 109, 111807. [Google Scholar] [CrossRef] [PubMed]
- Ball, P. Quantum Theory Rebuilt from Simple Physical Principles, Quanta Magazine. 2017. Available online: https://www.quantamagazine.org/quantum-theory-rebuilt-from-simple-physical-principles-20170830/ (accessed on 11 April 2021).
- Coddens, G. The Exact Theory of the Stern-Gerlach Experiment and Why it Does Not Imply that a Fermion Can Only Have Its Spin Up or Down. Symmetry 2021, 13, 134. [Google Scholar] [CrossRef]
- Dieudonné, J. Pour L’honneur de L’esprit Humain-Les Mathématiques Aujourd’hui; Hachette: Paris, France, 1987. [Google Scholar]
- Coddens, G. A Solution of the Paradox of the Double-Slit Experiment. Available online: https://hal.archives-ouvertes.fr/cea-01459890v3 (accessed on 11 April 2021).
- Van der Waerden, B.L. Group Theory and Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Sagan, B.E. The Symmetric Group. Representations, Combinatorial Algorithms, and Symmetric Functions. In Springer Graduate Texts in Mathematics, 2nd ed.; Springer: New York, NY, USA, 2001; Volume 203. [Google Scholar]
- Deheuvels, R. Tenseurs et Spineurs; Presses Universitaires de France: Paris, France, 1993; p. 232. [Google Scholar]
- Rauch, H.; Zeilinger, A.; Badurek, G.; Wilfing, A.; Bauspiess, W.; Bonse, U. Verification of coherent spinor rotation of fermions. Phys. Lett. 1975, 54, 425–427. [Google Scholar] [CrossRef]
- Feynman, R.P.; Weinberg, S. Elementary Particles and the Laws of Physics; Cambridge University Press: New York, NY, USA, 1987. [Google Scholar]
- Staley, M. Understanding quaternions and the Dirac belt trick. Eur. J. Phys. 2010, 31, 467. [Google Scholar] [CrossRef]
- Marmier, P.; Sheldon, E. The Physics of Nuclei and Particles; Academic Press: New York, NY, USA, 1969; Volume I, p. 341. [Google Scholar]
- Biedenharn, K.C.; Louck, J.D. Angular Momentum in Quantum Mechanics, Theory and Application; Encyclopedia of Mathematics and Its Applications; Addison-Wesley: Reading, MA, USA, 1981; Volume 8. [Google Scholar]
- Lounesto, P. Clifford Algebras and Spinors; Camlbridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Gallier, J. Geometric Methods and Applications for Computer Science and Engineering, 2nd ed.; Texts in Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 38, Chapter 8. [Google Scholar]
- Newman, E.; Penrose, R. An Approach to Gravitational Radiation by a Method of Spin Coefficients. J. Math. Phys. 1962, 3, 566. [Google Scholar] [CrossRef]
- Ungar, A.A. Beyond the Einstein Addition Law and Its Gyroscopic Thomas Precession: The Theory of Gyrogroups and Gyrovector Spaces; Fundamental Theories of Physics; Kluwer: New York, NY, USA, 2002; Volume 117. [Google Scholar]
- Rhodes, J.A.; Semon, M.D. Relativistic velocity space, Wigner rotation and Thomas precession. Am. J. Phys. 2004, 72, 945. [Google Scholar] [CrossRef]
- Coddens, G. On Magnetic Monopoles, the Anomalous g-Factor of the Electron and the Spin-Orbit Coupling in the Dirac Theory. Available online: https://hal-cea.archives-ouvertes.fr/cea-01269569 (accessed on 11 April 2021).
- Coddens, G. A Linearly Polarized Electromagnetic Wave as a Swarm of Photons Half of Which Have Spin -1 and Half of Which Have Spin +1. Available online: https://hal.archives-ouvertes.fr/hal-02636464v3 (accessed on 11 April 2021).
- Coddens, G. A proposal to get some common-sense intuition for the paradox of the double-slit experiment. Available online: https://hal.archives-ouvertes.fr/cea-01383609v5 (accessed on 11 April 2021).
- Ballentine, L.E. Quantum Mechanics, A Modern Development, 2nd ed.; World Scientific: Singapore, 1998. [Google Scholar]
- Ballentine, L.E. The Statistical Interpretation of Quantum Mechanics. Rev. Mod. Phys. 1970, 42, 358. [Google Scholar] [CrossRef]
- Everett, H. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Cramer, J. The transactional interpretation of quantum mechanics. Rev. Mod. Phys. 2009, 58, 795–798. [Google Scholar]
- Bohm, D. A Suggested Interpretation of Quantum Theory in Terms of “Hidden” Variables I. Phys. Rev. 1952, 85, 166–179. [Google Scholar] [CrossRef]
- Bohm, D.; Hiley, B.J. The Undivided Universe: An Ontological Interpretation of Quantum Theory; Routledge: London, UK, 1993. [Google Scholar]
- Griffiths, R.B. Consistent histories and the interpretation of quantum mechanics. J.Stat. Phys. 1984, 36, 219–272. [Google Scholar] [CrossRef]
- Nelson, E. Derivation of the Schrödinger Equation from Newtonian Mechanics. Phys. Rev. 1966, 150, 1079–1085. [Google Scholar] [CrossRef]
- von Neumann, J. Mathematische Begründung der Quantenmechanik (Mathematical Foundation of Quantum Mechanics). In Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse; Göttinger Akademie der Wissenschaften: Göttingen, Germany, 1927; pp. 1–57. [Google Scholar]
- Messiah, A. Quantum Mechanics; North Holland: Amsterdam, The Netherland, 1965; Volume I. [Google Scholar]
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; Kameda, J.; Kasuga, S.; et al. (Super-Kamiokande Collaboration), Evidence for Oscillation of Atmospheric Neutrinos. Phys. Rev. Lett. 1998, 81, 1562–1567. [Google Scholar] [CrossRef]
- Tonomura, A.; Endo, J.; Matsuda, T.; Kawasaki, T. Demonstration of single-electron buildup of an interference pattern. Am. J. Phys. 1989, 57, 117. [Google Scholar] [CrossRef]
- Silverman, M.P. More than One Mystery, Explorations in Quantum Interference; Springer: Berlin/Heidelberg, Germany, 1995; p. 3. [Google Scholar]
- Duistermaat, J.J. Huygens’ Principle 1690–1990: Theory and Applications; Blok, H., Ferwerds, H., Kuiken, H.K., Eds.; Elsevier: Amsterdam, The Netherlands, 1992; p. 273. [Google Scholar]
- Hadamard, J. Le problème de Cauchy et Les Equations aux Dérivés Partielles Linéaires Hyperboliques; Jacques Gabay: Dover, UK; New York, NY, USA, 1952. [Google Scholar]
- Longhurst, R.S. Geometrical and Physical Optics, 2nd ed.; Longman Group: London, UK, 1967. [Google Scholar]
- Feynman, R.P. QED: The Strange Theory of Light and Matter; Princeton University Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Bohm, D. Quantum Theory; Dover Publications: Exeter, UK; New York, NY, USA, 1989. [Google Scholar]
- Greiner, W. Relativistic Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Laundau, L.D.; Lifchitz, E.M. Quantum Mechanics; Pergamon Press: Oxford, UK, 1959. [Google Scholar]
- Schwinger, J. Quantum Mechanics: Symbolism of Atomic Measurements; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1930. [Google Scholar]
- Heisenberg, W. The Physical Principles of the Quantum Theory; Dover Publications: Exeter, UK; New York, NY, USA, 1949. [Google Scholar]
- van der Waerden, B.L. Sources of Quantum Mechanics; Dover Publications: Exeter, UK; New York, NY, USA, 1968. [Google Scholar]
- Leite Lopes, J.; Escoubès, B. Sources et Evolution de la Physique Quantique, Textes Fondateurs; Masson: Paris, France, 1995. [Google Scholar]
- Wheeler, J.A.; Zurek, W.H. Quantum Theory and Measurement; Princeton University Press: Princeton, NJ, USA, 1983. [Google Scholar]
- Hansen, A.; Ravndal, F. Klein’s Paradox and Its Resolution. Phys. Scr. 1981, 23, 1036. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen Paradox. Physics 1965, 1, 195–200. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. Phys. Rev. Lett. 1982, 49, 1804. [Google Scholar] [CrossRef]
- Kupczynski, M. Closing the Door on Quantum Nonlocality. Entropy 2018, 20, 877. [Google Scholar] [CrossRef] [PubMed]
- Gell-Mann, M. Is nature simple? In The Nature of the Physical Universe, 1976 Nobel Conference; Huff, D., Prewett, O., Eds.; Wiley Interscience: New York, NY, USA, 1979; p. 29. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).