On the Roots of the Modified Orbit Polynomial of a Graph

Abstract

The definition of orbit polynomial is based on the size of orbits of a graph which is $O_G\left(x\right)={\sum }_i{x}^{|}{O}_i|$, where $O_1,\dots ,O_k$ are all orbits of graph G. It is a well-known fact that according to Descartes’ rule of signs, the new polynomial $1-O_G\left(x\right)$ has a positive root in $(0,1)$, which is unique and it is a relevant measure of the symmetry of a graph. In the current work, several bounds for the unique and positive zero of modified orbit polynomial $1-O_G\left(x\right)$ are investigated. Besides, the relation between the unique positive root of $O_G$ in terms of the structure of G is presented.

1. Introduction

The counting polynomials were first introduced in [1,2] and after it other types of counting polynomials were proposed. However, the subject received notable attention from both mathematicians and chemists. Some of them are matching polynomials [3,4,5], independence [6,7], king [8,9], color [9], star or clique polynomials [10,11], choromatic polynomials [12], and orbit polynomials [13], see [14] for more details about counting polynomials.

Recently, Dehmer et al. [15] defined the orbit polynomial of graph G as ${\displaystyle O_G\left(x\right)=\sum _{i=1}^k{x}^{|O_i|}}$ that uses the cardinalities of the orbits. The typical terms of the orbit polynomials are of the form $c{x}^n$, where $|O_i|$’s indicate the vertex orbit sizes. The modified version of this polynomial is defined as $O_G^{\star }\left(x\right)=1-O_G\left(x\right)$, which has a unique positive root $\delta \in (0,1]$, see [16,17,18,19,20,21,22,23,24,25]. In [23], the authors also studied the degeneracy of the orbit polynomial.

In [15], some bounds for the unique and positive zero of $O_G^{\star }$ were computed. The authors indicated that the unique positive root of this new polynomial can be served as a relative measure of a graph symmetry. Here, we compute the location of the unique positive root of several classes of graphs and, as a result, we determine it for a broom graph. In continuing, we analyze the value of the unique zeros of the modified version of orbit polynomials for several classes of real-world networks, and then we investigate the correlation between $\delta$ and the size of the automorphism group.

2. Preliminaries

The vertex-orbit or the orbit of a graph G, with automorphism group $\mathrm{Aut}\left(\mathit{G}\right)$, containing the vertex $v\in V\left(G\right)$ is defined as $\left[v\right]=\{v^{\alpha }:\alpha \in Aut\left(G\right)\}$. A graph is said to be vertex-transitive, if for each vertex $u\in V\left(G\right)$, we have $\left[u\right]=V\left(G\right)$ if and only if for each pair of vertices $u,v\in V\left(G\right)$, $\left[u\right]=\left[v\right]$ or equivalently $u^{\eta }=v$, where $\eta \in \mathrm{Aut}\left(\mathrm{G}\right)$ is an automorphism of G. In a similar way, an edge-transitive graph is a graph with $\left[e\right]=\left[f\right]$, for two arbitrary edges $e,f\in E\left(G\right)$.

The vertex-orbits, under the action of automorphisms on the set of vertices, constitute a partition which captures the symmetry structure of the graph, see [13,16,26,27,28,29,30]. In a complex network, the collections of similar vertices can be used to define communities with shared attributes, see [30].

The orbits of a graph show vertices with similar properties such as having the same degree or the same eccentricity. Conversely, if there exists a property that does not hold for two vertices, then these vertices are not in the same orbit. So, creating several kinds of polynomials on the set of orbits of a graph would help to distinguish vertices that have different properties and thus to separate them into different orbits.

Orbit Polynomial

The orbit polynomial is defined [16] as $O_G\left(x\right)={\sum }_{i=1}^t{x}^{|O_i|},$ where $\{O_1,\dots ,O_t\}$ indicates the set of orbits of graph G. The modified orbit polynomial can be defined as follows:

$$O_G^{\star }\left(x\right)=1-\sum _{i=1}^t{x}^{|O_i|}.$$

The vertex (or edge) orbits, under the action of automorphisms on the set of vertices, constitute a partition which captures the symmetry structure of the graph, see [13,16,26,27,28,29,30]. A decomposition of vertices, in such a way, defines an equivalence relation on the set of vertices of a graph. Hence, two vertices are similar if they are in the same orbit. In a complex network, the collections of similar vertices can be used to define communities with shared attributes, see [30].

3. Methods and Results

In [15], some bounds for the unique and positive zero of $O_G^{\star }$ are computed. In [15], the authors indicated that the unique positive root of this new polynomial can be considered a relevant measure of the symmetry of a graph. This quantity measures symmetry and can therefore be used to compare graphs with respect to this property. It is also shown that the unique positive roots of $O_G$ has useful applications in chemistry, bioinformatics, and structure-oriented drug design. Here, we propose new bounds for the positive zero of $O_G^{\star }$.

Example 1.

It is easy to prove that the cycle $C_n$ is vertex-transitive and then $O_{C_n}\left(x\right)=x^n$ and $O_{C_n}^{\star }\left(x\right)=1-x^n$.

It is clear that one cannot capture considerable information about the structural properties of a graph with the same orbit structure by the orbit polynomial. These properties include, for example, the structure of blocks of a graph and the structure of the automorphism group. In other words, both complete graph $K_n$ and the cycle graph $C_n$ have the same orbit polynomial equal to $O_G\left(x\right)=x^n$, while $\mathrm{Aut}\left({\mathit{K}}_{\mathit{n}}\right)={\mathbb{S}}_{\mathit{n}}$ and $\mathrm{Aut}\left({\mathit{C}}_{\mathit{n}}\right)={\mathit{D}}_{\mathit{2}\mathit{n}}$. In contrast, the orbit polynomial of a non-vertex-transitive graph explore some results about the structural properties of the graph. For example, by having the orbit polynomial of a tree, one can easily check whether it has a central vertex or a central edge. In the following example, we do this for the path graph $P_n$.

Example 2.

The path graph $P_n$ is not vertex-transitive. The automorphism group of this graph is ${\mathcal{Z}}_2$ and thus

$$\begin{array}{c}\hfill O_{P_n}\left(x\right)= \left\{\begin{array}{cc}\frac{n}{2}{x}^2,\hfill & 2\mid n\\ x+\frac{n-1}{2}{x}^2,\hfill & 2\mid n\end{array}\right.,\end{array}$$

and

$$\begin{array}{c}\hfill O_{P_n}^{\star }\left(x\right)= \left\{\begin{array}{cc}1-\frac{n}{2}{x}^2,\hfill & 2\mid n\\ 1-x-\frac{n-1}{2}{x}^2,\hfill & 2\mid n\end{array}\right..\end{array}$$

Example 3.

Consider the star graph $S_n$. It has two vertex-orbits. The central vertex compose a singleton orbit and the pendant vertices compose the second orbit. Hence,

$$\begin{array}{ccc}\hfill O_{S_n}\left(x\right)& =& x+x^{n-1},\hfill \\ \hfill O_{S_n}^{\star }\left(x\right)& =& 1-(x+x^{n-1}).\hfill \end{array}$$

A broom graph $G=B_{n,k}$ is a graph of order n, constructed by coinciding a pendant vertex of $P_k$ with the central vertex of star graph $S_{n-k+1}$ (see Figure 1). Each tree can be decomposed to the union of broom graphs. Hence, the orbit polynomial of all trees can be interpreted as the orbit polynomial of broom graphs.

Example 4.

It is not difficult to see that $\mathrm{Aut}\left(\mathit{G}\right)\cong {\mathbb{S}}_{\mathit{n}-\mathit{k}}$. Hence, the vertices $u_1,\dots ,u_{n-k}$ are in the same orbit, which yields that each vertex of the subgraph ${\mathbb{S}}_{n-k+1}$ compose an orbit. The vertices of the path graph $P_k$ compose k singleton sets. Hence, we obtain

$$\begin{array}{ccc}\hfill O_G\left(x\right)& =& x^{n-k}+kx,\hfill \\ \hfill O_G^{\star }\left(x\right)& =& 1-x^{n-k}-kx.\hfill \end{array}$$

It is well-known that $S_n$ is edge-transitive and thus it has at most two vertex-orbits. In other words, if $e=uv$ is an arbitrary edge of graph G, then $V_1=\left[u\right]$ and $V_2=\left[v\right]$ are two distinct orbits of G and so

$$\begin{array}{ccc}\hfill O_G\left(x\right)& =& x^{|V_1|}+x^{|V_2|},\hfill \\ \hfill O_G^{\star }\left(x\right)& =& 1-(x^{|V_1|}+x^{|V_2|}).\hfill \end{array}$$

In general, if the edge-transitive graph G is not vertex-transitive, then G is bipartite with partition $V\left(G\right)=V_1\left(G\right)\cup V_2\left(G\right)$, and so

$$\begin{array}{c}\hfill O_G\left(x\right)=x^{|V_1|}+x^{|V_2|},and{O}_G^{\star }\left(x\right)=1-(x^{|V_1|}+x^{|V_2|}).\end{array}$$

Roots of Orbit-Polynomial

The unique positive root (denoted by $\delta$) can be applied to quantify the symmetry of a graph. By regarding the numbers and sizes of orbits of automorphism group, it is reasonable to estimate that the graph $G_1$ is more symmetric than $G_2$, if $\delta \left(G_1\right)>\delta \left(G_2\right)$.

If a graph G has k equal sizes orbits, then $O_G\left(x\right)=k{x}^{\frac{n}{k}}$ and thus the orbit polynomial has only zero as a root. Conversly, if the orbit polynomial has only one zero $x=0$, then $O_G\left(x\right)=k{x}^t$, for some $k,t\in \mathbb{N}$. Since, orbits decompose the vertex set, we obtain $kt=n$ or equivalently $t=\frac{n}{k}$. It is clear in the case that $k=1$, G is vertex-transitive and for $k=n$, weconclude that G is asymmetric. We may conclude the following result.

Theorem 1.

The orbit polynomial O of graph G has only zero as its root, if and only if all orbits of G are of equal sizes.

Corollary 1.

$O_G^{\star }\left(x\right)=1-k{x}^{\frac{n}{k}}$ if and only if all orbits of G are of equal sizes.

Corollary 2.

The graph G is a vertex-transitive if and only if $x=1$ is a root of $O_G^{\star }\left(x\right)$.

Proof. 

Suppose G is vertex-transitive, by definition, we obtain $O_G^{\star }\left(x\right)=1-x^n$ which yields that $x=1$ is a root. Conversely, suppose $O_G^{\star }\left(x\right)=1-{\sum }_{i=1}^r{a}_i{x}^{|O_i|}$ and $x=1$ is a root of $O_G^{\star }$. It is not difficult to see that $O_G^{\star }\left(1\right)=1-a_1-\dots -a_r=0$. Since, $a_i\ge 1$, necessarily $r=1$ and $a_1=1$ and thus G has only one orbit. □

Theorem 2.

Suppose G is a graph with two orbits. If zero is the only root of orbit polynomial, then G is either a regular or a bi-regular graph.

Proof. 

Since G has two orbits such as $V_1$ and $V_2$, the orbit polynomial can be written as $O_G\left(x\right)=a_1{x}^{n_1}+a_2{x}^{n_2}$, where $n_1=\left|V_1\right|$, $n_2=\left|V_2\right|$ and $n_1+n_2=n$. If $n_1\ne n_2$, then without loss of generality, suppose $n_1<n_2$. Thus, $O_G\left(x\right)=x^{n_1}(1+x^{n_2-n_1})$ and so $O_G$ has a non-zero root, a contradiction. Hence, $n_1=n_2$ and by Theorem 1, G has two orbits $V_1$ and $V_2$ of equal sizes. If G is not regular, then G is bi-regular, since two vertices in the same orbit have equal degrees. □

Corollary 3.

If zero is a root of orbit polynomial of an edge-transitive graph G, then G is a regular or a bi-regular graph.

Example 5.

Consider three graphs G, H and K in Figure 2. The graph G has two orbits $V_1=\{1,3\}$ and $V_2=\{2,4\}$ and thus $O_G\left(x\right)=2x^2$. Hence, $x=0$ is the only zero of $O_G$ and G is bi-regular. H has two orbits and it is bi-regular. However, K is a 3-regular graph of order 12 with two vertex-orbits $V_1=\{1,2,5,6,8,12\}$ and $V_2=\{3,10,4,7,11,9\}$ which yields that $O_G\left(x\right)=2x^6$.

Theorem 3.

Suppose the multiplicity of the root $x=0$ is $i<n$. Then G has one orbit of size i and the size of other orbits is at least i.

Proof. 

Since the multiplicity of $x=0$ is i, we obtain $O_G\left(x\right)=x^{i}g\left(x\right)$, where $g\left(x\right)$ is a polynomial with $g\left(0\right)\ne 0$. Suppose $g\left(x\right)=b_0+\dots +b_l{x}^l$, where $b_i\in \mathbb{N}$ and $l<n$, then G has $b_0$ orbits of size i and the other orbits are of size at least $i+1$. □

Corollary 4.

Consider a graph G with two orbits $V_1$ and $V_2$, where $|V_1|=n_1<n_2=\left|V_2\right|$. Then $x=0$ is a root of $O_G\left(x\right)$ with multiplicity $n_1$ and the other roots are $i{\omega }^k$$(k=1,\dots ,n_2-n_1$, where $\omega =e^{\frac{2\pi }{n}i}$.

Example 6.

Consider the star graph $S_n$. It has two orbits of sizes 1 and $n-1$. Hence, $O_{S_n}\left(x\right)=x+x^{n-1}$ and its roots are $x=0$ and all roots of equation $x^{n-2}+1=0$. On the other hand, for the complete graph $K_n$, we obtain $O_{K_n}^{\star }\left(x\right)=1-x^n$ and it has n roots

$$1,\omega ,\dots ,{\omega }^{n-1},$$

where $\omega =e^{\frac{2\pi }{n}i}$.

Lemma 1.

For a graph G with n vertices, the maximum number of roots of $O_G\left(x\right)$ and $O_G^{\star }\left(x\right)$ are $n-1$ and n, respectively. In particular, a graph whose orbit polynomial has $n-1$ distinct roots has the structure $K_1+\mathcal{H}$, where $\mathcal{H}$ is a vertex-transitive of order $n-1$. The graph, G, in which $O_G^{\star }\left(x\right)$ has n distinct roots, is vertex-transitive.

Proof. 

It is not difficult to see that the complete graph $G=K_n$ the modified orbit polynomial has the maximum number of roots. For $G\ne K_n$, if $O_G^{\star }\left(x\right)$ has n distinct roots, then necessarily G is vertex-transitive and the first assertion follows. On the other hand, if $O_G$ is a polynomial of degree n, then necessarily, $O_G\left(x\right)=x^n$, which has only $x=0$ as its root. The star graph $S_n$ has $n-1$ distinct roots and we are done. If for a graph $G\ne S_n$, $O_G$ has $n-1$ roots, then necessarily $O_G\left(x\right)$ is of degree $n-1$ and thus G has an orbit of size $n-1$. It is not difficult to see that all graphs by this property have the structure $K_1+\mathcal{H}$, where $\mathcal{H}$ is a vertex-transitive of order $n-1$. □

Dehmer et al. in [15] determined the location of positive zero of modified orbit polynomial a graph in general. They also explored this problem for the path graph $P_n$, the star graph $S_n$ and the complete bipartite graph $K_{m,n}$. In [31], the authors continued this method to investigate the unique positive roots of bi-star graph $B_{m,n}$ and for exhaustive sets of isomers of hydrocarbons with 14 carbon atoms. Here, we state the location of graph measure $\delta$, for the broom graph and a class of graphs with a specific orbit polynomial.

Let $f\left(z\right)={\sum }_{i=0}^n{a}_i{z}^i$, where $a_n\ne 0$ and $a_i\in \mathbb{C}$ $(i=0,1,\cdots ,n)$ be a complex polynomial. The set $K(z_0,r)=\{z\in \mathbb{C}:|z-z_0|\le r\}$, represent a closed disk with central point $z_0$ and radius r. Let $\widehat{K}(z_0,r)=\{z\in \mathbb{C}:|z-z_0|<r\}$.

Theorem 4. 

(Dehmer et al. [18]) Let $f\left(z\right)=a_n{z}^n+a_{n-1}{z}^{n-1}+\cdots +a_0$, where $a_n{a}_{n-1}\ne 0$, be a complex polynomial. All zeros of $f\left(z\right)$ lie in the closed disk

$$\begin{array}{c}\hfill K(0,\frac{1+\mu }{2}+\frac{\sqrt{{(\mu -1)}^2+4M}}{2}),\end{array}$$

where $\mu = |\frac{a_n-a_{n-1}}{a_n}|$, $M={max}_{1\le j\le n}|\frac{a_{n-j}-a_{n-j-1}}{a_n}|$ and $a_{-1}=0$.

Theorem 5.

Suppose G to be a graph on n vertices in which the orbit polynomial is $O_G\left(x\right)=x^{\frac{n}{2}}+2{\sum }_{1\le r\le \frac{n}{2}-1}{x}^r$ and n is even. Then for $n\ge 4$ all roots of $H_u(C_n;x)$ are in $K(0,2)$ and for $n\ge 6$ they are in $\widehat{K}(0,2)$.

Proof. 

We define $F\left(x\right)=(1-x)O_G\left(x\right)$ and suppose $\left|x\right|>1$. Hence, $\left|F\left(x\right)\right|=|-x^{\frac{n}{2}+1}-x^{\frac{n}{2}}+2x|$ and two following cases hold:

Case (1)

If $n=4$, then $|F\left(x\right)|\ge |x|\{|x^{\frac{n}{2}}|-|x^{\frac{n}{2}-1}|-2\}$ and by putting $S\left(\right|x\left|\right)={\left|x\right|}^2-\left|x\right|-2$, we have $\left|F\right(x\left)\right|>0$ when $\left|x\right|>2$ and so all roots are in $K(0,2)$.

Case (2)

If $n\ge 6$, then

$$\begin{array}{ccc}\hfill {\left|x\right|}^{\frac{n}{2}}-{\left|x\right|}^{\frac{n}{2}-1}& =\hfill & \hfill {\left|x\right|\left\{\right|x|}^{\frac{n}{2}-1}-{\left|x\right|}^{\frac{n}{2}-2}{\}>|x|}^{\frac{n}{2}-1}-{\left|x\right|}^{\frac{n}{2}-2}{>\cdots >\left|x\right|}^3-{\left|x\right|}^2\\ & >\hfill & \hfill {\left|x\right|}^2-\left|x\right|.\end{array}$$

For $\left|x\right|\ge 2$ we have ${\left|x\right|}^{\frac{n}{2}}-{\left|x\right|}^{\frac{n}{2}-1}-{2>\left|x\right|}^2-\left|x\right|-2\ge 0$. This means that for $n\ge 6$ all roots of F are in $\widehat{K}(0,2)$. This completes the proof.

□

Theorem 6.

Suppose $f_n\left(x\right)=1-O_G\left(x\right)$. Then

(1)

For each $n\in N$, $f_n$ has exactly a unique real root in $(0,1)$.

(2)

If $\left\{{\delta }_n\right\}$ is the sequence of roots of $f_n\left(x\right)$’s, then ${\delta }_n$ tends to $\frac{1}{3}$ if n is sufficiently large.

Proof. 

(1)

Since the number of sign changes in $f_n$ is one, the Descartes rule of signs yields that $f_n$ has at most one positive root. On the other hand, $f_n\left(0\right)>0$ and $f_n\left(1\right)<0$, by using Mean Value Theorem, we conclude that for each n, $f_n$ has a root in $(0,1)$.

(2)

Suppose ${\delta }_n$ is a real root of $f_n$. We have

$$\begin{array}{ccc}\hfill f_n\left(x\right)& =& 1-(x^{\frac{n}{2}}+2\sum _{r=1}^{\frac{n}{2}-1}{x}^r)=1-(x^{\frac{n}{2}}+x^{\frac{n}{2}}-x^{\frac{n}{2}}+2\sum _{r=1}^{\frac{n}{2}}{x}^r)\hfill \\ & =& 1+x^{\frac{n}{2}}-2\sum _{r=1}^{\frac{n}{2}}{x}^r.\hfill \end{array}$$

We claim that the roots of $f_n$ and $g_n\left(x\right)=x^{\frac{n}{2}+1}+x^{\frac{n}{2}}-3x+1$ are the same in interval $(0,1)$. To do this, we know ${\sum }_{r=1}^{\frac{n}{2}}{x}^r=\frac{x(1-x^{\frac{n}{2}})}{1-x}$ and thus $f_n\left(x\right)=0$ implies that $(1-x)(1+x^{\frac{n}{2}})-2x(1-x^{\frac{n}{2}})=0$, or equivalently, $1+x^{\frac{n}{2}}-x-x^{\frac{n}{2}+1}-2x+2x^{\frac{n}{2}+1}=0$. This yields that $x^{\frac{n}{2}+1}+x^{\frac{n}{2}}=3x-1$. The polynomial $f_n\left(x\right)$ has no real zero in $(0,\frac{1}{3})$, since for $0<x<\frac{1}{3}$, we have $3x-1<0$. We obtain

$$\begin{array}{c}\hfill 3x-1<0<x^{\frac{n}{2}+1}+x^{\frac{n}{2}}.\end{array}$$

This implies that for each $x\in (0,\frac{1}{3})$, we have $0<x^{\frac{n}{2}+1}+x^{\frac{n}{2}}-3x+1=f_n\left(x\right)$. On the other hand, $f_n\left(1\right)<0$. This yields that $f_n$ has a root in $[\frac{1}{3},1)$. Finally, suppose $g_n\left({\delta }_n\right)=0$. Hence, ${\delta }_n^{\frac{n}{2}+1}+{\delta }_n^{\frac{n}{2}}-3{\delta }_n+1=0$. Since for each $n\in \mathbb{N}$, ${\delta }_n^{\frac{n}{2}+1}+{\delta }_n^{\frac{n}{2}}=3{\delta }_n-1$, all terms of $3{\delta }_n-1$ are positive. For given $ϵ>0$, put $N=2\left[{log}_{{\delta }_n}^{\frac{ϵ}{2}}\right]+2$. Then for $n\ge N$, we have

$$\begin{array}{c}\hfill {\delta }_n^{\frac{n}{2}+1}+{\delta }_n^{\frac{n}{2}}\le 2{\delta }_n^{\frac{n}{2}}\le 2{\delta }_n^{\frac{N}{2}}=2({\delta }_n^{[{log}_{{\delta }_n}^{\frac{ϵ}{2}}]+1})<2(\frac{ϵ}{2})=ϵ.\end{array}$$

Hence, if n is sufficiently large, then ${\delta }_n^{\frac{n}{2}+1}+{\delta }_n^{\frac{n}{2}}$ or equivalents $3{\delta }_n-1$ tends to zero. This means that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\delta }_n=\frac{1}{3}.\end{array}$$

□

Theorem 7.

Let $g_{n,k}\left(x\right)=-x^{n-k}-kx+1$ and $1\le k\le n$. Then, $g_{n,k}\left(x\right)$ has a unique positive root in the interval $(\frac{1}{k+1},\frac{1}{\sqrt[n-k]{k+1}})$. If $\left\{z_{n,k}\right\}$ is a sequence of positive roots $g_{n,k}$, then $z_{n,k}$ tends to $\frac{1}{k}$, if n is sufficiently large.

Proof. 

By using Descartes’ rule of signs, we yield that $g_{n,k}\left(x\right)$ has at most one real root. On the other hand, one can see that $g_{n,k}\left(0\right)=1>0$ and $g_{n,k}\left(1\right)=-k<0$ implies that $g_{n,k}\left(x\right)$ has a unique positive root in $(0,1)$. For $n-k=1$, the unique positive root of $g_{n,k}\left(x\right)$ is $z_{n,k}=\frac{1}{1+k}$. Let $n-k>1$, for all $x\in (0,1)$, we obtain

$$\begin{array}{c}\hfill x^{n-k}<xand-x<-x^{n-k}.\end{array}$$

Hence

$$\begin{array}{c}\hfill -(1+k)x+1<-x^{n-k}-kx+1<-(1+k)x^{n-k}+1.\end{array}$$

The left side yields that $-(1+k)x+1=0$ if $x=\frac{1}{1+k}$. So, $0<-x^{n-k}-kx+1$ for $x=\frac{1}{1+k}$. Similarly, the right side yields to $-x^{n-k}-kx+1<0$ if $x=\frac{1}{\sqrt[n-k]{1+k}}$. This complete the first assertion. Now, suppose, $z_{n,k}$ is the positive root of polynomial $g_{n,k}$. Thus

$$\begin{array}{c}\hfill -z_{n,k}^{n-k}-k{z}_{n,k}+1=0,\end{array}$$

and

$$\begin{array}{c}\hfill z_{n,k}^{n-k}=1-k{z}_{n,k}.\end{array}$$

Since $z_{n,k}\in (0,1)$, $z_{n,k}^{n-k}$ tends to zero if n is sufficiently large and the proof is complete. □

Corollary 5.

The modified orbit polynomial of a broom graph $B_{n,k}$, has a unique positive root in

$$\begin{array}{c}\hfill (\frac{1}{k+1},\frac{1}{\sqrt[n-k]{k+1}}).\end{array}$$

In addition, this root tends to $\frac{1}{k}$, if n is sufficiently large.

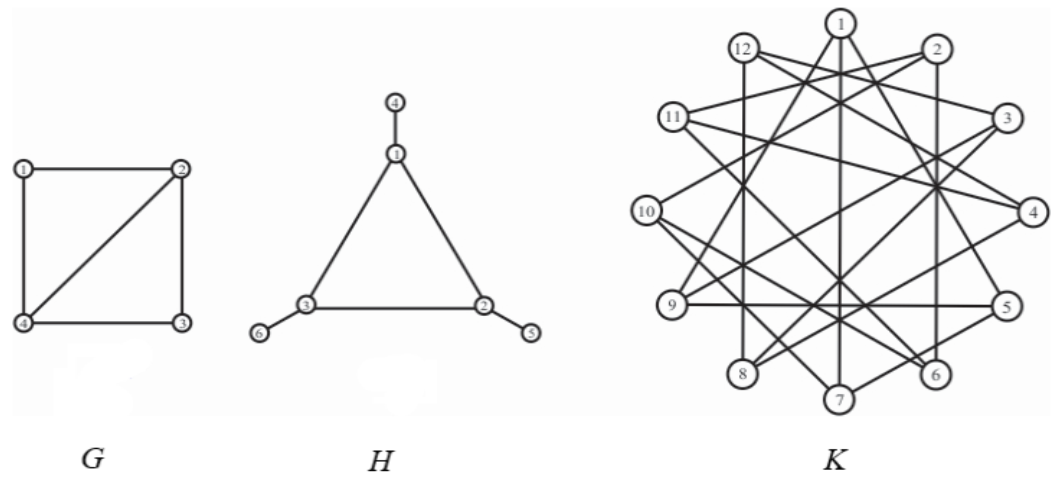
4. Applications

As we showed in the last section, the orbit polynomial has a unique positive root in interval $(0,1]$ and this value can be considered as a relevant measure of the symmetry of a graph, see [15]. In [15,32], it is shown that $\delta$ is a degenerate measure for sorting distinct graphs with the same vertex-orbits. Several classes of graphs were applied to determine some properties of graphs such as branching, symmetry, cyclicity and connectedness. In [15], six classes of trees of orders 15–19, where chosen and the results indicated a weak correlation between $\delta$ and S. Although, all considered graphs are without loops and directed or multiple edges, but the definition of orbit polynomial and then the positive root can be generalized for non-simple graphs, especially for weighted graphs. For instance, for a molecular graph with heteroatoms and multiple bonds [30].

It is clear that if a graph G on n vertices is asymmetric, then the modified orbit polynomial is $1-nx$ and thus the unique positive root is $\frac{1}{n}$. For a vertex-transitive graph, $O_G^{\star }=1-x^n$ which means that for two vertex-transitive graphs of the same order $\delta =1$. So, a natural question arises: "What is the relation between the unique positive roots of graphs with the size of automorphism groups?". On the other hand, applying the automorphism group method enables us to analyze networks by capturing information about the number of interconnections of components.

Example 7.

Consider the graph $\mathcal{G}$ as depicted in Figure 3. It is the basic building of most of real world networks. In [30], the authors showed that $O_{\mathcal{G}}\left(x\right)=12x+5x^2+x^3+2x^4$ and $O_{\mathcal{G}}^{\star }\left(x\right)=1-[11x+6x^2+x^3+2x^4]$. They showed that $\delta \left(O_{\mathcal{G}}^{\star }\right)=0.46$.

Continuing this paper, a set of well-known real-world networks with distinct topologies are collected in

Table 1. The size of the automorphism group and the real positive roots of some real-world networks.

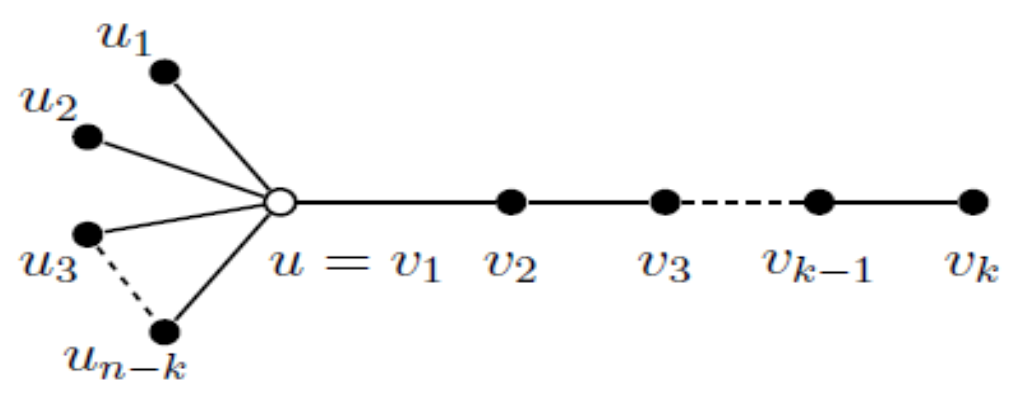
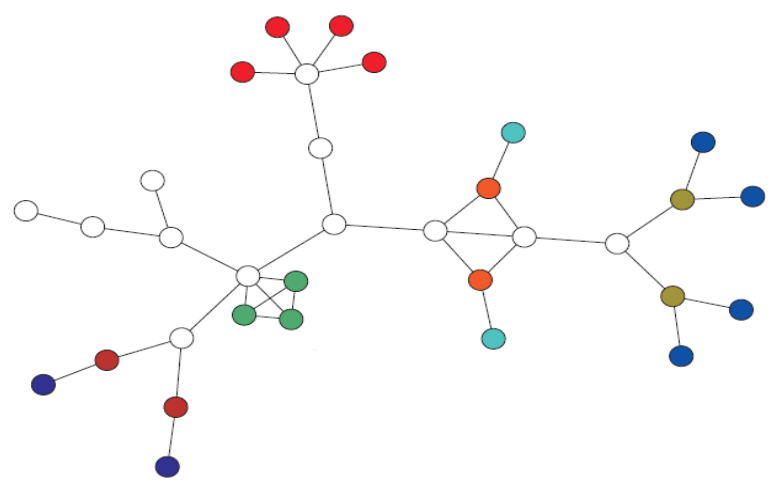
Biological Networks	n	$\left|\mathbf{Aut}\right|$	$\mathit{\delta }$
Biological Networks
Human B Cell Genetic	5.930	$5.937\times {10}^{13}$	$0.00017099$
Caenorhabditis elegans Genetic	2.060	$6.998\times {10}^{161}$	$0.00062575$
BioGRID Human	7.013	$1.260\times {10}^{485}$	$0.00017639$
BioGRID Saccharomyccs cerevisiae	5.29	$6.8622\times {10}^{64}$	$0.00019580$
BioGRID Drosophila	7.371	$3.068\times {10}^{493}$	$0.00016897$
BioGRID Mus musculus	209	$5.348\times {10}^{125}$	$0.022144$
Yeast Protein Interactions	1.458	$1.066\times {10}^{254}$	$0.0011599$
c. elegans metabolic	453	$1.932\times {10}^{10}$	$0.0025702$
Technological networks
Internet	22.332	$1.282\times {10}^{11298}$	$0.00010350$
US Power Grid	4.941	$5.185\times {10}^{152}$	$0.00023803$
US Airports	332	$2.591\times {10}^{24}$	$0.00404718$
www California search subnet	5.925	$1.241\times {10}^{1298}$	$0.00028200$
www EPA.gov subnet	4.253	$1.277\times {10}^{2321}$	$0.00049924$
www Political Blogs	1.222	$2.399\times {10}^{35}$	$0.00087411$
Social networks
Email	1.133	$1.528\times {10}^9$	$0.00092164$
Media ownership	4.475	$3.363\times {10}^{4818}$	$0.0013278$
Geometry Co-authorship	3.621	$1.899\times {10}^{320}$	$0.00044185$
Erdös Collaboration	6.927	$3.461\times {10}^{4222}$	$0.00054912$
PhD network	1.025	$2.981\times {10}^{292}$	$0.00252451$

. Analyzing the reported data shows that the symmetry measure $\delta$ is not highly correlated with the size of the automorphism group. In other words, for two equal size graphs with the same automorphism group, the positive root of the modified orbit polynomial may not capture structural information meaningfully.

5. Summary and Conclusions

Studying the structural complexity of networks has yielded plenty of effective results in the theory of graph and applied branches such as engineering and data analysis. The current work aims to make a further contribution to this research area. It is focused on measures designed for comparing graphs with respect to symmetry. In other words, in this text, we have investigated the orbit polynomial for some classes of graphs. On the other hand, subtracting the orbit polynomial from 1 results in a modified orbit polynomial that has a unique positive root in the interval $(0,1]$, which can serve as a respective measure of the graph symmetry. The importance of this root is expressive of symmetry and can thus be used to contrast graphs with respect to that property. We proved several inequalities on the unique positive roots of a modified version of the orbit polynomial corresponding to the given graph.

As a result, we showed that, for the broom graph $B_{n,k}$, if n is sufficiently large then the unique positive root tends to $\frac{1}{k}$. Finally, we have analyzed the value of the unique zeros of the modified version of orbit polynomial for several classes of real-world networks. Analyzing the reported data show that the symmetry measure $\delta$ is not highly correlated with the size of the automorphism group. This means that the degeneracy of this root relative to the existing symmetry measure is quite low and for two equal size graphs with the same automorphism group, $\delta$ may not meaningfully capture structural information.