Abstract
Random variables in biology, social and health sciences commonly follow skewed distributions. Many of these variables can be represented by exGaussian functions; however, in practice, they are sometimes considered as Gaussian functions when statistical analysis is carried out. The asymmetry can play a fundamental role which can not be captured by central tendency estimators such as the mean. By means of Monte Carlo simulations, the effect of a small asymmetry in the generating functions of the chi distribution is studied. To this end, the k generating functions are taken as exGaussian functions. The limits of this approximation are tested numerically for the practical case of three health-related variables: one physical (body mass index) and two cognitive (verbal fluency and short-term memory). This work is in line with our previous works on a physics-inspired mathematical model to represent the reaction times of a group of individuals.
1. Introduction
The chi and chi-squared distributions are well-known continuous probability distributions widely used in Applied Statistics [1,2,3,4,5]. The fact that they can be generated by a set of Gaussian-distributed random variables makes them amenable to simulations. We devoted a previous work to study the percentile ratios in a chi distribution [6].
A chi distribution of degrees of freedom is found in physics to model the velocities of the independent particles of an ideal gas in thermodynamic equilibrium. Similarly, a chi-squared distribution models the energies of the particles in the same physical system. Another typical case from physics is the Rayleigh distribution (chi of k = 2 degrees of freedom).
In one of our previous works [7], we found a new interesting application of the chi distribution of k = 3 degrees of freedom, that is, of the Maxwell–Boltzmann (MB) distribution. In reference [8] we proved that the reaction times (RTs) of children responding independently to visual stimuli in a short time (hundreds of milliseconds) and without exchanging information are correlated. We interpreted this fact as an experimental evidence for the existence of a system of individuals (or collective). In order to gain insights into this correlation, we developed a physics-inspired mathematical model in reference [7] to represent these correlations. In fact, we could elucidate a correspondence between a system of particles and a group of correlated individuals.
We are rather interested in the conceptual modelling of different situations using the chi distribution. In this respect, in our recent work we have been studying the limits within which the chi distribution can still represent well probability distributions originated from generating functions which are not necessarily Gaussians of equal variances. For example, in reference [9], we studied the limits of the chi modelling for the case of unequal variances in the generating Gaussians. We also proposed a discrete model and an ansatz to calculate the only parameter of this distribution as a function of the unequal variances of the generating Gaussian.
In line with our previous works [7,9], we have extended here the simulation study of the chi distribution for the case of asymmetric generating functions. In this respect, the exGaussian function is a simple, flexible and intuitive function that can be used to represent a skewed distribution as it results from the convolution between the Gaussian and exponential decay functions. The convolution between two functions can be easily simulated as the sum of the respective randomly generated variables. Two practical examples which can be represented by exGaussians are the reaction time distributions in Experimental Psychology [10,11,12,13,14,15,16,17] or the peaks in Chromatography [18].
In this paper we will carry out Monte Carlo simulations to study the distribution Z that originates from combining k generating functions with certain asymmetry (), as , and will evaluate the result by means of a fit to a chi distribution. The level of asymmetry is considered by using exGaussians as generating functions. Our aim is to explore the level of asymmetry for which the fit to chi distribution can be still considered reasonably good for practical applications. Our approach is useful to model multiple situations in health and social sciences where random variables commonly follow asymmetrical distributions. In this respect, an example involving health-related variables is also included in this work.
2. Methodology
2.1. Generalities on the Chi Distribution
The chi distribution is a continuous probability distribution of a random variable defined as
where each of the , , is a Gaussian-distributed independent random variable. Each one of the k variables follows a Gaussian distribution with mean zero and variance to achieve unity. In Ref. [9] we analysed the case of different values of the variance for each Gaussian component j. In the present paper we propose to study the case in which the components deviate from exact Gaussianity, instead exhibiting a certain degree of asymmetry. We propose to model the deviation of each component from pure Gaussianity, considering them as exGaussian distributions. The exGaussian distribution [10] is given by
where erfc is the complementary error function. The above is the result of convoluting the pure Gaussian
with the exponential distribution
where and are the mean and standard deviation of the Gaussian component and the decay constant of the exponential. Let us recall that, if a random variable X is distributed according to (3), and a random variable Y is distributed according to (4), then the sum is distributed according to the exGaussian (2). In this way, the parameters , are not the mean and the standard deviation of the exGaussian distribution (2), but those of its Gaussian component (3). Thus the parameter is a measure of the skewness of the exGaussian distribution, i.e., of its deviation from pure Gaussianity. The value corresponds to a pure symmetric Gaussian [9].
On the other hand, the probability density function corresponding to (1) is given by
In the case when all the variances of the k generating Gaussians take a value different from one, then the above generalises to [9]
where B is related to the variance of distribution (6). The chi distribution as stated in (1) describes a k-dimensional ideal gas of free, independent particles. In this latter case, the k variances are all equal. The cumulative distribution function corresponding to (6) is given by
where is the upper incomplete gamma function [19].
A particularly interesting case of the above appears in the statistical mechanics of ideal gases [20]. This is the case of a chi distribution with degrees of freedom. Then the random variables are the three components of the velocities of the particles. These components are Gaussian-distributed, and their modulus is distributed according to (6). This special case, called the Maxwell–Boltzmann distribution [21,22], is such that all three component distributions are centered around , and the three variances are all equal (and proportional to the temperature of the gas). A k-dimensional ideal gas would be represented by (6).
2.2. Monte Carlo Simulations for Non-Gaussian Generating Distributions
In this paper we will perform Monte Carlo simulations to generate one random variable Z obtained as . Each one of the is a random variable whose probability density function resembles a Gaussian but however has some degree of asymmetry (for the exGaussian [10]). In this work we considered (see Figure 1, and Table 1 and Table 2). This asymmetry will be implemented considering distributions such as the exGaussians presented in (2). As we have stated above, a random variable following an exGaussian can be simulated by summing a random variable following a Gaussian distribution and another random variable following an exponential decay distribution. We will first simulate k generating exGaussians, each one with a vanishing value of the mean and standard deviations all equal to one. A total of random numbers were generated to obtain the probability distribution of the variable Z. The generating exGaussian random variables () will be chosen to have different levels of asymmetry. All fittings are performed by using the non-linear fitting algorithm of Levenberg–Marquardt [23,24]. We used the FORTRAN 90 programming language to make all calculations. The machine epsilon is for the “double precision” real type. The same methodology as in our previous article [9] to study the modified chi distribution for the case of unequal variances in the generating Gaussians was followed. The cases of k = 3 and k = 5 degrees of freedom are developed hereafter in a general way.
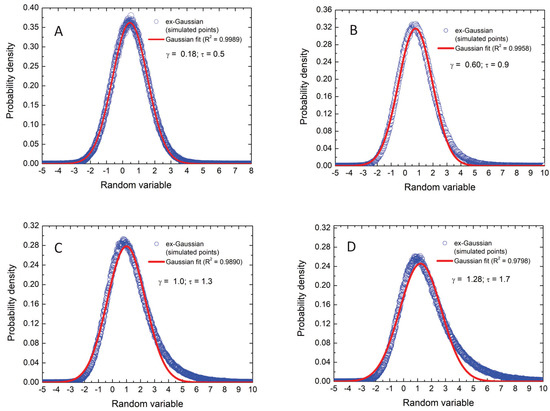
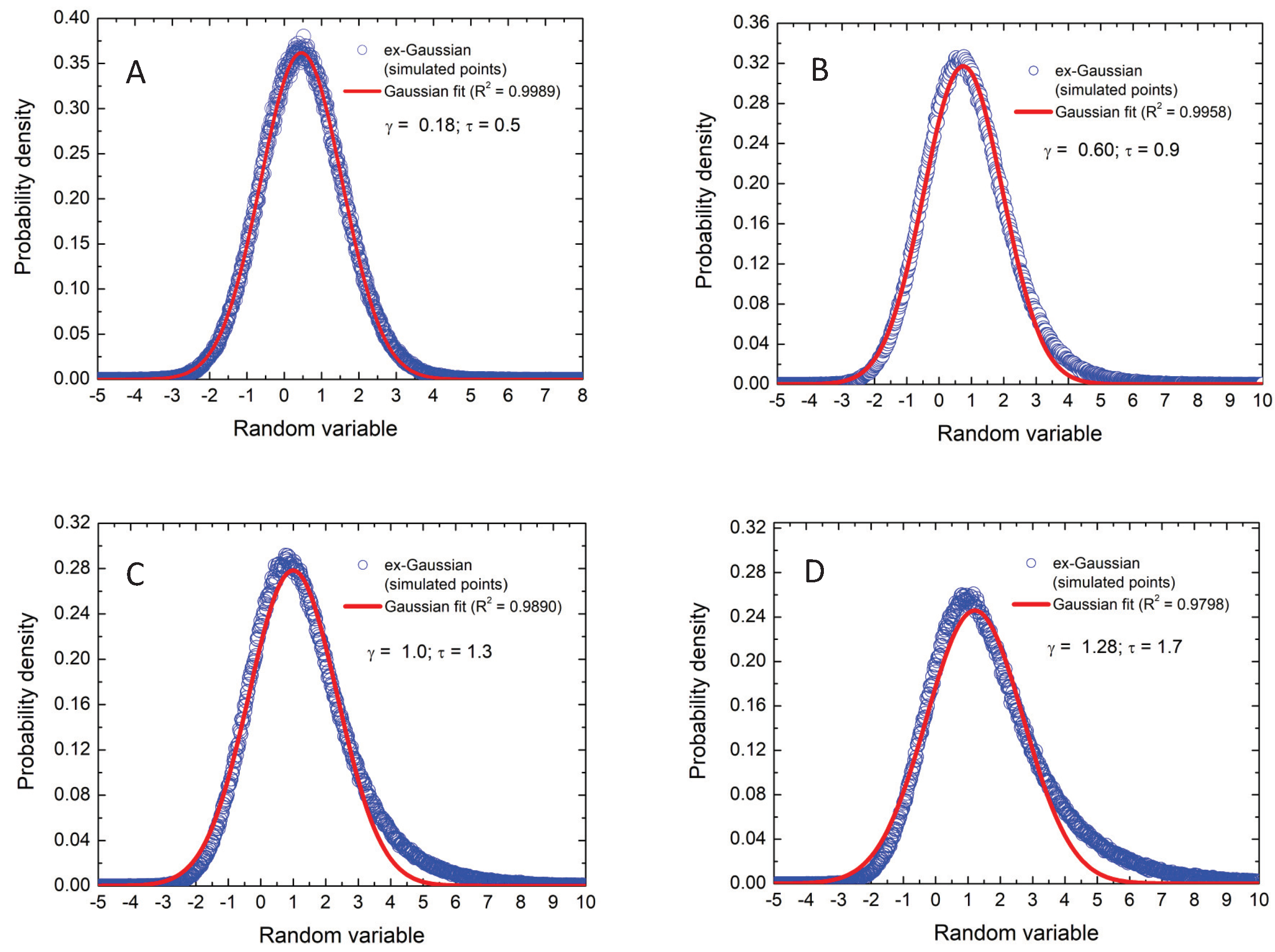
Figure 1.
Gaussian fittings to exGaussian functions generated from Monte Carlo simulations. Several increasing values for the asymmetry were chosen, that is, = 0.18 (panel (A)), = 0.60 (panel (B)), = 1.0 (panel (C)), and = 1.28 (panel (D)).

Table 1.
Results for different levels of asymmetry when considering generating ex-Gaussians. The columns in order show: the set number, the values of for each of the generating exGaussians (, , and ), the corresponding percentage difference between the smallest and the largest value of (), the mean asymmetry among the three generating exGaussians (⟨⟩), the calculated parameter (), the fitted parameter (), the mean coefficient of determination (⟨⟩), and the mean percentage difference between and over the values within the set (⟨⟩).

Table 2.
Results for different levels of asymmetry when considering generating exGaussians. The columns in order show: the set number, the values of for each of the generating exGaussians (, , , , and ), the corresponding percentage difference between the smallest and the largest value of (), the mean asymmetry among the five generating exGaussians (⟨⟩), the calculated parameter , the fitted parameter (), the mean coefficient of determination (⟨⟩), and the mean percentage difference between and over the values within the set (⟨⟩).
2.3. Measurement of Goodness of Fit between Data and Models
Statistical analysis was performed to measure the quality of the proposed model with respect to the data, including both simulations and real health-related variables. The goodness of fit of the model with respect to the data was first studied by the coefficient of determination . It quantifies the percentage of data variance that can be explained by the model [25] with values in the range [0, 1] representing from a null fit to a perfect fit.
In addition, a non-parametric test was assessed to quantify the equality between the two continuous probability distributions under comparison in each case: the ex-Gaussians, and the distributions for the simulated or real data. Kolmogorov–Smirnov (KS) distance is the maximum vertical distance between the cumulative density functions (CDFs) of the simulated/real data, and the model [26,27]. This statistic is sensitive to differences in both location and shape of the CDFs [28,29]. We also checked the associated p-value to check whether both distributions can be considered to follow the same distribution (i.e., the null hypothesis is true).
Finally, quantile–quantile (Q-Q) plots are also depicted to study the goodness of fit between data and models [30]. Each point of the plot corresponds to one of the quantiles of the first distribution (simulated/real data) which is compared against the same quantile of the second distribution (the model). Thus, points in the Q-Q plot lie approximately on the line when data follow the same distribution. We used these probability plots to confirm that both probability distributions (simulated/real data and the model) had good fitting agreement.
3. Results and Discussion
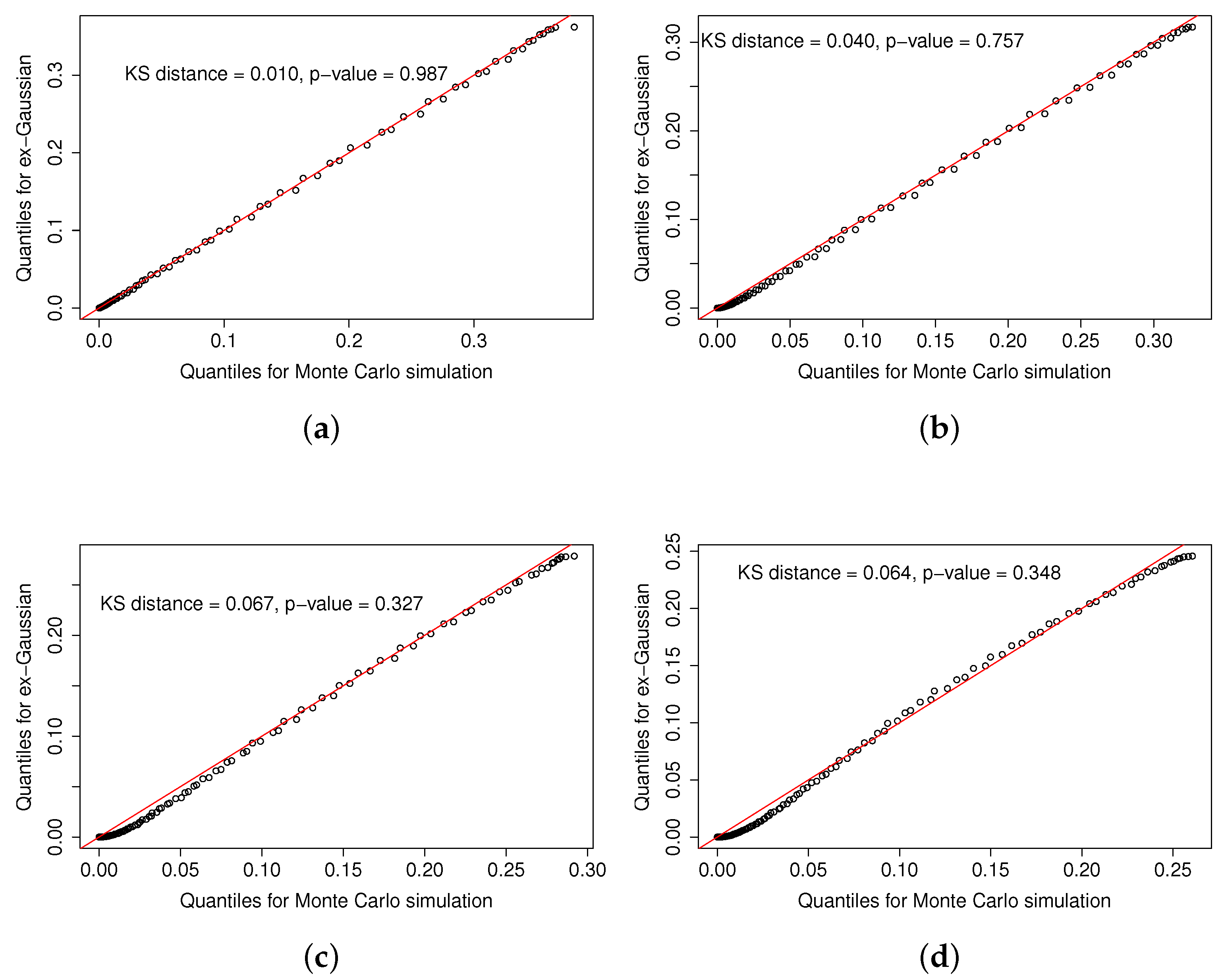
Figure 1 shows the probability densities of the exGaussian random variables () obtained for four different values of the parameter and therefore of the asymmetry in the generating exGaussians. The coefficient of determination () of a Gaussian fit (red solid line) has also been included. The larger the value of the lower the values of , as expected. For the sake of clarity, quantile–quantile plots of these probability densities are also shown in Figure 2. The good quality of the fittings can be observed since the points lie approximately in a line. This is also remarked with the low values of Kolmogorov–Smirnov distances, and the p-values higher than 0.5 which show strong acceptance of the null hypothesis: data follow the same distribution.
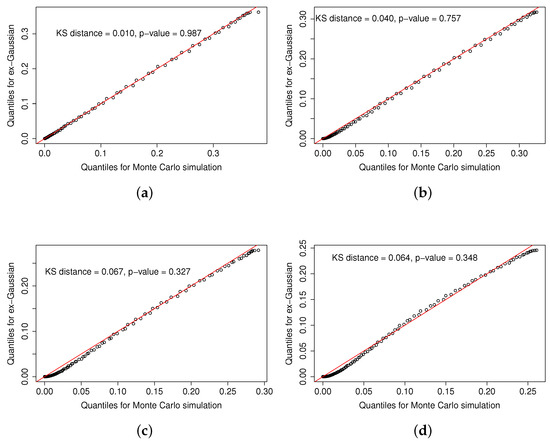
Figure 2.
Quantile–quantile plots of the Gaussian fittings to exGaussian functions generated from Monte Carlo simulations for the different asymmetry values shown in Figure 1, that is, = 0.18 (panel (a)), = 0.60 (panel (b)), = 1.0 (panel (c)), and = 1.28 (panel (d)). Each panel also includes the Kolmogorov–Smirnov distance and the associated p-value.
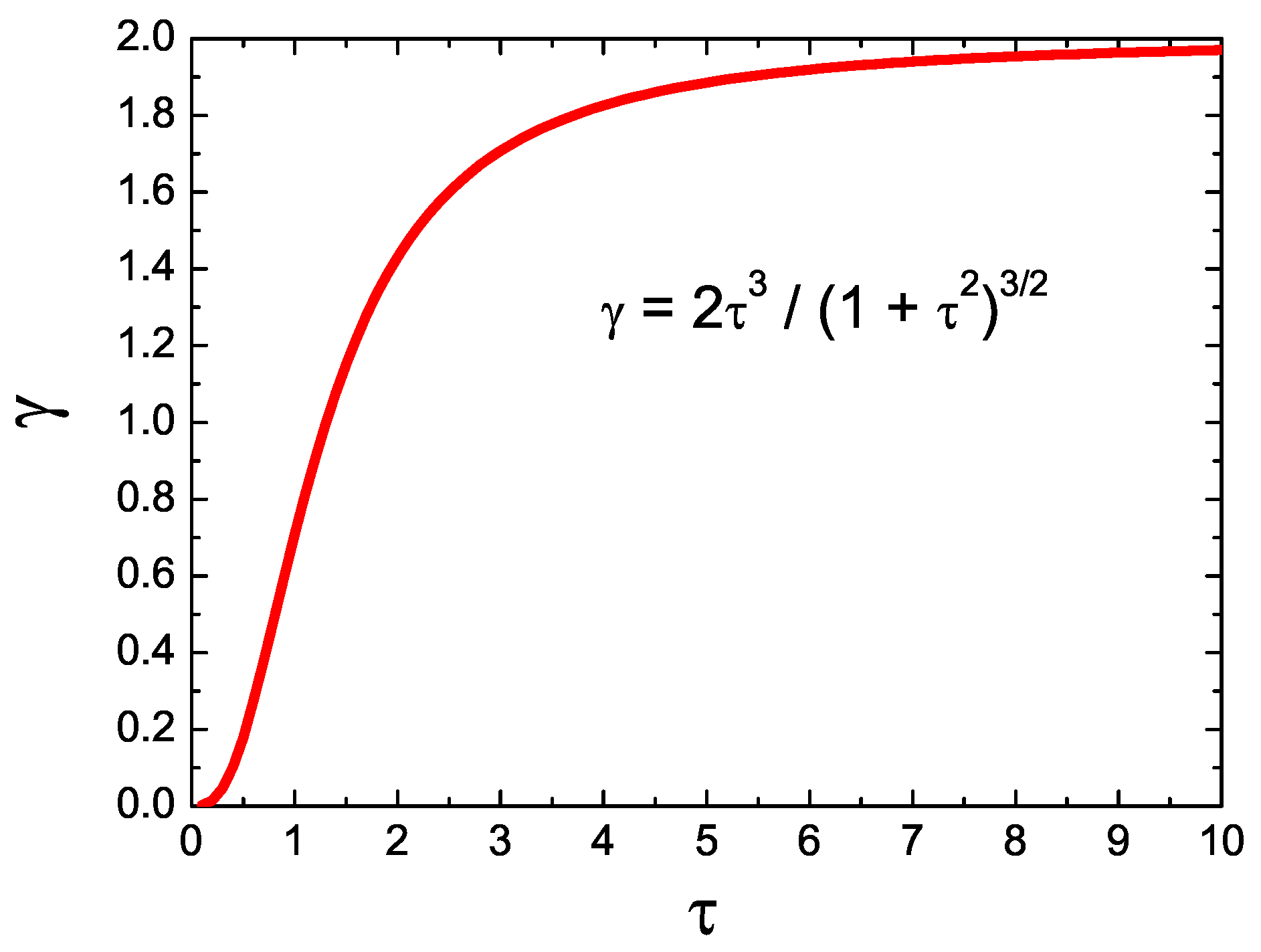
Figure 3 includes the asymmetry of the generating exGaussian random variables () as a function of for (mean value) and (standard deviation). It can be seen that almost a constant value of the asymmetry is reached when increases. Values of asymmetry in the linear region of this curve were chosen for this work (). A linear fit for yields a coefficient of determination of 0.97.
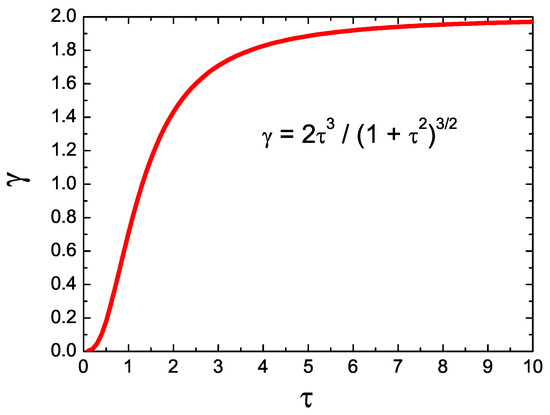
Figure 3.
Asymmetry of the exGaussian distribution as a function of for and .
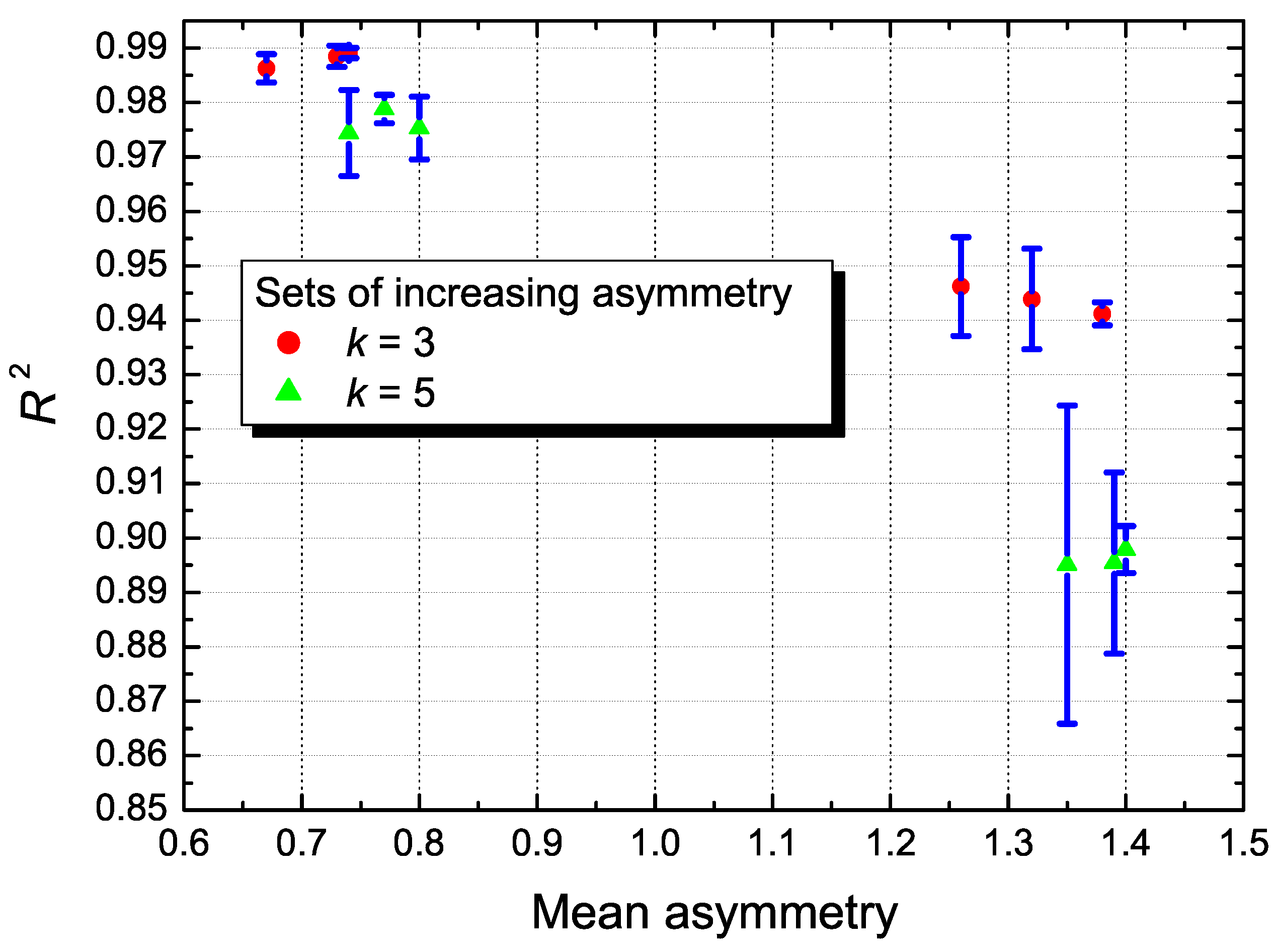
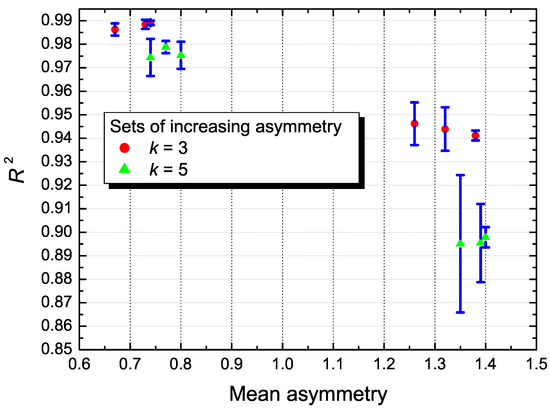
The resulting distributions of the variable Z for three and five generating exGaussians, and for different values of the asymmetry were fitted by using chi distributions of and degrees of freedom, respectively. All the generating exGaussians were centered at and divided by the corresponding mode in order to standardise the resulting distribution. The mean asymmetry is calculated over the asymmetry values within each of the sets shown in Table 1 and Table 2. The values of the coefficient of determination are represented in Figure 4 versus the mean asymmetry for several increasing values of asymmetry. A total of random numbers were used to obtain the probability distributions to which chi distributions are fitted.
A change in the values of the generating exGaussians leads to a change in their variances () as they depend on this parameter as [10]. In Figure 5, the values of (the fitted B parameter of the chi distribution (6)) are compared with the B value as calculated from . This expression is an extended version of the ansatz defined in our previous reference [9], , but for the case when a small asymmetry is present. It should be noticed that the exGaussian parameters involved in the calculation of (i.e., and ) should be divided by the corresponding mode of each generating Gaussian.
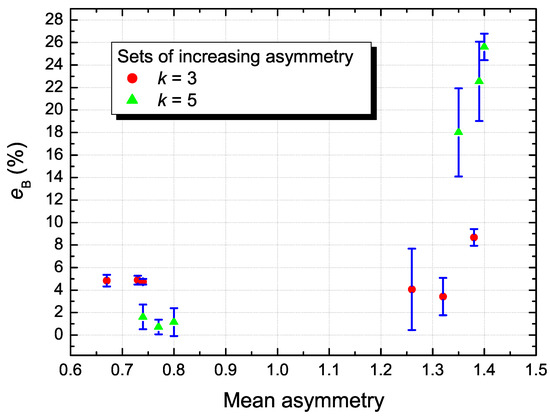
Figure 5.
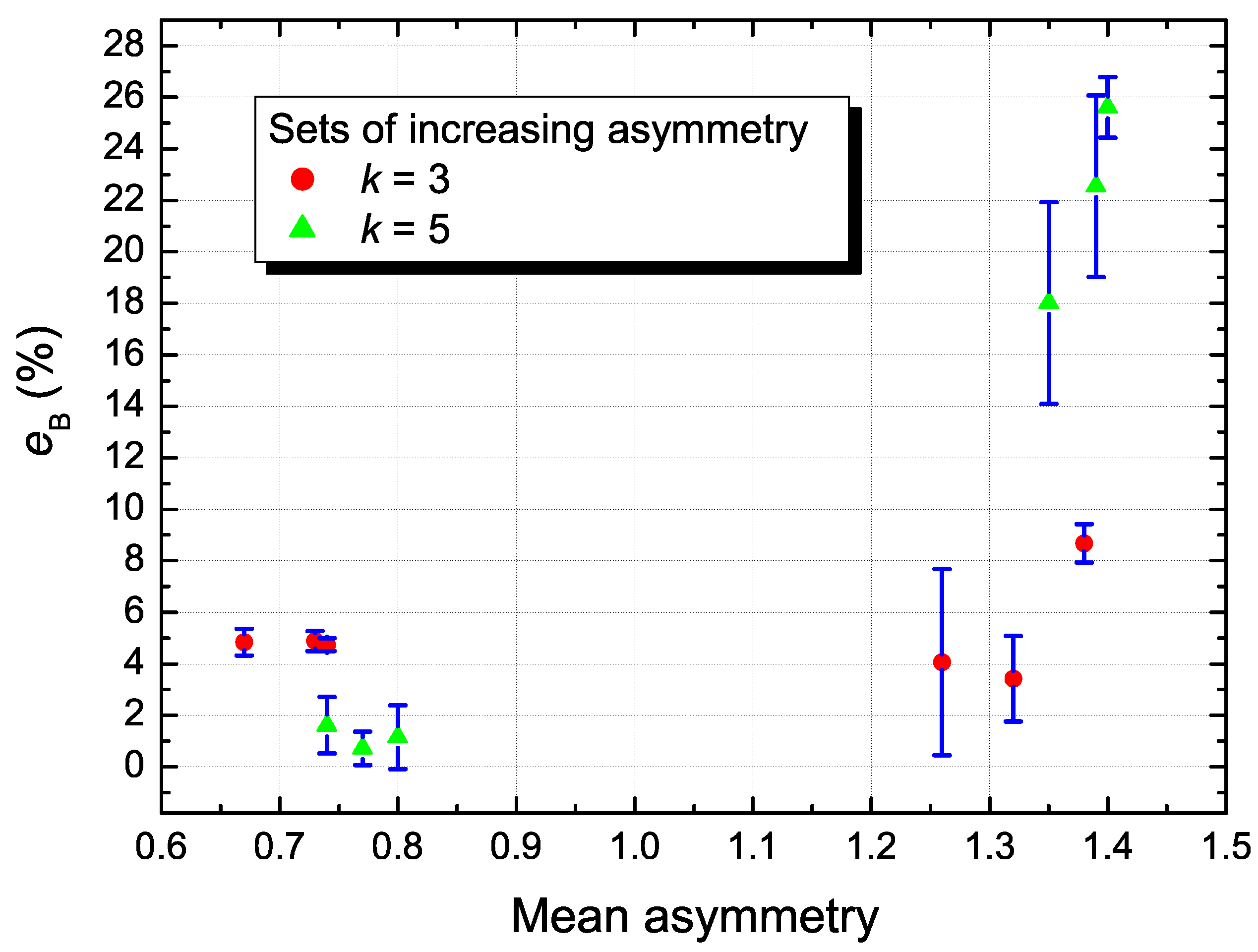
Percentage difference () between the fitted () and calculated parameter () of the chi distribution (of and ) when used to fit the simulated distribution (Z). The error bars represent the standard deviations over the values within each set.
The results shown in Figure 4 and Figure 5 are summarised in Table 1 and Table 2, respectively. For very low values of asymmetry (<0.8), the difference between and (i.e., the error ) remains very small (<6%) and is reasonably good (>0.97). However, for asymmetry values larger than 1.2 the results for are higher and lower, especially for k = 5, where is below 0.9 and higher than 18%.
In order to illustrate the presented work with real data, three health-related variables were chosen from the seventh wave of SHARE (Survey of Health, Ageing and Retirement in Europe) (released 17 December 2020) [31,32,33]. The three variables in this example were: one related to physical health (body mass index–BMI), and two related to cognitive frailty (verbal fluency, measured as the number of animals named within a minute; and short-term memory, measured as the number of words the participant was able to repeat from a 10-word list). We considered a sample formed by 1503 participants from several European countries. We chose those three variables to illustrate results since they were numeric and not categorical, in which case the proposed representation may be compromised.
The empirical probability distributions of these variables were fitted by exGaussian functions (Figure 6A–C) with a good coefficient of determination. For the sake of clarity, quantile–quantile plots of these probability densities are also shown in Figure 7, where it is depicted that both probability distributions match to a straight line. In addition, the good quality of the fittings can be visually checked with the small Kolmogorov–Smirnov distance values, while p-values are higher than 0.05, showing no-significant differences.
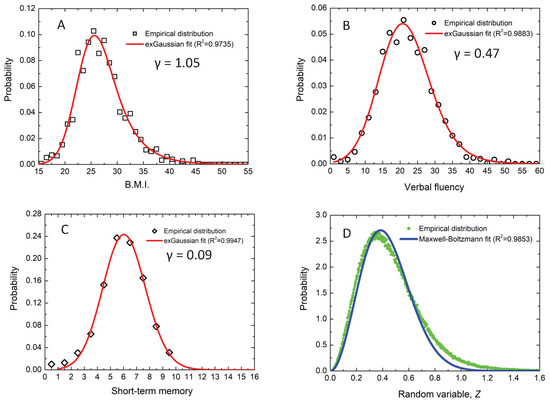
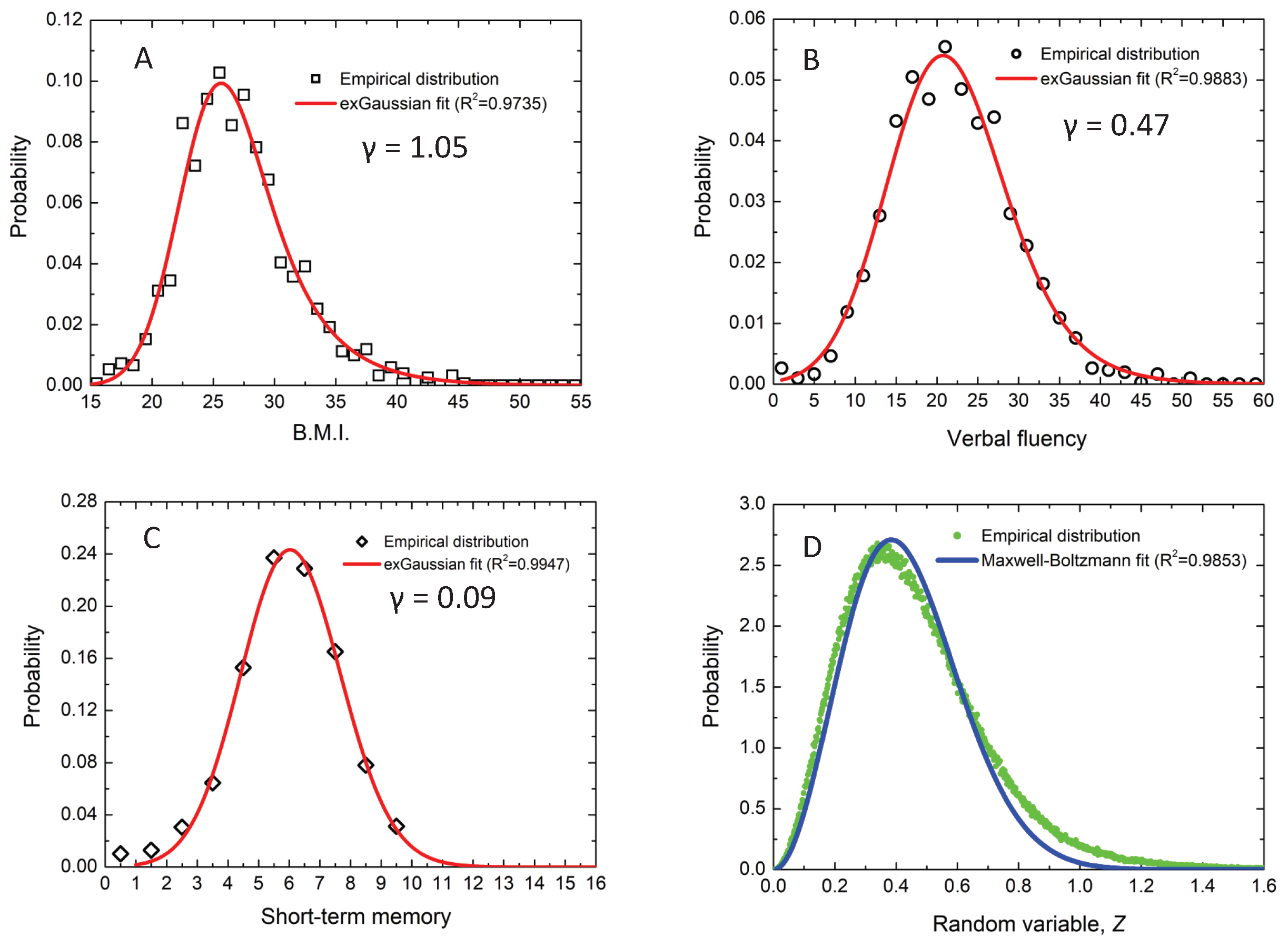
Figure 6.
Experimental probability distributions (open symbols) and exGaussian fittings (solid lines) to body mass index (panel (A)), verbal fluency (panel (B)), and short-term memory (panel (C)) variables. The random variable in panel (D) represents . The asymmetry values (panels A–C) and the coefficients of determination () (in all panels) are also included. The corresponding MB curve along the fitting is included in panel (D).
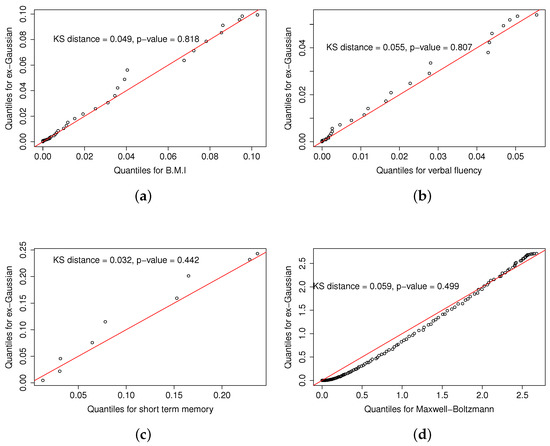
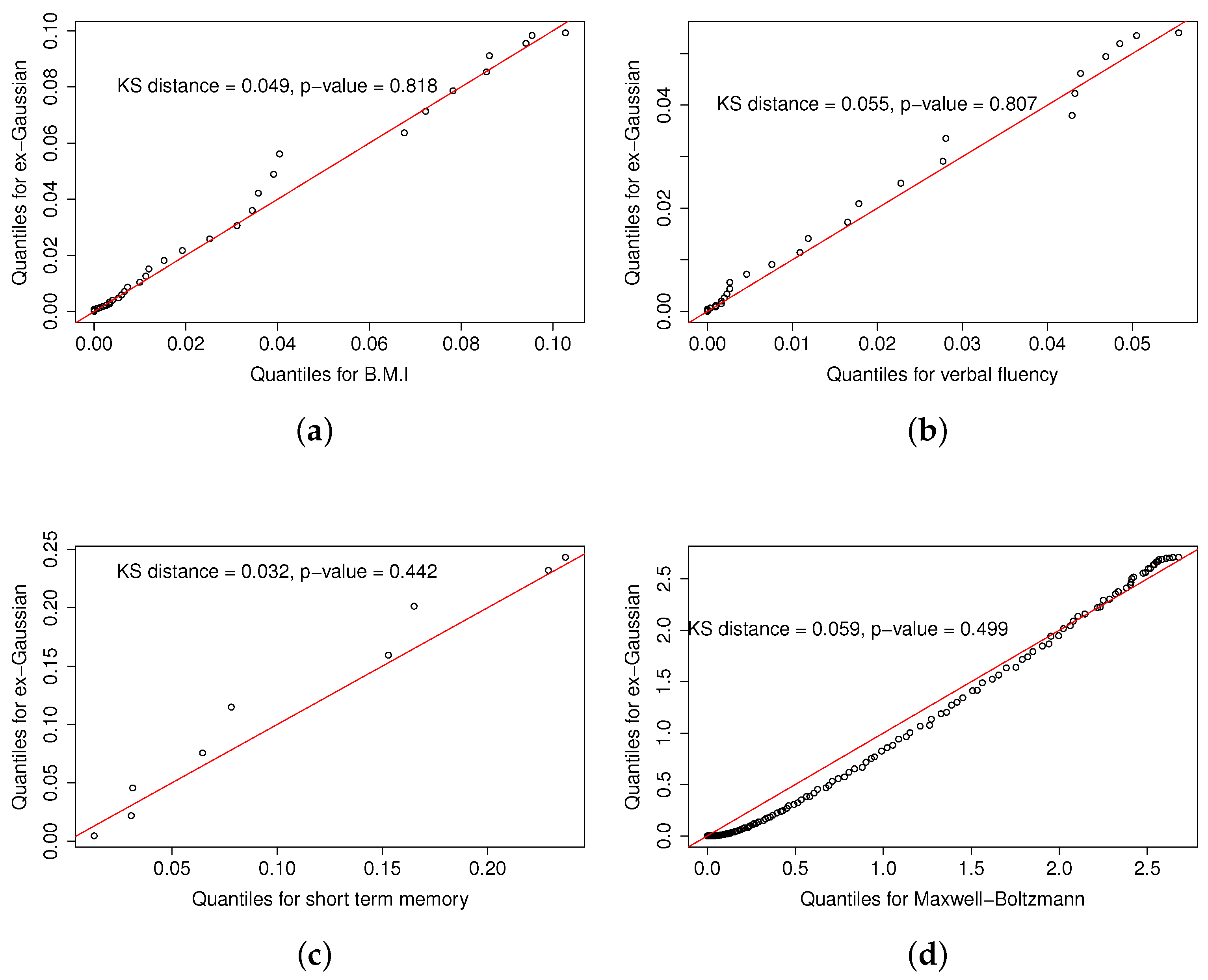
Figure 7.
Quantile–quantile plots of the exGaussian fittings and the empirical probability distributions of the three health-related variables shown in Figure 6: (a) BMI, (b) verbal fluency, (c) short-term memory, and the corresponding fit to a MB distribution (d). Each panel also shows the Kolmogorov–Smirnov distance and the associated p-value.
Figure 6D shows the probability distribution of the random variable and the corresponding fit to a MB distribution (see (6) for ). The variables stand for body mass index, verbal fluency, and short-term memory, which were standardised [7,9]. The parameters, uncertainties, and coefficients of determination () from the exGaussian and MB fittings are included in Table 3. This new variable, Z, combines the values of the three health-related variables in a unique value for each individual, which can be considered as a new index able to characterise each individual in the sample. The MB-like distribution in Figure 6D models the probability distribution of Z in the sample. Thus, the entire sample can be modelled by only one parameter, namely, the parameter B of the MB distribution. We illustrated this methodology for three variables but it can be extended for any number of k variables. The methodology developed in this work can have potential applications in diverse areas, for instance, to model health-related [34] and psychological variables [16,35].

Table 3.
Parameters (, , and ), uncertainties (, , and ), and coefficient of determination () from the exGaussian fitting of the analysed variables. In the last two rows, the results for the MB fitting are included. The fitted parameter () is compared with the calculated parameter (, with the ansatz introduced in this work) yielding a percentage difference of = 7.17 %.
4. Conclusions
The influence of the asymmetry in the chi distribution was investigated by means of fitting this function to the distribution resulting by taking three and five generating exGaussian functions. The results indicate that, for very small asymmetries () in the generating functions, good values for the coefficient of determination () are still obtained when the simulated distribution is fitted with a chi function for both and . The results for are also good for asymmetries larger than 1.2 while they worsen for . We also extend the ansatz proposed in [9] to include small asymmetries. As a practical example to illustrate the results of the Monte Carlo simulations, three health-related non-dichotomic variables (body mass index, verbal fluency and short-term memory) were studied. These variables were combined by taking the square root of the sum of their squares. The resulting new variable can be fitted by a Maxwell–Boltzmann (MB) distribution. Thus, the entire sample can be characterised by a one-parameter distribution, namely, B. The values of the MB variable can be considered as a new index Z able to characterise each individual in the sample. In this article, we chose three variables but this methodology can be extended to any number of variables that can be combined into a single scalar which is the variable of the resulting chi distribution.
Author Contributions
Conceptualisation and methodology design: N.O., M.O.-P., J.C.C.-P., P.F.d.C. and J.M.I.; data analysis and simulations: N.O., M.O.-P., J.C.C.-P., P.F.d.C. and J.M.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by grant number RTI2018-102256-B-I00 of MINECO/FEDER (Spain). N. Ortigosa acknowledges the support from Generalitat Valenciana under grant Prometeo/2017/102, and from Spanish MINECO under grant MTM2016-76647-P.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available upon request.
Acknowledgments
The authors thank the Instituto Universitario de Matemática Pura y Aplicada, Universitat Politècnica de València (IUMPA) for the support with the computational facilities.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 6th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Fisher, R. On the Interpretation of χ2 from Contingency Tables, and the Calculation of P. J. R. Stat. Soc. 1922, 85, 87–94. [Google Scholar] [CrossRef]
- Fisher, R.A. The Conditions Under Which χ2 Measures the Discrepancy Between Observation and Hypothesis. J. R. Stat. Soc. 1924, 87, 442–450. [Google Scholar]
- Bolboacă, S.D.; Jäntschi, L.; Sestraş, A.F.; Sestraş, R.E.; Pamfil, D.C. Pearson-Fisher Chi-Square Statistic Revisited. Information 2011, 2, 528–545. [Google Scholar] [CrossRef]
- Castro-Palacio, J.C.; Fernández-de-Córdoba, P.; Isidro, J.M.; Navarro-Pardo, E.; Selva-Aquilar, R. Aguilar. Percentile study of Chi distribution. Application to response time data. Mathematics 2020, 8, 514. [Google Scholar] [CrossRef]
- Castro-Palacio, J.C.; Navarro-Pardo, E.; Isidro, J.M.; Sahu, S.; Fernández-de-Córdoba, P. Brain reaction times. Linking individual and collective behavior through Physics modeling. Symmetry 2021, 13, 451. [Google Scholar] [CrossRef]
- Iglesias-Martínez, M.E.; Hernaiz-Guijarro, M.; Castro-Palacio, J.C.; Fernández-de-Córdoba, P.; Isidro, J.M.; Navarro-Pardo, E. Machinery Failure Approach and Spectral Analysis to Study the Reaction Time Dynamics over Consecutive Visual Stimuli: An Entropy-Based Model. Mathematics 2020, 8, 1979. [Google Scholar] [CrossRef]
- Castro-Palacio, J.C.; Isidro, J.M.; Navarro-Pardo, E.; Velázquez-Abad, L.; Fernández-de-Córdoba, P. Monte Carlo Simulation of a Modified Chi Distribution with Unequal Variances in the Generating Gaussians. A Discrete Methodology to Study Collective Response Times. Mathematics 2021, 9, 77. [Google Scholar] [CrossRef]
- Moret-Tatay, C.; Gamermann, D.; Navarro-Pardo, E.; Fernández-de-Córdoba, P. ExGUtils: A Python Package for Statistical Analysis with the ex-Gaussian Probability Density. Front. Psycol. 2018, 9, 612. [Google Scholar] [CrossRef]
- Ratclif, R.; Murdock, B.B. Retrieval processes in recognition memory. Psychol. Rev. 1976, 83, 190. [Google Scholar] [CrossRef]
- Gmehlin, D.; Fuermaier, A.B.M.; Walther, S.; Debelak, R.; Rentrop, M.; Westermann, C.; Sharma, A.; Tucha, L.; Koerts, J.; Tucha, O.; et al. Intraindividual variability in inhibitory function in adults with ADHD. An ex-Gaussian approach. PLoS ONE 2014, 9, e112298. [Google Scholar] [CrossRef] [PubMed]
- Adamo, N.; Hodsoll, J.; Asherson, P.; Buitelaar, J.K.; Kuntsi, J. Ex-Gaussian, frequency and reward analyses reveal specificity of reaction time fluctuations to ADHD and not autism traits. J. Abnorm. Child Psychol. 2019, 47, 557. [Google Scholar] [CrossRef] [PubMed]
- Xavier Castellanos, F.; Sonuga-Barke, E.J.S.; Scheres, A.; Di Martino, A.; Hyde, C.; Walters, J.R. Varieties of Attention-Defficit/Hyperactivity Disorder-Related Intra-Individual Variability. Biol. Psychiatry 2005, 57, 1416. [Google Scholar] [CrossRef]
- Navarro-Pardo, E.; Navarro-Prados, A.B.; Gamermann, D.; Moret-Tatay, C. Differences between young and old university students on a lexical decision task: Evidence through an ex-gaussian approach. J. Gen. Psychol. 2013, 140, 251–268. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Moret-Tatay, C.; Moreno-Cid, A.; de Lima Argimon, I.I.; Quarti Irigaray, T.; Szczerbinski, M.; Murphy, M.; Vázquez-Martínez, A.; Vázquez-Molina, J.; Sáiz-Mauleón, B.; Navarro-Pardo, E.; et al. The effects of age and emotional valence on recognition memory: An ex-Gaussian components analysis. Scand. J. Psychol. 2014, 55, 420–426. [Google Scholar] [CrossRef]
- Hernáiz-Guijarro, M.; Castro-Palacio, J.C.; Navarro-Pardo, E.; Isidro, J.M.; Fernández-de-Córdoba, P. A probabilistic classification procedure based on response time analysis towards a quick pre-diagnosis of student’s attention deficit. Mathematics 2019, 7, 473. [Google Scholar] [CrossRef]
- Li, J.A. Simplified Exponentially Modified Gaussian Function for Modeling Chromatographic Peaks. J. Chromatogr. Sci. 1995, 33, 568–572. [Google Scholar] [CrossRef]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series and Products; Academic Press: Boston, MA, USA, 2007. [Google Scholar]
- Tolman, R. The Principles of Statistical Mechanics; Dover Publications Inc.: New York, NY, USA, 2003. [Google Scholar]
- Boltzmann, L. Studies on the balance of kinetic energy between moving material points. Wiener Berichte 1868, 58, 517–560. [Google Scholar]
- Fodor, M.P.; Bolboacă, S.D.; Jäntschi, L. Distribution of Molecules by Kinetic Energy Revisited. Bull. UASVM Hortic. 2013, 70, 10–18. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Devore, J.L. Probability and Statistics for Engineering and the Sciences; Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Conover, W.J. Practical Nonparametric Statistics; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Kolmogoroff, A. Confidence Limits for an Unknown Distribution Function. Ann. Math. Stat. 1941, 12, 461–463. [Google Scholar] [CrossRef]
- Jäntschi, L. A Test Detecting the Outliers for Continuous Distributions Based on the Cumulative Distribution Function of the Data Being Tested. Symmetry 2019, 11, 835. [Google Scholar] [CrossRef]
- Jäntschi, L. Detecting Extreme Values with Order Statistics in Samples from Continuous Distributions. Mathematics 2020, 8, 216. [Google Scholar] [CrossRef]
- Wilk, M.B.; Gnanadesikan, R. Probability plotting methods for the analysis of data. Biom. Biom. Trust 1968, 55, 1–17. [Google Scholar] [CrossRef]
- Börsch-Supan, A. Survey of Health, Ageing and Retirement in Europe (SHARE) Wave 7; Release Version: 7.1.1; SHARE-ERIC: München, Germany, 2020. [Google Scholar]
- Bergmann, M.; Scherpenzeel, A.; Börsch-Supan, A. SHARE Wave 7 Methodology: Panel Innovations and Life Histories; Munich Center for the Economics of Aging (MEA): München, Germany, 2019. [Google Scholar]
- Börsch-Supan, A.; Brandt, M.; Hunkler, C.; Kneip, T.; Korbmacher, J.; Malter, F.; Schaan, B.; Stuck, S.; Zuber, S. Data Resource Profile: The Survey of Health, Ageing and Retirement in Europe (SHARE). Int. J. Epidemiol. 2013, 42, 992–1001. [Google Scholar] [CrossRef]
- Fernandez-de-las-Penas, C.; Fernandez-Munoz, J.J.; Palacios-Cena, M.; Navarro-Pardo, E. Sleep disturbances in tension-type headache and migraine. Ther. Adv. Neurol. Disord. 2017, 11, 1–6. [Google Scholar] [CrossRef]
- Viguer, P.; Carlos Melendez, J.; Valencia, S.; Cantero, M.-J.; Navarro, E. Grandparent-Grandchild Relationships from the Children’s Perspective: Shared Activities and Socialization Styles. Span. J. Psychol. 2010, 13, 708–717. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).