Leader-Following Regional Multiple-Bipartite Consensus for Networked Lagrangian Systems with Coopetition Interactions

Abstract

This paper investigates the leader-following regional multiple-bipartite consensus problems of networked Lagrangian systems (NLSs) in coopetition networks. Our framework expands the application scopes of traditional regional consensus in cooperative networks. With the aid of a novel auxiliary variable embedded in the control protocols, the final states of NLSs are guaranteed to realise multi-regional symmetry in the constructed multiple symmetric regions. By utilising the characteristic of acyclic topology in the structurally balanced graph, the stability of the closed system is performed by perturbation analysis theory, nonlinear control theory, functional analysis theory, and so on. Finally, the effectiveness of our approach is verified by numerical simulations.

1. Introduction

In the past few decades, the cooperative control problems of NLSs have attracted a great deal of attention because of their merits in terms of applicability and simplicity in a range of fields, such as modern assembly production [1], autonomous vehicles [2], flying spacecrafts [3], and underwater robots [4]. Usually, consensus-based approaches are bound up with cooperative control strategies, in which one of the strong points is the extensive robustness to distributed control. Consensus appertains to the behavior evolution where all agents converge to a common state, and the leaderless case and the leader-following case are two regular classifications. In the leader-following case, the final states of the followers asymptotically agree with their leader’s motion. In light of its advantages of maneuverability and practicability over the leaderless case, the leader-following tracking consensus approaches are widely developed in many fields [5,6,7,8,9,10,11].

The aforementioned studies concentrate on the consensus scenarios in traditional networks including cooperative interactions only. A more realistic case taking antagonistic interactions into account (i.e., bipartite consensus) has been investigated. Bipartite consensus refers to the collective behavior where all agents converge to the symmetric modulus states in coopetition networks; therein, a structurally balanced network often arises [12], which is widely used in multi-agent networks and social networks [13,14,15,16], just to name a couple scenarios.

Due to the influence of environmental changes, indeterminacy, and multi-task requirements, it should be noted that the final states of the agents may not be one consistent case. For instance, the formation tracking control of multi-agent systems usually has multiple targets [17]. Qin and Yu [18] investigated group consensus control for generic linear multi-agent systems in cooperative networks. Liu et al. [19] integrated the evolutions of bipartite consensus and group consensus, realising intra-symmetric consensus in first-order multi-agent systems. On the other hand, from a the practical perspective, the workplaces of NLSs often meet with disturbances which may cause system oscillation and procure instability. To improve the performance of individual robot systems, many control theoretical methods have been studied, including disturbance observer-based control [20], robust damping control [21], and region-based reaching control [22]. For multirobot systems, Yao et al. [23] studied task-space tracking control problems of NLSs with input disturbances using passivity approaches. Moreover, resorting to a recursion-like method, the regional group consensus problems were investigated in [24]. However, these works did not consider the antagonistic information exchanges among the robots.

The abovementioned motivation prompts us greatly to investigate the leader-following regional multiple-bipartite consensus problems of NLSs with coopetition interactions. The key challenge is to render the final states of NLSs to realise regional symmetry on the basis of ensuring the stability between groups. By leveraging the characteristic of acyclic topology in the structurally balanced graph, stability analysis is conducted in the constructed multi-group symmetric regions with Laplacian matrix integrated leaders and followers. The main contributions of this paper are listed below. (1) The research framework introduces antagonistic interactions in the network, effectively extending the application scopes of complete consensus such as [8,9], and group consensus such as [17,25]. Our scheme provides a more complex dynamic behavior scenario compared with those in cooperative networks. In addition, it is not required that antagonistic relations exist between different groups only, which is more in accordance with actual situations. (2) To overcome the difficulties mentioned above, a novel auxiliary interaction variable is embedded in the designed algorithm, guaranteeing that the final states of the robots converge to multi-group symmetric regions. Our method realises regional complete consensus and regional group consensus simultaneously, reflecting the multi-group symmetric tasks in a more realistic case, so the results in [23,24] represent the special cases of ours.

The rest of this paper is organised as follows: Section 2 introduces algebraic graph theory and problem formulations. Section 3 presents the leader-following regional multiple-bipartite consensus results of the NLSs. Section 4 illustrates numerical simulations to verify the effectiveness of our approach. Section 5 summarizes this paper and puts forward the future prospects.

2. Preliminaries

2.1. Algebraic Graph Theory

Before moving on, necessary notes are given in this subsection. $\mathbb{R}$ denotes a set of real numbers, ${\mathbb{R}}^w$ and ${\mathbb{R}}^{w\times z}$ are, respectively, a set of w-dimensional Euclidean space, and a set of $w\times z$ real matrices. Square matrix $I_p$ is a $p\times p$ identity matrix. ${\mathbf{0}}_m$ represents a column vector with all entries 0, and ${\mathbf{0}}_{m\times m}$ is a square matrix with all entries 0. “Sgn” is the notation of the sign function, and ⊗ represents the Kronecker product. Denote $\parallel ·\parallel$ as the matrix-induced 2–norm. The symbol $\mathcal{G}=(\mathbb{V},\mathbb{E},\mathbb{A})$ stands for the network topology, where $\mathbb{V}=\{1,2,\cdots ,n\}$, $\mathbb{E}\subseteq \mathbb{V}\times \mathbb{V}$, and $\mathbb{A}=\left[a_{{\nu }_i{\nu }_j}\right]\in R^{n\times n}$ is the weighted adjacency matrix associated with $\mathcal{G}$, in which the elements are expressed as $a_{{\nu }_i{\nu }_j}=0$ if $({\nu }_j,{\nu }_i)\notin \mathbb{E}$; otherwise, $a_{{\nu }_i{\nu }_j}\ne 0$ if $({\nu }_j,{\nu }_i)\in \mathbb{E}$. A directed path in the graph is such that there exists a set of different edges of $({\nu }_1,{\nu }_2),({\nu }_2,{\nu }_3),\cdots ,({\nu }_{j-1},{\nu }_j)$, where $({\nu }_z,{\nu }_{z+1})\in \mathbb{E},z=1,2,\cdots ,j-1.$ It is said that $\mathcal{G}$ has a spanning tree if there is at least one directed path from i to all the other nodes j, $i\ne j$. A structurally balanced graph is defined as the case where if two subsets $\left\{{\mathbb{V}}^{\left(1\right)},{\mathbb{V}}^{\left(2\right)}\right\}$ of $\mathbb{V}$ satisfy ${\mathbb{V}}^{\left(1\right)}\bigcap {\mathbb{V}}^{\left(2\right)}=\varnothing$, ${\mathbb{V}}^{\left(1\right)}\bigcup {\mathbb{V}}^{\left(2\right)}=\mathbb{V}$, $a_{{\nu }_i{\nu }_j}\ge 0$ when ${\nu }_i$ and ${\nu }_j$ are in the same subset ${\mathbb{V}}^{\left(m\right)}$, $m=1,2$, otherwise $a_{{\nu }_i{\nu }_j}\le 0$.

2.2. Problem Formulations

Assume that NLSs consist of n robots and that the Lagrangian equation of the ith system can be compactly formulated as

$$\begin{array}{c}{M}_i\left({\mathrm{q}}_i\right){\ddot{\mathrm{q}}}_i+C_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i){\dot{\mathrm{q}}}_i+g_i\left({\mathrm{q}}_i\right)={\tau }_i+{\tau }_{d_i},\hfill \\ i=1,2,\cdots ,n,\hfill \end{array}$$

(1)

where $M_i\left({\mathrm{q}}_i\right)$ and $C_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i)$$\in {\mathbb{R}}^{p\times p},$${\mathrm{q}}_i$, ${\dot{\mathrm{q}}}_i$, $g_i\left({\mathrm{q}}_i\right)$, ${\tau }_i$ and ${\tau }_{d_i}\in {\mathbb{R}}^p$. ${\mathrm{q}}_i$ and ${\dot{\mathrm{q}}}_i$ are, respectively, the generalised coordinate vector and the generalised velocity vector, $M_i\left({\mathrm{q}}_i\right)$ represents the symmetric positive definite inertia matrix, $C_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i)$ stands for the Coriolis and centrifugal matrix, $g_i\left({\mathrm{q}}_i\right)$ represents the gravitational torque, ${\tau }_i$ is the generalised force vector, and ${\tau }_{d_i}:{\mathbb{R}}^{+}\cup \left\{0\right\}\to {\mathbb{R}}^p$ is the norm-bounded external disturbance function, that is, there exists $\varsigma \ge 0$, satisfying $\parallel {\tau }_d\left(t\right)\parallel \le \varsigma$, where ${\tau }_d={[{\tau }_{d_1}^{\mathrm{T}},\cdots ,{\tau }_{d_n}^{\mathrm{T}}]}^{\mathrm{T}}$, $\forall t\ge 0$. Next, according to [26], three important properties of system (1) are given below.

Property 1.

${\chi }_{{}_{p1}},{\chi }_{{}_{p2}}$ and ${\chi }_{{}_{p3}}$ are positive constants such that

$$0\le {\chi }_{{}_{p1}}{I}_p\le M_i\left({\mathrm{q}}_i\right)\le {\chi }_{{}_{p2}}{I}_p,$$

$$||C_i(u,v)w||\le {\chi }_{{}_{p3}}||v||||w||,\forall u,v,w\in {\mathbb{R}}^p.$$

Property 2.

${\dot{M}}_i-2C_i$ is skew symmetric.

Property 3.

For system (1), there exists a dynamic parameter ${\mathcal{P}}_i$ which is a constant vector, satisfying

$$\begin{array}{c}\hfill M_i\left({\mathrm{q}}_i\right)w+C_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i)z+G_i\left({\mathrm{q}}_i\right)=Y_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i,w,z){\mathcal{P}}_i,\end{array}$$

(2)

where $w,z\in {\mathbb{R}}^p$ are differentiable vectors and $Y_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i,w,z)$ is the regression matrix.

Consider the network topology $\mathcal{G}=(\mathbb{V},\mathbb{E},\mathbb{A})$ in regard to NLSs. In the following discussion, an acyclic partition $\{{\mathbb{V}}_l,{\mathbb{V}}_2,\cdots ,{\mathbb{V}}_k\}$ of $\mathbb{V}$ is taken into account for the advantage of the stable structure of one-way information transmission, depicting many engineering applications for complex tasks. Then the node set of each group ${\mathbb{V}}_l$ is assigned as ${\mathbb{V}}_l=\{{\sum }_{z=0}^{l-1}{h}_z+1,\cdots ,{\sum }_{z=0}^l{h}_z\},$ $h_0=0$, ${\sum }_{l=1}^k{h}_l=n$, and $n_l={\sum }_{z=1}^l{h}_z$, $l=1,2,\cdots ,k$. Accordingly, in view of the structure of acyclic partition, k leaders are associated with the groups of $\mathbb{V}$. Assume that the lth leader is expressed as ${\zeta }_l$, and that the derivatives ${\dot{\zeta }}_l$, ${\ddot{\zeta }}_l$ are all bounded, $l=1,2,\cdots ,k$. Denote $\overline{\mathcal{G}}=(\overline{\mathbb{V}},\overline{\mathbb{E}},\overline{\mathbb{A}})$, reflecting the interactions between k leaders and n followers. $\overline{\mathbb{V}}=\{{\overline{\mathbb{V}}}_l,{\overline{\mathbb{V}}}_2,\cdots ,{\overline{\mathbb{V}}}_k\}$, where ${\overline{\mathbb{V}}}_l$ involves the corresponding lth leader, $l\in \{1,2,\cdots ,k\}$.

Assumption 1.

Each leader in ${\overline{\mathbb{V}}}_l$ has a directed path to every follower in ${\overline{\mathcal{G}}}_l$, where the diagraph ${\overline{\mathcal{G}}}_l$ is associated with ${\overline{\mathbb{V}}}_l,l=1,2,\cdots ,k.$

Assumption 2.

${\overline{\mathcal{G}}}_l$ is structurally balanced, $l=1,2,\cdots ,k.$

Under Assumption 2, each ${\overline{\mathbb{V}}}_l$, $l=1,2,\cdots ,k$, can be divided into two subsets ${\overline{\mathbb{V}}}_l^{\left(1\right)}$ and ${\overline{\mathbb{V}}}_l^{\left(2\right)}$ such that ${\overline{\mathbb{V}}}_l^{\left(1\right)}\cap {\overline{\mathbb{V}}}_l^{\left(2\right)}=\varnothing$, ${\overline{\mathbb{V}}}_l^{\left(1\right)}\cup {\overline{\mathbb{V}}}_l^{\left(2\right)}={\overline{\mathbb{V}}}_l$. Let ${\overline{\varphi }}_i\in \{-1,1\}$ (see [27]) such that ${\overline{\varphi }}_i=1$ if $i\in {\overline{\mathbb{V}}}_l^{\left(1\right)}$, otherwise ${\overline{\varphi }}_i=-1$ if $i\in {\overline{\mathbb{V}}}_l^{\left(2\right)}$, $i\in \{1,2,\cdots ,n\}$. Subsequently, denote ${\overline{\mathsf{\Phi }}}_l=\mathrm{diag}\{{\overline{\varphi }}_{{}_{0l}},{\overline{\varphi }}_{h_{l-1}+1},\cdots ,{\overline{\varphi }}_{h_l}\},$ ${\overline{\varphi }}_{{}_{0l}}=1$ if the lth leader ${\zeta }_l$ lies in ${\mathbb{V}}_l^{\left(1\right)}$, otherwise, ${\overline{\varphi }}_{{}_{0l}}=-1$, $l=1,2,\cdots ,k$. Introduce the index set: $\widehat{i}=l$, that is, $i\in {\overline{\mathbb{V}}}_l$, $l=1,2,\cdots ,k$. According to [19], the Laplacian matrix of $\overline{\mathcal{G}}$ is defined as $\overline{L}=\left[{\sigma }_{ij}\right]\in R^{n\times n}$, ${\sigma }_{ii}={\sum }_{j\notin {\overline{\mathbb{V}}}_{\widehat{i}}}{\overline{\varphi }}_j{a}_{ij}+{\sum }_{j\in {\overline{\mathbb{V}}}_{\widehat{i}}}|a_{ij}|,i\in \{1,2,\cdots ,n\}$, and ${\sigma }_{ij}=-a_{ij},i\ne j$. Under the acyclic partition, denote ${\overline{L}}_i=\left[\begin{array}{ccc}{\overline{L}}_{11}& \cdots & {\mathbf{0}}_{n_1\times n_i}\\ ⋮& \ddots & ⋮\\ {\overline{L}}_{i1}& \dots & {\overline{L}}_{ii}\end{array}\right],$ where ${\overline{L}}_{ij}$ describes the communication transmission from ${\overline{\mathcal{G}}}_j$ to ${\overline{\mathcal{G}}}_i,$ $i\ge j$, $i,j\in \{1,2,\cdots ,k\}.$ It is clear that ${\overline{L}}_k$ is the Laplacian matrix $\overline{L}$.

Assumption 3.

The sum of each row in ${\overline{\mathsf{\Phi }}}_i{\overline{L}}_{ij}{\overline{\mathsf{\Phi }}}_j$ is zero, $i\ne j,i,j=1,2,\cdots ,k$.

Remark 1.

Assumption 3 integrates the leader into the homologous Laplacian matrix form ${\overline{L}}_{ij}$, which naturally generalises the widely used conditions in cluster/group consensus (see [18,25]).

Lemma 1

([19]). If Assumptions 1–3 hold, then the Laplacian matrix $\overline{L}$ possesses k simple zero eigenvalues, and the other eigenvalues have positive real parts. In addition, the k left eigenvectors associated with the zero eigenvalue can be explicitly described as ${\rho }_1={\left({\alpha }_{10},{\alpha }_{11},{\alpha }_{12},\cdots ,{\alpha }_{1h_1},0,\cdots ,0\right)}^{\mathrm{T}},$ ${\rho }_2=\left({\beta }_{10}^{\left(2\right)},{\beta }_{11}^{\left(2\right)},\cdots ,\right.$ ${\left.{\beta }_{1h_1}^{\left(2\right)},{\alpha }_{20},{\alpha }_{21},{\alpha }_{22},\cdots ,{\alpha }_{2h_2},0,\cdots ,0\right)}^{\mathrm{T}},$ ⋯${\rho }_k=\left({\beta }_{10}^{\left(k\right)},\right.$ ${\beta }_{11}^{\left(k\right)},$ $\cdots ,{\beta }_{1h_1}^{\left(k\right)},\cdots ,$ ${\beta }_{(k-1),0}^{\left(k\right)},{\beta }_{(k-1),1}^{\left(k\right)},\cdots ,$ $\cdots ,{\beta }_{(k-1),h_{k-1}}^{\left(k\right)},{\alpha }_{k0},{\alpha }_{k1},$ ${\left.\cdots ,{\alpha }_{k{h}_k}\right)}^{\mathrm{T}}$ such that ${\overline{\mathsf{\Phi }}}_i{\alpha }_i^{\mathrm{T}}$ are nonnegative vectors, ${\alpha }_i{\overline{\mathsf{\Phi }}}_i{\mathbf{1}}_{h_i+1}=1$ and ${\beta }_i^{\left(j\right)}{\overline{\mathsf{\Phi }}}_i{\mathbf{1}}_{h_i+1}=0$, $i\in \{1,2,\cdots ,k\}$, $j\in \{2,\cdots ,k\}$, where ${\alpha }_i=\left({\alpha }_{i0},{\alpha }_{i1},\cdots ,{\alpha }_{i{h}_i}\right)$, ${\beta }_i^{\left(j\right)}=\left({\beta }_{i0}^{\left(j\right)},{\beta }_{i1}^{\left(j\right)},\cdots ,{\beta }_{i{h}_i}^{\left(j\right)}\right)$.

For convenience of the following discussion, define the group error vector of NLSs as ${\varpi }_{{\mu }_1}=[{({\overline{\varphi }}_1{\mathrm{q}}_1-{\overline{\varphi }}_{{}_{01}}{\zeta }_1)}^{\mathrm{T}},\cdots ,$${({\overline{\varphi }}_1{\mathrm{q}}_{n_1}-{\overline{\varphi }}_{{}_{01}}{\zeta }_1)}^{\mathrm{T}}{]}^{\mathrm{T}}$, ⋯, ${\varpi }_{{\mu }_k}=\left[\right({\overline{\varphi }}_{n_{k-1}+1}$${\mathrm{q}}_{n_{k-1}+1}-{\overline{\varphi }}_{{}_{0k}}$${\zeta }_k{)}^{\mathrm{T}},$ ⋯, ${({\overline{\varphi }}_{n_k}{\mathrm{q}}_{n_k}-{\overline{\varphi }}_{{}_{0k}}{\zeta }_k)}^{\mathrm{T}}{]}^{\mathrm{T}}$. Based on the above preparations, the concept of leader-following regional multiple-bipartite consensus is defined as follows.

Definition 1.

Given that the acyclic partition $\overline{\mathbb{V}}=\{{\overline{\mathbb{V}}}_1,\cdots ,{\overline{\mathbb{V}}}_k\}$, it is said that system (1) realises leader-following regional multiple-bipartite consensus by using ${\tau }_i$, $i=1,2,\cdots ,n$, if ${lim}_{t\to \infty }$$\parallel {\varpi }_{{\mu }_l}\parallel \le {\gamma }_l$, $l=1,2,\cdots ,k,$ for k predefined positive error bounds ${\gamma }_1,\cdots ,{\gamma }_k$, and arbitrary initial values.

3. Presentation of Leader-Following Regional Multiple-Bipartite Consensus

To realise leader-following regional multiple-bipartite consensus for NLSs, the control algorithm is proposed in this section. First, for the ith ($i\in {\mathbb{V}}_{\widehat{i}}$) robot, the auxiliary variable ${\dot{\mathrm{q}}}_{ri}\in {\mathbb{R}}^p$ is defined as

$$\begin{array}{c}\hfill {\dot{\mathrm{q}}}_{ri}={\overline{\varphi }}_i{\dot{\zeta }}_{\widehat{i}}+{\eta }_i({\zeta }_{\widehat{i}}-\mathrm{sgn}\left({\eta }_i\right){\mathrm{q}}_i)\\ \hfill +{\Sigma }_{j\in {\mathbb{V}}_{\widehat{i}}}{a}_{ij}\left[{\mathrm{q}}_j-\mathrm{sgn}\left(a_{ij}\right){\mathrm{q}}_i\right]+{\Sigma }_{j\notin {\mathbb{V}}_{\widehat{i}}}{a}_{ij}\left({\mathrm{q}}_j-{\overline{\varphi }}_j{\mathrm{q}}_i\right),\end{array}$$

(3)

where ${\eta }_i\ne 0$ if the ith robot is pinned with ${\zeta }_i$—that is, only a portion of followers receive information from the leader directly.

Second, define the sliding vector ${\mathrm{s}}_i\in {\mathbb{R}}^p$ as

$$\begin{array}{c}\hfill {\mathrm{s}}_i={\dot{\mathrm{q}}}_i-{\dot{\mathrm{q}}}_{ri}.\end{array}$$

(4)

Subsequently, the control protocol is designed by

$${\tau }_i=Y_i\left({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i,{\ddot{\mathrm{q}}}_{ri},{\dot{\mathrm{q}}}_{ri}\right){\overline{\mathcal{P}}}_i-{\kappa }_i{\mathrm{s}}_i-{\tau }_{di},$$

(5)

where ${\overline{\mathcal{P}}}_i$ represents the estimation of ${\mathcal{P}}_i$, and ${\kappa }_i$ is positive definite. Then the adaptive law of ${\overline{\mathcal{P}}}_i$ is correspondingly given as follows

$${\dot{\overline{\mathcal{P}}}}_i=-{\mathsf{\Gamma }}_i{Y}_i^{\mathrm{T}}\left({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i,{\ddot{\mathrm{q}}}_{ri},{\dot{\mathrm{q}}}_{ri}\right){\mathrm{s}}_i,$$

(6)

where ${\mathsf{\Gamma }}_i$ represents a positive definite matrix.

With the aid of (5) and (6), system (1) is reformulated as

$$\begin{array}{c}\hfill M_i\left({\mathrm{q}}_i\right){\dot{\mathrm{s}}}_i=-C_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i){\mathrm{s}}_i-Y_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i,{\ddot{\mathrm{q}}}_{ri},{\dot{\mathrm{q}}}_{ri}){\tilde{\mathcal{P}}}_i-{\kappa }_i{\mathrm{s}}_i-{\tau }_{di},\end{array}$$

(7)

where ${\tilde{\mathcal{P}}}_i={\mathcal{P}}_i-{\overline{\mathcal{P}}}_i$.

For the sake of convenient analysis, Equation (4) can be written as the compact form

$$\begin{array}{c}\hfill \dot{\overline{\mathbf{q}}}=-\left(\overline{L}\otimes I_p\right)\overline{\mathbf{q}}+\mathsf{\Lambda },\end{array}$$

(8)

where $\overline{\mathbf{q}}={({\zeta }_1^{\mathrm{T}},{\mathrm{q}}_1^{\mathrm{T}},\cdots ,{\mathrm{q}}_{n_1}^{\mathrm{T}},{\zeta }_2^{\mathrm{T}},{\mathrm{q}}_{n_1+1}^{\mathrm{T}},\cdots ,{\mathrm{q}}_{n_2}^{\mathrm{T}},\cdots ,{\mathrm{q}}_n^{\mathrm{T}})}^{\mathrm{T}}$, and $\mathsf{\Lambda }=({\mathbf{0}}_p^{\mathrm{T}},{({\mathrm{s}}_1+{\overline{\varphi }}_1{\dot{\zeta }}_1)}^{\mathrm{T}},\cdots ,$${({\mathrm{s}}_{n_1}+{\overline{\varphi }}_{n_1}{\dot{\zeta }}_{n_1})}^{\mathrm{T}},{\mathbf{0}}_p^{\mathrm{T}},$$({\mathrm{s}}_{n_1+1}$

$+{\overline{\varphi }}_{n_1+1}{\dot{\zeta }}_{n_1+1}{)}^{\mathrm{T}},$$\cdots ,{({\mathrm{s}}_n+{\overline{\varphi }}_n{\dot{\zeta }}_n)}^{\mathrm{T}}{\left)\right)}^{\mathrm{T}}$.

Let ${\xi }_1^{\left(1\right)}={\alpha }_1^{\mathrm{T}}$, ${\mathsf{\Xi }}_1={({{\xi }_1^{\left(1\right)}}^{\mathrm{T}},{\mathsf{\Xi }}_{\left\{1\right\}}^{\mathrm{T}})}^{\mathrm{T}}$, where ${\mathsf{\Xi }}_{\left\{1\right\}}$ can be expressed as

$${\mathsf{\Xi }}_{\left\{1\right\}}=\left[\begin{array}{ccccc}-{\overline{\varphi }}_{{}_{01}}& {\overline{\varphi }}_1& 0& \cdots & 0\\ & \cdots & & \cdots & \\ -{\overline{\varphi }}_{{}_{01}}& 0& 0& \cdots & {\overline{\varphi }}_{n_1}\end{array}\right].$$

According to Lemma 1, ${\mathsf{\Xi }}_1{\overline{L}}_1{\mathsf{\Xi }}_1^{-1}=\mathrm{diag}\{0,{\overline{L}}_{{\mu }_1}\}$ and $-{\overline{L}}_{{\mu }_1}$ is Hurwitz stable. Consequently, for the robots in the first group, Equation (8) is written as

$${\dot{\overline{\mathbf{q}}}}_{{\mu }_1}=-({\overline{L}}_1\otimes I_p){\overline{\mathbf{q}}}_{{\mu }_1}+{\mathsf{\Lambda }}_{{\mu }_1},$$

(9)

where ${\overline{\mathbf{q}}}_{{\mu }_1}={({\zeta }_1^{\mathrm{T}},{\mathrm{q}}_1^{\mathrm{T}},\cdots ,{\mathrm{q}}_{n_1}^{\mathrm{T}})}^{\mathrm{T}},$ and ${\mathsf{\Lambda }}_{{\mu }_1}=({\mathbf{0}}_p^{\mathrm{T}},{({\mathrm{s}}_1+{\overline{\varphi }}_1{\dot{\zeta }}_1)}^{\mathrm{T}},$$\cdots ,$${({\mathrm{s}}_{n_1}+{\overline{\varphi }}_{n_1}{\dot{\zeta }}_{n_1})}^{\mathrm{T}}{)}^{\mathrm{T}}.$ Making the coordinate transformation

$${\varpi }_1=({\mathsf{\Xi }}_1\otimes I_p){\overline{\mathbf{q}}}_{{\mu }_1},$$

(10)

note from the structure of ${\mathsf{\Xi }}_1$, ${\varpi }_1={({{\varpi }_{\left(1\right)}}^{\mathrm{T}},{\varpi }_{{\mu }_1}^{\mathrm{T}})}^{\mathrm{T}}$, where ${\varpi }_{\left(1\right)}=({{\xi }_1^{\left(1\right)}}^{\mathrm{T}}\otimes I_p){\overline{\mathbf{q}}}_{{\mu }_1}$ and ${\varpi }_{{\mu }_1}=[{(-{\overline{\varphi }}_{{}_{01}}{\zeta }_1+{\overline{\varphi }}_1{\mathrm{q}}_1)}^{\mathrm{T}},\cdots ,$ ${(-{\overline{\varphi }}_{{}_{01}}{\zeta }_1+{\overline{\varphi }}_{n_1}{\mathrm{q}}_{n_1})}^{\mathrm{T}}{]}^{\mathrm{T}}$. Thus, Equation (9) can be expressed as ${\dot{\varpi }}_1=-({\mathsf{\Xi }}_1{\overline{L}}_1{\mathsf{\Xi }}_1^{-1}\otimes I_p){\varpi }_1+({\mathsf{\Xi }}_1\otimes I_p){\mathsf{\Lambda }}_{{\mu }_1}.$ For further decomposition, one has

$${\dot{\varpi }}_{\left(1\right)}=({{\xi }_1^{\left(1\right)}}^{\mathrm{T}}\otimes I_p){\mathsf{\Lambda }}_{{\mu }_1},$$

(11)

and

$${\dot{\varpi }}_{{\mu }_1}=-({\overline{L}}_{{\mu }_1}\otimes I_p){\varpi }_{{\mu }_1}+s_{{\varpi }_1},$$

(12)

where $s_{{\varpi }_1}$ is the column vector with respect to $s_i$, $i=1,2,\cdots ,n_1$. Because all of the eigenvalues of ${\overline{L}}_{{\mu }_1}$ possess positive real parts, there exists a positive definite matrix $X_1$ such that $Z_1={\overline{L}}_{{\mu }_1}^{\mathrm{T}}{X}_1+X_1{\overline{L}}_{{\mu }_1}$, where $Z_1$ is also positive definite.

Next, let ${\xi }_1^{\left(2\right)}={({\alpha }_1,{\mathbf{0}}_{h_2+1}^{\mathrm{T}})}^{\mathrm{T}}$, ${\xi }_2^{\left(2\right)}={({\beta }_1^{\left(2\right)},{\alpha }_2)}^{\mathrm{T}}$, and ${\mathsf{\Xi }}_2={({{\xi }_1^{\left(2\right)}}^{\mathrm{T}},{{\xi }_2^{\left(2\right)}}^{\mathrm{T}},{\mathsf{\Xi }}_{\left\{2\right\}}^{\mathrm{T}})}^{\mathrm{T}}$, ${\mathsf{\Xi }}_{\left\{2\right\}}=\mathrm{diag}\{{\mathsf{\Xi }}_{\left\{1\right\}},{\mathsf{\Xi }}_{\left\{2\right\}}^{\left(1\right)}\}$

$${\mathsf{\Xi }}_{\left\{2\right\}}^{\left(1\right)}=\left[\begin{array}{ccccc}-{\overline{\varphi }}_{{}_{02}}& {\overline{\varphi }}_{n_1+1}& 0& \cdots & 0\\ & \cdots & & \cdots & \\ -{\overline{\varphi }}_{{}_{02}}& 0& 0& \cdots & {\overline{\varphi }}_{n_2}\end{array}\right],$$

thus, ${\mathsf{\Xi }}_2{\overline{L}}_2{\mathsf{\Xi }}_2^{-1}$$=\mathrm{diag}\{{\mathbf{0}}_{2\times 2},{\overline{L}}_{{\mu }_2}\}$ and $-{\overline{L}}_{{\mu }_2}$ is Hurwitz stable. For the robots in the second group, Equation (8) is written as

$${\dot{\overline{\mathbf{q}}}}_{{\mu }_2}=-({\overline{L}}_2\otimes I_p){\overline{\mathbf{q}}}_{{\mu }_2}+{\mathsf{\Lambda }}_{{\mu }_2},$$

(13)

where ${\overline{\mathbf{q}}}_{{\mu }_2}={({\zeta }_1^{\mathrm{T}},\cdots ,{\mathrm{q}}_{n_2}^{\mathrm{T}})}^{\mathrm{T}},$ and ${\mathsf{\Lambda }}_{{\mu }_2}=({\mathbf{0}}_p^{\mathrm{T}},{({\mathrm{s}}_1+{\overline{\varphi }}_1{\dot{\zeta }}_1)}^{\mathrm{T}},\cdots ,$ ${({\mathrm{s}}_{n_1}+{\overline{\varphi }}_{n_1}{\dot{\zeta }}_{n_1})}^{\mathrm{T}},{\mathbf{0}}_p^{\mathrm{T}},\cdots ,$ ${({\mathrm{s}}_{n_2}+{\overline{\varphi }}_{n_2}{\dot{\zeta }}_{n_2})}^{\mathrm{T}}{)}^{\mathrm{T}}.$ Similarly, by introducing the following coordinate transformation

$${\varpi }_2=({\mathsf{\Xi }}_2\otimes I_p){\overline{\mathbf{q}}}_{{\mu }_2},$$

(14)

where ${\varpi }_2={({{\varpi }_{\left(21\right)}}^{\mathrm{T}},{{\varpi }_{\left(22\right)}}^{\mathrm{T}},{\varpi }_{{\mu }_2}^{\mathrm{T}})}^{\mathrm{T}}$, ${\varpi }_{\left(21\right)}=({{\xi }_1^{\left(2\right)}}^{\mathrm{T}}\otimes I_p){\overline{\mathbf{q}}}_{{\mu }_2},$ ${\varpi }_{\left(22\right)}=({{\xi }_2^{\left(2\right)}}^{\mathrm{T}}\otimes I_p){\overline{\mathbf{q}}}_{{\mu }_2},$ and ${\varpi }_{{\mu }_2}=[{(-{\overline{\varphi }}_{{}_{01}}{\zeta }_1+{\overline{\varphi }}_1{\mathrm{q}}_1)}^{\mathrm{T}},\cdots ,$${(-{\overline{\varphi }}_{{}_{02}}{\zeta }_2+{\overline{\varphi }}_{n_2}{\mathrm{q}}_{n_2})}^{\mathrm{T}}{]}^{\mathrm{T}}$, Equation (13) can be expressed as

$${\dot{\varpi }}_{\left(21\right)}=({{\xi }_1^{\left(2\right)}}^{\mathrm{T}}\otimes I_p){\mathsf{\Lambda }}_{{\mu }_2},$$

(15)

$${\dot{\varpi }}_{\left(22\right)}=({{\xi }_2^{\left(2\right)}}^{\mathrm{T}}\otimes I_p){\mathsf{\Lambda }}_{{\mu }_2},$$

(16)

and

$${\dot{\varpi }}_{{\mu }_2}=-({\overline{L}}_{{\mu }_2}\otimes I_p){\varpi }_{{\mu }_2}+s_{{\varpi }_2},$$

(17)

where $s_{{\varpi }_2}$ is the column vector with respect to $s_i$, $i=1,2,\cdots ,n_2$. According to Lemma 1, $-{\overline{L}}_{{\mu }_2}$ is Hurwitz-stable, and there exists a positive definite matrix $X_2$ such that $Z_2={\overline{L}}_{{\mu }_2}^{\mathrm{T}}{X}_2+X_2{\overline{L}}_{{\mu }_2}$, where $Z_2$ is positive definite. Through the analogous method one can get a series of positive definite matrices $X_l$, $Z_l$ and error vectors ${\varpi }_{{\mu }_l}$, $l=1,2,\cdots ,k$. Then the major findings are given in Theorem 1.

Theorem 1.

Given the error bounds ${\gamma }_{{}_l}>0$, $l=1,2,\cdots$$\cdots ,k$, if Assumptions 1–3 are satisfied, and ${\lambda }_{min}\left({\kappa }_{{}_l}\right)>{max}_{j\in \{l,l+1,\cdots ,k\}}\left\{\frac{2{max}_{j\in \{1,2,\cdots ,l\}}\left\{{\varsigma }_j\right\}{\lambda }_{max}\left(X_l\right)}{{\lambda }_{min}\left(Z_l\right){\gamma }_{{}_l}}\right\},$ then the leader-following regional multiple-bipartite consensus problems of NLSs are solved under (5) and (6).

Proof. 

First, denote ${\mathsf{\Phi }}_l=\mathrm{diag}\{{\overline{\varphi }}_1,{\overline{\varphi }}_2,\cdots ,$${\overline{\varphi }}_{h_{l-1}+1},\cdots ,$${\overline{\varphi }}_{h_l}\},$$l=1,2,\cdots ,k.$ Second, the Lyapunov function of the ith ($i\in \mathbb{V}$) system is selected as $V_i=\frac{1}{2}{\mathrm{s}}_i^{\mathrm{T}}{M}_i\left({\mathrm{q}}_i\right){\mathrm{s}}_i+\frac{1}{2}{\tilde{\mathcal{P}}}_i^{\mathrm{T}}{\mathsf{\Gamma }}_i^{-1}{\tilde{\mathcal{P}}}_i.$ Due to (7) and Property 3, ${\dot{V}}_i=-{\mathrm{s}}_i^{\mathrm{T}}{\kappa }_i{\mathrm{s}}_i+{\mathrm{s}}_i^{\mathrm{T}}{\tau }_{di}$. Thus, $|{\mathrm{s}}_i^{\mathrm{T}}{\tau }_{di}|\le \frac{\parallel {\mathrm{s}}_i{\parallel }^2}{\parallel {\mathrm{s}}_i\parallel }\parallel {\tau }_d\parallel$, and

$${\dot{V}}_i\le \left(\frac{{\varsigma }_{\widehat{i}}}{\parallel {\mathrm{s}}_i\parallel }-{\lambda }_{min}\left({\kappa }_i\right)\right){\parallel {\mathrm{s}}_i\parallel }^2.$$

(18)

Construct

$${\mathcal{Q}}_{i1}^{\left(z\right)}=\left\{{({\overline{\varphi }}_i{\mathrm{q}}_i^{\mathrm{T}},{\overline{\varphi }}_i{\dot{\mathrm{q}}}_i^{\mathrm{T}})}^{\mathrm{T}}|\parallel {\mathrm{s}}_i\parallel <\frac{{\varsigma }_1}{{\lambda }_{min}\left({\kappa }_i\right)}\right\},z=1,2.$$

Let ${\mathcal{U}}_i\left({\mathrm{s}}_i\right)=0,$ if ${({\overline{\varphi }}_i{\mathrm{q}}_i^{\mathrm{T}},{\overline{\varphi }}_i{\dot{\mathrm{q}}}_i^{\mathrm{T}})}^{\mathrm{T}}\in {\mathcal{Q}}_{i1}^{\left(z\right)};$ if not, ${\mathcal{U}}_i\left({\mathrm{s}}_i\right)=-{\overline{\varphi }}_i\left(\frac{\varsigma }{\parallel {\mathrm{s}}_i\parallel }-{\lambda }_{min}\left({\kappa }_i\right)\right){\parallel {\mathrm{s}}_i\parallel }^2,$ if ${({\overline{\varphi }}_i{\mathrm{q}}_i^{\mathrm{T}},{\overline{\varphi }}_i{\dot{\mathrm{q}}}_i^{\mathrm{T}})}^{\mathrm{T}}\in {\mathbb{R}}^{2p}/{\mathcal{Q}}_{i1}^{\left(z\right)}.$ Assume that $\mathcal{R}\in {\mathbb{R}}^{2p}$ is a compact set, and that ${({\overline{\varphi }}_i{\mathrm{q}}_i^{\mathrm{T}},{\overline{\varphi }}_i{\dot{\mathrm{q}}}_i^{\mathrm{T}})}^{\mathrm{T}}$ are the solution trajectories from initial points in $\mathcal{R}$. Subsequently, the following analysis will demonstrate that ${({\overline{\varphi }}_i{\mathrm{q}}_i{\left(t\right)}^{\mathrm{T}},{\overline{\varphi }}_i{\dot{\mathrm{q}}}_i\left(t\right))}^{\mathrm{T}}$ converge to ${\mathcal{Q}}_{i1}^{\left(z\right)}$ with time. As a matter of fact, ${\mathrm{s}}_i\left(t\right)$ and ${\tilde{\mathcal{P}}}_i\left(t\right)$ are bounded, implying that $V_i\left(t\right)$ is bounded. If ${\overline{\varphi }}_i=-1$, from (18), it arrives that ${\overline{\varphi }}_i\parallel {\mathrm{s}}_i\left(t\right)\parallel <{\overline{\varphi }}_j\frac{{\varsigma }_1}{{\lambda }_{min}\left({\kappa }_i\right)}$, ${\dot{V}}_i\left(t\right)<0$. Thus, ${lim}_{t\to \infty }{V}_i\left(t\right)$ exists. Combining the above result with ${\mathcal{U}}_i$ gives rise to $-\infty <{lim}_{t\to \infty }{V}_i\left(t\right)-V_i\left(t_0\right)\le {lim}_{t\to \infty }{\int }_{t_0}^t{\mathcal{U}}_i\left({\mathrm{s}}_i\left(t\right)\right)$$dt\le 0$. The similar process applies when ${\overline{\varphi }}_i=1.$ Due to (7), one obtains that ${\dot{s}}_i\left(t\right)$, and that ${\mathcal{U}}_i\left({\mathrm{s}}_i\left(t\right)\right)$ is uniformly continuous. Consequently, ${lim}_{t\to \infty }{\mathcal{U}}_i\left({\mathrm{s}}_i\left(t\right)\right)=0$ as the result of Barbalat’s lemma. It can be concluded that $V_i\left(t\right)$ converges to ${\mathcal{Q}}_{i1}^{\left(z\right)}$, so $\parallel {\mathrm{s}}_i\left(t\right)\parallel <\frac{{\varsigma }_1}{{\lambda }_{min}\left({\kappa }_i\right)}$ when $t>t_i$, $t_i\in {\mathbb{R}}^{+}$.

Subsequently, for the robots in the first group, another Lyapunov function is selected as $V_{10}=\frac{1}{2}{\varpi }_{{\mu }_1}^{\mathrm{T}}(X_1\otimes I_p){\varpi }_{{\mu }_1}$, then the derivative of $V_{10}$ is formulated as ${\dot{V}}_{10}={\varpi }_{{\mu }_1}^{\mathrm{T}}(X_1\otimes I_p){\dot{\varpi }}_{{\mu }_1}=-{\varpi }_{{\mu }_1}^{\mathrm{T}}\left(Z_1\otimes I_p\right){\varpi }_{{\mu }_1}+{\varpi }_{{\mu }_1}^{\mathrm{T}}\left(X_1\otimes I_p\right)s_{{\varpi }_1}$. Thus, one has

${\dot{V}}_{10}\le \left(\frac{2{\varsigma }_1{\lambda }_{max}\left(X_1\right)}{{\lambda }_{min}\left({\kappa }_i\right)\parallel {\varpi }_{{\mu }_1}\parallel }-{\lambda }_{min}\left(Z_1\right)\right){\parallel {\varpi }_{{\mu }_1}\parallel }^2$.

Taking ${\mathcal{Q}}_1=\left\{({\mathsf{\Phi }}_1\otimes I_p){\mathbf{q}}_{{\mu }_1}^{\mathrm{T}},({\mathsf{\Phi }}_1\otimes I_p){\dot{\mathbf{q}}}_{{\mu }_1}^{\mathrm{T}})|\parallel {\varpi }_{{\mu }_1}\parallel \right.$ $\left.<\frac{2{\varsigma }_1{\lambda }_{max}\left(X_1\right)}{{\lambda }_{min}\left({\kappa }_i\right){\lambda }_{min}\left(Z_1\right)}\right\},$ where ${\mathbf{q}}_{{\mu }_1}$ and ${\dot{\mathbf{q}}}_{{\mu }_1}$ are the respective column stack vectors of ${\mathrm{q}}_i$ and ${\dot{\mathrm{q}}}_i$, $i=1,2,\cdots ,n_1$, it arrives readily that the initial states from $\mathcal{R}$ eventually drop into the region ${\mathcal{Q}}_1$. Conducting similar processes, serial regions ${\mathcal{Q}}_l$ can be derived such that ${\mathcal{Q}}_l=\{({\mathsf{\Phi }}_l\otimes I_p){\mathbf{q}}_{{\mu }_l}^{\mathrm{T}},({\mathsf{\Phi }}_l\otimes I_p){{\dot{\mathbf{q}}}_{{\mu }_l}}^{\mathrm{T}})|\parallel {\varpi }_{{\mu }_1}\parallel <\frac{2{\varsigma }_1{\lambda }_{max}\left(X_1\right)}{{\lambda }_{min}\left({\kappa }_i\right){\lambda }_{min}\left(Z_1\right)},$ $\cdots ,$ $\parallel {\varpi }_{{\mu }_l}\parallel <\frac{2{max}_{j\in \{1,\cdots ,l\}}\left\{{\varsigma }_j\right\}{\lambda }_{max}\left(X_l\right)}{{min}_{j\in \{1,\cdots ,l\}}\left\{{\lambda }_{min}\left({\kappa }_j\right)\right\}{\lambda }_{min}\left(Z_l\right)}\}$, where ${\mathbf{q}}_{{\mu }_l}$ and ${\dot{\mathbf{q}}}_{{\mu }_l}$ are the respective column stack vectors of ${\mathrm{q}}_i$ and ${\dot{\mathrm{q}}}_i$, $i=1,2,\cdots ,n_l$, $l=1,2,\cdots ,k$. Accordingly, if ${\lambda }_{min}\left({\kappa }_{{}_l}\right)>$ ${max}_{j\in \{l,l+1,\cdots ,k\}}$ $\left\{\frac{2{max}_{j\in \{1,2,\cdots ,l\}}\left\{{\varsigma }_j\right\}{\lambda }_{max}\left(X_l\right)}{{\lambda }_{min}\left(Z_l\right){\gamma }_{{}_l}}\right\},$ $l=1,2,\cdots$$\cdots ,k$, then leader-following regional multiple-bipartite consensus is realised. Theorem 1 is proved. □

Remark 2.

Regional multiple-bipartite consensus requires that system evolution should follow the principle of multiple objective regional symmetry emphasised in practical circumstances. Although the concept of multiple-bipartite consensus was proposed in [28], realising multiple symmetry of final states of NSLs, our problem framework, system control method, and stability analysis are different from the previous study which is the concrete embodiment of our mathematical models of a network system to tackle multiple complex tasks. The results in our paper cannot be obtained nor generalised by virtue of existing methods. Therefore, our work has further expansion and embodies great practical significance compared with the abovementioned literature.

Remark 3.

Integrating the structurally balanced topology with acyclic partition, it can always select the appropriate control gain coefficient to make the state variable converge to the predefined region, which is flexible and in line with the realistic situation. Obviously, Theorem 1 extends the results in complete consensus [23]. When $\overline{\mathsf{\Phi }}=I_{n+k}$, the problem degenerates into the traditional regional group consensus in [24], which is a special case of the problems discussed in Theorem 1.

Remark 4.

The sign function “Sgn” of the control component is inspired by Altafini [12], which is a traditional feedback control input in terms of the architecture of coopetition network topology. “${\overline{\varphi }}_i$” is introduced in [27] as a supplementary state feedback protocol to apply to the agents from different groups. Our work can be seen as an effective generalisation of regional group consensus and bipartite consensus of NLSs in realising regional multiple-bipartite consensus.

Remark 5.

In the realisation of regional multiple-bipartite consensus, ${\mathrm{s}}_i$ is embedded in ${\tau }_i$, guaranteeing that ${\mathrm{q}}_i$ converges to the desired region. In addition, it is not required that the condition of antagonistic relations only exists between different groups. Our results reflect the characteristics of acyclic partition topology: the information of the first group directly or indirectly affects the latter group, so the requirement of control gain is more strict than that of latter groups.

4. Simulations

In order to achieve leader-following regional multiple-bipartite consensus for NLSs, our algorithm is demonstrated through the state evolution of two groups composed of seven two-link mechanical manipulators. $M_i\left({\mathrm{q}}_i\right),C_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i)$, and $g_i\left({\mathrm{q}}_i\right)$ in system (1) are given as follows:

$$M_i\left({\mathrm{q}}_i\right)=\left[\begin{array}{cc}{\vartheta }_{i1}+2{\vartheta }_{i2}cos{\mathrm{q}}_{i2}& {\vartheta }_{i3}+{\vartheta }_{i2}cos{\mathrm{q}}_{i2}\\ {\vartheta }_{i3}+{\vartheta }_{i2}cos{\mathrm{q}}_{i2}& {\vartheta }_{i3}\end{array}\right],$$

$$C_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i)=\left[\begin{array}{cc}-{\vartheta }_{i2}{\dot{\mathrm{q}}}_{i2}sin{\mathrm{q}}_{i2}& -{\vartheta }_{i2}({\dot{\mathrm{q}}}_{i1}+{\dot{\mathrm{q}}}_{i2})sin{\mathrm{q}}_{i2}\\ {\vartheta }_{i2}{\dot{\mathrm{q}}}_{i1}sin{\mathrm{q}}_{i2}& 0\end{array}\right],$$

$$g_i\left({\mathrm{q}}_i\right)=\left[\begin{array}{c}{\vartheta }_{i4}g{\dot{\mathrm{q}}}_{i2}cos{\mathrm{q}}_{i1}+{\vartheta }_{i5}gcos({\mathrm{q}}_{i1}+{\mathrm{q}}_{i2})\\ {\vartheta }_{i5}gcos({\mathrm{q}}_{i1}+{\mathrm{q}}_{i2})\end{array}\right],$$

where ${\mathrm{q}}_i={({\mathrm{q}}_{i1},{\mathrm{q}}_{i2})}^{\mathrm{T}},$ $g=9.8\mathrm{m}/{\mathrm{s}}^2,$ ${\vartheta }_{i1}=m_{i1}{d}_{ci1}^2+m_{i2}(d_{i1}^2+d_{ci2}^2)+J_{i1}+J_{i2},$ ${\vartheta }_{i2}=m_{i2}{d}_{i1}{d}_{ci1},$ ${\vartheta }_{i3}=m_{i2}{d}_{ci2}^2+J_{i2},$ ${\vartheta }_{i4}=m_{i1}{d}_{ci1}+m_{i2}{d}_{i1},$ ${\vartheta }_{i5}=m_{i2}{d}_{ci2}.$ Here $m_{i1}=1.2+0.2i$ kg, $m_{i2}=1.4+0.12i$ kg, $d_{i1}=1.8+0.08i$ m, $d_{i2}=2.3+0.04i$ m, $d_{ci1}=d_{i1}/2,$ $d_{ci2}=d_{i2}/2,$$J_{i1}=m_{i1}{d}_{ci1}^2/3$ kg m${}^2$, $J_{i2}=m_{i2}{d}_{ci2}^2/3$ kg m${}^2$. Then the regressor matrix can be expressed as

$$Y_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i,w,z)=\left[\begin{array}{ccccc}{w}_1& Y_{12}& w_2& gcos{\mathrm{q}}_{i1}& gcos({\mathrm{q}}_{i1}+{\mathrm{q}}_{i2})\\ 0& Y_{21}& w_1+w_2& 0& gcos({\mathrm{q}}_{i1}+{\mathrm{q}}_{i2})\end{array}\right],$$

where $Y_i({\mathrm{q}}_i,{\dot{\mathrm{q}}}_i,w,z)\in {\mathbb{R}}^{2\times 5}$. Denote ${\mathcal{P}}_i={({\vartheta }_{i1},{\vartheta }_{i2},{\vartheta }_{i3},{\vartheta }_{i4},{\vartheta }_{i5})}^{\mathrm{T}}$, where $w={(w_1,w_2)}^{\mathrm{T}},$ $z={(z_1,z_2)}^{\mathrm{T}}$, $Y_{12}=2w_{1}cos{\mathrm{q}}_{i2}+w_{2}cos{\mathrm{q}}_{i2}-{\dot{\mathrm{q}}}_{i2}{z}_{1}sin{\mathrm{q}}_{i2}-({\dot{\mathrm{q}}}_{i1}+{\dot{\mathrm{q}}}_{i2})z_{2}sin{\mathrm{q}}_{i2},$ $Y_{21}=w_{1}cos{\mathrm{q}}_{i2}$$+{\dot{\mathrm{q}}}_{i1}{z}_{1}sin{\mathrm{q}}_{i2}.$

The topology graph $\overline{\mathcal{G}}$ is shown in Figure 1. $\overline{\mathbb{V}}=\{{\zeta }_1,1,2,3,$$4,{\zeta }_2,5,6,7\}={\overline{\mathbb{V}}}_1\cup {\overline{\mathbb{V}}}_2$, where ${\overline{\mathbb{V}}}_1=\{{\zeta }_1,1,2,3,4\}$ and ${\overline{\mathbb{V}}}_2=\{{\zeta }_2,5,6,7\}$. In addition, ${\overline{\mathbb{V}}}_1^{\left(1\right)}=\{{\zeta }_1,1,2\}$ and ${\overline{\mathbb{V}}}_1^{\left(2\right)}=\{3,4\}$, ${\overline{\varphi }}_{{}_{01}}={\overline{\varphi }}_1={\overline{\varphi }}_2=1$, ${\overline{\varphi }}_3={\overline{\varphi }}_4=-1$; ${\overline{\mathbb{V}}}_2^{\left(1\right)}=\{{\zeta }_2,5\}$ and ${\overline{\mathbb{V}}}_2^{\left(2\right)}=\{6,7\},$${\overline{\varphi }}_{{}_{02}}={\overline{\varphi }}_5=1$, ${\overline{\varphi }}_3={\overline{\varphi }}_4=-1$. The leaders ${\zeta }_1$ and ${\zeta }_2$ in the two groups are described as follows:

$${\zeta }_1={\left(2\sin \left(t\right),2\cos \left(t\right)\right)}^{\mathrm{T}},$$

$${\zeta }_2={\left(2+\left(1/2\right)\sin \left(t\right),-2+\left(1/2\right)\cos \left(t\right)\right)}^{\mathrm{T}}.$$

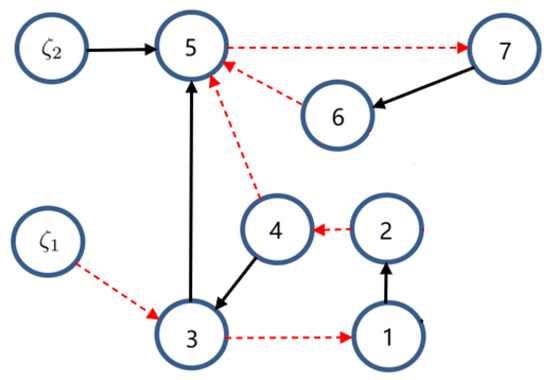
Figure 1. Communication topology graph $\overline{\mathcal{G}}$ with two leaders (${\zeta }_1$ and ${\zeta }_2$) and seven followers (1, 2, 3, 4, 5, 6, 7).

Denote the error functions as $\parallel {\mathrm{q}}_1-{\mathrm{q}}_2\parallel$, $\parallel {\mathrm{q}}_3-{\mathrm{q}}_4\parallel$, $\parallel {\mathrm{q}}_5+{\mathrm{q}}_6\parallel$, and $\parallel {\mathrm{q}}_6-{\mathrm{q}}_7\parallel$. The selection of initial values are from $[-3,3]$ randomly and the predefined tracking errors are selected as ${\gamma }_l=0.5$, $l=1,2,\cdots ,7.$ Assume the external disturbance functions ${\tau }_d=\mathrm{rand}(14,1)$ and that control gains are taken as ${\kappa }_i=22\mathrm{diag}\{2.3,1.5\}$. Figure 2 and Figure 3 exhibit the state evolutions of leader-following regional multiple-bipartite consensus. Figure 4 and Figure 5 show that $\parallel {\varpi }_{{\mu }_1}\parallel =\parallel (\overline{{\varphi }_1}{\mathrm{q}}_1-{\overline{\varphi }}_{{}_{01}}{\zeta }_1),$$(\overline{{\varphi }_2}{\mathrm{q}}_2-{\overline{\varphi }}_{{}_{01}}{\zeta }_1),$$(\overline{{\varphi }_3}{\mathrm{q}}_3-{\overline{\varphi }}_{{}_{01}}{\zeta }_1),$$(\overline{{\varphi }_4}{\mathrm{q}}_4-{\overline{\varphi }}_{{}_{01}}{\zeta }_1)\parallel <0.5$, and $\parallel {\varpi }_{{\mu }_2}\parallel =\parallel (\overline{{\varphi }_5}{\mathrm{q}}_5-{\overline{\varphi }}_{{}_{02}}{\zeta }_2),$$(\overline{{\varphi }_6}{\mathrm{q}}_6-{\overline{\varphi }}_{{}_{02}}{\zeta }_2),$$(\overline{{\varphi }_7}{\mathrm{q}}_7-{\overline{\varphi }}_{{}_{02}}{\zeta }_2)\parallel <0.5$, implying that the group error vectors associated with leaders converge to the desired predefined regions. In a word, satisfactory results are presented by exploiting the proposed protocol (5), so the leader-following regional multiple-bipartite consensus problems are well settled.

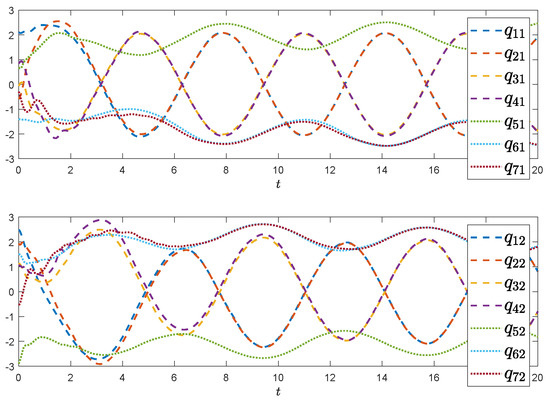
Figure 2. Position tracking evolution for two groups of mechanical manipulators.

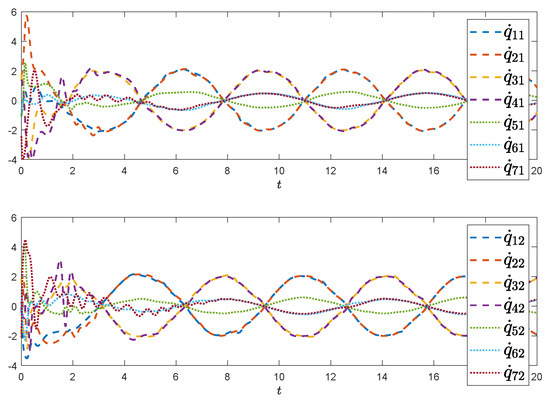
Figure 3. Velocity tracking evolution for two groups of mechanical manipulators.

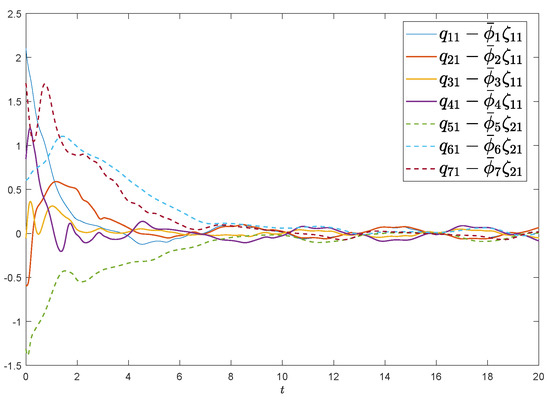
Figure 4. X-coordinate error evolution for two groups of mechanical manipulators with leaders.

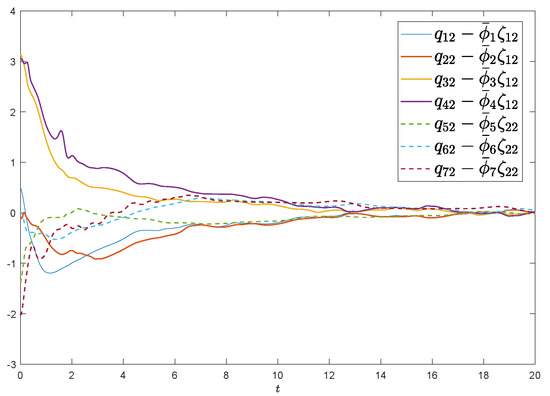
Figure 5. Y-coordinate error evolution for two groups of mechanical manipulators with leaders.

5. Conclusions

This paper studied the leader-following regional multiple-bipartite consensus problems of NLSs in coopetition networks. By introducing antagonistic interactions in each group, the research framework effectively extended the application scopes of that of complete consensus and regional consensus in cooperative networks. In addition, it is more in line with the actual situation that antagonistic relations can exist in the same group. To realise the objective that the final states of NLSs converge to the predefined multi-regional symmetry on the basis of ensuring system stability, a novel auxiliary vector was integrated into the control protocols to offset the impacts between different groups. Moreover, the control gain selection of our algorithm guaranteed that the final states of NLSs achieved regional symmetry, reflecting the important role of the characteristics of acyclic partition topology, in which the former groups need more strict rules than the latter groups. The validity of the proposed approach was illustrated by numerical simulations.

One of the future research directions will be the regional multiple-bipartite consensus problem of NLSs on varied and more complex robot structures due to its potential applicability. For instance, resorting to the control algorithm and method in [29], we hope to develop a relevant algorithm for NLSs with six degrees of freedom, which will be worthy of thorough research. In addition, for multirobot systems with nonholonomic constraints [30], determining how to develop appropriate strategies to circumvent the underactuated features and realise the multiple two-coordinate regional symmetry control objective will also deserve our further pursuit. We also hope to realise leader-following regional multiple-bipartite consensus for NLSs under switching topology, delay limitation, and event-triggered mechanism in further study.