Abstract
Majorana bound states in topological superconductors have attracted intense research activity in view of applications in topological quantum computation. However, they are not the only example of topological bound states that can occur in such systems. Here, we study a model in which both Majorana and Tamm bound states compete. We show both numerically and analytically that, surprisingly, the Tamm state remains partially localized even when the spectrum becomes gapless. Despite this fact, we demonstrate that the Majorana polarization shows a clear transition between the two regimes.
1. Introduction
Non-Abelian quasiparticles have attracted intense theoretical and experimental research activities in the last several years, in view of their potential applications in topologically protected quantum computation [1]. Several proposals for the experimental realization or detection of such exotic states of matter in interacting systems have hence been put forward [2,3,4,5,6,7,8,9,10,11,12,13]. Despite steady progress, the need to enforce the coexistence of superconductivity and electronic interactions makes their experimental realization challenging [14,15,16]. In the absence of interactions, the possibility to engineer non-Abelian Majorana zero modes [17] in spinless p-wave superconductors has been predicted [18,19]. The unambiguous experimental realization of such states is again far from straightforward, due to the fact that spinless p-wave superconductivity is rare in nature. However, it has been realized that this kind of pairing could be achieved by means of proximity-induced superconductivity on semiconducting structures with pronounced spin-dependent properties. One of the first example of a system that, once proximitized, can host Majorana bound states is represented by topological insulators [20,21,22], where strong spin–orbit coupling gives rise to inverted bands behavior. However, it additionally requires the presence of magnetic barriers to allow for Majorana bound state formation. The difficulty in implanting magnetic barriers has slowed down the development of such a platform. Recently, the possibility to employ quantum point contacts [23] instead of magnetic barriers has been considered, providing a promising alternative for topological insulator-based Majorana platforms [24,25]. Several other platforms have been proposed, ranging from ferromagnetic atomic chains with superconducting pairing [26], planar Josephson junctions in 2D semiconductors [27,28,29], and the more popular setup based on spin–orbit-coupled quantum wire with proximity superconductivity and applied magnetic fields [30,31].
In the last case, several experiments have reported signatures compatible with the presence of Majorana zero modes [32]. However, a clear evidence of the quantization of the zero bias peak, which is one of the predicted signatures ascribed to the presence of Majorana zero modes, or other unambiguous fingerprints of their formation are still lacking to date. Indeed, an additional challenge in the field is posed by the fact that Majorana zero modes behave, in many terms, similarly to more conventional Andreev bound states, which do not exhibit non-Abelian statistics, and are thus less useful in quantum computation [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. Indeed, on one hand, it is still possible to distinguish between trivial Andreev bound states that emerge at finite chemical potential in clean systems and Majorana bound states due to the fact that the phase containing Majorana fermions and the one with the trivial bound states are separated by a region with extended states only [51]. On the other hand, the distinction becomes more subtle in the presence of disorder, spatial variations of the confinement potentials, or whenever the formation of quantum dots [52] takes place. A detailed analysis of the scenarios in which Majorana fermions and other bound states coexist is hence in order.
In this work, we concentrate on this aspect by studying a simple model where different bound states may coexist. To this end, we consider a one-dimensional finite size spinless p-wave superconductor in the presence of a spatially periodic modulation of the local chemical potential. The system is numerically investigated by means of extensive exact diagonalization. We find that the bulk of the system is always gapped at the chemical potential, except for a gapless point that marks the boundary between two phases dominated either by the periodic local potential (A) or the superconducting one (B). In the A phase, either a bound state is localized at one end of the system or no boundary states are present, depending on the phase of the modulated potential. The possible boundary state is adiabatically connected with the system in the absence of superconductivity and hence is, qualitatively speaking, a Tamm state [53,54,55]. In the B phase, one recovers the more conventional Majorana scenario, with the zero mode split into two Majorana modes at both ends of the system. Surprisingly, at the transition between A and B, the Tamm state remains partially localized. This behavior poses the question if the Majorana fermions in the B phase are still topological in nature or if the reminiscence of the Tamm state eventually spoils their properties.
In the second part of the work, we answer this question, deriving and analyzing a linearized low-energy model that can be analytically solved. This allows us to interpret and discuss the physics observed in the first part in terms of Goldstone–Wilczek charges [54,56,57,58,59,60,61,62,63].
Finally, to elucidate the interplay between the different kinds of bound states, and to possibly discriminate between them, we evaluate the Majorana polarization [64,65,66] associated to the boundary states. This quantity is one of the standard tools introduced to characterize topological superconductors. This allows us to conclude that phase B is indeed characterized by the presence of Majorana fermions.
In more details, the article is divided as follows. In Section 2, we analyze the results for the p-wave superconductor model. In Section 3, we derive the exactly solvable model and discuss it. Section 4 contains the calculation of the Majorana polarization. Our conclusions are finally drawn in Section 5.
2. The Quadratic Model
2.1. Hamiltonian
The system we inspect is a finite-size, spinless one-dimensional p-wave superconductor in the presence of an additional periodic potential [67]. More specifically, the Hamiltonian, defined on a segment of length L, is
with the Bogoliubov–de Gennes (BdG) Hamiltonian density given by ()
and , where is a fermionic annihilation field. We impose open boundary conditions, implying . In the Hamiltonian, m is the effective mass, sets the filling with (Note that, in view of the finite size of the system, we also impose , with a positive integer.) , the strength of the p-wave superconducting pairing and () are the Pauli matrices. For future use, we also introduce as the 2 × 2 identity matrix. Finally, we set
with the phase kept as a free parameter. Here, is a periodic potential that can emerge due to external gates [68] or via a coupling to the phonons [69]. The parameter B parametrizes the strength of the term, while the phase , which is clearly an irrelevant parameter when periodic boundary conditions are imposed, becomes essential in the case of open boundary conditions. The manipulation of the phase can be envisioned if is due to external finger gates [68]. In this case, the spatial variations of the potential can be fully manipulated.
The energy spectrum and the wavefunctions are evaluated via a numerical exact diagonalization procedure, which consists of expanding the eigenfunctions of the Hamiltonian on the basis of the states of a free particle in a infinite 1D box of length L
and diagonalizing the associated matrix of the Hamiltonian on this basis. This allows us to obtain the energy spectrum and the weights of the eigenfunctions of the problem. It is here worth mentioning that since we adopt the Bogoliubov–de Gennes formalism, we artificially double the spectrum by introducing a redundant chiral symmetry, and hence only half of the eigenfunctions of the Hamiltonian matrix have physical meaning. Indeed, by only taking the positive energy eigenstates, one recovers the correct excitation spectrum. The diagonalization is performed in Mathematica (TM) and up to 450 box states per BdG sector are employed depending on the values of B and , to ensure numerical convergence with a relative error on the energy spectrum.
2.2. Tamm States
We begin our analysis by considering the case .
Figure 1 shows the energy spectrum for different values of the strength B and different phases . As a general feature, we observe that, for , the periodic potential opens a gap at zero energy—where the chemical potential is set. Secondary gaps can occur when the amplitude B becomes large, . This additional gap, visible in Figure 1a for , opens, having in mind periodic boundary conditions and a folded scheme for taking into account the periodic perturbation, at . For the same magnitudes of B, an additional feature appears for small (see the blue and red curves). This is due to the change in nature of the lowest energy states, which, for , are dominated by the periodic potential. Comparing Figure 1a,b, one can observe that for almost all the states, the overall shape of the energy spectrum depends weakly on the phase , being almost insensitive to it for . However, inspecting the case , one can observe that a zero-energy mode occurs within the gap, which suggests that the low-energy sector of the spectrum may exhibit a more pronounced dependence on .
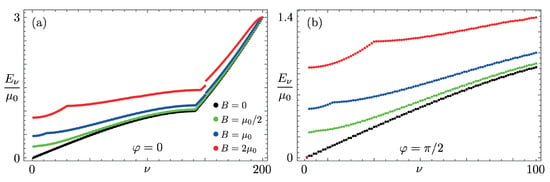
Figure 1.
Plots of the energy spectrum for different values of the amplitude of the periodic potential: (black); (green); (blue); (red). The case is shown in panel (a) for the first 200 eigenstates, while in panel (b) for the first 100 eigenstates.
To check this fact, Figure 2a shows the behavior of the first eight eigenstates with as a function of for the representative case of . As one can clearly see, the lowest energy state exhibits a quite dramatic dependence on the phase, becoming a zero mode for with p an integer. The wavefunction of such a zero-energy state is shown for in Figure 2b and it corresponds to a localized state, which, in this context, is usually referred to as a Tamm state. Such a state is respectively localized either at the right () or at the left () edge of the system. Such a Tamm state is starkly different from the delocalized states obtained at , which extend over the entire length of the system; see the representative example reported in Figure 2c for the case . In general, for , a bound state within the gap always occurs, possibly with a nonzero energy and a larger localization length.
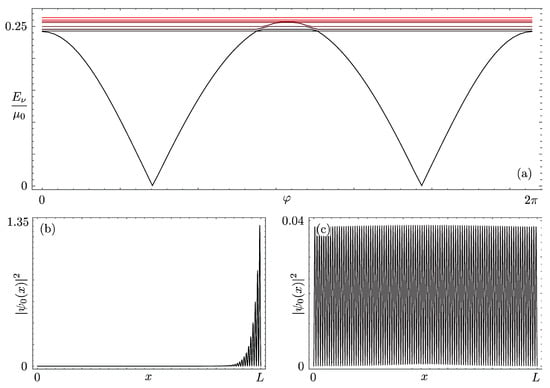
Figure 2.
Plot of for (from black to red) as a function of (panel a) and probability density of the state (units ) as a function of x for (panel b) and (panel c). In all panels, the amplitude of the periodic potential is set at .
2.3. Majorana States
The regime with is more known since it represents the paradigmatic model that hosts Majorana bound states: even in this case a gap opens around the chemical potential and a fermionic zero-energy mode appears in the spectrum.
The BdG wave function corresponding to this fermionic state is significantly nonzero close to both ends of the segment (see Figure 3). Formally, one can interpret this nonlocal fermionic state as two local Majorana states, each one localized close to one end only. This is obviously meaningful only when the localization length is smaller than the length of the system.
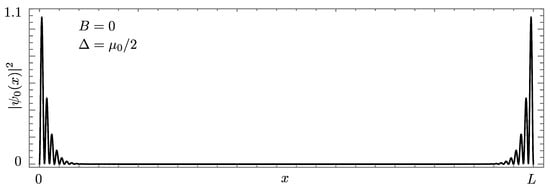
Figure 3.
Probability density of the zero-energy Majorana state (units ) as a function of x for and .
2.4. Competition between Tamm and Majorana States
Let us now address the case when both B and are nonzero and thus the two gaps induced by the oscillating potential and by the p-wave pairing compete. We are particularly interested into the interplay between the two (qualitatively different) localized Tamm and Majorana states, and thus we set from now on to achieve the most dramatic effects. Indeed, corresponds to a maximally localized Tamm state. As a general feature, we find that in this case, for any value of a zero-energy mode occurs.
Figure 4a–e shows the probability amplitude of this zero-energy mode for and increasing values of the superconducting pairing. As is increased from zero, the localized state broadens (see panel (b)). However, when (see panel (c)), a peculiar phenomenon occurs: the former Tamm state gets sharper once again while the wavefunction in the rest of the system becomes nonzero and with a flat envelope. When (see panel (d)), a second localized state develops. Finally, when , the wavefunction tends to recover a symmetric shape localized at both ends of the system.
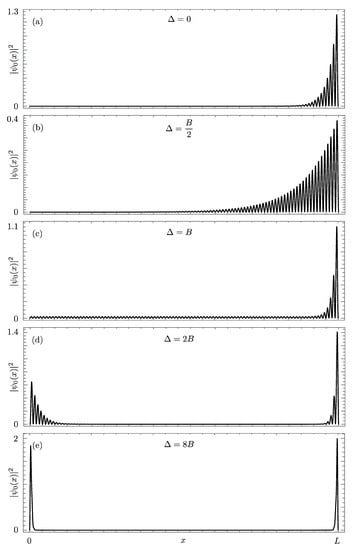
Figure 4.
Probability density of the zero-energy state (units ) as a function of x for different values of the p-wave pairing strength: (a); (b); (c); (d); (e). In all panels, and .
To better understand what is going on, we study the spectral weight , shown as a density plot as a function of the box state index n and the energy E in Figure 5 for energies around . (Note that due to the finite size of the system, the spectrum is always discrete and a binning of the energies has been performed to produce the plots.) In general, this tool allows us to get a glimpse of the structure of the energy spectrum of the system. Indeed, panel (a) shows, as a warm-up, the case . As one can see, the spectral weight is sharply peaked on one box state per energy value and the yellow traces faithfully reproduce the energy spectra of the particle () and hole () sectors of the BdG picture for the Hamiltonian . Panel (b) shows the situation for and , when a Tamm state occurs. The energy gap is clearly visible and the blurry feature at is the spectral representation of the Tamm state, whose amplitude is smeared across many delocalized box states in order to produce a state localized in space. The situation is somewhat similar for —see panel (d)—again consistent with the picture of a wavefunction with sharp peaks at the system ends. However, the situation for , shown in panel (c), is peculiar. At this transition point, the spectrum is gapless and exhibits two linear modes around . Thus, the zero-energy mode is embedded into a gapless spectrum, and yet it still represents a bound state.
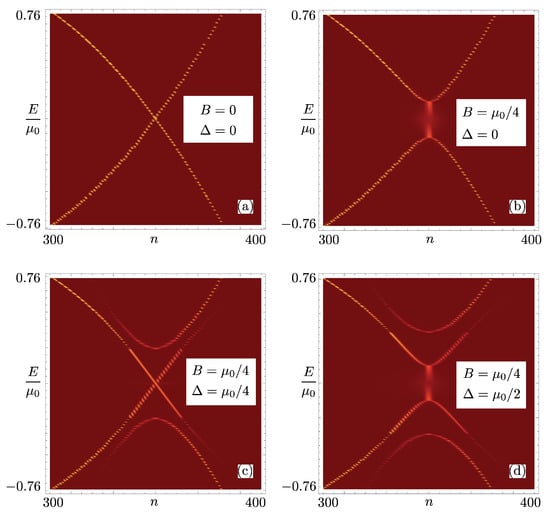
Figure 5.
Density plot of the spectral weight (see text) as a function of the index n labeling the eigenstates of a particle in a box of length L and energy E (units ) for different values of B and : (a); , (b); (c); , (d).
To summarize our findings so far, even though a gap closing is present at the level of the bulk spectrum, bound states can exist for every value of B and . However, assessing the nature of such bound states (Tamm- or Majorana-like) is not a trivial affair in the context of the full quadratic model, which can only be solved numerically. A notable exception is represented by the point . In that case, indeed, no Tamm state is present and a bound state is necessarily a Majorana state. However, the general case needs further inspection. In order to tackle this problem and provide an answer, we now proceed with development of an analytically solvable low-energy model that is able to capture all of the features described so far.
3. Effective Low-Energy Model
3.1. Linearization
To develop an effective, low-energy model valid around the chemical potential, we consider a linear dispersion relation instead of the quadratic one. This is meaningful as long as is the largest energy scale involved [70,71,72]. In detail, we approximate the fermionic operator as [73,74,75,76]
with fermionic operators for right- or left-moving electrons. In particular, using the particle-in-a-box states, one can write
and ensuring, together with the periodicity of the fields, that open boundary conditions are satisfied. Here, the fermionic operators are associated to the nth eigenstate of a particle in a box. Note that, as an approximation, the sum is here extended to all integers and, consequently, a slight notation abuse has been adopted, having defined the operators for all the integer values n. This approximation scheme is always performed when discussing the bosonization procedure, and is discussed, for example, in [77].
The kinetic energy is then approximated with
with representing the Fermi velocity.
In order to write the full Hamiltonian within the linear approximation, it is useful to introduce the enlarged BdG spinor
By imposing that is the largest energy scale (we indeed neglect terms proportional to with respect to terms proportional to ), we finally get the approximate form for the Hamiltonian
with
In order to interpret the boundary conditions and the peculiar effects that they may have on the bound states, it is useful to think in the following way. Consider a pair of chiral fermions and , independent from each other and organized in the BdG spinor , defined on the whole real axis, and with Hamiltonian
where we have introduced a localized backscattering potential
with the backscattering strength. It can be easily shown in the limit that the wavefunctions in the region become disconnected and acquire the boundary conditions , [78,79,80]. The Schrodinger problem associated to , when considered for and when , is hence perfectly equivalent to the one related to H in Equation (9).
The advantage in resorting to is conceptual, since it allows to give a simple interpretation to the results described in the previous section. Indeed, from a physical point of view, is equivalent to the Hamiltonian of a quantum spin Hall liquid gapped by both superconductivity, with gap , and a magnetic mass pointing in the direction given by in the presence of two strong backscattering centers with opposite magnetization localized at .
3.2. Qualitative Interpretation of the Results
The first insight into the results comes from the computation of the spectrum as obtained by neglecting the presence of boundaries. If we consider the Hamiltonian given by
where the operators are now being defined, with a slight abuse of notation, on the whole real axis, one can obtain the energy spectrum. The spectrum is promptly found to be with and is shown in Figure 6.
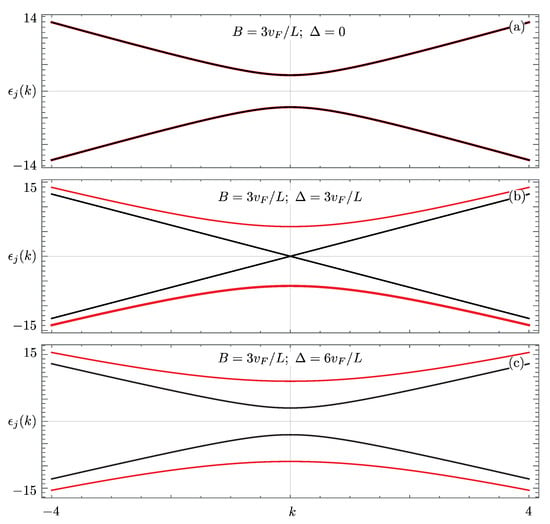
Figure 6.
Plot of (units ) as a function of k (units ) for: , (a); , (b); , (c). In all panels, red lines represent ; black lines correspond to .
As can be seen, the spectrum is always gapped for all except for —see panel (b)—where is gapless. The phase space point marks a quantum phase transition where the gap changes from magnetic () to superconducting (). However, it is crucial to notice the presence of a secondary gap of magnitude in , which is always present for every . Notice also the qualitative similarity between these spectra and the spectral features found in the quadratic model substantiating the validity of the linear approximation at low energies, compared to .
Turning to the inspection of bound states, it is crucial to observe that the addition of a confining term proportional to produces a magnetic gap in the spectrum. It is well known [81] that in the superconducting dominated regime (), Majorana bound states appear at the boundaries of the system. However, in the opposite case, when the situation is more subtle, as this model would implement the physics of so-called Goldstone–Wilczek fractional solitons [62]. Since this regime is adiabatically connected to , in order to build some physical intuition, one can refer to the case in which superconductivity is absent. The system is then equivalent to a quantum spin Hall liquid, in the absence of superconductivity, gapped by two magnets of equal strength at and characterized by different magnetization angles: it hence hosts bound states. Assuming the decay length of these bound states to be shorter than the system size L, the two bound states are essentially independent, and thus it is sufficient to concentrate on a single boundary to capture the relevant physics.
3.3. Linear Model with One Boundary and
We thus inspect a simpler linear model in the regime , considering the bound state localized around . Its wavefunction , that since superconductivity is now absent (), has only the two right- and left-moving components, can be easily obtained and reads
The solution is only acceptable (normalizable) for . The corresponding energy is . Note that for the state, mimicking the Tamm state of the quadratic model, is at zero energy. The scenario just derived perfectly agrees with the behavior of the left boundary of the quadratic model, although in that case the wavefunction in Equation (14) by means of Equation (5) has one component only, and is rebuilt from the condition in Equation (5). Moreover, in the quadratic model, the unphysical particle–hole symmetry of the Bogoliubov–de Gennes equation is present while here the redundancy [82,83] is not needed since superconductivity is not present. Hence, we have a single bound state instead of two at opposite energies.
The addition of a second physical boundary at produces effects that can be now easily understood by leveraging on the single boundary case just discussed. Indeed, the bound state at the boundary at is present when —that is, for —when the bound state is absent at . Such exponentially increasing solution is admissible due to the added barrier at —which prevents the divergence of the wavefunction—and its decay through the dot. This again is perfectly compatible with the results of the quadratic model discussed in Section 2.
A final comment for this section is the behavior at . For those values of the angle, the energy of the bound state reaches the bulk bands and the bound state becomes delocalized, and hence, effectively, disappears.
In the following, we will concentrate on the case in which the bound state is maximally localized around —that is, for .
3.4. The Wavefunction of the Bound State for
A further interesting behavior of the bound state found within the quadratic model is the fact that, when present, it does not become completely delocalized at the quantum phase transition . To confirm that this fact occurs also within the linearized model, we here report the BdG expression of the wavefunction of the bound state characterizing the linearized model in Equation (9), together with the condition in Equation (5), for and arbitrary . We find
where
Both the particle and the hole components and are characterized by a profile that is peaked around the edge, even at the transition point .
This case is shown in Figure 7, where a plot of and is reported for : one can clearly notice that, although the wavefunction is sharply localized at , it does not completely decay exponentially to zero at the transition point. This fact is in excellent agreement with the results obtained in the full quadratic model. As apparent from the analytical form of the wavefunction, this fact is due to the presence of the energy scale.
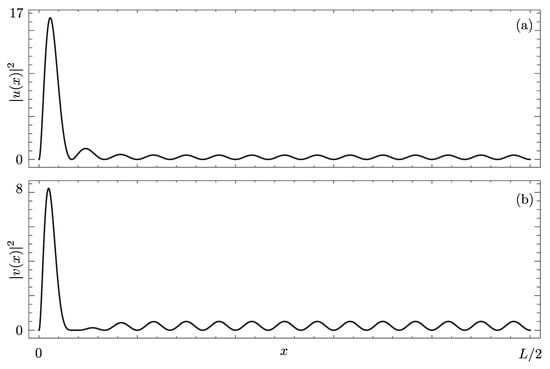
Figure 7.
Plot of the probability amplitude of particle and hole components of the zero-mode wavefunction (units ) as a function of x: (a); (b). Here, and .
A natural question hence arises: are the Majorana zero modes, in the superconducting-dominated phase , influenced by the persistence of the Tamm state across the quantum phase transition?
4. Majorana Polarization
The Majorana polarization [64] is a quantity that has been proposed in order to discriminate between Majorana fermions and other types of Andreev bound states. We now evaluate the Majorana polarization associated to the state , defined as
where
This absolute value of is close to one (in the large gap limit) if the bound state is a Majorana bound state, while it reaches different values for regular Andreev bound states, which allows us to assess the character of . In the case under examination, we find
Looking at the previous expressions, two limiting cases can be extracted. For , one finds , with when . For (and ), we find , and thus . From the point of view of the Majorana polarization, we hence have that, in the phase dominated by the magnetic field, the Majorana polarization is small, while it approaches, in modulus, the unity in the large gap limit. A transition takes place for . However, such a transition does not happen at the exact value of the gap closing, even for , that is . This behavior of shows, despite the fact that the Majorana phase indeed hosts polarized Majorana fermions, that a reminiscence of the Tamm state is, however, present—and visible—for .
The Majorana polarization is shown in Figure 8.
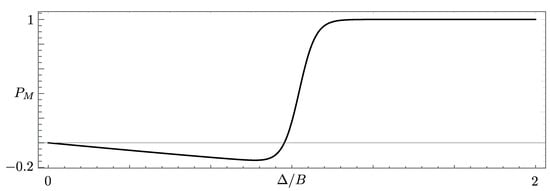
Figure 8.
Plot of the Majorana polarization as a function of for and .
5. Conclusions
In this work, we have characterized a simple model for a finite-size, one-dimensional topological superconductor in the presence of a competing normal gapping mechanism arising from a position-dependent potential. The first part of the article deals with the numerical inspection of the model. We find that the model has two phases: one characterized by Majorana fermions at both ends, and the other by, at most, a single Tamm bound state localized at one side. The energy of the bound state, when present, strongly depends on the phase of the position-dependent potential. Surprisingly, we find that the wavefunction of the bound state remains strongly peaked close to the edges, even at the gap closing point separating the two phases. In the second part of the article, we develop an exactly solvable model for interpreting the results of the first part. Finally, in the last section, we evaluate the Majorana polarization for a fully developed bound state of the model and show that, despite the fact that the Tamm state is not completely delocalized at the transition point, deep in the superconducting phase, the Majorana bound states are not strongly affected by the position-dependent potential.
Author Contributions
Conceptualization, M.C., N.T.Z., and F.C.; methodology, L.V.; software, M.C. and F.C.; validation, F.C., M.C., and L.V.; formal analysis, L.V. and N.T.Z.; writing—original draft preparation, N.T.Z. and F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We acknowledge fruitful discussions with Simone Traverso and Maura Sassetti.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian Anyons and Topological Quantum Computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef] [Green Version]
- Read, N.; Rezayi, E. Beyond paired quantum hall states: Parafermions and incompressible states in the first excited landau level. Phys. Rev. B 1999, 59, 8084. [Google Scholar] [CrossRef] [Green Version]
- Blasi, A.; Braggio, A.; Carrega, M.; Ferraro, D.; Maggiore, N.; Magnoli, N. Non-Abelian BF theory for 2+1 dimensional topological states of matter. New J. Phys. 2012, 14, 013060. [Google Scholar] [CrossRef]
- Zhang, F.; Kane, C.L. Time-Reversal-Invariant Z4 Fractional Josephson Effect. Phys. Rev. Lett. 2014, 113, 036401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orth, C.P.; Tiwari, R.P.; Meng, T.; Schmidt, T.L. Non-Abelian parafermions in time-reversal-invariant interacting helical systems. Phys. Rev. B 2015, 91, 081406. [Google Scholar] [CrossRef] [Green Version]
- Klinovaja, J.; Loss, D. Fractional charge and spin states in topological insulator constrictions. Phys. Rev. B 2015, 92, 121410. [Google Scholar] [CrossRef] [Green Version]
- Fleckenstein, C.; Traverso Ziani, N.; Trauzettel, B. Z4 parafermions in Weakly Interacting Superconducting Constrictions at the Helical Edge of Quantum Spin Hall Insulators. Phys. Rev. Lett. 2020, 122, 066801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rossini, D.; Carrega, M.; Calvanese Strinati, M.; Mazza, L. Anyonic tight-binding models of parafermions and of fractionalized fermions. Phys. Rev. B 2019, 99, 085113. [Google Scholar] [CrossRef] [Green Version]
- Carrega, M.; Principi, A.; Vera-Marun, I. Tunneling spectroscopy as a probe of fractionalization in 2D magnetic heterostructures. Phys. Rev. B 2020, 102, 085412. [Google Scholar] [CrossRef]
- Ronetti, F.; Carrega, M.; Ferraro, D.; Rech, J.; Jonckheere, T.; Martin, T.; Sassetti, M. Polarized heat current generated by quantum pumping in two-dimensional topological insulators. Phys. Rev. B 2017, 95, 115412. [Google Scholar] [CrossRef] [Green Version]
- Schiller, N.; Cornfeld, E.; Berg, E.; Oreg, Y. Predicted signatures of topological superconductivity and parafermion zero modes in fractional quantum Hall edges. Phys. Rev. Res. 2020, 2, 023296. [Google Scholar] [CrossRef]
- Michelsen, A.B.; Schmidt, T.L.; Idrisov, E.G. Current correlations of Cooper-pair tunneling into a quantum Hall system. Phys. Rev. B 2020, 102, 125402. [Google Scholar] [CrossRef]
- Zhao, L.; Arnault, E.G.; Bondarev, A.; Seredinski, A.; Larson, T.F.Q.; Draelos, A.W.; Li, H.; Watanabe, K.; Taniguchi, T.; Amet, F.; et al. Interference of chiral Andreev edge states. Nat. Phys. 2020, 16, 862. [Google Scholar] [CrossRef]
- Amet, F.; Ke, C.T.; Borzenets, I.V.; Wang, J.; Watanabe, K.; Taniguchi, T.; Deacon, R.S.; Yamamoto, M.; Bomze, Y.; Tarucha, S.; et al. Supercurrent in the quantum Hall regime. Science 2016, 352, 966. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, G.-H.; Huang, K.-F.; Efetov, D.K.; Wei, D.S.; Hart, S.; Taniguchi, T.; Watanabe, K.; Yacoby, A.; Kim, P. Inducing Superconducting Correlation in Quantum Hall Edge States. Nat. Phys. 2017, 13, 693. [Google Scholar] [CrossRef]
- Gül, O.; Ronen, Y.; Lee, S.Y.; Shapourian, H.; Zauberman, J.; Lee, Y.H.; Watanabe, K.; Taniguchi, T.; Vishwanath, A.; Yacoby, A.; et al. Induced superconductivity in the fractional quantum Hall edge. arXiv 2020, arXiv:2009.07836. [Google Scholar]
- Mourik, V.; Zuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 2012, 336, 1003. [Google Scholar] [CrossRef] [Green Version]
- Lutchyn, R.M.; Sau, J.D.; Das Sarma, S. Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef] [Green Version]
- Oreg, Y.; Refael, G.; von Oppen, F. Helical Liquids and Majorana Bound States in Quantum Wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, L.; Kane, C.L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, L.; Kane, C.L. Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction. Phys. Rev. B 2009, 79, 161408. [Google Scholar] [CrossRef] [Green Version]
- Akhmerov, A.R.; Nilsson, J.; Beenakker, C.W.J. Electrically detected interferometry of Majorana fermions in a topological insulator. Phys. Rev. Lett. 2009, 102, 216404. [Google Scholar] [CrossRef] [Green Version]
- Strunz, J.; Wiedenmann, J.; Fleckenstein, C.; Lunczer, L.; Beugeling, W.; Müller, V.L.; Shekhar, P.; Traverso Ziani, N.; Shamim, S.; Kleinlein, J.; et al. Interacting topological edge channels. Nat. Phys. 2020, 16, 83. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Pan, W.; Bernevig, B.A.; Lutchyn, R.M. Detection of Majorana Kramers Pairs Using a Quantum Point Contact. Phys. Rev. Lett. 2016, 117, 046804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fleckenstein, C.; Traverso Ziani, N.; Calzona, A.; Sassetti, M.; Trauzettel, B. Formation and detection of Majorana modes in quantum spin Hall trenches. Phys. Rev. B 2021, 103, 125303. [Google Scholar] [CrossRef]
- Nadj-Perge, S.; Drozdov, I.K.; Li, J.; Chen, H.; Jeon, S.; Seo, J.; MacDonald, A.H.; Bernevig, B.A.; Yazdani, A. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 2014, 6209, 602. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Pientka, F.; Hart, S.; Pierce, A.T.; Kosowsky, M.; Lunczer, L.; Schlereth, R.; Scharf, B.; Hankiewicz, E.M.; Molenkamp, L.W.; et al. Topological superconductivity in a phase-controlled Josephson junction. Nature 2019, 569, 93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guiducci, S.; Carrega, M.; Biasiol, G.; Sorba, L.; Beltram, F.; Heun, S. Toward Quantum Hall Effect in a Josephson Junction. Phys. Status Solidi RRL 2019, 13, 1800222. [Google Scholar] [CrossRef]
- Guiducci, S.; Carrega, M.; Taddei, F.; Biasiol, G.; Courtois, H.; Beltram, F.; Heun, S. Full electrostatic control of quantum interference in an extended trenched Josephson junction. Phys. Rev. B 2019, 99, 235419. [Google Scholar] [CrossRef] [Green Version]
- Krogstrup, P.; Ziino, N.L.B.; Chang, W.; Albrecht, S.M.; Madsen, M.H.; Johnson, E.; Nygard, J.; Marcus, C.M.; Jespersen, T.S. Epitaxy of semiconductor–superconductor nanowires. Nat. Mater. 2015, 14, 400. [Google Scholar] [CrossRef]
- Deng, M.T.; Vaitiekenas, S.; Hansen, E.B.; Danon, J.; Leijnse, M.; Flensberg, K.; Nygard, J.; Krogstrup, P.; Marcus, C.M. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 2016, 354, 1557. [Google Scholar] [CrossRef] [Green Version]
- Aguado, R. Majorana quasiparticles in condensed matter. La Riv. Del Nuovo Cimento 2017, 40, 523. [Google Scholar]
- Asano, Y.; Tanaka, Y.; Kashiwaya, S. Phenomenological theory of zero-energy Andreev resonant states. Phys. Rev. B 2004, 69, 134501. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, Y.; Kashiwaya, S.; Yokoyama, T. Theory of enhanced proximity effect by midgap Andreev resonant state in diffusive normal-metal/triplet superconductor junctions. Phys. Rev. B 2005, 71, 094513. [Google Scholar] [CrossRef] [Green Version]
- Golubov, A.A.; Brinkman, A.; Tanaka, Y.; Mazin, I.I.; Dolgov, O.V. Andreev Spectra and Subgap Bound States in Multiband Superconductors. Phys. Rev. Lett. 2009, 103, 077003. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, Y.; Mizuno, Y.; Yokoyama, T.; Yada, K.; Sato, M. Anomalous Andreev Bound State in Noncentrosymmetric Superconductors. Phys. Rev. Lett. 2012, 105, 097002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Potter, A.C.; Law, K.T.; Lee, P.A. Zero-Bias Peaks in the Tunneling Conductance of Spin-Orbit-Coupled Superconducting Wires with and without Majorana End-States. Phys. Rev. Lett. 2012, 109, 267002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kells, G.; Meidan, D.; Brouwer, P.W. Near-zero-energy end states in topologically trivial spin-orbit coupled superconducting nanowires with a smooth confinement. Phys. Rev. B 2012, 86, 100503. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.; Bondyopadhaya, N.; Tewari, S. Topologically trivial zero-bias conductance peak in semiconductor Majorana wires from boundary effects. Phys. Rev. B 2013, 88, 020502. [Google Scholar] [CrossRef] [Green Version]
- Stanescu, T.D.; Tewari, S. Disentangling Majorana fermions from topologically trivial low-energy states in semiconductor Majorana wires. Phys. Rev. B 2013, 87, 140504. [Google Scholar] [CrossRef] [Green Version]
- Cayao, J.; Prada, E.; San-Jose, P.; RAguado, R. SNS junctions in nanowires with spin-orbit coupling: Role of confinement and helicity on the subgap spectrum. Phys. Rev. B 2015, 91, 024514. [Google Scholar] [CrossRef] [Green Version]
- San-Jose, P.; Cayao, J.; Prada, E.; Aguado, R. Majorana bound states from exceptional points in non-topological superconductors. Sci. Rep. 2016, 6, 21427. [Google Scholar] [CrossRef]
- Liu, C.-X.; Sau, J.D.; Stanescu, T.D.; Das Sarma, S. Andreev bound states versus Majorana bound states in quantum dot-nanowire-superconductor hybrid structures: Trivial versus topological zero-bias conductance peaks. Phys. Rev. B 2017, 96, 075161. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.-X.; Sau, J.D.; Das Sarma, S. Distinguishing topological Majorana bound states from trivial Andreev bound states: Proposed tests through differential tunneling conductance spectroscopy. Phys. Rev. B 2018, 97, 214502. [Google Scholar] [CrossRef] [Green Version]
- Moore, C.; Stanescu, S.T.; Tewari, S. Two-terminal charge tunneling: Disentangling Majorana zero modes from partially separated Andreev bound states in semiconductorsuperconductor heterostructures. Phys. Rev. B 2018, 97, 165302. [Google Scholar] [CrossRef] [Green Version]
- Moore, C.; Zeng, C.; Stanescu, T.D.; Tewari, S. Quantized zero-bias conductance plateau in semiconductorsuperconductor heterostructures without topological Majorana zero modes. Phys. Rev. B 2018, 98, 155314. [Google Scholar] [CrossRef] [Green Version]
- Fleckenstein, C.; Dominguez, F.; Traverso Ziani, N.; Trauzettel, B. Decaying spectral oscillations in a Majorana wire with finite coherence length. Phys. Rev. B 2018, 97, 155425. [Google Scholar] [CrossRef] [Green Version]
- Awoga, O.A.; Cayao, J.; Black-Schaffer, A.M. Supercurrent Detection of Topologically Trivial Zero-Energy States in Nanowire Junctions. Phys. Rev. Lett. 2019, 123, 117001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marra, P.; Nitta, M. Topologically nontrivial Andreev bound states. Phys. Rev. B 2019, 100, 220502. [Google Scholar] [CrossRef] [Green Version]
- Cayao, J.; Black-Schaffer, A.M. Distinguishing trivial and topological zero energy states in long nanowire junctions. arXiv 2020, arXiv:2011.10411. [Google Scholar]
- Pan, H.; Das Sarma, S. Physical mechanisms for zero-bias conductance peaks in Majorana nanowires. Phys. Rev. Res. 2020, 2, 013377. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Pan, H.; Liu, C.-X.; Sau, J.D.; Stanescu, T.D.; Das Sarma, S. Metamorphosis of Andreev bound states into Majorana bound states in pristine nanowires. Phys. Rev. Lett. 2018, 98, 144511. [Google Scholar] [CrossRef] [Green Version]
- Gangadharaiah, S.; Trifunovic, L.; Loss, D. Localized End States in Density Modulated Quantum Wires and Rings. Phys. Rev. Lett. 2012, 108, 136803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Traverso Ziani, N.; Fleckenstein, C.; Vigliotti, L.; Trauzettel, B.; Sassetti, M. From fractional solitons to Majorana fermions in a paradigmatic model of topological superconductivity. Phys. Rev. B 2020, 101, 195303. [Google Scholar] [CrossRef]
- Henriques, J.C.G.; Rappoport, T.G.; Bludov, Y.V.; Vasilevskiy, M.I.; Peres, N.M.R. Topological photonic Tamm states and the Su-Schrieffer-Heeger model. Phys. Rev. A 2020, 101, 043811. [Google Scholar] [CrossRef] [Green Version]
- Jackiw, R.; Rebbi, C. Solitons with fermion number 1/2. Phys. Rev. D 1976, 13, 3398. [Google Scholar] [CrossRef]
- Goldstone, J.; Wilczek, F. Fractional Quantum Numbers on Solitons. Phys. Rev. Lett. 1981, 47, 986. [Google Scholar] [CrossRef] [Green Version]
- Kivelson, S.; Schrieffer, J.R. Wannier functions in one-dimensional disordered systems: Application to fractionally charged solitons. Phys. Rev. B 1982, 25, 6447. [Google Scholar] [CrossRef]
- Qi, X.-L.; Hughes, T.L.; Zhang, S.-C. Fractional charge and quantized current in the quantum spin Hall state. Nat. Phys. 2008, 4, 273. [Google Scholar] [CrossRef]
- Väyrynen, J.I.; Ojanen, T. Chiral Topological Phases and Fractional Domain Wall Excitations in One-Dimensional Chains and Wires. Phys. Rev. Lett. 2011, 107, 166804. [Google Scholar] [CrossRef] [PubMed]
- Klinovaja, J.; Stano, P.; Loss, D. Transition from Fractional to Majorana Fermions in Rashba Nanowires. Phys. Rev. Lett. 2012, 109, 236801. [Google Scholar] [CrossRef]
- Fleckenstein, C.; Traverso Ziani, N.; Trauzettel, B. Chiral anomaly in real space from stable fractional charges at the edge of a quantum spin Hall insulator. Phys. Rev. B 2016, 94, 241406. [Google Scholar] [CrossRef] [Green Version]
- Gresta, D.; Blasi, G.; Taddei, F.; Carrega, M.; Braggio, A.; Arrachea, L. Signatures of Jackiw-Rebbi resonance in the thermal conductance of topological Josephson junctions with magnetic islands. Phys. Rev. B 2021, 103, 075439. [Google Scholar] [CrossRef]
- Sticlet, D.; Bena, C.; Simon, P. Spin and Majorana Polarization in Topological Superconducting Wires. Phys. Rev. Lett. 2012, 108, 096802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sedlmayr, N.; Bena, C. Visualising Majorana bound states in 1D and 2D using the generalized Majorana polarization. Phys. Rev. B 2015, 92, 115115. [Google Scholar] [CrossRef] [Green Version]
- Bena, C. Testing the formation of Majorana states using Majorana polarization. Comptes Rendus Phys. 2017, 18, 349. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L. Topological Insulators and Topological Superconductors; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Malard, M.; Japaridze, G.I.; Johannesson, H. Synthesizing Majorana zero-energy modes in a periodically gated quantum wire. Phys. Rev. B 2016, 94, 115128. [Google Scholar] [CrossRef] [Green Version]
- Peierls, R.A. Zur Theorie der elektrischen und thermischen Leitfähigkeit von Metallen. Ann. Phys. 1930, 4, 121. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Effective harmonic-fluid approach to low-energy properties of one-dimensional quantum fluids. Phys. Rev. Lett. 1981, 47, 1840. [Google Scholar] [CrossRef]
- Cuniberti, G.; Sassetti, M.; Kramer, B. Transport and elementary excitations of a Luttinger liquid. J. Phys. Condens. Matter 1996, 8, L21. [Google Scholar] [CrossRef] [Green Version]
- Guinea, F.; Santos, G.G.; Sassetti, M.; Ueda, M. Asymptotic tunneling conductance in Luttinger liquids. Europhys. Lett. 1995, 30, 561. [Google Scholar] [CrossRef] [Green Version]
- Fabrizio, M.; Gogolin, A.O. Interacting one-dimensional electron gas with open boundaries. Phys. Rev. B 1995, 51, 17827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Traverso Ziani, N.; Cavaliere, F.; Sassetti, M. Signatures of Wigner correlations in the conductance of a one-dimensional quantum dot coupled to an AFM tip. Phys. Rev. B 2012, 86, 125451. [Google Scholar] [CrossRef] [Green Version]
- Traverso Ziani, N.; Cavaliere, F.; Sassetti, M. Theory of the STM detection of Wigner molecules in spin-incoherent CNTs. Europhys. Lett. 2013, 102, 47006. [Google Scholar] [CrossRef]
- Porta, S.; Gambetta, F.M.; Traverso Ziani, N.; Kennes, D.M.; Sassetti, M.; Cavaliere, F. Nonmonotonic response and light-cone freezing in fermionic systems under quantum quenches from gapless to gapped or partially gapped states. Phys. Rev. B 2018, 97, 035433. [Google Scholar] [CrossRef] [Green Version]
- Giamarchi, T. Quantum Physics in One Dimension; Oxford University Press: Oxford, UK, 2004; ISBN 9780198525004. [Google Scholar]
- Timm, C. Transport through a quantum spin Hall quantum dot. Phys. Rev. B 2012, 86, 155456. [Google Scholar] [CrossRef] [Green Version]
- Dolcetto, G.; Traverso Ziani, N.; Biggio, M.; Cavaliere, F.; Sassetti, M. Spin textures of strongly correlated spin Hall quantum dots. Phys. Stat. Sol. (RRL) 2013, 7, 1059. [Google Scholar] [CrossRef] [Green Version]
- Kylänpää, I.; Cavaliere, F.; Traverso Ziani, N.; Sassetti, M.; Räsänen, E. Thermal effects on the Wigner localization and Friedel oscillations in many-electron nanowires. Phys. Rev. B 2016, 94, 115417. [Google Scholar] [CrossRef]
- Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. J. Rep. Prog. 2012, 75, 076501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Franchini, F. An Introduction to Integrable Techniques for One-Dimensional Quantum Systems; Lecture Notes in Physics; Springer: Berlin, Germany, 2017; Volume 940. [Google Scholar]
- Porta, S.; Cavaliere, F.; Sassetti, M.; Ziani, N.T. Topological classification of dynamical quantum phase transitions in the xy chain. Sci. Rep. 2020, 10, 642. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).